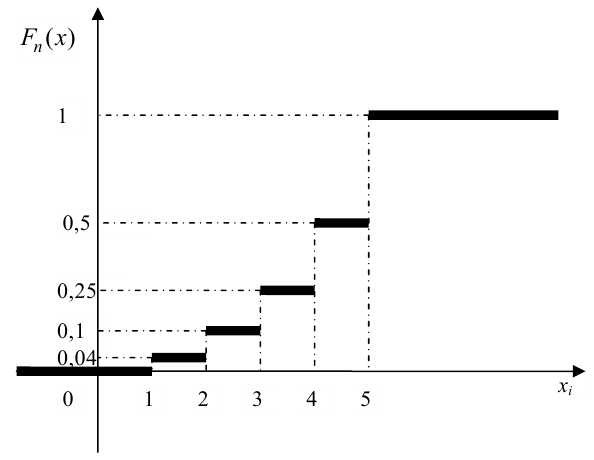
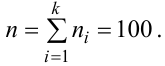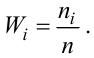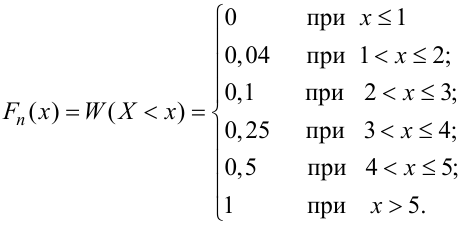В качестве примера
дискретных случайных величин нами была
рассмотрены: бросание кубика, бросание
монеты.
Рассмотрим теперь
примеры непрерывных случайных величин.
Равномерно
распределённая случайная величина.
Плотность
распределения такой случайной величины
есть функция, отличная от нуля только
в пределах отрезка от a
до b.
Е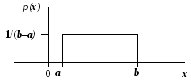
уровень в пределах отрезка отa
до b
постоянен и обратно пропорционален
длине отрезка:
Равномерно
распределённая случайная величина
наиболее проста для понимания и описания.
Также как на рисунке
выглядит слой, который образуют случайно
вылетающие из распылителя капельки
краски при нанесении изображения через
трафарет.
Равномерное
распределение имеют ошибки округления
при измерениях или вычислениях.
Например, взвешиваем
образец товара из проверочной закупки.
Его масса может принимать любое значение,
но мы, глядя, на шкалу весов, определяем
ближайшее деление. Ошибка снятия
показаний по шкале имеет равномерное
распределение.
Эта случайная
величина будет использоваться нами в
практических работах.
Нормально
распределённая случайная величина.
Примером нормально
распределённой случайной величины
является координата попадания шарика
на ось в опыте с доской Гальтона, который
рассматривался нами в вопросе «Первые
статистические опыты».
Ещё говорят, что
такая случайная величина имеет нормальное
распределение.
Случайные величины
с нормальным распределением имеют
исключительно широкое распространение
в природе.
Отсюда и название:
нормальное,
что значит типовое, характерное.
Математическая
запись нормальной плотности распределения
следующая (формула страшная):

.
Здесь
= 3,14…, е
= 2,72… – основание натурального логарифма.
Параметрами
нормального распределения являются
величины m
и
,
имеющие специальные названия:
m
– математическое
ожидание
или среднее;
–дисперсия
или рассеяние
(обозначается маленькой греческой
буквой «сигма»).
Более подробно
смысл этих понятий будет объяснён позже.
На графике плотность
распределения вероятности нормально
распределённой случайной величины
выглядит как колоколообразная кривая.
Это знакомая нам
огибающая уровней шариков в ячейках в
опыте Гальтона.
Вершина распределения
имеет абсциссу, равную математическому
ожиданию x
= m.
Площадь, заключённая
между кривой и горизонтальной осью
равна 1.
7.14. Среднее арифметическое
Закон распределения
или плотность распределения вероятности
несёт полную информацию о случайной
величине.
На практике довольно
часто требуется сравнить две случайные
величины. Сравнение распределений
подразумевает сравнение каких-либо их
существенных черт. Удобно, чтобы они
выражались числами, тогда сравнение
становится совсем простым.
Поэтому хотелось
бы иметь числовые
характеристики,
которые описывали бы как закон
распределения, так и плотность вероятности,
причём любого вида.
Наиболее простыми
и практически важными числовыми
характеристиками случайной величины
являются математическое
ожидание
(среднее) и дисперсия
(рассеяние).
Математическое
ожидание случайной величины Х
является вероятностным обобщением
понятия среднего арифметического,
которое применяется в статистике. С
него и начнём.
Вначале рассмотрим
дискретную случайную величину Х
с N
возможными значениями. (У кубика – 6
возможных значений.)
Пусть с этой
случайной величиной проделано n
одинаковых опытов («эн» маленькое).
При этом случайная
величина Х
(икс большое)
значение
приняла
раз, т.е.
–
значение
приняла
раз, т.е.
–
и так далее …,
значение
приняла
раз, т.е.
–
.
Общее количество
появления всех значений равно n,
т.е.
Найдём среднее
арифметическое случайной величины Х
по n
опытам.
Среднее арифметическое
– это, как известно, сумма всех значений,
делённая на их количество:

Преобразуем это
выражение, учтя повторяемость значений:
Теперь для сокращения
длины формулы воспользуемся специальным
знаком суммы, который мы уже рассматривали,
Дробь в каждом
слагаемом – это вычисленная по n
опытам частота события, состоящего в
том, что случайная величиной Х
примет
значение
.
Мы её обозначали так:.
В итоге получаем:
Так, введя некоторые
обозначения, мы преобразовали выражение
для среднего арифметического.
Из полученного
выражения видно, что среднее арифметическое
вычисляется как сумма значений случайной
величины, взятых с множителями, в качестве
которых выступают частоты.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти среднее значение распределения вероятностей (с примерами)
17 авг. 2022 г.
читать 2 мин
Распределение вероятностей говорит нам о вероятности того, что случайная величина примет определенные значения.
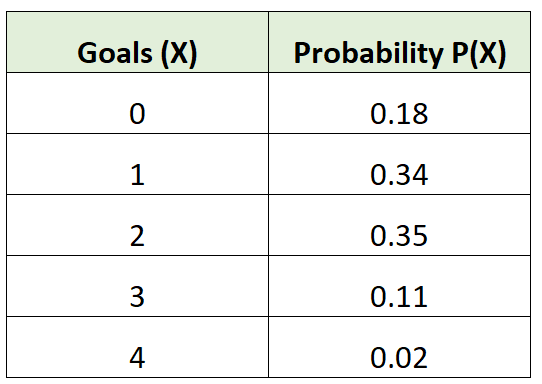
Например, следующее распределение вероятностей говорит нам о вероятности того, что определенная футбольная команда забьет определенное количество голов в данной игре:
Примечание.Вероятности в действительном распределении вероятностей всегда будут в сумме равны 1. Мы можем подтвердить, что это распределение вероятностей действительно: 0,18 + 0,34 + 0,35 + 0,11 + 0,02 = 1.
Чтобы найти среднее (иногда называемое «ожидаемым значением») любого распределения вероятностей, мы можем использовать следующую формулу:
Mean (Or "Expected Value") of a Probability Distribution:
μ = Σx * P(x)
where:
•x: Data value
•P(x): Probability of value
Например, рассмотрим наше распределение вероятностей для футбольной команды:
Среднее количество голов для футбольной команды будет рассчитываться как:
μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 гола.
В следующих примерах показано, как вычислить среднее значение распределения вероятностей в нескольких других сценариях.
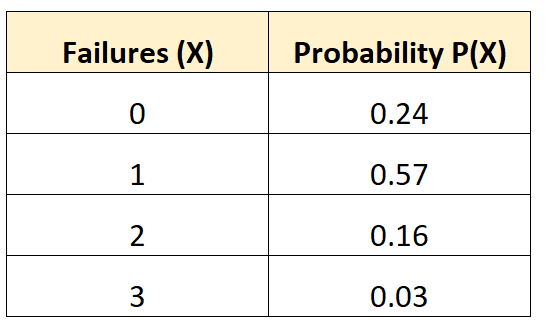
Пример 1: Среднее количество отказов транспортных средств
Следующее распределение вероятностей говорит нам о вероятности того, что данное транспортное средство испытает определенное количество отказов батареи в течение 10-летнего периода:
Вопрос: Каково среднее количество ожидаемых отказов для этого автомобиля?
Решение.Среднее количество ожидаемых отказов рассчитывается как:
μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 отказов.
Пример 2: Среднее количество побед
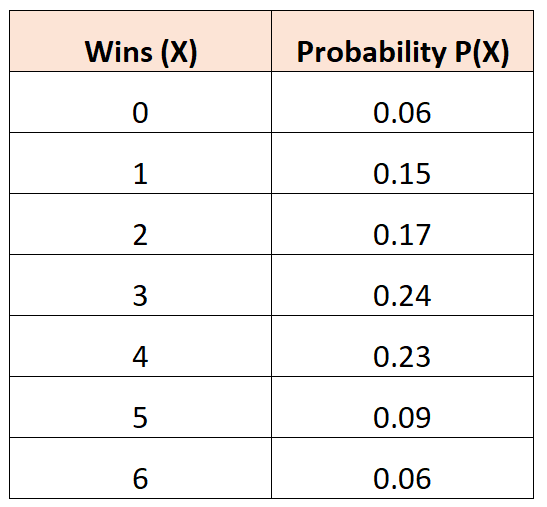
Следующее распределение вероятностей говорит нам о вероятности того, что данная баскетбольная команда выиграет определенное количество игр в турнире:
Вопрос: Каково среднее количество ожидаемых побед для этой команды?
Решение: Среднее количество ожидаемых выигрышей рассчитывается как:
μ = 0*0,06 + 1*0,15 + 2*0,17 + 3*0,24 + 4*0,23 + 5*0,09 + 6*0,06 = 2,94 победы.
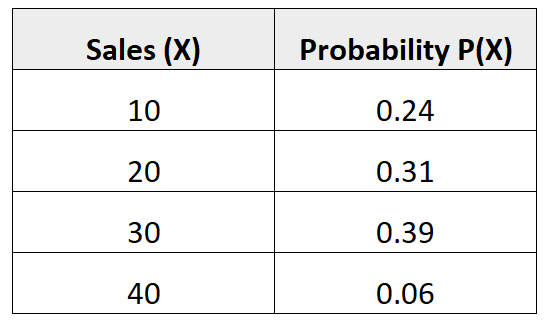
Пример 3: Среднее количество продаж
Следующее распределение вероятностей говорит нам о вероятности того, что данный продавец совершит определенное количество продаж в предстоящем месяце:
Вопрос: Каково среднее количество ожидаемых продаж этого продавца в предстоящем месяце?
Решение: Среднее количество ожидаемых продаж рассчитывается как:
μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 продаж.
Бонус: калькулятор распределения вероятностей
Вы можете использовать этот калькулятор для автоматического расчета среднего значения любого распределения вероятностей.
Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся
Рассмотрим свойства математического ожидания.
- Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
- Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
- Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
- Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
- Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
- Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
Для дискретной случайной величины X эта формула принимает вид:
Для непрерывной случайной величины: 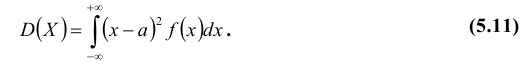
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 

Рассмотрим свойства дисперсии.
- Дисперсия постоянной величины равна нулю:
- Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.
- Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.
- Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 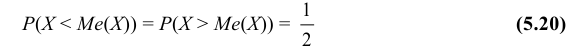
Пример №2
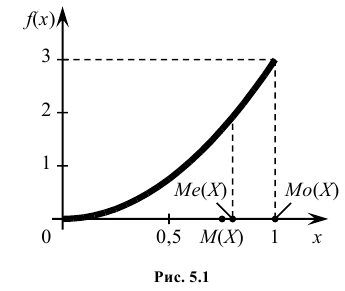
Найти моду, медиану случайной величины Х с плотностью вероятности
Решение:
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 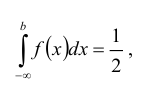
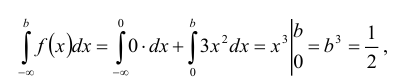
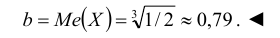
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.
Пример №3
По данным примера 5.3 найти квантиль
Решение:
Находим функцию распределения 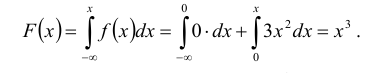
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 

Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
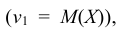
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
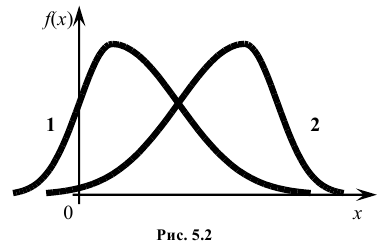
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 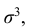
Полученная величина А называется коэффициентом асимметрии случайной величины: 
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом случайной величины называется число 
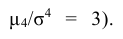
Числовые характеристики независимых испытаний
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин 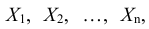
Обозначим среднее арифметическое n взаимно независимых случайных величин через
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 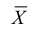
- Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
- Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в
раз меньше дисперсии D каждой из величин:
- Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:
Пример:
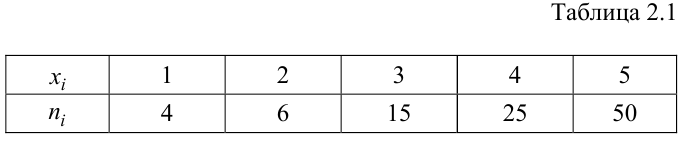
По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.
Решение. Определяем объем выборки:
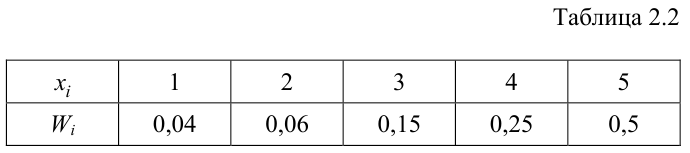
Определяем относительные частоты вариант (табл. 2.2):
Так как значение 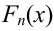
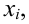
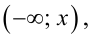
График примет вид:
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
Среднее арифметическое, мода и медиана
- Предмет, цели и методы математической статистики
- Метод выборочных исследований
- Средняя арифметическая, простая и взвешенная
- Мода и медиана
- Примеры
Предмет, цели и методы математической статистики
Начиная с XVIII века, в общем направлении статистических исследований начинает активно формироваться математическая статистика.
Математическая статистика – раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений.
В зависимости от предмета исследований математическая статистика делится на:
- статистику чисел;
- многомерный статистический анализ;
- анализ функций (процессов) и временных рядов;
- статистику объектов с нечисловыми характеристиками.
В зависимости от цели и методов исследований математическая статистика делится на: описательную статистику; теорию оценивания; теорию проверки гипотез.
| Описательная статистика | Теория оценивания | Теория проверки гипотез | |
| Цель | Обработка и систематизация эмпирических данных | Оценивание ненаблюдаемых данных и сигналов от объектов наблюдения на основе наблюдаемых данных | Обоснование предположений о виде распределения и свойствах случайной величины |
| Методы |
1. Наглядное представление в форме графиков и таблиц. 2. Количественное описание с помощью статистических показателей. |
1. Параметрические методы (наименьших квадратов, максимального правдоподобия и др.). 2. Непараметрические методы. |
1. Последовательный анализ. 2. Статистические критерии. |
Метод выборочных исследований
Статистика получила признание в различных областях человеческой деятельности благодаря заметной экономии времени и прочих ресурсов. Её основная идея: не нужно измерять всё, измерьте только часть всего и сделайте предположение об остальном.
«Всё» в статистике называется генеральной совокупностью.
«Часть всего», которую мы тщательно исследуем, называется выборкой.
Метод выборочных исследований – способ определения свойств группы объектов (генеральной совокупности) на основании статистического исследования её части (выборки).
Например, чтобы оценить средние размеры апельсина, который продаётся в магазине в декабре, необязательно денно и нощно мерить все апельсины во всех ящиках (сколько же для этого нужно времени и людей?!). Достаточно сделать выборку – мерить по одному апельсину из каждого ящика в течение месяца (тут уже и один человек справится).
Статистика предоставляет методику и оценки для того, чтобы правильно провести выборку и на основании знаний о среднем размере апельсина в выборке (выборочной средней) судить о средних размерах всех декабрьских апельсин (генеральной средней).
Средняя арифметическая, простая и взвешенная
Статистическое исследование опирается на собранные данные о каком-то признаке (рост, вес, возраст, доход и т.п.).
Варианта – полученное эмпирическое значение признака.
Вариационный ряд – совокупность собранных вариант.
Пусть мы сделали выборку, провели N измерений и получили x_1,x_2,…,x_N вариант.
Вариационный ряд, состоящий из отдельных вариант, называют дискретным.
Чтобы найти выборочную среднюю дискретного вариационного ряда, нужно вычислить среднюю арифметическую простую:
$$ x_{cp} = frac{1}{N} sum_{i=1}^N x_i ,i = overline{1,N} $$
Знак Σ означает «сумма», i — это индекс полученных вариант, который пробегает все значения, от 1 до N.
Например:
На протяжении четверти школьник получил такие оценки по алгебре: 5,4,3,5,4,4,5,4,3,5,5,4,3,5,4,4. Найдите среднюю оценку за четверть.
Считаем среднюю арифметическую простую:
$$ x_cp = frac{5+4+3+⋯+4}{16} ≈ 4,2 $$
Нетрудно заметить, что оценки повторяются, и вычисления можно упростить, если вместо сложения одинаковых оценок использовать умножение оценок на их количество.
Чтобы найти выборочную среднюю при повторяющихся вариантах, удобно вычислять среднюю арифметическую взвешенную:
$$ x_{cp} = frac{1}{N} sum_{i=1}^K x_i n_i , N = sum_{i=1}^K n_i , i = overline{1,K} $$
где K – количество групп с повторяющимися вариантами, $x_i$ — значение варианты в -й группе, $n_i$ – частота варианты $x_i$.
Например:
Рассматриваем тот же ряд оценок: 5,4,3,5,4,4,5,4,3,5,5,4,3,5,4,4 и составляем таблицу:
$$ x_cp = frac{3cdot3+4cdot7+5cdot6}{3+7+6} ≈ 4,2 $$
Вычисления заметно упростились.
Мода и медиана
Мода дискретного вариационного ряда – это варианта с максимальной частотой. Мод может быть несколько. Тогда говорят, что ряд мультимодальный.
В примере с оценками по алгебре мода $M_0 = 4$ — эта оценка встречается чаще всего, её частота равна 7.
Медиана дискретного вариационного ряда – это значение варианты посредине упорядоченного ряда.
Алгоритм:
-
Отсортировать ряд по возрастанию.
-
Если общее количество измерений N нечётное, найти m = $lceil frac{N}{2}rceil$ и округлить в сторону увеличения. $M_e = x_m$ — искомая медиана.
-
Если общее количество измерений N чётное, найти $m = frac{N}{2}$ и вычислить медиану как среднее $M_e = frac{x_m+x_{m+1}}{2}$.
В примере с оценками по алгебре N = 16 — четное. $m = frac{N}{2} = 8 $.
Сортируем ряд оценок по возрастанию: 3,3,3,4,4,4,4, 4,4, 4,5,5,5,5,5,5
$$ x_8 = 4, x_9 = 4 Rightarrow M_e = frac{4+4}{2} = 4 $$
Внимание!
Мода и медиана учитывают индивидуальные варианты и поэтому важны для характеристики вариационного ряда.
Особенное значение мода и медиана приобретают в рядах с выбросами – одиночными очень большими или очень малыми вариантами. В этом случае они оберегают от выводов на основании «средней температуры по больнице».
Примеры
Пример 1. В исследовании месячных доходов десяти человек были получены следующие данные: 200,100,300,300,1000,5000,100,200, 300,400 (дол.).
Найдите выборочную среднюю, моду и медиану.
Почему при оценке доходов мода и медиана предпочтительней выборочной средней?
Составим таблицу:
$x_i$, дол.
100
200
300
400
1000
5000
$sum$
$n_i$, чел.
2
2
3
1
1
1
10
$x_i n_i$
200
400
900
400
1000
5000
7900
Выборочная средняя:$ x_{cp} = frac{7900}{10} = 790$ (дол.)
Мода: $M_o$ = 300 (дол.) – максимальная частота 3
Медиана:
100, 100, 200, 200, 300, 300, 300, 400, 1000, 5000
$$ m = frac{10}{2} = 5, x_5 = x_6 = 300, M_e = frac{300+300}{2} = 300 (дол.) $$
Выборочная средняя не отражает доходов большей части людей в выборке, поскольку даже один человек с большими доходами может резко сместить оценку вправо. Мода и медиана хорошо отражают доходы большей части людей в выборке.
Пример 2. Исследовалось время решения задачи. В исследовании принимало участие 20 человек, из них двое задачу не решили. Время решения остальных участников:
$x_i$, мин
10
15
20
25
30
Найдите выборочную среднюю, моду и медиану.
При подборе задач для контрольной работы, сколько времени следует отвести на решение подобной задачи?
Проведём вычисления:
$x_i$
10
15
20
25
30
$sum$
$x_i n_i$
20
75
100
100
60
355
$$x_cp = frac{355}{18} ≈ 19,7 мин $$
В выборке 2 моды: $M_{o1}$ = 15 мин, $M_{o2}$ = 20 мин
Положение медианы: $m = frac{N}{2} = frac{18}{2} = 9, x_9 = x_10 = 20, Me = 20$ мин
Средняя, одна из мод и медиана равны 20 мин. Поэтому при составлении контрольной следует отвести на подобную задачу 20 мин.
Пример 3. работа по геометрии показала следующие результаты:
Найдите выборочную среднюю, моду и медиану.
Что вы можете сказать об уровне понимания материала?
Проведём вычисления:
$x_i n_i$
10
66
40
10
126
$$x_cp = frac{126}{39} ≈ 3,2$$
Мода: $M_o$ = 3 — эта оценка получена 22 раза
Положение медианы: $m = ⌈ frac{N}{2}⌉ = ⌈frac{39}{2}⌉ = 20, x_{20} = 3, Me = 3$
Средняя, мода и медиана равны 3.
Уровень понимания удовлетворительный, «на троечку».
Среднее арифметическое нескольких величин – это отношение суммы величин к их количеству.
Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.
Например: найдем среднее арифметическое чисел 2; 6; 9; 15.
У нас четыре числа, значит надо их сумму разделить на четыре. Это и будет среднее арифметическое данных чисел: (2 + 6 + 9 + 15) : 4 = 8.
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.
Например: найдем размах чисел 2; 5; 8; 12; 33.
Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т. е.: 33 – 2 = 31.
Мода ряда чисел – это число, которое встречается в данном ряду чаще других.
Например: найдем моду ряда чисел 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 8.
Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.
Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.
Например: в ряде чисел 2; 5; 9; 15; 21 медианой является число 9, находящееся посередине.
Найдем медиану в ряде чисел 4; 5; 7; 11; 13; 19.
Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел: (7 + 11) : 2 = 9. Число 9 является медианой данного ряда чисел.
-
В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3; 5; 5; 4; 4; 4; 3; 2; 4; 5.
Какую оценку получали чаще всего? Каков средний балл сдавшей зачет группы?
-
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите медиану и размах ряда.
-
Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.
Найдите моду ряда и среднее арифметическое ряда.
-
Имеются следующие данные о месячной заработной плате пяти рабочих (тг): 126000; 138000; 132000; 141000; 150000.
Найдите среднюю заработную плату.
-
Магазин продает 8 видов булочек по следующим ценам: 31; 22; 24; 27; 30; 36; 19; 27.
Найдите разность среднего арифметического и медианы этого набора.
-
Найдите объем и медиану числового ряда.
9; 7; 1; 1; 11; 5; 1.
-
Товарные запасы хлопчатобумажных тканей в магазине за первое полугодие составили (тыс. тг) на начало каждого месяца:
I II III IV V VI VII 37 34 35 32 36 33 38 Определите средний товарный запас хлопчатобумажных тканей за первое полугодие.
-
Провели несколько измерений случайной величины: 2,5; 2,2; 2; 2,4; 2,9; 1,8.
Найдите среднее арифметическое этого набора чисел.
-
Провели несколько измерений случайной величины: 6; 18; 17; 14; 4; 22.
Найдите медиану этого набора чисел.
-
Провели несколько измерений случайной величины:
800; 3200; 2000; 2600; 2900; 2000. Найдите моду этого набора чисел.
-
Магазин продает 8 видов хлеба по следующим ценам: 60, 75, 80, 85, 90, 100, 110, 120 тенге.
Найдите разность среднего арифметического и медианы этого набора.
-
Дан числовой ряд: 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 7,8.
Найдите среднее арифметическое, размах и моду.


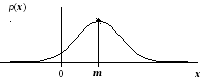



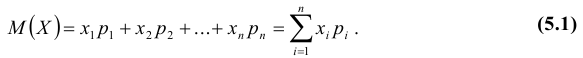
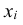
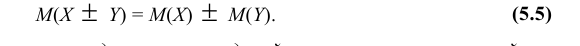


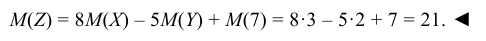







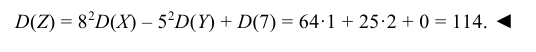
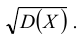


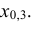
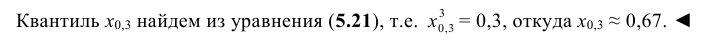



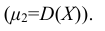
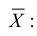
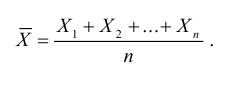

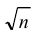 раз меньше дисперсии D каждой из величин:
раз меньше дисперсии D каждой из величин: