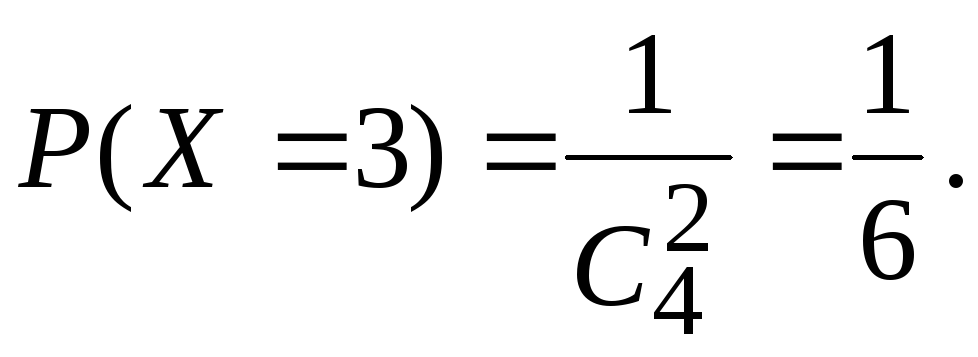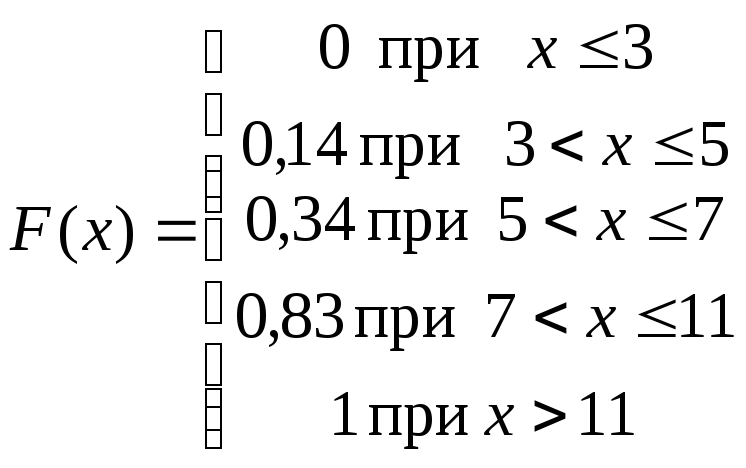Как найти среднее число бросаний

71

В
приложениях теории вероятностей основное
значение имеет количественная
характеристика эксперимента. Величина,
которая может быть количественно
определена и которая в результате
эксперимента может принимать в зависимости
от случая различные значения, называется
случайной
величиной.

Примеры случайных
величин:

1. Число выпадений
четного числа очков при десяти бросаниях
игральной кости.

2. Число попаданий
в мишень стрелком, который производит
серию выстрелов.

3. Число осколков
разорвавшегося снаряда.

В каждом из
приведенных примеров случайная величина
может принимать лишь изолированные
значения, то есть значения, которые
можно пронумеровать с помощью натурального
ряда чисел.

Такая
случайная величина, возможные значения
которой есть отдельные изолированные
числа, которые эта величина принимает
с определенными вероятностями, называется
дискретной.

Число возможных
значений дискретной случайной величины
может быть конечным или бесконечным
(счетным).

Законом
распределения
дискретной случайной величины называют
перечень её возможных значений и
соответствующих им вероятностей. Закон
распределения дискретной случайной
величины можно задать в виде таблицы
(ряд распределения вероятностей),
аналитически и графически (многоугольник
распределения вероятностей).

При
осуществлении того или иного эксперимента
возникает необходимость оценивать
изучаемую величину «в среднем». Роль
среднего значения случайной величины
играет числовая характеристика,
называемая математическим
ожиданием, которая
определяется формулой

где
x₁,
x₂
,.. , x_n
– значения случайной величины X,
а p₁,
p₂,
… , p_n
– вероятности этих значений (заметим,
что p₁
+ p₂
+…+ p_n = 1).

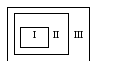
Пример. Производится
стрельба по мишени (рис. 11).

Рис. 11

Попадание в I дает
три очка, в II – два очка, в III – одно очко.
Число очков, выбиваемых при одном
выстреле одним стрелком, имеет закон
распределения вида

Xi	1	2	3
Pi	0,4	0,2	0,4

Для другого стрелка
ряд распределения вероятностей имеет
вид

Xi	1	2	3
Pi	0,2	0,5	0,3

Для
сравнения мастерства стрелков достаточно
сравнить средние значения выбиваемых
очков, т.е. математические ожидания M(X)
и M(Y):

M(X)
=
1
0,4
+ 2 
0,2
+ 3 
0,4
= 2,0,

M(Y)
=
1
0,2
+ 2 
0,5
+ 3 
0,3
= 2,1.

Второй стрелок
дает в среднем несколько большее число
очков, т.е. при многократной стрельбе
он будет давать лучший результат.

Отметим свойства
математического ожидания:

1. Математическое
ожидание постоянной величины равно
самой постоянной:

M(C)
=
C.

2. Математическое
ожидание суммы случайных величин равно
сумме математических ожиданий слагаемых:

M
= (X₁+X₂+…+X_n)=M(X₁)+M(X₂)+…+M(X_n).

3. Математическое
ожидание произведения взаимно независимых
случайных величин равно произведению
математических ожиданий cомножителей

M(X₁X₂…X_n)
=
M(X₁)M(X₂)…M(X_n).

4. Математическое
отрицание биноминального распределения
равно произведению числа испытаний на
вероятность появления события в одном
испытании (задача 4.6).

M(X)
= пр.

Для оценки того,
каким образом случайная величина «в
среднем» уклоняется от своего
математического ожидания, т.е. для того
чтобы охарактеризовать разброс значений
случайной величины в теории вероятностей
служит понятие дисперсии.

Дисперсией
случайной величины X
называют математическое ожидание
квадрата отклонения:

D(X)
=
M[(X
— M(X))²].

Дисперсия является числовой характеристикой
рассеивания случайной величины. Из
определения видно, что чем меньше
дисперсия случайной величины, тем кучнее
располагаются её возможные значения
около математического ожидания, то есть
тем лучше значения случайной величины
характеризуются её математическим
ожиданием.

Из определения
следует, что дисперсия может быть
вычислена по формуле

.

Дисперсию
удобно вычислять по другой формуле:

D(X)
=
M(X²)
— (M(X))².

Дисперсия обладает следующими свойствами:

1. Дисперсия
постоянной равна нулю:

D(C)
= 0.

2. Постоянный множитель можно выносить
за знак дисперсии, возводя его в квадрат:

D(CX)
=
C²D(X).

3. Дисперсия
суммы независимых случайных величин
равна сумме дисперсии слагаемых:

D(X₁+X₂+X₃+…+X_n)=D(X₁)+D(X₂)+…+D(X_n)

4. Дисперсия
биномиального распределения равна
произведению числа испытаний на
вероятность появления и непоявления
события в одном испытании:

D(X)
=
npq.

В теории вероятностей
часто используется числовая характеристика,
равная корню квадратному из дисперсии
случайной величины. Эта числовая
характеристика называется средним
квадратным отклонением и обозначается
символом

.

Она
характеризует примерный размер уклонения
случайной величины от её среднего
значения и имеет одинаковую со случайной
величиной размерность.

4.1.
Стрелок проводит по мишени три выстрела.
Вероятность попадания в мишень при
каждом выстреле равна 0,3.

Построить ряд
распределения числа попаданий.

Решение.
Число попаданий является дискретной
случайной величиной X.
Каждому значению x_n
случайной
величины X
отвечает определенная вероятность P_n.

Закон распределения дискретной случайной
величины в данном случае можно задать
рядом распределения.

В данной задаче Xпринимает значения 0, 1, 2, 3. По формуле
Бернулли

,

найдем
вероятности возможных значений случайной
величины:

Р₃(0)
= (0,7)³ =
0,343,

Р₃(1)
=0,3(0,7)²
= 0,441,

Р₃(2)
=(0,3)²0,7
= 0,189,

Р₃(3)
= (0,3)³ =
0,027.

Расположив значения случайной величины
Xв возрастающем
порядке, получим ряд распределения:

Xn	0	1	2	3
n	0,343	0,441	0,189	0,027

Заметим, что сумма

означает
вероятность того, что случайная величина
Xпримет хотя бы одно
значение из числа возможных, а это
событие достоверное, поэтому

.

4.2.В урне имеются четыре шара с
номерами от 1 до 4. Вынули два шара.
Случайная величинаX– сумма номеров шаров. Построить ряд
распределения случайной величиныX.

Решение. Значениями случайной
величиныXявляются
3, 4, 5, 6, 7. Найдем соответствующие
вероятности. Значение 3 случайной
величиныXможет
принимать в единственном случае, когда
один из выбранных шаров имеет номер 1,
а другой 2. Число всевозможных исходов
испытания равно числу сочетаний из
четырех (число возможных пар шаров) по
два.

По классической формуле вероятности
получим

Аналогично,

Р(Х = 4) =Р(Х = 6) =Р(Х
= 7) = 1/6.

Сумма 5 может появиться в двух случаях:
1 + 4 и 2 + 3, поэтому

.

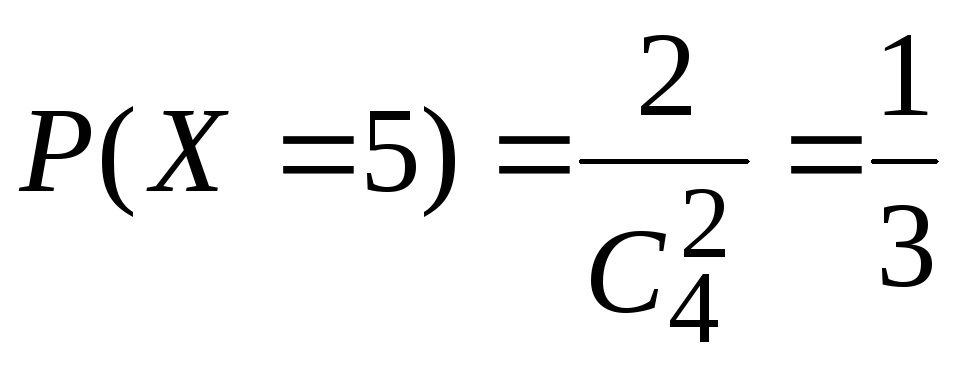
Ряд распределения случайной величины
Химеет вид:

Xn	3	4	5	6	7
n	1/6	1/6	1/3	1/6	1/6

4.3.Случайная величинаХзадана
рядом распределения

Xn	3	5	7	11
Pn	0,14	0,20	0,49	0,17

Найти функцию распределения F(x)
случайной величиныXи построить ее график. Вычислить дляXее математическое ожидание и дисперсию.

Решение. Закон распределения
случайной величины может быть задан
функцией распределения

F(x)
= P(X

x).

Функция распределения F(x)
– неубывающая, непрерывная слева
функция, определенная на всей числовой
оси, при этом

F (—)=0,F
(+)=1.

Для
дискретной случайной величины эта
функция выражается формулой

.

Поэтому
в данном случае

График функции распределения F(x)
представляет собой ступенчатую линию
(рис. 12)

	F(x) 1
	0,5
	0	3	5	7	11	x

Рис. 12

Математическое ожидание М(Х)
является взвешенной средней арифметической
значенийх₁,
х₂,……х_n
случайной величиныХпри весахρ_1,
ρ_2,……,ρ_n
и называется средним значением
случайной величиныХ. По формуле

М(Х)
= х₁
ρ₁
+ х₂
ρ₂
+ ……+ х_n
ρ_n

находим

М(Х) = 3·0,14+5·0,2+7·0,49+11·0,17 = 6,72.

Дисперсияхарактеризует степень
рассеяния значений случайной величины
от своего среднего значения и обозначаетсяD(Х):

D(Х)
=М[(Х-М(Х))²]
= М(Х
²)
–[М(Х)]².

Для дискретной случайной величины
дисперсия имеет вид

или
она может быть вычислена по формуле

.

Подставляя
числовые данные задачи в формулу,
получим:

М(Х²)
= 3²
∙ 0,14+5²
∙ 0,2+7²
∙ 0,49+11²
∙ 0,17 = 50,84

D(Х)
= 50,84-6,72²
= 5,6816.

4.4.Две игральные кости одновременно
бросают два раза. Написать биномиальный
закон распределения дискретной случайной
величиныХ— числа выпадений четного
суммарного числа очков на двух игральных
костях.

Решение. Введем в рассмотрение
случайное событие

А= {на двух костях при одном бросании
выпало в сумме четное число очков}.

Используя
классическое определение вероятности
найдем

Р(А)=
,

где n
— число всевозможных исходов испытания
находим по правилу

умножения:

n = 6∙6 =36,

m
—число благоприятствующих событиюАисходов — равно

m= 3∙6=18.

Таким
образом, вероятность успеха в одном
испытании равна

ρ = Р(А)=1/2.

Задача решается с применением схемы
испытаний Бернулли. Одним испытанием
здесь будет бросание двух игральных
костей один раз. Число таких испытаний
n = 2. Случайная
величинаХпринимает значения 0, 1,
2 с вероятностями

Р₂(0)
=,Р₂(1)
=∙,Р₂(2)
=

Искомое биноминальное распределение
случайной величины Хможно представить
в виде ряда распределения:

хn	0	1	2
ρn

4.5. В партии из шести деталей имеется
четыре стандартных. Наудачу отобраны
три детали. Составить распределение
вероятностей дискретной случайной
величиныХ– числа стандартных
деталей среди отобранных и найти ее
математическое ожидание.

Решение. Значениями случайной
величиныХявляются числа 0,1,2,3. Ясно,
чтоР(Х=0)=0,
поскольку нестандартных деталей всего
две.

Р (Х=1) ==1/5,

Р
(Х=2) =
= 3/5,

Р (Х=3) =
= 1/5.

Закон распределения случайной величины
Х представим в виде ряда распределения:

хn	0	1	2	3
ρn	0	1/5	3/5	1/5

Математическое ожидание

М(Х)=1
∙ 1/5+2 ∙ 3/5+3 ∙ 1/5=2.

4.6. Доказать, что математическое
ожидание дискретной случайной величиныХ— числа появлений событияАвnнезависимых испытаниях, в каждом
из которых вероятность появления события
равнаρ– равно произве-дению числа
испытаний на вероятность появления
события в одном испыта-нии, то есть
доказать, что математическое ожидание
биноминального распределения

М(Х)
=n^.ρ,

а
дисперсия

D(X)
=np .

Решение.Случайная величинаХможет принимать значения 0, 1, 2…,n.
ВероятностьР(Х = к) находится
по формуле Бернулли:

Р(Х=к)=Р_n
(к)=ρ^к
(1-ρ)^n-к

Ряд распределения случайной величины
Х имеет вид:

хn	0	1	2	…..	n
ρn	qn	ρqn-1	ρqn-2	……	ρn

где q=1—ρ.

Для
математического ожидания имеем выражение:

М(Х)=ρq^n—1
+2

ρ²
q^n—2
+…+.n


ρⁿ

В случае одного испытания, то есть при
n = 1для случайной величиныХ₁–числа появлений событияА— ряд
распределения имеет вид:

хn	0	1
ρn	q	Р

Тогда

M(X₁)=0
∙ q+1
∙ p
= p

D(X₁)
= p
– p²
= p(1—p)
= pq.

Если Х_к– число появлений событияАв к-ом
испытании, тоР(Х_к)=
ρ и

Х=Х₁+Х₂+….+Х_n.

Отсюда
получаем

М(Х)=М(Х₁)+М(Х₂)+
… +М(Х_n)=nρ,

D(X)=D(X₁)+D(X₂)+
…
+D(X_n)=npq.

4.7.ОТК проверяет изделия на
стандартность. Вероятность того, что
изделие стандартно, равна 0,9. В каждой
партии содержится 5 изделий. Найти
математическое ожидание дискретной
случайной величиныХ-числа партий,
в каждой из которых окажется равно 4
стандартных изделия – если проверке
подлежит 50 партий.

Решение. Вероятность того, что в
каждой произвольно выбранной партии
окажется 4 стандартных изделия, постоянна;
обозначим ее черезρ.Тогда
математическое ожидание случайной
величиныХ равноМ(Х)=50∙ρ.

Найдем вероятность ρпо формуле
Бернулли:

ρ=Р₅(4)== 0,94∙0,1=0,32.

Тогда

М(Х)=50∙0,32=16.

4.8. Бросаются три игральные кости.
Найти математическое ожидание суммы
выпавших очков.

Решение.Можно найти распределение
случайной величиныХ— суммы выпавших
очков и затем ее математическое ожидание.
Однако такой путь слишком громоздок.
Проще использовать другой прием,
представляя случайную величинуХ,
математическое ожидание которой
требуется вычислить, в виде суммы
нескольких более простых случайных
величин, математическое ожидание которых
вычислить легче. Если случайная величинаХ_i
– это число очков, выпавших наi– й кости (i= 1, 2, 3), то
сумма очковХвыразится в виде

Х
= Х₁
+ Х₂
+ Х_3.

Для вычисления
математического ожидания исходной
случайной величины останется лишь
воспользоваться свойством математического
ожидании

М
(Х₁
+
Х₂
+ Х₃)
= М(Х₁)
+ М(Х₂)
+ М(Х₃).

Очевидно, что

Р
(Х_i
= К)=1/6, К
=
1, 2, 3, 4, 5, 6, i=1,
2, 3.

Следовательно,
математическое ожидание случайной
величины Х_i
имеет вид

М
(Х_i)
= 1/6∙1
+ 1/6∙2
+1/6∙3
+ 1/6∙4
+ 1/6∙5
+ 1/6∙6
= 7/2,

а значит

М(Х)
= 3∙7/2 = 10,5.

4.9.
Определить математическое ожидание
числа приборов, отказавших в работе за
время испытаний, если:

а)
вероятность отказа для всех приборов
одна и та же равна р,
а число испытуемых приборов равно n;

б)
вероятность отказа для i
– го прибора
равна p_i
,
i=1,
2, … , n.

Решение.
Пусть случайная величина Х
– число
отказавших приборов, тогда

Х
= Х₁
+ Х₂
+ … + Х_n,

где

X_i
=

Ясно, что

Р(Х_i=1)=Р_i, Р(Х_i=0)=1–Р_i, i=1,
2,
…,
n.

Так как

М(Х_i)=1∙Р_i+0∙(1–Р_i)=Р_i,

то

М(Х)=М(Х₁)+М(Х₂)+
… +М(Х_n)=Р₁+Р₂+
… +Р_n.

В случае «а»
вероятность отказа приборов одна и та
же, то есть

Р_i=p,
i=1,
2, …
,
n.

Поэтому

М(Х)=np.

Этот
ответ можно было получить сразу, если
заметить, что случайная величина Х
имеет биномиальное распределение с
параметрами (n,
p).

4.10.
Две игральные кости бросают одновременно
два раза. Написать биномиальный закон
распределения дискретной случайной
величины Х
– числа
выпадения четного числа очков на двух
игральных костях.

Решение. Пусть

А
={выпадение
четного числа на первой кости},

В
={выпадение
четного числа на второй кости}.

Выпадение
четного числа на обеих костях при одном
бросании выразится произведением АВ.
Тогда

Р
(АВ)
= Р(А)∙Р(В)
=
.

Результат второго
бросания двух игральных костей не
зависит от первого, поэтому применима
формула Бернулли при

n
= 2, р
= 1/4, q
= 1
– р = 3/4.

Случайная
величина Х
может
принимать значения 0, 1, 2,
вероятность которых найдем по формуле
Бернулли:

Р
(Х=0)
= Р₂
(0)
= q
²
= 9/16,

Р
(Х=1)
= Р₂
(1)
= С
,
р∙q
= 6/16,

Р
(Х=2)
= Р₂
(2)
= С
,
р²
= 1/16.

Ряд
распределения случайной величины Х:

Х	0	1	2
Р	9/16	6/16	1/16

4.11.
Устройство состоит из большого числа
независимо работающих элементов с
одинаковой очень малой вероятностью
отказа каждого элемента за время t.
Найти среднее число отказавших за время
t
элементов, если вероятность того, что
за это время откажет хотя бы один элемент,
равна 0,98.

Решение.
Число
отказавших за время t
элементов – случайная величина Х,
которая распределена по закону Пуассона,
поскольку число элементов велико,
элементы работают независимо и вероятность
отказа каждого элемента мала. Среднее
число появлений события в n
испытаниях равно

М
(Х)
= np.

Поскольку
вероятность отказа К
элементов из n
выражается формулой

Р_n
(К)
,

где

= np,
то вероятность того, что не откажет ни
один элемент за время t
получим при
К = 0:

Р_n
(0)
= е^—.

Поэтому
вероятность противоположного события
– за время t
откажет хотя
бы один элемент – равна 1
— е^—
.
По условию задачи эта вероятность равна
0,98. Из уравнения

1
— е^—
= 0,98,

находим

е^—
= 1 – 0,98 =
0,02,

отсюда

= -ln
0,02

4.

Итак,
за время t
работы устройства откажет в среднем 4
элемента.

4.12.
Игральная кость бросается до тех пор,
пока не выпадет «двойка». Найти среднее
число бросаний.

Решение.
Введем случайную величину Х
– число испытаний, которое надо
произвести, пока интересующее нас
событие не наступит. Вероятность того,
что Х =
1 равна вероятности того, что при одном
бросании кости выпадет «двойка», т.е.

Р(Х=1)
= 1/6.

Событие Х = 2 означает, что при первом
испытании «двойка» не выпала, а при
втором выпала. Вероятность событияХ = 2 находим по правилу умножения
вероятностей независимых событий:

Р
(Х=2)
= (5/6)∙(1/6)

Аналогично,

Р(Х=3)
= (5/6)²∙1/6, Р(Х=4)
= (5/6)²∙1/6

и т.д. Получим ряд
распределения вероятностей:

Х	1	2	3	…	К	…
Р	1/6	5/6∙1/6	(5/6)2∙1/6	…	(5/6)к ∙1/6	…

Среднее
число бросаний (испытаний) есть
математическое ожидание

М(Х)
= 1∙1/6 +
2∙5/6∙1/6 + 3∙(5/6)²∙1/6
+ … + К
(5/6)^К-1∙1/6
+ … =

=
1/6∙(1+2∙5/6 +3∙(5/6)²
+ … + К
(5/6)^К-1
+ …)

Найдем
сумму ряда:

Кg
^К-1
= (g^К)
_g^
.

Следовательно,

М(Х)
= (1/6) (1/ (1 –
5/6)²
= 6.

Таким образом, нужно осуществить в
среднем 6 бросаний игральной кости до
тех пор, пока не выпадет «двойка».

4.13.
Производятся независимые испытания с
одинаковой вероятностью появления
события А
в каждом испытании. Найти вероятность
появления события А,
если дисперсия числа появлений события
в трех независимых испытаниях равна
0,63.

Решение.
Число появлений события в трех испытаниях
является случайной величиной Х,
распределенной по биномиальному закону.
Дисперсия числа появлений события в
независимых испытаниях (с одинаковой
вероятностью появления события в каждом
испытании) равна произведению числа
испытаний на вероятности появления и
непоявления события (задача 4.6)

D(Х)
= npq.

По
условию n
= 3,
D(Х)
= 0,63, поэтому
можно р
найти из уравнения

0,63
= 3∙р(1-р),

которое
имеет два решения р₁
= 0,7
и р₂
= 0,3.

Здесь можно всё посчитать с помощью рядов, но проще воспользоваться рекуррентными соотношениями.

а) Пусть $%S$% — искомое среднее значение. Если выпадает решка, то далее нам снова надо ждать в среднем $%S$% шагов, и с учётом первого бросания, общее среднее число составит $%S+1$%. Это происходит с вероятностью $%frac12$%.

Теперь пусть выпал орёл. Далее либо снова выпадает орёл, и число шагов равно двум, либо выпадает решка, и ждать далее приходится в среднем $%S$% шагов. Итого с вероятностью $%frac14$% получается $%2$%, и с такой же вероятностью $%S+2$%.

По формуле полной вероятности, $%S=frac12(S+1)+frac14cdot2+frac14(S+2)$%, то есть $%S=6$%.

б) Здесь рассуждаем аналогично. Искомое среднее значение снова обозначаем через $%S$%. Если выпадает 1, то ждать придётся опять $%S$% шагов, и это даёт слагаемое $%frac12(S+1)$%. Если выпадает 0, то обозначим среднее число шагов ожидания 1 через $%T$%. Вычислим $%T$% по тому же принципу: с вероятностью $%frac12$% шаг потребуется один, а если выпал 0, то далее ждать придётся $%T$% шагов. Отсюда $%T=frac12+frac12(T+1)$%, и $%T=2$%. (Это согласуется с результатом одной из предыдущих задач, где выпадения первого орла надо было в среднем ждать в среднем 2 шага.)

Из первого рассмотрения $%S=frac12(S+1)+frac12(T+1)$%, то есть $%S=4$%.

То, что ответы получились разные, может показаться парадоксальным, но это имеет своё объяснение. А для выпадения 000 в среднем надо ждать 14 шагов, в то время как для 001 всего 8.

Saragashev писал(а):

Задача по теории вероятности

Нет такой теории.
Saragashev
Исходы Вы рассмотрели правильно, только надо найти вероятности этих исходов.

Обозначим [math]X[/math] — орёл, [math]Y[/math] — решка, [math]A[/math] — любой исход, [math]P_i[/math] — вероятность, что эксперимент закончится на [math]i[/math]-м броске.

[math]P_1=P(X)=frac{1}{2}[/math]

[math]P_2=P(Y,X)=frac{1}{2}cdot frac{1}{2}=frac{1}{4}[/math]

[math]P_3=P(Y,Y,X)=frac{1}{2}cdot frac{1}{2} cdot frac{1}{2}=frac{1}{8}[/math]

[math]P_4=P(Y,Y,Y,A)=frac{1}{2}cdot frac{1}{2} cdot frac{1}{2} cdot 1=frac{1}{8}[/math]

А теперб найдём среднее число бросков, или, как говорят в народе, матожидание: [math]M=1cdot P_1+2 cdot P_2+3 cdot P_3+4 cdot P_4=1,875[/math]

Enter the max die roll (sum of all dice) and the number of dice into the calculator to determine the average dice roll value.

• Dice Probability Calculator
• Coin Flip Probability Calculator
• Post Test Probability Calculator
• Empirical Probability Calculator

Dice Average Formula

The following equation is used to calculate the average value of a set of dice.

AV = ( (M + 1 )/ 2 ) * N

• Where AV is the average dice value
• M is the max value of all dice
• N is the total number of die

To calculate the average dice value, add 1 to the max value of all dice, divide the result by 2, then multiply that result by the number of dies.

Dice Average Definition

A dice average is defined as the total average value of the rolling of dice. That is the average of the values facing upwards when rolling dice.

Dice Average Example

Let’s look at a simple example of how to use the equation above.

1. First, we need to determine the max value of 1 dice. For this example will assume standard dice so the max value is 6.
2. Next, we need to determine the number of dice. Simply count them up. For this, we will say 10 dice.
3. Finally, enter the information into the formula above. We get the results (6+1/2)*6 = 21 average roll value.

FAQ

What is dice average?

A dice average is the total average value of a rolled set of dice.

---

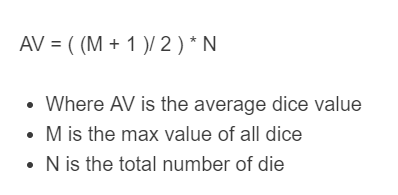
Применим теоремы 1 и 2 для решения общей задачи о лампочках.

Здания и лампочки.

Есть n-этажное здание. Известно, что если бросить лампочку с последнего, n-го этажа, то она разобьётся. У нас есть запас лампочек для экспериментов — мы можем бросать их с других этажей и смотреть, разбилась лампочка или нет. Естественно, если лампочка разбилась с какого-то этажа, то она разобьётся и с любого этажа с большим номером.

Задача лампочкобросателя — определить наименьший этаж, на котором лампочка разбивается.

Если запас лампочек бесконечен, то алгоритм действий очевиден — скажем, при n=100 нужно бросить лампочку с 50-го этажа, дальше, в зависимости от результата, с 25-го или 75-го и так далее, сужая интервал «кандидатов в ответ» в два раза при каждом бросании. После примерно семи бросаний мы узнаем точный ответ.

Наилучшее среднее число бросаний.

Все знают или верят, что этот алгоритм половинного деления оптимален по параметру «число бросаний в самом плохом случае». Однако, мы будем использовать другой критерий качества алгоритма — среднее число бросаний.

Что это за величина? Ответ для более подкованных: это математическое ожидание числа бросаний при условии, что наименьший этаж, на котором лампочка разбивается, с равной вероятностью равен 1, 2, …, n.

Ответ для менее подкованных: предположим, у нас есть n домов — в первом наименьший бьющий этаж равен 1, во втором 2, в третьем 3 и так далее, в n-ом доме лампочка бьётся только с n-го этажа. Мы применили алогритм в каждом доме, при этом каждый раз пришлось выполнить сколько-то бросаний. Эти n количеств бросаний мы усреднили — сложили и поделили на n. Это и есть среднее число бросаний алгоритма.

Никто, я думаю, не удивится, что при бесконечном запасе лампочек алгоритм половинного деления лучший и по этому показателю тоже. Но строгое доказательство этого факта и вычисление среднего числа попыток для этого алгоритма, пожалуй, потянет на задачку для районной олимпиады. Вот здесь проведено это доказательство и заодно показано, что среднее число попыток равно a(n)/n, где последовательность a(n) определяется рекуррентно: a(1)=0, a(2n)=2*a(n)+2n, a(2n+1)=a(n)+a(n+1)+(2n+1). Желающие могут найти явную формулу для a(n).

Конечный запас лампочек.

Но всё меняется, если запас лампочек у нас конечен. Например, если у нас только одна лампочка, то ни о каком половинном делении и речи быть не может. Бросишь её с 50-го этажа, она разобьётся, и мы так ничего и не узнаем. С одной лампочкой алгоритм вообще только один: бросить её с 1-го этажа, если не разбилась, то со 2-го и так далее. Среднее число бросаний для такого алгоритма равно (1+2+3+…+(n-1)+(n-1))/n=(n-1)*(n+2)/2n.

Упражнение. Почему (n-1) в сумме повторено дважды?

Если лампочек две или больше, то алгоритмов много. Например, можно действовать осторожно, как с одной лампочкой, а остальные вообще не использовать. Но это, конечно, не оптимально. Можно действовать половинным делением, пока не останется одна лампочка, а уже тогда действовать осторожно. Но, оказывается, не оптимально и это.

Вот здесь найдено наилучшее среднее число попыток для двух лампочек и указан наилучший алгоритм. Рядом опубликовано другое решение для двух лампочек и n=100 (правда, я его не понял).

Наилучшее среднее число попыток, оказывается, равно b(n)/n, где b(n) = сумма (h(k) + 1) от k=1 до n-1. Здесь h(k) это последовательность 1, 2, 2, 3, 3, 3, 4, 4, 4, 4… Достигается это наилучшее число попыток при таком алгоритме: бросить лампочку с этажа h(n)-1; если разбилась, то оставшуюся одну лампочку использовать единственно возможным образом, перебирая этажи с 1-го по h(n)-2; если не разбилась, то у нас есть две лампочки и та же самая задача для n1=n-(h(n)-1) этажей. Соответственно, надо бросить лампочку с (h(n1)-1)-го этажа и так далее.

Например, если n=100, то первый бросок надо сделать с h(100)-1 = 13-го этажа. Если лампочка не разбилась, то мы остаёмся фактически с 87-этажным домом и той же задачей, так что следующий бросок надо сделать с h(87)-1 = 12-го этажа этого 87-этажного дома, то есть с 25-го этажа исходного дома. И так далее.

Общий случай.

Решение для двух лампочек подсказывает общий подход к решению для p лампочек в запасе, который мы сейчас и реализуем.

В предыдущих постах было определено и исследовано замедление последовательности. Если g — неубывающая последовательность натуральных чисел, в которой встречаются все натуральные числа (так называемая натуральная гамма, простейший пример — натуральный ряд 1, 2, 3…), то её замедление Lrg[g] — другая натуральная гамма. Точное определение см. в предыдущих постах. У неё тоже есть замедление Lrg[Lrg[g]] — ещё одна последовательность, которую мы будем обозначать Lrg^2(g). Аналогично, Lrg^3[g]=Lrg[Lrg^2[g]] и так далее. Lrg^0[g] это сама последовательность g.

Кстати, обозначение Lrg — сокращение от музыкального термина largo или allargando. Замедление «звучит» медленнее, чем исходная гамма.

Теорема. Пусть N — натуральный ряд, и пусть h=Lrg^(p-1)[N] — это (p-1)-е замедление натурального ряда. Тогда для задачи про n этажей и p лампочек в запасе имеем:

а) Наилучшее среднее число бросаний равно H(n)/n, где H(n)=sum (h(k)+1) от k=1 до n-1.

б) Этаж, с которого надо бросить в первый раз, определяется так (при n>=2). Пусть l — номер h(n-1) в «серии» значений, равных h(n-1), в последовательности h. Пусть l1 — число членов в последовательности h, равных h(n-1)-1. Тогда начальный этаж равен max(l, l1).

Для доказательства теоремы нам понадобится слегка модифицированный принцип математической индукции:

Лемма (двумерный принцип математической индукции) Пусть S(p, n) — некое утверждение, своё при каждых натуральных p и n. Предположим, что:

A) S(1, n) верно при любом n.
B) Если p>1 и S(p-1, k) и S(p, k) верны при всех k < n, то верно и S(p, n).

Тогда S(p, n) верно при любых p и n.

Доказательство. Для натурального q>1 определим утверждение T(q) так: T(q) = утверждения S(p, n) верны при всех p и n таких, что p+n <= q. Докажем T(q) по индукции. T(2) верно по условию A. Пусть T(q-1) верно и пусть p+n=q. Если p=1, то S(p, n) верно по условию А. Если p>1, то S(p, n) верно по условию B. Доказательство закончено.

Доказательство теоремы.

Проверим, что теорема верна при p=1 (одна лампочка) для всех n. Поскольку h в этом случае просто натуральный ряд, имеем H(n)/n= 2+…+n=((n-1)(n+2)/2n. Эта формула уже была получена выше прямым вычислением (раздел «конечный запас лампочек»). Все серии в натуральном ряду имеют длину 1, поэтому б) советует бросать с 1 этажа, что тоже верно.

Теперь совершим индукционный переход. Пусть a) верно для p-1 и p лампочек и k этажей при всех k < n. Любой алгоритм для n этажей начинается с указания какого-то первого этажа бросания k.

Если лампочка на этом этаже разобьётся (вероятность этого k/n), то мы оказываемся с задачей для p-1 лампочек и k этажей, и по индукционному предположению для неё наилучшее среднее число бросаний равно G(k)/k, где G(k)= sum (g(i)+1) от i=1 до k-1. Здесь g=Lrg^(p-2)[N].

Если лампочка на этом этаже не разобьётся (вероятность этого (n-k)/n), то мы оказываемся с задачей для p лампочек и n-k этажей, и по индукционному предположению для неё наилучшее среднее число бросаний равно H(n-k)/(n-k).

Отсюда следует, что нилучшее среднее число бросаний для задачи (p, n) равно минимуму по k=1..n-1 выражения 1+(k/n)*(G(k)/k)+((n-k)/n)*H(n-k)/(n-k) = (n+G(k)+H(n-k))/n. Нам остаётся показать, что этот минимум равен H(n)/n и достигается в точке, указанной в части б).

Изменение выражения n + G(k)+H(n-k) при увеличении k на 1 равно g(k)-h(n-1-k). По Теореме 2 из предпредыдущего поста, если определить k_min, как указано в части б), то при k < k_min эта разность будет отрицательной, а при k >= k_min — неотрицательной. Отсюда следует, что минимум выражения n + G(k) + H(n-k) действительно достигается в точке k_min и равен

n + G(k_min) + H(n-k_min) = n + [sum (g(k)+1)) от k=1 до k_min-1] + [sum (h(k)+1) от k=1 до n-k_min-1] = n + [sum (g(k)+1) от k=1 до k_min-1] + H(n) — [sum (h(k)+1) от k=n-k_min до n-1] = n + [sum ((g(k) — h(n-1-k)) от k=1 до k_min-1] — (h(n-1)+1) + H(n)

Применяя Теорему 1 из того же поста, получаем, что это равно n + [h(n-1) — (n-1)] — (h(n-1)+1) + H(n) = H(n), что и требовалось доказать.