Решение задач про вероятность попаданий при выстрелах
Спасибо за ваши закладки и рекомендации
Общая постановка задачи следующая:
Вероятность попадания в цель при одном выстреле равна $p$. Производится $n$ выстрелов. Найти вероятность того, что цель будет поражена в точности $k$ раз (будет $k$ попаданий).
Применяем формулу Бернулли и получаем:
$$
P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k} = C_n^k cdot p^k cdot q^{n-k}. qquad (1)
$$
Здесь $C_n^k$ — число сочетаний из $n$ по $k$.
Если в задаче речь идет о нескольких стрелках с разными вероятностями попадания в цель, теорию, примеры решения и калькулятор вы можете найти здесь.
Видеоурок и шаблон Excel
Посмотрите наш ролик о решении задач о выстрелах в схеме Бернулли, узнайте, как использовать Excel для решения типовых задач.
Расчетный файл Эксель из видео можно бесплатно скачать и использовать для решения своих задач.
Примеры решений задач о попаданиях в цель в серии выстрелов
Рассмотрим несколько типовых примеров.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,705. Найти вероятность того, что при этом будет ровно 5 попаданий.
Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах по мишени), всего производится $n=7$ выстрелов, вероятность попадания при каждом $p=0,705$, вероятность промаха $q=1-p=1-0,705=0,295$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$
P_7(5)=C_{7}^5 cdot 0,705^5 cdot 0,295^2 = 21cdot 0,705^5 cdot 0,295^2= 0,318.
$$
Пример 2. Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится четыре независимых выстрела. Найти вероятность того, что будет хотя бы одно попадание в мишень.
Изучаем задачу и выписываем параметры: $n=4$ (выстрела), $p=0,4$ (вероятность попадания), $k ge 1$ (будет хотя бы одно попадание). Используем формулу для вероятности противоположного события (нет ни одного попадания):
$$
P_4(k ge 1) = 1-P_4(k lt 1) = 1-P_4(0)=
$$
$$
=1-C_{4}^0 cdot 0,4^0 cdot 0,6^4 =1- 0,6^4=1- 0,13=0,87.
$$
Вероятность попасть хотя бы один раз из четырех равна 0,87 или 87%.
Пример 3. Вероятность поражения мишени стрелком равна 0,3. Найти вероятность того, что при 6 выстрелах мишень будет поражена от трех до шести раз.
В отличие от предыдущих задач, здесь нужно найти вероятность того, что число попаданий будет находится в некотором интервале (а не равно в точности какому-то числу). Но формула используется прежняя.
Найдем вероятность того, что мишень будет поражена от трех до шести раз, то есть будет или 3, или 4, или 5, или 6 попаданий. Данные вероятности вычислим по формуле (1):
$$
P_6(3)=C_{6}^3 cdot 0,3^3cdot 0,7^3 = 0,185.
$$
$$
P_6(4)=C_{6}^4 cdot 0,3^4cdot 0,7^2 = 0,06.
$$
$$
P_6(5)=C_{6}^5 cdot 0,3^5cdot 0,7^1 = 0,01.
$$
$$
P_6(6)=C_{6}^6 cdot 0,3^6cdot 0,7^0 = 0,001.
$$
Так как события несовместные, искомая вероятность может быть найдена по формуле сложения вероятностей:
$$
P_6(3 le k le 6 )=P_6(3)+P_6(4)+P_6(5)+P_6(6)=$$
$$ = 0,185+0,06+0,01+0,001=0,256.$$
Пример 4. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.
Обозначим вероятность попадания в цель при одном выстреле. Введем событие:
$A = $ (Из четырех выстрелов хотя бы один попадет в цель),
а также противоположное ему событие, которое можно записать как:
$overline{A} = $ (Все 4 выстрела будут мимо цели, ни одного попадания).
Запишем формулу для вероятности события $A$. Выпишем известные значения: $n=4$, $P(A)=0,9984$. Подставляем в формулу (1) и получаем:
$$
P(A)=1-P(overline{A})=1-P_4(0)=1-C_{4}^0 cdot p^0 cdot (1-p)^4=1-(1-p)^4=0,9984.
$$
Решаем получившееся уравнение:
$$
1-(1-p)^4=0,9984,\
(1-p)^4=0,0016,\
1-p=0,2,\
p=0,8.
$$
Итак, вероятность попадания в цель при одном выстреле равна 0,8.
Понравилось? Добавьте в закладки
Полезные ссылки
- Решения разных задач о стрелках и выстрелах
- Примеры контрольных по теории вероятностей
- Заказать контрольную по теории вероятностей
Найдите готовые задачи в решебнике:
Характеристика случайной величины в виде таблицы или Функции распределения представляет полное задание случайной величины Однако для разрешения ряда вопросов в теории вероятностей и К Статистике с успехом применяется более простая характеристика случайной величины — ее среднее значение X, или, что то же, математическое ожидание — М(Х)=а.
Пусть дана таблица распределения случайной величины с конечным числом возможных значений:
|
|
|
|
… |
|
|
|
|
|
… |
|
Введем следующее определение: Средним значением, или математическим ожиданием, случайной величины называется сумма произведений всех возможных значений случайной ВЕличины на соответствующие вероятности:
Или
Здесь важно отметить, что , А это показывает, что ИСчерпываются все возможные значения случаЙНоЙ величины, составляющие полную систему событий.
Пример 4. Проводится беспроигрышная лотерея на 200 выигрышей, из которых 1 выигрыш составляет 100 руб., 5 выигрышей по 20 руб., 10 выигрышей по 5 руб. и 184 выигрыша по 2 руб. Определить справедливую цену одного билета, рассчитанную так, чтобы сумма выплаченных выигрышей равнялась сумме, вырученной за продажу билетов.
Решение. Для применения формулы среднего значения случайной величины мы предварительно составляем в соответствии с данными о количестве отдельных выигрышей таблицу распределения:
|
|
2 |
5 |
20 |
100 |
|
|
|
|
|
|
Поэтому
Таким образом, справедливая цена одного лотерейного билета должна составить 3 руб. 09 коп.
Пример 5. Найти среднее значение числа попаданий в мишень при 6 выстрелах, если дана вероятность попадания прИ отдельном выстреле
Решение. Распределение случайной величины (числа попаданий X) в этом примере подчиняется биномиальному закону:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
|
После вычисления соответствующих членов биномиального распределения по формуле
Имеем
Переходя к основным свойствам математического ожидания случайных величин, введем понятие об их независимости.
Определение. Случайные величины Х и Y называются независимыми, если законы распределения каждой из них не меняются, когда становится известным, что другая приняла какое-либо одно (безразлично какое) значение.
Примером двух независимых случайных величин могут служить суммы выигрышей по каждому из двух билетов по двум различным денежно-вещевым лотереям.
Здесь ставший известным размер выигрыша по билету одной лотереи не влияет на ожидаемый размер выигрыша и соответствующую ему вероятность по билету другой лотереи.
В виде другого примера независимых случайных величин можно привести данные о числе километров суточного пробега для двух машин из различных гаражей.
Свойство 1°. Математическое ожидание постоянной величины равно этой же постоянной величине.
В самом деле, таблица распределЕНия для постоянной величины С имеет вид:
Поэтому
Свойство 2°. Математическое ожидание суммы случаЙНых величИн равно сумме их математических ожиданий.
Пусть две случайные величины Х и Y заданы соотвЕТствуЮщИми таблицами распределения.
Докажем, что .
Рассмотрим простейший случай, когда каждая из случайных величин принимает лишь по два значения:
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
В этих условиях сумма Х+у как случайная величина Характеризуется следующей таблицей:
|
|
|
|
|
|
|
|
|
|
|
|
Здесь произведения вида обозначают вероятности соответствующих значений суммы случайных величин Х+Y, так как эти вероятности определяются по теореме умножения вероятностей.
В самом деле, обозначает вероятность того, что
и
, т. е. имеет место совместное наступление двух событий: 1) случайная величина Х принимает значение
и 2) случайная величина Y принимает значение
.
ПоэтОМу , где
и
Отсюда
Переходя к математическому ожиданию рассматриваемой сУммы, Имеем
Раскрывая в правой части скобки и группируя слагаемые по каждому значению случайной величины, получаем
Заметив далее, что суммы в каждой скобке определяют соответственные вероятности значений и
1), имеем
Это свойство можно распространить на любое конечное Число Слагаемых, т. Е.
Или
Это свойство справедливо и для независимых, и для зависимых случайных величин, хотя приведенное доказательство применимо лишь для независимых случайных величин.
Пример 6. Проверить свойство 2° для двух независимых случайных величин Х и Y, заданных следующими распределениями:
|
|
3 |
5 |
7 |
И |
|
2 |
6 |
|
|
0.3 |
0.5 |
0.2 |
|
0.6 |
0.4 |
Решение. Составляем распределение суммы :
|
|
3+2 |
3+6 |
5+2 |
5+6 |
7+2 |
7+6 |
|
|
0,18 |
0,12 |
0,3 |
0,2 |
0,12 |
0,08 |
Отсюда
Определим теперь математическое ожИДанИЕ каждой из заданных случайных величин:
Таким образом, 4.8+3.6 = 8.4, чем подтверждается свойстВО Математического ожидания суммы случайных величин.
Пример 7. Найти математическое ожидание чисЛА Т Появлений События А в П повторных испытаниях, если вероятность Появления Его в отдельном испытании равна Р.
РЕШеНИЕ. Здесь число появлений события А в каждом Испытании представляет собой случайНую величину со следующим распределением:
|
|
1 |
0 |
|
|
P |
Q |
Математическое ожидание этой случайнОй величины в каждом Испытании одинаково:
Число Т появлений события А в П испытаниях Представляет Собой также случайную величину, являющуюся суммой случайных величин :
Применяя поэтому к числу Т свойство 2° математического Ожидания суммы случайных величин, получаем
.
Так как каждое из этих П слагаемых равно Р, то Или
Заметим, что результат этого примера позволяет сразу находитЬ Среднее значение числа Т для любого случая биномиального распределения, не прибегая к сложному вычислению, проведенному в примере 5.
В отношении математического ожидания суммы случайных величин применение свойства не связано с вопросом о зависимости или независимости случайных величин. Следующая теорема—о математическом ожидании произведения случайных величин—применима только к независимым случайным величинам.
Свойство 3°. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Пусть Х и Y—Две независимые случайные величины, таблИЦы распределения которых даются ниже:
|
|
|
|
… |
|
И |
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
… |
|
Докажем, что .
Рассматривая XY как случайную величину, мы устанаВЛиваем, что она принимает все значеНИя вИДа , число которых опредеЛЯется произведением Kl. Вероятность каждого значения произведеНИя
находится по теореме умножения вероятностей:
.
Поэтому .
| < Предыдущая | Следующая > |
|---|
Математическое ожидание случайных величин
Определение
математического ожидания с.в. зависит
от того, является ли она дискретной или
непрерывной.
-
Пусть Х
– дискретная случайная величина с
законом распределения:
|
Х |
х1 |
х2 |
… |
xn |
|
Р |
p1 |
p2 |
… |
pn |
Математическим
ожиданием д.с.в.
Х
называется число, обозначаемое М(Х)
и вычисляемое по формуле
-
Пусть Х
– непрерывная случайная величина с
плотностью вероятности f(x).
Математическим
ожиданием н.с.в.
Х
называется число, обозначаемое также
М(Х)
и вычисляемое по формуле
Понятно, что если
н.с.в. Х
сосредоточена на некотором отрезке
[a,b]
(т.е. по принятому выше определению
плотность ее вероятности f(x)
обращается в 0 вне этого отрезка), то
формула для математического ожидания
переходит в следующую:
.
Убедимся (для
случая дискретных случайных величин),
что таким образом введенному математическому
ожиданию случайной величины можно
действительно придать смысл среднего
значения этой величины. Напомним, что
арифметическим средним n
чисел х1,
х2,
… , xn
называется число, равное
.
Пусть не все числах1,
х2,
… , xn
разные, а разных среди них только k
штук, причем имеется n1
чисел, равных х1,
n2
чисел, равных х2,
… , nk
чисел, равных xk
(понятно,
что n1+…+nk
= n,
а если все числа разные, то это просто
означает, что k=n,
n1=n2=…=nk=1).
Тогда сумма всех чисел может быть
представлена в виде
.
Поэтому формула для среднего всех данных
чисел может быть представлена в виде
.
Далее будет
использована именно эта формула среднего
для набора из n
чисел, среди
которых имеется n1
чисел, равных х1,
n2
чисел, равных х2,
… , nk
чисел, равных xk
(n1+…+nk
= n).
Итак, пусть имеется
д.с.в. Х ,
возможные значения которой
х1,
х2,
… , xk
и принимаются они с вероятностями p1,
p2,
… , pk.
Таким образом, д.с.в. Х
имеет следующий закон распределения
вероятностей:
|
Х |
х1 |
х2 |
… |
xk |
|
Р |
p1 |
p2 |
… |
pk |
Проведем n
случайных экспериментов, в каждом из
которых д.с.в. Х
приняла одно из своих возможных значений.
Пусть свое первое значение х1
было принято n1
раз, значение х2
было принято n2
раз, …, значение хk
принято nk
раз (n1+n2+…+nk
= n).
Составим теперь среднее значение с.в.
Х
в этих n
экспериментах,
обозначив его
.
По приведенной выше формуле для среднего
получаем:
.
Понятно, что это
число
может меняться при переходе от одной
серии изn
экспериментов
к другой, а также зависит и от числа n
проведенных
экспериментов. Поэтому полученное число
не может быть принято в качестве среднего
значения с.в.Х
как таковой.
Посмотрим, как будет меняться это среднее
при неограниченном увеличении числа
проводимых экспериментов, т.е. попробуем
вычислить предельное значение
приn→∞:
.
Найдем значение
первого в этой сумме предела
.
Под знаком предела стоит отношение
числа экспериментовn1,
в которых с.в. Х
приняла значение х1
(т.е. произошло событие Х=х1),
к общему числу проведенных
экспериментов
n
. Когда мы
проходили ранее статистическое
определение вероятности, то для
произвольного события А
отношение числа экспериментов, в которых
это событие появилось, к общему числу
экспериментов n
мы называли относительной частотой
события А
в n
испытаниях и обозначали Wn(A).
Поэтому отношение
есть ни что иное, как относительная
частота события (Х=х1)
в проведенных n
экспериментах :
.
В той же теме о статистическом определении
вероятности мы говорили о том, что,
благодаря свойству устойчивости
относительных частот, при неограниченном
увеличении числа испытаний относительная
частота любого событияА
стремится к его вероятности:
.
Поэтому исследуемый предел
равен вероятности
для исследуемой с.в. Х
принять свое первое значение х1.
Но такая вероятность по выписанному
выше закону распределения для с.в. Х
равна р1.
Поэтому можно окончательно записать,
что
.
Аналогичные формулы можно получить и
для остальных пределов. В результате
получаем, что
.
Поэтому для предела
среднего значения с.в. Х
при неограниченном увеличении числа
испытаний получается формула
.
Но в правой части
мы получили то, что выше было названо
математическим ожиданием М(Х)
для с.в. Х
. Таким образом
,
а потому математическое
ожидание мы действительно можем считать
средним значением случайной величины
при большом
(так как n→∞)
числе испытаний. По этой причине
математическое ожидание некоторой
случайной величины называют еще и
средним значением этой величины.
Полученная формула
говорит о том, чтопри
большом числе
экспериментов n
среднее значение с.в. Х
в этих испытаниях приближенно равно
математическому ожиданию этой с.в. :
.
С другой стороны, записав это приближенное
равенство в виде,
получим способ оценки математического
ожидания с.в.Х,
если неизвестен закон ее распределения.
Этот способ оценки математического
ожидания и используется в математической
статистике.
Рассмотрим некоторые
примеры на нахождение математического
ожидания. Если в задаче требуется найти
среднее некоторой величины, то (по
изложенным выше причинам) это означает,
что требуется найти ее математическое
ожидание.
Пример.
Найти среднее число очков, выпадающих
на игровом кубике.
Решение. Пусть с.в.
Х
– число очков на кубике при его
подбрасывании. Требуется найти
математическое ожидание М(Х)
этой случайной
величины. Мы уже выписывали закон
распределения для числа выпавших на
кубике очков:
|
Х |
1 |
2 |
3 |
4 |
5 |
6 |
|
Р |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
Тогда по определению
.
Отметим, что среднее значение случайной
величины не обязано совпадать с одним
из своих возможных значений, что
показывает данный пример.
Пример.
Найти среднее число продаваемых за день
автомобилей в задаче об автосалоне
(данные по этой задаче были даны выше).
Решение. В этой задаче уже был дан
закон распределения с.в. Х
– число продаваемых за день автомобилей:
|
Х |
0 |
1 |
2 |
3 |
|
Р |
0.4 |
0.3 |
0.2 |
0.1 |
Поэтому среднее
число продаваемых за день автомобилей
М(Х)=0∙0.4+1∙0.3+2∙0.2+3∙0.1=1
. Поэтому в среднем продается одна машина
в день. Отметим, что в данном примере
математическое ожидание случайной
величины совпало с одним из ее возможных
значений.
Пример.
У охотника имеется 4 патрона. Он стреляет
по зайцу, пока не попадет или пока не
закончатся патроны. Найти среднее число
израсходованных патронов.
Пример (доходы
страхования).
По статистике 40-летний человек доживает
до 50-летнего возраста с вероятностью
0.927 . При страховании жизни на 10 лет на
сумму 1000 у.е. такой человек платит 100
у.е. страхового взноса. Найти средний
доход страховой компании за 10 лет от
одного клиента.
Пример.
Найти математическое ожидание непрерывной
с.в. Х,
если плотность ее вероятности
Решение. Поскольку
эта случайная величина сосредоточена
на отрезке [0,1] (т.к. вне этого отрезка
плотность вероятности обращается в 0),
то
.
Рассмотрим свойства
математического ожидания, которые
справедливы как для дискретных, так и
для непрерывных случайных величин.
-
Если с.в С
принимает только одно значение с=const
(при любом исходе эксперимента), то она
уже не является случайной. В этом случае
она называется постоянной величиной.
Но такую величину тоже можно рассматривать
как д.с.в. с законом распределения
|
C |
с |
|
Р |
1 |
Тогда, очевидно,
что ее математическое ожидание равно
единственному принимаемому этой
величиной числу: М(С)=
с ∙1
= с. Итак,
М(С)=с.
-
Постоянный
множитель можно выносить за знак
математического ожидания:
М(с∙Х)=с∙М(Х),
где c=const.
-
Математическое
ожидание суммы случайных величин равно
сумме их математических ожиданий:
M(X+Y)=M(X)+M(Y).
Это свойство
справедливо для суммы любого числа
случайных величин и помогает находить
математическое ожидание некоторых
с.в., закон распределения которых
неизвестен либо его нахождение вызывает
значительные трудности.
Пример (о том же
автосалоне).
Найти среднюю ежедневную прибыль
автосалона.
Решение. Пусть
снова с.в. Х
– число проданных за день автомобилей,
а с.в. Y
– ежедневная прибыль автосалона. Ранее
было получено, что Y=100
∙X
−
50, а М(Х)=1.
Поэтому, используя приведенные выше
свойства, получаем среднее значение
ежедневной прибыли М(Y)=M(100
∙X
−
50)=100 ∙M(X)
−50 =50 у.е. .
Пример.
Найти среднее значение суммы числа
очков при подбрасывании двух кубиков.
Решение. Пусть
с.в. Х
– сумма очков на двух кубиках. Требуется
найти М(Х).
Введем вспомогательные с.в. : Х1
– число очков на 1-м кубике, а Х2
– на втором. Очевидно, что Х=Х1+Х2.
Уже не так просто составить закон
распределения с.в. Х
(для того, чтобы вычислить ее матожидание
по определению). А если бы подбрасывалось
100 кубиков, то составить закон распределения
было бы необычайно сложно. Однако
используя рассматриваемое свойство и
учитывая, что ранее вычисленное
матожидание числа очков на одном кубике
равно 3.5, получаем М(Х)=M(X1+Х2)=M(X1)+M(Х2)=3.5+3.5=7.
Понятно, что средняя сумма числа очков
для 100 кубиков равна 350.
-
Математическое
ожидание произведения независимых
случайных величин Х
и Y
равно произведению их математических
ожиданий:∙
M(X∙Y)=M(X)∙M(Y)
.
Еще раз отметим,
что если свойство матожидания суммы
случайных величин справедливо для всех
с.в., то для гарантированной справедливости
этой формулы с.в. Х
и Y
должны быть независимыми.
Пример.
Найти среднее значение произведения
числа очков при подбрасывании двух
кубиков.
Решение. Пусть
с.в. Х
– произведение очков на двух кубиках.
Требуется найти М(Х).
Снова введем те же вспомогательные с.в.
: Х1
– число очков на 1-м кубике, а Х2
– на втором. Очевидно, что Х=Х1
∙Х2,
а с.в.
Х1
и
Х2
независимы. Тоже не так просто составить
закон распределения с.в. Х
(для того, чтобы вычислить ее матожидание
по определению). Однако используя
рассматриваемое свойство и учитывая,
что ранее вычисленное матожидание числа
очков на одном кубике равно 3.5, получаем
М(Х)=M(X1
∙Х2)=M(X1)∙M(Х2)=3.52=12.25
.
Пример.
Пусть Х
и Y
– независимые с.в. . Найти математическое
ожидание с.в. Z=2X–5Y+4X∙Y+3,
если М(Х)=1,
M(Y)=3.
-
Укажем формулы
для вычисления математического ожидания
функции от случайной величины.
|
Х |
х1 |
х2 |
… |
xn |
|
Р |
p1 |
p2 |
… |
pn |
1) Пусть Х
– дискретная случайная величина с
законом распределения
а с.в. Y=g(X).
Тогда
.
Доказательство
этой формулы очевидно, если вспомнить,
как выглядит закон распределения с.в.
Y=g(X)
и определение математического ожидания.
2) Пусть Х
– непрерывная случайная величина с
плотностью вероятности f(x),
а с.в. Y=g(X).
Тогда
.
-
Рассмотрим теперь
нахождение математического ожидания
в часто встречающихся ситуациях. Пусть
производится n
независимых
испытаний, в каждом из которых некоторое
событие А
может появиться с вероятностью, зависящей
в общем случае от номера испытания.
Пусть р1
–
вероятность появления событий А
в 1-oм
испытании, …, рn
–
вероятность появления событий А
в n-oм
испытании. Рассмотрим с.в. Х
– число появлений события А
во всех n
испытаниях (как говорят – «число
успехов» в n
испытаниях). Тогда математическое
ожидание числа успехов:
.
Доказательство.
Рассмотрим вспомогательные случайные
величины: Х1
– число появлений события А
в 1-ом
испытании, …,
Хn
– число
появлений события А
в n-ом
испытании .
Все введенные с.в. могут принимать
значения 0
или 1
(событие А
в испытании может появиться или нет),
причем значение 1
по условию принимается в k-ом
испытании с вероятностью pk
(вероятность появления события А
в k-ом
испытании), а значение 0
с вероятностью (1–
pk)
(вероятность противоположного события
– не появления события А
в k-ом
испытании), k=1,…,
n.
Поэтому эти величины имеют следующие
законы распределения:
|
Х1 |
0 |
1 |
|
Р |
1–р1 |
р1 |
|
Хn |
0 |
1 |
|
Р |
1–рn |
рn |
, … ,
Поэтому средние
значения этих величин: М(Х1)=0∙(1–р1)+1∙
р1=
р1
, …, М(Хn)=0∙(1–рn)+1∙
рn=
рn
. Ясно, что
общее число появлений события А
во всех испытаниях равно сумме «успехов»
по всем испытаниям: Х=Х1+Х2+…+Xn
. Пользуясь свойством математического
ожидания суммы случайных величин,
получаем: М(Х)=М(Х1)+М(Х2)+…+М(Xn)=р1+…+рn
, что и требовалось доказать.
Пример.
Первый стрелок попадает в мишень с
вероятностью р1=0.5,
второй с вероятностью р2=0.6,
а третий с вероятностью р3=0.7
. Найти
среднее число попаданий в мишень при
одном залпе этих стрелков по мишени.
Решение. Этот
пример в точности укладывается в
изложенную схему. Событие А
в данном случае – попадание в мишень.
В каждом из трех испытаний (выстрелы
стрелков) оно появляется со своей
вероятностью (р1=0.5
либо р2=0.6,
либо р3=0.7)
.
С.в. Х
– общее число попаданий в мишень есть
общее число появлений события А.
Поэтому М(Х)=
р1+р2+р3=1.8
. Итак, среднее число попаданий в мишень
в данной ситуации равно 1.8
(ясно, что оно не является одним из
возможных значений общего числа попаданий
в мишень).
-
Математическое
ожидание числа успехов в схеме Бернулли.
Пусть
производится n
независимых
испытаний, в каждом из которых некоторое
событие А
может появиться с одной и той же
вероятностью р.
Рассмотрим с.в. Х
– число появлений события А
во всех n
испытаниях. Тогда математическое
ожидание числа успехов:
.
Эта формула следует
из предыдущего свойства, так как в
рассматриваемом случае вероятности
успеха в каждом испытании одинакова:
р1=р2=…=рn=р
.
Пример.
Стрелок попадает в мишень с вероятностью
р=0.6 .
Найти среднее число попаданий в мишень
при трех выстрелах.
Ответ: 3∙0.6=1.8
.
С помощью последнего
свойства теперь можно строго обосновать
наше интуитивное понимание вероятности
наступления некоторого события в
эксперименте. Например, если получалось,
что вероятность некоторого события А
оказывалась равной, к примеру, р
= 0.1 , то
говорилось, что это событие происходит
в среднем один раз в 10
испытаниях. И действительно, если мы
произведем 10
испытаний на появление этого события,
то по выведенной формуле для среднего
числа успехов в схеме Бернулли получили
бы, что среднее число появлений события
А
в этих испытаниях действительно равно
10 ∙0.1=1.
Если в формуле
для схемы Бернулли взять n=1,
то получим М(Х)=р.
Поэтому вероятность р
некоторого события можно интерпретировать
как среднее число появлений этого
события в одном испытании.
Пример.
Вася с Петей снова затеяли ту же игру.
Если при подбросе кубика выпадет 6, то
Вася дает Пете 4 рубля, а в противном
случае Петя дает Васе 1 рубль. Найти
среднее значение Васиного выигрыша.
Пример.
Играющий платит некоторую сумму
(начальная ставка) за проведение игры
ее устроителю. Четыре раза бросается
монета. Если выпадает 4 орла, то играющий
получает 10 рублей, если 3 орла, то 1 рубль.
В остальных случаях − ничего. Какова
должна быть начальная ставка в игре,
чтобы игра была «безобидной» (т.е. средний
общий выигрыш с учетом начальной ставки
равен 0).
Пример.
На двух столах лежат по 2 внешне одинаковых
коробки конфет. На первом столе в одной
из коробок 1 конфета, а в другой 7 конфет.
На втором столе в одной из коробок 2
конфеты, а в другой 5 конфет. Ребенок
выбирает стол, с которым он будет играть.
Игра заключается в выборе одной из двух
лежащих на столе коробок. Если ребенок
выбрал первый стол, то он сможет с ним
сыграть 10 раз, а если второй, то 11 раз.
Какой стол ему лучше выбрать?
Содержание:
Формула полной вероятности:
Пусть событие А может произойти в результате появления одного и только одного события
События этой группы обычно называются гипотезами.
Теорема: Вероятность события А равна сумме парных произведений вероятностей всех гипотез, образующих полную группу, на соответствующие условные вероятности данного события А, т. е.
(формула полной вероятности), причем здесь
Доказательство. Так как
причем, ввиду несовместности событий 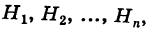
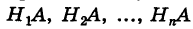
что и требовалось доказать.
Пример:
В магазин для продажи поступает продукция трех фабрик, относительные доли которых есть: I — 50%, II — 30%, III — 20%. Для продукции фабрик брак соответственно составляет: I — 2%, II — 3%, III — 5%. Какова вероятность того, что изделие этой продукции, случайно приобретенное в магазине, окажется доброкачественным (событие А)?
Решение:
Здесь возможны следующие три гипотезы: 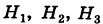
Соответствующие условные вероятности события А равны
По формуле полной вероятности имеем
Формула Бейеса:
Пример:
Имеется полная группа несовместных гипотез
вероятности которых 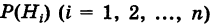
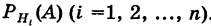
Например, очевидно, следует отбросить гипотезы, отрицающие появление события А. Вообще, проблема состоит в том, что, имея новую информацию, мы должны переоценить вероятности наших гипотез.
Иными словами, нам нужно определить условные вероятности
На основании теоремы умножения вероятностей имеем
отсюда
Для нахождения вероятности Р(А) можно использовать формулу полной вероятности
Отсюда имеем формулу вероятностей гипотез после опыта (<формулу Бейеса)
Пример:
Вероятность поражения самолета при одиночном выстреле для 1-го ракетного расчета (событие А) равна 0,2, а для 2-го (событие В) — 0,1. Каждое из орудий производит по одному выстрелу, причем зарегистрировано одно попадание в самолет (событие С). Какова вероятность, что удачный выстрел принадлежит первому расчету?
Решение:
До опыта возможны четыре гипотезы: 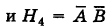
Вероятности их, при независимом действии расчетов, соответственно равны
причем
Условные вероятности для наблюдаемого события С при данных гипотезах будут
Следовательно, гипотезы 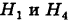
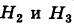
Таким образом, с вероятностью приблизительно 0,7 можно утверждать, что удачный выстрел принадлежит 1-му расчету,
Формула полной вероятности
Пусть событие А еще не произошло, но вскоре должно произойти. Событие А может протекать в различных условиях, относительно характера которых сделано 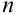
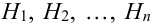
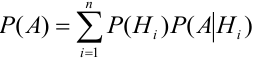
Доказательство.
По условию теоремы гипотезы 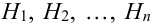
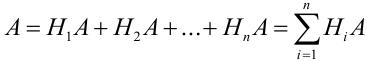
Т.к. гипотезы несовместны, то и комбинации 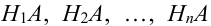
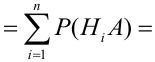
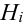
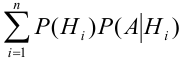
Пример:
Имеется пять урн:
2 урны состава 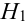
1 урна состава 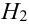
2 урны состава 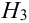
Наудачу выбирается урна, и из нее наудачу выбирается шар. Чему равна вероятность события А = {будет вынут белый шар}?
Решение.
Событие А еще не произошло. Шар может быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 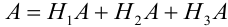
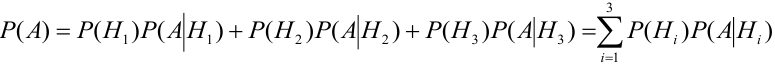
Найдем отдельно вероятности событий:
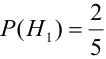
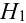
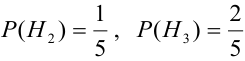
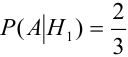
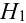
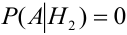
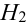
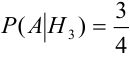
Подставим найденные вероятности в формулу (*): 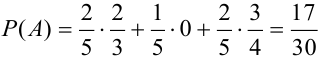
Формула полной вероятности и решение задач
Пример:
В двух одинаковых коробках имеется по 100 резисторов. В 1-й — 60 резисторов по 100 КОм, во 2-й 30 — резисторов по 100 КОм. Определить вероятность того, что взятый наугад из какой-либо коробки резистор будет 100 КОм.
Решение:
Пусть событие 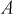
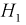
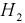
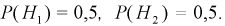
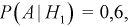
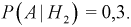
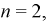
Пример №1
В первой коробке находится 20 деталей, из них 18 стандартных, во второй коробке – 10 деталей, из них 9 стандартных. Из второй коробки наудачу взята одна деталь и переложена в первую коробку.
Какова вероятность того, что деталь, наудачу извлечённая после этого из первой коробки, окажется стандартной?
Решение. Обозначим события:
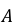
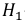
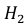
Событие А может наступить при условии наступления одного из событий 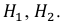
Вероятность того, что из второй коробки извлечена нестандартная деталь
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена стандартная деталь,
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена нестандартная деталь,
Искомая вероятность того, что из первой коробки будет извлечена стандартная деталь, по формуле полной вероятности равна:
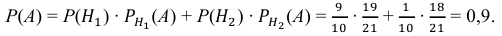
Ответ: 0,9.
Пример №2
Два станка производят одинаковые детали, которые поступают на общий конвейер. Производительность первого станка в два раза больше производительности второго станка. Первый производит 60 % деталей высшего сорта, а второй – 84 %. Наудачу взятая с конвейера деталь оказалась высшего сорта. Какова вероятность того, что эта деталь произведена на первом станке?
Решение. Обозначим события:
А – деталь, взятая с конвейера, оказалась высшего сорта.
Это событие наступит с одним из двух событий (гипотез):
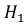
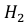
Поскольку производительность первого станка в два раза больше производительности второго станка, вероятности гипотез равны:
Условные вероятности события А даны:
По формуле полной вероятности находим:
По формуле Байеса найдём условную вероятность того, что взятая наудачу деталь высшего сорта произведена на первом станке:
Ответ:
Пример №3
В ящике 20 белых и 10 чёрных шаров. Поочерёдно извлекают 4 шара, причём каждый извлечённый шар возвращают в ящик перед извлечением следующего. Какова вероятность того, что среди четырёх извлечённых шаров окажется два белых?
Решение. Вероятность извлечения белого шара одна и та же во всех четырёх испытаниях, так как каждый извлечённый шар возвращается в ящик:
Тогда вероятность извлечения чёрного шара во всех четырёх испытаниях равна
Используя формулу Бернулли, находим вероятность того, что из четырёх извлечённых шаров два шара будут белыми:
Ответ:
Пример №4
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена 75 раз?
Решение. По условию задачи
Так как n – достаточно большое число, воспользуемся локальной формулой Лапласа:
В таблице значений функции 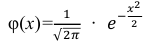
0,1826.
Следовательно,
Ответ: 0,04565.
Пример №5
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена
а) не менее 75 раз и не более 90 раз?
б) не менее 75 раз?
в) не более 74 раз?
Решение.
Воспользуемся интегральной формулой Лапласа:
где 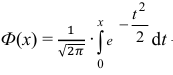
а) По условию задачи 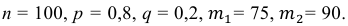
б) Требование того, чтобы событие наступило не менее 75 раз, означает следующее: число появлений события может быть равно либо 75, либо 76, … , либо 100.
Тогда следует принять 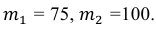
в) Событие «мишень поражена не более 74 раз» и событие «мишень поражена не менее 75 раз» являются противоположными. Поэтому сумма их вероятностей равна 1. Следовательно, искомая вероятность
Ответ: а) 0,8882; б) 0,8944; в) 0,1056.
Пример №6
Учебник издан тиражом 100000 экземпляров.
Вероятность того, что один учебник сброшюрован неправильно, равна 0,0001. Какова вероятность того, что тираж содержит 5 бракованных книг?
Решение. По условию задачи n = 100000, p = 0,0001.
События «из n книг ровно m книг сброшюрованы неправильно», где m = 0,1,2, … ,100000, являются независимыми. Так как число n велико, а вероятность p мала, вероятность 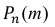
В рассматриваемой задаче 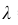
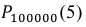
Ответ: 0,0375.
Формула Байеса (Бейеса)
Пусть событие А произошло, причем А могло протекать в различных условиях, относительно характера которых было сделано 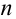
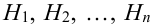
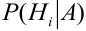
Решение:
По условию теоремы гипотезы 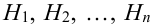
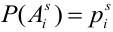
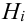
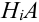
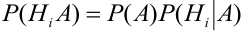
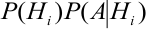
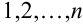
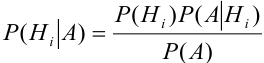
Выразим Р(А) с помощью формулы полной вероятности:
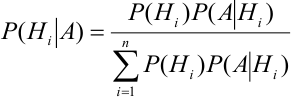
Пример №7
Имеется пять урн:
2 урны состава 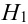
2 урны состава 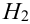
1 урна состава 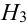
Из одной наудачу выбранной урны взят шар. Он оказался белым (событие А). Чему равна после опыта вероятность события, что шар вынут из урны третьего состава.
Решение.
Событие А произошло. Шар мог быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 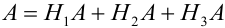
Найдем вероятности событий:
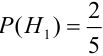
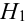
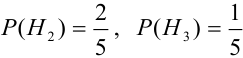
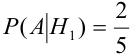
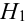
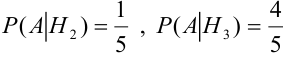
По формуле Байеса найдем условную вероятность 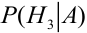
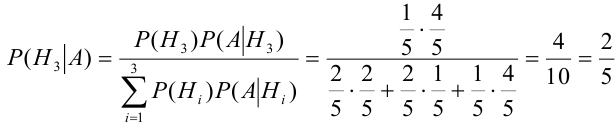
Пример №8
Вероятность дождливого дня в городе равна 0,2. Известно, что вероятность выиграть футбольный матч команде этого города в дождливый день равна 0,4, а в сухой — 0,7. Известно, что команда выиграла матч. Определить, что в этот день шел дождь.
Решение:
Событие 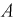
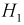
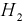
Чтобы ответить на вопрос, пересмотрим вероятность 1-й гипотезы с учетом результата опыта-появилось событие 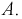
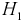
Из полученного результата видим, что с учетом события 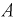
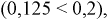
Независимые испытания
Под испытанием станем понимать осуществление определенного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства 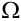
Определение 26. Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.
В каждом испытании вероятность появления события А одинакова.
Ряд задач связан с экспериментом, в котором проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Рассматривается последовательность п независимых испытаний, под которой будем понимать дискретное новое пространство 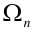
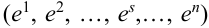
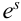

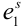
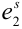
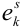
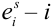



Пример №9
Пусть испытание состоит в подбрасывании игральной кости. Пространство элементарных событий 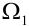
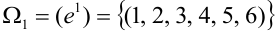
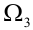
Обычно исходы обозначали большими заглавными буквами. Переобозначим! Пусть происходит 



Обозначим событие 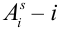



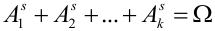
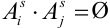
Обозначим вероятность 
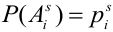
Пусть при первом испытании произошло событие под номером 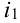
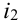

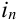

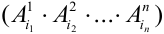
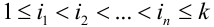
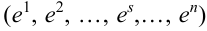
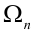
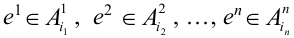
Испытания — независимые, следовательно, по теореме 4, имеет место равенство:
В случае, когда вероятности событий 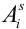
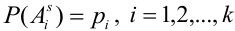
В силу несовместности и единственной возможности исходов, очевидно, что 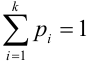
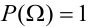
Теорема. Если данные 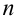
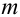
Теорема. Для того, чтобы 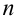
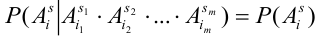
для любой группы чисел 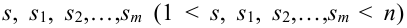
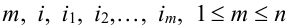
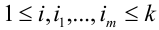
Формулы Бернулли
Пусть проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Схема независимых испытаний является математической моделью серии испытаний, повторяющихся при неизменных условиях. Такая схема называется полиномиальной.
Простейшим классом повторяющихся независимых испытаний является последовательность независимых испытаний с двумя исходами (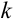
Определение 27. Независимые испытания при двух исходах называются испытаниями Бернулли.
Пример №10
Определить вероятность того, что в результате проведения 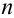

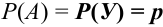
Решение.
Искомую вероятность обозначим 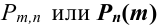
Событие А в данных испытаниях может появиться ровно 
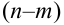
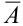
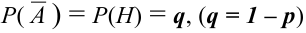
Сначала найдем вероятность того, что события У наступают при определенных 

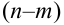
По условию данные события — независимые, следовательно, по теореме 4 для произведения независимых событий можем записать, что
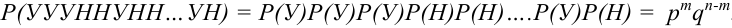
Число успехов и неудач задано. Можно менять только их расположения в цепочках, которое однозначно определяется выбором из 

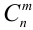
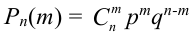
В данной задаче мы доказали теорему Бернулли.
Теорема Бернулли. Если 


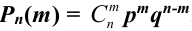
Следствие. 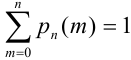

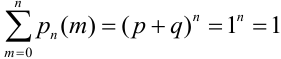
Пример №11
Пусть монета брошена 5 раз. Требуется найти вероятность того, что выпало ровно 3 орла.
Решение.
В каждом из 5 независимых испытаниях (
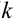
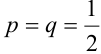

По формуле Бернулли 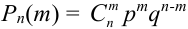
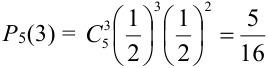
Замечания.
Замечание 1. Вероятность 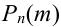
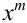
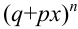
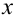
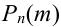
Замечание 2. Рассмотрим схему испытаний с произвольным количеством исходов. Пусть каждое из 
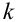
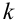
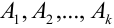
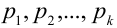

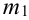
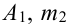
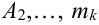
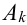

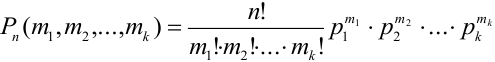
Эта совокупность вероятностей является коэффициентом при 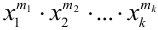
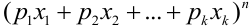
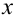
Например. При 

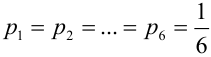
Если различать только «6» и «не 6», то получим схему Бернулли с двумя исходами (
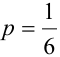
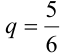
Замечание 3. При вычислении вероятности события, состоящего в том, что число успехов m лежит, например, между а и b, приходится находить числовые значения сумм вероятностей вида: 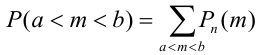
Например, вероятность того, что событие наступит а) менее 



a) 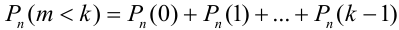
b) 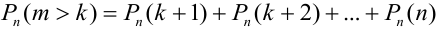
c) 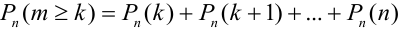
d) 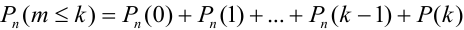
В некоторых случаях удобнее перейти к противоположному событию, например, 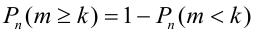
Пример №12
Пусть монета брошена 5 раз. Требуется найти вероятность того, что 1) менее двух раз выпал орел, 2) не менее двух раз выпал орел.
Решение.
Два исхода (
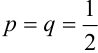
1) Орел выпал менее двух раз, значит, не выпал или выпал раз.
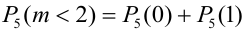
2) Орел выпал не менее двух раз, т.е. выпал два раза или три или четыре или пять:
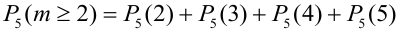
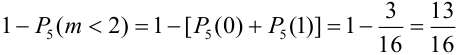
Замечание 4. В примере на формулу Бернулли вычисления проводятся очень легко, однако часто приходится вычислять вероятности при очень больших значениях n и m, например, при n = 1000, m = 500. Также затруднения при вычислении возникают при малых значениях р или q.
В этих случаях удается заменить формулу Бернулли какой-нибудь приближенной асимптотической формулой. Существуют три предельные теоремы, содержащие такие формулы.
Предельные теоремы в схеме Бернулли
Теорема Пуассона (асимптотическая формула для случая малых значений р)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, причем 

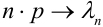
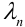
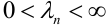
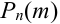

Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при 
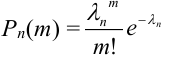
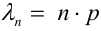
2. Формулой пользуются при больших n и малых р. Например, при n > 100, 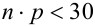
3. Теорема имеет место и в том случае, когда вероятность события А в каждом испытании равна нулю. В этом случае 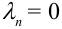
4. Существуют таблицы значений данной вероятности (стр. 410, 411 в задачнике Ефимова -Демидовича).
Пример №13
Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более пулями, если число выстрелов равно 5000.
Решение.
Считаем каждый выстрел за испытание и попадание в цель за событие. Количество испытаний n = 5000 (велико), р = 0,001 (мало). По формуле Бернулли считать сложно. Поэтому применим формулу Пуассона.
Найдем среднее число попаданий: 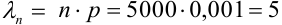
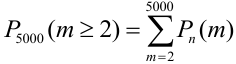
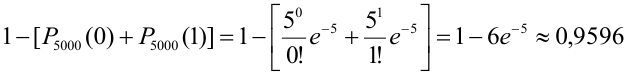
По точной формуле (формуле Бернулли) 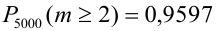
Локальная предельная теорема Муавра — Лапласа (асимптотическая формула для случая больших значений n и m)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, (0 < р < 1), то вероятность 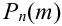

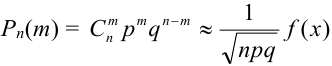
где 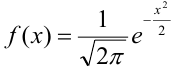
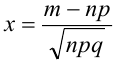
Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при 
2. Формулой пользуются при больших n и m. Например, при п > 100, 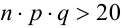
3. Из того, что 
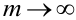
4. Существуют таблицы значений функции 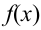
Пример №14
Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение.
Количество испытаний n = 243, количество успехов m = 70, вероятность успеха р = 0,25, вероятность неудачи q = 1 — 0,25 = 0,75.
По формуле Бернулли считать сложно. Так как n и m велики, поэтому применим формулу Муавра — Лапласа.
Найдем сначала х и 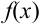
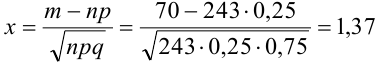
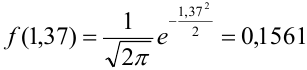
Можно было не считать значение 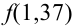
Подставим найденное значение 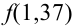
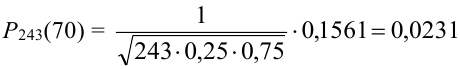
Предельная интегральная теорема Муавра — Лапласа (асимптотическая формула для случая, когда число успехов m лежит в некоторых пределах)
Теорема 1. Если m — число наступлений события А в n независимых испытаниях, в каждом из которых вероятность этого события равна р (0 < р < 1), то равномерно относительно а и b 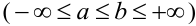
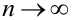
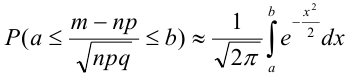
В некоторых источниках 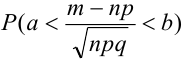
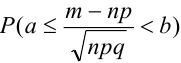
Ранее вывели, что 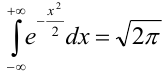
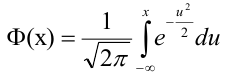
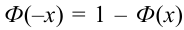
Либо, функция Лапласа может быть в виде: 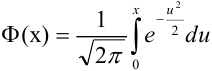
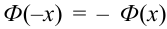
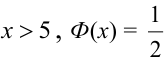
Теорема 2. (Теорема Муавра-Лапласа) Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие А наступит не менее 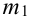
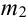
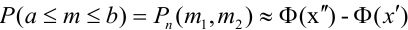
где Ф(х) — функция Лапласа, значения 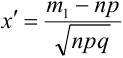
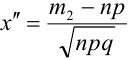
Теорема 3. (Закон больших чисел или теорема Бернулли).
При неограниченном увеличении числа однородных независимых опытов частота события будет сколь угодно мало отличаться от вероятности события в отдельном опыте.
Иначе, вероятность того, что отклонение относительной частоты наступления события 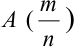
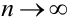
Доказательство.
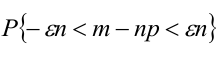
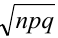
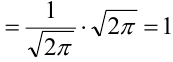
Пример №15
Вероятность появления события А в каждом из 100 независимых испытаний постоянна и равна 0,8. Найти вероятность того, что событие появиться не менее 75 раз и не более 90 раз.
Решение.
Количество испытаний n = 100, вероятность успеха р = 0,8, вероятность неудачи q = 1 — 0,8 = 0,2 , 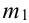
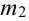
Найдем 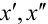
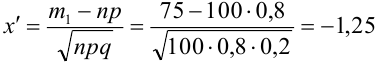
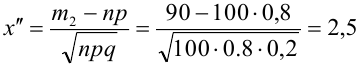
По теореме 2:
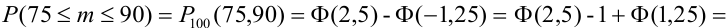
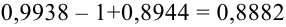
Наивероятнейшее число появления события в независимых испытаниях
Определение 28. Число 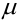
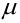
Наивероятнейшее число 
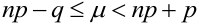
причем 1) если (np — q) -дробное, то существует одно 

Пример №16
Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержат испытание и вероятность этого числа.
Решение.
Количество испытаний n = 15, вероятность успеха р = 0,9, вероятность неудачи q = 0,1.
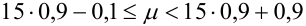
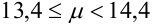
Т.к. 

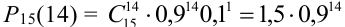
Всё о формуле полной вероятности
Пусть событие 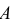
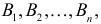
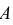
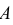
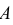
В силу несовместимости событий можно записать
Используя теорему умножения вероятностей, получаем формулу
которая и называется формулой полной вероятности.
Обычно ее записывают кратко:
Пример №17
Имеется две коробки деталей, в каждой из которых по 10 деталей. В первой коробке среди деталей две низкого сорта, а во второй четыре низкосортных детали. Из первой коробки для нужд производства взяли наугад половину деталей, а оставшиеся высыпали во вторую коробку. Через некоторое время из второй коробки взяли наугад деталь. Какова вероятность того, что это деталь низкого сорта?
Решение. Обозначим через A событие, состоящее в выборе из второй коробки детали низкого сорта. Возможность этого выбора зависит от того, какие именно детали были добавлены во вторую коробку. На этот счет можно выдвинуть следующие предположения: B1 – во вторую коробку добавили пять годных деталей; B2 – добавили одну деталь низкого сорта и четыре доброкачественные; B3 – добавили две детали низкого сорта и три доброкачественные. Пять деталей во вторую коробку можно переложить 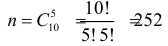
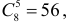
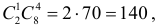
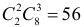
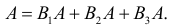

Ответ. 1/ 3.
Всё о Формуле Байеса
Пусть событие A может наступить только при появлении одного из несовместных событий 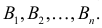

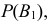
Проделан опыт, в результате которого событие A произошло. Тогда вероятности событий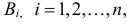
Формулы Байеса позволяют переоценивать вероятности гипотез (событий 
Пример №18
По каналу связи передается одна из последовательностей букв 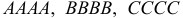
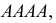
Решение. Для краткости записи формулы обозначим 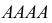
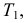
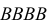
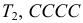
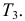
Ответ. 8/9.
Пример №19
Три стрелка производят по одному выстрелу в одну и ту же мишень. Вероятности попадания в мишень при одном выстреле для этих стрелков соответственно равны 0,8; 0,7; 0,6. Какова вероятность того, что третий стрелок промахнулся, если в мишени оказалось две пробоины?
Решение. Обозначим через А событие, состоящее в появлении двух пробоин в мишени. В отношении двух пробоин могут быть три предположения: В1 – попали первый и второй стрелки, а третий не попал, вероятность чего равна 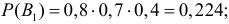
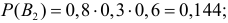
Заметим, что 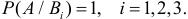
Ответ.
Пример №20
В партии из 10 изделий с равными шансами может оказаться от нуля до трех бракованных. Наугад взяли и проверили три изделия. Они оказались годными. Какова вероятность того, что остальные изделия в партии тоже годные?
Решение. Насчет содержания в партии бракованных изделий по условиям задачи может быть четыре предположения 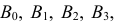
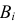
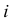
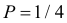
Заметим, что 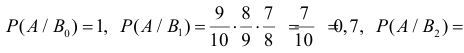
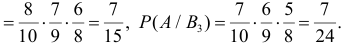
Ответ.
Пример №21
Вероятность того, событие B произойдет в течение часа, равна 0,9. Оказалось, что в течение первых 40 мин. событие B не произошло. Какова вероятность того, что это событие появится в оставшиеся 20 мин. времени?
Решение. В отношении события 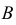
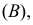
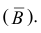
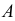
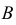
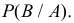
В задаче по умолчанию предполагается, что событие 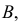
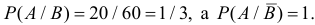
Ответ. 3/4.
Пример №22
В кошельке лежат четыре монеты. Три монеты обычных, а у четвертой на той и другой стороне изображен герб. Наугад взяли монету и подбросили три раза. Все три раза выпал герб. Какова вероятность того, что и при четвертом подбрасывании выпадет герб?
Решение. Обозначим через B1 – выбор монеты с одним гербом, через B2 – выбор монеты с двумя гербами. Априорные вероятности этих событий равны: 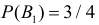
Обозначим через A – выпадение трех гербов подряд. Апостериорные вероятности по формулам Байеса равны:
Тогда по формуле полной вероятности (2.4.1):
P(выпадения герба в четвертый раз)
Ответ.
Подробное объяснение формулы полной вероятности
Постановка задачи: Пусть 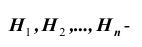
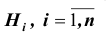


Требуется найти вероятность события A.
Выведем формулу решения этой задачи. Имеем
маршрутов (схема дорог). Какова вероятность того, что он попадет в пункт А ?
Решение. Как видим из схемы дорог, путь туриста обязательно проходит через один из пунктов 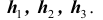
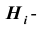
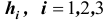
Заметим, что события (гипотезы)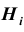
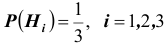
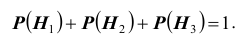
видеть (см. схему), что 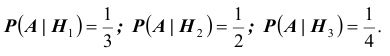
Пример №23 (о мудреце и властелине).
Властелин, разгневавшись на мудреца, приказал отрубить ему голову. Но затем, смягчившись, дал мудрецу возможность попытаться спастись. Итак, властелин взял 2 белых и 2 черных шара и предложил мудрецу распределить их по своему усмотрению по двум одинаковым урнам. После чего, палач сначала наугад выберет одну из урн, а затем также наугад, не глядя, вытащит из неё один шар. Мудрец будет помилован, если вытянутый шар оказался белым. Какую стратегию распределения шаров по урнам должен
выбрать мудрец, чтобы быть помилованным? Какова максимальная вероятность спастись мудрецу? Какая стратегия наименее выгодна для него?
Решение. Выдвинем гипотезы (предположения) 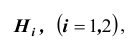
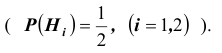
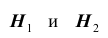
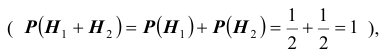
палачом вытянут белый шар. Далее, рассмотрим следующие варианты распределения мудрецом шаров по
урнам:
1). В первой урне 2 белых, а во второй 2 черных шара. Тогда
2 Хотим заметить, что далеко не всегда властелины были глупыми людьми, не знающими математики. Так, например, Наполеон был немного математиком, интересовался, в частности, геометрией. Он вёл дискуссии с Лагранжем и Лапласом, когда ещё не был правителем Франции.
Как-то в одной из таких дискуссий Лаплас резко оборвал Бонапарта: «Менее всего мы хотим от Вас, генерал, урока геометрии». В дальнейшем Лаплас стал его главным военным инженером. Наполеону приписывают теорему: «Если на сторонах произвольного треугольника во внешнюю сторону построены равносторонние треугольники, то их центры образуют равносторонний треугольник» — это так называемый вешний треугольник Наполеона.Так же ему приписывают один из знаменитых палиндромов (читается в обе стороны одинаково): «ABLE WAS I ERE I SAW ELBA» — я был силён, пока не увидел Эльбу.
2). В первой и во второй урнах по 1 белому и 1 черному шару. Тогда
3). В первой урне 1 белый, а во второй 1 белый и 2 черных шара. Тогда
4). В первой урне 1 черный, а во второй 2 белых и 1 черный шары. Тогда
5). Первая урна оказалась пустой, т.е. все шары во второй урне. Тогда
Как видим, наиболее предпочтительной является 3-я стратегия, ей соответствует вероятность быть помилованным равная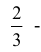
Вероятность гипотез. Формула Байеса
Постановка задачи: Пусть 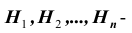
и пусть событие A может произойти лишь совместно с каким — либо одним из этих событий (гипотез) — ситуация аналогичная той, которая была ранее. И пусть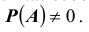
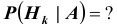
По теореме об умножении вероятностей
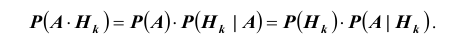
Полученная формула называется формулой Байеса (Бейеса) для переоценки гипотез. Другими словами: вероятность 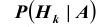
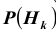
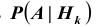
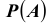
Пример №24
При обследовании больного имеется подозрение (т.е. делаются предположения или, что то же самое, выдвигаются гипотезы)
на одно из двух заболеваний 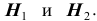
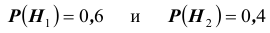
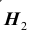
Решение. Во — первых, очевидно, что события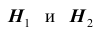
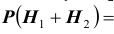
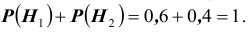
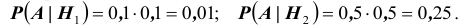
Как видим, при данных результатах обследования следует предполагать болезнь
Повторение испытаний
Формула Бернулли (схема повторения опытов)
Опыты называются независимыми , если вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты. Независимые опыты могут проводиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления какого — либо события A во всех опытах одна и та же, во втором случае — она меняется от опыта к опыту. Ниже мы воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми. Итак, пусть производится n независимых опытов в одинаковых условиях, в каждом из которых некоторое событие A может произойти с одной и той же вероятностью 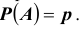
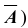
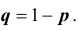
Итак, еще раз: схемой Бернулли называется последовательность n независимых испытаний, проводимых при одних и тех же условиях, в каждом из которых событие A либо происходит с постоянной вероятностью p , не зависящей от номера испытания, либо не происходит с вероятностью
Ставятся задачи:
Задача №1. Найти вероятность 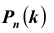
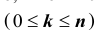
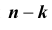
Задача № 2. Найти вероятность 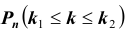
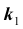
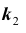
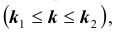
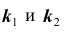
Задача № 3. Найти наивероятнейшее число 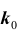
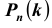
Решение №1.
Вероятность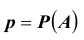
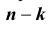
Таких несовместных событий столько, сколько сочетаний из n элементов по k элементов в каждом. Поэтому по теореме о вероятности суммы несовместных событий получим формулу, называемую формулой Бернулли:
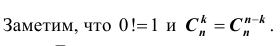
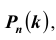
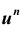
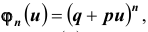
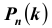
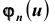
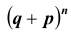
которую называют биномиальным законом распределения вероятностей события A в n испытаниях схемы Бернулли.
Заметим, что вероятность хотя бы одного появления события A в n испытаниях схемы Бернулли равна: 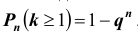
следующим вопросом: честное ли пари вам предлагают, если вы выиграете в том случае, когда при 24-х кратном бросании двух игральных костей хотя бы один раз одновременно появятся две шестёрки? Ответ дайте в конце пары.
(РЕШЕНИЕ. Вероятность одновременного выпадения двух шестерок при одном подбрасывании равна 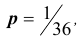
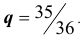
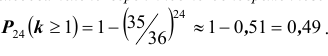
Другие примеры на применение формулы Бернулли, рассмотрим немного позднее, а именно после того, как решим задачи № 2 и № 3
Решение № 2.
Нетрудно показать, что вероятность 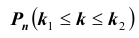
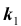
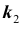
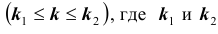
Решение № 3
Важной является задача № 3 о наивероятнейшем числе 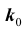
Рассмотрим отношение:
Из полученного следует, что:
1) если 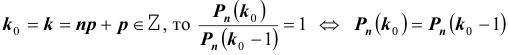
два максимума;
2) если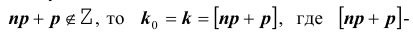
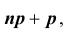
Пример №25
При некоторых условиях стрельбы вероятность p попадания в цель при одном выстреле равна
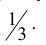
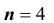
- а). Каково наивероятнейшее число попаданий в цель?
- б). Какова его вероятность?
- в). Какова вероятность двух попаданий?
- г). Какова вероятность хотя бы одного попадания?
Пример №26
Некто Сэмюэль Пепайс обратился к Исааку Ньютону с вопросом: какое из событий наиболее вероятно —
- появление по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей;
- хотя бы двух «шестерок» при подбрасывании 12-ти;
- хотя бы трех «шестерок» при подбрасывании 18-ти?
Решение.
Вероятность q непоявления «шестерки» при одном подбрасывании, как известно, равна 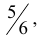
5 . Таким образом, вероятность появления по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей может быть найдена по формуле:
Событие «хотя бы две» противоположно событию «либо ни разу, либо один раз», т.е.
Событие «хотя бы три» противоположно событию «либо ни разу, либо один раз, либо два раза», т.е.
Таким образом, как видим, предпочтительнее первая стратегия – таким и был ответ Ньютона.
Замечу, что при больших значениях числа n испытаний в схеме Бернулли формула для подсчета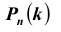
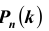
ТЕОРЕМА Пуассона 3. Пусть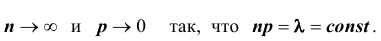
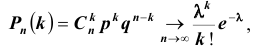
Доказательство
Что и требовалось доказать.
При доказательстве можно воспользоваться приближенной формулой Стирлинга.
Следствие: при указанных выше условиях, т.е. при 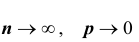
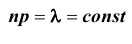
Пример №27
Телефонная станция обслуживает 800 абонентов. Для каждого абонента вероятность того, что в течении часа он позвонит на станцию равна p =0,01. Найти вероятность того, что четыре абонента позвонят на станцию в течении часа.
Решение
Теорема Муавра — Лапласа (локальная)
Остановлюсь еще на двух предельных теоремах в схеме Бернулли — локальной теореме Муавра — Лапласа (её доказательство получим как частный случай закона больших чисел — предельной теоремы Ляпунова, доказательство которой нам ещё предстоит провести) и интегральной теореме Муавра — Лапласа. Итак:
причем, во-первых, погрешность этой формулы есть величина порядка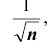
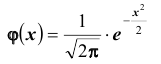
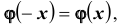
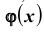
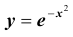
интегральная приближенная формула Лапласа ( при больших
Для функции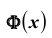
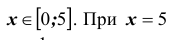
равносильно условию 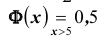
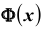
Замечание: если функция Лапласа записана в виде 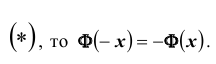
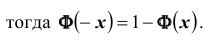
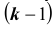
Формула полной вероятности и сложные задачи
В данном разделе мы рассмотрим более сложные задачи, имеющие большое практическое значение. Эти задачи встречается на практике в случае, если имеются несколько возможных сценариев развития событий (несколько вероятных гипотез). Известны как величины вероятности реализации каждого из сценариев, так и вероятность наступления интересующего нас события для любого из этих сценариев, а нас интересует, какова полная (совокупная) вероятность наступления интересующего нас события.
Предположим, что в результате опыта может произойти одно из n несовместных событий (гипотез) 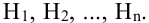
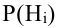
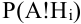
Пример №28
Из 40 деталей 10 изготовлены в первом цехе, 25 — во втором, а остальные — в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех — с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?
Решение:
Обозначим событие А = {выбрана деталь отличного качества}, Hi= {выбранная деталь изготовлена в i цехе}, i = 1, 2, 3. Тогда
По условию задачи 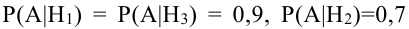
Пример №29
На рисунке изображена схема дорог. Найти вероятность того, что турист, вышедший из пункта А, попадет в пункт В, если на развилке он наугад выбирает любую дорогу (кроме обратной).
Решение:
Обозначим Нi = {приход туриста в пункт Hi}, i = 1, 2, 3, 4. Поскольку, выйдя из пункта А, он выбирает любую дорогу наугад, то 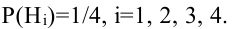
Исходя из схемы дорог, определяем, что
Таким образом, по формуле полной вероятности
Пример №30
Из двенадцати лотерейных билетов пять выигрышных. Билеты вытягиваются по одному без возвращения. Какова вероятность того, что во второй раз вытянут выигрышный билет?
Решение:
Как обычно, вдоль каждой ветви «дерева вероятностей» значения вероятностей перемножаются, а затем значения на концах нужных веток между собой складываются. В результате получаем ответ:
Случайные события независимые в совокупности
Следует различать попарно независимые случайные события и случайные события независимые в совокупности.
Определение: События называются попарно независимыми событиями, если любые два из них независимы.
Определение: События 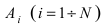
Замечание: Из определений видно, что из попарной независимости еще не следует, что эти события независимы в совокупности. Это означает, что условие независимости в совокупности является более сильным, чем условие попарной независимости случайных событий.
Теорема: Вероятность наступления хотя бы одного из событий 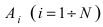
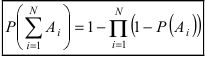
Доказательство: Обозначим через А событие, состоящее в том, что наступит хотя бы одно из событий 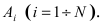
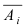
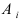
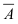
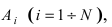
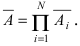
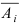
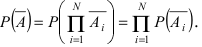
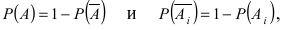
Пример №31
Пусть прибор содержит N последовательно соединенных блоков. Определить вероятность того, что цепь будет разорвана, если вероятность работы каждого блока равна р и она не зависит от работы других блоков.
Решение:
Пусть А — событие, которое состоит в том, что данная цепь разорвана. Это событие происходит, если выходит из строя хотя бы один из блоков, так как блоки включены последовательно. Противоположное событие состоит в том, что все блоки работают, т.е. 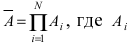
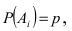
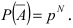
Теорема сложения вероятностей для совместных событий
Если случайные события одновременно появляются в условиях опыта, то имеет место следующая теорема.
Теорема: Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их произведения:
Доказательство: Пусть в результате опыта возможно n равно возможных, несовместных, элементарных исходов. При этом в 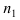
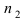
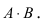
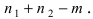
Замечание: Методом математической индукции вышеприведенная теорема может быть обобщена на любое число совместных событий, например, в случае 3 совместных событий А, В и С теорема принимает вид:
Пример №32
Найти вероятность того, что взятое наугад число из чисел от 10 до 20 делится или на 2, или на 3.
Решение:
Всего равновозможных, элементарных исходов 11 (числа от 10 включительно до 20 включительно). В 6 случаях (10, 12, 14, 16, 18, 20) число кратно 2; в 3 случаях (12, 15, 18) число кратно 3; в 2 случаях (12, 18) число кратно и 2, и 3. Пусть событие А состоит в том, что наугад взятое число кратно 2, а событие В состоит в том, что наугад взятое число кратно 3. Сложное событие С состоит в том, что наугад взятое число делится или на 2, или на 3, т.е. С = А + В. Следовательно, вероятность этого события равна:
Все вышерассмотренные теоремы объединяются в теории вероятностей общим названием “основные теоремы теории вероятностей”.
Формула полной вероятности и события
Формула полной вероятности является следствием основных теорем теории вероятностей: теорем сложения и умножения вероятностей событий.
Пусть некоторое случайное событие А наступает с одним и только с одним из несовместных событий
Определение: События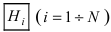
Теорема: Формула полной вероятности определяет вероятность случайного
события л, как сумму произведений вероятности каждой гипотезы 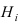
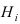
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 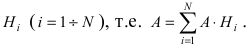
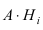
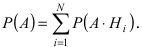
Пример №33
Пусть на сборку поступают детали с двух автоматических станков. Первый станок дает в среднем 0.3 % брака, а второй — 0.15 % брака. Производительность второго станка в два раза выше, чем первого станка. Найти вероятность того, что наугад взятая деталь окажется бракованной.
Решение:
Пусть событие А состоит в том, что наугад взятая деталь окажется бракованной. Тогда гипотеза 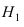
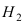
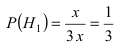
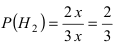
Вероятности события А при условии реализации первой и второй гипотез равны: 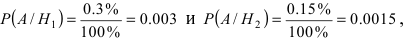
Формула вероятностей гипотез (формула Байеса)
Ниже будет получена формула, которая является следствием основных теорем теории вероятностей и формулы полной вероятности. Эта формула применяется для решения задач следующего типа. Пусть проводится эксперимент, в результате которого может появиться или не появиться событие л, которое наступает с одним и только с одним из несовместных событий 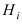
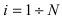
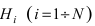
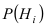
Теорема: Вероятность гипотезы 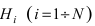
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 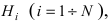
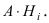
Следовательно, 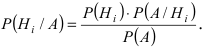
Пример №34
Однотипные пластмассовые детали изготавливаются на 3 прессах. Первый пресс выпускает 50 % всех деталей, второй — 40 %, третий — 10 % . При этом с первого пресса сходит в среднем 0.025 нестандартных деталей, со второго — 0.02 и с третьего — 0.015. Все детали поступают на сборку. Взятая наудачу деталь оказалась нестандартной. Какова вероятность того, что она изготовлена на первом прессе.
Решение:
Событие А состоит в том, что наудачу взятая деталь изготовлена на первом прессе. Гипотеза 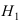
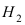
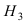
По условию задачи 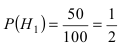
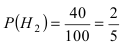
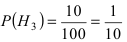
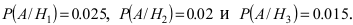
Используя формулу Байеса, получим
Независимые испытания и формула Бернулли
Пусть испытания повторяются n раз, причем событие А появляется в каждом опыте с одной и той же вероятностью р или не появляется с одной и той же вероятностью
Определение: Испытания называются независимыми, если вероятность события А не зависит от того, какие события появились в предыдущих опытах, или появятся в последующих экспериментах.
Пример:
Независимы ли следующие испытания: а) многократное бросание кубика; б) извлечение карты из колоды без ее возвращения в колоду (выяснить самостоятельно).
Формула Бернулли
Теорема: Пусть проводится серия из n независимых испытаний, в каждом из которых событие А появляется с постоянной вероятностью 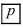
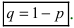
Доказательство: Пусть 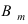
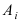
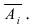
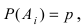
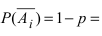
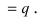
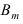
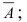
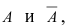
Воспользуемся теоремой умножения вероятностей для независимых событий, получим: 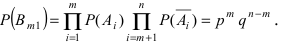
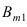
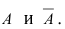
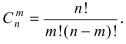
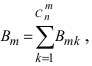
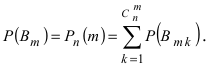
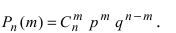

Пример №35
Монета подбрасывается 6 раз. Определить вероятность того, что герб выпадет а) 5 раз; б) от 2 до 4 раз.
Решение:
Вероятность выпадения герба не изменяется от опыта к опыту и равна 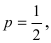
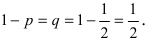
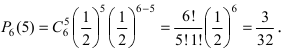
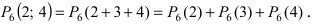
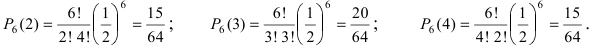
При больших значениях чисел m и n применение формулы Бернулли затруднительно, так как вычисление коэффициентов 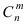
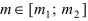
Формула Пуассона
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А мала (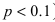
Формулы Муавра-Лапласа
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А р>0.1, то при больших значениях чисел m и n применяют дифференциальную формулу Муавра-Лапласа: 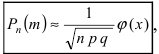
Замечание: В общем случае дифференциальная формула Муавра-Лапласа применяется при выполнении неравенств
Если при проведении серии испытаний по схеме Бернулли числа m и n принимают большие значения, причем число m принимает значения от 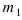
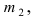
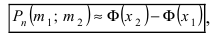
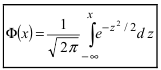
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Теоремы сложения и умножения вероятностей
АННОТАЦИЯ
С использованием генератора случайных чисел исследованы зависимости ошибки в определении показателей кучности спортивной винтовки от числа выстрелов в группе m и числа групп n при стрельбе группами.
На основе проведённых статистических исследований кучности стрельбы по мишеням построены простые таблицы кучности, позволяющие по количеству выстрелов в группе и количеству групп определить ошибку таких показателей кучности, как средний радиус и среднее квадратичное значение радиуса точек попаданий в мишень.
Полученные таблицы будут полезны для практического использования не только спортсменам, увлекающимся стрельбой по мишеням, но и охотникам и любителям спортивной стрельбы, желающим правильно оценить кучность своих винтовок.
ABSTRACT
Using a random number generator, the dependences of the error in determining the accuracy of a sports rifle on the number of shots in group m and the number of groups n when shooting in groups were investigated.
Based on the conducted statistical studies of accuracy of target shooting, simple accuracy tables are constructed that allow determining the error of accuracy indicators such as the average radius and the average quadratic value of the radius of the points of hits to the target by the number of shots in a group and the number of groups.
The resulting tables will be useful for practical use not only for athletes who are fond of target shooting, but also for hunters and sports shooting enthusiasts who want to correctly assess the accuracy of their rifles.
Ключевые слова: показатель кучности, генератор случайных чисел, спортивная винтовка, оценка кучности, таблица кучности.
Keywords: accuracy index, random number generator, sports rifle, accuracy score, accuracy table.
Кучность спортивной винтовки является одним из самых важных ее качеств. Очень популярным показателем кучности винтовки является экстремальный размер группы [1,2,4,5,9,11,17]. Однако, наряду с простотой и другими достоинствами, у него есть и недостатки, такие как невысокая информативность и большая чувствительность к максимальным отклонениям пробоин. В этом плане большей информативностью и устойчивостью обладают показатели среднего радиуса Rcp и среднего квадратичного размера радиуса RSD точек попадания в мишень, поскольку они учитывают не только крайние, но и все остальные пробоины [5,13,14]. Более сложная структура показателей Rcp и RSD, трудности с их измерениями и вычислениями до недавнего времени были препятствием к их применению, несмотря на большую информативность и точность, однако с появлением программ сканирования и обработки мишеней типа GRT, On Target TDS, subMOA Pro [15,22] проблема расчета этих показателей перестала существовать, что увеличило перспективы их использования. В связи с этим стала актуальной задача планирования оценки кучности по более информативным показателям. Рассмотрим особенности указанной задачи и возможные способы ее решения.
Распределение пробоин по мишени носит вероятностный характер. Соответственно, кучность — это статистический показатель, имеющий вероятностные границы, связанные с количеством выстрелов и выбранной доверительной вероятностью оценки.
Допустим, по 10 выстрелам получена выборочная точечная оценка среднего радиуса попаданий 0.5 МОА. Понятно, что формулировка «кучность равна 0.5 МОА» будет неправильной, потому что мы не знаем, что она равна 0.5 МОА, мы лишь имеем результаты одного отстрела с оценкой 0.5 МОА, то есть, одно из возможных значений кучности из некоторого вероятного диапазона. Повторив стрельбу много раз, мы увидим, что каждый раз следующая оценка кучности будет отличаться от первой. Вычислив дисперсию этой оценки по многим опытам, мы увидим, что статистическая ошибка в определении кучности для 10 выстрелов с доверительной вероятностью 0.9 составляет, например, 20%. Тогда истинное значение кучности лежит в диапазоне (0.4-0.6) МОА. Учитывая, что заход за нижний предел 0.4 это хорошо, можно опустить его. Тогда полная формулировка будет звучать так: «по 10 выстрелам мы с вероятностью 90% уверены, что кучность винтовки не хуже 0.6 МОА». Это, конечно, не значит, что такая винтовка. Это значит, что количество выстрелов недостаточно, чтобы уверенно говорить о ещё лучшей кучности. Добавив ещё 10 выстрелов, мы сузим диапазон неопределенности и сможем сказать: мы на 90% уверены, что по результатам обработки 20 выстрелов истинное значение кучности лежит в диапазоне (0.45 — 0.55) МОА.
Если мы вместо 10 выстрелов будем делать 2 серии по 5 выстрелов, оценка кучности изменится, значения, полученные по 10 выстрелам одной серией и по 5 выстрелам двумя сериями окажутся несопоставимы. Таким образом, величина показателя и точность его оценки оказывается связанной со структурой и количеством выстрелов.
Целью данной работы являлось исследование доверительных интервалов распределения пробоин на мишени и создание простого способа оценки кучности стрельбы по показателям Rcp и RSD при стрельбе группами в зависимости от числа выстрелов в группе m и числа групп n.
Средний радиус точек попадания Rcp определяется как среднее отклонение точек попадания (пробоин) относительно выборочной средней точки попадания (СТП). СТП группы определяется несколькими известными способами [20,21]. Для определения кучности с высокой достоверностью необходимо произвести большое число выстрелов. Но если много стрелять в одну мишень, зона попаданий на мишени превратится в одно сплошное пятно, и замерить все радиусы точек попадания не будет никакой возможности. Выходом из этой ситуации является стрельба группами по разным мишеням. При этом возникает вопрос, как объединять результаты выстрелов, полученные на разных мишенях? При объединении мишеней по общей точке прицеливания трудностей не возникает. Они просто накладываются одна на другую, после чего пересчитывается общая СТП и от неё рассчитываются расстояния до каждой пробоины. Но, например, в бенчресте, или при перенастройке прицела после каждой группы, или при изучении мишеней с неполной информацией общей точки прицеливания как бы не существует, она неизвестна. Для такого случая математически корректная задача состоит в объединении координат пробоин на всех мишенях с совмещением по их выборочным СТП, пересчету радиусов по новой совместной СТП и постоянной коррекции общей СТП и радиусов по мере добавления все новых групп. Однако такая задача содержит неопределенность интервала нахождения истинного значения СТП и главное, совершенно непрактична в использовании. Поэтому мы выбрали более простой и более практичный показатель кучности, такой как «средний средних» радиусов или «среднее средних» квадратичных радиусов, получаемых простым сложением этих радиусов по каждой группе и делением суммы на количество групп.
Для решения поставленной задачи мы приняли предположение, что распределение пробоин на мишенях подчиняется двумерному нормальному распределению, или распределению Рэлея [6,7,8,10,19].
Сумма средних радиусов каждой группы подчиняется теореме Чебышева [3,20], в соответствии с которой выборочное значение суммы средних радиусов, делённое на количество членов суммы, с увеличением числа групп n стремится к его математическому ожиданию, а дисперсия среднего радиуса стремится к 0. Заданным значениям m и n соответствует заданное значение дисперсии среднего радиуса. При этом коэффициент вариации v зависит только от числа выстрелов в группе m и числа групп n [1,2,18]. Это позволяет создать простые таблицы кучности, по которым можно в зависимости от числа выстрелов в группе m и числа групп n определять точность показателя Rcp, или по точности показателя Rcp планировать количество групп m и число выстрелов в группе n.
Наши исследования с применением генератора случайных чисел [1,2,8,19,12] показали, что ошибка в определении истинного значения показателя Rcp больше зависит от общего числа выстрелов, чем от числа выстрелов в группе.
На рис. 1 приведены зависимости показателя Rcp от количества групп в серии n при различных значениях выстрелов в группе m (рис.1а) и от общего количества выстрелов k (рис.1б). Закономерности поведения функций Rcp(k) при разных m похожи. Функции Rcp(m, n) стабилизируются примерно к 15-20 выстрелам.
|
|
|
|
а) |
б) |
Рисунок 1. Зависимость Rcp от общего количества групп в серии n (а) и от общего числа выстрелов (б)
Однако само значение показателя Rcp зависит от количества выстрелов m в группе. Полученные значения показателя Rcp при разном количестве выстрелов в группе m несопоставимы между собой и могут сравниваться только c использованием коэффициентов приведения.
На рис. 2 приведены зависимости СКО (дисперсии) показателя Rcp от общего количества групп в серии n (рис. 2а) и общего количества выстрелов k (рис. 2б). Сходимость функций к низкой дисперсии достигается примерно за 10-30 выстрелов [5,9,11,17,24].
Динамика изменения показателя Rcp и дисперсии хорошо наблюдается на рис. 3, где представлены данные об изменении численных значений Rcp для 100 независимых циклов испытаний по 50 серий в каждом для серий по 2 выстрела (рис.3а) и для серий по 10 выстрелов (рис.3б). С ростом числа выстрелов в группе в диапазоне до 10-30 выстрелов дисперсия Rcp резко уменьшается, а затем переходит в стадию все более медленного нелинейного уменьшения. При этом для начального периода испытаний с ростом m характерно уменьшение дисперсии.
|
|
|
|
а) |
б) |
Рисунок 2. Зависимость дисперсии (СКО) показателя Rcp от общего количества групп в серии n (а) и общего количества выстрелов k (б)
|
а) |
|
|
б) |
|
Рисунок 3. Случайные реализации показателя Rcp для 100 независимых испытаний в зависимости от количества серий выстрелов при m = 2 (a) и m = 10 (б)
На основе указанных исследований разработана простая таблица кучности, связывающая точность определения показателя кучности Rcp c числом выстрелов в группе m и числом групп n (табл. 1).
Таблица 1.
Взаимосвязь ошибки оценки показателя Rcp с числом выстрелов в группе и числом групп
|
Количество выстрелов в серии |
|||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
10 |
||
|
Требуемая точность оценки кучности, % |
50% |
2 |
1 |
1с |
1 |
1 |
1 |
1 |
1 |
|
45,00% |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
40,00% |
4 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
35,00% |
4 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
30,00% |
5 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
25,00% |
7 |
3 |
2 |
2 |
2 |
2 |
1 |
1 |
|
|
20,00% |
11 |
4 |
3 |
3 |
3 |
2 |
2 |
1 |
|
|
19,00% |
12 |
4 |
3 |
3 |
3 |
3 |
2 |
1 |
|
|
18,00% |
15 |
5 |
4 |
3 |
4 |
3 |
2 |
2 |
|
|
17,00% |
15 |
6 |
4 |
4 |
4 |
3 |
2 |
2 |
|
|
16,00% |
17 |
7 |
4 |
4 |
4 |
4 |
3 |
2 |
|
|
15,00% |
18 |
8 |
5 |
5 |
5 |
4 |
3 |
2 |
|
|
14,00% |
21 |
9 |
5 |
5 |
5 |
4 |
3 |
3 |
|
|
13,00% |
24 |
11 |
6 |
6 |
6 |
5 |
4 |
3 |
|
|
12,00% |
31 |
13 |
7 |
6 |
7 |
5 |
5 |
3 |
|
|
11,00% |
39 |
15 |
8 |
7 |
7 |
6 |
6 |
5 |
|
|
10,00% |
44 |
10 |
9 |
8 |
8 |
7 |
7 |
6 |
|
|
9,00% |
19 |
12 |
11 |
10 |
9 |
8 |
7 |
||
|
8,00% |
26 |
12 |
14 |
12 |
11 |
9 |
8 |
||
|
7,00% |
35 |
17 |
18 |
16 |
14 |
12 |
9 |
||
|
6,00% |
49 |
27 |
21 |
20 |
18 |
16 |
12 |
||
|
5,00% |
36 |
33 |
32 |
24 |
20 |
18 |
|||
|
4,00% |
47 |
36 |
33 |
31 |
Вторым показателем кучности мы рассматриваем средний квадратичный размер радиусов RSD относительно СТП. Он более сложный и в большей степени учитывает влияние наиболее удаленных пробоин, чем показатель Rcp. Задача решается аналогично предыдущей, только в качестве суммируемых данных фигурирует показатель RSD каждой новой выборки и выполняются необходимые преобразования на каждом шаге суммирования.
Сумма квадратов радиусов подчиняется той же закономерности, что и сумма средних радиусов. На рис. 4 приведены зависимости показателя RSD от общего количества групп в серии n (рис. 4а) и общего количества выстрелов k (рис. 4б).
|
|
|
|
а) |
б) |
Рисунок 4. Зависимость показателя RSD от числа серий (а) и от общего количества выстрелов k (б)
Такие же закономерности мы видим в поведении среднего квадратичного отклонения (рис.5) и динамики зависимости дисперсии показателя RSD от количества выстрелов в группе и количества серий (рис.6).
|
|
|
|
а) |
б) |
Рисунок 5. Зависимость дисперсии (СКО) показателя RSD от количества серий n (а) и общего количества выстрелов k (б)
|
а) |
|
|
б) |
|
Рисунок 6. Случайные реализации показателя RSD для 100 независимых испытаний в зависимости от количества серий выстрелов при m = 2 (a) и m = 10 (б)
Табл. 2 является аналогом табл. 1 и содержит данные о необходимом количестве групп выстрелов для обеспечения заданной точности по показателю RSD.
Таблица 2.
Взаимосвязь ошибки оценки показателя RSD с числом выстрелов в группе и числом групп
|
Количество выстрелов в серии |
|||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
10 |
||
|
Требуемая точность оценки кучности, % |
50% |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
45,00% |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
40,00% |
3 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
35,00% |
4 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
30,00% |
5 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
25,00% |
7 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
|
|
20,00% |
11 |
4 |
2 |
2 |
2 |
2 |
1 |
1 |
|
|
19,00% |
11 |
4 |
2 |
3 |
3 |
2 |
2 |
1 |
|
|
18,00% |
11 |
4 |
2 |
3 |
3 |
2 |
2 |
1 |
|
|
17,00% |
15 |
5 |
3 |
3 |
3 |
3 |
2 |
1 |
|
|
16,00% |
16 |
6 |
3 |
4 |
4 |
3 |
2 |
1 |
|
|
15,00% |
17 |
7 |
3 |
4 |
4 |
3 |
2 |
1 |
|
|
14,00% |
18 |
8 |
4 |
4 |
4 |
4 |
3 |
1 |
|
|
13,00% |
21 |
9 |
5 |
5 |
5 |
4 |
3 |
2 |
|
|
12,00% |
24 |
11 |
6 |
6 |
6 |
5 |
4 |
2 |
|
|
11,00% |
27 |
14 |
7 |
7 |
7 |
5 |
5 |
3 |
|
|
10,00% |
40 |
17 |
8 |
7 |
7 |
6 |
6 |
5 |
|
|
9,00% |
45 |
19 |
9 |
8 |
8 |
7 |
7 |
6 |
|
|
8,00% |
24 |
12 |
11 |
11 |
9 |
8 |
7 |
||
|
7,00% |
31 |
18 |
15 |
15 |
11 |
9 |
8 |
||
|
6,00% |
42 |
22 |
19 |
18 |
15 |
14 |
9 |
||
|
5,00% |
31 |
25 |
24 |
19 |
18 |
14 |
|||
|
4,00% |
44 |
38 |
36 |
32 |
24 |
20 |
Какие выводы мы можем сделать из проведённых исследований?
Сравнение показателей Rcp и RSD показывает, что они ведут себя во многом схоже. Информативность показателей примерно одинаковая. Показатель RSD демонстрирует более высокую сходимость по точности, но вместе с тем, он более сложный в расчетах и менее понятный в интерпретации. Поэтому на данном этапе исследований мы бы не отдавали предпочтения показателю RSD.
Нужно обратить внимание, что для достижения высокой точности показателей Rcp и RSD необходимо нереально большое количество выстрелов. Даже для достижения не самой высокой точности 5% требуется около 150 выстрелов. Поэтому мы не советуем стремиться к очень высокой точности и екомендуем оптимальный диапазон ошибки 10-20%, соответствующий 10-30 выстрелам.
Стремиться к высокой точности не стоит также из-за того, что при разработке модели сделан ряд предположений о распределении пробоин, которые в действительности могут быть не совсем точны в области низких вероятных диапазонов. Достигнуть высокой точности показателей кучности Rcp и RSD и быть уверенным в ней возможно только при специальных исследованиях кучности с очень большим количеством реальных выстрелов после их тщательной статистической обработки.
Меньше 10 выстрелов мы бы также не рекомендовали из-за слишком большой ошибки.
Используя таблицы, мы можем делать разные утверждения. Реальность состоит в том, что истинное значение кучности с заданной доверительной вероятностью расположено между двумя числами. Но, как мы думаем, учитывая, что выход за нижний предел — это хорошо, лучше записать односторонний предел, например: мы на 80% уверены, что кучность не хуже чем Rcp·(1 + k·v) МОА. На наш взгляд, односторонний предел будет восприматься стрелками легко и однозначно. Но и это не все предложения.
Мы хорошо понимаем, что стрелки, будучи конкретными людьми, тяготеют к детерминистическому мышлению, им непонятен и некомфортен сам факт представления кучности неким расплывчатым диапазоном. Они хотят видеть одну цифру. Второе, что они хотели бы делать, это не тратить слишком большое количество боеприпасов на оценку кучности. Идя навстречу их желаниям, мы предлагаем считать минимально достаточной точность 20% и вводим три показателя — R3, R5 и R10. Для получения оценки кучности R3, R5 и R10 нужно будет на выбор отстрелять соответственно 4 серии по 3 группы, 2-3 серии по 5 групп или 1 серию из 10 выстрелов. Если будет выполнено одно из этих условий, то можно будет сказать, что кучность, например, R5 = 0.5 МОА. То, что она определена с ошибкой 20% при доверительной вероятности 0.8 можно по умолчанию опустить. Думаем, такое предложение устроит стрелков. Значения кучностей, определенные по разному числу выстрелов в группе, будут несопоставимы между собой. Коэффициенты приведения к группе 5 будут иметь следующие значения: k5/3 = 1,01 и k5/10 = 0,90 для показателя Rcp·; k5/3 = 1,09 и k5/10 = 0,94 для показателя RSD. Для ещё большего упрощения мы бы предложили один показатель R5 и 3 группы по 5. Можно, наконец, пойти ещё дальше и предложить определять кучность по 10 выстрелам, сделанным в любой конфигурации групп.
Наиболее часто используемыми для оценки кучности спортивных винтовок являются группы по 3, 5 или 10 выстрелов. Хотя мы допускаем, что практические соображения могут внести свои коррективы.
ПРИМЕР 1. Определим по табл. 1 количество групп при стрельбе группами по 5 для оценки кучности с ошибкой не хуже 15%. Заходим в табл. 1, по пересечению точности 15% и числу выстрелов в группе 5 видим соответствующее им цифру количества групп, равную 5. Отстреляв 5 групп по 5, мы получили, например, оценку кучности 0.5 МОА. Прибавляя к этой цифре 15%, мы получаем, что оценка кучности не хуже 0.58 МОА. Или оценка 0.5 МОА с точностью 15%.
ПРИМЕР 2. Определим общее количество выстрелов для оценки кучности с точностью 10%. Заходим, например, в табл. 2 и по требуемой точности 10%, определяем серий и количество выстрелов. Для группы с m=7 находим, что требуется выполнить отстрел 6 серий, что соответствует 42 выстрелам; для группы с m=6 находим, что требуется выполнить отстрел 7 серий, что так же соответствует 42 выстрелам. При выполнении отстрелов группами по 5 выстрелов получаем, что необходимое количество групп равно 7, а общее количество выстрелов уменьшается и равно 35. Выбор для последующих испытания типа групп, обеспечивающих минимальное необходимое количество выстрелов, позволяет оптимизировать процесс испытаний.
Выводы
- Проведены исследования ошибок оценки показателей кучности Rcp и RSD с помощью генератора случайных чисел в зависимости от числа выстрелов в группе m и числа групп n.
- Выявленные закономерности позволили создать простые и понятные таблицы для оценки точности показателей кучности Rcp и RSD в зависимости от числа выстрелов в группе и числа групп.
- Созданные таблицы могут быть использованы в качестве основы стандарта или сертификата оценки кучности спортивных винтовок, а также охотниками и любителями спортивной стрельбы.
- Предложено упростить оценку кучности введением стандартов R3, R5 или R10, не требующих записи интервалов при соблюдении требований по числу выстрелов в группе и числу групп.
Список литературы:
- Богословский В. Н., Кадомкин В.В. Метод оценки кучности нарезного гражданского оружия // Universum: технические науки. — 2022.-№11(104)
- Богословский В. Н., Кадомкин В.В., Жуков И.Г. Показатели кучности нарезного гражданского оружия // Universum: технические науки. — 2022.-№11(104)
- Вентцель Е. С. Теория вероятностей; Учебник для вузов. — 6-е изд. — М.: «Наука», 1999 — 576с.
- ГОСТ 25291–82 Винтовки малокалиберные произвольные. Основные параметры и общие технические требования // [Электронный ресурс] URL https://standartgost.ru/g/%D0%93%D0%9E%D0%A1%D0%A2_25291-82?ysclid=la1jj6kwr2345870310 (Дата обращения 03.11.2022)
- Group Sizes & Statistics By «Joe B.» // [Электронный ресурс] URL www.castpics.net https://castpics.net/subsite2/GeneralReference/ GroupSizesandStatsbyJB.pdf (Дата обращения 03.11.2022).
- Двумерный закон распределения случайной величины //Wikipedia [Электронный ресурс] URL www.wikipedia.org . (Дата обращения 20.10.2022).
- Двухмерное нормальное распределение // Bstudy.net [Электронный ресурс] URL www.bstudy.net. (Дата обращения 20.10.2022).
- Дроздова И. И., Жилин В. В. Генераторы случайных и псевдослучайных чисел // Технические науки в России и за рубежом: материалы VII Междунар. науч. конф. (г. Москва, ноябрь 2017 г.). — Москва: Буки-Веди, 2017. — С. 13–16. — URL: https://moluch.ru/conf/tech/archive/286/13233 . (Дата обращения: 20.10.2022).
- Geladen. Разбросало кучу // www.geladen.livejournal.com. [Электронный ресурс] URL https://geladen.livejournal.com/tag/%D1%80%D0%B0%D0%B7%D0%B1%D1%80%D0%BE%D1%81%D0%B0%D0%BB%D0%BE%20%D0%BA%D1%83%D1%87%D1%83. (Дата обращения 20.10.2022).
- Законы распределения случайных величин [Электронный ресурс] URL ru.wikipedia.org (Дата обращения 03.11.2022).
- Записки Флинта: два, три, четыре, пять…// Оружейный форум [Электронный ресурс] URL https://guns.allzip.org/topic/2/483355.html . (Дата обращения 20.10.2022).
- Кадомкин В.В. Применение численных методов в теории надежности систем защиты: Учебно-методическое пособие / Кадомкин В.В., Журавлев, С. И., Трубиенко О.В. — М.: МИРЭА – Российский технологический университет, 2020 -144с.
- Наставление по стрелковому делу. Основы стрельбы из стрелкового оружия. -М.: Военное издательство, 1984 -177с.
- Наставление по стрелковому делу СВД // [Электронный ресурс] URL https://coollib.com/b/224033/read?ysclid=la1jcem2fs500788041 (Дата обращения: 03.11.2022).
- OnTarget TDS // [Электронный ресурс] URL https://ontargetshooting.com/ontarget-tds (Дата обращения 03.11.2022)
- Официальная мишенная система //Арсенал-Инфо. [Электронный ресурс] URL https://arsenal-info.ru/b/book/1407702771/14 . (Дата обращения 20.10.2022).
- Chris Long, AKA techshooter. Статистический анализ размера групп // 6mmbr.com [Электронный ресурс] URL https://forum.accurateshooter.com/threads/group-analysis.3888603. (Дата обращения 20.10.2022).
- Связь полярных координат с прямоугольными // Matematicus.ru. net [Электронный ресурс] URL www.matematicus.ru . (Дата обращения: 20.10.2022).
- Слеповичев И.И. Генераторы псевдослучайных чисел //Studylib. [Электронный ресурс] URL https://studylib.ru/doc/6222742/slepovichev-i.i.-generatory-psevdosluchaynyh-chisel-2017-1 . (Дата обращения: 20.10.2022).
- Статистика для стрелков. PrecisionRifleBlog.com [Электронный ресурс] URL .https://translated.turbopages.org/proxy_u/en-ru.en.6a7bfd3b-63594fb5-3f36a848-74722d776562/https/precisionrifleblog.com /2020/12/12/measuring-group-size-statistics-for-shooters. (Дата обращения: 20.10.2022).
- Статистические оценки параметров генеральной совокупности //Высшая математика для заочников и не только [Электронный ресурс] URL http://mathprofi.ru/matematicheskaya_statistika.html . (Дата обращения: 20.10.2022)
- TARAN. Инструкция по эксплуатации // Guns@Ptosis [Электронный ресурс] URL guns.ptosis.ch. (Дата обращения 20.10.2022).
- Bryan Litz. Accuracy and Precision for Long Range Shooting: A Practical Guide for Riflemen. Applied Ballistics LLC, 2011.-578 p.
- Choosing the most accurate ammunition is probably. Jeroen Hogema May 2006/April 2019 // [Электронный ресурс] URL info@sport-shooters-OTS.com (Дата обращения 03.11.2022)


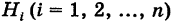
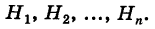
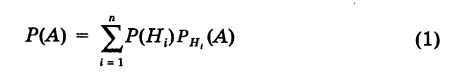

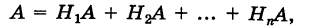
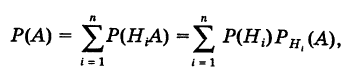
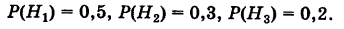
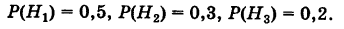
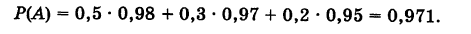
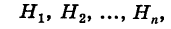
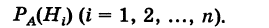
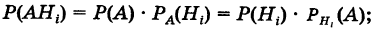
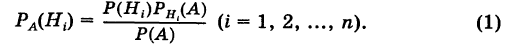
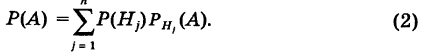
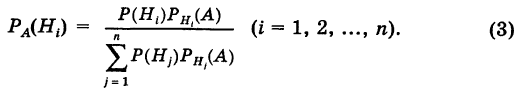
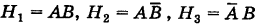
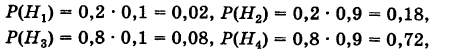
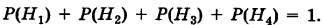
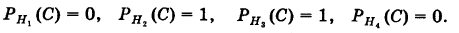
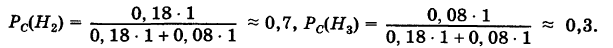
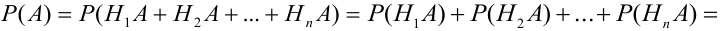
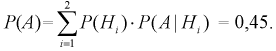
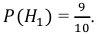
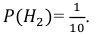
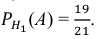
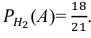
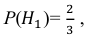
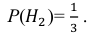
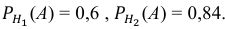
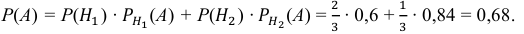
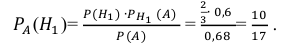
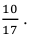
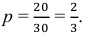
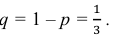
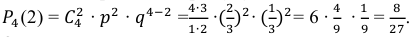
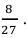
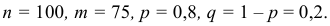
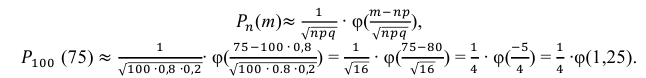
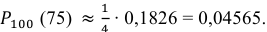
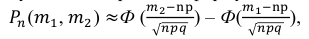
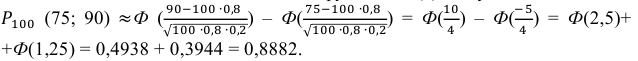
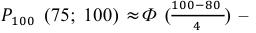
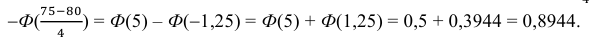
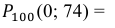
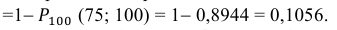
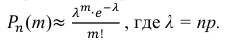
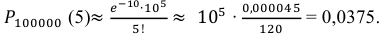
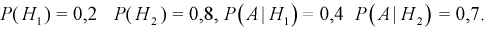
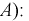
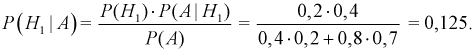
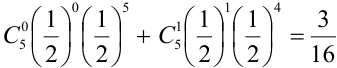
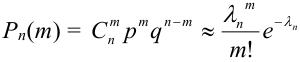
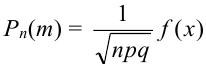
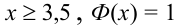
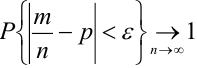
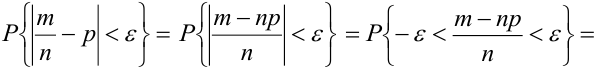
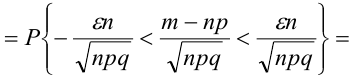
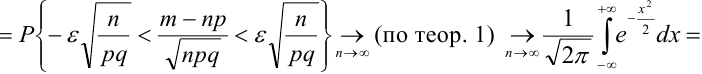
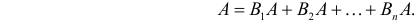
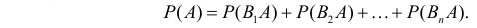
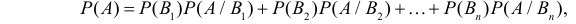
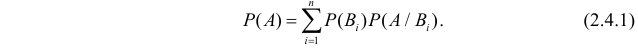
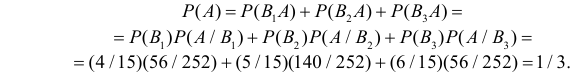
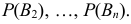
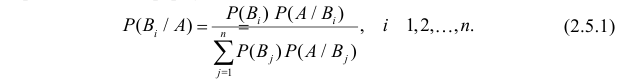

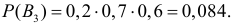
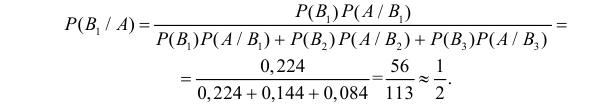
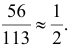
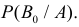
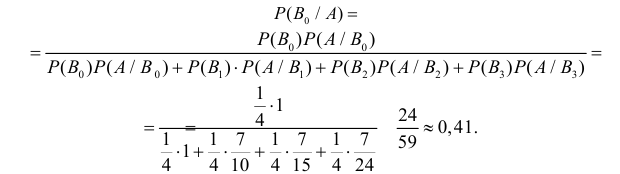
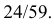
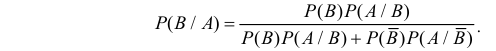
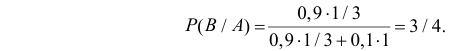
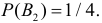
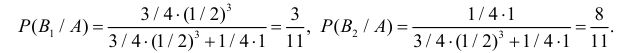
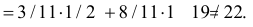
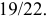
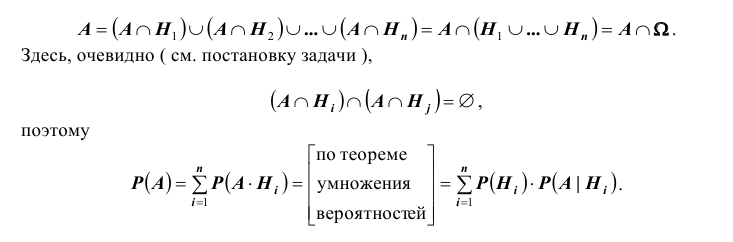
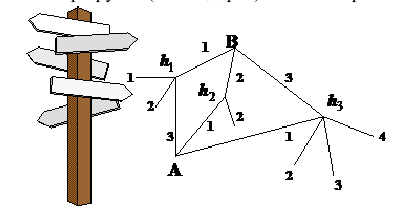
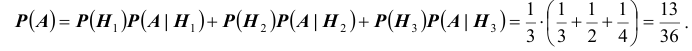

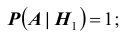
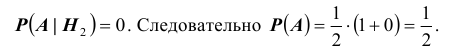
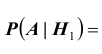
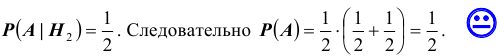
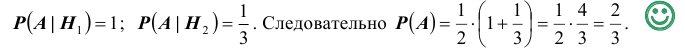
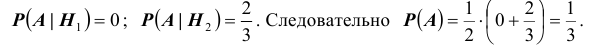
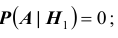
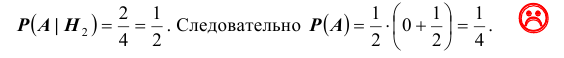

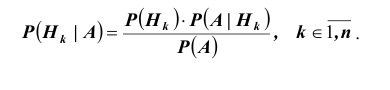
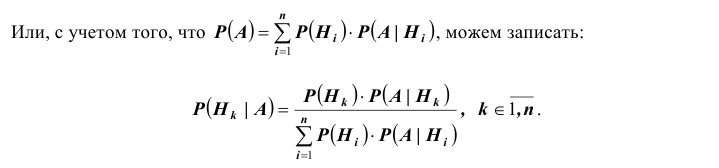

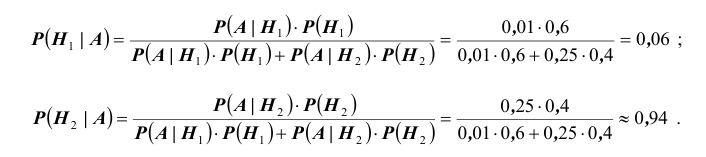
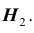
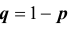
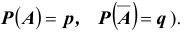
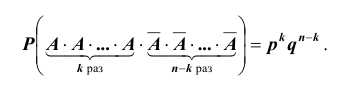
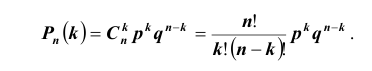


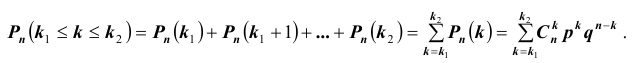
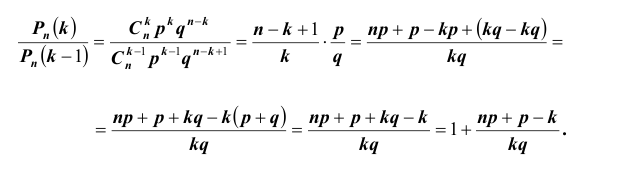
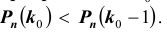

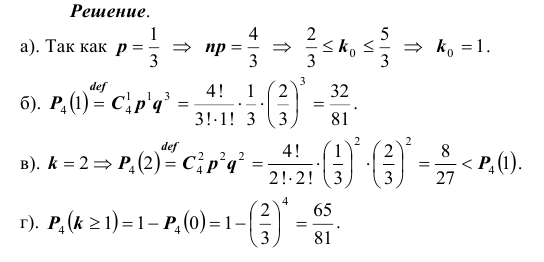
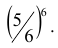
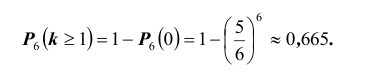
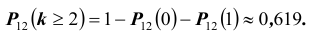
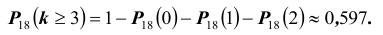
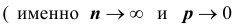
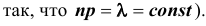
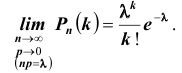

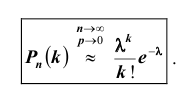
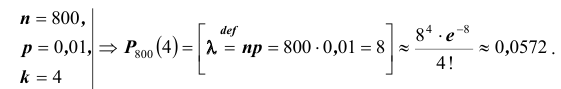

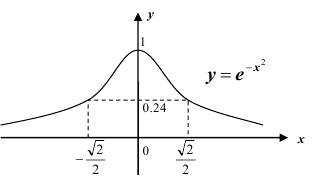
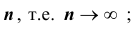
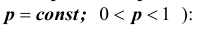

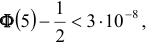
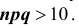
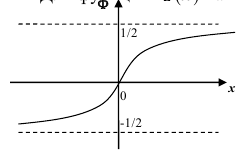
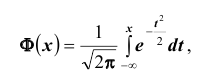
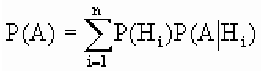
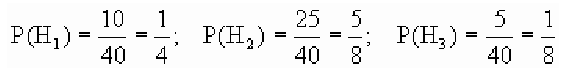
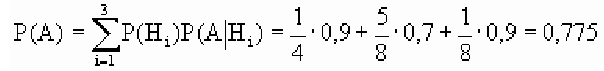
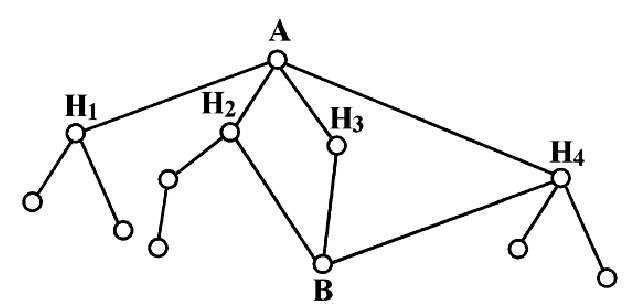
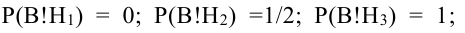
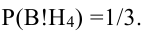
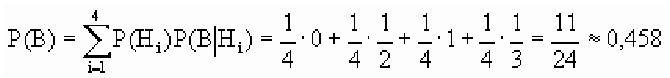
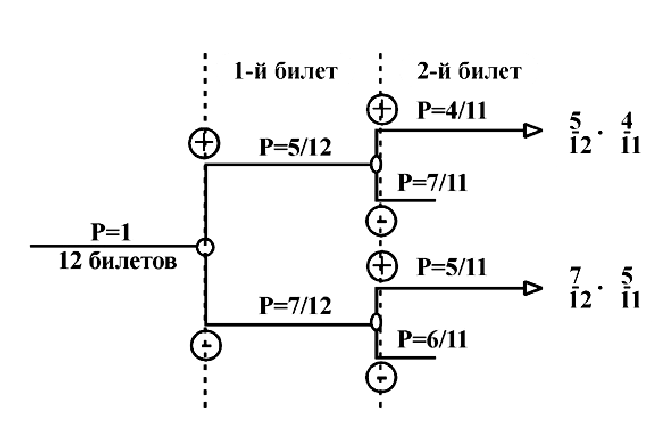
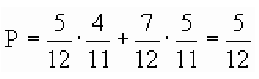
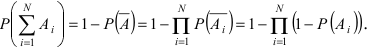
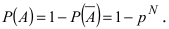
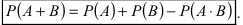
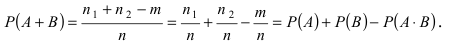
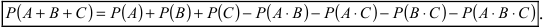
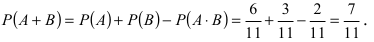
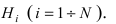
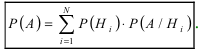
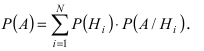
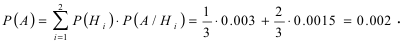
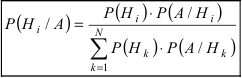
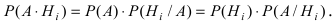
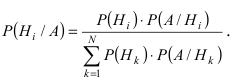
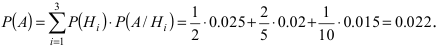
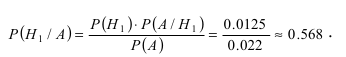
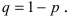

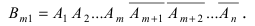
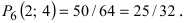
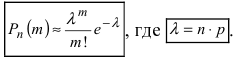
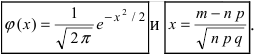
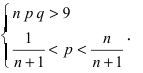
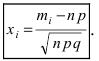
/Bogoslovskii1.files/image001.jpg)
/Bogoslovskii1.files/image002.jpg)
/Bogoslovskii1.files/image003.jpg)
/Bogoslovskii1.files/image004.jpg)
/Bogoslovskii1.files/image005.jpg)
/Bogoslovskii1.files/image006.jpg)
/Bogoslovskii1.files/image007.jpg)
/Bogoslovskii1.files/image008.jpg)
/Bogoslovskii1.files/image009.jpg)
/Bogoslovskii1.files/image010.jpg)
/Bogoslovskii1.files/image011.png)
/Bogoslovskii1.files/image012.jpg)