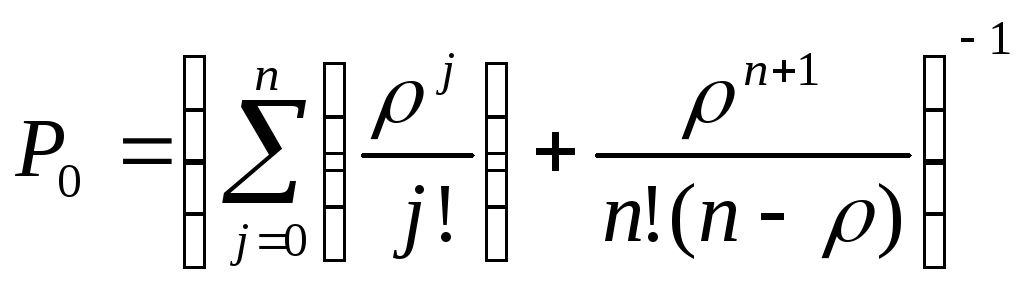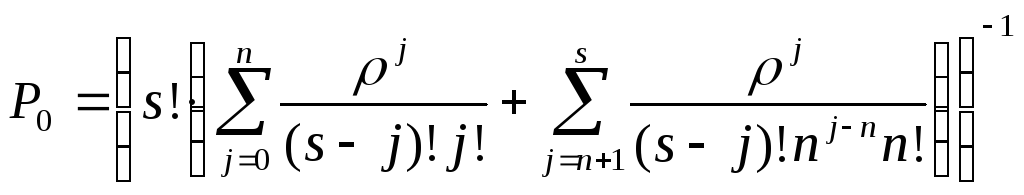Как найти среднее число занятых каналов - Исправление недочетов и поиск решений вместе с Examum.ru

и
ограниченной длиной очереди

Пусть имеется n
— канальная СМО с
очередью, на которую не наложено
ограничений ни по длине очереди, ни по
времени ожидания. В силу неограниченности
очереди каждая заявка рано или поздно
будет обслужена, поэтому Для
СМО с неограниченной очередью накладывается
ограничениеЕслиэто условие нарушено,
то очередь растет до бесконечности,
наступает явление «взрыва».
Вероятность простоя каналов равна

Вероятность занятости
обслуживанием
каналов равна

Вероятность занятости
обслуживанием всех каналов при отсутствии
очереди равна

Вероятность наличия очереди есть
вероятность того, что число требований
в системе больше числа каналов:

Вероятность попадания
заявки в очередь есть вероятность
занятости всех каналов. Эта вероятность
равна сумме вероятностей наличия очереди
и занятости всех п
каналов при отсутствии
очереди:

Среднее число занятых
обслуживанием каналов равна

Доля каналов, занятых обслуживанием
равна,

Среднее число заявок в очереди (длина
очереди) равно

Среднее число заявок в
системе равно

M
= L+
T
=L+p.

Среднее время ожидания заявки в очереди
равно

Среднее время пребывания заявки в
системе равно

Имеется n-канальная
система с ожиданием, в которой количество
заявок, стоящих в очереди, ограничено
числом т, т.е.
заявка, заставшая все каналы занятыми,
становится в очередь, только если в ней
находится менее т
заявок. Если число
заявок в очереди равно т,
то последняя прибывшая
заявка в очередь не становится и покидает
систему необслуженной.

Системы с ограниченной
очередью являются обобщением двух
рассмотренных ранее СМО: при т
= 0 получаем СМО с
отказами, при
получаем СМО с ожиданием.

Вероятность простоя каналов

Вероятность отказа в обслуживании равна
вероятности
того, что в очереди уже стоятт
заявок:

Относительная пропускная способность
есть величина, дополняющая вероятность
отказа до 1, т.е. вероятность обслуживания

Абсолютная пропускная способность
определяется равенством

Среднее число занятых каналов определяется
равенством

Средняя длина очереди системы, т.е.
среднее число заявок в очереди определяется
равенством

Среднее время ожидания обслуживания в
очереди равно

Среднее число заявок в СМО равно

M
= L+
к.

Среднее время пребывания заявки в СМО
равно

6. Замкнутые системы массового обслуживания

До сих пор мы рассматривали
СМО, в которых входящий поток никак не
связан с выходящим. Такие системы
называются разомкнутыми.
В некоторых же случаях требования,
которые были обслужены, после задержки
опять могут поступать на вход.

Такие системы
массового обслуживания
называются замкнутыми.
Например, такие объекты, как, поликлиника,
обслуживающая данную территорию, бригада
рабочих, закрепленная за группой станков,
являются примерами замкнутых систем.
В замкнутой СМО циркулирует одно и то
же конечное число потенциальных
требований. Пока потенциальное требование
не реализовалось в качестве требования
на обслуживание, считается, что оно
находится в блоке задержки. В момент
реализации оно поступает в саму систему.
Например, рабочие обслуживают группу
станков. Каждый станок является
потенциальным требованием, превращаясь
в действующее в момент своей поломки.
Пока станок работает, он находится в
блоке задержки, а с момента поломки до
момента окончания ремонта — в самой
системе. Каждый рабочий является
каналом обслуживания.

Пусть
общее
число каналов
обслуживания,
число
потенциальных заявок,
,—
интенсивность потока заявок каждого
потенциального требования,интенсивность
обслуживания. Тогда, в соответствии
наших обозначений коэффициент загрузки
системы равнаВероятность простоя
системы определяется формулой

Финальные вероятности
состояний системы определяются в виде:

Через эти вероятности выражается среднее
число занятых каналов

Через

находим абсолютную
пропускную способность системы

А =
,

а также среднее число заявок в системе

Рассмотрим некоторые примеры.

Пример 3.
На вход трехканальной СМО с отказами
поступает поток заявок с интенсивностью
равной 4
заявки в минуту, время обслуживания
заявки одним каналом t_обсл
= 1/μ = 0,5 мин. Выгодно ли с точки зрения
пропускной способности СМО заставить
все три канала обслуживать заявки сразу,
при этом среднее время обслуживания
уменьшается втрое? Как это скажется на
среднем времени пребывания заявки в
СМО?

Решение.
Вероятность
простоя трехканальной СМО согласно
формуле равна

Вероятность отказа определяем по формуле
вероятности отказа:

Относительная пропускная
способность системы равна

Абсолютная пропускная
способность системы равна

Среднее число занятых
каналов

1,58,
доля каналов, занятых обслуживанием
равно,

Среднее время пребывания
заявки в СМО находим как вероятность
того, что заявка принимается к обслуживанию,
умноженную на среднее время обслуживания:
t
0,395
мин.

Объединяя все три канала в
один, получаем одноканальную систему
с параметрами μ = 6,
= 2/3. Для одноканальной системы вероятность
простоя равна

вероятность отказа равна

относительная пропускная способность
равна

абсолютная пропускная способность
равна

Среднее время пребывания
заявки в СМО равно

В результате объединения каналов в
один, пропускная способность системы
снизилась, так как увеличилась вероятность
отказа. Тем самым, среднее время пребывания
заявки в системе уменьшилось.

Пример 4.
На вход трехканальной СМО с неограниченной
очередью поступает поток заявок с
интенсивностью λ = 4
заявки в час, среднее время обслуживания
одной заявки t=
1/μ 0,5 ч. Найти показатели
эффективности работы системы.

Решение. Для
рассматриваемой системы п
= 3, λ=
4, μ
= 1/0,5 = 2,
=λ /μ
= 2,

/n
= 2/3
< 1.
Определяем вероятность простоя системы:

Среднее число заявок в очереди находим
по формуле:

Среднее время ожидания заявки в очереди
определяется по формуле:

ч.

Среднее время пребывания
заявки в системе равно

Пример 5.
В парикмахерской работают 3 мастера, а
в зале ожидания расположены 3 стула.
Поток клиентов имеет интенсивность X
= 12 клиентов в час.
Среднее время обслуживания t
⁼
20 мин. Определить относительную и
абсолютную пропускную способность
системы, среднее число занятых кресел,
среднюю длину очереди, среднее время,
которое клиент проводит в парикмахерской.

Решение. Для
данной задачи п = 3,
т = 3,
λ
= 12, μ= 3,
= 4,/п
= 4/3.

Вероятность простоя равна:

Вероятность отказа в обслуживании
определяем по формуле:

Относительная пропускная способность
системы, т.е. вероятность обслуживания

Абсолютная пропускная способность

Среднее число занятых каналов

Средняя длина очереди
.

Среднее время ожидания
обслуживания в очереди ч.

Среднее число заявок в СМО

Среднее время пребывания заявки в СМО

ч.

Пример 6.
Рабочий обслуживает 4 станка. Каждый
станок отказывает с интенсивностью λ
= 0,5 отказа в час,
среднее время ремонта
= 1/μ = 0,8 ч. Определить пропускную
способность системы.

Решение. Эта
задача рассматривает «замкнутую СМО»,
μ = 1,25,
= 0,5/1,25 = 0,4. Вероятность простоя рабочего:

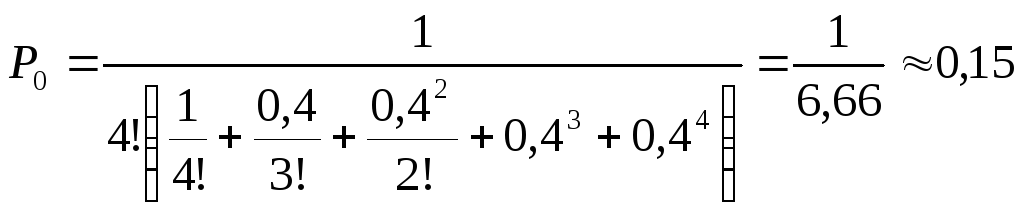
Вероятность занятости
рабочего
P0,85.
Если рабочий занят,
он налаживает μ станков в единицу
времени, пропускная способность системыстанков в час.

В заключении читателю
рекомендуется обратиться к более
обстоятельным учебникам, с целью
получения углубленного знания по этому
разделу [Карлин С.]

Соседние файлы в папке Теория вероятностей от исмоилова

#
06.02.20163.8 Mб65~WRL3455.tmp
#
06.02.20163.95 Mб67~WRL3470.tmp
#
06.02.20163.21 Mб65~WRL3784.tmp
#
06.02.20162.41 Mб65~WRL3792.tmp
#
06.02.20164.29 Mб65~WRL3856.tmp
#
#

Источник

СМО с отказами: определения и формулы

В качестве показателей эффективности СМО с отказами будем рассматривать:

1) — абсолютную пропускную способность СМО, т.е. среднее число заявок, обслуживаемых в единицу времени;

2) — относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой;

3) $P_{text{otk}}$ — вероятность отказа, т.е. того, что заявка покинет СМО необслуженной;

4) overline{k} — среднее число занятых каналов (для многоканальной системы).

Одноканальная система (СМО) с отказами

Рассмотрим задачу. Имеется один канал, на который поступает поток заявок с интенсивностью lambda . Поток обслуживании имеет интенсивность . Найти предельные вероятности состояний системы и показатели ее эффективности.

Примечание. Здесь и в дальнейшем предполагается, что все потоки событий, переводящие СМО из состояния в состояние, будут простейшими. К ним относится и поток обслуживании — поток заявок, обслуживаемых одним непрерывно занятым каналом. Среднее время обслуживания $overline{t}_{text{ob.}}$ обратно по величине интенсивности , т.е. $overline{t}_{text{ob.}}=1/mu$ .

Система (СМО) имеет два состояния: S_0 — канал свободен, S_1 — канал занят. Размеченный граф состояний представлен на рис. 6.

Размеченный граф состояний одноканальной системы с отказами

В предельном, стационарном режиме система алгебраических уравнений для вероятностей состояний имеет вид (см. выше правило составления таких уравнений)

$begin{cases}lambdacdot p_0=mucdot p_1,\mucdot p_1=lambdacdot p_0,end{cases}$

(18)

т.е. система вырождается в одно уравнение. Учитывая нормировочное условие p_0+p_1=1 , найдем из (18) предельные вероятности состояний

$p_0=frac{mu}{lambda+mu},quad p_1=frac{lambda}{lambda+mu},,$

(19)

которые выражают среднее относительное время пребывания системы в состоянии S_0 (когда канал свободен) и S_1 (когда канал занят), т.е. определяют соответственно относительную пропускную способность системы и вероятность отказа $P_{text{otk}}:$

$Q=frac{mu}{lambda+mu},,$

(20)

$P_{text{otk}}=frac{lambda}{lambda+mu},.$

(21)

Абсолютную пропускную способность найдем, умножив относительную пропускную способность на интенсивность потока отказов

$A=frac{lambdamu}{lambda+mu},.$

(22)

Пример 5. Известно, что заявки на телефонные переговоры в телевизионном ателье поступают с интенсивностью lambda , равной 90 заявок в час, а средняя продолжительность разговора по телефону $overline{t}_{text{ob.}}=2$ мин. Определить показатели эффективности работы СМО (телефонной связи) при наличии одного телефонного номера.

Решение. Имеем lambda=90 (1/ч), $overline{t}_{text{ob.}}=2$ мин. Интенсивность потока обслуживании $mu=frac{1}{overline{t}_{text{ob.}}}=frac{1}{2}=0,!5$ (1/мин) =30 (1/ч). По (20) относительная пропускная способность СМО $Q=frac{30}{90+30}=0,!25$ , т.е. в среднем только 25% поступающих заявок осуществят переговоры по телефону. Соответственно вероятность отказа в обслуживании составит $P_{text{otk}}=0,!75$ (см. (21)). Абсолютная пропускная способность СМО по (29) A=90cdot0,!25=22,!5 , т.е. в среднем в час будут обслужены 22,5 заявки на переговоры. Очевидно, что при наличии только одного телефонного номера СМО будет плохо справляться с потоком заявок.

Многоканальная система (СМО) с отказами.

Рассмотрим классическую задачу Эрланга. Имеется каналов, на которые поступает поток заявок с интенсивностью lambda . Поток обслуживании имеет интенсивность . Найти предельные вероятности состояний системы и показатели ее эффективности.

Система (СМО) имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе): S_0,S_1,S_2,ldots,S_k,ldots,S_n , где S_k — состояние системы, когда в ней находится заявок, т.е. занято каналов.

Граф состояний СМО соответствует процессу гибели и размножения и показан на рис. 7.

Граф состояний СМО, соответствующий процессу гибели и размножения

Поток заявок последовательно переводит систему из любого левого состояния в соседнее правое с одной и той же интенсивностью lambda . Интенсивность же потока обслуживании, переводящих систему из любого правого состояния в соседнее левое состояние, постоянно меняется в зависимости от состояния. Действительно, если СМО находится в состоянии S_2 (два канала заняты), то она может перейти в состояние S_1 (один канал занят), когда закончит обслуживание либо первый, либо второй канал, т.е. суммарная интенсивность их потоков обслуживании будет 2mu . Аналогично суммарный поток обслуживании, переводящий СМО из состояния S_3 (три канала заняты) в S_2 , будет иметь интенсивность 3mu , т.е. может освободиться любой из трех каналов и т.д.

В формуле (16) для схемы гибели и размножения получим для предельной вероятности состояния

$p_0={left(1+ frac{lambda}{mu}+ frac{lambda^2}{2!mu^2}+ldots+frac{lambda^k}{k!mu^k}+ldots+ frac{lambda^n}{n!mu^n}right)!}^{-1},$

(23)

где члены разложения $frac{lambda}{mu},,frac{lambda^2}{2!mu^2},,ldots,,frac{lambda^k}{k!mu^k},,ldots,, frac{lambda^n}{n!mu^n}$ , будут представлять собой коэффициенты при p_0 в выражениях для предельных вероятностей p_1,p_2,ldots,p_k,ldots,p_n . Величина

$rho=frac{lambda}{mu}$

(24)

называется приведенной интенсивностью потока заявок или интенсивностью нагрузки канала. Она выражает среднее число заявок, приходящее за среднее время обслуживания одной заявки. Теперь

$p_0={left(1+rho+frac{rho^2}{2!}+ldots+frac{rho^k}{k!}+ldots+frac{rho^n}{n!}right)!}^{-1},$

(25)

$p_1=rhocdot p,quad p_2=frac{rho^2}{2!}cdot p_0,quad ldots,quad p_k=frac{rho^k}{k!}cdot p_0,quad ldots,quad p_n=frac{rho^n}{n!}cdot p_0.$

(26)

Формулы (25) и (26) для предельных вероятностей получили названия формул Эрланга в честь основателя теории массового обслуживания.

Вероятность отказа СМО есть предельная вероятность того, что все я каналов системы будут заняты, т.е.

$P_{text{otk}}= frac{rho^n}{n!}cdot p_0.$

(27)

Относительная пропускная способность — вероятность того, что заявка будет обслужена:

$Q=1- P_{text{otk}}=1-frac{rho^n}{n!}cdot p_0.$

(28)

Абсолютная пропускная способность:

$A=lambdacdot Q=lambdacdotleft(1-frac{rho^n}{n!}cdot p_0right)!.$

(29)

Среднее число занятых каналов overline{k} есть математическое ожидание числа занятых каналов:

$overline{k}=sum_{k=0}^{n}(kcdot p_k),$

где p_k — предельные вероятности состояний, определяемых по формулам (25), (26).

Однако среднее число занятых каналов можно найти проще, если учесть, что абсолютная пропускная способность системы есть не что иное, как интенсивность потока обслуженных системой заявок (в единицу времени). Так как каждый занятый канал обслуживает в среднем заявок (в единицу времени), то среднее число занятых каналов

$overline{k}=frac{A}{mu}$

(30)

или, учитывая (29), (24):

$overline{k}=rhocdotleft(1-frac{rho^n}{n!}cdot p_0right)!.$

(31)

Пример 6. В условиях примера 5 определить оптимальное число телефонных номеров в телевизионном ателье, если условием оптимальности считать удовлетворение в среднем из каждых 100 заявок не менее 90 заявок на переговоры.

Решение. Интенсивность нагрузки канала по формуле (25) $rho=frac{90}{30}=3$ , т.е. за время среднего (по продолжительности) телефонного разговора $overline{t}_{text{ob.}}=2$ мин. поступает в среднем 3 заявки на переговоры.

Будем постепенно увеличивать число каналов (телефонных номеров) n=2,3,4,ldots и определим по формулам (25), (28), (29) для получаемой n-канальной СМО характеристики обслуживания. Например, при n=2 имеем

$з_0={left(1+3+ frac{3^2}{2!}right)!}^{-1}=0,!118approx0,!12;quad Q=1-frac{3^2}{2!}cdot0,!118=0,!471approx0,!47;quad A=90cdot0,!471=42,!4$ и т.д.

Значение характеристик СМО сведем в табл. 1.

По условию оптимальности Qgeqslant0,!9 , следовательно, в телевизионном ателье необходимо установить 5 телефонных номеров (в этом случае Q=0,!9 — см. табл. 1). При этом в час будут обслуживаться в среднем 80 заявок (A=80,!1) , а среднее число занятых телефонных номеров (каналов) по формуле (30) $overline{k}=frac{80,!1}{30}=2,!67$ .

Расчёт значений характеристик СМО

Пример 7. В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Среднее время работы с одним заказом составляет 3 ч. Интенсивность потока заявок 0,25 (1/ч). Найти предельные вероятности состояний и показатели эффективности работы вычислительного центра.

Решение. По условию n=3,~lambda=0,!25 (1/ч), $overline{t}_{text{ob.}}$ =3 (ч). Интенсивность потока обслуживании $mu=frac{1}{overline{t}_{text{ob.}}}=frac{1}{3}=0,!33$ . Интенсивность нагрузки ЭВМ по формуле (24) $rho=frac{0,!25}{0,!33}=0,!75$ . Найдем предельные вероятности состояний:

– по формуле (25) $p_0={left(1+0,!75+ frac{0,!75^2}{2!}+ frac{0,!75^3}{3!}right)!}^{-1}=0,!476$ ;

– по формуле (26) $p_1=0,!75cdot0,!476= 0,!357;~p_2= frac{0,!75^2}{2!}cdot0,!476= 0,!134;~p_3=frac{0,!75^3}{3!}cdot0,!476=0,!033$ ;

т.е. в стационарном режиме работы вычислительного центра в среднем 47,6% времени нет ни одной заявки, 35,7% — имеется одна заявка (занята одна ЭВМ), 13,4% — две заявки (две ЭВМ), 3,3% времени — три заявки (заняты три ЭВМ).

Вероятность отказа (когда заняты все три ЭВМ), таким образом, $P_{text{otk}}=p_3=0,!033$ .

По формуле (28) относительная пропускная способность центра Q=1-0,!033=0,!967 , т.е. в среднем из каждых 100 заявок вычислительный центр обслуживает 96,7 заявок.

По формуле (29) абсолютная пропускная способность центра A=0,!25cdot0,!967=0,!242 , т.е. в один час в среднем обслуживается. 0,242 заявки.

По формуле (30) среднее число занятых ЭВМ $overline{k}=frac{0,!242}{0,!33}=0,!725$ , т.е. каждая из трех ЭВМ будет занята обслуживанием заявок в среднем лишь на $frac{72,!5}{3}= 24,!2%.$ .

При оценке эффективности работы вычислительного центра необходимо сопоставить доходы от выполнения заявок с потерями от простоя дорогостоящих ЭВМ (с одной стороны, у нас высокая пропускная способность СМО, а с другой стороны — значительный простой каналов обслуживания) и выбрать компромиссное решение.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Многоканальная СМО с неограниченной очередью

Краткая теория

Пусть в n-канальную систему массового обслуживания (СМО) поступает с
интенсивностью

простейший поток требований. Длительность
обслуживания распределена по показательному закону со средним временем
обслуживания

.
Если же все каналы обслуживания заняты, то вновь поступившее требование
становится в очередь за ранее поступившими не обслуженными требованиями.
Освободившийся канал приступает к обслуживанию очередного требования из
очереди. Определим основные характеристики работы такой системы. Так как число
требований, стоящих в очереди, может быть бесконечно большим, то и число
состояний системы также может быть бесконечно большим.

Вероятность свободного состояния
системы:

Последнее выражение получено при
условии

, которое является условием
стационарности СМО. В случае

система не справляется с обслуживанием,
очередь неограниченно возрастает. Отношение

обозначается через

и называется уровнем загрузки системы:

Определим основные характеристики
многоканальной СМО с ожиданием.
Вероятность получения отказа равна нулю. Относительная пропускная способность

—это величина, которая дополняет
вероятность отказа до единицы:

.
Абсолютная пропускная способность

. Определим среднее число занятых
каналов: каждый занятый канал обслуживает в единицу времени в среднем

заявок, а вся система —

заявок. Тогда:

Коэффициент занятости каналов
обслуживания:

Образование очереди возможно,
когда вновь пост пившее требование застанет в системе не менее n требований, т. е. когда в
системе будет находиться

, требований. Эти события
независимы, поэтому вероятность того, что все каналы заняты, равна сумме
вероятностей

Отсюда вероятность образования очереди:

Среднее число заявок в очереди

можно вычислить как математическое ожидание,
складывая произведения возможного числа
заявок на вероятность того, что число заявок будет в очереди:

Среднее число заявок, связанных с
системой:

Определим среднее время ожидания
заявки в очереди

. Очередь образуется, если все

каналов заняты. Так как интенсивность
обслуживания

, то поток освобожденных каналов
имеет интенсивность

. Если заявка поступила в момент,
когда заняты все

каналов и очереди нет, то время ожидания
составит в среднем

, а если застанет одно требование
в очереди, то

, и так далее. Среднее время
ожидания заявок в очереди найдем, суммируя произведения среднего времени
ожидания на соответствующую вероятность:

Среднее время пребывания заявок в
системе:

Формулы Литтла:

Среднее число простаивающих
каналов обслуживания:

Коэффициент простоя каналов:

Пример решения задачи

Задача

На строительном складе работают
четыре кладовщика. Поток посетителей имеет

пуассоновское распределение с
интенсивностью 2 заявки в минуту. Время обслуживания имеет показательное
распределение со средним значением 1,5 минуты на заявку. Определить показатели
работы склада.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Имеем:

Отсюда
следует, что вероятность того, что все четыре кладовщика простаивают, равна
0,05. Определим другие показатели работы системы.

Абсолютная
пропускная способность склада, т. е. количество обслуживаемых
в единицу времени требовании,

(заявки в минуту). Среднее число занятых
кладовщиков

. Вероятность образования
очереди, т. е. вероятность того, что в момент обращения заказчика все четыре
кладовщика заняты:

Среднее
число заявок в очереди:

Среднее
время простаивания в очереди:

Среднее
число заявок в системе:

Среднее
время пребывания заявки в системе:

Среднее
число простаивающих кладовщиков:

Источник

УДК 519.872

А. П. Кирпичников, Нгуен Тхань Банг, Чан Куанг Куи РАСЧЁТ СРЕДНЕГО ЧИСЛА ЗАНЯТЫХ КАНАЛОВ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ОГРАНИЧЕННЫМ СРЕДНИМ ВРЕМЕНЕМ ПРЕБЫВАНИЯ ЗАЯВКИ В ОЧЕРЕДИ

Ключевые слова: система массового обслуживания, поток требований, очередь, обслуживающее устройство.

Представлена математическая модель открытой многоканальной системы массового обслуживания с ограниченным средним временем пребывания заявки в очереди и вычислено среднее число занятых каналов обслуживания этой системы.

Keywords: queuing system, flow of requirements, queue, serving device.

Presented the mathematical model of multi-channel queuing system of open type with bounded mean residence time in the queue and calculated the average number of busy service channels of this system.

Настоящая работа является продолжением цикла публикаций авторов, начатого в работах [1, 2] и по-свящённого разработке математических основ функционирования системы массового обслуживания (СМО) с очередью конечной длины и ограниченным средним временем пребывания заявки в очереди. Напомним, что в этих работах рассмотрена система массового обслуживания, в интенсивностью у = 1/1. Интенсивность обслуживания заявки в системе при этом обозначается как ¡1, а интенсивность поступающего в систему потока заявок как Л.

В работе [1] рассмотрен такой вариант постановки задачи, в котором фиксировано максимальное число требований, ожидающих обслуживания; в частности, предположено, что в очереди одновременно могут находиться не более N заявок и что любое поступившее сверх этого числа требование получает отказ и немедленно покидает систему без обслуживания. Поступление новых требований происходит по закону Пуассона, времена их обслуживания распределены экспоненциально со средней интенсивностью обслуживания л заявок в единицу времени. При этом, однако, в систему допускаются только те требования, которые застают в ней строго меньше заявок, чем m+N . Ясно, что при N такая система массового обслуживания сводится к изученной в цикле работ [2-4]. Граф системы массового обслуживания такого рода изображён на рис. 1. В этом случае приведённая интенсивность потока поступающих в систему заявок равна р = Лл. Физический смысл этой величины заключается, очевидно, в том, что она показывает, какое число заявок в среднем поступило в систему за среднее время обслуживания в системе одной заявки.

В работе [1] были впервые получены формулы для вероятностных характеристик системы массового обслуживания такого рода, в частности, для вероятности полного простоя системы Ро

Р0 =1 em-1-p)+p

m-1

I-mlp)EN{cemlP)

N + 1

-1 +

-mlP+N)T-mlP+N)

= (1)

-m-1)!

+ ч.

+ 3.

д T

где ет(р) — неполная экспонента [3, 4] (напомним, что ео( р) =1). В этих формулах

N к

к = 0

г(#+к)

(2)

— неполная функция Г. Миттаг-Леффлера первого порядка, введённая в рассмотрение в работе [1]. В предельном случае, когда N ^ да, третье слагаемое в квадратных скобках этого соотношения стремится к нулю и тогда формула (1) переходит в известное соотношение

-1

Ро-

,т-1

ет-1(р)+т1) [г(т рЕ-т р)-1 ]

модели [3, 4], как и следовало ожидать. При этом формулы для вероятностей стационарных состояний системы имеют вид

Рк

Рк =кРо при к<т;

„к-т

Рк =

Ро =

Р ‘ т

т (т/р+1)к-

кк-т г(т/р+1) г(т/р+1 + к-т)

__хк-т+1 г(т/ р)

(т-1) (т/р+к-т) г(т/р+к-т) m<k<m+N,

Ро

т -1

Ро при

где (а)к =а(а + 1)(а + 2) … (а + к -1); (0)0 = 1 -символ Л. Похгаммера [5]. Величина а = р /р = Л/у, очевидно, показывает, какое среднее число заявок поступает в систему за среднее время пребывания в очереди одной «нетерпеливой» заявки. При этом р = у/ /и — приведённая интенсивность ухода «нетерпеливых» заявок из очереди — величина, которая показывает, сколько в среднем заявок покидает систему необслуженными за среднее время обслуживания системой одной заявки.

В работе [2] найдены вероятность отказа в обслуживании вновь поступившей в систему заявки

ротк = pm+N =

т -1

N+1

г(т/Р)

(т-1) (mP+N) г(т/р+!

Ро.

(3)

и вероятность ожидания обслуживания поступившей заявкой, то есть вероятность того, что поступающее требование найдет все каналы занятыми (вне зависимости от того, будет оно дожидаться обслуживания или нет). Эта вероятность определяется формулой

од-т.^ [г(тр)Е1л/(«;тр)-1 ]. (4)

В предельном случае, когда N ^ да, соотношение (4), как и следовало ожидать, переходит в известную

мультипликативную зависимость [3, 4] рт -1 Р

Рожнд =т_ 1)0 [г(т р)Е1{а,тР)-1 ].

Для дальнейших расчетов нам ещё потребуется найти выражение для такой важнейшей характеристики данного типа СМО, как среднее число требований, находящихся под обслуживанием (среднее число занятых каналов). По определению имеем

m + N

т=Х кРк + X тРк =Р0 X ккЛ

к=0 к=т+1 к=0

т _ т + 1

Р Р0 V а

—л^ х т

к-т

к = т + т к-1

1 (тр+1)к-т „к

+ р Р0 X

=РР0 Й(к-1)^ (т-1)^=1 (тР+1)к

к=0

и тогда в силу соотношения (2)

Рт Р0

(т 1)

(тр+1)/

-1

т=р

=РР0ет-1(р)+рт-Ц гЦр+Е (о;тР+1)-(т-1 Но

, как показано в работе [1], для неполной функции Г. Миттаг-Леффлера справедливо рекуррентное соотношение

-N1

Р Р0

г(т/ р +1) Е™ (а т/ Р +1) = -N1

Л1 г(т1р)Е»(ат1Р)-1+^-, ,г(тр) ч 1 (5)

р 1 (т/р+^гт/р+^г7

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

и тогда имеем

т = рР0 ет-1(р)+ ^ [г(тР)Е?{а,т1 Р)-1 ]+

т р

т-1

N + 1

г(тр)

РтР0

(т-1) (т/р-И^т/р-И) (т-1) ‘

Подставляя в это соотношение формулы (3) и (4) для вероятности отказа и вероятности ожидания начала обслуживания заявкой в свою очередь, очевидно, имеем

т=

р Р0

РР0 ет-1{р)+тРотк +тРожид -(т-)

Заметим далее, что из соотношений (1), (3) и (4) следует ет-1 (Р)Р0 =1-Ротк — Рожид , что

достаточно очевидно, поскольку физический смысл величины ет-1(р)Р0 — это вероятность

немедленного обслуживания поступившей в систему заявки. Подставляя указанное соотношение в формулу (6), найдём окончательно

т = р-(т-р)[Рожид(°)-Рожид -Ротк ]

где

Рожид (°) :

Р Р0

(т- 1)(т-р)

— это выражение для вероятности ожидания системы с неограниченной очередью и «терпеливыми»

заявками, известное из модели М/М/т [3, 4]. Заметим, что хотя по форме это соотношение совпадает с аналогичным выражением модели М/М/т, однако, в отличие от него, содержит внутри себя ещё и зависимость от параметров р и N, содержащуюся внутри вероятности полного отсутствия заявок в системе Ро = Ро согласно формуле (1). Очевидно, что при NроТк ^0 и тогда соотношение (6) переходит в известную формулу [3, 4] т = р-(т-РДРожид(0)-Рожид ].

Отсюда коэффициент загрузки СМО этого типа

кз = т -11 -т 1 [Рожид(о)-Рожид -Ротк ]

соответственно коэффициент простоя

К.П. = 1 -K.5. = Çl-m)[l + Рожид(0)-Рожид -Ротк ]•

Заметим, что к. з.<к. з.(о), к. п. >к. п(о).

Дисперсия числа занятых каналов

соответственно

m <ю

mm = y k Pk + y m2 Pk-m2 =

k=0

m k=m+1

m k mp m + N ak-m = P0 y k2y m2 -—-—^—m2 =

k! m! . k=0 k = m +

1/1 —,-ч-

1 (mß+i)k-

m k m m Р m+N k-m

P m k(k-i+i)k y —m2-

k=0

k! (m-i)! k=m+i (mß+l)k-

k-m

m k-2 m k-1 mPm p N k

2 P P mp p ^ a —2

=P p kS и+PP0k=1 (k-i)i+-^5 m+k ~m

m pk-1 pm-1 m k-1

=p2 p0 y (bir-p2 p0mû+pp0 y P +

=1 (k-1)! » — (m-1)!

m Pm Р N

+ m p p0 y

1 (k -1)!

mp’ p0 _2 0 -m2.

(m-1)! (mß+1)k (m-1)!

Воспользовавшись теперь последовательно соотношениями (2), (5), (3) и (4), отсюда имеем

2 2 2 P

°m =P P0 em-1(PP-P P0

m -1

(m-1)!

+ PP0 em-1(PP +

m2 Pm-1

+m P,. [r(mß)^1 (-;mß)-1 ]+

m2 Pm-1 -N+1

r(m/ß)

(m-1)!

(m-1)! (m/ß+N)r(m/ ß+N)

mP p0 _2

^ —m2 =

(m-1)!

Pm p

= P2 P0 em-1 (P) + PP0 em-1(P)-P (m+

Pm p

2 2 P P0 —2

+ m Рожид + m Ротк-m(m-1)! -m =

= P(1 + P)P0 em- 1(P) + m2 Pожид+m2 Ротк —

-(m2-P2

)-m2 .

)Рожид(0)»

Но em-1 (p)p0 =1-Ротк — Рожид и тогда, очевидно, ==p-p(p0жид+ Ротк) — (m2 -P2 ) [ Рожид (0) — Рожид — Ротк ]+P2 -m2

или

^ =Р-Р(Рожид + Ротк)-(т-т)(Р-т),

поскольку в соответствии с соотношением (7)

(т -Р)[Рожид(о)-Рожид -Ротк ]=Р-т .

При Nполучаем отсюда известное соотношение [3, 4]

=p-p рожид—m-m) -p-m), которое, в свою очеред, при р =0 переходит в формулу cr2m = p-pрожид{0) (модель M/M/m), что очевидно, поскольку в этом случае имеем m = p в соответствии с результатами модели M/M/m.

Литература

1. А.П. Кирпичников, Нгуен Тхань Банг, Чан Куанг Куи, Вероятностные характеристики открытой многоканальной системы массового обслуживания с очередью конечной длины и ограниченным средним временем пребывание в очереди // Вестник технол. ун-та. 2016. Т. 19. № 11. С. 136-139.

2. А.П. Кирпичников, Нгуен Тхань Банг, Чан Куанг Куи, Вероятность отказа и вероятность ожидания начала обслуживания в системе с очередью конечной длины и ограниченным средним временем пребывания заявки в очереди // Вестник технол. ун-та. 2016. Т. 19. № 21. С. 151-153.

3. А.П. Кирпичников, Прикладная теория массового обслуживания. Казань, Изд-во Казан. гос. ун-та, 2008. 112 с.

4. А.П. Кирпичников, Методы прикладной теории массового обслуживания. Казань, Изд-во Казан. ун-та, 2011. 200 с.

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

5. А.П. Прудников, Ю.А. Брычков, О.И. Маричев, Интегралы и ряды. Специальные функции. Наука, Москва, 1983. 664 с.

© А. П. Кирпичников — д. ф.-м. н., зав. каф. интеллектуальных систем и управления информационными ресурсами КНИТУ, kirpichnikov@kstu.ru; Нгуен Тхань Банг — асп. той же кафедры, nguyenthanhbang.nd.vn@gmail.com; Чан Куанг Куи — асп. той же кафедры, tranquangquy88@gmail.com.

© A. P. Kirpichnikov — Dr. Sci, Head of the Department of Intelligent Systems & Information Systems Control, KNRTU, kirpichni-kov@kstu.ru; Nguyen Thanh Bang — postgraduate of the Department of Intelligent Systems & Information Systems Control, KNRTU, nguyenthanhbang.nd.vn@gmail.com; Tran Quang Quy — postgraduate of the Department of Intelligent Systems & Information Systems Control, KNRTU, tranquangquy88@gmail.com.

Источник