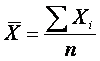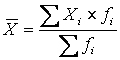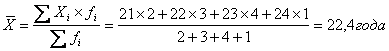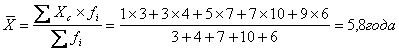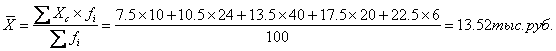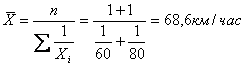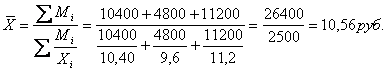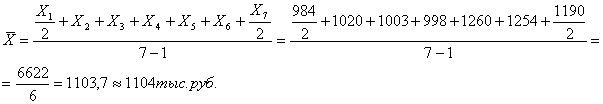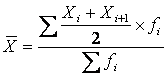Как найти среднее кубическое

Средняя геометрическая

Средняя геометрическая
применяется в тех случаях, когда
индивидуальные значения признака
представляют собой, как правило,
относительные величины динамики,
построенные в виде цепных величин, как
отношение к предыдущему уровню каждого
уровня в ряду динамики, то есть
характеризует средний коэффициент
роста.

Средняя
геометрическая
исчисляется извлечением корня степени
n
из произведений отдельных значений –
вариантов признака х.

(5.11)

где n
– число вариантов;

П – знак произведения.

Наиболее широкое
применение средняя геометрическая
получила для определения средних темпов
изменения в рядах динамики, а также в
рядах распределения.

Средняя квадратическая и средняя кубическая

В ряде случаев в
экономической практике возникает
потребность расчета среднего размера
признака, выраженного в квадратных или
кубических единицах измерения. Тогда
применяется средняя
квадратическая
(например, для вычисления средней
величины стороны n
квадратных участков, средних диаметров
труб, стволов и т.п.) и средняя
кубическая
(например, при определении средней длины
стороны n
кубов).

Формулы для расчета
средней квадратической:

• Средняя
  квадратическая простая
  является квадратным корнем из частного
  от деления суммы квадратов отдельных
  значений признака на их число:

(5.12)

• Средняя
  квадратическая взвешенная

(5.13)

где f
– веса.

Формулы для расчета
средней кубической аналогичны:

• Средняя кубическая
  простая

(5.14)

• Средняя кубическая
  взвешенная

(5.15)

Средние квадратическая
и кубическая имеют ограниченное
применение в практике статистики. Широко
пользуется статистика средней
квадратической, но не из самих вариантов
х, и из их отклонений от средней ()
при расчете показателей вариации.

Средняя может быть
вычислена не для всех, а для какой-либо
части единиц совокупности. Примером
такой средней может быть средняя
прогрессивная
как одна из частных средних, вычисляемая
не для всех, а только для «лучших»
(например, для показателей выше или ниже
средних индивидуальных).

5.5. Структурные средние.

Для изучения
структуры исследуемой совокупности
применяют так называемые структурные
средние: моду и медиану.

Модой в
статистике называют наиболее часто
встречающиеся в исследуемой совокупности
значение признака.

В дискретном
вариационном ряду моду определяют по
наибольшей частоте. По
следующим данным дискретного ряда
распределении определим моду:

Дневная выработка
рабочего, шт 10 12 15
25 25 30

Число рабочих,
имеющих

данную выработку,
чел. 5 10 8
12 9 7

Просматривая
частоты ряда (число рабочих), видим, что
наибольшая частота-12. Она соответствует
дневной выработке 20 шт. Таким образом,
мода показывает, что в данной совокупности
наибольшее число рабочих имеют выработку
20 шт. деталей в день.

В интервальном
ряду мода определяется по формуле:

,
(

где x₀—
нижняя граница модального интервала
(модальным называется интервал, имеющий
наибольшую частоту);

i
— величина
модального интервала;

f_mo
— частота
модального интервала;

f_mo-1
—
частота
интервала, предшествующего модальному;

f_mo
+1 —
частота
интервала, следующая за модальным.

Несколько иначе
определяется мода для интервального
вариационного ряда. В качестве примера
воспользуемся данными табл. 16.

Сначала найдем
модальный интервал, на который должна
приходиться наибольшая частота; по
условию задачи это будет интервал
100-105, так как ему соответствует наибольшая
частота – 16 чел. Подставив соответствующие
значения в формулу, получим:

M₀=
100 + 5 *(16-3 / (16 – 3) + (16 – 8)) = 103 %/

Наибольшее число
рабочих выполняют месячное задание на
103 %.

Медианой в
статистике называют такое значение
признака, которое расположено в середине
упорядоченного ряда.

Медиана определяется
по – разному для дискретного и
интервального вариационного рядов.
Медиана
дискретного вариационного ряда,
расположенного в ранжированном порядке,
имеет серединное
значение.
Если дискретный ряд включает четное
число единиц, то медиана (Ме) определяется
как средняя из двух центральных значений.
Медиана в интервальном ряду определяется
по формуле:

где x_Ме
— нижняя
граница медианного интервала ( медианным
называется первый интервал, накопленная
частота которого превышает половину
общей суммы частот);

i
— величина
медианного интервала;

∑ f
—
сумма
частот;

S_me-1
– накопленная
частота интервала, предшествующего
медианному

f_me
– частота
медианного интервала.

По следующим данным
дискретного ряда распределения,
расположенного в ранжированном порядке
(в порядке возрастания) определим
медиану:

Номер по порядку
рабочего….1 2 3 4 5

Стаж работы, лет
…………… .7 8 9 10 11

Так как медиана
имеет значение признака, находящееся
в середине упорядоченного ряда, то для
данного ряда распределения она составит
9 лет. Это значит, что половина совокупности
рабочих имеет стаж работы до 9 лет,
половина – более 9 лет.

Несколько сложнее
определяется сложнее определяется
медиана для интервального вариационного
ряда (табл.16)

Таблица 16

Распределение
рабочих по проценту выполнения месячного
задания

Выполнение месячного задания, %	Число рабочих, чел.	Накопленные частоты от начала ряда
95 — 100	3	3
100 — 105	16	19
105 — 110	8	27
110 — 115	7	34
115 — 120	6	40

Прежде находится
медианный интервал, на который должно
приходиться 50% накопленных частот
данного ряда, что по условию задачи
40/2=20. Сумма частот первых двух интервалов
равна 19, что меньше 20. Следовательно,
медианный интервал будет находиться
не во второй группе, а в третьей, т.е. в
пределах границ 105 — 110.

Подставим
соответствующие значения в формулу:

М_е
= 105 + 5 * (
(40 + 2) — 19/8 ) =
105,6 %.

Таким образом, 50%
всех рабочих выполняют производственное
задание менее чем на 105,6%, 50% — более чем
на 105,6%.

Моду и медиану в
интервальном ряду можно определить
графически. Мода определяется по
гистограмме
распределения.
Для этого выберем
самый высокий прямоугольник,
который является модальным. Затем правую
вершину модального прямоугольника
соединяем с правым верхним углом
предыдущего прямоугольника, а левую
вершину модального прямоугольника
соединяем с правым верхним углом
последующего прямоугольника. Из точки
пересечения отпускаем перпендикуляр
на ось абсцисс. Абсцисса точки пересечения
этих прямых и будет модой распределения.

Медиана рассчитывается
на кумуляте.
Для ее определения из точки на шкале
накопленных частот, соответствующей
50 %, проводится прямая, параллельная оси
абсцисс, до пересечения с кумулятой.
Затем из точки пересечения указанной
прямой с кумулятой опускается
перпендикуляр на ось абсцисс. Абсцисса
точки пересечения является медианой.

Аналогично с
нахождением медианы в вариационных
рядах распределения можно найти значение
признака у любой по порядку единицы
ранжированного ряда. Можно найти значение
признака у единиц, делящих ряд на четыре
равные части, на десять, сто частей. Эти
величины называются квартили, децили,
перцентили.

Квартили
представляют
собой значения признака, делящие
ранжированную совокупность на четыре
равные части. Различают квартиль нижний
(Q1),
отделяющий ¼ часть совокупности с
наименьшими значениями признака, и
квартиль верхний (Q3),
отделяющий ¼ с наибольшими значениями
признака. Это означает, что 25 % единиц
совокупности будут по величине меньше
Q1;
25 % будут заключены между Q1
и Q2,
25 % между Q2
и Q3,
а остальные 25 % превосходят Q3.
Средним квартилем Q2
является медиана.

Для расчета
квартилей по интервальному вариационному
ряду используются формулы:

¼
∑ f – S_Q1-1

Q₁
=
xq1 + i
*———————
;

f
_Q1

¾
∑ f – S_Q3-1

Q₃
= xQ3
+ i
*———————
;

f
_Q3

где xq1
– нижняя граница интервала, содержащая
нижний квартиль (интервал определяется
по накопленной частоте, первой превышающей
25 %);

xQ3
— нижняя граница интервала, содержащая
верхний квартиль (интервал определяется
по накопленной частоте, первой превышающей
75 %);

i
– величина интервала;

SQ1-1
– накопленная частота интервала,
предшествующего интервалу, содержащему
нижний квартиль;

SQ3
– 1 – то же для верхнего квартиля;

f
Q1
– частота интервала, содержащего нижний
квартиль;

f
Q3
– то же для верхнего квартиля;

Рассмотрим на
примере (табл. 17).

Таблица 17

Распределение
семей города по размеру среднедушевого
дохода в январе 2007 г.

Группы семей по размеру дохода, руб.	Число семей	Накопленные частоты	Накопленные частоты, % к итогу
До 5000 5000-6000 6000-7000 7000-8000 8000-9000 9000-10000 свыше 10000	600 700 1700 2500 2200 1500 800	600 1300 3000 5500 7700 9200 10000	6 13 30 55 77 92 100
Итого	10000	—	—

Нижний квартиль
находится в интервале 6000-7000, накопленная
частота которого равна 30 %. Верхний
квартиль лежит в интервале 8000-9000 с
накопленной частотой 77 %. Поэтому
получаем:

Q1=
6000 + 100*((1/4 10000 – 1300) / 1700) = 6710 руб.

Q3
=8000 + 100 * ((3/4 10000 – 5500) / 2200) = 8910 руб.

Итак, 25 % семей
имеют среднедушевой доход менее 6710
руб., 255 семей – свыше 8910 руб., а остальные
имеют доход в пределах 6710 — 8910 руб.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

From Wikipedia, the free encyclopedia

The cubic mean (written as ) is a specific instance of the generalized mean with .

Definition[edit]

For real numbers the cubic mean is defined as:

   ^[1][2][3]

For example, the cubic mean of two numbers is:

.

Applications[edit]

It is used for predicting the life expectancy of machine parts.^[3][4][5][6]

The cubic mean wind speed has been used a measure of local potential for wind energy.^[7]

The cubic mean is also used in biology to measure the mean dimensions of spherical bacteria (cocci)^[8] and of larger animals that are (approximately) spheroidal in shape.^[9] In this case using the conventional arithmetic mean will not give an accurate result because the size of a spherical bacterium increases as the cube of the radius.

References[edit]

Среднее кубическое (также средняя кубическая^[1]) — число [math]displaystyle{ x }[/math], равное кубическому корню из среднего арифметического кубов данных чисел [math]displaystyle{ a_1, a_2,…, a_n }[/math]:

[math]displaystyle{ x=sqrt[3]{frac {a_1^3+ a_2^3+ ldots+ a_n^3} {n}} }[/math]

Свойства

Среднее кубическое — частный случай среднего степенного и потому подчиняется неравенству о средних. В частности, для любых чисел оно не меньше среднего арифметического:

[math]displaystyle{ frac{a_1+a_2+ldots+a_n}{n}leqslantsqrt[3]{frac {a_1^3+ a_2^3+ ldots+ a_n^3} {n}} }[/math]

Применение

Среднее кубическое является характеристикой объёмных признаков. Может использоваться, например, для расчёта среднего объёма предметов по их диаметрам. Так, если известны диаметры яиц, то их средний объём может быть рассчитан с помощью среднего кубического^[1]. Среднее кубическое находит применение в статистике^[2].

Среднее кубическое для функции

Среднее кубическое можно также определить для непрерывной функции [math]displaystyle{ f(t) }[/math], заданной на отрезке [math]displaystyle{ [T_1,, T_2] }[/math], по формуле

[math]displaystyle{ x = sqrt[3]{dfrac{1}{T_2 — T_1} intlimits_{T_1}^{T_2} f^3(t) , dt,} }[/math]

а также для непрерывной функции [math]displaystyle{ f(t) }[/math], определённой на положительной полуоси:

[math]displaystyle{ x = lim_{Trightarrow infty} sqrt[3]{dfrac{1}{T} intlimits_{0}^{T} f^3(t) , dt.} }[/math]

Среднее кубическое для периодической функции по положительной полуоси равно среднему кубическому по периоду функции.

Пример вычисления

Рассмотрим функцию синуса

[math]displaystyle{ x(t) = A sin(omega t), }[/math]

где [math]displaystyle{ t }[/math] — время, [math]displaystyle{ A }[/math] — амплитуда, а [math]displaystyle{ omega }[/math] — частота в радианах на единицу времени. Тогда

[math]displaystyle{ omega = dfrac{2 pi}{T} }[/math]

и среднее кубическое вычисляется как

[math]displaystyle{ x = sqrt[3]{dfrac{1}{T} intlimits_{0}^{T} A^3 sin^3left(dfrac{2pi}{T} tright) , dt} = dfrac{A}{sqrt[3]{2 pi}} sqrt[3]{intlimits_{0}^{2pi} sin^3(t) , dt.} }[/math]

Примечания

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3.

Расчёт степенных средних величин.

Студент должен:

знать:

—     область применения и методику расчёта
степенных средних величин;

уметь:

—     исчислять
степенные средние
величины;

—     формулировать вывод по полученным
результатам.

Методические указания

Средней величиной называется обобщающая величина
статистической совокупности, выражающая типический уровень изучаемого признака.
Она выражает величину признака, отнесённую к единице совокупности.

К степенным средним
относятся средняя арифметическая, средняя
гармоническая, средняя хронологическая, средняя геометрическая, средняя квадратическая, средняя кубическая.

Средняя величина всегда
обобщает количественную вариацию признака, т. е. в средних величинах погашаются
индивидуальные различия признака у отдельных единиц совокупности, обусловленные
случайными обстоятельствами. Средняя величина позволяет сравнивать значения
признака у единиц, относящихся к разным совокупностям.

Принципы применения средних величин:

1)               
Необходим
обоснованный выбор признака у единиц совокупности, для которого рассчитывается
средняя.

2)               
При
определении средней величины в каждом конкретном случае следует исходить из
качественного содержания осредняемого признака,
учитывать взаимосвязь изучаемых признаков и особенность имеющихся исходных
данных;

3)               
Средняя
величина должна, прежде всего, рассчитываться по однородной совокупности.
Однородную совокупность позволяет получить метод группировки.

4)               
Общие
средние должны подкрепляться групповыми средними.

5)               
Средняя
величина не может быть меньше минимального значения и больше максимального
значения признака в совокупности.

Область применения и методика расчёта степенных
средних величин:

1. Средняя арифметическая

1.1 Средняя
арифметическая простая.

При небольшом объёме
исходной информации, когда исходные данные не сгруппированы, применяется средняя
арифметическая простая,которая рассчитывается по формуле:

где    ΣX_i — сумма
значений;

n— число
значений.

Например: В
бригаде четверо рабочих в возрасте  21,
22, 23 и 24 года. Средний возраст рабочего бригады составляет

1.2 Средняя арифметическая взвешенная.

Когда исходные данные сгруппированы,
то расчёт средней производится по

формуле средней арифметической
взвешенной:

где f_i –
частота ряда распределения, с которой отдельные варианты встречаются в
совокупности (или удельный вес отдельных значений во всей совокупности).

Например: Рабочие бригады по возрасту распределились следующим
образом:

Возраст рабочих, лет (X)	21	22	23	24
Численность рабочих, чел. (fi)	2	3	4	1

Средний возраст рабочего
бригады составляет

Если
исходная информация представлена в виде
интервального ряда распределения,
то средняя арифметическая взвешенная определяется по формуле:

 

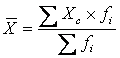
где X_c —
центральное (серединное) значение признака в интервале.

Например: По
имеющимся данным определить средний стаж рабочего бригады:

Стаж работы, лет	0 — 2	2 — 4	4 — 6	6 — 8	8 — 10
Численность рабочих, чел. (fi)	3	4	7	10	6

Для расчёта средней
арифметической взвешенной интервального ряда распределения определим центральное
(серединное) значение признака в каждом интервале. Среднее значение интервала
находится как полусумма нижней границы данного
интервала и нижней границы следующего интервала:

Стаж работы, лет	0 — 2	2 — 4	4 — 6	6 — 8	8 — 10
(Xc )

Оформим исходные данные
а следующем виде:

Стаж работы, лет	0 — 2	2 — 4	4 — 6	6 — 8	8 — 10
(Xc )	1	3	5	7	9
Численность рабочих, чел. (fi)	3	4	7	10	6

Средний стаж рабочего бригады
составляет

Если в интервальном ряду
распределения имеются «открытые» интервалы, то для установления центральных
(серединных) значений «открытых» интервалов на каждый из них условно
распространяется величина смежного «закрытого» интервала.

Например: Работники организации по величине заработной платы за январь 2010 года
распределились следующим образом:

Группы работающих по величине заработной платы за январь 2010 года, тыс.руб.	Численность работников, в % к итогу (fi)
До 9	10
9 — 12	24
12 — 15	40
15 — 20	20
20 и выше	6
Итого:	100

Определить по имеющимся данным
среднюю зарплату работников организации.

Для расчёта средней
арифметической взвешенной интервального ряда распределения определим центральное
(серединное) значение признака в каждом интервале. На каждый открытый интервал
условно распространим величину смежного закрытого интервала:

Группы работающих по величине заработной платы за январь 2010 года, тыс.руб.	Численность работников, в % к итогу (fi)	Центральное (серединное) значение интервала (Xc), руб
До 9	10
9 — 12	24
12 — 15	40
15 — 20	20
20 и выше	6
Итого:	100

Частоты
при расчете средних арифметических могут быть выражены
не только абсолютными величинами, но и относительными величинами – частостями Результаты применительно к одинаковым
вариантам будут совпадать. В данном примере численность работников
выражена не частотами, а частостями – удельными
весами численности отдельных групп во всей совокупности, что не влияет на
порядок расчёта средней.

Средняя зарплата работников
организации составляет:

Необходимо небольшое
пояснение применительно к расчету средней в
интервальных рядах распределения. В действительности распределение отдельных
вариантов в пределах интервала может оказаться неравномерным. В этом случае
середина интервала будет в той или иной степени отличаться от
фактической средней по интервалу. Это в свою очередь может повлиять на
правильность общей средней, исчисленной по данным интервального ряда. Степень
расхождения зависит от ряда причин. Во-первых, от числа вариант, чем больше
число вариант, тем вероятнее, что середина интервала будет мало отличаться от групповой средней. Во-вторых, от величины интервала. Если
интервал невелик, то ошибка будет незначительной, т.к. групповая средняя будет
мало отличаться от середины интервала. В-третьих, от характера распределения.
Чем симметричнее распределение, тем ошибка меньше. В-четвертых, размер ошибки
зависит от принципа построения интервального ряда. При равных интервалах
середина интервала будет ближе к средней по данной
группе. При наличии открытых интервалов расхождение, как правило, взрастает
из-за условного обозначения неизвестных границ. Общая
средняя равна средней из частных (групповых) средних, взвешенных по численности
соответствующих частей совокупности. Это правило имеет большое значение для
всей статистики – организации сбора и обработки данных, их анализа.

Свойства средней арифметической:

1. Произведение средней на сумму частот всегда равно сумме
произведений вариант на частоты. Другими словами, постоянный
множитель может быть вынесен за знак средней.

2. Если от каждой варианты отнять (прибавить) какое-либо
произвольное число, то новая средняя уменьшится (увеличится) на то же число:

3. Если каждую варианту умножить (разделить) на какое-то произвольное
число, то средняя арифметическая увеличится
(уменьшится) во столько раз

4. Если все частоты (веса) разделить или умножить на
какое-либо число, то средняя арифметическая от этого не изменится. Дело в том,
что веса при исчислении средней арифметической выполняют роль
удельного веса (соотношений между группами по количеству единиц). Поэтому
замена частот частостями не меняет значения средней.

5. Сумма отклонений отдельных вариантов от средней
арифметической всегда равняется нулю.

Перечисленные свойства могут быть использованы для того,
чтобы облегчить технику исчисления средней арифметической.

Например. Можно из всех значений признака вычесть произвольную
постоянную величину (лучше значение серединной варианты или варианты с
наибольшей частотой), полученные разности сократить на общий множитель (лучше
на величину интервала), а частоты выразить частостями
(в процентах) и исчисленную среднюю умножить на общий множитель и прибавить
произвольную постоянную величину. Иногда этот способ расчета средней
арифметической также называется способом расчета от условного нуля. Широкое
применение для обработки статистических материалов современных ЭВМ сужает
необходимость исчисления средних по упрощенным схемам.

2. Средняя гармоническая

2.2 Средняя гармоническая простая. Если объёмы явлений, т.е. произведения  Х_i ×f_i  по каждой
единице равны, то для расчёта средней применяется формула средней гармонической простой:

 

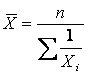
Например: Две
автомашины прошли один и тот же путь: первая со скоростью 60 км/ч, вторая со
скоростью 80 км/ч.
Определить среднюю скорость движения автомашины.

2.2 Средняя гармоническая взвешенная. Учитывая, что средние выражают
качественные свойства изучаемых явлений, важно правильно выбрать вид средней  исходя из
взаимосвязей явлений и признаков. Когда статистическая информация не содержит
частот (f_i ) у отдельных вариант (X), а представлена как их произведение M_i=(X_i × f_i), то для
расчёта средней применяется формула средней гармонической взвешенной:

 

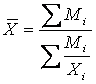
Например: По
имеющимся данным о продаже хлеба «Дарницкий»
определить среднюю цену одной булки хлеба

№ торгового павильона	Цена одной булки хлеба «Дарницкий» весом 0,5 кг, руб. (Xi)	Сумма выручки от продажи хлеба «Дарницкий», руб. (Mi)	Количество проданных булок , шт
1	10,40	10400	1000
2	9,60	4800	500
3	11,20	11200	1000
Итого:		26400	2500

Средняя цена одной булки хлеба может
быть определена делением общей суммы выручки от продажи хлеба на общее
количество проданных булок

 (1). Но количество
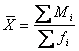
проданных булок в каждом торговом павильоне неизвестно, его можно выразить,
учитывая особенность исходных данных, делением суммы выручки от продажи хлеба
на цену одной булки  (2). Подставим
значение (f_i) – формулу (2) в формулу (1) и
получим

 — формулу средней гармонической взвешенной

Средняя цена одной булки хлеба
составляет:

Используя для расчёта
средней цены формулу средней арифметической простой, получим , что является неверным результатом, так как не учтено
количество проданных булок.

Средняя гармоническая представляет собой
обратную величину средней арифметической из обратных значений осредняемого признака. Если определить частоты ряда
распределения, то можно использовать формулу средней арифметической взвешенной,
но формула средней гармонической взвешенной позволяет избежать промежуточных расчётов.

3.Средняя геометрическая

3.1 Средняя
геометрическая простая применяется для характеристики  средних темпов роста в рядах динамики с
равноотстоящими уровнями и исчисляется по формуле:

где    Х_i — цепной коэффициент роста уровня ряда динамики.

n –
число цепных коэффициентов роста в ряду динамики.

3.2 Средняя
геометрическая взвешенная применяется для характеристики  средних темпов роста в рядах динамики с неравноотстоящими уровнями и исчисляется по формуле:

где f_i – промежуток времени между датами.

4. Средняя хронологическая

4.1 Средняя хронологическая простая

Средний уровень моментного ряда
динамики с равноотстоящими уровнями характеризует средняя хронологическая простая,
которая исчисляется по

формуле:

где    X_i – значение уровня моментного ряда
динамики;

n – число
уровней моментного ряда динамики.

Например: По
имеющимся данным определить средний товарный запас за первое полугодие

Дата	1 января	1 февраля	1 марта	1 апреля	1 мая	1 июня	1 июля
Товарный запас на указанную дату, тыс. руб.	984	1020	1003	998	1260	1254	1190
обозначение	X1	X2	X3	X4	X5	X6	X7

п=7

Средний товарный запас за
полугодие составляет

4.2 Средняя хронологическая взвешенная

Средний уровень моментного ряда
динамики с неравноотстоящими уровнями характеризует средняя
хронологическая взвешенная, которая исчисляется по формуле:

X_i  и X_i+1 
– значение
уровня моментного ряда динамики и уровня, следующего за ним;.  

где f_i – промежуток времени между датами.

Например: Известна списочная численность персонала организации на  некоторые даты 2009 года. Определить
среднесписочную численность персонала за год.

Дата	1.01.2009	1.03.2009	1.06.2009	1.09.2009	1.01.2010
Численность персонала по списку на указанную дату, чел.	1200	1100	1250	1500	1350

Среднесписочная
численность персонала за 2009 год составляет

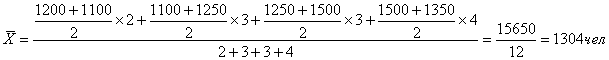
5. Средняя квадратическая

5.1 Средняя квадратическая простая применяется, когда возникает
потребность расчета среднего размера признака, выраженного в квадратных
единицах измерения, для несгруппированных данных. Она
исчисляется как квадратный корнень
из частного от деления суммы квадратов отдельных значений признака на их число
по формуле:

.

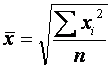
где f_i –
частота ряда распределения или удельный вес в совокупности.

5.2. Средняя квадратическая взвешенная применяется,
когда возникает потребность расчета среднего размера признака, выраженного в
квадратных единицах измерения, для сгруппированных данных. Исчисляется по
формуле:

,

где f_i –
частота ряда распределения или удельный вес в совокупности.

6. Средняя кубическая

6.1 Средняя кубическая простая применяется, когда возникает потребность расчета
среднего размера признака, выраженного в кубических единицах измерения, для несгруппированных данных. Исчисляется по формуле:

 

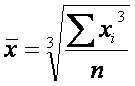
6.2 Средняя кубическая взвешенная применяется, когда возникает потребность расчета
среднего размера признака, выраженного в кубических единицах измерения, для
сгруппированных данных. Исчисляется по формуле:

.

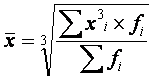
Правило мажорантности
средних величин

Если
рассчитать все виды средних для одних и тех же исходных данных, то значения их
окажутся неодинаковыми. Здесь действует правило мажорантности
средних: с
увеличением показателя степени m увеличивается и
соответствующая средняя величина:

В статистической практике чаще, чем
остальные виды средних взвешенных, используются
средние арифметические и средние гармонические взвешенные.

Кубическое среднее (записать в виде ) представляет собой конкретный экземпляр обобщенных среднего с .

Определение

Для действительных чисел среднее кубическое значение определяется как:

   

Например, среднее кубическое значение двух чисел:

.

Приложения

Он используется для прогнозирования ожидаемого срока службы деталей машин .

Рекомендации