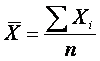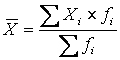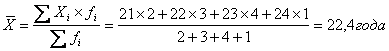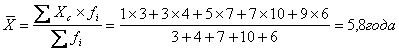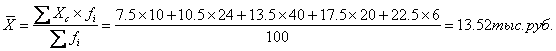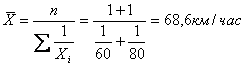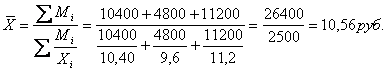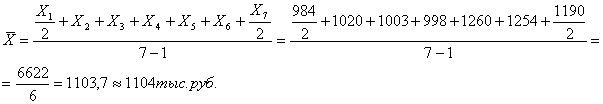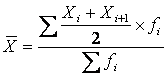Как найти среднее квадратическое взвешенное - Исправление недочетов и поиск решений вместе с Examum.ru

Для определения
степени колеблемости признаков
используется среднее квадратическое
отклонение, широко применяемое в
экономических расчетах.

Среднее квадратическое
отклонение бывает простое и взвешенное.
Оно обозначается буквой σ.

—простое квадратическое
отклонение;
—взвешенное
квадратическое отклонение.

Рассмотрим порядок
вычисления взвешенного среднего
квадратического отклонения.

Вычисляют СА
взвешенную величину из ряда
.

Определяют
отклонения отдельных вариантов от
средней.

Полученные
отклонения возводят в квадрат.
Квадраты отклонений
делят на увеличивают на число случаев
в этих отклонениях, то есть на частоты
.
Затем полученные отклонения суммируют.
Сумму квадратов
отклонений сумму всех чисел членов
ряда:

Таким
образом, получается дисперсия, или
средний квадрат отклонений.

Из величины,
выражающей дисперсию, извлекают
квадратный корень:

Пример. Произведем
вычисление простого и взвешенного
среднеквадратического отклонения. В
табл. 12 показано распределение кип
шерсти по массе при отгрузке.

Таблица
.12

Распределение кип шерсти при отгрузке

Масса одной кипы (), кг	Количество отгруженных кип (f), шт
86	10
90	20
94	10
96	30
100	15
110	15
ИТОГО	100

Требуется определить
СА простую и взвешенную, среднее
квадратическое отклонение простое и
взвешенное.

Определяем средний
вес одной кипы, для чего используем
формулу средней арифметической простой:

Подставим значения:

2. Среднее
квадратическое простое отклонение (не
взвешенное) определяем по формуле:

Для расчета
квадратического отклонения построим
расчетную таблицу(таб. .13).
Таблица .13

Данные для расчета квадратического отклонения

Масса кипы шерсти, кг	Отклонение от средней (= 96 кг)	Квадраты отклонений (х-х_а)²
86	-10(86-96)	100
90	-6	36
94	-2	4
96	0	0
100	+4	16
110	+14	196
ИТОГО

Что характеризует
полученное квадратическое отклонение?

Масса отдельных
кип шерсти отклоняется от средней (96
кг) в одних случаях на большую величину,
в других— на меньшую. В среднем это
отклонение от средней составляет ±7,7
кг. Из этих данных видно и другое: простое
среднее квадратическое отклонение
выражается в тех же именованных числах,
что и средняя величина. Поэтому оно
составляет так называемое абсолютное
отклонение от средней величины. По
данным примера рассчитаем также среднее
квадратическое отклонение (взвешенное)
для характеристики ряда распределения
с неравными частотами. Для этого примем
во внимание количество отгруженных
кип, которые будут составлять частоты(f).

Расчет производим
по формуле:

Построим расчетную
таблицу (табл. .14).

Сначала определяем
среднюю арифметическую взвешенную:

Рассчитаем среднее
квадратическое отклонение (взвешенное):

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.12.2018130.46 Кб297.docx
#
#
#
#
#
#
#
#
#
#

Источник

Средняя арифметическая взвешенная применяется в том случае, когда отдельные значения признака (варианты) встречаются в ряду распределения не с одинаковой частотой (f₁≠ f₂≠ …f_n) и число вариантов не совпадает с частотой их появления.

Пример расчета:

средней арифметической взвешенной
среднего линейного отклонения (показатель вариации)
среднеквадратического отклонения взвешенного (показатель вариации)

При расчете средней арифметической по интервальному вариационному ряду необходимо сначала найти середину интервалов. Это и будут значения x_i, а количество единиц совокупности в каждой группе f_i.При наличии открытого интервала, его ширина принимается равной ширине примыкающего (рядом стоящего) интервала.

Стаж работника, лет

Число работников, чел.

(f_i)

Середина интервала, лет

(x_i)

1-3

3-5

5-7

7-9

9-11

Итого

100

1. Средний стаж работников предприятия определяется по средней арифметической взвешенной. Он будет равен:

$[overline x = frac{{Sigma {xi}{fi}}}{{Sigma {fi}}} Rightarrow ]$

$[overline x = frac{{{x1}{f1} + {x2}{f2} + ... + {xn}{fn}}}{{{f1} + {f2} + ... + {fn}}}]$

$[overline x = frac{{2*10 + 4*28 + 6*48 + 8*10 + 10*4}}{{100}} = frac{{540}}{{100}} = 5,4;]$

2. Размах вариации R=Хmax-Хmin зависит только от двух крайних значений признака: R=11-1=10(лет).

3. Взвешенное среднее линейное отклонение (средний модуль) является средней величиной из абсолютных значений отклонений индивидуальных значений признака от общей средней арифметической величины:

$[begin{array}{l} overline d = frac{{sum left| {{X_i} - overline X } right| times {f_i}}}{{sum {f_i}}} = frac{{left| {2 - 5,4} right|*10 + left| {4 - 5,4} right|*28 + left| {6 - 5,4} right|*48 + left| {8 - 5,4} right|*10 + left| {10 - 5,4} right|*4}}{{100}} = frac{{147.4}}{{100}} = 1.474; end{array}]$

4. Взвешенное среднее квадратическое отклонение определяется как квадратный корень из дисперсии. На столько, в среднем, отклоняется средний стаж работников предприятия по каждой группе от общей средней (среднего стажа по предприятию).

$[mathop sigma nolimits_X = sqrt {frac{{{{sum {left( {mathop Xnolimits_i - mathop {bar X}nolimits_{} } right)} }^2}*mathop fnolimits_i }}{{sum {mathop fnolimits_i } }}} ]$

или

$[mathop sigma nolimits_X = sqrt {frac{{sum {{{mathop Xnolimits_i }^2}*mathop fnolimits_i } }}{{sum {mathop fnolimits_i } }} - mathop {{{bar X}^2}}nolimits_{} } ]$

$[begin{array}{l} {sigma _x} = sqrt {frac{{{{left( {2 - 5,4} right)}^2}*10 + {{left( {4 - 5,4} right)}^2}*28 + {{left( {6 - 5,4} right)}^2}*48 + {{left( {8 - 5,4} right)}^2}*10 + {{left( {10 - 5,4} right)}^2}*4}}{{100}}} = = sqrt {frac{{340}}{{100}}} = 1,84 end{array}]$

5. Коэффициент вариации характеризует колеблемость признака около средней. Если коэффициент вариации не превышает 33%, то совокупность, по рассматриваемому признаку, можно считать однородной. Данная совокупность характеризуется сильной вариацией, т.е. разброс значений по отдельным группам относительно общего среднего стажа по предприятию значителен.

$[V = frac{sigma }{{bar {rm X}}}*100,% = frac{{1,84}}{{5,4}}*100,% = 34,07,% ]$

Техника расчета средней арифметической «способом моментов»

$[overline {x'} = frac{{sum {left( {frac{{x - A}}{K}} right) cdot f} }}{{sum f }}]$

Заработная плата

Число рабочих

Центр интервала

Х-А^*

Х’=(Х-А):К^**

Х’f

до 250

250 – 275

275 – 300

300 – 325

325 и более

237,5

262,5

287,5

312,5

337,5

– 50

– 25

+25

+50

– 2

– 1

– 20

-15

+12

+10

Итого

-13

* – в качестве (А) обычно берут значение х, стоящее в середине вариационного ряда (А=287,5)

** -( K) обычно равно ширине интервала (K=25)

$[overline {x'} = frac{{sum {x' cdot {f_i}} }}{{sum {{f_i}} }} = frac{{ - 13}}{{60}} = - 0,2176]$

Источник

Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).

Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.

Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.

Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.

Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.

Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу.

Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.

ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:

средняя арифметическая;
средняя гармоническая;
средняя геометрическая;
средняя квадратическая.

Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.

Средняя арифметическая простая (невзвешенная) – вычисляется когда каждый вариант совокупности встречается только один раз.
Средняя арифметическая (взвешенная) – варианты повторяются различное число раз, при этом число повторений вариантов называется частотой, или статистическим весом.

ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН

Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле (8.8):

(8.8 -формула средней арифметической простой)

где х_i – вариант, а n – количество единиц совокупности.
Пример вычисления средней арифметической простой. Провели опрос о желаемом размере заработной платы у пяти сотрудников офиса. По результатам опроса выяснили, что желаемый размер заработной платы составляет соответственно для каждого сотрудника: 50000, 100000, 200000, 350000, 500000 рублей человек. Рассчитаем среднюю арифметическую простую по формуле (8.8):Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
Средняя арифметическая взвешенная формула 8.9.

(8.9 -формула средней арифметической взвешенной)

где х_i – вариант, а f_i – частота или статистический вес.
Пример вычисления средней арифметической взвешенной. Результаты опроса всех работников офиса приведены в табл. 8.2.

Таблица 8.2 – Результаты опроса работников офиса

Желаемый размер заработной платы, тыс.руб х_i	Количество работников f_i	х_if_i
1	2	3
50 100 200 350 500	6 10 20 9 5	300 1000 4000 3150 2500
Итого	50	10950

Пример. Вычислим (ориентируясь на итоговые строки таблицы) желаемый размер заработной платы, 50 сотрудников офиса (используем формулу 8.9):

Пример вычисления средней арифметической взвешенной

Вывод: в среднем желаемый размер заработной платы по результатам опроса 50 человек составил 219 тысяч рублей.

Среднеарифметическая – всегда обобщающая количественная характеристика варьирующего признака совокупности.

Средняя гармоническая вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины.
Средняя гармоническая простая представлена ниже:

(8.10 – формула средней гармонической простой)

Средняя гармоническая взвешенная определяется по формуле

(8.11- формула средней гармонической взвешенной)

где x_i – вариант, n – количество вариантов, V_i – веса для обратных значений x_i.

Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, чем взвешенная. Для иллюстрации области ее применения воспользуемся упрощенным условным примером.

Пример (вычисление средней гармонической простой (невзвешенной)).

Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 5 мин., второй – 15 мин.

Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?

На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. если используем среднюю арифметическую простую получим: (5+15):2=10, мин.

Проверим обоснованность такого подхода на примере одного часа (60 минут) работы. За этот час первый работник обрабатывает 12 заказов (60:5), второй – 4 заказа (60:15), что в сумме составляет 16 заказов.

Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится: (60/10) + (60/10) = 12 заказов (что не соответствует истине).

Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов, т.е. используем среднюю гармоническую:

Пример вычисления средней гармонической простой (невзвешенной)

Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится: (60/7,5) + (60/7,5) = 16 заказов

Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения Wj для единиц совокупности равны (в рассмотренном примере рабочий день у сотрудников одинаковый).

Пример (вычисление средней гармонической взвешенной) В ходе торгов на валютной бирже за первый час работы заключено пять сделок. Данные о сумме продажи рублей и курсе рубля по отношению к доллару США приведены в табл.8.3.

Таблица 8.3 – Данные о ходе торгов на валютной бирже (цифры условные)

Номер сделки	Сумма продажи V, млн руб.	Курс рубля x, руб. за 1 дол.	V/x
1	2	3	4
1 2 3 4 5	455,00 327,50 528,00 266,00 332,50	65,00 65,50 66,00 66,50 66,50	7,00 5,00 8,00 4,00 5,00
итого	1909,00	–	29,00

Для того чтобы определить средний курс рубля по отношению к доллару, нужно найти соотношение между суммой продажи рублей, которые затрачены на покупку долларов в ходе всех сделок, и суммой приобретенных в результате этих сделок долларов.

Вывод: средний курс за один доллар составил 65,83 руб.;
Если бы для расчета среднего курса была использована средняя арифметическая простая:то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.

Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин как отношение каждого уровня ряда к предыдущему уровню.
Средняя геометрическая простая рассчитывается по формуле 8.12

(8.12)

Если использовать частоты m, получим формулу средней геометрической взвешенной
Средняя геометрическая взвешенная рассчитывается по формуле 8.13

(8.13)

Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.

Для несгруппированных данных используют формулу средней квадратической простой

Средняя квадратическая простая (формула 8.14)

8.14

Для сгруппированных данных используют формулу средней квадратической взвешенной

Средняя квадратическая взвешенная (формула 8.15)

(8.15) – Формула -средняя квадратическая взвешенная

Средние арифметическая, гармоническая, геометрическая и квадратическая, рассчитанные для одного и того же ряда вариантов, отличаются друг от друга. Их численное значение возрастает с ростом показателя степени в формуле степенной средней правило мажорантности средних А.Я. Боярского, т.е.

Мода и Медиана (структурные средние) формулы и примеры вычисления см. по ссылке

Источник

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3.

Расчёт степенных средних величин.

Студент должен:

знать:

— область применения и методику расчёта
степенных средних величин;

уметь:

— исчислять
степенные средние
величины;

— формулировать вывод по полученным
результатам.

Методические указания

Средней величиной называется обобщающая величина
статистической совокупности, выражающая типический уровень изучаемого признака.
Она выражает величину признака, отнесённую к единице совокупности.

К степенным средним
относятся средняя арифметическая, средняя
гармоническая, средняя хронологическая, средняя геометрическая, средняя квадратическая, средняя кубическая.

Средняя величина всегда
обобщает количественную вариацию признака, т. е. в средних величинах погашаются
индивидуальные различия признака у отдельных единиц совокупности, обусловленные
случайными обстоятельствами. Средняя величина позволяет сравнивать значения
признака у единиц, относящихся к разным совокупностям.

Принципы применения средних величин:

1)
Необходим
обоснованный выбор признака у единиц совокупности, для которого рассчитывается
средняя.

2)
При
определении средней величины в каждом конкретном случае следует исходить из
качественного содержания осредняемого признака,
учитывать взаимосвязь изучаемых признаков и особенность имеющихся исходных
данных;

3)
Средняя
величина должна, прежде всего, рассчитываться по однородной совокупности.
Однородную совокупность позволяет получить метод группировки.

4)
Общие
средние должны подкрепляться групповыми средними.

5)
Средняя
величина не может быть меньше минимального значения и больше максимального
значения признака в совокупности.

Область применения и методика расчёта степенных
средних величин:

1. Средняя арифметическая

1.1 Средняя
арифметическая простая.

При небольшом объёме
исходной информации, когда исходные данные не сгруппированы, применяется средняя
арифметическая простая,которая рассчитывается по формуле:

где ΣX_i— сумма
значений;

n— число
значений.

Например: В
бригаде четверо рабочих в возрасте 21,
22, 23 и 24 года. Средний возраст рабочего бригады составляет

1.2 Средняя арифметическая взвешенная.

Когда исходные данные сгруппированы,
то расчёт средней производится по

формуле средней арифметической
взвешенной:

где f_i –
частота ряда распределения, с которой отдельные варианты встречаются в
совокупности (или удельный вес отдельных значений во всей совокупности).

Например: Рабочие бригады по возрасту распределились следующим
образом:

Возраст рабочих, лет (X)	21	22	23	24
Численность рабочих, чел. (f_i)	2	3	4	1

Средний возраст рабочего
бригады составляет

Если
исходная информация представлена в виде
интервального ряда распределения,
то средняя арифметическая взвешенная определяется по формуле:

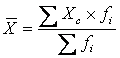
где X_c —
центральное (серединное) значение признака в интервале.

Например: По
имеющимся данным определить средний стаж рабочего бригады:

Стаж работы, лет	0 — 2	2 — 4	4 — 6	6 — 8	8 — 10
Численность рабочих, чел. (f_i)	3	4	7	10	6

Для расчёта средней
арифметической взвешенной интервального ряда распределения определим центральное
(серединное) значение признака в каждом интервале. Среднее значение интервала
находится как полусумма нижней границы данного
интервала и нижней границы следующего интервала:

Стаж работы, лет	0 — 2	2 — 4	4 — 6	6 — 8	8 — 10
(X_c)

Оформим исходные данные
а следующем виде:

Стаж работы, лет	0 — 2	2 — 4	4 — 6	6 — 8	8 — 10
(X_c)	1	3	5	7	9
Численность рабочих, чел. (f_i)	3	4	7	10	6

Средний стаж рабочего бригады
составляет

Если в интервальном ряду
распределения имеются «открытые» интервалы, то для установления центральных
(серединных) значений «открытых» интервалов на каждый из них условно
распространяется величина смежного «закрытого» интервала.

Например: Работники организации по величине заработной платы за январь 2010 года
распределились следующим образом:

Группы работающих по величине заработной платы за январь 2010 года, тыс.руб.	Численность работников, в % к итогу (f_i)
До 9	10
9 — 12	24
12 — 15	40
15 — 20	20
20 и выше	6
Итого:	100

Определить по имеющимся данным
среднюю зарплату работников организации.

Для расчёта средней
арифметической взвешенной интервального ряда распределения определим центральное
(серединное) значение признака в каждом интервале. На каждый открытый интервал
условно распространим величину смежного закрытого интервала:

Группы работающих по величине заработной платы за январь 2010 года, тыс.руб.	Численность работников, в % к итогу (f_i)	Центральное (серединное) значение интервала (X_c), руб
До 9	10
9 — 12	24
12 — 15	40
15 — 20	20
20 и выше	6
Итого:	100

Частоты
при расчете средних арифметических могут быть выражены
не только абсолютными величинами, но и относительными величинами – частостями Результаты применительно к одинаковым
вариантам будут совпадать. В данном примере численность работников
выражена не частотами, а частостями – удельными
весами численности отдельных групп во всей совокупности, что не влияет на
порядок расчёта средней.

Средняя зарплата работников
организации составляет:

Необходимо небольшое
пояснение применительно к расчету средней в
интервальных рядах распределения. В действительности распределение отдельных
вариантов в пределах интервала может оказаться неравномерным. В этом случае
середина интервала будет в той или иной степени отличаться от
фактической средней по интервалу. Это в свою очередь может повлиять на
правильность общей средней, исчисленной по данным интервального ряда. Степень
расхождения зависит от ряда причин. Во-первых, от числа вариант, чем больше
число вариант, тем вероятнее, что середина интервала будет мало отличаться от групповой средней. Во-вторых, от величины интервала. Если
интервал невелик, то ошибка будет незначительной, т.к. групповая средняя будет
мало отличаться от середины интервала. В-третьих, от характера распределения.
Чем симметричнее распределение, тем ошибка меньше. В-четвертых, размер ошибки
зависит от принципа построения интервального ряда. При равных интервалах
середина интервала будет ближе к средней по данной
группе. При наличии открытых интервалов расхождение, как правило, взрастает
из-за условного обозначения неизвестных границ. Общая
средняя равна средней из частных (групповых) средних, взвешенных по численности
соответствующих частей совокупности. Это правило имеет большое значение для
всей статистики – организации сбора и обработки данных, их анализа.

Свойства средней арифметической:

1. Произведение средней на сумму частот всегда равно сумме
произведений вариант на частоты. Другими словами, постоянный
множитель может быть вынесен за знак средней.

2. Если от каждой варианты отнять (прибавить) какое-либо
произвольное число, то новая средняя уменьшится (увеличится) на то же число:

3. Если каждую варианту умножить (разделить) на какое-то произвольное
число, то средняя арифметическая увеличится
(уменьшится) во столько раз

4. Если все частоты (веса) разделить или умножить на
какое-либо число, то средняя арифметическая от этого не изменится. Дело в том,
что веса при исчислении средней арифметической выполняют роль
удельного веса (соотношений между группами по количеству единиц). Поэтому
замена частот частостями не меняет значения средней.

5. Сумма отклонений отдельных вариантов от средней
арифметической всегда равняется нулю.

Перечисленные свойства могут быть использованы для того,
чтобы облегчить технику исчисления средней арифметической.

Например. Можно из всех значений признака вычесть произвольную
постоянную величину (лучше значение серединной варианты или варианты с
наибольшей частотой), полученные разности сократить на общий множитель (лучше
на величину интервала), а частоты выразить частостями
(в процентах) и исчисленную среднюю умножить на общий множитель и прибавить
произвольную постоянную величину. Иногда этот способ расчета средней
арифметической также называется способом расчета от условного нуля. Широкое
применение для обработки статистических материалов современных ЭВМ сужает
необходимость исчисления средних по упрощенным схемам.

2. Средняя гармоническая

2.2 Средняя гармоническая простая. Если объёмы явлений, т.е. произведения Х_i×f_i по каждой
единице равны, то для расчёта средней применяется формула средней гармонической простой:

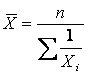
Например: Две
автомашины прошли один и тот же путь: первая со скоростью 60 км/ч, вторая со
скоростью 80 км/ч.
Определить среднюю скорость движения автомашины.

2.2 Средняя гармоническая взвешенная. Учитывая, что средние выражают
качественные свойства изучаемых явлений, важно правильно выбрать вид средней исходя из
взаимосвязей явлений и признаков. Когда статистическая информация не содержит
частот (f_i ) у отдельных вариант (X), а представлена как их произведение M_i=(X_i× f_i), то для
расчёта средней применяется формула средней гармонической взвешенной:

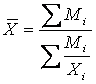
Например: По
имеющимся данным о продаже хлеба «Дарницкий»
определить среднюю цену одной булки хлеба

№ торгового павильона	Цена одной булки хлеба «Дарницкий» весом 0,5 кг, руб. (*X_i*)	Сумма выручки от продажи хлеба «Дарницкий», руб. (*M_i*)	Количество проданных булок , шт
1	10,40	10400	1000
2	9,60	4800	500
3	11,20	11200	1000
Итого:		26400	2500

Средняя цена одной булки хлеба может
быть определена делением общей суммы выручки от продажи хлеба на общее
количество проданных булок

(1). Но количество
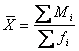
проданных булок в каждом торговом павильоне неизвестно, его можно выразить,
учитывая особенность исходных данных, делением суммы выручки от продажи хлеба
на цену одной булки (2). Подставим
значение (f_i) – формулу (2) в формулу (1) и
получим

— формулу средней гармонической взвешенной

Средняя цена одной булки хлеба
составляет:

Используя для расчёта
средней цены формулу средней арифметической простой, получим , что является неверным результатом, так как не учтено
количество проданных булок.

Средняя гармоническая представляет собой
обратную величину средней арифметической из обратных значений осредняемого признака. Если определить частоты ряда
распределения, то можно использовать формулу средней арифметической взвешенной,
но формула средней гармонической взвешенной позволяет избежать промежуточных расчётов.

3.Средняя геометрическая

3.1 Средняя
геометрическая простая применяется для характеристики средних темпов роста в рядах динамики с
равноотстоящими уровнями и исчисляется по формуле:

где Х_i— цепной коэффициент роста уровня ряда динамики.

n –
число цепных коэффициентов роста в ряду динамики.

3.2 Средняя
геометрическая взвешенная применяется для характеристики средних темпов роста в рядах динамики с неравноотстоящими уровнями и исчисляется по формуле:

где f_i – промежуток времени между датами.

4. Средняя хронологическая

4.1 Средняя хронологическая простая

Средний уровень моментного ряда
динамики с равноотстоящими уровнями характеризует средняя хронологическая простая,
которая исчисляется по

формуле:

где X_i – значение уровня моментного ряда
динамики;

n – число
уровней моментного ряда динамики.

Например: По
имеющимся данным определить средний товарный запас за первое полугодие

Дата	1 января	1 февраля	1 марта	1 апреля	1 мая	1 июня	1 июля
Товарный запас на указанную дату, тыс. руб.	984	1020	1003	998	1260	1254	1190
обозначение	X₁	X₂	X₃	X₄	X₅	X₆	X₇

п=7

Средний товарный запас за
полугодие составляет

4.2 Средняя хронологическая взвешенная

Средний уровень моментного ряда
динамики с неравноотстоящими уровнями характеризует средняя
хронологическая взвешенная, которая исчисляется по формуле:

X_i и X_i₊₁
– значение
уровня моментного ряда динамики и уровня, следующего за ним;.

где f_i– промежуток времени между датами.

Например: Известна списочная численность персонала организации на некоторые даты 2009 года. Определить
среднесписочную численность персонала за год.

Дата	1.01.2009	1.03.2009	1.06.2009	1.09.2009	1.01.2010
Численность персонала по списку на указанную дату, чел.	1200	1100	1250	1500	1350

Среднесписочная
численность персонала за 2009 год составляет

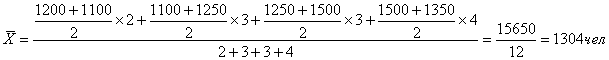
5. Средняя квадратическая

5.1 Средняя квадратическая простая применяется, когда возникает
потребность расчета среднего размера признака, выраженного в квадратных
единицах измерения, для несгруппированных данных. Она
исчисляется как квадратный корнень
из частного от деления суммы квадратов отдельных значений признака на их число
по формуле:

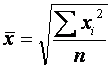
где f_i –
частота ряда распределения или удельный вес в совокупности.

5.2. Средняя квадратическая взвешенная применяется,
когда возникает потребность расчета среднего размера признака, выраженного в
квадратных единицах измерения, для сгруппированных данных. Исчисляется по
формуле:

где f_i –
частота ряда распределения или удельный вес в совокупности.

6. Средняя кубическая

6.1 Средняя кубическая простая применяется, когда возникает потребность расчета
среднего размера признака, выраженного в кубических единицах измерения, для несгруппированных данных. Исчисляется по формуле:

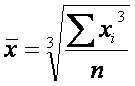
6.2 Средняя кубическая взвешенная применяется, когда возникает потребность расчета
среднего размера признака, выраженного в кубических единицах измерения, для
сгруппированных данных. Исчисляется по формуле:

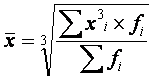
Правило мажорантности
средних величин

Если
рассчитать все виды средних для одних и тех же исходных данных, то значения их
окажутся неодинаковыми. Здесь действует правило мажорантности
средних: с
увеличением показателя степени m увеличивается и
соответствующая средняя величина:

В статистической практике чаще, чем
остальные виды средних взвешенных, используются
средние арифметические и средние гармонические взвешенные.

Источник

Распределение кип шерсти при отгрузке

Данные для расчета квадратического отклонения

Техника расчета средней арифметической «способом моментов»

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://stat-ist.ru/wp-content/uploads/2019/11/Srednie-pokazateli-300x258.jpg" alt="Средние" width="140" height="120" />

ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН