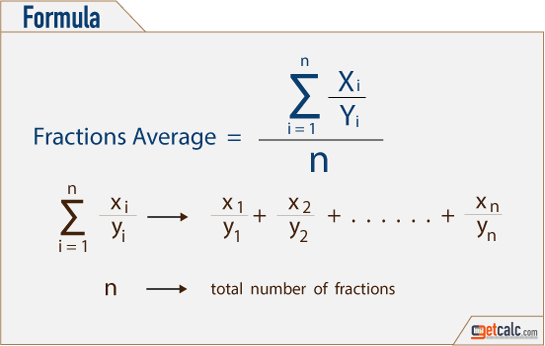Multiple Fractions Average
Arithmetic Operator :
Fractions & Mixed Numbers:
enter space separated input values
Average :
share
feedback
calculator
info
history
</>
Average of Fractions and Mixed Numbers Calculator
getcalc.com’s Fractions and Mixed Numbers Average calculator is an online basic math function tool to find an equivalent fraction for the average between two or more fractions with same or different (equal or unlike) denominators, positive or negative fractions, regular or irregular fractions, mixed numbers and whole numbers. This calculator also featured to generate the complete work with steps for any given valid input values to assist elementary or grade school students to solve the fractions average worksheet or homework problems effectively. Users can generate the step by step calculation for the corresponding input values or verify the similar calculation results by using this fractions and mixed numbers average calculator.
More Fraction Calculators
Multiple Fractions Average and Formula
Average of Multiple Fractions is a basic arithmetic operation used to find the average between two or more fractions with same or different (equal or unlike) denominators, positive or negative fractions, regular or irregular fractions, mixed numbers and whole numbers. The below formula is the mathematical representation for average of multiple fractions with like or unlike denominators, positive or negative fractions or mixed or whole numbers.
How to Find the Average of Two or More Fractions
The average of fractions is the sum of all fractions divided by the count of total number of fractional numbers. Any whole number in the group of fractions considered as a fraction with denominator 1. For fractions with same or equal denominators, the sum is the simplified fraction of sum of numerators divided by the common denominators, whereas, for fractions with unlike, unequal or different denominators, the LCM (least common multiple) of all denominators must be multiplied with both numerators and denominators of each fractions to bring the common denominator to perform the addition between them. By using this tool and associated information, users may refer the below solved examples with step by step calculation to learn how to find the average of two, three or more fraction numbers with same or different denominators, or the average of regular, irregular, positive or negative fractions and whole numbers. user may found the answers for the following queries
Average of Three Fractions with Different Denominators
The below solved example with step by step calculation or workout may help users to learn how to find the average of three fractions with unlike, unequal or different denominators.
Problem
Find the average of fractions 1/2, 1/3 and 1/4.Step by step workout
step 1 Address formula and input values.
Input values:
1/2, 1/3 , 1/4
Total count = 3
(1/2 + 1/3 + 1/4)/3 = ?
step 2 To find the sum for fractions with different denominators, find the LCM (least common multiple) for all denominators.
12 is the LCM for 2, 3 and 4.
step 3 Multiply LCM 12 with each numerators and denominators
= (1 x 12)/(2 x 12) + (1 x 12)/(3 x 12) + (1 x 12)/(4 x 12)
step 4 Simplify the above expression to bring same denominators for all fractions.
= 6/12 +4/12+3/12
= (6 + 4 + 3)/12
step 5 Add all numerators and rewrite it in a single form.
= 13/12
1/2+1/3+1/4= 13/12
step 6 Divide the sum by total count of fractions.
(1/2 + 1/3 + 1/4)/3 = (13/12)/3
13/12is the average of three fractions 1/2, 1/3 and 1/4.
Average of Three Fractions with Same Denominators
The below solved example with step by step calculation or workout may help users to learn how to find the average of three fractions with same, equal or common denominators.
Problem
Find the average of fractions 5/9, 6/9 and 7/9.
Step by step workout
step 1 Address formula and input values.
Input values:
5/9,6/9,7/9
Total count = 3
(5/9 + 6/9 + 7/9)/3 = ?
step 2 Find the sum of all fractions.
(5 + 6 + 7)/9=18/9
=18/9
step 3 Divide the sum by total count of fractions and simplify
= (18/9)/3
(5/9 + 6/9 + 7/9)/3 = 2/3 in fraction form
(5/9 + 6/9 + 7/9)/3 = 0.66 in decimal form
2/3 or 0.66 is the average of three fractions 5/9, 6/9 and 7/9.
Average of Multiple Fractions and Whole Numbers
The below solved example with step by step workout may help users to learn how to find the average of multiple regular or irregular fractions with like or different denominators and whole numbers.
Problem
Find the average of fractions and whole numbers 2/3, 3/4, 6, 4/5, 3, 5/6 and 8/9.Step by step workout
step 1 Address formula and input values.
Input values:
2/3,3/4,6,4/5, 3 ,5/6,8/9
Total count = 7
2/3,3/4,6,4/5, 3 ,5/6,8/9 = ?
step 2 Convert whole numbers to fractions and rewrite as below
Any whole number or integer is a rational number (quotient of 1), hence the denominators for all whole numbers is 1 and can be written as
6 =6/1
3 =3/1
step 3 Arrange all the numbers as fractions
2/3+3/4+6/1+4/5+ 3/1+5/6+ 8/9
step 4 To find the sum for fractions with different denominators, find the LCM (least common multiple) for all denominators.
180 is the LCM for 3, 4, 1, 5, 1, 6 and 9.
step 5 multiply LCM 180 with each numerators and denominators
=(2 x 180)/(3 x 180)+(3 x 180)/(4 x 180) +(6 x 180)/(1 x 180)+ (4 x 180)/(5 x 180)+(3 x 180)/(1 x 180)+(5 x 180)/(6 x 180)+(8 x 180)/(9 x 180)
step 6 simplify the above expression to bring same denominators for all fractions.
=120/180+135/180+1080/180+144/180+540/180+150/180+160/180
=(120 + 135 + 1080 + 144 + 540 + 150 + 160)/180
step 7 add all numerators and rewrite it in a single form.
=2329/180
=2/3+3/4+6/1+4/5+ 3/1+5/6+ 8/9=2329/180
step 8 Divide the sum by total count of fractions.
(2/3 + 3/4 + 6/1 + 4/5 + 3/1 + 5/6 + 8/9)/7 = (2329/180)/7
= 2329/1260
2329/1260 is the average of fractions and whole numbers 2/3, 3/4, 6, 4/5, 3, 5/6 and 8/9.
Average of Multiple Positive and Negative Fractions
The below solved example with step by step calculation may help users to learn how to find the average of multiple whole numbers, positive and negative fractions (with unlike or different denominators).
Problem
Find the average of multiple whole numbers, positive and negative fractions 2/3, 2/4, -2/5, 6, 2/7, -3/9 and 2/9.Step by step workout
step 1 Address formula and input values.
Input values:
2/3,2/4,-2/5, 6 ,2/7,-3/9
Total count = 6
(2/3 + 2/4 + -2/5 + 6 + 2/7 + -3/9)/6 = ?
step 2 Convert the whole numbers to fractions, if any
6 = 6/1
step 3 Arrange all the numbers as fractions.
2/3+2/4+-2/5+6/1+2/7+-3/9
step 4 To find the sum for fractions with different denominators, find the LCM (least common multiple) for all denominators.
1260 is the LCM for 3, 4, 5, 1, 7 and 9.
step 5 Multiply LCM 1260 with each numerators and denominators
=(2 x 1260)/(3 x 1260)+(2 x 1260)/(4 x 1260)—(2 x 1260)/(5 x 1260)+(6 x 1260)/(1 x 1260)+(2 x 1260)/(7 x 1260)—(3 x 1260)/(9 x 1260)
step 6 Simplify the above expression to bring same denominators for all fractions.
=(2 x 420)/(1260)+(2 x 315)/(1260)—(2 x 252)/(1260)+(6 x 1260)/(1260)+(2 x 180)/(1260)—(3 x 150)/(1260)
=840/1260+ 630/1260— 504/1260 + 7560/1260 + 360/1260 — 450/1260
step 7add all numerators and rewrite it in a single form.
=(840 + 630 + 504 + 7560 + 360 + 450)/1260
=10344/1260
=862/105
(2/3 + 2/4 + -2/5 + 6 + 2/7 + -3/9) = 862/105
step 8 Divide the sum by total count of fractions.
(2/3 + 3/4 + 6/1 + 4/5 + 3/1 + 5/6 + 8/9)/6 = (862/105)/6
= (431/105)/3
=431/315
431/315 is the average of multiple whole numbers, positive and negative fractions 2/3, 2/4, -2/5, 6, 2/7, -3/9 and 2/9.
Average of Two or More Fractions and Mixed Numbers
The below solved example for average of two or more fractions, mixed numbers and whole numbers. The fraction numbers include regular, irregular, negative or positive fractions with same or unlike denominators. The below step by step work guides how to find equivalent fraction for the average between multiple fractions, mixed and whole numbers 2/3, 4/5, 6/7, 3(8/9), 6(1/2) and 9.
Problem
Find the average between multiple fractions, mixed and whole numbers 2/3, 4/5, 6/7, 3(8/9), 6(1/2) and 9.Step by step workout
step 1 Address formula and input values.
Input values:
2/3,4/5,6/7, 3 8/9, 6 1/2, 9
Total count = 6
(2/3 + 4/5 + 6/7 + 3(8/9) + 6(1/2) + 9)/6 = ?
step 2 Convert the whole numbers to fractions, if any
9 = 9/1
step 3 Convert the mixed fractions to fractions, if any
38/9= ((3 x 9) + 8)/9= 35/9
61/2= ((6 x 2) + 1)/2= 13/2
step 4 Arrange all the numbers as fractions.
2/3+4/5+6/7+35/9+13/2+9/1
step 5 To find the sum for fractions with different denominators, find the LCM (least common multiple) for all denominators.
630 is the LCM for 3, 5, 7, 9, 2 and 1.
step 6 Multiply LCM 630 with each numerators and denominators
=(2 x 630)/(3 x 630)+(4 x 630)/(5 x 630)+(6 x 630)/(7 x 630)+(35 x 630)/(9 x 630)+(13 x 630)/(2 x 630)+(9 x 630)/(1 x 630)
step 7 Simplify the above expression to bring same denominators for all fractions.
=(2 x 210)/(630)+(4 x 126)/(630)+(6 x 90)/(630)+(35 x 70)/(630)+(13 x 315)/(630)+(9 x 630)/(630)
=420/630+504/630+54/630+2450/630+4095/630+5670/630
step 8 Add all numerators and rewrite it in a single form.
=(420 + 504 + 54 + 2450 + 4095 + 5670)/630
=13193/630
(2/3 + 4/5 + 6/7 + 3(8/9) + 6(1/2) + 9) = 13193/630
step 9 Divide the sum by total count of fractions.
(2/3 + 4/5 + 6/7 + 3(8/9) + 6(1/2) + 9)/6 = (13193/630)/6
=13193/3780
13193/3780 is the average of multiple fractions, mixed and whole numbers 2/3, 4/5, 6/7, 3(8/9), 6(1/2) and 9.
Правила ввода
Вводить можно целые(1, 2, 3, -7), десятичные(0.25, -1.15), дробные(-1/8, 32/9). Если необходимо ввести смешанное число, то нужно перед вводом перевести его в неправильную обыкновенную дробь. Т.е. 1 целая 1/2 вводить нужно будет как 3/2.
При вводе десятичных дробей использовать точку. Запятая зарезервирована под разделитель.
В качестве разделителя можно использовать любой символ кроме цифр(0-9), слэша(/), точки(.), знака минус(-). Остальные символы и перенос строки будут программой заменены на разделители.
Определение среднего арифметического
Среднее арифметическое чисел это число, равное отношению этих чисел к их количеству.
Формула среднего арифметического
m = (a1+a2+a3+…+an)/n
где a1, a2, a3…an — ряд чисел
n — количество чисел
Пример нахождения среднего арифметического
Дан ряд чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 необходимо найти среднее арифметичское этих чисел.
Для решения этой задачи нам необходимо сумму этих чисел 55 разделить на количество этих чисел 10.
m = (1+2+3+4+5+6+7+8+9+10)/10 = 55/10 = 5.5
Пример нахождения среднего арифметического дробей
Даны дроби 1/2, 1/4, 1/8, 1/16 необходимо найти среднее арифметичское этих чисел.
Для решения этой задачи нам необходимо просуммировать эти дроби 1/2+1/4+1/8+1/16=(8+4+2+1)/16=15/16. Затем полученное число разделить на количество этих дробей (15/16)/4=(15/16)×(1/4)=15/64
m = (1/2+1/4+1/8+1/16)/4=15/64
Пример нахождения среднего арифметического десятичных дробей
Даны десятичные дроби 0.2, 0.3, 0.4 необходимо найти среднее арифметичское этих дробей.
Для решения этой задачи нам необходимо просуммировать эти дроби 0.2+0.3+0.4=0.9. Затем полученное число разделить на количество этих дробей 0.9/3=0.3
m = (0.2+0.3+0.4)/3=0.3
Возможно, вы слышали выражения «средний балл за контрольную», «среднее количество осадков» или «средняя годовая температура». Этот урок посвящён среднему арифметическому: тому, что это такое, как найти среднее арифметическое натуральных чисел и дробей, и где это может пригодиться.
Знакомство со средним арифметическим
Решавр, Вообразавр и Иксератопс собирали грибы. Решавр нашёл $5$ грибов, Вообразавр – $7$, а Иксератопс целых $9$! Друзья решили разделить найденное количество грибов поровну.
Они сложили все грибы в кучку, а потом каждый взял себе равное число грибов, то есть они поделили общее количество на $3$.
$5 + 7 + 9 = 21$
$21 : 3 = 7$
То число грибов, которое получилось у каждого из друзей, будет средним арифметическим.
Среднее арифметическое нескольких чисел – это сумма этих чисел, разделённая на количество слагаемых.
Задачи на нахождение среднего арифметического натуральных чисел
Автомобиль $2$ часа ехал через город со скоростью $30$ км/ч, по пригороду час со скоростью $60$ км/час, а затем ещё $3$ часа по трассе со скоростью $100$ км/час. Вычислите среднюю скорость автомобиля.
Сначала найдём сумму всех расстояний. У нас получится $30 cdot 2 + 60 + 100 cdot 3 = 420$
Теперь разделим эту сумму расстояний на количество часов.
$$420 : 6 = 70$$
Следовательно, если бы автомобиль ехал со скоростью $70$ км/ч в течение такого же времени ($6$ часов), он проехал бы такое же расстояние.
Рассмотрим другую задачу.
Первый рабочий за рабочий день собирает $50$ деталей, второй – $44$ более сложные детали, а третий работает над самыми сложными и делает за день гораздо меньше деталей. Сколько деталей он делает, учитывая, что средняя производительность всех трёх рабочих $38$ деталей за смену?
Зная, что средняя производительность $38$, а рабочих трое, мы можем найти сумму деталей, которые они собирают за день.
$$38 cdot 3 = 114$$
Теперь просто вычтем из этого числа то, что делают первые двое рабочих и найдём количество деталей, которые делает третий.
$$114-50-44 = 20$$
Показать проверку
Скрыть
$$(50 + 44 + 20) : 3 = 114 : 3 = 38$$
Как найти среднее арифметическое десятичных дробей
Решать задачи на среднее арифметическое достаточно просто, если речь идёт о натуральных числах. Ненамного сложнее дело обстоит с десятичными дробями.
На рисунке 3 изображены три отрезка. Длина отрезка АВ $5.9$ см, отрезка CD – $7.3$ см, а отрезок EF равен среднему арифметическому первых двух отрезков. Какова длина отрезка EF?
Сложим длины отрезков АВ и CD и вычислим их среднюю длину.
$$5.9 + 7.3 = 13.2$$
$$13.2 : 2 = 6.6$$
Теперь решим задачу на нахождение слагаемых. Два кролика ели морковку, серый кролик съел в $1.4$ раза больше морковки, чем белый. Сколько морковки съел каждый, если среднее количество съеденного – $7.5$ морковок?
Начинаем «распутывать» наш пример. Если мы знаем, что среднее арифметическое двух чисел – $7.5$, значит, их сумма – $7.5 cdot 2 = 15$
Примем количество съеденного белым кроликом за $x$, тогда серый съел $1.4 cdot x$. Можно составить уравнение:
$$1.4 cdot x + x = 15$$
Вычислим, сколько съел каждый из кроликов.
Показать решение
Скрыть
Сначала найдём значение выражения.
$$1.4 cdot x + x = 2.4 cdot x = 15$$
$$x = 15 : 2.4 = 6.25$$
Мы получили число моркови, которую съел белый кролик. Теперь давайте определим, сколько съел серый.
$$6.25 cdot 1.4 = 8.75$$
Проверим наше решение, сложив количество съеденного обоими кроликами и найдя среднее арифметическое.
$$8.75 + 6.25 = 15$$
$$15 : 2 = 7.5$$
Значит, наше решение было верным.
Как найти среднее арифметическое обыкновенных дробей
Вычислять среднее арифметическое обыкновенных дробей приходится не так уж часто. Но давайте рассмотрим, как это делается.
Особенность поиска среднего арифметического обыкновенных дробей состоит в том, что нужно складывать их, а, значит, приводить к общему знаменателю.
Напомним, что приведение к общему знаменателю основывается на основном свойстве дроби, которое позволяет умножить обе части дроби на одно и то же число без изменения значения. Таким образом, мы можем найти для дробных слагаемых дополнительные множители, с помощью которых знаменатели слагаемых станут одинаковыми.
Найдём среднее арифметическое дробей $frac{2}{3}$ и $frac{4}{7}$.
Мы можем выполнить сложение только в том случае, если у обоих слагаемых будет одинаковый знаменатель. Сначала нужно понять, к какому наименьшему общему знаменателю нужно привести эти дроби. Для этого требуется найти число, которое делится и на $3$, и на $7$. Это число будет называться НОК (наименьшее общее кратное). Для чисел $3$ и $7$ это будет произведение этих чисел, $21$.
Для того чтобы вычислить дополнительные множители, нужно разделить НОК на каждый из знаменателей. Таким образом, для $3$ дополнительным множителем будет $7$, а для $7$ это будет $3$.
Умножаем обе части дроби на один и тот же дополнительный множитель.
$$frac{2}{3} = frac{2cdot 7}{3 cdot 7} = frac{14}{21}$$
$$frac{4}{7} = frac{4cdot 3}{7 cdot 3} = frac{12}{21}$$
Теперь у нас две дроби с одинаковым знаменателем, и мы можем легко их сложить.
$$frac{14}{21} + frac{12}{21} = frac{14 + 12}{21} = frac{26}{21}$$
Осталось только разделить эту сумму на число слагаемых. При делении обыкновенной дроби нужно умножить знаменатель дроби на делитель:
$$frac{26}{21} : 2 = frac{26}{21 cdot 2} = frac{26}{42}$$
Эту дробь можно сократить, разделив обе части на $2$. У нас получится $frac{13}{21}$.
Многие операции, которые мы разобрали подробно, можно сделать и устно – здесь они расписаны так только для того, чтобы немного повторить пройденный материал.
Разберём ещё пример со смешанными дробями. Найдём среднее арифметическое для дробей $2frac{1}{6}$ и $3frac{1}{15}$.
Сначала нужно перевести каждую из этих смешанные дробей в неправильную. Для этого нужно умножить целое число на знаменатель и прибавить числитель.
$$2frac{1}{6} = frac{(2 cdot 6) + 1}{6} = frac{13}{6}$$
$$3frac{1}{15} = frac{(3 cdot 15) + 1}{15} = frac{46}{15}$$
Теперь приведём эти дроби к общему знаменателю. НОК $(15$ и $6) = 30$
Теперь подбираем дополнительные множители и складываем наши дроби.
$$frac{13 cdot 5}{6 cdot 5} + frac{46 cdot 2}{15 cdot 2}$$
$$frac{65}{30} + frac{92}{30} = frac{65 + 92}{30} = frac{157}{30}$$
Мы могли бы выделить целую часть из этой дроби, но нет необходимости, так как мы не закончили вычисления. Для нахождения среднего арифметического разделим полученное число на $2$ (другими словами, умножим дробь на число, обратное делителю, в данном случае $frac{1}{2}$).
$$frac{157}{30} : 2 = frac{157}{30 cdot 2} = frac{157}{60} = 2 frac{37}{60}$$
Если мы захотим поделить $37$ на $60$, у нас получится периодическая дробь: $0.61(6) $
Если нужно записать ответ в виде десятичной дроби, то можно использовать периодическую дробь. В некоторых случаях можно округлить эту дробь, например, $0.61(6) $ приблизительно равно $0.62$
Но если в условиях не сказано, что нужна именно десятичная дробь, лучше оставить обыкновенную, так как она будет точно передавать значение выражения.
Как найти среднее арифметическое
Это пригодится не только для решения школьных задачек, но и при различных подсчётах в обычной жизни.
Что такое среднее арифметическое
Среднее арифметическое — это сумма всех чисел в ряду, разделённая на количество слагаемых.
Как найти среднее арифметическое
Например, перед вами ряд чисел «1, 2, 3, 4, 5, 6». Как следует из определения, чтобы узнать среднее арифметическое, нужно сложить все данные вам числа, а потом разделить получившийся результат на количество этих чисел. В приведённом примере — на шесть. Вот как это выражается формулой:
Допустим, вам нужно определить среднее арифметическое для чисел 4, 5 и 6. Складываем 4 + 5 + 6 = 15. Теперь делим 15 на 3 и получаем 5. Это и будет среднее арифметическое.
Таким же образом оно подсчитывается для десятичных и обыкновенных дробей.
Пример расчёта среднего арифметического для обыкновенных дробей будет выглядеть так:
А это пример, как найти среднее арифметическое для десятичных дробей:
Как это пригодится в жизни
Среднее арифметическое помогает описать множество цифровых значений всего одним числом. Например, по выше представленной формуле можно подсчитать усреднённую цену на товар или среднюю зарплату сотрудников в одной организации, среднюю посещаемость заведения. Это полезно для ведения статистики и в случаях, когда нужно сжато изложить информацию.
Читайте также 🧐
- 7 причин полюбить математику
- 7 способов найти площадь прямоугольника
- 6 способов посчитать проценты от суммы с калькулятором и без
- Как освоить устный счёт школьникам и взрослым
- 10 увлекательных задач от советского математика
Нахождение среднего значения набора чисел также известно как нахождение среднего значения. Единственная разница между десятичными и целыми числами состоит в том, что десятичные дроби представляют собой часть целого числа, которое может или не может быть объединено с самим целым числом. Если вы хотите найти среднее значение для набора десятичных дробей, вам нужно использовать только базовые математические навыки, такие как сложение и деление.
Добавьте список десятичных знаков. Например, рассмотрим следующий список: 0, 45, 1, 6, 2, 9 и 0, 84. В сумме эти значения равны 5, 79.
Подсчитайте количество десятичных знаков в наборе, который вы добавили. В этом примере вы добавили четыре десятичных знака.
Разделите сумму из шага 1 на количество десятичных знаков в вашем наборе (как определено в шаге 2). В этом примере вы разделите 5, 79 на 4, чтобы получить 1, 4475. Это среднее значение для вашего набора.