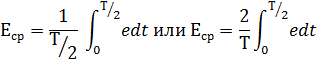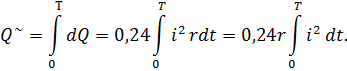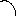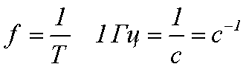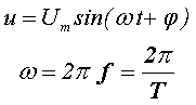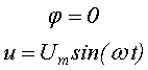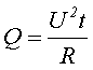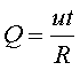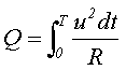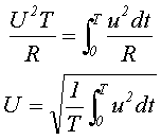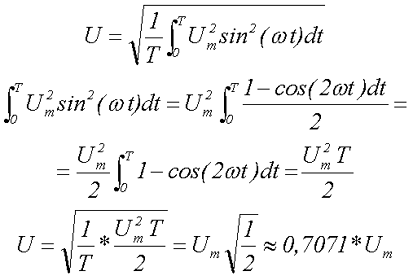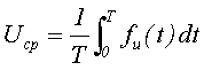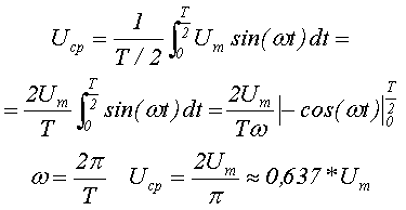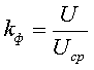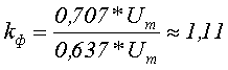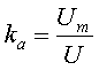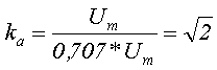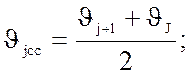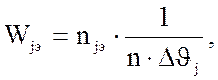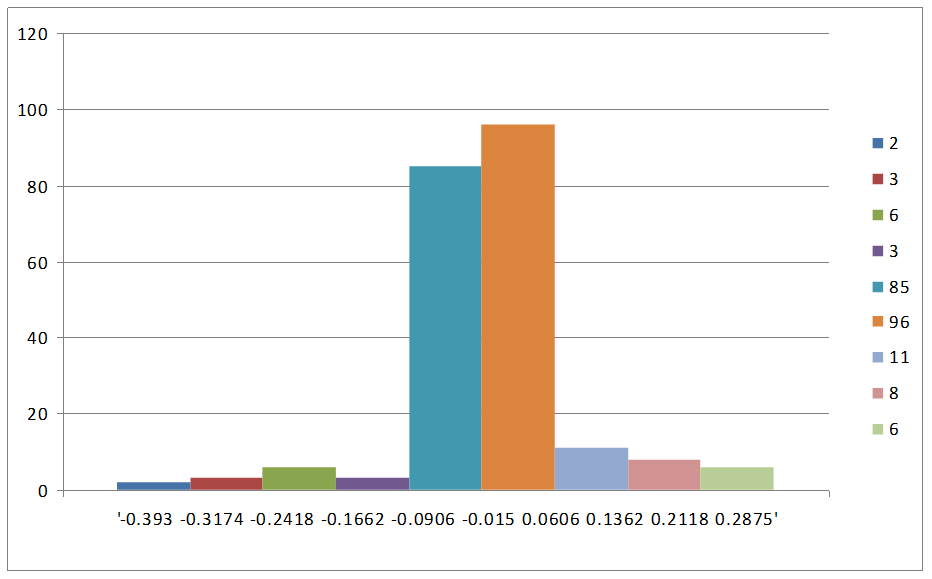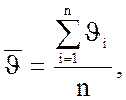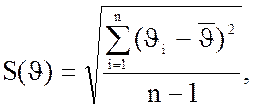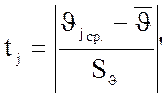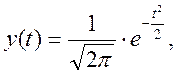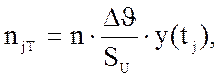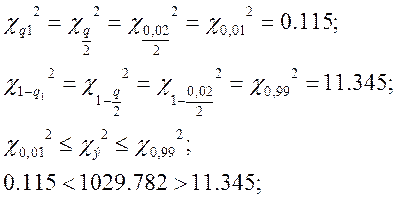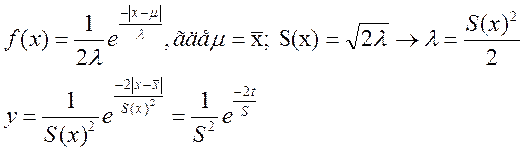Как оценить среднее значение и медиану любой гистограммы
17 авг. 2022 г.
читать 2 мин
Гистограмма — это диаграмма, которая помогает нам визуализировать распределение значений в наборе данных.
По оси X гистограммы отображаются интервалы значений данных, а по оси Y указано, сколько наблюдений в наборе данных приходится на каждый интервал.
Хотя гистограммы полезны для визуализации распределений, не всегда очевидно, что представляют собой средние и медианные значения, просто взглянув на гистограммы.
И хотя невозможно найти точное среднее и срединное значения распределения, просто взглянув на гистограмму, можно оценить оба значения. В этом руководстве объясняется, как это сделать.
Как оценить среднее значение гистограммы
Мы можем использовать следующую формулу, чтобы найти наилучшую оценку среднего значения любой гистограммы:
Наилучшая оценка среднего: Σm i n i / N
куда:
- m i : середина i -го бина
- n i : частота i -го бина
- N: общий размер выборки
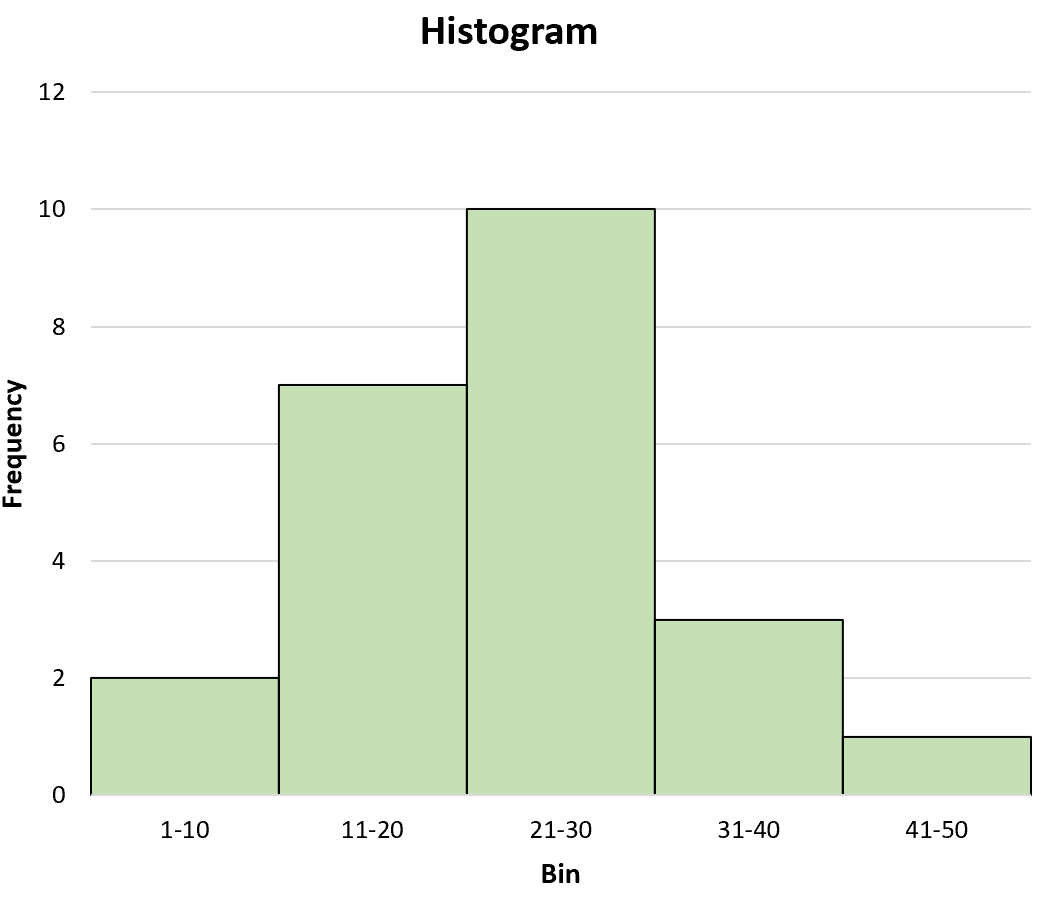
Например, рассмотрим следующую гистограмму:
Наилучшей оценкой среднего значения будет:
Среднее значение = (5,5*2 + 15,5*7 + 25,5*10 + 35,5*3 + 45,5*1) / 23 = 22,89 .
Глядя на гистограмму, это кажется разумной оценкой среднего значения.
Как оценить медиану гистограммы
Мы можем использовать следующую формулу, чтобы найти наилучшую оценку медианы любой гистограммы:
Наилучшая оценка медианы: L + ((n/2 – F)/f) * w
куда:
- L: Нижний предел средней группы
- n: общее количество наблюдений
- F: кумулятивная частота до средней группы
- f: частота срединной группы
- w: ширина срединной группы
Еще раз рассмотрим следующую гистограмму:
Наилучшей оценкой медианы будет:
Медиана = 21 + ((25/2 – 9)/10) * 9 = 24,15 .
Глядя на гистограмму, это также кажется разумной оценкой медианы.
Связанный: Как оценить стандартное отклонение любой гистограммы
Дополнительные ресурсы
Как найти среднее значение, медиану и моду в диаграммах «стебель-и-листья»
Как рассчитать среднее значение из таблиц частот
Когда использовать среднее значение против медианы
Рассмотрите гистограмму напряжение электросети найдите приблизительно а среднее напряжение
Рейтинг:
Пользуясь критерием Шарлье, отбрасывают результат, для значения которого в ряду из n наблюдений выполняется неравенство |хi — х̅| > КШSx .
Вариационный критерий Диксона удобный и достаточно мощный (с малыми вероятностями ошибок). При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд х1, х2, . . ., xn (x1 Zq) = q. Значения Zf( приведены в табл. 7.3 [56].
Пример 7.2. Было проведено пять измерений напряжения в электросети. Получены следующие данные: 127,1; 127,2; 126,9; 127,6; 127,2 В. Результат 127,6 В существенно (на первый взгляд) отличается от остальных. Проверить, не является ли он промахом.
Составим вариационный ряд из результатов измерений напряжения в электросети: 126,9; 127,1; 127,2; 127,2; 127,6 В. Для крайнего члена этого ряда (127,6 В) критерий Диксона
Кд = (127,6 — 127,2) /(127,6 — 126,9) = 0,4 / 0,7 » 0,57.
Как следует из табл.7.3, по этому критерию результат 127,6 В может быть отброшен как промах лишь на уровне значимости q = 0,10.
Применение рассмотренных критериев требует осмотрительности и учета объективных условий измерений. Конечно, оператор должен исключить результат наблюдения с явной грубой погрешностью и выполнить новое измерение. Но он не имеет права отбрасывать более или менее резко отличающиеся от других результаты наблюдений. В сомнительных случаях лучше сделать дополнительные измерения (не взамен сомнительных, а кроме них) и затем привлекать на помощь рассмотренные выше статистические критерии. Кроме рассмотренных критериев, существуют и другие, например критерии Граббса и Шовенэ.
1. Что такое грубые погрешности и промахи? Как определить их присутствие в выборке по виду закона распределения или гистограмме?
2. Расскажите о критерии «трех сигм» и его модификациях.
3. Как применить критерий Романовского для исключения из выборки промахов?
4. В чем суть критерия Шарлье?
5. Расскажите об использовании вариационного критерия Диксона для нахождения промахов.
Источник
Что показывает вольтметр, или математика розетки
О чем эта статья
Сегодня я ненадолго отступлю от своей обычной темы о визуальном программировании контроллеров и обращусь к теме измерений напряжения прямо в ней, в розетке!
Родилась эта статья из дискуссий за чаем, когда разразился спор среди «всезнающих и всеведающих» программистов о том, чего многие из них не понимают, а именно: как измеряется напряжение в розетке, что показывает вольтметр переменного напряжения, чем отличается пиковое и действующие значения напряжений.
Скорее всего, это статья будет интересна тем, кто начинает творить свои устройства. Но, возможно, поможет и кому-то опытному освежить память.
В статье рассказано о том, какие напряжения есть в сети переменного тока, как их измеряют и о том, что следует помнить при проектировании электронных схем.
Всему дано краткое и упрощённое математическое обоснование, чтобы было ясно не только «как», но и «почему».
Кому не интересно читать про интегралы, ГОСТы и фазы — могут сразу переходить к заключению.
Вступление
Когда люди начинают говорить о напряжении в розетке, очень часто стереотип «в розетке 220В» скрывает от их взора реальное положение дел.
Начнем с того, что согласно ГОСТ 29322-2014, сетевое напряжение должно составлять 230В±10% при частоте 50±0,2Гц (межфазное напряжение 400В, напряжение фаза-нейтраль 230В). Но в том же ГОСТ имеется примечание: «Однако системы 220/380 В и 240/415 В до сих пор продолжают применять».
Согласитесь, что это уже совсем не то однозначное «в розетке 220В», к которому мы привыкли. А когда речь начинает идти о «фазном», «линейном», «действующем» и «пиковом» напряжениях — вообще каша получается знатная. Так сколько же вольт в розетке?
Чтобы ответить на этот вопрос начнем с того, как измеряется напряжение в сети переменного тока.
Как измерять переменное напряжение?
Прежде, чем углубиться в дебри цепей переменного тока и напряжения, вспомним школьную физику цепей тока постоянного.
Цепи постоянного тока — вещь простая. Если мы возьмем некоторую активную нагрузку (пусть это будет обычная лампа накаливания, как на рисунке) и воткнем ее в цепь постоянного тока, то все, что происходит в нашей цепи будет характеризоваться всего двумя величинами: напряжением на нагрузке U и током, протекающим через нагрузку I. Мощность, которая потребляется нагрузкой однозначно вычисляется по формуле, известной со школы: .
Или, если учесть, что по закону Ома , то мощность P, потребляемую нагрузкой-лампочкой, можно вычислить по формуле
.
С переменным напряжением все куда сложнее: в каждый момент времени — оно может иметь разное мгновенное значение. Следовательно, в разные моменты времени, на нагрузке, подключенной к источнику переменного напряжения (например, на лампе накаливания, воткнутой в розетку) будет выделяться разная мощность. Это очень неудобно с точки зрения описания электрической цепи.
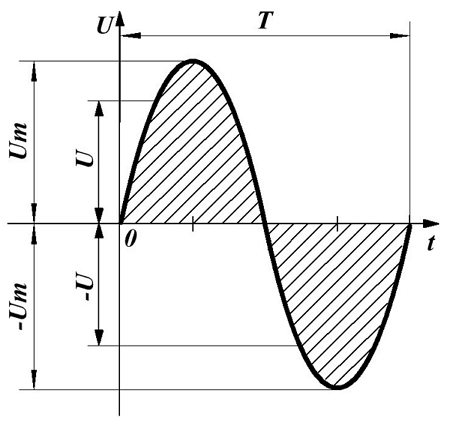
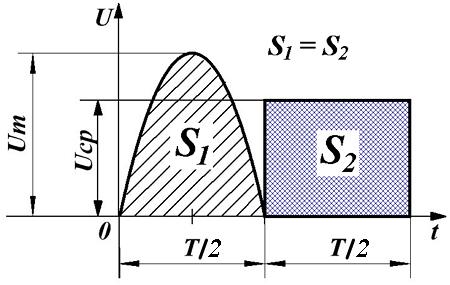
Но нам повезло: форма напряжения в розетке синусоидальная. А синусоида, как известно, полностью описывается тремя параметрами: амплитудой, периодом и фазой. В однофазных сетях (а обычная розетка с двумя дырочками именно и есть однофазная сеть) про фазу можно забыть. На рисунке подробно показаны два периода сетевого однофазного напряжения. Того самого, что в розетке.
Рассмотрим, что означают все эти буковки на рисунке.
Период T — это время между двумя соседними минимумами или соседними максимумами синусоиды. Для осветительной сети РФ этот период составляет 20 миллисекунд, что соответствует частоте 50Гц. Частота колебаний напряжения электрической сети выдерживается очень точно, до долей процента.
Очевидно, что в любых двух точках синусоиды, отстоящих друг от друга на целое число периодов, напряжения всегда равны между собой.
Амплитуда Um — это максимальное напряжение, пик синусоиды. Про действующее напряжение Uд поговорим чуть ниже.
Напряжение в розетке (или однофазной сети) описывается формулой
где t — текущий момент времени, Um — амплитуда (или пиковое значение) напряжения, T — период сетевого напряжения.
Если с однофазным переменным напряжением более или менее все ясно, то попробуем посчитать мощность, которая выделяется на нашей любимой лампе накаливания, при втыкании ее прямо в розетку.
Так как лампа накаливания является активной нагрузкой (а это значит, что ее сопротивление не зависит от частоты напряжения и тока), то мгновенная мощность, выделяемая на лампе накаливания, воткнутой в розетку, будет вычисляться по формуле
где t — текущий момент времени, а R — сопротивление лампы накаливания при нагретой спирали. Зная амплитуду переменного напряжения Um, можно записать:
Понятно, что мгновенная мощность — неудобный параметр, да и на практике не особо нужный. Поэтому практически обычно применяется мощность, усредненная за период.
Именно усредненная мощность указана на лампочках, нагревателях и прочих бытовых утюгах.
Рассчитывается усредненная мощность в общем случае по формуле:
А для нашей синусоиды — по гораздо более простой формуле:
Можете сами подставить вместо функцию
и взять интеграл, если не верите.
Не думайте, что про мощность я вспомнил просто так, из вредности. Сейчас поймете, зачем она нам была нужна. Переходим к следующему вопросу.
Что же показывает вольтметр?
Для цепей постоянного тока, тут все однозначно — вольтметр показывает единственное напряжение между двумя контактами.
С цепями переменного тока все опять сложнее. Некоторые (и этих некоторых не так мало, как я убедился) считают, что вольтметр показывает пиковое значение напряжения Um, но это не так!
На самом деле, вольтметры обычно показывают действующее или эффективное, оно же среднеквадратичное, напряжение в сети Uд.
Разумеется, речь идет о вольтметрах переменного напряжения! Поэтому, если будете измерять вольтметром напряжение сети, обязательно убедитесь, что он находится в режиме измерения переменного напряжения.
Оговорюсь, что «пиковые вольтметры», показывающие амплитудные значения напряжения, тоже существуют, но на практике при измерении напряжения питающей сети в быту обычно не применяются.
Разберемся, почему такие сложности. Почему бы не измерять просто амплитуду? Зачем выдумали какое-то «действующее значение» напряжения?
А все дело в потребляемой мощности. Я ведь не просто так писал о ней. Дело в том, что действующее (эффективное) значение переменного напряжения равно величине такого постоянного напряжения, которое за время, равное одному периоду этого переменного напряжения, произведет такую же работу, что и рассматриваемое переменное напряжение.
Или, по-простому, лампочка накаливания будет светить одинаково ярко, воткнем ли мы ее в сеть постоянного напряжения 220В или в цепь переменного тока с действующим значением напряжения 220В.
Для тех, кто уже знаком с интегралами или еще не забыл математику, приведу общую формулу расчета действующего напряжения произвольной формы:
Из этой формулы также становится ясно, почему действующее (эффективное) значение переменного напряжения также называют «среднеквадратичным».
Заметим, что подкоренное выражение и есть та самая «усредненная за период мощность», стоит только поделить это выражение на сопротивление нагрузки R.
Применительно к синусоидальной форме напряжения, страшный интеграл после несложных преобразований превратится в простую формулу:
где Uд — действующее или среднеквадратичное значение напряжение (то самое, которое обычно показывает вольтметр), а Um — амплитудное значение.
Действующее напряжение хорошо тем, что для активной нагрузки, расчет усредненной мощности полностью совпадает с расчетом мощности на постоянном токе:
Это и не удивительно, если вспомнить определение действующего значения напряжения, которое было дано чуть выше.
Ну и, наконец, посчитаем, чему же равна амплитуда напряжения в розетке «на 220В«:
В худшем случае, если у вас сеть на 240В, да еще и с допуском +10%, амплитуда будет аж !
Поэтому, если хотите, чтобы ваши устройства, питающиеся от сети, работали стабильно и не сгорали, выбирайте элементы, которые выдерживают пиковые напряжения не менее 400В. Разумеется, речь идет об элементах, на которые непосредственно подаётся сетевое напряжение.
Отмечу, что для не-синусоидальной формы сигнала действующее значение напряжения рассчитывается по иным формулам. Кому интересно — могут сами взять интегралы или обратиться к справочникам. Нас же интересует питающая сеть, а там всегда должна быть синусоида.
Фазы, фазы, фазы…
Помимо обычной однофазной осветительной сети
220В все слышали и о трехфазной сети
380В. Что такое 380В? А это межфазное эффективное напряжение.
Помните, я сказал, что в однофазной сети про фазу синусоиды можно забыть? Так вот, в трехфазной сети этого делать нельзя!
Если говорить по простому, то фаза — это сдвиг во времени одной синусоиды относительно другой. В однофазной сети мы всегда могли принять за начало отсчета любой момент времени — на расчеты это не влияло. В трехфазной сети необходимо учитывать насколько одна синусоида отстоит от другой. В трехфазных сетях переменного тока каждая из фаз отстоит от другой на треть периода или на 120 градусов. Напомню, что период измеряется также в градусах и полный период равен 360 градусов.
Если мы возьмем осциллограф с тремя лучами и прицепимся к трем фазам и одному нулю, то увидим такую картину.
«Синяя» фаза — начинается от нуля отсчета. «Красная» фаза — на треть периода (120 градусов) позже. И, наконец «зеленая» фаза начинается на две трети периода (240 градусов) позже «синей». Все фазы абсолютно симметричны друг относительно друга.
Какую именно фазу брать за точку отсчета — не важно. Картина будет одинаковой.
Математически можно записать уравнения всех трех фаз:
«Синяя» фаза:
«Красная» фаза:
«Зеленая» фаза:
Если измерить напряжение между любой из фаз и нулем в трехфазной сети — то получим обычные 220В (или 230В или 240В — как повезет, см. ГОСТ).
А если измерить напряжение между двумя фазами — то получим 380В (или 400В или 415В — не забываем об этом).
То есть трехфазная сеть — многолика. Ее можно использовать как три однофазные сети с напряжением 220В или как одну трехфазную сеть с напряжением 380В.
Откуда взялось 380В? А вот откуда.
Если мы подставим в формулу расчета действующего напряжения наши данные о двух любых фазах, то получим:
Uдф — действующее межфазное, оно же линейное напряжение.
Учитывая, что амплитуда каждой фазы получим, что
для межфазного напряжения. На рисунке наглядно показано, как образуется межфазное напряжение, которое обозначено F1-F2 из двух фазных напряжений фаз F1 и F2. Напряжение фаз F1 и F2 измеряется относительно нулевого провода. Линейное напряжение F1-F2 измеряется между двумя разными фазными проводами.
Как видим, что действующее межфазное напряжение больше амплитуды синусоидального напряжения одной фазы.
Амплитуда межфазного напряжения составляет:
Для наихудшего случая (сеть 240В и межфазное напряжение 415В, да еще 10% сверху) амплитуда межфазного напряжения составит:
Учтите это при работе в трехфазных сетях и выбирайте элементы, рассчитанные не менее, чем на 650В, если им предстоит работать между двумя фазами!
Надеюсь, теперь понятно что показывает вольтметр переменного тока?
Заключение
Итак, очень кратко, почти на пальцах, мы ознакомились с тем какие напряжения действуют в бытовых сетях переменного тока. Подведем краткие итоги всего, изложенного выше.
- Фазное напряжение — это напряжение между фазой и нулевым проводом.
- Линейное или межфазное напряжение — это напряжение между двумя разными фазными проводами одной трехфазной сети.
- В сетях переменного тока РФ действуют три, хоть и близких, но разных стандарта (фазное/линейное): 220В/380В, 230В/400В и 240В/415В переменного тока с частотой 50Гц.
- Вольтметр переменного тока обычно показывает действующее (оно же среднеквадратичное, оно же эффективное) напряжение, которое в
раза меньше, чем пиковое (амплитудное) напряжение в сети.
- В наихудшем с точки зрения стандартов случае пиковое фазное напряжение составляет примерно 373В, а пиковое линейное напряжение — 645B. Это следует учитывать при разработке электронных схем.
Надеюсь эта статья помогла кому-то разобраться в теме и ответить для себя на некоторые вопросы.
Источник
Среднее
значение переменного напряжения, ЭДС
и тока за период равно нулю, так как
площадь отрицательных и положительных
полуволн синусоид равны по величине и
различны по знаку (рис.2.6).

e

i

t

T/2
T
Рис.2.6
Поэтому,
когда говорят о среднем значении
переменного тока i,
напряжения u
или
ЭДС е,
под ним подразумевается среднее значение
за половину периода Т/2 между двумя
нулевыми значениями величины 0 и .
Например,
среднее значение переменной ЭДС любого
вида определяется так:
Если
ЭДС изменяется по синусоидальному
закону е
, то можно установить простую зависимость
между средним значением ЭДС Eср
и
его амплитудным значением Еm.
а
так как ,
то
=0,637
.
Аналогично
получим средние значения напряжения и
тока:
2.1.4. Действующее значение переменного тока и напряжения.
В
электротехнике часто приходится иметь
дело с тепловыми и механическими
действиями переменного тока.
Механическая
сила взаимодействия двух проводников
с одинаковыми токами и тепловое действие
тока пропорциональны квадрату мгновенных
значений тока. Для переменного тока
тепловое или механическое действие
определяется средним значением квадратов
токов за период, называемым действующим
значением тока.
Иначе
говоря, действующее значение переменного
тока равняется постоянному току,
выделяющему за время, равное периоду,
в каком-либо проводнике такое же
количество тепла, что и данный переменный
ток.
Количество
теплоты, выделяемое постоянным током
в резисторе с активным сопротивлением
r
за промежуток времени Т, равный периоду
переменного тока, составляет:
=0,24
Количество
теплоты, выделяемое переменным током
в том же эелементе за промежуток времени
dt,
равно:
Количество
теплоты, выделяемое за период Т, равно:
Приравнивая
количество теплоты, выделяемое постоянным
и переменным током, получим:
=
Отсюда
получим действующее значение тока:
Аналогично
для напряжений и ЭДС переменного тока
имеем:
Выражения
для I,U
и Е определяют в общем виде действующие
периодические токи, напряжение и ЭДС
при любом законе их изменения.
Для
синусоидального переменного тока i=
будем иметь:
Второй
интеграл равен нулю, и для действующего
синусоидального тока имеем:
Аналогично
получим выражение для действующих
синусоидальных ЭДС и напряжения:
.
Градация
вольтметров и амперметров, предназначенных
для работы в цепи синусоидального тока,
обычно показывает непосредственно
действующие значения напряжения или
тока.
2.1.5.Векторные диаграммы переменного тока.
Как
было установлено, гармонически
изменяющееся напряжение в общем виде
определяется выражением:
Зная
амплитуду напряжения
и аргумент синусоидальной функции ,
можно с помощью несложных математических
операций определить мгновенные значения
напряжения u
в
любой момент времени. Наряду с аналитическим
способом расчета получить u
можно
графически, например, по временной
диаграмме гармонической переменной
(рис.2.7).
Однако
при различных расчетах бывает удобнее
пользоваться методом векторных диаграмм.
Применение векторных диаграмм при
исследовании цепей переменного тока
позволяет наглядно представить
рассматриваемые процессы и упрощать
производимые расчеты.

U

Х u

Рис.2.7
Синусоидальный
ток и напряжение можно представить как
вектор, движущийся по окружности со
скоростью
Мгновенные значения будут равны проекции
этого вектора на ось Y.
Суть
данного метода заключается в следующем:
если какая-нибудь точка движется с
постоянной скоростью по окружности, то
её проекция на любой диаметр (горизонтальный-
воображаемая ось Х или вертикальная-
ось Y)
совершает гармонические(синусоидальные
колебания). Радиус-вектор ( в дальнейшем
для краткости будем называть просто
вектор) этой точки вращается с постоянной
угловой скоростью
Um
U


0
Um
Рис.2.8
Если
этот вектор (рис.2.8) в известном, произвольно
выбранном масштабе изображающий
амплитуду напряжения (
тока и ЭДС), занимает в начальный момент
времени (t=0)
горизонтальное положение, вправо от
центра вращения 0 и вращается против
часовой стрелки с угловой скоростью
,
то в произвольный момент времени t,
когда он образует с горизонталью угол
,
проекция его на вертикальную ось Y
в том же масштабе покажет соответствующее
мгновенное напряжение:

же вектор
в начальный момент расположен не
горизонтально, а образует с осью абсцисс
Х угол ,
то проекция на ось Y
покажет мгновенное значение напряжения
опережающее
предыдущее на часть периода .
Представим этот случай графически.
Расположим под углом
относительно положительной оси абсцисс
вектора ,длина
которого в заранее выбранном масштабе
равна амплитуде изображаемой гармонической
величины (рис.2.9).



Рис.2.9
Положительные
углы ( начальные фазы напряжения ,
а так же только принято
откладывать в направлении против часовой
стрелки, а отрицательные( )-по
часовой стрелке ( рис.2.9, показана
положительная начальная фаза напряжения
).

что вектор
, начиная с момента времени t=0,
вращается вокруг начала координат
против часовой стрелки с постоянной
частотой вращения ,
равной угловой частоте изображаемого
напряжения.

момент времени t
вектор
повернется на угол
и будет расположен под углом
по отношению к оси абсцисс X.
Проекция
этого вектора на ось координат Y
в выбранном масштабе равна мгновенному
значению изображаемого напряжения .

величину, изменяющуюся гармонически
во времени, можно изображать вращающимся
вектором. При начальной фазе, равной
нулю (
когда ,
вектор
для t=0.
(рис.2.8) расположен на оси абсцисс.
При
больше или меньше 0 положение вектора
для t=0
определяется знаком и величиной начальной
фазы напряжения.
Обычно
при расчете цепи используются действующие
ЭДС, напряжения и токи( или амплитуды
этих величин), а так же их сдвиг по фазе
относительно друг друга. Поэтому
рассматриваются неподвижные векторы
для некоторого момента времени, который
выбирается так, чтобы диаграмма была
наглядней. Такая диаграмма называется
векторной. Иными словами векторная
диаграмма является совокупностью
векторов, изображающих движущие
синусоидальные ЭДС, напряжение и токи
или их амплитудные значения. Углы сдвига
по фазе
откладываются в направлении вращении
векторов (против часовой стрелки), если
они положительны (например, ,
и в обратном направлении, если они
отрицательны (.
Если, например, начальный фазовый угол
ЭДС
больше начального фазового угла
(см.временную диаграмму на рис.2.10), то
соответственно сдвиг по фазе
и этот угол откладывается в положительном
направлении от вектора тока (рис.2.10).

значения ЭДС и тока в начальный момент
отсчета
( для
определяются проекциями амплитудных
значений их векторов
на ось ординат Y
в заданном масштабе расчетных параметров
e
и i.
Рассмотрим
сложение ЭДС, токов и напряжений на
векторной диаграмме. При исследовании
цепи переменного тока часто приходится
складывать ЭДС, токи и напряжения одной
и той же частоты.

e,i


0
Рис.2.10
Предположим,
что требуется сложить две ЭДС:
Такое
сложение можно осуществить аналитически
( путем математических вычислений) и
графически с помощью векторных диаграмм.
Последний способ более нагляден и прост.
Две складываемые ЭДС е1
и е2
в определенном масштабе представлены
векторами
и

e e1
e2

Em
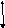
E1

E2m

Ψe
Ψ1e

Ψ1e
Ψe
Ψ2e
Рис.2.11

вращении этих векторов с одинаковой
частотой вращения, равной угловой
частоте переменного тока ,
взаимное расположение вращающихся
векторов относительно друг друга
остается неизменным. Сумма проекций
вращающихся векторов
и
на ось ординат (е1
и е2)
равна проекции на ту же ось Y
вектора ,
равного геометрической сумме векторов
и :
.
Указанный
способ сложения двух ЭДС универсален,
его можно применить для сложения и
вычитания любого числа ЭДС, напряжений
и токов одной частоты. При этом операцию
вычитания можно представить в виде
сложения, проведя элементарные
преобразования.
Например,
,
то есть уменьшаемая величина складывается
с вычитаемой, взятой с обратным знаком.
На
практике векторные диаграммы, как
правило, строятся не для амплитудных
значений переменных ЭДС, напряжений и
токов, а для действующих величие E,U
и I,
пропорциональных амплитудных значениям
так
как все расчеты цепей выполняются для
действующих значений ЭДС, напряжений
и токов.
Всем доброго времени суток! В прошлой статье я рассказал, как рассчитать индуктивность катушки выполненной на разомкнутом сердечнике (например, ферритовой антенны, контурных катушек радиоприёмников, катушек с построечными сердечниками и т. д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.
Что такое переменное напряжение?
Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.
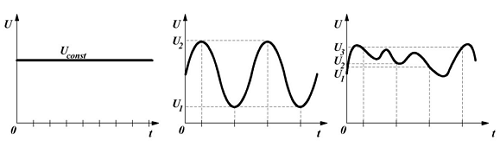
Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.
Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид
где Т – период.
Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда
Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже
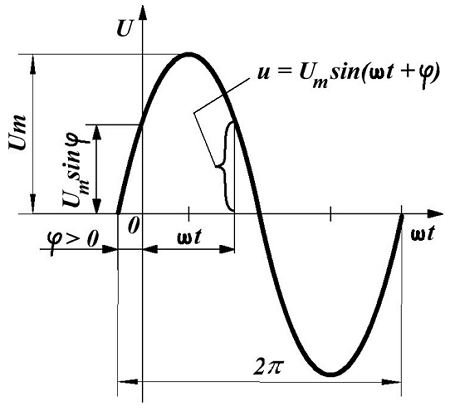
Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.
Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла),
φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.
Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.
Таким образом, амплитуда Um, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.
Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда
В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.
Что такое действующее напряжение переменного тока?
Как я писал выше, одним из основных параметров переменного напряжения является амплитуда Um, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному Um ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?
Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения
Для переменного напряжения мгновенное значение выделяемой энергии составит
где u – мгновенное значение напряжения
Тогда количество энергии за полный период от t0 = 0 до t1 = T составит
Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения
Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.
Действующее значение синусоидального напряжения.
Вычислим действующее значение синусоидального напряжения
Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.
Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение
Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения
Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.
С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.
Что такое среднее значение переменного напряжения?
Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением
где Т – период переменного напряжения,
fu(t) – функциональная зависимость напряжения от времени.
Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией fu(t) и осью Ox за период Т.
Среднее значение переменного напряжения.
В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.
Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла).
Какие коэффициенты, характеризуют переменное напряжение?
Иногда возникает необходимость охарактеризовать форму переменного напряжения. Для этой цели существует ряд параметров данного переменного напряжения:
1. Коэффициент формы переменного напряжения kф – показывает как относится действующее значение переменного напряжения U к его среднему значению Ucp.
Так для синусоидального напряжения коэффициент формы составит
2. Коэффициент амплитуды переменного напряжения kа – показывает как относится амплитудное значение переменного напряжения Um к его действующему значению U
Так для синусоидального напряжения коэффициент амплитуды составит
На сегодня всё, в следующей статье я рассмотрю прохождение переменного напряжения через сопротивление, индуктивность и емкость.
Таблица
8.5 – Экспериментальные частоты каждого интервала.
|
n1 |
n2 |
n3 |
n4 |
n5 |
n6 |
n7 |
n8 |
n9 |
|
2 |
3 |
6 |
3 |
85 |
96 |
11 |
8 |
6 |
8.4 Находим среднее
значение каждого интервала
Таблица 8.6 – Средние
значения каждого интервала измерений
|
υ1ср |
υ2ср |
υ3ср |
υ4ср |
υ5ср |
υ6ср |
υ7ср |
υ8ср |
υ9ср |
|
-0,3552 |
-0,2796 |
-0,204 |
-0,1284 |
-0,0528 |
0,0228 |
0,0984 |
0,174 |
0,2497 |
8.5
Подсчитываем плотности распределения вероятности для каждого интервала
где
n и — постоянные
величины для измеряемой выборки.
Шаг для каждого интервала группы
измерений –= 0,0756.
Таблица 8.7 – Плотности
распределения вероятности для каждого интервала 1-ой группы
|
|
|
|
|
|
|
|
|
|
|
0,12 |
0,18 |
0,36 |
0,18 |
5,1 |
5,76 |
0,66 |
0,48 |
0,36 |
8.6
Построим гистограммы экспериментального распределения.
Построим
гистограмму распределения в виде прямоугольников, откладывая по оси абсцисс
интервалы в порядке возрастания их номеров, а
по оси ординат — экспериментальные частоты ,
пропорциональные плотности распределения вероятностей.
Рис 8.1 – Экспериментальная гистограмма распределения
отклонений напряжений
8.7
Построим теоретическую гистограмму распределения.
Проверку
на нормальность экспериментального распределения при большом числе результатов
измерений проведём путём построения теоретической гистограммы и оценивания её
соответствия экспериментальной гистограмме.
Вычислим
нормированные отклонения середины каждого интервала гистограммы от САЗ
напряжений .
Находим
значение САЗ отклонений по формуле:
v=0/220=0.
Находим
значение СКО
=0,09
Нормированные
отклонения середины каждого интервала гистограммы от САЗ напряжений:
Таблица
8.9 — Нормированные отклонения середины каждого интервала гистограммы от САЗ
напряжений 1-ой группы
|
|
|
|
|
|
|
|
|
|
|
3,95 |
3,11 |
2,27 |
1,43 |
0,59 |
0,25 |
1,09 |
1,93 |
2,77 |
Определим
по таблице нормированной функции нормального распределения плотность
вероятности для каждого интервала гистограммы:
Таблица
8.10 — Плотность вероятности для каждого интервала гистограммы.
|
y(3,95) |
y(3,11) |
y(2,27) |
y(1,43) |
y(0,59) |
y(0,25) |
y(1,09) |
y(1,93) |
y(2,77) |
|
0,0002 |
0,0032 |
0,0303 |
0,1435 |
0,3352 |
0,3867 |
0,2203 |
0,062 |
0,0086 |
Вычисляем
теоретические частоты (теоретическое число
результатов измерения), соответствующие каждому интервалу:
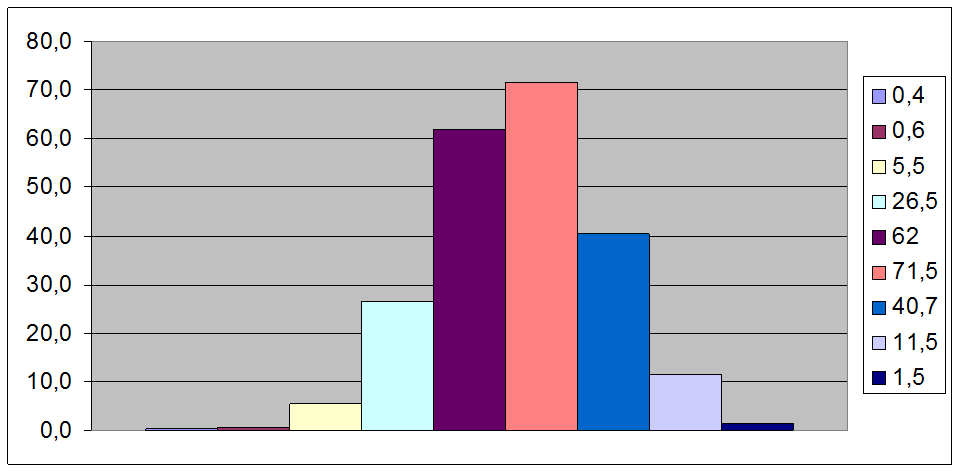
Таблица 8.11 — Теоретическое
число результатов измерения.
|
|
|
|
|
|
|
|
|
|
|
0,4 |
0,6 |
5,5 |
26,5 |
62 |
71,5 |
40,5 |
11,5 |
1,5 |
Рис 8.3 – Теоретическая гистограмма распределения
отклонений напряжений
8.8 Проверяем
соответствие экспериментальной гистограммы теоретической.
При
большом числе опытов проверка соответствия экспериментальной и теоретической
гистограмм выполняется с использованием критерия согласия — Пирсона, обеспечивающего
минимальную ошибку принятия гипотезы по сравнению с другими критериями.
Показатель
разности частот экспериментального и теоретического распределений можно
вычислить по формуле
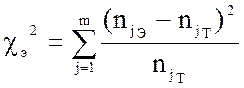
где
m- число интервалов гистограммы после их укрупнения.
Для
1-ой группы измерений:
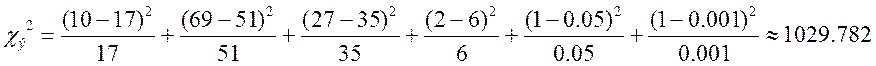
Критерий зависит
от числа степеней свободы k и выбираемого уровня значимости q.
Число степеней свободы , где d-
число независимых условий (ограничений), принятых при определении значений
плотности вероятности. Для нормального распределения существуют три таких
условия(d=3):
Уровень значимости q должен быть
достаточно малым, чтобы была малой вероятность отклонения правильной гипотезы.
С другой стороны, чрезмерно малый уровень значимости увеличивает вероятность
принятия ложной гипотезы. Из опыта практического применения критерия следует ограничить выбор q-интервалом
.
По
уровню значимости q и числу степеней свободы k=r-3,
по таблице — распределения находят границу
критической области критерия . Если оказывается, что
,то гипотеза о нормальности
отвергается, если то экспериментальное
распределение относят к нормальному.
Вместо
односторонней критической области часто применяют
двусторонние критические области и
, соответствующие
и
.
Для
нахождения и
уровень
значимости делится на две части обычно (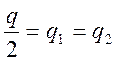
По таблице критерия для выбранного уровня
значимости и числа степеней свободы k=r-3 определяют для
и
для
.
Гипотеза
о нормальности проверяемого распределения принимается, если .
Для
1-ой группы измерений:
1)
к =m-3,где m-число интервалов гистограммы после их укрупнения,
тогда:
k=9-3=6;
интервал:;
пусть
при
k=3 и q=0,02 имеем (15,033 и
16,812)
2)
k=6-3=3;
Следовательно,
данное распределение является ненормальным.
Предположим,
что данные распределения подчиняются експонециальному закону распределения, а
именно двойному експонециальному закону распределения (Лапласа), который имеет
вид:
Для
1-ой группы измерений:
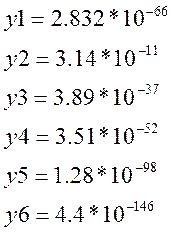
По
расчетным значениям нормированных функций двойного экспоненциального
распределения (Лапласа) видно, что
данное распределение не является экспоненциальным. Следовательно, нам не нужно
проверять соответствие экспериментальной гистограммы теоретической по критерию
согласия — Пирсона для данного закона
распределения.