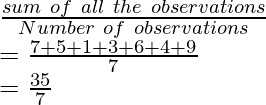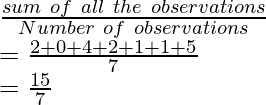Как найти среднее отклонение среднего арифметического - Исправление недочетов и поиск решений вместе с Examum.ru

Представление результатов исследования

В научных публикациях важно представление результатов исследования. Очень часто окончательный результат приводится в следующем виде: M±m, где M – среднее арифметическое, m –ошибка среднего арифметического. Например, 163,7±0,9 см.

Прежде чем разбираться в правилах представления результатов исследования, давайте точно усвоим, что же такое ошибка среднего арифметического.

Ошибка среднего арифметического

Среднее арифметическое, вычисленное на основе выборочных данных (выборочное среднее), как правило, не совпадает с генеральным средним (средним арифметическим генеральной совокупности). Экспериментально проверить это утверждение невозможно, потому что нам неизвестно генеральное среднее. Но если из одной и той же генеральной совокупности брать повторные выборки и вычислять среднее арифметическое, то окажется, что для разных выборок среднее арифметическое будет разным.

Чтобы оценить, насколько выборочное среднее арифметическое отличается от генерального среднего, вычисляется ошибка среднего арифметического или ошибка репрезентативности.

Ошибка среднего арифметического обозначается как m или

Ошибка среднего арифметического рассчитывается по формуле:

где: S — стандартное отклонение, n – объем выборки; Например, если стандартное отклонение равно S=5 см, объем выборки n=36 человек, то ошибка среднего арифметического равна: m=5/6 = 0,833.

Ошибка среднего арифметического показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего выборочное среднее.

Так как при небольшом объеме выборки истинное значение генерального среднего не может быть определено сколь угодно точно, поэтому при вычислении выборочного среднего арифметического нет смысла оставлять большое число значащих цифр.

Правила записи результатов исследования

В записи ошибки среднего арифметического оставляем две значащие цифры, если первые цифры в ошибке «1» или «2».
В остальных случаях в записи ошибки среднего арифметического оставляем одну значащую цифру.
В записи среднего арифметического положение последней значащей цифры должно соответствовать положению первой значащей цифры в записи ошибки среднего арифметического.

Представление результатов научных исследований

В своей статье «Осторожно, статистика!», опубликованной в 1989 году В.М. Зациорский указал, какие числовые характеристики должны быть представлены в публикации, чтобы она имела научную ценность. Он писал, что исследователь «…должен назвать: 1) среднюю величину (или другой так называемый показатель положения); 2) среднее квадратическое отклонение (или другой показатель рассеяния) и 3) число испытуемых. Без них его публикация научной ценности иметь не будет “с. 52

В научных публикациях в области физической культуры и спорта очень часто окончательный результат приводится в виде: (М±m) (табл.1).

Таблица 1 — Изменение механических свойств латеральной широкой мышцы бедра под воздействием физической нагрузки (n=34)

	Эффективный модуль упругости (Е), кПа	Эффективный модуль вязкости (V), Па с
Этап эксперимента	Рассл.	Напряж.	Рассл.	Напряж.
До ФН	7,0±0,3	17,1±1,4	29,7±1,7	46±4
После ФН	7,7±0,3	18,7±1,4	30,9±2,0	53±6

Литература

Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
Зациорский В.М. Осторожно — статистика! // Теория и практика физической культуры, 1989.- №2.
Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.

Источник

В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).

Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

Определите среднее (простое среднее арифметическое ряда значений).
Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Порода собаки	Рост в миллиметрах
Ротвейлер	600
Бульдог	470
Такса	170
Пудель	430
Мопс	300

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее $=frac{600+470+170+430+300}{5} = 394$ мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить отклонение роста каждой из собак от среднего:

$[ begin{array}{l} 1: 600-394 = 206 \ 2: 470-394 = 76 \ 3: 170-394 = -224\ 4: 430-394 = 36\ 5: 300-394 = -94 end{array} ]$

Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Дисперсия $= frac{206^2+76^2+(-224)^2+36^2+(-94)^2}{5} = 21704$ мм².

Таким образом, дисперсия составляет 21704 мм².

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

мм (округлено до ближайшего целого значения в мм).

Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть значений, то:

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

Дисперсия выборки = $frac{108520}{4}=27130$ мм².

При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Примечание. Почему именно квадраты разностей?

Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:

$frac{4+4-4-4}{4}=0$ .

Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?

$frac{4+4+|-4|+|-4|}{4} = frac{4+4+4+4}{4}=4$ .

На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:

$frac{7+1+|-6|+|-2|}{4} = frac{7+1+6+2}{4}=4$ .

Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.

А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).

Для первого примера получится:

$sqrt{frac{4^2+4^2+(-4)^2+(-4)^2}{4}}=4$ .

Для второго примера получится:

$sqrt{frac{7^2+1^2+(-6)^2+(-2)^2}{4}}=4.74$ .

Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.

Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.

И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.

О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич

Источник

The science of collecting, analyzing, presenting data is known as statistics. In statistics, the deviation is known as the variation obtained between the observed value and other values of a variable. Let’s learn more about this topic and learn what a men deviation is in statistics,

Mean Deviation

The mean deviation of a given standard distribution is a measure of the central tendency. It can be computed using the Arithmetic Mean, Median, or Mode of the data. It is used to show how far the observations are situated from the average of the data observations. Each of these deviations is considered to be an absolute value. This implies that the negative signs are ignored. In addition to this, the deviations on both sides of the mean value are equivalent in nature. Therefore, the mean deviation of the given data distribution is the mean of the absolute deviations of the observations or values from a suitable average. This suitable average can be either mean, median, or mode of the data. For instance, the mean deviation formula for an individual series or a continuous series, etc.

Mean Deviation Types

Individual Series

For a given set of raw data, when the data is presented individually in the form of a series, it is known as individual series. It is basically a sequence of raw data in such a form that forms an arrangement individually. Items are represented singly in the individual series. It is used to depict numerical values. For instance, let’s assume the following marks out of 100 to be secured by students in a class :

56, 77, 88, 49, 60, 92, 70, 81, 69, 51,

The above data is not conclusive about how many students got 56 marks or more than 77 in a single sight.

Discrete Series

The discrete series is used to reflect data for each specific value of the observation variable. Each of the variables corresponds to an integer value. The exact measurement of the items in the data is visible. For instance, the wages earned by 30 workers are depicted below in the tables as:

Wages	Number of workers (frequency)
2500	7
3000	9
4000	5
4500	6
5000	3

Conclusively, 7 workers are getting wages equivalent to Rs. 2500, and 9 workers are getting Rs. 3000 and so on.

Continuous Series

A continuous series contains data items maintained in certain definite classes. The data items contained in classes lose their individual identity, and the individual items are merged in one or the other class group. The classes have continuity, that is the end of the first class is marked by the beginning of the next class. Thus, the name continuous series. For instance, the continuous series is depicted using the following data:

Age Group	Frequency
10-20	15
20-30	10
30-40	13
40-50	12
50-60	18
60-70	4
70-80	8

Individual Series

Mean Deviation (M.D) = $frac{sum|x-bar x|}{N}$

Where,

∑ – Summation

x – Observation

– Mean

N – Number of observation

Discrete Series

Mean Deviation (M.D) = $frac{sum f|x-bar x|}{sum f}$

Where,

∑ – Summation

x – Observation

– Mean

f – frequency of observation

Continuous Series

Mean Deviation (M.D) = $frac{sum f|x-bar x|}{sum f}$

Where,

∑ – Summation

x – Mid-value of the class

– Mean

f – frequency of observation

Mean deviation from Median

Individual Series

Mean Deviation (M.D) = $frac{sum |x-M|}{N}$

Where,

∑ – Summation

x – Observation

M – Median

N – Number of observation

Discrete Series

Mean Deviation (M.D) = $frac{sum f |x-M|}{sum f}$

Where,

∑ – Summation

x – Observation

M – Median

N – Frequency of observations

Continuous Series

Mean Deviation (M.D) = $frac{sum f |x-M|}{sum f}$

Where,

∑ – Summation

x – Observation

M – Median

N – Frequency of observations

Mean deviation from Mode

Individual Series

Mean Deviation (M.D) = $frac{sum |x-Mode|}{sum N}$

Where,

∑ – Summation

x – Observation

M – Mode

N – Number of observations

Discrete Series

Mean Deviation (M.D) = $frac{sum f |x-Mode|}{sum f}$

Where,

∑ – Summation

x – Observation

M – Mode

N – Frequency of observations

Continuous Series

Mean Deviation (M.D) = $frac{sum f |x-Mode|}{sum f}$

Where,

∑ – Summation

x – Observation

M – Mode

N – Frequency of observations

Steps to Calculate the Mean Deviation

Calculate the mean, median, or mode of the series.
Calculate the deviations from the Mean, median, or mode and do ignore the minus signs.
Multiply the deviations with the frequency. The step is required only in the discrete and continuous series.
Sum up all the deviations.
Apply the formula.

Examples;

Example 1: What are the advantages of using the mean deviation?

Solution:

The advantages of using mean deviation are:

It is based on all the data values given, and hence it provides a better measure of dispersion.

It is easy to understand and calculate.

Example 2: Mention the procedure to find the mean deviation.

Solution:

The procedure to find the mean deviation are:

Step 1: Calculate the mean value for the data given.

Step 2: Then, the mean is subtracted from each data value (distance).

Step 3: Finally, the mean is found for the distance.

Example 3: Find the mean deviation of the following data?

7, 5, 1, 3, 6, 4, 10

Solution:

To find the mean deviation,

First, calculate the mean value of the given data

Mean = $frac{sum of all the observations}{Number of observations}\ = frac{7+ 5+ 1+ 3+ 6+ 4+ 9}{7}\ =frac{35}{7}$

Mean = 5

Now subtract the mean from each data value {ignore negative (-)}

7 – 5 = 2

5 – 5 = 0

1 – 5 = 4

3 – 5 = 2

6 – 5 = 1

4 – 5 = 1

10 – 5 = 5

Further find the mean of these values obtained

2, 0, 4, 2, 1, 1, 5

Mean = $frac{sum of all the observations}{Number of observations}\ = frac{2+ 0+ 4+ 2+ 1+ 1+ 5}{7}\ =frac{15}{7}$

Mean = 2.14

Therefore,

Mean deviation for 7, 5, 1, 3, 6, 4, 10 is 2.14

Example 4: Find the mean deviation of the following data?

11, 9, 7, 3, 2, 8, 10, 12, 15, 13

Solution:

To find the mean deviation,

First, calculate the mean value of the given data

Mean = $frac{sum of all the observations}{Number of observations}\ = frac{11+ 9+ 7+ 3+ 2+ 8+ 10+ 12+ 15+ 13}{10}\ =frac{80}{10}$

Mean = 8

Now subtract the mean from each data value {ignore negative (-)}

11 – 8 = 3

9 – 8 = 1

7 – 8 = 1

3 – 8 = 5

2 – 8 = 6

8 – 8 = 0

10 – 8 = 2

12 – 8 = 4

15 – 8 = 7

13 – 8 = 5

Further find the mean of these values obtained

3, 1, 1, 5, 6, 0, 2, 4, 7, 5.

Mean = $frac{sum of all the observations}{Number of observations}\ = frac{3+ 1+ 1+ 5+ 6+ 0+ 2+ 4+ 7+ 5 }{10}\ =frac{34}{10}$

Mean = 3.4

Therefore,

Mean deviation for 11, 9, 7, 3, 2, 8, 10, 12, 15, 13 is 3.4.

Last Updated :
09 Nov, 2021

Like Article

Save Article

Источник

Условное
обозначение средней арифметической
величины через М (от латинского слова
Media) чаще применяется в медицинских и
педагогических исследованиях. В
математической статистике предпочитают
обозначение через .
Средняя арифметическая величина является
производной, обобщающей количественные
признаки ряда однородных показателей
(совокупности). Выражая одним числом
определенную совокупность, она как бы
ослабляет влияние случайных индивидуальных
отклонений, и акцентирует некую обобщенную
количественную характеристику, наиболее
типичное свойство изучаемого ряда
показателей.

Определяя
значение средней арифметической
величины, следует придерживаться
некоторых правил.

1.
Средняя арифметическая величина может
характеризовать только те признаки
изучаемого объекта, которые присущи
всей совокупности, но в разной
количественной мере (например, уровень
развития быстроты движений характерен
для каждого человека, хотя и в разной
количественной мере). Средняя арифметическая
величина не может характеризовать
количественную меру тех признаков,
которые одной части совокупности
присущи, а другой нет, т. е. она не может
отражать присутствие или отсутствие
того или иного признака (например, умение
или неумение выполнять то или иное
двигательное действие).

2.
Средняя арифметическая величина должна
включать все показатели, полученные в
данном исследовании. Произвольное
исключение даже некоторых из них
неизбежно приведет к искажению конечного
результата.

3.
Средняя арифметическая величина обязана
отражать только однородную совокупность.
Нельзя, например, определять средний
уровень физического развития школьников,
не разделив их предварительно по возрасту
и полу.

4.
Средняя арифметическая величина должна
вычисляться на достаточно большой
совокупности, размеры которой определяются
в каждом конкретном случае отдельно
(см. «Подбор исследуемых»).

5.
Необходимо стремиться к тому, чтобы
средняя арифметическая величина имела
четкие и простые свойства, позволяющие
легко и быстро ее вычислять.

6.
Средняя арифметическая величина должна
обладать достаточной устойчивостью к
действию случайных факторов. Только в
этом случае она будет отражать
действительное состояние изучаемого
явления, а не его случайные изменения.

7.
Точность вычисления средней арифметической
величины должна соответствовать
содержанию изучаемого педагогического
явления. В некоторых случаях нет
необходимости в расчетах с большой
точностью, в других — большая точность
нужна при вычислениях, но совершенно
не нужна в выводах. Например, при расчете
средних величин числа подтягиваний на
перекладине можно пользоваться и сотыми
долями целого, но представлять и выводах,
что исследуемые в среднем подтянулись
7,83 раза, было бы неграмотна, так как
невозможно измерение с подобной
точностью. В этом случае необходимо в
выводах представлять числа, округленные
до целых единиц.

В
простейшем случае этот показатель
вычисляется путем сложения всех
полученных значений (которые называются
вариантами) и деления суммы на число
вариант:

где
S — знак суммирования;

V
— полученные в исследовании значения
(варианты);

п
— число вариант.

По
этой формуле вычисляется так называемая
простая средняя арифметическая величина.
Применяется она в тех случаях, когда
имеется небольшое число вариант.

При
большом числе вариант прибегают к
вычислению так называемой взвешенной
средней арифметической величины. С этой
целью строят ряд распределения, или
вариационный ряд, который представляет
собой ряд вариант и их частот,
характеризующих какой-нибудь признак
в убывающем или возрастающем порядке.
Например, в нашем случае измерение
точности попадания мячом в цель дало
125 вариант, т. е. в группе I, где применялась
методика обучения «А», одноразово
исследовалось 125 детей с числовым
выражением от 0 (точное попадание в цель)
до 21,5 см (максимальное отклонение от
цели). Каждое числовое выражение
встречалось в исследовании один и более
раз, например «0» встретился 28 раз.
Другими словами, 28 участников эксперимента
точно попали в цель. Этот показатель
называется числом наблюдений или
частотой вариант и условно обозначается
буквой «Р» (число наблюдений составляет
часть числа вариант).

Для
упрощения числовых операций все 125
вариант разбиваются на классы с величиной
интервала 1,9 см. Число классов зависит
от величины колебаний вариант (разности
между максимальной и минимальной
вариантами), наличия вариант для каждого
класса (если, например, для первого
класса — «0 — 1,9» — нет соответствующих
вариант, т.е. ни один исследуемый не имел
точных попаданий или отклонений от цели
в пределах от 0 до 1,9 см, то подобный класс
не вносится в вариационный ряд) и,
наконец, требуемой точности вычисления,
(чем больше классов, тем точность
вычисления выше). Вполне понятно, что
чем больше величина интервала, тем
меньше число классов при одной и той же
величине колебаний вариант.

После
разбивки вариант по классам в каждом
классе определяется срединная варианта
«V_c»,
и для каждой срединной варианты
проставляется число наблюдений. Пример
этих операций, и дальнейший ход вычислений
приведены в следующей таблице:

Классы	Серединные варианты V_C	Число набл, р	V_CP	V_C-M=d	d²	d²P
0 – 1.9	1	28	28	-4.6	21.16	592.48
2 – 3.9	3	29	87	-2.6	6.76	196.04
4 – 5.9	5	22	110	-0.6	0.36	7.92
6 – 7.9	7	13	91	1.4	1.96	25.48
8 – 9.9	9	11	99	3.4	11.56	127.16
10 – 11.9	11	13	143	5.4	29.16	379.08
12 – 13.9	13	4	52	7.4	54.76	219.04
14 – 15.9	15	2	30	9.4	88.36	176.72
16 – 17.9	17	1	17	11.4	130.00	130.00
18 – 19.9	19	1	19	13.4	179.60	179.60
20 – 21.9	21	1	21	15.4	237.20	237.20
		125	697			2270.72

Очередность
числовых операций:

1)
вычислить сумму числа наблюдений (в
нашем примере она равна 125);

2)
вычислить произведение каждой срединной
варианты на ее частоту (например, 1*28 =
28);

3)
вычислить сумму произведений срединных
вариант на их частоты (в нашем примере
она равна 697);

4)
вычислить взвешенную среднюю арифметическую
величину по формуле:

Средняя
арифметическая величина позволяет
сравнивать и оценивать группы изучаемых
явлений в целом. Однако для характеристики
группы явлений только этой величины
явно недостаточно, так как размер
колебаний вариант, из которых она
складывается, может быть различным.
Поэтому в характеристику группы явлений
необходимо ввести такой показатель,
который давал бы представление о величине
колебаний вариант около их средней
величины.

Вычисление
средней ошибки среднего арифметического.
Условное обозначение средней ошибки
среднего арифметического — т. Следует
помнить, что под «ошибкой» в статистике
понимается не ошибка исследования, а
мера представительства данной величины,
т. е. мера, которой средняя арифметическая
величина, полученная на выборочной
совокупности (в нашем примере — на 125
детях), отличается от истинной средней
арифметической величины, которая была
бы получена на генеральной совокупности
(в нашем примере это были бы все дети
аналогичного возраста, уровня
подготовленности и т. д.). Например, в
приведенном ранее примере определялась
точность попадания малым мячом в цель
у 125 детей и была получена средняя
арифметическая величина примерно равная
5,6 см. Теперь надо установить, в какой
мере эта величина будет характерна,
если взять для исследования 200, 300, 500 и
больше аналогичных детей. Ответ на этот
вопрос и даст вычисление средней ошибки
среднего арифметического, которое
производится по формуле:

Для
приведенного примера величина средней
ошибки среднего арифметического будет
равна:

Следовательно,
M±m = 5,6±0,38. Это означает, что полученная
средняя арифметическая величина (M =
5,6) может иметь в других аналогичных
исследованиях значения от 5,22 (5,6 — 0,38 =
5,22) до 5,98 (5,6+0,38 = 5,98).

Источник

Вычисление среднего отклонения может быть эффективным способом анализа изменчивости в наборе данных. Независимо от точного характера собранных данных, знание их среднего отклонения может помочь вам в их интерпретации. Знание того, как рассчитать среднее отклонение — ценный навык, но он требует изучения и практики. В этой статье мы обсудим, что такое среднее отклонение, как его рассчитать, а также различия между абсолютным и средним отклонением, средним средним и средним отклонением от среднего и стандартным отклонением в сравнении со средним отклонением.

Что такое среднее отклонение?

Среднее отклонение набора данных — это среднее значение всех отклонений от заданной центральной точки. Это статистический инструмент для измерения расстояния от среднего значения или медианы, где среднее значение — это среднее значение всех чисел в наборе данных, а медиана — это точное среднее число, когда мы упорядочиваем набор данных от самого низкого до самого высокого числа. Среднее отклонение набора данных также называется средним абсолютным отклонением (MAD) или средним абсолютным отклонением.

Хотя при работе с относительно небольшими наборами данных вы можете рассчитать среднее отклонение вручную, для больших наборов данных обычно требуется специальное программное обеспечение, которое выполняет расчеты за вас после ввода исходных данных.

Как рассчитать среднее отклонение

Рассмотрим эти шаги при расчете среднего отклонения набора данных:

1. Рассчитать среднюю медиану

Первый шаг — вычисление среднего значения. Вы можете сделать это, сложив все значения в наборе данных и разделив полученную сумму на общее количество значений.

Также можно вычислить медиану, если вы хотите использовать ее вместо среднего значения. Расположите все числа в числовом порядке и подсчитайте, сколько их всего. Затем, если общее число нечетное, разделите его на два и округлите, чтобы найти положение медианы. Если общее число четное, разделите его на два и сделайте среднее между числом в этой позиции и числом в следующей более высокой позиции.

2. Рассчитайте отклонение от среднего значения

После расчета среднего значения можно рассчитать отклонение от среднего для каждого значения в наборе данных. Вычислите разницу между ранее рассчитанным средним и каждым значением в наборе данных и запишите абсолютное значение получившихся чисел. Абсолютное значение числа — это его модуль или неотрицательное значение. Поскольку направление каждого отклонения не имеет значения при расчете среднего отклонения, все результирующие числа положительны.

3. Вычислите сумму всех отклонений

После вычисления отклонения от среднего значения для каждого значения в наборе данных необходимо сложить их вместе. Поскольку это операция с абсолютным значением, каждое значение должно быть положительным числом.

4. Вычислить среднее отклонение

Наконец, рассчитайте среднее отклонение вашего набора данных, разделив ранее рассчитанную сумму всех отклонений на общее количество отклонений, которые вы сложили вместе. Полученное число — это среднее отклонение от среднего.

Пример

Рассмотрите этот пример при расчете среднего отклонения от среднего значения.

Баскетболист сыграл 5 игр в этом сезоне. Числа очков в каждой игре: 23, 30, 31, 15 и 46.

Первый шаг — вычисление среднего значения. Вы делаете это, складывая очки и деля результат на пять игр.

23+30+31+15+46=145

1455=29

Теперь, когда вы определили, что игрок набирал в среднем 29 очков за игру, вам нужно рассчитать отклонение от среднего значения для каждой игры.

23-29=6

30-29=1

31-29=2

15-29=14

46-29=17

Далее необходимо вычислить сумму всех вариаций.

6+1+2+14+17=40

Среднее отклонение — это сумма всех отклонений, деленная на общее количество записей.

Среднее отклонение=405=8

Среднее отклонение от среднего значения по очкам, набранным в первых пяти играх сезона, составляет 8.

Абсолютное отклонение vs. среднее отклонение

Вычисление абсолютного отклонения является важным шагом для определения среднего отклонения. Абсолютное отклонение — это разница между средним значением набора данных и каждым значением в соответствующем наборе данных. Название абсолютного отклонения происходит от того, что все полученные числа записываются как абсолютные числа. Мера выражает расстояние между средним и каждым значением, поэтому отрицательное или положительное число не имеет значения.

После расчета абсолютного отклонения для каждого значения в наборе данных можно рассчитать среднее отклонение, сложив их все вместе и разделив на общее количество значений в наборе данных.

Среднее значение против. среднее отклонение от среднего

Вычисление среднего значения также является важным шагом для определения среднего отклонения от среднего значения. Среднее среднее — это просто сумма всех значений, включенных в набор данных, деленная на общее количество значений. Вычисление среднего значения помогает определить отклонение от среднего путем вычисления разницы между средним и каждым значением. Далее разделите сумму всех ранее рассчитанных значений на количество отклонений, сложенных вместе, и в результате получите среднее отклонение от среднего.

Стандартное отклонение против. среднее отклонение

Стандартное отклонение также является мерой изменчивости в наборе данных, так как оно показывает размер отклонения между всеми значениями в наборе данных. Основное различие между ними заключается в том, что значения, полученные в результате вычитания среднего из значения каждой точки данных, записываются как абсолютные только при вычислении среднего отклонения. Чтобы рассчитать стандартное отклонение, полученные значения записываются не в абсолютных величинах, а в квадрате. Затем необходимо вычислить среднее арифметическое всех квадратных значений. Квадратный корень из этого среднего значения является стандартным средним значением.

Стандартное отклонение чаще всего используется для измерения изменчивости, являясь очень популярным инструментом для расчета волатильности финансовых инструментов и потенциальной инвестиционной доходности. Более высокая волатильность обычно означает, что существует повышенный риск того, что инвестиции принесут убытки. Это означает, что инвестор, который берет на себя риск высоковолатильной ценной бумаги, обычно ожидает от нее высокой доходности. Среднее отклонение также используется в качестве финансового инструмента, но, как правило, реже, чем стандартное отклонение.

Источник