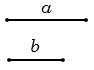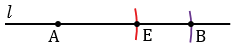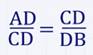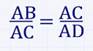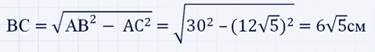- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Построения циркулем и линейкой
- Среднее пропорциональное
Среднее пропорциональное положительных чисел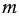 
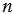
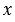
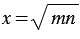
и 
— это такое число 
, которое равно квадратному корню из произведения этих чисел, т.е. 
.
Среднее пропорциональное носит такое название, потому что число 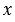является средним членом пропорции 
.
Средним пропорциональным (или средним геометрическим) двух отрезков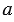 
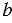
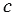
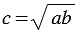
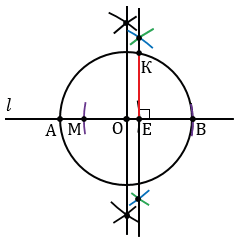
и 
, называется такой отрезок 
, что: 
.
Чтобы построить среднее пропорциональное двух отрезков используют циркуль и линейку.
Ход построения:
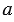
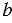
Пусть нам даны два отрезка и , строим их.
Затем строим с помощью линейки прямую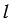 
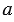
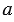
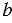
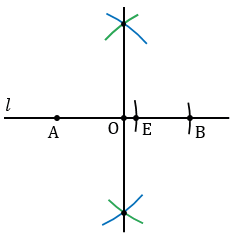
, отмечаем на ней точку А и строим отрезок АЕ, равный отрезку . Для этого строим с помощью циркуля окружность радиуса с центром А (полностью окружность строить необязательно, смотри выделенное красным цветом). Затем, аналогично строим отрезок ЕВ, равный отрезку .
Далее найдем середину отрезка АВ. Для этого строим две окружности с центрами А и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая пересечет отрезок АВ в его середине О.
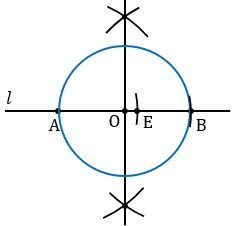
Теперь строим окружность с центром О радиуса ОА.
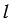
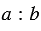
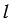
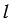
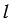
Затем построим перпендикуляр к прямой так, чтобы он проходил через точку Е, которая делит отрезок АВ в отношении 
. Для этого строим окружность произвольного радиуса с центром Е (полностью окружность строить необязательно, смотри выделенное фиолетовым цветом), данная окружность пересечет прямую в двух точках М и В (точку В мы берем как точку пересечения данной окружности и данной прямой для того, чтобы не добавлять на рисунке лишние элементы, но важно помнить, что точки пересечения окружности с центром Е и прямой могут быть и другие, все зависит от того, каким мы возьмем радиус окружности с центром Е). Далее строим две окружности с центрами М и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая будет перпендикулярна к прямой и пересечет окружность с центром О в точке К.
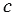
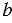
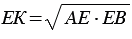
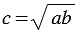
Длина отрезка ЕК и есть искомый отрезок , равный среднему пропорциональному отрезков и , т.е. 
или .
Советуем посмотреть:
Построение угла, равного данному
Построение биссектрисы угла
Построение перпендикулярных прямых
Построение середины отрезка
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольник
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 1270,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Пропорциональные отрезки в прямоугольном треугольнике
В этом уроке познакомимся с понятием «среднее геометрическое» или «среднее пропорциональное» для отрезков, выведем формулы для вычисления высоты и катетов прямоугольного треугольника через понятие среднее пропорциональное, рассмотрим задачу на применение формул.
Решим задачу:
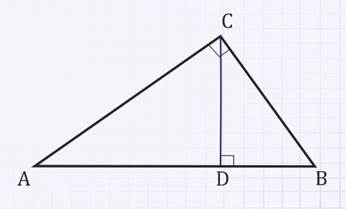
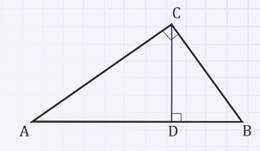
Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Дано:
∆АВС – прямоугольный треугольник,
СD – высота, проведенная из вершины С к гипотенузе АВ.
Доказать:
∆АВС ~ ∆АСD;
∆АВС ~ ∆CBD
∆АСD ~ ∆CBD.
Доказательство:
1)Рассмотрим треугольники АВС и АСD.
Так как ∠А–общий,
∠АСВ = ∠АDС = 90°, отсюда следует, что треугольники АВС и АСD подобны по первому признаку подобия треугольников, т.е. по двум равным углам.
2)Рассмотрим треугольники АВС и СВD.
Так как ∠В–общий,
∠АСВ = ∠ВDС = 90°, то треугольники АВС и СВD тоже подобны по первому признаку подобия треугольников. А раз так, то ∠А = ∠ВСD.
3)Рассмотрим треугольники АСD и СВD.
Так как ∠АDС = ∠СDВ = 90° и ∠А = ∠ВСD, то треугольники АСD и СВD подобны по первому признаку подобия треугольников.
Что и требовалось доказать.
В геометрии в формулировках ряда утверждений и при решении отдельных задач используется понятие «среднее пропорциональное отрезков» или «среднее геометрическое».
Отрезок ХУ называется средним пропорциональным (или средним геометрическим) для отрезков АВ и СD, если выполняется равенство:
Исходя из доказанной выше задачи, можно выделить два утверждения.
1.Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
Для вывода данного утверждения воспользуемся доказанным, а именно, что:
поэтому:
Применяя основное свойство пропорции, получим
2.Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.
Также по выше доказанному в задаче:
поэтому:
и, следовательно:
Решим задачу, применяя данные утверждения.
Задача:
Найдите катеты прямоугольного треугольника АВС, если АD = 24 см, ВD = 6 см.
Решение:
Найдем гипотенузу данного прямоугольного треугольника:
Теперь воспользуемся равенством второго утверждения:
Для вычисления второго катета воспользуемся теоремой Пифагора:
или равенством все того же второго утверждения:
Планиметрия
6. Подобие фигур
6.7. Средние пропорциональные отрезки в прямоугольном треугольнике
Когда говорят о среднем пропорциональном отрезке 
между двумя данными отрезками 
и 
, то имеют в виду следующее соотношение между их длинами (числами) : 
или 
.
Теоремы
Если в прямоугольном треугольнике опущена высота на гипотенузу, то:
1) высота является средним пропорциональным между проекциями катетов на гипотенузу;
2) каждый из катетов есть среднее пропорциональное между всей гипотенузой и его проекцией на гипотенузу.
Дано : 
, 
, 
.
Требуется доказать:
1) 
;
2) 
; 
.
Доказательство:
1) 
, так как у них имеется по прямому углу и 
(углы с соответственно перпендикулярными сторонами). Катет 
в 
сходственен катету 
в 
(лежат против равных углов) и другие катеты и 
этих треугольников также сходственны. В подобных треугольниках отношения сходственных сторон равны: 
, 
.
2) 
(они прямоугольные и 
общий). Сходственны их гипотенузы 
и 
, а также катеты, прилежащие к общему углу, и : 
; .
Аналогично рассматриваем подобные треугольники 
и 
, из которых получаем, что 
.
Начнём с повторения уже известных нам сведений о
прямоугольном треугольнике.
Прямоугольным называется треугольник,
у которого один из углов прямой.
Сторону, лежащую против прямого угла, называют гипотенузой,
а две другие — катетами.
Вы уже знакомы с очень важной теоремой, теоремой
Пифагора. Она гласит, что в прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов.
А также вам известны признаки равенства
прямоугольных треугольников. Они могут быть равны: по двум катетам, по катету и
прилежащему к нему углу, по гипотенузе и острому углу, по катету и гипотенузе.
Сегодня поговорим о пропорциональных отрезках в
прямоугольном треугольнике. И начнём с задачи.
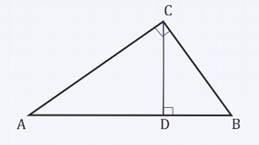
Задача. Докажите, что
высота прямоугольного треугольника, проведенная из вершины прямого угла,
разделяет треугольник на два подобных прямоугольных треугольника, каждый из
которых подобен данному треугольнику.
Доказательство.
1.
2.
3.
Так мы доказали, что высота прямоугольного
треугольника, проведенная из вершины прямого угла, разделяет треугольник на два
подобных прямоугольных треугольника, каждый из которых, в свою очередь, подобен
данному треугольнику.
Определение.
Отрезок называется
средним пропорциональным
(или средним геометрическим) для отрезков и
,
если .
Опираясь на данное определение и задачу, решённую нами, докажем
следующие утверждения:
высота прямоугольного треугольника, проведенная из
вершины прямого угла, есть среднее пропорциональное для отрезков, на которые
делится гипотенуза этой высотой.
В предыдущей задаче нами уже было доказано, что
треугольники
катет прямоугольного треугольника есть среднее
пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между
катетом и высотой, проведенной из вершины прямого угла.
Докажем второе утверждение.
Для этого воспользуемся подобием треугольников ABC
и ACD. Запишем отношение
соответствующих сторон.
Отсюда получаем, что АЦ равно корню квадратному из
произведения АБ и АД.
Выполним задание.
Задача. Найдите элементы
прямоугольного треугольника по известным данным.
а)
б)
в)
г)
Решение.
а)
б)
в)
г)
Задача. По данным
рисунка нужно найти площадь .
Решение.
а)
1.
2.
3.
б)
1.
2.
3.
4.
Ответ: а) , б)
.
Задача. —
ромб, равно
12, .
Найдите площадь ромба.
Решение.
1.
2. Пусть
3.
4.
Ответ: .
Подведём итоги урока.
Сегодня вы познакомились с определением среднего
геометрического и узнали, как это понятие связано с прямоугольным
треугольником.
А именно:
Высота прямоугольного треугольника, проведенная из
вершины прямого угла, есть среднее пропорциональное для отрезков, на которые
делится гипотенуза этой высотой.
Катет прямоугольного треугольника есть среднее
пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между
катетом и высотой, проведенной из вершины прямого угла.
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Признак подобия прямоугольных треугольников
Введем для начала признак подобия прямоугольных треугольников.
Признак подобия прямоугольных треугольников: два прямоугольных треугольника подобны тогда, когда у них есть по одному равному острому углу (рис. 1).
прямоугольные треугольники»>
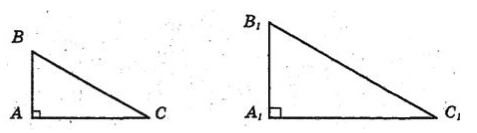
Рисунок 1. Подобные прямоугольные треугольники
Доказательство.
Пусть нам дано, что $angle B=angle B_1$. Так как треугольники прямоугольные, то $angle A=angle A_1={90}^0$. Следовательно, они подобны по первому признаку подобия треугольников.
Теорема доказана.
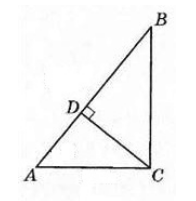
Теорема о высоте в прямоугольном треугольнике
Теорема 2
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Доказательство.
Пусть нам дан прямоугольный треугольник $ABC$ с прямым углом $C$. Проведем высоту $CD$ (рис. 2).
Рисунок 2. Иллюстрация теоремы 2
Докажем, что треугольники $ACD$ и $BCD$ подобны треугольнику $ABC$ и что треугольники $ACD$ и $BCD$ подобны между собой.
-
Так как $angle ADC={90}^0$, то треугольник $ACD$ прямоугольный. У треугольников $ACD$ и $ABC$ угол $A$ общий, следовательно, по теореме 1, треугольники $ACD$ и $ABC$ подобны.
-
Так как $angle BDC={90}^0$, то треугольник $BCD$ прямоугольный. У треугольников $BCD$ и $ABC$ угол $B$ общий, следовательно, по теореме 1, треугольники $BCD$ и $ABC$ подобны.
-
Рассмотрим теперь треугольники $ACD$ и $BCD$
[angle A={90}^0-angle ACD] [angle BCD={90}^0-angle ACD=angle A]
Следовательно, по теореме 1, треугольники $ACD$ и $BCD$ подобны.
«Пропорциональные отрезки в прямоугольном треугольнике» 👇
Теорема доказана.
Среднее пропорциональное
Определение 1
Отрезок $x$ называется средним пропорциональным или средним геометрическим дл отрезков $a$ и $b$, если выполняется следующее равенство
[x=sqrt{ab}]
Теорема 3
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые высота делит гипотенузу данного треугольника.
Доказательство.
В доказательстве теоремы будем пользоваться обозначениями из рисунка 2.
По теореме 2, имеем, что треугольники $ACD$ и $BCD$ подобны, следовательно
Теорема доказана.
Теорема 4
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из вершины угла.
Доказательство.
В доказательстве теоремы будем пользоваться обозначениями из рисунка 2.
По теореме 2, имеем, что треугольники $ACD$ и $ABC$ подобны, следовательно
Теорема доказана.
Примеры задач на использование пропорциональных отрезков в прямоугольном треугольнике
Пример 1
Катеты прямоугольного треугольника $ABC$ с прямым углом $C$ относятся как $2:3$, а гипотенуза равна $39$ см. Найти отрезки, на которые высота $CD$ делит гипотенузу данного треугольника.
Решение.
Изобразим условие на рисунке:
Рисунок 3.
По теореме 4, с одной стороны, получим
[AC=sqrt{ABcdot AD}]
А с другой стороны, получим
[BC=sqrt{ABcdot BD}]
Тогда
[frac{AC}{BC}=frac{sqrt{ABcdot AD}}{sqrt{ABcdot BD}}=sqrt{frac{AD}{BD}}=frac{2}{3}]
Следовательно
[frac{AD}{BD}=frac{4}{9}] [AD=frac{4}{9}BD]
Так как $AD+BD=AB=39$, то
[frac{4}{9}BD+BD=39] [13BD=39cdot 9] [BD=27] [ AD=12]
Ответ: $12$ и $27$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме