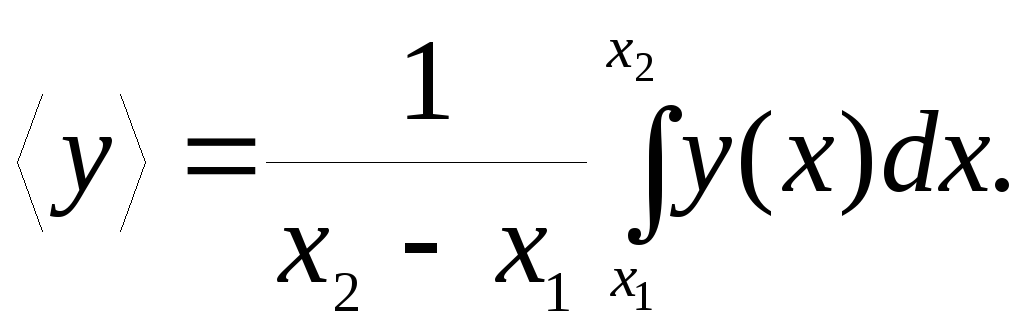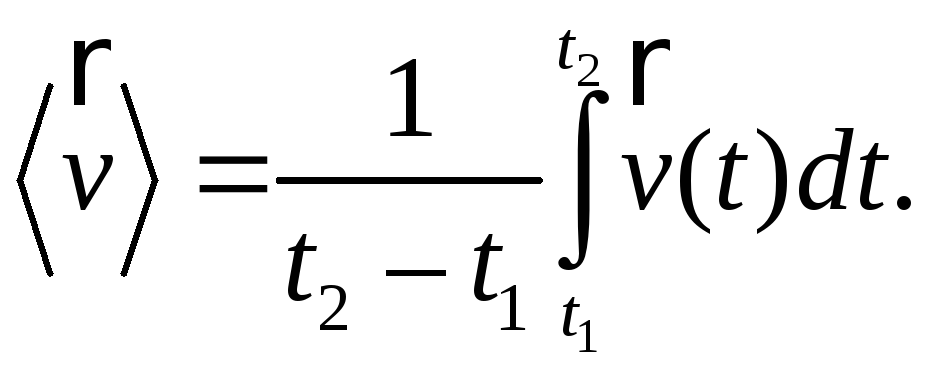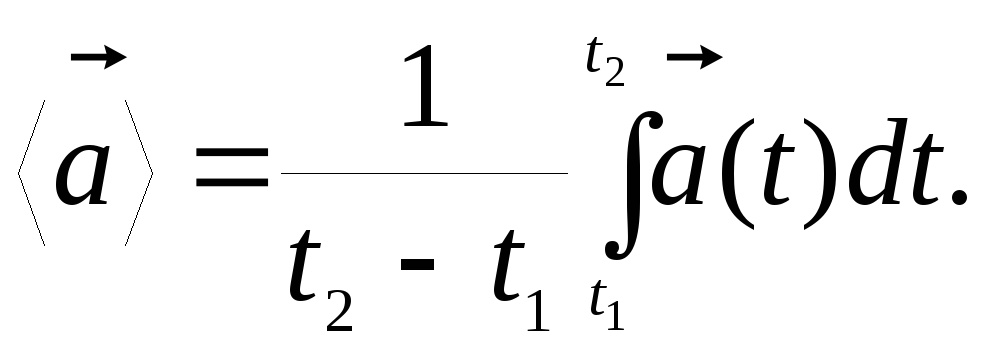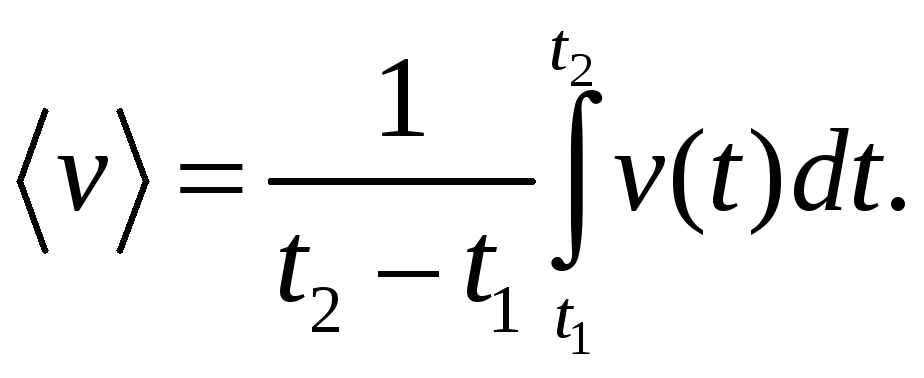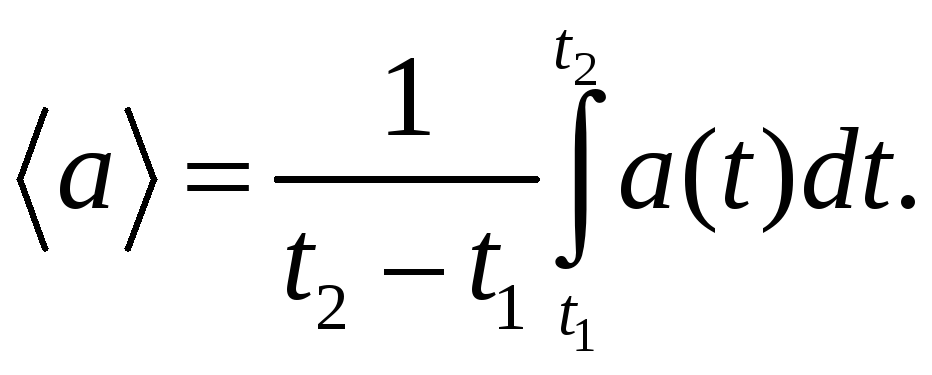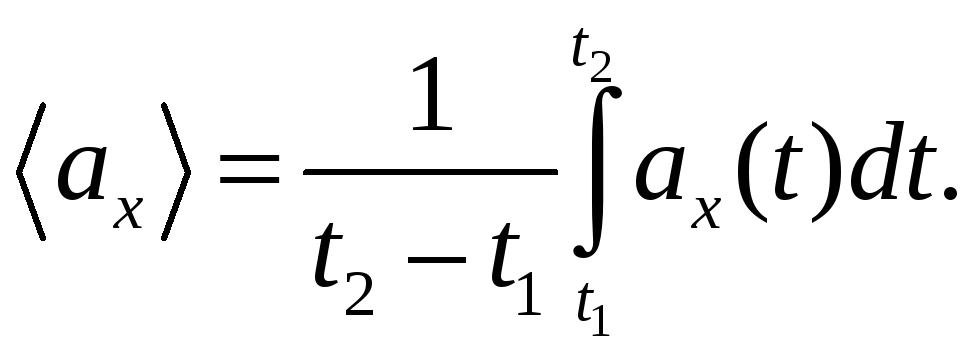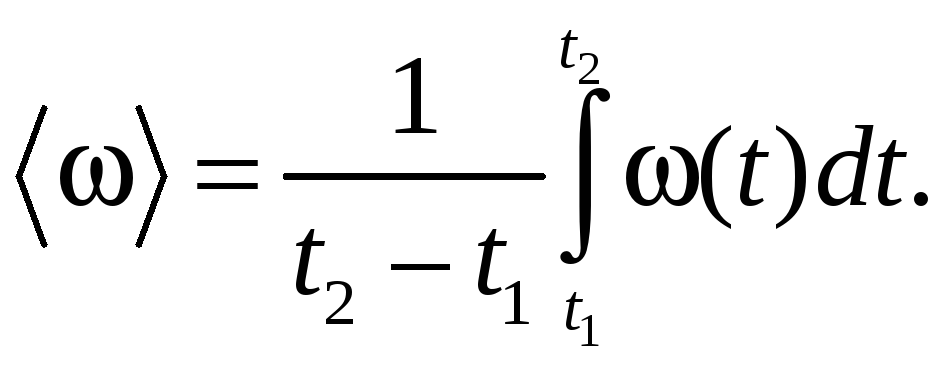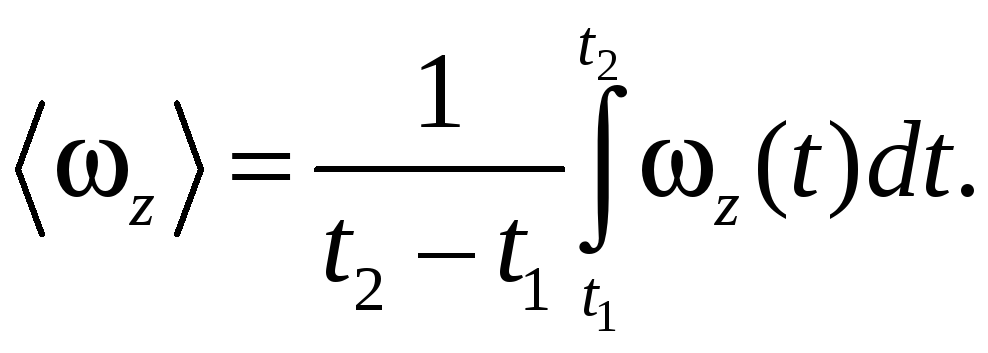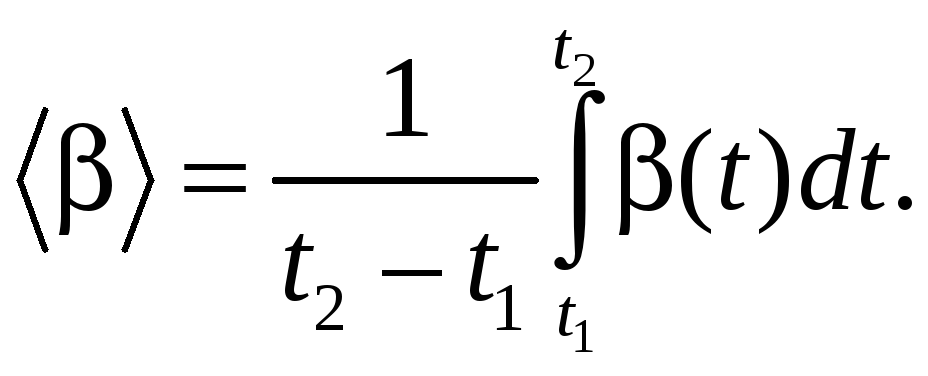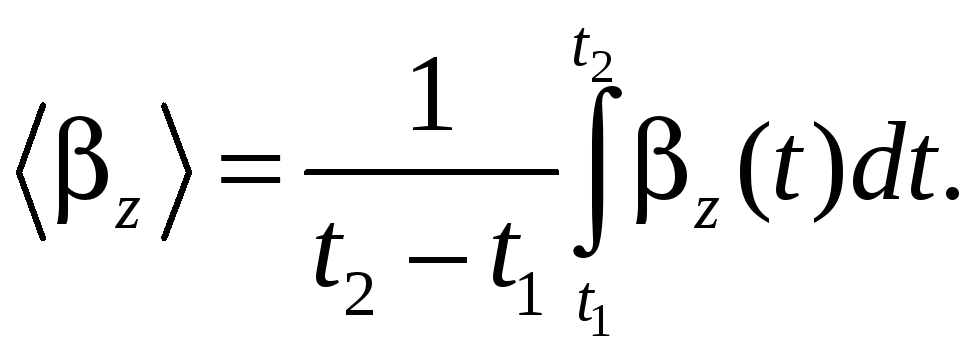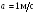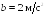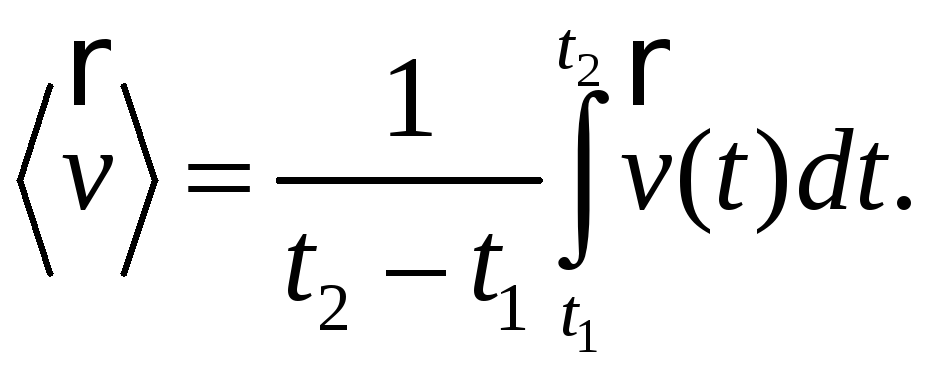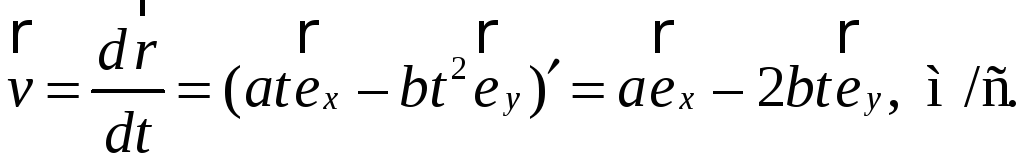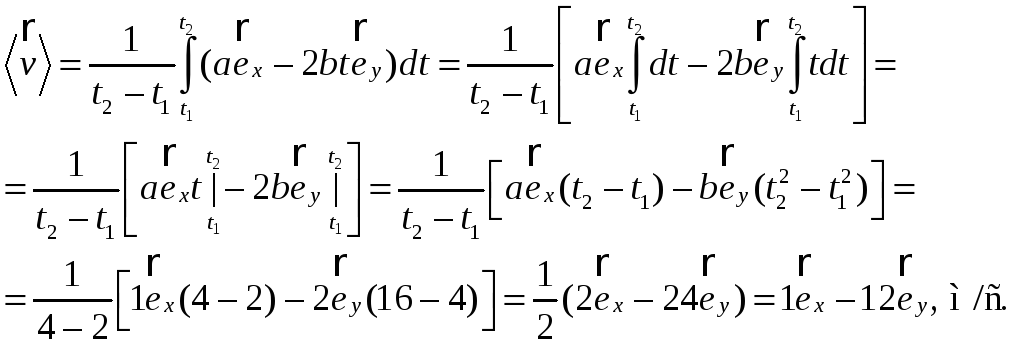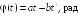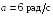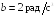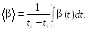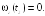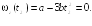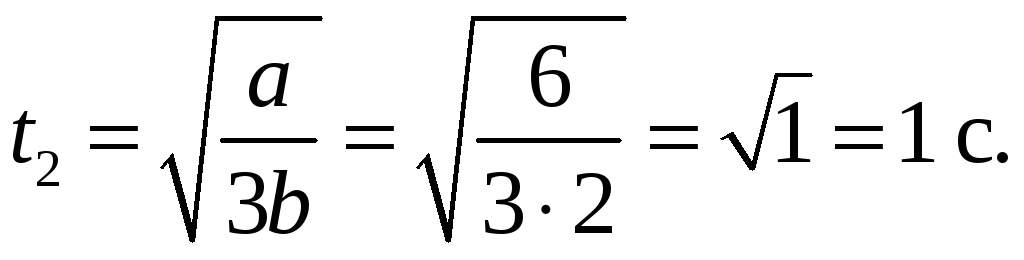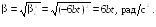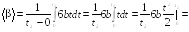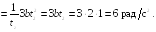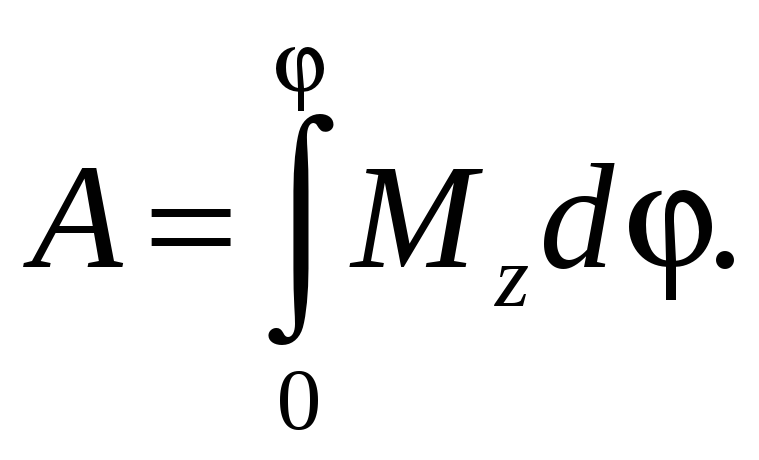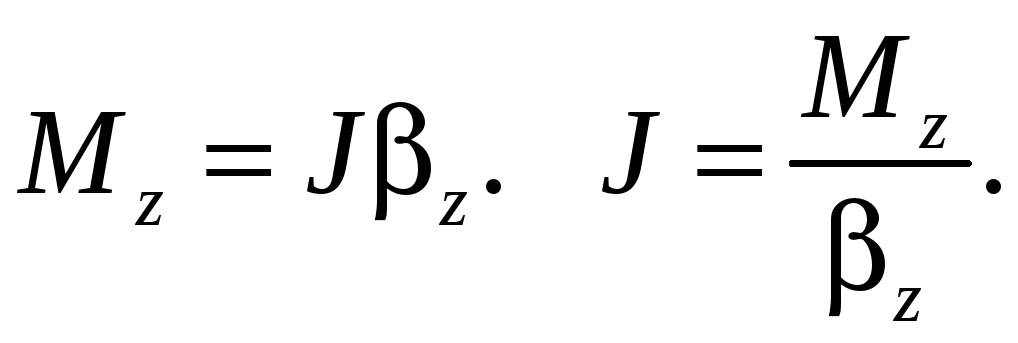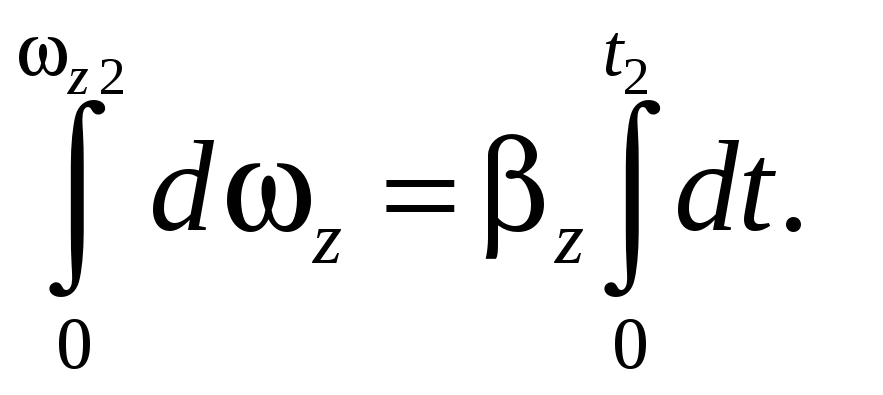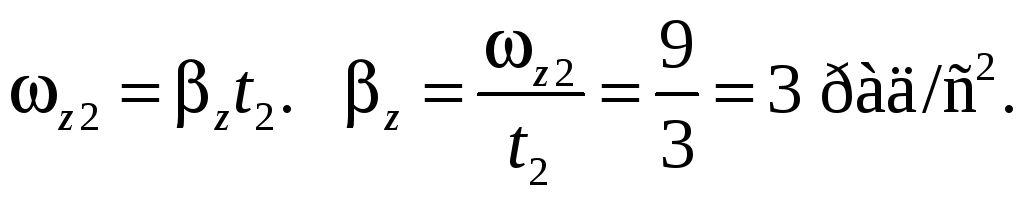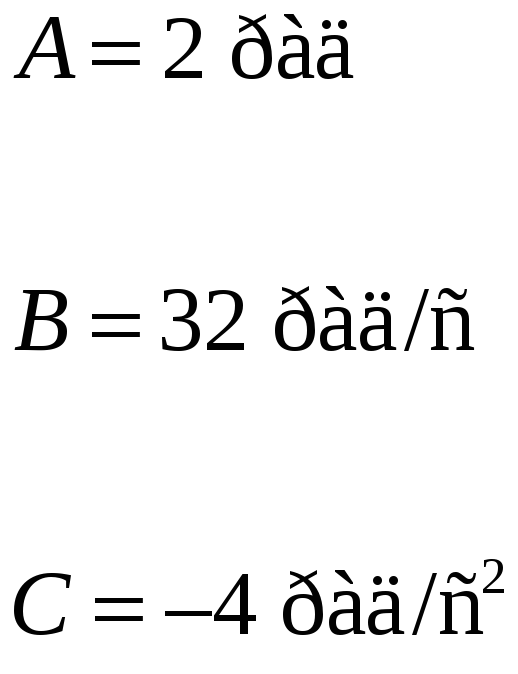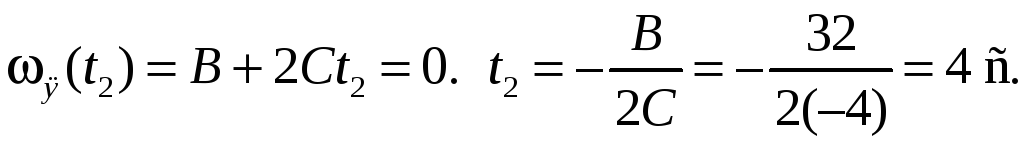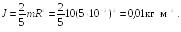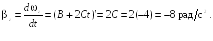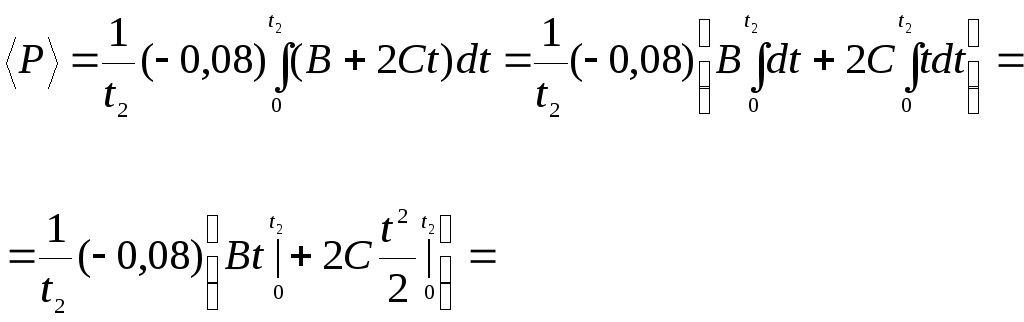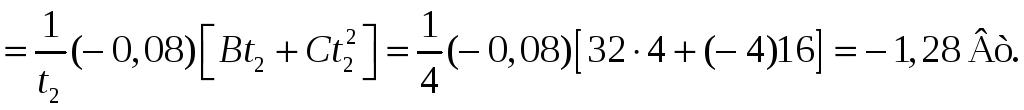Как найти среднее ускорение за время движения - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Ускорение характеризует быстроту изменения скорости как по величине, так и по направлению. Можно найти среднее ускорение, чтобы определить среднюю быстроту изменения скорости тела в течение определенного периода времени. Возможно, вы не знаете, как вычислить ускорение (так как это неповседневная задача), но с правильным подходом это не составит труда.

1
Определение ускорения. Ускорение — это быстрота увеличения или уменьшения скорости,^[1] или просто быстрота изменения скорости с течением времени.^[2] Ускорение — векторная величина, имеющая направление (включите его в ответ).
- Обычно, если тело ускоряется при движении «вправо», «вверх» или «вперед», то ускорение имеет положительное (+) значение.
- Если тело ускоряется при движении «влево», «вниз» или «назад», то ускорение имеет отрицательное (+) значение.
2
Запишите определение ускорения в виде формулы. Как упоминалось выше, ускорение — это быстрота изменения скорости с течением времени.^[3] Есть два способа записать это определение в виде формулы:
- a_ср = ^Δv/_Δt (символ дельта «Δ» означает «изменение»).
- a_ср = ^{(v_к — v_н)}/_{(t_к — t_н)}, где v_к — конечная скорость, v_н — начальная скорость.
3
Найдите начальную и конечную скорости тела. Например, автомобиль, начинающий движение (вправо) со стоянки, имеет начальную скорость 0 м/с, а конечную скорость 500 м/с.^[4]
- Движение вправо описывается положительными значениями, поэтому далее мы не будем указывать направление движения.
- Если автомобиль начинает движение вперед, а заканчивает его движением назад, конечная скорость имеет отрицательное значение.
4
Обратите внимание на изменение времени. Например, автомобилю может понадобиться 10 секунд, чтобы достичь конечной скорости. В этом случае t_к = 10 с, а t_н = 0 с.^[5]
- Убедитесь, что скорость и время даются в соответствующих единицах измерения. Например, если скорость дана в км/ч, то время должно измеряться в часах.
5
Подставьте данные вам значения скорости и времени в формулу для вычисления среднего ускорения. В нашем примере:
- a_ср = ^{(500 м/с — 0 м/с)}/_{(10с – 0с)}
- a_ср = ^{(500 м/с)}/_(10с)
- a_ср = 50 м/с / с, то есть 50 м/с².
6
Интерпретация результата. Среднее ускорение задает среднюю быстроту изменения скорости в течение определенного промежутка времени.^[6] В приведенном выше примере машина в среднем ускорялась на 50 м/с за каждую секунду. Запомните: параметры движения могут быть разными, но среднее ускорение будет таким же, только если изменение скорости и изменение времени не меняются:
- Автомобиль может начать движение со скоростью 0 м/с и разогнаться за 10 секунд до 500 м/с.
- Автомобиль может начать движение со скоростью 0 м/с и разогнаться до 900 м/с, а затем сбросить скорость до 500 м/с за 10 секунд.
- Автомобиль может начать движение со скоростью 0 м/с, стоять на месте в течение 9 секунд, а затем за 1 секунду разогнаться до 500 м/с.
Реклама

1
Определение положительной и отрицательной скорости. Скорость имеет направление (так как это векторная величина), но указывать его, например, как «вверх» или «на север», весьма утомительно. Вместо этого в большинстве задач предполагается, что тело движется вдоль прямой линии. При движении в одном направлении скорость тела положительна, а при движении в противоположном направлении скорость тела отрицательна.^[7]
- Например, синий поезд движется на восток со скоростью 500 м/с. Красный поезд движется на запад с такой же скоростью, но так как он движется в противоположном направлении, его скорость записывается так: -500 м/с.
2
Используйте определение ускорения, чтобы определить его знак (+ или -). Ускорение — быстрота изменения скорости с течением времени. Если вы не знаете, какой знак написать у значения ускорения, найдите изменение скорости:
- v_{конечная} — v_{начальная} = + или — ?
3
Ускорение в разных направлениях. Например, синий и красный поезда движутся в противоположных направлениях со скоростью 5 м/с. Представьте это движение на числовой прямой; синий поезд движется со скоростью 5 м/с в положительном направлении числовой прямой (то есть вправо), а красный поезд движется со скоростью -5 м/с в отрицательном направлении числовой прямой (то есть влево). Если каждый поезд увеличивает скорость на 2 м/с (в направлении его движения), то какой знак имеет ускорение?^[8] Давайте проверим:
- Синий поезд движется в положительном направлении, поэтому его скорость с 5 м/с возрастает до 7 м/с. Конечная скорость равна 7 — 5 = +2. Поскольку изменение скорости положительно, то и ускорение положительно.
- Красный поезд движется в отрицательном направлении и увеличивает скорость с -5 м/с до -7 м/с. Конечная скорость равна -7 — (-5) = -7 + 5 = -2 м/с. Поскольку изменение скорости отрицательно, то и ускорение отрицательно.
4
Замедление.^[9] Например, самолет летит со скоростью 500 км/ч, а затем замедляется до 400 км/ч. Хотя самолет движется в положительном направлении, его ускорение отрицательно, так как он замедляется (то есть уменьшает скорость). Это можно проверить через вычисления: 400 — 500 = -100, то есть изменение скорости отрицательно, поэтому и ускорение отрицательно.^[10]
- С другой стороны, если вертолет движется со скоростью -100 км/ч и разгоняется до -50 км/ч, то его ускорение положительно, потому что изменение скорости положительно: -50 — (-100) = 50 (хотя такого изменения скорости было недостаточно, чтобы изменить направление движения вертолета).
Реклама

Советы

Ускорение и скорость — векторные величины, которые задаются как значением, так и направлением. Величины, задающиеся только значением, называются скалярными (например, длина).^[11]

Об этой статье

Эту страницу просматривали 46 718 раз.

Была ли эта статья полезной?

Источник

Download Article

If you’ve ever watched a bright red Ferrari fly ahead of your Honda Civic after a stoplight, you’ve experienced differing rates of acceleration firsthand. Acceleration is the rate of change in the velocity of an object as it moves. You can calculate this rate of acceleration, measured in meters per second, based on the time it takes you to go from one velocity to another, or based on the mass of an object.^[1]

1
Define Newton’s Second Law of Motion. Newton’s second law of motion states that when the forces acting on an object are unbalanced, the object will accelerate. This acceleration is dependent upon the net forces that act upon the object and the object’s mass.^[2] Using this law, acceleration can be calculated when a known force is acting on an object of known mass.
- Newton’s law can be represented by the equation F_net = m x a, where F_net is the total force acting on the object, m is the object’s mass, and a is the acceleration of the object.
- When using this equation, keep your units in the metric system. Use kilograms (kg) for mass, newtons (N) for force, and meters per second squared (m/s²) for acceleration.
2
Find the mass of your object. To find the mass of an object, simply place it on a balance or scale and find its mass in grams. If you have a very large object, you may need to find a reference that can provide you with the mass.^[3] Larger objects will likely have a mass with the unit of kilograms (kg).
- For this equation, you will want to convert the mass into kilograms. If the mass you have is in grams simply divide that mass by 1000 to convert to kilograms.
Advertisement
3
Calculate the net force acting on your object. A net force is an unbalanced force. If you have two forces opposing each other and one is larger than the other, you will have a net force in the direction of the larger force.^[4] Acceleration happens when an unbalanced force acts on an object, causing it to change speeds towards the direction the force is pushing or pulling it.
- For example: Let’s say you and your big brother are playing tug-of-war. You pull the rope to the left with a force of 5 newtons while your brother pulls the rope in the opposite direction with a force of 7 newtons. The net force on the rope is 2 newtons to the right, in the direction of your brother.
- In order to properly understand the units, know that 1 newton (N) is equal to 1 kilogram X meter/second squared (kg X m/s²).^[5]
4
Rearrange the equation F = ma to solve for acceleration. You can change this formula around to solve for acceleration by dividing both sides by the mass, so: a = F/m.^[6] To find the acceleration, simply divide the force by the mass of the object being accelerated.
- Force is directly proportional to the acceleration, meaning that a greater force will lead to a greater acceleration.
- Mass is inversely proportional to acceleration, meaning that with a greater mass, the acceleration will decrease.
5
Use the formula to solve for acceleration. Acceleration is equal to the net force acting on an object divided by the mass of the object. Once you’ve established the values for your variables, do the simple division to find the acceleration of the object.
- For example: A 10 Newton force acts uniformly on a mass of 2 kilograms. What is the object’s acceleration?
- a = F/m = 10/2 = 5 m/s²

1
Define the equation for average acceleration. You can calculate the average acceleration of an object over a period of time based on its velocity (its speed traveling in a specific direction), before and after that time. To do this you need to know equation for acceleration: a = Δv / Δt where a is acceleration, Δv is the change in velocity, and Δt is the amount of time it took for that change to occur.^[7]
- The unit for acceleration is meters per second per second or m/s².^[8]
- Acceleration is a vector quantity, meaning it has both a magnitude and a direction.^[9] The magnitude is the total amount of acceleration whereas the direction is the way in which the object is moving. If it is slowing down the acceleration will be negative.
2
Understand the variables. You can further define Δv and Δt: Δv = v_f — v_i and Δt = t_f — t_i where v_f is the final velocity, v_i is the initial velocity, t_f is the ending time, and t_i is the starting time.^[10]
- Because acceleration has a direction, it is important to always subtract the initial velocity from the final velocity. If you reverse them, the direction of your acceleration will be incorrect.
- Unless otherwise stated in the problem, the starting time is usually 0 seconds.
3
Use the formula to find acceleration. First write down your equation and all of the given variables. The equation is a = Δv / Δt = (v_f — v_i)/(t_f — t_i). Subtract the initial velocity from the final velocity, then divide the result by the time interval. The final result is your average acceleration over that time.
- If the final velocity is less than the initial velocity, acceleration will turn out to be a negative quantity or the rate at which an object slows down.
- Example 1: A race car accelerates uniformly from 18.5 m/s to 46.1 m/s in 2.47 seconds. What is its average acceleration?
  - Write the equation: a = Δv / Δt = (v_f — v_i)/(t_f — t_i)
  - Define the variables: v_f = 46.1 m/s, v_i = 18.5 m/s, t_f = 2.47 s, t_i = 0 s.
  - Solve: a = (46.1 – 18.5)/2.47 = 11.17 meters/second².
- Example 2: A biker traveling at 22.4 m/s comes to halt in 2.55 s after applying brakes. Find his deceleration.
  - Write the equation: a = Δv / Δt = (v_f — v_i)/(t_f — t_i)
  - Define the variables: v_f = 0 m/s, v_i = 22.4 m/s, t_f = 2.55 s, t_i = 0 s.
  - Solve: a = (0 – 22.4)/2.55 = -8.78 meters/second².

Understand the Direction of Acceleration. The physics concept of acceleration doesn’t always match how we would use the term in everyday life. Every acceleration has a direction, usually represented as positive if it’s UP or RIGHT, and negative if DOWN or LEFT. See if your answer makes sense based on this breakdown:

Behavior of a Car	How is Velocity Changing?	Direction of Acceleration
Driver moving right (+) hits gas pedal	+ → ++ (more positive)	positive
Driver moving right (+) hits brakes	++ → + (less positive)	negative
Driver moving left (-) hits gas pedal	— → — (more negative)	negative
Driver moving left (-) hits brakes	— → — (less negative)	positive
Driver moves at constant velocity	remains the same	acceleration is zero

2
Understand the Direction of Force. Remember, a force only causes acceleration in the direction of the force. Some problems may try to trick you with irrelevant values.
- Example Problem: A toy boat with mass 10kg is accelerating north at 2 m/s². A wind blowing due west exerts a force of 100 Newtons on the boat. What is the boat’s new northward acceleration?
- Solution: Because the force is perpendicular to the direction of motion, it does not have an effect on motion in that direction. The boat continues to accelerate north at 2 m/s².
3
Understand Net Force. If more than one force acts on an object, combine them into a net force before you calculate acceleration. For a problem in two dimensions, this looks something like this:
- Example Problem: April is pulling a 400 kg container right with a force of 150 newtons. Bob stand on the left of the container and pushes with a force of 200 newtons. A wind blowing left exerts a force of 10 newtons. What is the acceleration of the container?
- Solution: This problem uses tricky language to try and catch you. Draw a diagram and you’ll see the forces are 150 newtons right, 200 newtons right, and 10 newtons left. If «right» is the positive direction, the net force is 150 + 200 — 10 = 340 newtons. Acceleration = F / m = 340 newtons / 400 kg = 0.85 m/s².

Calculator, Practice Problems, and Answers

Add New Question

Question

How do you solve acceleration word problems?

Sean Alexander is an Academic Tutor specializing in teaching mathematics and physics. Sean is the Owner of Alexander Tutoring, an academic tutoring business that provides personalized studying sessions focused on mathematics and physics. With over 15 years of experience, Sean has worked as a physics and math instructor and tutor for Stanford University, San Francisco State University, and Stanbridge Academy. He holds a BS in Physics from the University of California, Santa Barbara and an MS in Theoretical Physics from San Francisco State University.

Academic Tutor

Expert Answer
Question

What is the SI unit for acceleration?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor

Staff Answer

SI units are standardized units that are used internationally in scientific writing. When describing acceleration, use the SI units meters per seconds squared (m/s^2).
Question

How do you calculate acceleration without time?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor

Staff Answer

If you know that acceleration is constant, you can solve for it without time if you have the initial and final velocity of the object as well as the amount of displacement. Use the formula v^2=u^2+2as where v is the final velocity, u is the initial velocity, a is acceleration, and s is displacement. Solve for a to find acceleration.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

References

About This Article

Article SummaryX

To calculate acceleration, use the equation a = Δv / Δt, where Δv is the change in velocity, and Δt is how long it took for that change to occur. To calculate Δv, use the equation Δv = vf — vi, where vf is final velocity and vi is initial velocity. To caltulate Δt, use the equation Δt = tf — ti, where tf is the ending time and ti is the starting time. Once you’ve calculated Δv and Δt, plug them into the equation a = Δv / Δt to get the acceleration. To learn how to calculate acceleration from a force, read the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 1,763,841 times.

Reader Success Stories

DrDave Alpenschnee

Mar 5, 2018

«I am an Alpine ski instructor, and was interested in how unbalanced forces cause one ski to accelerate more than…» more

Did this article help you?

Источник

Среднее ускорение

Среднее ускорение неравномерно ускоренного поступательного движения, формула

По определению

[ textit{Среднее ускорение} = frac{textit{Изменение скорости}}{textit{Время движения}} ]

[ a_{cред} = frac{∆u}{∆t} ]

Среднее ускорение для интервала времени, формула

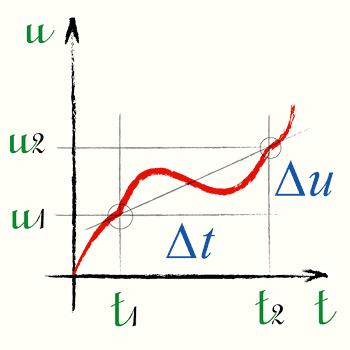
Среднее ускорение для интервала времени — график скорости

Среднее ускорение для некоторого интервала времени вычисляется по формуле:

[ a_{cред} = frac{u_2-u_1}{t_2-t_1} = frac{∆u}{∆t} ]

Среднее ускорение неравномерно ускоренного поступательного движения	стр. 406

Источник

Из
математики известно, что среднее значение
функции

(скалярной или векторной) на промежутке
от

до

определяется выражением

(5.1)

Если
известны зависимости скорости

и ускорения

частицы от времени

при ее движении по траектории, то,
используя выражение (5.1), можно определить
их средние значения за любой промежуток
времени

Можно написать

(5.2)

(5.3)

Аналогично
можно записать выражения для средних
значений модуля вектора и его проекций
на координатные оси, например, на ось
x:

(5.4)

(5.5)

(5.6)

(5.7)

В случае вращения
твердого тела имеем

(5.8)

(5.9)

(5.10)

(5.11)

Пример
5.1. Закон
движения частицы

Найти среднюю скорость

частицы за промежуток времени от t₁=2
с до t₂=4
с.

Дано:

t₁=2
с

t₂=4
с

Решение

– ?

Ответ:

Пример
5.2. Закон
вращения тела

где a
= 6 рад/c,
b =
= 2 рад/с³.
Найти средний модуль

углового ускорения тела за промежуток
времени от

до момента

остановки тела.

Дано:

Решение

– ?

Ответ:
=
6 рад/с².

§ 6. Момент силы

Пусть
частица движется под действием силы

и ее положение в пространстве в некоторый
момент времени

определяет радиус-вектор
,
проведенный из точки 0, являющейся
началом координат (рис.
6.1).

Назовем
моментом
силы

относительно
точки 0 вектор
,
равный векторному произведению векторов

и
:

(6.1)

Рис. 6.1

Направления
векторов

и
связаны
правилом правого винта (если направить
указательный палец правой руки по
вектору
,
а средний — по вектору
,
то отогнутый большой палец покажет
направление вектора

(рис. 6.1)).
Модуль момента силы

(6.2)

где

и

— модули векторов

и
;
α — угол между векторами

и

Назовем
прямую, вдоль которой направлена сила,
линией
действия силы, а
расстояние

от линии действия силы до точки 0 —
плечом силы
относительно
точки 0. Как видно из рис.
6.1,

откуда

(6.3)

Проекция

вектора

на координатные оси

называют моментами силы относительно
этих осей. Например,

— момент силы относительно оси
.

Теперь
перейдем к рассмотрению вращения
твердого тела вокруг неподвижной оси
.
Причиной этого вращения может быть сила
,
приложенная к какой-либо частице тела,
отстоящей от оси

на некотором расстоянии
.
Под действием силы

эта частица, а также все остальные
частицы твердого тела будут двигаться
по различным окружностям, центры которых
лежат на оси
,
а твердое тело вращаться с ускорением

вокруг оси
.

Расчет
показывает, что для данного твердого
тела и определенной оси вращения

проекция

углового ускорения пропорциональна
проекции
момента
силы
:

(6.4)

где

— положительная скалярная величина,
называемая моментом
инерции твердого
тела относительно оси
.

По определению

(6.5)

где

и

— масса и расстояние
-й
частицы тела от z;

N
— число частиц, из которых состоит тело.

Для
нахождения момента инерции твердого
тела от выражения (6.5) переходят к формуле

(6.6)

где

— масса элемента тела, находящего на
расстоянии

от оси

В
Приложении приведены моменты инерции

некоторых однородных твердых тел
относительно оси
,
проходящей через центр масс тела. Зная
момент инерции
,
можно определить момент инерции

относительно любой оси, параллельной
оси

и отстоящей от нее на расстоянии

(теорема
Штейнера):

(6.7)

где

— масса тела.

Соотношение (6.4),
записанное в виде

(6.8)

называют
основным
уравнением динамики вращения твердого
тела.

Если
на тело действует не одна, а несколько
сил, то в уравнении (6.8) M_z —
суммарный момент сил относительно оси

При
повороте тела на элементарный угол dφ
сила

совершает элементарную работу

(6.9)

Работа
силы

при повороте тела на угол

(6.10)

Мощность этой силы

(6.11)

где

— проекция угловой скорости тела на
ось вращения
.

Пример
6.1. Колесо
диаметром D
= 60 см вращается под действием касательной
к ее ободу силы F
= 10 H.
Найти момент инерции

колеса относительно неподвижной оси
,
проходящей через центр колеса
перпендикулярно его плоскости, если за
промежуток времени от

до t₂
= 3 c
проекция

угловой скорости колеса изменилась от
0 до 9 рад/с.

Дано:

D
= 60 см

F = 10 H

t₂
= 3 c

Решение

_J_–_?

Ответ:

Пример
6.2. Закон
вращения шара,
где А
= 2 рад,

Шар вращается вокруг оси
,
проходящей через его центр. Найти среднюю
мощность
,
развиваемую силой, действующей на шар
при его вращении от

до момента времени

его остановки. Радиус шара

Масса шара

Дано:

Решение

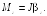
(см.
Приложение А)

Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В физике рассмотрением особенностей движения макроскопических твердых тел занимается кинематика. Этот раздел механики оперирует такими понятиями, как скорость, ускорение и путь. В данной статье мы сосредоточим свое внимание на вопросах, что такое мгновенное ускорение и скорость. Также рассмотрим, какими формулами можно определить эти величины.

Нахождение скорости

Об этом понятии известно каждому школьнику, начиная уже с младших классов. Все ученики знакомы с приведенной ниже формулой:

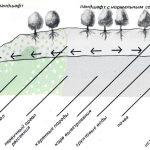
Вам будет интересно:Геохимический барьер: определение термина, особенности

v = S/t.

Здесь S — путь, который преодолело движущееся тело за время t. Данное выражение позволяет рассчитать некоторую среднюю скорость v. Действительно, нам ведь неизвестно, каким образом двигалось тело, на каком участке пути оно перемещалось быстрее, а на каком медленнее. Даже не исключена ситуация, что в некоторой точке пути оно находилось в состоянии покоя какое-то время. Единственное, что известно, это пройденный путь и соответствующий ему временной отрезок.

В старших классах школ скорость, как физическая величина, рассматривается в новом свете. Ученикам предлагают следующее ее определение:

v = dS/dt.

Чтобы понять это выражение, нужно знать, как вычисляется производная от некоторой функции. В данном случае — это S(t). Поскольку производная характеризует поведение кривой в данной конкретной точке, то вычисляемая по формуле выше скорость называется мгновенной.

Ускорение

Если механическое движение является переменным, то для его точного описания необходимо знать не только скорость, но и величину, которая показывает, как она изменяется во времени. Это — ускорение, которое является производная по времени скорости. А та, в свою очередь, есть производная по времени пути. Формула мгновенного ускорения имеет вид:

a = dv/dt.

Благодаря этому равенству можно определить изменение величины v в любой точке траектории.

По аналогии со скоростью, среднее ускорение вычисляется по такой формуле:

a = Δv/Δt.

Здесь Δv — это изменение модуля скорости тела за промежуток времени Δt. Очевидно, что в течение этого периода тело способно как ускоряться, так и замедляться. Величина a, определенная из выражения выше, покажет лишь в среднем быстроту изменения скорости.

Движение с постоянным ускорением

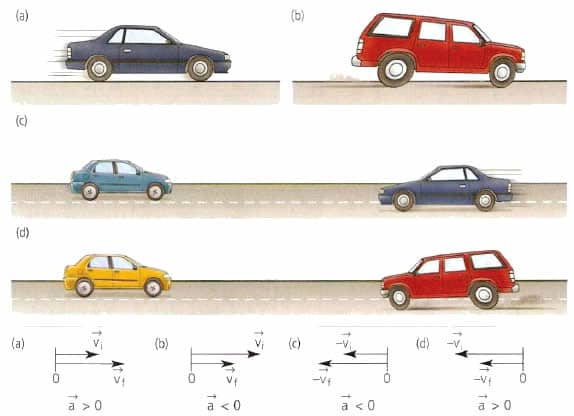
Отличительной особенностью этого типа перемещения тел в пространстве является постоянство величины а, то есть a=const.

Это движение также называют равноускоренным или равнозамедленным в зависимости от взаимного направления векторов скорости и ускорения. Ниже такое перемещение рассмотрим на примере двух наиболее распространенных траекторий: прямой линии и окружности.

При перемещении по прямой линии во время равноускоренного движения мгновенная скорость и ускорение, а также величина пройденного пути, связаны следующими равенствами:

v = v0 ± a*t;

S = v0*t ± a*t2/2.

Здесь v0 — это значение скорости, которым тело обладало до появления ускорения a. Заметим один нюанс. Для данного типа перемещения бессмысленно говорить о мгновенном ускорении, поскольку в любой точке траектории оно будет одним и тем же. Иными словами, мгновенная и средняя величины его будут равны друг другу.

Что касается скорости, то первое выражение позволяет определить ее в любой момент времени. То есть это будет мгновенный показатель. Для расчета средней скорости необходимо воспользоваться представленным выше выражением, то есть:

v = S/t = v0 ± a*(t1 + t2)/2.

Здесь t1 и t2 — это моменты времени, между которыми вычисляют среднюю скорость.

Знак «плюс» во всех формулах соответствует ускоренному передвижению. Соответственно знак «минус» — замедленному.

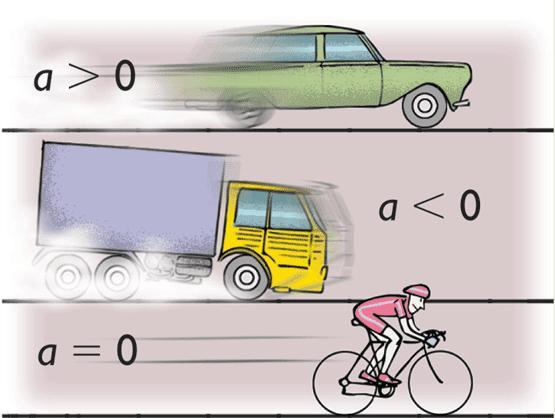
При изучении движения по окружности с постоянным ускорением в физике используют угловые характеристики, которые аналогичны соответствующим линейным. К ним относится угол поворота θ, угловая скорость и ускорение (ω и α). Эти величины связаны в равенства, аналогичные выражениям равноускоренного движения по прямой линии, которые приводятся ниже:

ω = ω0 ± α*t;

θ = ω0*t ± α*t2/2.

При этом угловые характеристики связаны с линейными следующим образом:

S = θ*R;

v = ω*R;

a = α*R.

Здесь R — радиус окружности.

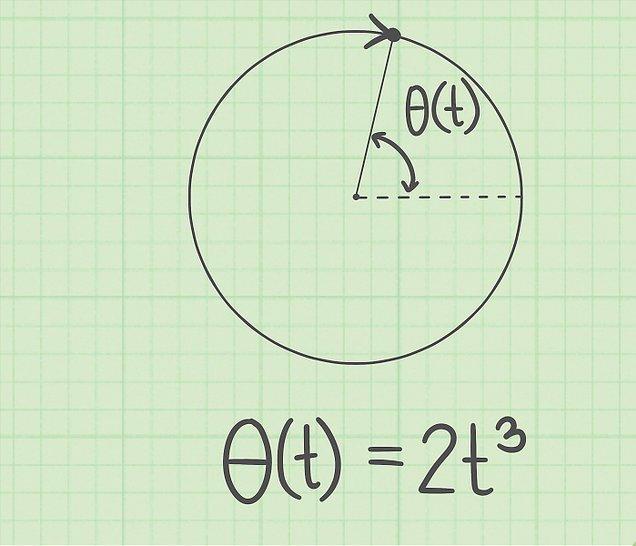
Задача на определение среднего и мгновенного ускорения

Известно, что тело движется по сложной траектории. Его мгновенная скорость меняется по времени следующим образом:

v = 10 — 3*t + t3.

Чему равно мгновенное ускорение тела в момент t=3 (секунды)? Найти среднее ускорение за промежуток времени от двух до четырех секунд.

На первый вопрос задачи ответить несложно, если вычислить производную от функции v(t). Получаем:

a = |dv/dt|t=2;

а = |3*t2 — 3|t=2 = 24 м/с2.

Для определения среднего ускорения, следует воспользоваться таким выражением:

a = (v2 — v1)/(t2 — t1);

а = ((10 — 3*4 + 43) — (10 — 3*2 + 23))/2 = 25 м/c2.

Из расчетов следует, что среднее ускорение немного превышает мгновенное в середине рассмотренного временного промежутка.

Источник