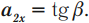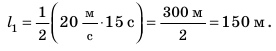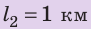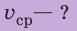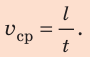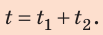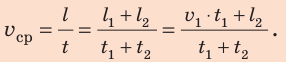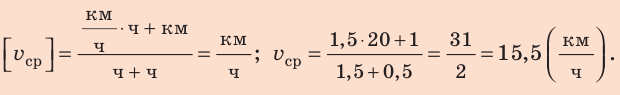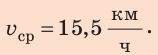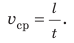Расчёт
пути и времени движения
«Движение
– это жизнь»
Аристотель
В
данной теме будем применять приобретённые знания о механическом движении на
практике. Прежде чем начать решать задачи, вспомним, необходимые определения. Путь
– это физическая величина, равная длине траектории, по которой двигалось тело,
в течение данного промежутка времени. Путь является скалярной величиной,
то есть, не имеет направления. Скорость при равномерном движении – это
величина, равная отношению пройденного пути к промежутку времени, за который
этот путь пройден.
Скорость
является векторной величиной, то есть, характеризуется как числовым значением,
так и направлением.
Средняя
скорость при неравномерном движении – это величина, равная отношению всего
пройденного пути к общему времени в пути.
Задача
1.
Какой путь пройдет автомобиль, двигаясь равномерно со скоростью 75 км/ч за 20 минут?
В
первую очередь, необходимо научиться правильно оформлять задачи по физике.
При решении любой задачи нужно писать «дано». То есть, в левой части
листа необходимо записать слово «дано», после которого ставится двоеточие, а
дальше в столбик перечисляете все исходные данные, которые указаны в условии
задачи. В нашем случае – это скорость и время в пути. После этого, нужно
очеркнуть данные и ниже (уже под линией) записать, что необходимо найти.
В задаче спрашивается, какой путь пройдет автомобиль. Дальше приступаем
непосредственно к решению задачи.
А
теперь обратите внимание вот на что: скорость в условии задачи дана в км/ч, то есть,
сколько километров автомобиль проходит за час. А время в условии дано в
минутах. Поэтому, прежде чем делать вычисления, необходимо перевести минут в
часы.
В
общем и целом, этот способ правильный. Но, чтобы не запутаться с единицами
измерения, можно (и даже нужно) переводить данные в систему СИ сразу после
того, как записано «дано». Напомним, что для перевода км/ч в м/с или м/с в
км/ч необходимо
1 м/с = 3,6 км/ч
1 км/ч = 1/3,6 м/с
Время
в системе СИ измеряется в секундах. В одной минуте шестьдесят секунд, поэтому,
чтобы перевести минуты в секунды, нужно минуты умножить на 60. После того, как
перевели все данные в систему СИ, необходимо очеркнуть и эту колонку, а правее
пишитсяе само решение. Решение и ответ будут одинаковыми. Однако рекомендуется
переводить данные в систему СИ.
Задача
2.
Мотоциклист проехал 5 км вдвое быстрее, чем следующие 7 км. Найдите его среднюю скорость, если общее время в пути составило 10 минут.
Получившееся
выражение, в котором остались, только те величины, которые были даны
изначально, называется расчетной формулой. Только в расчетную формулу необходимо
подставлять числовые значения, а до этого, все делается в буквенном виде.
Задача
3.
Самолет взлетел, после чего пролетел 120 км на определенной высоте, а потом приземлился. Известно, что пути, пройденные в процессе взлета и посадки равны 120 км каждый. Во время взлета и посадки, скорость самолета была равна 200 м/с, а во время остального
пути – 250 м/с. Какое время самолет затратил на весь путь? Какова средняя
скорость?
Сразу
хочется обратить ваше внимание на распространенную ошибку. Среднюю
скорость нельзя находить как среднее арифметическое разных скоростей на разных
участках движения. В этом можно убедиться с помощью простых расчетов:
если подсчитать среднюю скорость, как среднее арифметическое скоростей, то
получим 216,7 м/с. Этот результат неправильный. Теперь подсчитаем среднюю
скорость как отношение всего пройденного пути к общему времени в пути. В
результате получим 214,3 м/с. Получается вроде небольшая разница. В
результате неверных расчётов за каждую секунду, пройденное расстояние
увеличивается на 2,4 м/с. Поэтому, при неверном расчете за час пройденное
расстоянии будет больше на 8,6 км, а это существенно.
Задача
4.
Средняя скорость движения велосипедиста равна 8 м/с. Известно, что первую часть
своего пути велосипедист проехал за 3 минуты. За какое время велосипедист
проехал вторую часть, если общий путь составил 2 км?
Задача
5.
Определите по графику скорость равномерного движения тела.
Здесь,
конечно, никаких данных, кроме самого графика нет, поэтому, «дано» писать не
нужно. В таких заданиях, в первую очередь нужно посмотреть на оси графика:
какие величины они обозначают и в каких единицах измеряются. Вертикальная ось –
обозначает пройденный путь в метрах, а горизонтальная ось – время в минутах.
Значит, это график зависимости пройденного пути от времени. При равномерном
движении скорость постоянна, значит, можно путь, пройденный за определенный
промежуток времени, разделить на это время и, таким образом, найти скорость.
Для наибольшей точности желательно найти точку, на графике, наиболее близкую к
пересечению клеточек. Когда нашли такую точку, смотрим на соответствующие
координаты, то есть, на значения пути и времени. Для этого из точки опускаем
перпендикуляры на обе оси. Теперь, когда получили значение координат, можно определить скорость.
Основные
выводы:
В
качестве итогов урока, рассмотрим общий алгоритм решения задач на движение.
На прошлых уроках мы познакомились с определением механического движения, узнали, каким бывает движение, изучили его свойства и характеристики. Теперь нам известны формулы для расчета скорости при равномерном движении ($upsilon = frac{S}{t}$) и средней скорости при неравномерном ($upsilon_{ср} = frac{S}{t}$).
На данном уроке мы посмотрим на эти формулы с другой стороны — научимся использовать их для расчета пути и времени движения, а также рассмотрим графики скорости и пути для равномерного движения.
Формулы для расчета пути и времени движения при равномерном движении тела
Скорость тела при равномерном движении вычисляется по формуле $upsilon = frac{S}{t}$. Отсюда, если мы знаем скорость и время, то можем найти пройденный путь:
$S = upsilon t$.
Чтобы определить путь, пройденный телом при равномерном движении, нужно скорость тела умножить на время его движения.
Выразим время:
$t = frac{S}{upsilon}$.
Чтобы рассчитать время при равномерном движении, нужно путь, пройденный телом, разделить на скорость его движения.
Формулы для расчета пути и времени движения при неравномерном движении тела
При неравномерном движении мы используем определение средней скорости, которую можем найти по формуле:
$upsilon_{ср} = frac{S}{t}$.
Чтобы определить путь при неравномерном движении, нужно среднюю скорость движения умножить на время:
$large S = upsilon_{ср} t$.
Также мы можем рассчитать время, разделив путь, пройденный телом, на среднюю скорость его движения:
$t = frac{s}{upsilon_{ср}}$.
График скорости равномерного движения
Так как скорость – это векторная величина, она характеризуется и модулем, и направлением. В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.
На рисунке 1 изображен динозавр, автомобиль и дом. Зададим ось координат $x$.
Если динозавр начнет двигаться к дому, то его скорость будет положительной, так как направление движения совпадает с направлением оси $x$. Если же динозавр направится к автомобилю, то его скорость будет отрицательной, так как направление движения противоположно направлению оси $x$.
Итак, график скорости равномерного движения имеет вид, представленный на рисунке 2.
Из графика видно, что скорости с течением времени не изменяется – они постоянны в любой выбранный момент времени. Если мы посмотрим на график положительной скорости, то увидим, что $upsilon = 6 frac{м}{с}$, на график отрицательной — $upsilon = -4 frac{м}{с}$.
Зная скорость и время, мы можем рассчитать пройденный путь за определенный промежуток времени. Рассчитаем какой путь пройдет тело с положительной скоростью за $4 space с$.
$S = upsilon t = 6 frac{м}{с} cdot space 4 c = 24 space м$.
График пути равномерного движения
Пример графика зависимости пути равномерного движения представлен на рисунке 3.
Здесь $S$ — ось пройденных путей, $t$ — ось времени. По этому графику мы можем найти путь, пройденный телом за определенный промежуток времени. Например, за 1 с тело проходит путь длиной 2 м, за 2 с – 4 м, за 3 с – 6 м.
Зная путь и время, мы можем рассчитать скорость. Для удобства расчета возьмем самый первый отрезок пути: $t = 1 space с$, $S = 2 space м$. Тогда,
$upsilon = frac{S}{t} = frac{2 space м}{1 space с} = 2 frac{м}{с}$.
Задачи
Задача №1
Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.
Переведем единицы измерения скорость в СИ и решим задачу.
$120 frac{км}{ч} = 120 cdot frac{1000 space м}{3600 space с} approx 33 frac{м}{с}$.
Дано:
$upsilon = 120 frac{км}{ч}$
$t = 3 space c$
СИ:
$upsilon = 33 frac{м}{с}$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гепард двигается равномерно в течение 3 с.
Путь, который он проходит за это время:
$S = upsilon t$,
$S = 33 frac{м}{с} cdot 3 с approx 100 space м$
Ответ: $S = 100 space м$.
Задача №2
Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 frac{км}{ч}$. Сколько времени у них занимает такой полет?
Переведем единицы измерения скорость в СИ и решим задачу.
$40 frac{км}{ч} = 40 cdot frac{1000 м}{3600 с} approx 11 frac{м}{с}$,
$900 space км = 900 space 000 м$.
Дано:
$upsilon_{ср} = 40 frac{км}{ч}$
$S = 900 space км$
CИ:
$upsilon_{ср} = 11 frac{м}{с}$
$S = 900 space 000 space м$
$t-?$
Показать решение и ответ
Скрыть
Решение:
Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:
$t = frac{s}{upsilon_{ср}}$,
$t = frac{900 space 000 space м}{11 frac{м}{с}} approx 82 space 000 space с$.
Переведем время в часы:
$1 space ч = 60 space мин = 60 cdot 60 space c = 3600 space c$.
Тогда:
$t = frac{82 space 000 space c}{3600 space c} approx 23 space ч$.
Ответ: $t = 23 space ч$.
Больше задач на расчет пути и времени движения с подробными решениями смотрите в отдельном уроке.
Упражнения
Упражнение №1
Пользуясь таблицей 1 из прошлого урока, найдите скорости страуса, автомобиля, искусственного спутника Земли. Определите пути, пройденные ими за $5 space с$.
Дано:
$upsilon_1 = 22 frac{м}{с}$
$upsilon_2 = 20 frac{м}{с}$
$upsilon_3 = 8000 frac{м}{с}$
$t = 5 space с$
$S_1 — ?$
$S_2 — ?$
$S_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь, пройденный страусом:
$S_1 = upsilon_1 t$,
$S_1 = 22 frac{м}{с} cdot 5 space с = 110 space м$.
Путь, пройденный автомобилем:
$S_2 = upsilon_2 t$,
$S_2 = 20 frac{м}{с} cdot 5 space с = 100 space м$.
Путь, пройденный искусственным спутником Земли:
$S_3 = upsilon_3 t$,
$S_3 = 8000 frac{м}{с} cdot 5 space с = 40 space 000 space м = 40 space км$.
Ответ: $S_1 = 110 space м$, $S_2 = 100 space м$, $S_3 = 40 space км$.
Упражнение №2
На велосипеде можно без особого напряжения ехать со скоростью $3 frac{м}{с}$. На какое расстояние можно уехать за $1.5 space ч$?
Дано:
$t = 1.5 space ч$
$upsilon = 3 frac{м}{с}$
СИ:
$t = 5400 space с$
$S — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем путь, который можно проехать на велосипеде с указанной скоростью:
$S = upsilon t$,
$S = 3 frac{м}{с} cdot 5400 space с = 16 space 200 space м = 16.2 space км$.
Ответ: $S = 16.2 space км$.
Упражнение №3
На рисунке 4 показан график зависимости пути равномерного движения тела от времени ($S$ — ось пройденного пути, $t$ — ось времени). По этому графику найдите, чему равен путь, пройденный телом за $2 space ч$. Затем рассчитайте скорость тела.
Определим из графика путь, пройденный телом за $2 space ч$. Этому времени на графике соответствует значение пути, равное $200 space км$. Запишем условие задачи и решим ее.
Дано:
$S = 200 space км$
$t = 2 space ч$
$upsilon — ?$
Показать решение и ответ
Скрыть
Решение:
Скорость равномерного движения рассчитываем по формуле:
$upsilon = frac{S}{t}$.
$upsilon = frac{200 space км}{2 space ч} = 100 frac{км}{ч}$.
Ответ: $upsilon = 100 frac{км}{ч}$.
Упражнение №4
График зависимости скорости равномерного движения тела от времени представлен на рисунке 5. По этому графику определите скорость движения тела. Рассчитайте путь, который пройдет тело за $2 space ч$, $4 space ч$.
Из графика видно, что скорость тела равна $8 frac{м}{с}$. Этот график представляет собой прямую, параллельную оси времени, потому что движение равномерное, и скорость тела не изменяется с течением времени. Запишем условие задачи и решим ее.
Дано:
$t_1 = 2 space ч$
$t_2 = 4 space ч$
$upsilon = 8 frac{м}{с}$
СИ:
$t_1 = 7200 space с$
$t_2 = 14 space 400 space с$
$S_1 — ?$
$S_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Путь рассчитаем по формуле: $S = upsilon t$.
За $2 space ч$ тело пройдет путь:
$S_1 = upsilon t_1$,
$S_1 = 8 frac{м}{с} cdot 7200 space с = 57 space 600 space м = 57.6 space км$.
За $4 space ч$ тело пройдет путь:
$S_2 = upsilon t_2$,
$S_2 = 8 frac{м}{с} cdot 14 space 400 space с = 115 space 200 space м = 115.2 space км$.
Ответ: $S_1 = 57.6 space км$, $S_2 = 115.2 space км$.
Упражнения №5
По графикам зависимости путей от времени (рисунок 6) двух тел, движущихся равномерно, определите скорости этих тел. Скорость какого тела больше?
Для того, чтобы рассчитать скорость тела, нам нужно знать путь и время, за которое этот путь был пройден. Возьмем эти значения для двух тел из их графиков. Первое тело (I) проходит путь, равный $4 space м$, за $2 space с$. Второе тело (II) проходит путь, равный $4 space м$, за $4 space с$. Запишем условие задачи и решим ее.
Дано:
$S = 4 space м$
$t_1 = 2 space с$
$t_2 = 4 space с$
$upsilon_1 — ?$
$upsilon_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем скорость первого тела:
$upsilon_1 = frac{S}{t_1}$,
$upsilon_1 = frac{4 space м}{2 space с} = 2 frac{м}{с}$.
Рассчитаем скорость второго тела:
$upsilon_2 = frac{S}{t_2}$,
$upsilon_2 = frac{4 space м}{4 space с} = 1 frac{м}{с}$.
Получается, что скорость первого тела больше скорости второго.
Ответ: $upsilon_1 = 2 frac{м}{с}$, $upsilon_2 = 1 frac{м}{с}$, $upsilon_1 > upsilon_2$.
Неравномерное прямолинейное движение. Средняя скорость
- График скорости при неравномерном прямолинейном движении
- Как найти путь и перемещение по графику скорости?
- Средняя скорость и средняя путевая скорость
- Задачи
- Лабораторная работа №3. Определение средней скорости движения тела
п.1. График скорости при неравномерном прямолинейном движении
Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.
Движение с переменной скоростью называют неравномерным.
Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.
Например, пусть велосипедист добрался из города A в город B за 1 час. Первые полчаса он ехал со скоростью 9 км/ч, а потом проколол шину, и вторые полчаса шел пешком со скоростью 3 км/ч.
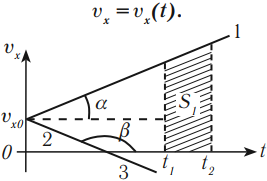
Направим ось ОХ также от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=3 text{км/ч} $$ Построим график скорости для этого случая:
Графиком скорости (v_x=v_x(t)) при неравномерном прямолинейном движении, которое можно разбить на участки с постоянной скоростью, является ломаная линия.
п.2. Как найти путь и перемещение по графику скорости?
Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком (triangle t) на оси (t) (см. §8 данного справочника).
В таком случае, путь велосипедиста в нашем примере:
Общий путь велосипедиста равен 6 км. Расстояние между городами 6 км.
Если принять город A за начало отсчета с (x_0=0), то координата велосипедиста в конце пути: $$ x_{к}=x_0+s=0+6=6 text{(км)} $$ Перемещение по оси ОХ: (triangle x=x_{к}-x_0=6 text{(км)}).
Теперь рассмотрим другую ситуацию. Пусть велосипедист выехал из A в B и двигался со скоростью 9 км/ч в течение получаса. Но, после того как проколол шину, он развернулся и пошел пешком назад в A. Где будет находиться велосипедист через полчаса после разворота?
Снова направим ось ОХ от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=-3 text{км/ч} $$ Построим график скорости для этого случая:
Путь велосипедиста по-прежнему будет равен сумме площадей прямоугольников, которые образует ломаная (v_x(t)) с осью (t): begin{gather*} x=v_{x1}cdot triangle t_1+|v_{x2}|cdottriangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*}
Если мы учтем знак (v_{x2}) и уберем модуль, то получим величину перемещения по оси ОХ: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ triangle x=9cdot 0,5-3cdot 0,5=4,5-1,5=3 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км в обратном направлении.
Конечная координата: $$ x_{к}=x_0+triangle x=0+3=3 text{(км)} $$
Ответ на вопрос задачи найден. Через полчаса после разворота велосипедист будет находиться в точке D в 3 км от города A.
Пусть неравномерное прямолинейное движение разбито на (n) участков с постоянными скоростями. Каждому такому участку соответствует промежуток времени (triangle t_i) и постоянная скорость (v_{xi}, i=overline{1,n}).
Тогда:
Весь пройденный путь равен сумме площадей прямоугольников на графике скорости: $$ s=|v_{x1}|cdottriangle t_1+|v_{x2}|cdottriangle t_2+…+|v_{xn}|cdottriangle t_n $$ Величина перемещения по оси ОХ равна сумме площадей прямоугольников с учетом знака: $$ triangle x=v_{x1}cdottriangle t_1+v_{x2}cdottriangle t_2+…+v_{xn}cdottriangle t_n $$ Конечная координата равна: (x_{к}=x_0+triangle x).
п.3. Средняя скорость и средняя путевая скорость
Средняя скорость на нескольких участках движения равна отношению общего перемещения к общему времени, затраченному на это перемещение: $$ overrightarrow{v_{cp}}=frac{overrightarrow{r_1}+overrightarrow{r_2}+…+overrightarrow{r_n}}{t_1+t_2+…+t_n}=frac{overrightarrow{r}}{t} $$
Средняя путевая скорость на нескольких участках движения равна отношению общего пути к общему времени, затраченному на этот путь: $$ v_{cp.п}=frac{s_1+s_2+…+s_n}{t_1+t_2+…+t_n}=frac{s}{t} $$
Если тело все время движется в одном направлении, величина средней скорости равна средней путевой скорости, т.к. на каждом участке путь совпадает с модулем перемещения.
Если тело меняет направление движения, величина средней скорости меньше средней путевой скорости.
В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 61=6 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости равна средней путевой скорости.
А вот для случая, когда велосипедист развернулся и пошел обратно: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 31=3 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости меньше средней путевой скорости.
п.4. Задачи
Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.
a)
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=1 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=2 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+1cdot 2+2cdot 2=21 text{(м)} end{gather*} Все проекции скоростей положительны, тело двигалось в одном направлении, общее перемещение равно общему пути: (triangle x=s=21) (м)
Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (с)
Величина средней скорости равна средней путевой скорости: $$ |overrightarrow{v_{cp}}|=v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|=v_{cp.п}=3 text{(м/с)})
б)
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=-2 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=1 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+2cdot 2+1cdot 2=21 text{(м)} end{gather*} Проекции скоростей имеют разные знаки, тело двигалось вперед и назад.
Общее перемещение будет меньше общего пути: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2+v_{x3}cdot triangle t_3\ triangle x=5cdot 3-2cdot 2+1cdot 2=13 text{(м)} end{gather*} Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (c)
Величина средней скорости: $$ |overrightarrow{v_{cp}}|=frac{triangle x}{t}=frac{13}{7}approx 1,86 text{(м/с)} $$ Средняя путевая скорость: $$ v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|approx 1,86 text{(м/с)}; v_{cp.п}=3 text{(м/с)})
Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.
Мотоциклист двигался все время в одном направлении, величина средней скорости равна средней путевой скорости: (v_{cp}=frac st), где (s) — весь путь, (t) — все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 40 | (frac{2d}{40}=frac{d}{20}) | (2d) |
| 2й участок | 80 | (frac{d}{80}) | (d) |
| Сумма | — | (t=frac{d}{20}+frac{d}{80}) | (s=2d+d=3d) |
Упростим сумму дробей: $$ t=frac{d}{20}+frac{d}{80}=frac{4d+d}{80}=frac{5d}{80}=frac{d}{16} $$ Получаем: $$ v_{cp}=frac st=frac{3d}{d/16}=3cdot 16=48 text{(км/ч)} $$
Ответ: 48 км/ч
Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) — весь путь, (t) — все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 90 | (frac{s}{2cdot 90}=frac{s}{180}) | (frac s2) |
| 2й участок | 30 | (frac{s}{2cdot 30}=frac{s}{60}) | (frac s2) |
| Сумма | — | (t=frac{s}{180}+frac{s}{60}) | (s) |
Упростим сумму дробей: $$ t=frac{s}{180}+frac{s}{60}=frac{s+3s}{180}=frac{4s}{180}=frac{s}{45} $$ Получаем: $$ v_{cp}=frac st=frac{s}{s/45}=45 text{(км/ч)} $$
Ответ: 45 км/ч
Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) — весь путь, (t) — все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (frac{d}{4t}) | (4t) | (d) |
| 2й участок | (frac{4d}{t}) | (t) | (4d) |
| 3й участок | (frac{45d}{20t}) | (20t) | (45d) |
| Сумма | — | (25t) | (50d) |
По условию средняя скорость: $$ v_{cp}=frac st=frac{50d}{25t}=2cdot frac dt=32Rightarrow frac dt=16 $$ Получаем: begin{gather*} v_1=frac{d}{4t}=frac{16}{4}=4 text{(км/ч)}\ v_2=frac{4d}{t}=4cdot 16=64 text{(км/ч)}\ v_3=frac{9d}{4t}=frac{9}{4}cdot 16=36 text{(км/ч)} end{gather*}
Ответ: 4 км/ч, 64 км/ч и 36 км/ч
Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?
Пусть (v) — скорость туриста при ходьбе пешком.
Найдем среднюю путевую скорость (v_{cp}) и сравним ее со скоростью (v).
Если (v_{cp}gt v), то турист выиграл время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (10v) | (frac{s}{2cdot 10v}=frac{s}{20v}) | (frac s2) |
| 2й участок | (frac{v}{2}) | (frac{s}{2cdot v/2}=frac sv) | (frac s2) |
| Сумма | — | (t=frac{s}{20v}+frac sv) | (s) |
Упростим сумму дробей: $$ t=frac{s}{20v}+frac sv=frac svleft(frac{1}{20}+1right)=frac{21}{20}cdot frac sv $$ Средняя скорость: $$ v_{cp}=frac{s}{frac{21}{20}cdotfrac sv}=frac{20}{21}vgt v $$Средняя скорость поездки оказалась меньше пешей скорости туриста.
Значит, он не выиграл по времени.
Ответ: нет
п.5. Лабораторная работа №3. Определение средней скорости движения тела
Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.
Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.
Величина средней скорости при движении на двух участках определяется как средняя путевая скорость: $$ v_{cp}=frac{s_1+s_2}{t_1+t_2} $$ где (s_1) и (s_2) – длина первого и второго участка; (t_1) и (t_2) — время движения по каждому из участков.
Длина участков измеряется с помощью мерной ленты с ценой деления (triangle=1) см,
инструментальная погрешность равна: (d=frac{triangle}{2}=0,5) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: (triangle s_1=triangle s_2=d=0,5) см
Погрешность суммы двух длин: (triangle(s_1+s_2)= triangle s_1+triangle s_2=2d=1) см
Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: (triangle(t_1+t_2)=triangle t_1+triangle t_2)
Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2} $$ Абсолютная погрешность определения средней скорости: $$ triangle v_{cp}=v_{cp}cdot delta_{v_{cp}} $$
Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с. 
3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин (delta_{s_1+s_2}=frac{triangle(s_1+s_2)}{s_1+s_2})
5. Проведите серии по 5 экспериментов для определения (t_1) и (t_2) с помощью секундомера.
6. Найдите (triangle t_1, triangle t_2, triangle(t_1+t_2), delta_{t_1+t_2})
7. По результатам измерений и вычислений найдите (v_{cp}, delta_{v_{cp}}) и (triangle v_{cp}).
8. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
1) Измерение длин
Цена деления мерной ленты (triangle =1) см
Инструментальная погрешность мерной ленты (d=frac{triangle}{2}=0,5) см
Результаты измерений:
(s_1=112) cм
(s_2=208) cм
Сумма длин участков: (s_1+s_2=112+208=320) (см)
Абсолютная погрешность суммы: (triangle (s_1+s_2)=triangle s_1+triangle s_2=2d=1) см
Относительная погрешность суммы: $$ delta_{s_1+s_2}=frac{triangle (s_1+s_2)}{s_1+s_2}=frac{1}{320}=0,3125% $$
2) Измерение времени
Цена деления секундомера (triangle =0,2) с
Инструментальная погрешность секундомера (d=frac{triangle}{2}=0,1) с
Время движения по наклонному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_1) c | 1,5 | 1,6 | 1,5 | 1,4 | 1,4 | 7,4 |
| (triangle) c | 0,02 | 0,12 | 0,02 | 0,08 | 0,08 | 0,32 |
Найдем среднее время спуска с наклонного желоба: $$ t_1=frac{1,5+1,6+1,5+1,4+1,4}{5}=frac{7,4}{5}=1,48 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_1): $$ triangle_1=|1,5-1,48|=0,02; triangle_2=|1,6-1,48|=1,02 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0,02+0,12+0,02+0,08+0,08}{5}=frac{0,32}{5}=0,064 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_1=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,064right}=0,1 text{c} $$ Округляем полученное значение времени до десятых. begin{gather*} t_1=(1,5pm 0,1) text{c}\ delta_{t_1}=frac{0,1}{1,5}=frac{1}{15}approx 6,7text{%} end{gather*} Время движения по горизонтальному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_2) c | 2,3 | 2,4 | 2,2 | 2,2 | 2,4 | 11,5 |
| (triangle) c | 0 | 0,1 | 0,1 | 0,1 | 0,1 | 0,4 |
Найдем среднее время движения по горизонтали: $$ t_2=frac{2,3+2,4+2,2+2,2+2,4}{5}=frac{11,5}{5}=2,3 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_2): $$ triangle_1=|2,3-2,3|=0; triangle_2=|2,4-2,3|=0,1 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0+0,1+0,1+0,1+0,1}{5}=frac{0,4}{5}=0,08 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_2=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,08right}=0,1 text{c} $$ Получаем: begin{gather*} t_2=(2,3pm 0,1) text{c}\ delta_{t_2}=frac{0,1}{2,3}=frac{1}{23}approx 4,4text{%} end{gather*}
3) Расчет погрешности суммы интервалов времени
Сумма интервалов времени: $$ t_1+t_2=1,5+2,3=3,8 text{(c)} $$ Абсолютная погрешность суммы: $$ triangle(t_1+t_2)=triangle t_1+triangle t_2=0,1+0,1=0,2 text{(c)} $$ Относительная погрешность суммы: $$ delta_{t_1+t_2}=frac{triangle (t_1+t_2)}{t_1+t_2}=frac{0,2}{3,8}=frac{1}{19}approx 5,3text{%} $$
4) Расчет средней скорости $$ v_{cp}=frac{s_1+s_2}{t_1+t_2}=frac{320}{3,8}approx 84,2 left(frac{text{см}}{text{c}}right) $$ Относительная ошибка частного: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2}=frac{1}{320}+frac{1}{19}approx 0,003125+0,0526approx 0,0557approx 0,056=5,6text{%} $$ (оставляем две значащие цифры).
Абсолютная ошибка: $$ v_{cp}=v_{cp}cdotdelta_{v_{cp}}=84,2cdot 0,056approx 4,7 left(frac{text{см}}{text{c}}right) $$ Получаем: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Кинематика
Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
- расстояние, которое проходит тело, много больше его размера;
- расстояние от данного тела до другого тела много больше его размера;
- тело движется поступательно.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
Содержание
- Механическое движение и его виды
- Относительность механического движения
- Правило сложения перемещений
- Правило сложения скоростей
- Относительная скорость
- Скорость
- Ускорение
- Равномерное движение
- График скорости (проекции скорости)
- График перемещения (проекции перемещения)
- Прямолинейное равноускоренное движение
- Свободное падение (ускорение свободного падения)
- Движение тела по вертикали
- Движение тела, брошенного горизонтально
- Движение тела, брошенного под углом к горизонту (баллистическое движение)
- Движение по окружности с постоянной по модулю скоростью
- Основные формулы по теме «Кинематика»
Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
- поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
- вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
- колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;
2. по виду траектории
- прямолинейным — это движение, траектория которого прямая линия;
- криволинейным — это движение, траектория которого кривая линия;
3. по скорости
- равномерным — движение, при котором скорость тела с течением времени не изменяется;
- неравномерным — это движение, при котором скорость тела с течением времени изменяется;
4. по ускорению
- равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
- равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.
Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:
где ( S ) — перемещение тела относительно неподвижной системы отсчета;
( S_1 ) — перемещение тела относительно подвижной системы отсчета;
( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:
где ( v ) — скорость тела относительно неподвижной системы отсчета;
( v_1 ) — скорость тела относительно подвижной системы отсчета;
( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_{12} ):
Определим скорость второго тела относительно первого ( v_{21} ):
Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:
Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:
Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — ( v ), единицы измерения — м/с (км/ч).
Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:
Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:
Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
Обозначение — ( a ), единица измерения — м/с2.
В векторном виде:
где ( v ) – конечная скорость; ( v_0 ) – начальная скорость;
( t ) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:
где ( a_n ) – нормальное ускорение, ( a_{tau} ) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:
Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:
Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_{tau} ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_{tau} ) = 0, ( a_n ) = 0, ( v ) ≠ 0, то тело движется равномерно по прямой;
если ( a_{tau} ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_{tau} ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_{tau} ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.
Равномерное движение
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:
Проекция вектора скорости на ось ОХ:
Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:
График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:
Проекция вектора перемещения на ось ОХ:
График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:
График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Координата тела при равномерном движении рассчитывается по формуле:
График координаты представляет собой зависимость координаты от времени: ( x=x(t) ).
График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:
График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:
Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:
При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:
При разгоне (в проекциях на ось ОХ):
При торможении (в проекциях на ось ОХ):
График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:
График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ( a_x ) > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) > 0.
График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_{0x} ) > 0, ( a_x ) < 0,
График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_{0x} ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ( t_2-t_1 ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:
Перемещение в ( n )-ую секунду при равноускоренном движении рассчитывается по формуле:
Координата тела при равноускоренном движении рассчитывается по формуле:
Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Обозначение – ( g ), единицы измерения – м/с2.
Важно! ( g ) = 9,8 м/с2, но при решении задач считается, что ( g ) = 10 м/с2.
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:
Если тело падает вниз без начальной скорости, то ( v_0 ) = 0.
Время падения рассчитывается по формуле:
Тело брошено вверх:
Если брошенное вверх тело достигло максимальной высоты, то ( v ) = 0.
Время подъема рассчитывается по формуле:
Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали со скоростью ( v_0=v_{0x} );
- равноускоренного движения по вертикали с ускорением свободного падения ( g ) и без начальной скорости ( v_{0y}=0 ).
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Дальность полета:
Угол между вектором скорости и осью ОХ:
Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали;
- равноускоренного движения по вертикали с ускорением свободного падения.
Уравнение скорости:
Уравнение координаты:
Скорость тела в любой момент времени:
Угол между вектором скорости и осью ОХ:
Время подъема на максимальную высоту:
Максимальная высота подъема:
Время полета:
Максимальная дальность полета:
Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ( v_0 ), с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ( alpha ), под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:
Это облегчает решение задач:
Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.
Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ( a_{цс} ), единицы измерения – м/с2.
Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ( T ), единицы измерения – с.
где ( N ) – количество оборотов, ( t ) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ( nu ), единицы измерения – с–1 (Гц).
Период и частота – взаимно обратные величины:
Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ( v ), единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:
Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ( omega ), единицы измерения – рад/с .
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:
Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:
Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:
Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ( v_1 ), и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ), то относительно дороги мгновенная скорость разных точек колеса различна.
Мгновенная скорость нижней точки ( (m) ) равна нулю, мгновенная скорость в верхней точке ( (n) ) равна удвоенной скорости ( v_1 ), мгновенная скорость точки ( (p) ), лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ( (c) ) – по теореме косинусов.
Основные формулы по теме «Кинематика»
Кинематика
3 (60.28%) 142 votes
Содержание:
Неравномерное движение:
Наверняка вам случалось ехать на автобусе или автомобиле из одного города в другой. Вспомните: транспортное средство время от времени тормозит, останавливается, потом снова набирает скорость… Стрелка спидометра все время колеблется и только иногда замирает на месте. Можно ли назвать такое движение равномерным? Конечно, нет. А как называют такое движение? Как его описывают?
В повседневной жизни мы обычно имеем дело с неравномерным движением. Так, неравномерным является движение автобуса (рис. 11.1) и других транспортных средств, движение падающих тел, движение спортсменов на беговой дорожке. А еще вспомните, например, как катится мяч, как вы движетесь во время прогулки, на уроках физкультуры и т. д.
Неравномерное движение — это движение, при котором тело за равные интервалы времени проходит разный путь. Обратите внимание! При неравномерном движении значение скорости движения тела со временем изменяется. Попробуйте привести примеры неравномерного движения. Теперь мы можем классифицировать виды механического движения (см. таблицу): по форме траектории — прямолинейное, криволинейное; по характеру движения тела — равномерное, неравномерное
Вычисляем среднюю скорость движения тела
Предположим, что поезд прошел 150 км (расстояние между двумя станциями) за 2,5 ч. Если разделить 150 км на 2,5 ч, получим скорость движения поезда — 60 км/ч. Но ведь поезд двигался неравномерно! В таком случае говорят, что получена средняя скорость движения поезда (рис. 11.2).
Средняя скорость движения тела 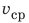
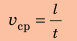
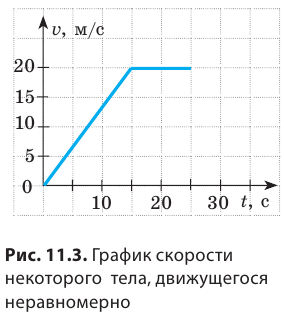
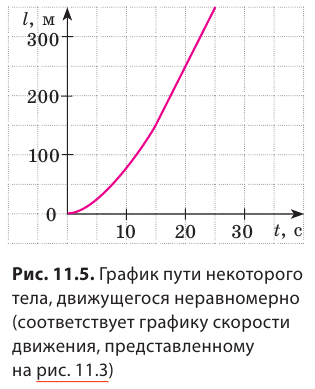
График скорости неравномерного движения тела
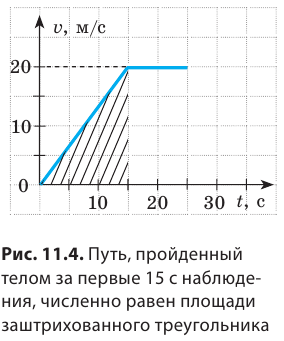
Рассмотрим график скорости неравномерного движения некоторого тела (рис. 11.3) и определим: как двигалось тело; какой путь прошло тело за 25 с наблюдения; какой была средняя скорость движения тела на данном пути. По графику видим, что скорость движения тела в течение первых 15 с равномерно увеличивалась от 0 до 20 м/с. Чтобы вычислить путь, пройденный телом за это время, вспомним: числовое значение пути, который прошло тело, равно числовому значению площади фигуры под графиком скорости движения этого тела. Итак, определим площадь заштрихованного треугольника (рис. 11.4). Из рисунка видим, что площадь заштрихованного треугольника равна половине площади прямоугольника с «длиной» 20 м/с и «шириной» 15 с. Площадь прямоугольника, в свою очередь, равна произведению его длины и ширины. Таким образом, путь 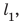
Следующий интервал времени 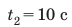
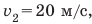
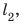
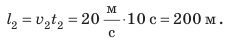
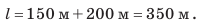
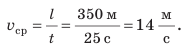
Обратите внимание! Путь не может уменьшаться, поэтому график пути либо поднимается, либо остается горизонтальным, но никогда не опускается.
- Заказать решение задач по физике
Пример
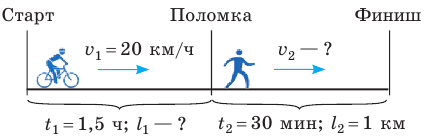
Полтора часа мальчик ехал на велосипеде со скоростью 20 км/ч. Потом велосипед сломался, и последний километр пути мальчик шел пешком. Какой была средняя скорость движения мальчика на всем пути, если пешком он шел полчаса? Анализ физической проблемы. Выполним пояснительный рисунок. Для определения средней скорости движения нужно найти путь, который преодолел мальчик, и время его движения. Время движения выражено в часах, путь — в километрах, поэтому среднюю скорость движения найдем в километрах в час.
Дано:
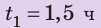
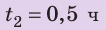
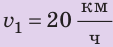
Найти:
Решение:
По определению:
Путь l, который преодолел мальчик, равен: 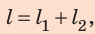
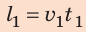
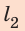
Подставив выражения для l и t в формулу средней скорости движения, получим:
Проверим единицу, найдем значение искомой величины:
Анализ результатов. Мальчик ехал на велосипеде со скоростью 20 км/ч, шел пешком со скоростью 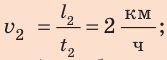
Ответ:
Итоги:
Неравномерное движение — это движение, при котором тело за равные интервалы времени проходит разный путь. Виды механического движения: по форме траектории — прямолинейное и криволинейное; по зависимости скорости движения от времени — равномерное и неравномерное. Средняя скорость движения тела равна отношению всего пути, пройденного телом, к интервалу времени, за который этот путь пройден:
- Вращательное движение тела
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники
- Относительность движения
- Поступательное движение
- Равномерное и неравномерное движение
- Равномерное движение