Как найти среднее время ожидания автобуса - Исправление недочетов и поиск решений вместе с Examum.ru

Парадокс времени ожидания, или почему мой автобус всегда опаздывает?

Время на прочтение
11 мин

Количество просмотров 64K

Источник: Wikipedia License CC-BY-SA 3.0

Если вы часто ездите на общественном транспорте, то наверняка встречались с такой ситуацией:

Вы приходите на остановку. Написано, что автобус ходит каждые 10 минут. Засекаете время… Наконец, через 11 минут приходит автобус и мысль: почему мне всегда не везёт?

По идее, если автобусы приходят каждые 10 минут, а вы придёте в случайное время, то среднее ожидание должно составлять около 5 минут. Но в действительности автобусы не прибывают точно по расписанию, поэтому вы можете ждать дольше. Оказывается, при некоторых разумных предположениях можно прийти к поразительному выводу:

При ожидании автобуса, который приходит в среднем каждые 10 минут, ваше среднее время ожидания будет 10 минут.

Это то, что иногда называют

парадоксом времени ожидания.

Идея встречалась мне раньше, и я всегда задавался вопросом, правда ли это на самом деле… насколько такие «разумные предположения» соответствуют действительности? В этой статье мы исследуем парадокс времени ожидания с точки зрения как моделирования, так и вероятностных аргументов, а затем взглянем на некоторые реальные данные автобусов в Сиэтле, чтобы (надеюсь) решить парадокс раз и навсегда.

Парадокс инспекции

Если автобусы прибывают ровно каждые десять минут, то действительно среднее время ожидания составит 5 минут. Можно легко понять, почему добавление вариаций в интервал между автобусами увеличивает среднее время ожидания.

Парадокс времени ожидания является частным случаем более общего явления — парадокса инспекции, который подробно обсуждается в толковой статье Аллена Дауни «Парадокс инспекции повсюду вокруг нас».

Короче говоря, парадокс инспекции возникает всякий раз, когда вероятность наблюдения количества связана с наблюдаемым количеством. Аллен приводит пример анкетирования студентов университета о среднем размере их классов. Хотя школа правдиво говорит о среднем количестве 30 студентов в группе, но средний размер группы с точки зрения студентов гораздо больше. Причина в том, что в больших классах (естественно) больше студентов, что и выявляется при их опросе.

В случае автобусного графика с заявленным 10-минутным интервалом иногда промежуток между прибытиями длиннее 10 минут, а иногда и короче. И если придти на остановку в случайное время, то у вас больше вероятность столкнуться с более длинным интервалом, чем с более коротким. И поэтому логично, что средний промежуток времени, между интервалами ожидания дольше, чем средний промежуток времени между автобусами, потому что более длинные интервалы чаще встречаются в выборке.

Но парадокс времени ожидания делает более сильное заявление: если средний интервал между автобусами составляет

$N$ минут, то среднее время ожидания для пассажиров составляет

$2N$ минут. Может ли такое быть правдой?

Имитация времени ожидания

Чтобы убедить себя в разумности этого, сначала смоделируем поток автобусов, которые прибывают в среднем за 10 минут. Для точности возьмём большую выборку: миллион автобусов (или примерно 19 лет круглосуточного 10-минутного трафика):

import numpy as np

N = 1000000  # number of buses
tau = 10  # average minutes between arrivals

rand = np.random.RandomState(42)  # universal random seed
bus_arrival_times = N * tau * np.sort(rand.rand(N))

Проверим, что средний интервал близок к

intervals = np.diff(bus_arrival_times)
intervals.mean()

9.9999879601518398

Теперь можем смоделировать прибытие большого количества пассажиров на автобусную остановку в течение этого промежутка времени и вычислить время ожидания, которое каждый из них испытывает. Инкапсулируем код в функцию для последующего использования:

def simulate_wait_times(arrival_times,
                        rseed=8675309,  # Jenny's random seed
                        n_passengers=1000000):
    rand = np.random.RandomState(rseed)
    
    arrival_times = np.asarray(arrival_times)
    passenger_times = arrival_times.max() * rand.rand(n_passengers)

    # find the index of the next bus for each simulated passenger
    i = np.searchsorted(arrival_times, passenger_times, side='right')

    return arrival_times[i] - passenger_times

Затем смоделируем время ожидания и вычислим среднее:

wait_times = simulate_wait_times(bus_arrival_times)
wait_times.mean()

10.001584206227317

Среднее время ожидания близко к 10 минутам, как и предсказывал парадокс.

Копаем глубже: вероятности и пуассоновские процессы

Как смоделировать такую ситуацию?

По сути, это пример парадокса инспекции, где вероятность наблюдения значения связана с самим значением. Обозначим через

$p(T)$ распределение интервалов

$T$ между автобусами по мере их прибытия на остановку. В такой записи ожидаемое значение времени прибытия будет:

В предыдущей симуляции мы выбрали

минут.

Когда пассажир прибывает на автобусную остановку в произвольное время, вероятность времени ожидания будет зависеть не только от

$p(T)$ , но и от самого

$T$ : чем больше интервал, тем больше в нём пассажиров.

Таким образом, можно написать распределение времени прибытия с точки зрения пассажиров:

$p_{exp}(T) propto T~p(T)$

Константа пропорциональности выводится из нормализации распределения:

$p_{exp}(T) = frac{T~p(T)}{int_0^infty T~p(T)~dT}$

Это упрощается до

$p_{exp}(T) = frac{T~p(T)}{E[T]}$

Тогда время ожидания

$E[W]$ будет составлять половину ожидаемого интервала для пассажиров, поэтому мы можем записать

$E[W] = frac{1}{2}E_{exp}[T] = frac{1}{2}int_0^infty T~p_{exp}(T)~dT$

что можно переписать более понятным образом:

$E[W] = frac{E[T^2]}{2E[T]}$

и теперь остаётся только выбрать форму для

$p(T)$ и вычислить интегралы.

Выбор p(T)

Получив формальную модель, каково же разумное распределение для

$p(T)$ ? Выведем картину распределения

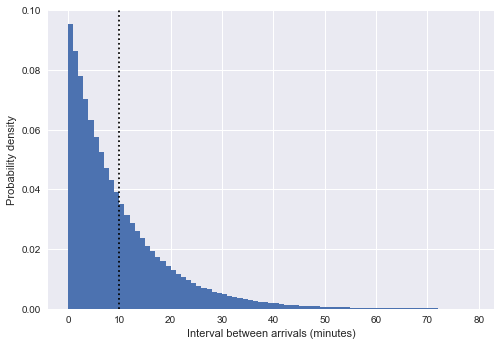
$p(T)$ в пределах наших моделируемых прибытий, построив гистограмму интервалов между прибытиями:

%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn')

plt.hist(intervals, bins=np.arange(80), density=True)
plt.axvline(intervals.mean(), color='black', linestyle='dotted')
plt.xlabel('Interval between arrivals (minutes)')
plt.ylabel('Probability density');

Здесь вертикальная пунктирная линия показывает средний интервал около 10 минут. Это очень похоже на экспоненциальное распределение, и не случайно: наше моделирование времени прибытия автобуса в виде однородных случайных чисел очень близко к процессу Пуассона, а для такого процесса распределение интервалов экспоненциально.

(Примечание: в нашем случае это только приблизительная экспонента; на самом деле интервалы

$T$ между

$N$ равномерно отобранными точками в пределах промежутка времени

$Ntau$ соответствуют бета-распределению

, которое в большом пределе

$N$ приближается к

. Для более подробной информации можете почитать, например, пост на StackExchange или эту ветку в твиттере).

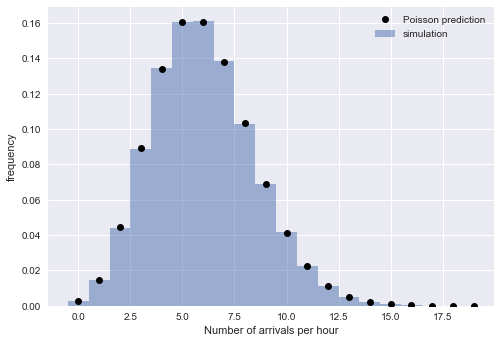
Экспоненциальное распределение интервалов подразумевает, что время прибытия следует за процессом Пуассона. Чтобы проверить это рассуждение, проверим наличие другого свойства пуассоновского процесса: что число прибытий в течение фиксированного промежутка времени является пуассоновским распределенем. Для этого разобъём симулированные прибытия на часовые блоки:

from scipy.stats import poisson

# count the number of arrivals in 1-hour bins
binsize = 60
binned_arrivals = np.bincount((bus_arrival_times // binsize).astype(int))
x = np.arange(20)

# plot the results
plt.hist(binned_arrivals, bins=x - 0.5, density=True, alpha=0.5, label='simulation')
plt.plot(x, poisson(binsize / tau).pmf(x), 'ok', label='Poisson prediction')
plt.xlabel('Number of arrivals per hour')
plt.ylabel('frequency')
plt.legend();

Близкое соответствие эмпирических и теоретических значений убеждает в правильности нашей интерпретации: для больших

$N$ смоделированное время прибытия хорошо описано пуассоновским процессом, который подразумевает экспоненциально распределённые интервалы.

Это означает, что можно записать распределение вероятностей:

$p(T) = frac{1}{tau}e^{-T/tau}$

Если подставить результат в предыдущую формулу, то мы найдём среднее время ожидания для пассажиров на остановке:

$E[W] = frac{int_0^infty T^2~e^{-T/tau}}{2int_0^infty T~e^{-T/tau}} = frac{2tau^3}{2(tau^2)} = tau$

Для рейсов с прибытиями по процессу Пуассона ожидаемое время ожидания идентично среднему интервалу между прибытиями.

Об этой проблеме можно рассуждать так: процесс Пуассона — это процесс без памяти, то есть история событий не имеет никакого отношения к ожидаемому времени следующего события. Поэтому по приходу на автобусную остановку среднее время ожидания автобуса всегда одинаково: в нашем случае это 10 минут, независимо от того, сколько времени прошло с момента предыдущего автобуса! При этом не имеет значения, как долго вы уже ждали: ожидаемое время до следующего автобуса всегда ровно 10 минут: в пуассоновском процессе вы не получаете «кредит» за время, проведённое в ожидании.

Время ожидания в реальности

Вышеизложенное хорошо, если реальные прибытия автобусов на самом деле описываются процессом Пуассона, но так ли это?

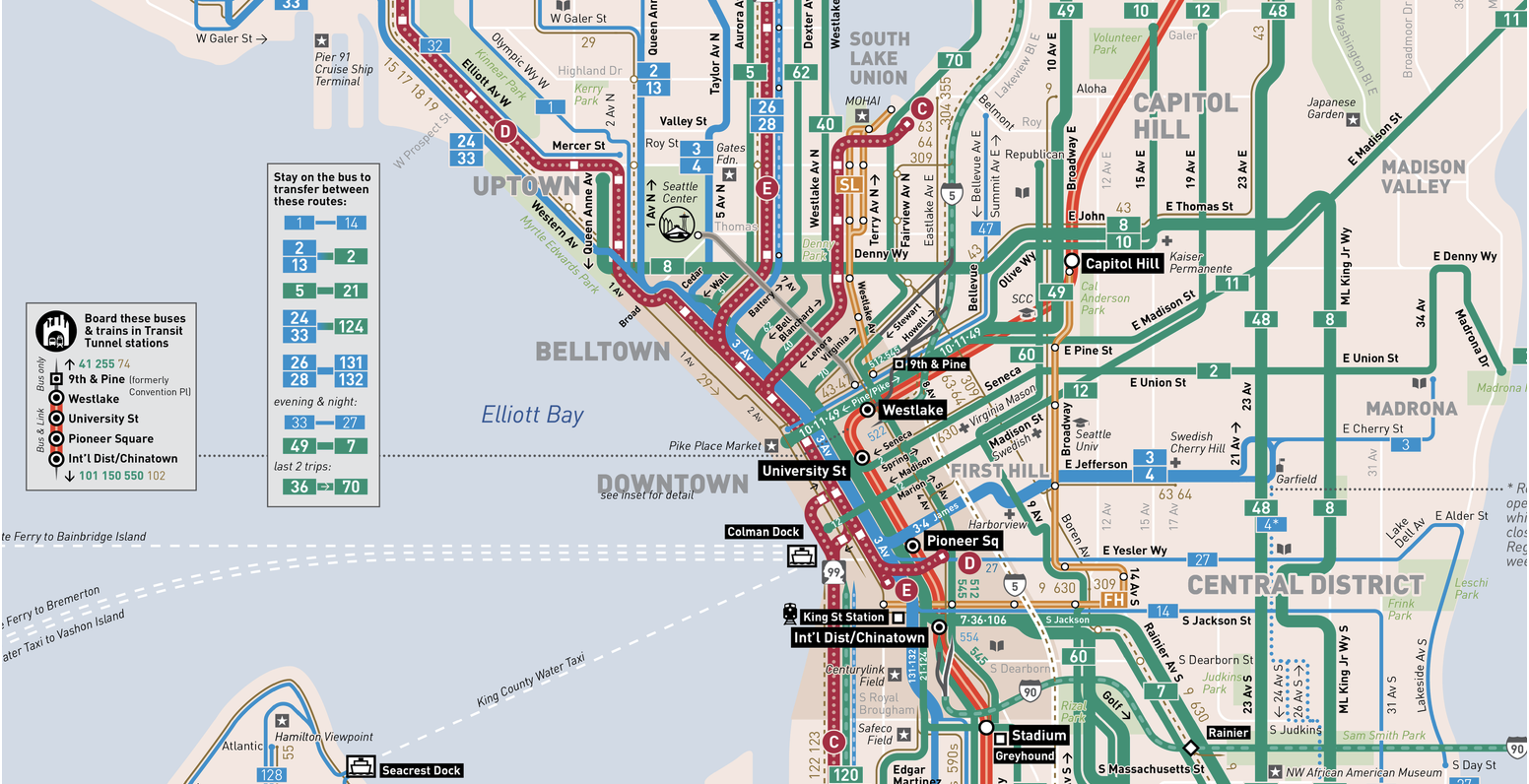
Источник: схема общественного транспорта Сиэтла

Попробуем определить, как парадокс времени ожидания согласуется с реальностью. Для этого изучим некоторые данные, доступные для загрузки здесь: arrival_times.csv (CSV-файл объёмом 3 МБ). Набор данных содержит запланированное и фактическое время прибытия для автобусов RapidRide маршрутов C, D и E на автобусной остановке 3rd&Pike в центре Сиэтла. Данные записаны во втором квартале 2016 года (огромное спасибо Марку Халленбеку из транспортного центра штата Вашингтон за этот файл!).

import pandas as pd
df = pd.read_csv('arrival_times.csv')
df = df.dropna(axis=0, how='any')
df.head()

	OPD_DATE	VEHICLE_ID	RTE	DIR	TRIP_ID	STOP_ID	STOP_NAME	SCH_STOP_TM	ACT_STOP_TM
0	2016-03-26	6201	673	S	30908177	431	3RD AVE & PIKE ST (431)	01:11:57	01:13:19
1	2016-03-26	6201	673	S	30908033	431	3RD AVE & PIKE ST (431)	23:19:57	23:16:13
2	2016-03-26	6201	673	S	30908028	431	3RD AVE & PIKE ST (431)	21:19:57	21:18:46
3	2016-03-26	6201	673	S	30908019	431	3RD AVE & PIKE ST (431)	19:04:57	19:01:49
4	2016-03-26	6201	673	S	30908252	431	3RD AVE & PIKE ST (431)	16:42:57	16:42:39

Я выбрал данные RapidRide в том числе потому что на протяжении большей части дня автобусы курсируют с регулярными интервалами 10−15 минут, не говоря уже о том, что я частый пассажир маршрута С.

Очистка данных

Для начала сделаем небольшую очистку данных, чтобы преобразовать их в удобный вид:

# combine date and time into a single timestamp
df['scheduled'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['SCH_STOP_TM'])
df['actual'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['ACT_STOP_TM'])

# if scheduled & actual span midnight, then the actual day needs to be adjusted
minute = np.timedelta64(1, 'm')
hour = 60 * minute
diff_hrs = (df['actual'] - df['scheduled']) / hour
df.loc[diff_hrs > 20, 'actual'] -= 24 * hour
df.loc[diff_hrs < -20, 'actual'] += 24 * hour
df['minutes_late'] = (df['actual'] - df['scheduled']) / minute

# map internal route codes to external route letters
df['route'] = df['RTE'].replace({673: 'C', 674: 'D', 675: 'E'}).astype('category')
df['direction'] = df['DIR'].replace({'N': 'northbound', 'S': 'southbound'}).astype('category')

# extract useful columns
df = df[['route', 'direction', 'scheduled', 'actual', 'minutes_late']].copy()

df.head()

	Маршрут	Направление	График	Факт. прибытие	Опоздание (мин)
0	C	юг	2016-03-26 01:11:57	2016-03-26 01:13:19	1.366667
1	C	юг	2016-03-26 23:19:57	2016-03-26 23:16:13	-3.733333
2	C	юг	2016-03-26 21:19:57	2016-03-26 21:18:46	-1.183333
3	C	юг	2016-03-26 19:04:57	2016-03-26 19:01:49	-3.133333
4	C	юг	2016-03-26 16:42:57	2016-03-26 16:42:39	-0.300000

На сколько опаздывают автобусы?

В этой таблице шесть наборов данных: направления на север и юг для каждого маршрута C, D и E. Чтобы получить представление об их характеристиках, давайте построим гистограмму фактического минус запланированного времени прибытия для каждого из этих шести:

import seaborn as sns
g = sns.FacetGrid(df, row="direction", col="route")
g.map(plt.hist, "minutes_late", bins=np.arange(-10, 20))
g.set_titles('{col_name} {row_name}')
g.set_axis_labels('minutes late', 'number of buses');

Логично предположить, что автобусы ближе к графику в начале маршрута и больше отклоняются от него к концу. Данные подтверждают это: наша остановка на южном маршруте С, а также на северных D и Е близка к началу маршрута, а в обратном направлении — недалеко от конечного пункта.

Запланированные и наблюдаемые интервалы

Посмотрим на наблюдаемые и запланированные интервалы между автобусами для этих шести маршрутов. Начнём с функции groupby в Pandas для вычисления этих интервалов:

def compute_headway(scheduled):
    minute = np.timedelta64(1, 'm')
    return scheduled.sort_values().diff() / minute

grouped = df.groupby(['route', 'direction'])
df['actual_interval'] = grouped['actual'].transform(compute_headway)
df['scheduled_interval'] = grouped['scheduled'].transform(compute_headway)

g = sns.FacetGrid(df.dropna(), row="direction", col="route")
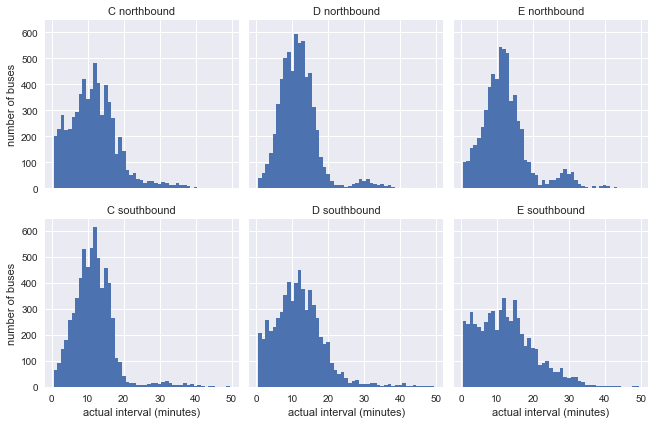
g.map(plt.hist, "actual_interval", bins=np.arange(50) + 0.5)
g.set_titles('{col_name} {row_name}')
g.set_axis_labels('actual interval (minutes)', 'number of buses');

Уже видно, что результаты не очень похожи на экспоненциальное распределение нашей модели, но это ещё ничего не говорит: на распределения могут влиять непостоянные интервалы в графике.

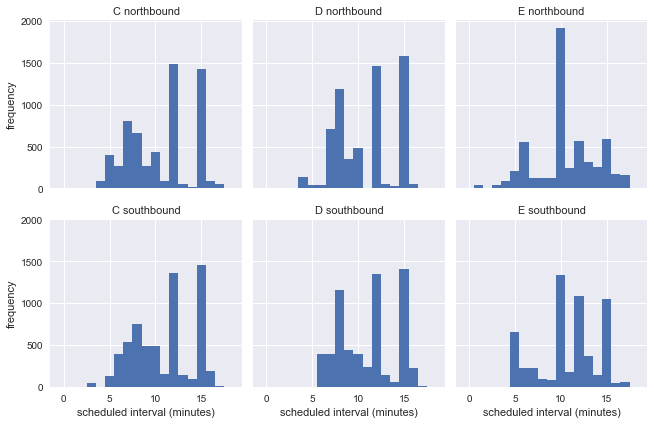
Повторим построение диаграмм, взяв запланированные, а не наблюдаемые интервалы прибытия:

g = sns.FacetGrid(df.dropna(), row="direction", col="route")
g.map(plt.hist, "scheduled_interval", bins=np.arange(20) - 0.5)
g.set_titles('{col_name} {row_name}')
g.set_axis_labels('scheduled interval (minutes)', 'frequency');

Это показывает, что в течение недели автобусы ходят с разными интервалами, так что мы не можем оценить точность парадокса времени ожидания по реальной информации с остановки.

Построение однородных расписаний

Хотя официальный график не даёт однородных интервалов, есть несколько конкретных промежутков времени с большим количеством автобусов: например, почти 2000 автобусов маршрута E в северную сторону с запланированным интервалом в 10 минут. Чтобы узнать, применим ли парадокс времени ожидания, давайте сгруппируем данные по маршрутам, направлениям и запланированному интервалу, а затем повторно сложим их, словно они произошли последовательно. Это должно сохранить все соответствующие характеристики исходных данных, облегчив при этом прямое сравнение с предсказаниями парадокса времени ожидания.

def stack_sequence(data):
    # first, sort by scheduled time
    data = data.sort_values('scheduled')
    
    # re-stack data & recompute relevant quantities
    data['scheduled'] = data['scheduled_interval'].cumsum()
    data['actual'] = data['scheduled'] + data['minutes_late']
    data['actual_interval'] = data['actual'].sort_values().diff()
    return data

subset = df[df.scheduled_interval.isin([10, 12, 15])]
grouped = subset.groupby(['route', 'direction', 'scheduled_interval'])
sequenced = grouped.apply(stack_sequence).reset_index(drop=True)
sequenced.head()

	Маршрут	Направление	Расписание	Факт. прибытие	Опоздание (мин)	Факт. интервал	Интервал по графику
0	C	север	10.0	12.400000	2.400000	NaN	10.0
1	C	север	20.0	27.150000	7.150000	0.183333	10.0
2	C	север	30.0	26.966667	-3.033333	14.566667	10.0
3	C	север	40.0	35.516667	-4.483333	8.366667	10.0
4	C	север	50.0	53.583333	3.583333	18.066667	10.0

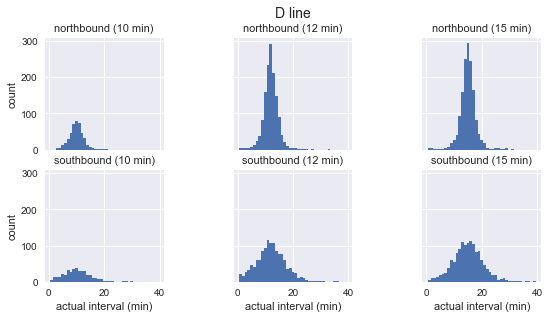
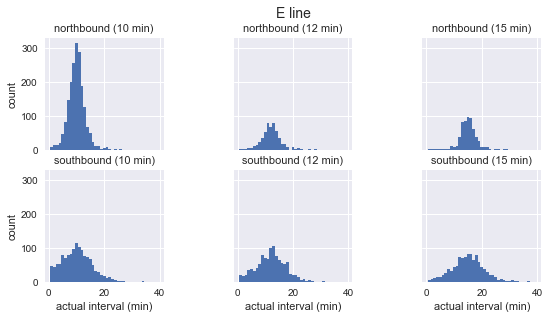
На очищенных данных можно составить график распределения фактического появления автобусов по каждому маршруту и направлению с частотой прибытия:

for route in ['C', 'D', 'E']:
    g = sns.FacetGrid(sequenced.query(f"route == '{route}'"),
                      row="direction", col="scheduled_interval")
    g.map(plt.hist, "actual_interval", bins=np.arange(40) + 0.5)
    g.set_titles('{row_name} ({col_name:.0f} min)')
    g.set_axis_labels('actual interval (min)', 'count')
    g.fig.set_size_inches(8, 4)
    g.fig.suptitle(f'{route} line', y=1.05, fontsize=14)

Мы видим, что для каждого маршрута распределение наблюдаемых интервалов почти гауссово. Оно достигает максимума около запланированного интервала и имеет стандартное отклонение, которое меньше в начале маршрута (на юг для C, на север для D/E) и больше в конце. Даже на глаз видно, что фактические интервалы прибытия определённо не соответствуют экспоненциальному распределению, что является основным предположением, на котором основан парадокс времени ожидания.

Мы можем взять функцию моделирования времени ожидания, которую использовали выше, чтобы найти среднее время ожидания для каждого автобусного маршрута, направления и расписания:

grouped = sequenced.groupby(['route', 'direction', 'scheduled_interval'])
sims = grouped['actual'].apply(simulate_wait_times)
sims.apply(lambda times: "{0:.1f} +/- {1:.1f}".format(times.mean(), times.std()))

маршрут  направление  интервал по расписанию
C        север        10.0                   7.8 +/- 12.5
                      12.0                   7.4 +/- 5.7
                      15.0                   8.8 +/- 6.4
         юг           10.0                   6.2 +/- 6.3
                      12.0                   6.8 +/- 5.2
                      15.0                   8.4 +/- 7.3
D        север        10.0                   6.1 +/- 7.1
                      12.0                   6.5 +/- 4.6
                      15.0                   7.9 +/- 5.3
         юг           10.0                   6.7 +/- 5.3
                      12.0                   7.5 +/- 5.9
                      15.0                   8.8 +/- 6.5
E        север        10.0                   5.5 +/- 3.7
                      12.0                   6.5 +/- 4.3
                      15.0                   7.9 +/- 4.9
         юг           10.0                   6.8 +/- 5.6
                      12.0                   7.3 +/- 5.2
                      15.0                   8.7 +/- 6.0
Name: actual, dtype: object

Среднее время ожидания, возможно, на минуту или две больше половины запланированного интервала, но не равно запланированному интервалу, как подразумевает парадокс времени ожидания. Другими словами, парадокс инспекции подтверждён, но парадокс времени ожидания не соответствует действительности.

Заключение

Парадокс времени ожидания был интересной отправной точкой для обсуждения, которое включило в себя моделирование, теорию вероятности и сравнение статистических предположений с реальностью. Хотя мы подтвердили, что в реальном мире автобусные маршруты подчиняются некоторой разновидности парадокса инспекции, приведённый выше анализ довольно убедительно показывает: основное предположение, лежащее в основе парадокса времени ожидания, — что прибытие автобусов следует статистике пуассоновского процесса — не является обоснованным.

Оглядываясь назад, это и не удивительно: процесс Пуассона — это процесс без памяти, который предполагает, что вероятность прибытия полностью независима от времени с момента предыдущего прибытия. На самом деле в хорошо управляемой системе общественного транспорта есть специально структурированные расписания, чтобы избежать такого поведения: автобусы не начинают свои маршруты в случайное время в течение дня, а стартуют по расписанию, выбранному для наиболее эффективной перевозки пассажиров.

Более важный урок в том, что следует быть осторожным относительно предположений, которые вы делаете к любой задаче анализа данных. Иногда процесс Пуассона — хорошие описание для данных о времени прибытия. Но только то, что один тип данных звучит как другой тип данных, не означает, что предположения, допустимые для одного, обязательно действительны для другого. Часто предположения, которые кажутся правильными, могут привести к выводам, которые не соответствуют действительности.

Источник

In [1]:

import numpy as np
import pandas as pd
from random import choices, shuffle
import scipy.stats as sps
import matplotlib.pyplot as plt

import seaborn as sns
sns.set(style='whitegrid', font_scale=1.3, palette='Set2')

1. Кошачий университет¶

Пусть у нас есть 20 групп котиков-студентов.

Вопрос: сколько котиков в среднем в группе?

Ответ деканата: посчитать количество котиков в каждой группе и взять среднее арифметическое полученных чисел.

Проведем эксперимент. Сгенерируем 20 групп, причем в каждой будет от 10 до 30 котиков.

In [2]:

groups_count = 20

groups_size = sps.randint(low=10, high=30).rvs(size=groups_count)
groups_size

Out[2]:

array([11, 26, 18, 17, 11, 13, 12, 27, 13, 26, 19, 19, 17, 26, 26, 10, 16,
       29, 17, 19])

Ответ получить очень просто:

Теперь предположим, что мы хотим провести эксперимент согласно тому, как учат в анализе данных:

возьмем случайную выборку котиков,
спросим у них, сколько котиков в их группе,
усредним полученные ответы.

Замечание. Следующие операции с точки зрения кода можно сделать более эффективно, однако приведенный код повышает эффектность изложения материала.

Для начала давайте создадим список всех студентов-котиков, каждому из которых присвоим номер группы.

In [4]:

students_group = []

for i in range(groups_count):
    students_group += [i] * groups_size[i]

Возьмем 30 случайных котиков, спросим их и усредним ответы

In [5]:

random_indexes = np.array(choices(students_group, k=30))
groups_size[random_indexes].mean()

Хм, среднее получилось больше, чем ответ деканата. Может случайно так получилось? Ведь эксперимент случайный.

Давайте повторим эксперимент 10 раз.

In [6]:

for _ in range(10):
    random_indexes = np.array(choices(students_group, k=30))
    print(np.round(groups_size[random_indexes].mean(), 2))

Что-то все равно не так…

А что будет если опросить вообще всех котиков? Навернято хоть тут должен получиться тот же ответ.

Попробуем

In [7]:

groups_size[np.array(students_group)].mean()

Хм, ответ все равно получился не тот, что сказали нам в деканате… В чем же дело?

Оказывается, дело в том, что выбирая случайного котика мы чаще попадаем на котика из большей группы. В самом деле, если

$n$ — общее количество котиков,
$n_j$ — количество котиков в группе $j$,

то вероятность того, что случайно выбранный котик учится в группе $j$ равна $n_j/n$.

Посчитаем теперь средний ответ котика. Пусть $xi$ — количество студентов в группе у случайно выбранного котика. Тогда
$$mathsf{E} xi = frac1n sum_{котик i} sum_{j} n_j cdot I{котик i из группы j} = frac1n sum_{j} n_j^2.$$

Проверим ответ:

In [8]:

(groups_size**2).sum() / groups_size.sum()

Это среднее можно посчитать другим способом:
$$mathsf{E} xi = sum_j n_j cdot mathsf{P}(случайный котик из группы j).$$

Если рассматривать в качестве данных сами группы, а не котиков, то такой тип усреднения называется взвешенным средним. Общая формула взвешенного среднего чисел $x_1, …, x_n$ с неотрицательными весами $w_1, …, w_n$, для которых выполнено $sum_{i=1}^n w_i=1$, имеет вид $$sum_{i=1}^n w_i x_i.$$

Выводы:

Деканат в качестве объектов данных рассматривает группы и берет по ним арифметическое среднее.
При проведении опроса объектами данных выступают котики, и арифметическое среднее по котикам отличается от результата деканата.
Деканат может взять взвешенное среднее и получить тот же ответ, что при проведении опроса.

Этот пример — частный случай парадокса инспекции, который можно охарактеризовать как непосредственную зависимость наблюдения количества с самим наблюдаемым количеством.

2. Средняя зарплата¶

Вопрос: какова средняя зарплата населения?

Важно отличать разные «виды средних»:

обычное среднее арифметическое,
медиана — значение, слева и справа от которого одинаковое количество элементов,
мода — самое частое значение.

Разницу между ними наглядно показывает иллюстрация из книги Huff D. How To Lie With Statistics. — New York: W.W. Norton & Company, 1954.

Посмотрим на численном примере. Сгенерируем зарплату 10 000 человек в соответствии с некоторым распределением.

In [9]:

count = 10000
salary = np.abs(sps.t(df=2, scale=100).rvs(size=count))

Посмотрим на описательные статистики. Как мы видим, среднее достаточно сильно отличается от медианы.

In [10]:

pd.Series(salary).describe()

Out[10]:

count    10000.000000
mean       143.361444
std        274.727742
min          0.014972
25%         35.979807
50%         81.488075
75%        162.664021
max       8320.602082
dtype: float64

Посмотрим на гистограмму распределения. Однако, в данном случае в выборке есть выбросы — сильно выделяющиеся по сравнению с остальными наблюдения. Видимо, выбросами у нас являются миллиардеры. В анализе данных существуют специальные методы для работы с выбросами, однако не редко их просто выбрасывают из анализа.

Выбросы сильно влияют на вид гистограммы. В данном случае видна широкая часть графика справа, в которой скорее какая-то пустота. Для наглядности стоит рисовать гистограмму в логарифмическом масштабе, на которой явно видно имеющиеся выбросы.

In [11]:

plt.figure(figsize=(20, 6))

plt.subplot(121)
plt.hist(salary, bins=50)
plt.xlabel('Зарплата')
plt.ylabel('Количество человек')
plt.title('Простая гистограмма')

plt.subplot(122)
plt.hist(salary, bins=50, log=True)
plt.xlabel('Зарплата')
plt.ylabel('Количество человек')
plt.title('Гистограмма в логарифмическом масштабе')

plt.show()

Попробуем убрать несколько выбросов и посчитать среднее по оставшимся элементам. Как видим, среднее достаточно сильно уменьшилось, хотя мы выкинули около 10 человек.

In [12]:

salary[salary < 3300].mean()

Такой вид усреднения обычно называется усеченное среднее. Чаще усеченное среднее рассматривают для симметричных распределений, исключая одинаковое количество минимальных и максимальных значений.

3. Когда придет мой автобус? Или каково среднее время ожидания автобуса.¶

Вы приходите на автобусную остановку. Согласно расписанию автобус ходит каждые 10 минут. Вы засекаете время, и получается, что автобусы обычно приходят через 9-11 минут.

Почему так не везет?

Казалось бы, если автобус ходит каждые 10 минут, то в среднем его нужно ждать 5 минут.
Однако, не все так просто. В действительности автобусы приезжают не точно по расписанию, а случайным образом. Оказывается, справедливо следующее утверждение.

Если автобусы приходят с одинаковой интенсивностью в 10 минут и независимо друг от друга, то среднее время ожидания составляет 10 минут.

Это называют парадоксом времени ожидания. Далее мы попробуем экспериментально проверить это утверждение. Теоретическое доказательство этих фактов ожидает вас на 3 курсе.

Для точности вычислений возьмем достаточно большую выборку — миллион автобусов, которые приходят с интенсивностью раз в 10 минут и сгенерируем интервалы прибытия между автобусами.

In [13]:

count = 1000000  # количество автобусов
tau = 10  # средний интервал между автобусами

bus_arrival_times = sps.uniform(scale=count*tau).rvs(size=count)
bus_arrival_times = np.sort(bus_arrival_times)

Посмотрим на гистограмму интервалов прибытия автобусов, сравнивая ее с графиком плотность равномерного распределения.

In [14]:

grid = np.linspace(-10, count*tau+10, 1010)

plt.figure(figsize=(8, 5))
plt.hist(bus_arrival_times, bins=50, density=True, label='Данные')
plt.plot(grid, sps.uniform(scale=count*tau).pdf(grid), lw=5, alpha=0.5, 
         label='Плотность $U[0, max]$', color='#FF3300')
plt.xlabel('Время прибытия автобуса')
plt.legend()
plt.show()

Прежде чем перейти к ответу на наш исходный вопрос, посмотрим, сколько в среднем автобусов приезжает на остановку в течении часа?
Поскольку у нам может не получится ровное количество часов, посчитаем для первых 100 000 часов.

In [15]:

hours_count = 100000  # количество часов

# количество автобусов за каждый интервал длиной в 1 час
hist = np.histogram(bus_arrival_times, bins=60*np.arange(hours_count))[0]
# количество интервалов, за которые приехало одинаковое количество автобусов
x, y = np.unique(hist, return_counts=True)

Посмотрим на гистограмму распределения количества автобусов за час и сравним его с графиком дискретной плотности пуассоновского распределения с параметром 6. Число 6 есть теоретически ожидаемое количество автобусов в час если их интенсивность движения есть в среднем 1 автобус за 10 минут.

In [16]:

grid = np.arange(25)

plt.figure(figsize=(8, 5))
plt.bar(x, y/y.sum(), label='Данные')
plt.plot(grid, sps.poisson(mu=60/tau).pmf(grid), marker='o', ms=10, lw=5, alpha=0.5, 
         label='Дискр.nплотность $Pois(60/\tau)$', color='#FF3300')
plt.xlabel('Количество автобусов в час')
plt.legend()
plt.show()

Теперь рассмотрим средние длины интервалов между прибытиями автобусов. Посчитаем также средний интервал. Как видим, он составляет примерно 10 минут.

In [17]:

intervals = np.diff(bus_arrival_times)
intervals.mean()

Посмотрим на гистограмму длин интервалов между прибытиями автобусов и сравним ее с плотностью экспоненциального распределения.

In [18]:

grid = np.linspace(-1, 70, 1000)

plt.figure(figsize=(8, 5))
plt.hist(intervals, bins=50, density=True, label='Данные', range=(0, 70))
plt.plot(grid, sps.expon(scale=tau).pdf(grid), lw=5, alpha=0.5, 
         label='Плотность $Exp(\tau)$', color='#FF3300')
plt.xlabel('Время между прибытиями автобусов')
plt.legend()
plt.show()

Проведем опрос миллиона пассажиров с целью выяснить, сколько времени они ждали автобус

In [19]:

n_passengers = 1000000  # количество пассажиров

# сгенерируем для каждого пассажира время его прибытия на остановку
passenger_times = sps.uniform(scale=bus_arrival_times.max()).rvs(size=n_passengers)
# найдем время прибытия следующего автобуса поиском по отсортированному массиву
i = np.searchsorted(bus_arrival_times, passenger_times, side='right')
# вычислим интервал ожидания
wait_times = bus_arrival_times[i] - passenger_times

wait_times.mean()

Посмотрим на гистограмму времени ожидания прибытия автобуса и сравним ее с плотностью ТОГО ЖЕ САМОГО экспоненциального распределения.

In [20]:

grid = np.linspace(-1, 70, 1000)

plt.figure(figsize=(8, 5))
plt.hist(wait_times, bins=50, density=True, label='Данные', range=(0, 70))
plt.plot(grid, sps.expon(scale=tau).pdf(grid), lw=5, alpha=0.5, 
         label='Плотность $Exp(\tau)$', color='#FF3300')
plt.xlabel('Время ожидания автобуса')
plt.legend()
plt.show()

Оказывается, оставшееся время ожидания автобуса не зависит от того времени, которое уже прошло с момента прибытия предыдущего автобуса. Это свойство называется свойством отсутствия памяти. Среди всех абсолютно непрерывных распределений таким свойством обладает только экспоненциальное распределение. Среди всех дискретных распредений — только геометрическое.

Если мы считаем, что у нас есть несколько маршрутов автобусов, причем все автобусы приходят независимо друг от друга с одинаковой интенсивностью, то количество автобусов, которое придется пропустить, имеет геометрическое распределение.

А сколько времени проходит между каждым пятым прибывающим автобусом? Посчитаем эти интервалы времени.

In [21]:

intervals = np.diff(bus_arrival_times[::5])
intervals.mean()

Посмотрим на гистограмму длин интервалов между прибытиями каждого 5-го автобуса и сравним ее с плотностью гамма-распределения.

In [22]:

grid = np.linspace(-1, 180, 1000)

plt.figure(figsize=(8, 5))
plt.hist(intervals, bins=50, density=True, label='Данные', range=(0, 180))
plt.plot(grid, sps.gamma(a=5, scale=tau).pdf(grid), lw=5, alpha=0.5, 
         label='Плотность $\Gamma(5, \tau)$', color='#FF3300')
plt.xlabel('Время между прибытиями каждого 5-го автобуса')
plt.legend()
plt.show()

Этот пример также показывает, что экпоненциальное распределение является частным случаем гамма-распредедения.

Источник

Равномерное случайное распределение

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Равномерным называют распределение вероятностей непрерывной случайной величины

, если на интервале

, которому принадлежат все возможные
значения

, плотность сохраняет постоянное значение.

Функция распределения
равномерного закона:

Числовые характеристики равномерного распределения

Математическое ожидание равномерно распределенной случайной величины:

Дисперсия
равномерного случайного
распределения:

Среднее квадратическое отклонение случайной величины, распределенной равномерно:

Для равномерного распределения коэффициент асимметрии:

Коэффициент эксцесса

При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.

Кроме равномерного, основные законы распределения непрерывных случайных величин:

Смежные темы решебника:

Непрерывная случайная величина
Нормальный закон распределения случайной величины
Экспоненциальный (показательный) закон распределения случайной величины

Примеры решения задач

Пример 1

Все
значения равномерно распределенной случайной величины X лежат на отрезке [2;8].
Найти вероятность попадания случайной величины X в промежуток (1;5).

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Плотность вероятности
равномерного распределения на интервале

Искомая вероятность:

Ответ:

Пример 2

Случайная
величина X равномерно распределена на интервале (2;7). Составить f(x), F(x),
построить графики. Найти M(X), D(X).

Решение

Плотность
вероятности случайной величины, распределенной равномерно на интервале

В нашем
случае

Получаем:

Функцию
распределения

найдем из
формулы:

Учитывая
свойства

, сразу можем
отметить, что:

Остается
найти выражение для

, когда х принадлежит интервалу

Получаем:

Построим
графики:

График плотности распределения

График функции распределения

Математическое
ожидание величины, распределенной равномерно:

Дисперсия:

Среднее
квадратическое отклонение:

Пример 3

Минутная
стрелка электрических часов перемещается скачком в конце каждой минуты. Найти
вероятность того, что в данное мгновение часы покажут время, которое отличается
от истинного не более чем на 20 с.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Плотность
равномерного распределения:

Вероятность
того, что в данное мгновение часы покажут время, которое отличается от
истинного не более чем на 20 с:

Ответ:

Пример 4

Пассажир
метро в случайный момент времени приходит на платформу. Известно, что среднее
квадратическое отклонение времени ожидания поезда равно 0,8 мин. Найти интервал
времени следования поездов в метро.

Решение

Дисперсия
равномерного распределения:

при
начале интервала

Искомый
интервал времени:

Ответ:

Задачи контрольных и самостоятельных работ

Задача 1

Случайные
величины X₂, X₃, X₄ имеют равномерное,
показательное и нормальное распределения соответственно. Найти вероятности
P(3<X_i<6), если у этих случайных величин
математические ожидания и средние квадратические отклонения равны 3.

Задача 2

Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите M(X), D(X),σ, x_mod, x_med, если известно, что
случайная величина X имеет равномерное распределение с параметрами a=2 и b=4.

Задача 3

Найти: M(X) НСВ X,
распределенной равномерно в интервале (1;9); функцию распределения F(x) и
функцию плотности вероятности f(x); вероятность попадания
НСВ X в интервал (2;7).

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 4

Непрерывная случайная величина X равномерно распределена на сегменте [1; 8.5].

Найти:

1) дифференциальную и интегральную
функцию распределения, а также построить их графики.

2) математическое ожидание и
дисперсию;

2) вероятность того, что X примет какое-нибудь значение из интервала (1;20).

Задача 5

Интервал движения парома 3 часа.
Найти: а) числовые характеристики времени ожидания для случайного пассажира; б)
вероятность времени ожидания менее 40 минут.

Задача 6

Равномерно распределенная случайная
величина

задана
плотностью распределения f(x)=0.125 в интервале (1;9) и f(x)=0 вне его.
Найти M(X), D(X), σ(X).

Задача 7

Случайная
величина X равномерно распределена на отрезке [5;11]. Найдите
математическое ожидание X, дисперсию X,
медиану, P(7<X<15), x_0.2.

Задача 8

Случайная
величина

равномерно распределена на отрезке [-1;9].
Запишите функцию плотности распределения, изобразите ее график. Найдите
вероятность того, что X примет значение в
интервале (-3;2). Найдите математическое ожидание X и медиану. Укажите
найденные значения на графике f(x).

Задача 9

Вычислить
вероятность того, что при 10 испытаниях значение X три раза попадет в
интервал [-1;1], если случайная величина X распределена по
равномерному закону на интервале [0;4].

Задача 10

Трамваи
данного маршрута идут с интервалом в 5 мин. Пассажир подходит к трамвайной
остановке в некоторый момент времени. Какова вероятность появления пассажира не
ранее чем через 1 мин после ухода предыдущего трамвая, но не позднее чем за 2
мин до отхода следующего трамвая?

Задача 11

Найти
функцию распределения, плотность, математическое ожидание и дисперсию случайной
величины, распределенной равномерно на отрезке [2,4].

Задача 12

Цена
деления шкалы прибора равна 0,4. Показания прибора округляют до ближайшего
деления. Найти вероятность того, что при отсчете будет сделана ошибка
округления, большая 0,05.

Задача 13

СВ X
распределена равномерно в промежутке [1∕3,5∕4]. Найти функцию плотности
распределения f(x), функцию распределения F(x),
математическое ожидание M(X), дисперсию D(X) и среднее квадратическое отклонение σ(X). Построить
графики функций f(x) и F(x). Найти вероятность того, что x∈[1,5∕4].

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 14

Шкала
рычажных весов, установленных в лаборатории, имеет цену делений 1 г. При
измерении массы химических компонентов смеси отсчет делается с точностью до
целого деления с округлением в ближайшую сторону. Какова вероятность, что
абсолютная ошибка определения массы будет заключена между значениями σ и 2σ.

Задача 15

Автобусы
некоторого маршрута идут строго по расписанию с интервалом 5 мин. Найти
вероятность того, что пассажир, подошедший к остановке будет ждать очередного
автобуса меньше трех минут.

Задача 16

Все
значения равномерно распределенной случайной величины Х принадлежат отрезку
[2,8]. Найти вероятность попадания случайной величины X в отрезок [3,5].

Задача 17

Случайная величина X имеет равномерное распределение на отрезке [1,6].
Найти дисперсию D(X) и вероятность попадания случайной величины X в интервал (2,4).

Задача 18

По маршруту
независимо друг от друга ходит два автобуса: №20 –через 10 и №15 –через 7
минут. Студент приходит на остановку в случайный момент. Какова вероятность
того, что ему придется ждать автобус менее трех минут.

Задача 19

Автобусы идут с интервалом 5 минут.
Считая, что случайная величина X – время
ожидания автобуса на остановке, распределена равномерно на указанном интервале,
найти среднее время ожидания и дисперсию времени ожидания.

Задача 20

Шкала
секундомера имеет цену деления 0,2 с. Какова вероятность сделать по этому
секундомеру отсчет времени с ошибкой менее 0,05 с, если отсчет делается наудачу
с округлением в ближайшую сторону, до целого деления?

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

There is an excellent answer to the more general question, «Expected Waiting time if the are many buses, which each stop every $m_k$ minutes«, can be found here.

As mentioned in the comments on this question and the linked one, the answer depends very much on the model used to describe the passage times of the buses. Here are two possible solutions, each based on slightly different assumptions, for two bus scenario, but which give quite different results.

Case 1. Fully random times.

Here the passage times of buses of type $k$ are a Poisson process of intensity $1/m_k$ and the passage times of buses of different types are independent.

Expected Time is $$mathbb E(T) = m, quad textrm{where } ; frac{1}{m} = frac{1}{m_1}+frac{1}{m_2}$$.

That is, $frac{1}{m} = (1/8+1/12) =frac{5}{24}$. So $m$ =4 minutes 48 seconds.

Case 2. Fully periodic passage times with random uniform initializations

Here, buses of type $k$ pass at times in $S_k+mkN$ where $S_k$ is uniform on $(0,m_k)$ and the random variables $(S_k)$ are independent.

$$
mathbb E(T)=m_1-frac{m_1^2}2left(frac1{m_1}+frac1{m_2}right)+frac{m_1^3}{3}left(frac1{m_1m_2}right),
$$
thus, with $m_1 =8, m_2 = 12$, we get
$$m=8-frac{64}{2}left(frac{1}{8}+frac{1}{12}right)+frac{512}{3}left(frac{1}{96}right) = 28/9$$
So $m=$ 3 minutes 7 seconds.

Thus, we can see from the quite different results that it depends a lot on what model/assumptions you use.

Источник

Равномерно распределенная случайная величина

На странице Непрерывная случайная величина мы разобрали примеры решений для произвольно заданных законов распределения (многочлены, логарифмы и т.п.). Здесь же мы разберем примеры только для одного типа СВ — распределенных по равномерному закону.

В сущности, равномерное распределение — самое простое из семейства непрерывных, и определяется тем, что плотность распределения постоянна (равна константе) на всем интервале: $f(x)=c=frac{1}{b-a}, xin (a;b)$ (а вне его равна нулю):

$$
f(x)=
left{
begin{array}{l}
0, x le a\
frac {1}{b-a}, a lt x le b, \
0, x gt b, \
end{array}
right.
$$

Функция распределения для нее вычисляется практически в уме:

$$
F(x)=
left{
begin{array}{l}
0, x le a\
frac {x-a}{b-a}, a lt x le b, \
1, x gt b, \
end{array}
right.
$$

Для равномерного на интервале $(a;b)$ распределения известны формулы для числовых характеристик. Математическое ожидание $M(X)=frac{a+b}{2}$, дисперсия $D(X)=frac{(b-a)^2}{12}$, среднее квадратическое отклонение $sigma(X)=frac{b-a}{2sqrt{3}}$.

В жизни равномерным распределением часто моделируют время ожидания транспорта, ошибки округления в пределах цены деления.

В этом разделе мы приведем разные примеры задач с полным решением, где используются равномерно распределенные случайные величины.

Лучшее спасибо — порекомендовать эту страницу

Примеры решений

Задача 1. Автобусы идут с интервалом 5 минут. Полагая, что случайная величина $xi$ — время ожидания автобуса на остановке — распределена равномерно на указанном интервале, найти среднее время ожидания и среднеквадратическое уклонение времени ожидания.

Задача 2. Телефонный звонок должен последовать от 10 ч до 10 ч 20 мин. Какова вероятность того, что звонок произойдет в последние 10 мин указанного промежутка, если момент звонка случаен?

Задача 3. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка: а) меньшая 0,04; б) большая 0,05.

Задача 4. В здании областной администрации случайное время ожидания лифта равномерно распределено в диапазоне от 0 до 3 минут. Найти а) плотность распределения времени ожидания, б) вероятность ожидания лифта более чем 2 минуты, в) вероятность того, что лифт прибудет в течение первых 15 секунд, г) среднее время ожидания лифта и дисперсию времени ожидания.

Задача 5. Случайная величина $X$ задана интегральной $F(x)$ или дифференциальной $f(x)$ функцией. Требуется:
а) найти параметр $C$;
б) при заданной интегральной функции найти дифференциальную функцию; а при заданной дифференциальной функции найти интегральную функцию;
в) построить графики функций $F(x)$ и $f(x)$;
г) найти математическое ожидание $M[X]$ дисперсию $D[X]$ среднее квадратическое отклонение $sigma[X]$;
д) вычислить вероятность попадания в интервал $P(alt X lt b)$;
е) определить, квантилем какого порядка является точка $x_p$;
ж) вычислить квантиль порядка $p$.

$$
f(x)=
left{
begin{array}{l}
{0,x lt -1,} \
{C, -1 le x le 1} \
{0, xgt 1.}
end{array}
right.
$$

Задача 6. Дана плотность распределения $p(x)$ случайной величины $xi$. Найти параметр $gamma$, математическое ожидание $Mxi$, дисперсию $Dxi$, функцию распределения случайной величины $xi$, вероятность выполнения неравенства $x_1 lt xi lt x_2$.
$$a=1, b=1,8, x_1=1,3, x_2=1,6.$$
$$
p(x)=
left{
begin{array}{l}
{1,x in [gamma; 1,8],} \
{0,x notin [gamma; 1,8].} \
end{array}
right.
$$

Задача 7. Случайная величина Х равномерно распределена в интервале (1;8). Найти:
а) дифференциальную функцию,
б) интегральную функцию,
в) математическое ожидание, дисперсию и среднее квадратическое отклонение,
г) вероятность попадания в интервал (3;5).

Задача 8. Функция распределения непрерывной случайной величины задана следующим образом:
$$
F(x)=
left{
begin{array}{l}
{0,x lt a,} \
{frac{x-1}{2}, x in [a,b]} \
{1, xgt b.}
end{array}
right.
$$
Определить параметры $а$ и $b$, найти плотность вероятности, числовые характеристики и вероятность попадания случайной величины в интервал $[-1, 2]$. Построить графики $р(x)$ и $F(x)$.

Мы отлично умеем решать задачи по теории вероятностей

Решебник по теории вероятности онлайн

Больше 11000 решенных и оформленных задач по теории вероятности:

Источник