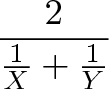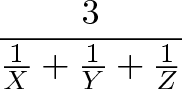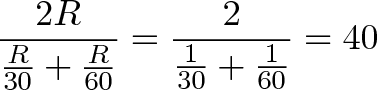В отделе заказов торговой фирмы занято трое работников, имеющих 8-часовой рабочий день. Первый работник на оформление одного заказа в среднем затрачивает 14 мин., второй – 15, третий – 19 мин. Определите средние затраты времени на 1 заказ в целом по отделу.
Решение:
На первый взгляд кажется, что задача легко решается по формуле средней арифметической простой:
Полученная средняя была бы правильной, если бы каждый работник отдела оформил только один заказ. Но в течение дня отдельными работниками было оформлено различное число заказов. Для определения числа заказов, оформленных каждым работником, воспользуемся следующим соотношением:
Число заказов, оформленных каждым работником, определяется отношением всего времени работы к среднему времени, затраченному на один заказ. Тогда среднее время, необходимое для оформления одного заказа, равно:
Это же решение можно представить иначе:
При решении данной задачи была использована формула средней гармонической простой:
Таким образом, средние затраты времени на 1 заказ в целом по отделу равны 15,73 минутам.
You can use the following formula to calculate an average time value in Excel:
=AVERAGE(A2:A11)
This particular formula calculates the average time value in the range A2:A11 and assumes that each value in the range is in a valid time format.
The following example shows how to use this formula in practice.
Suppose we have the following list of times in Excel:
To verify that the times are in a valid format, we can highlight the range A2:A11, then click the Number Format dropdown menu from the Number tab within the Home tab on the top ribbon:
Once we click More Number Formats, a new screen will appear that shows which format Excel has chosen for the values:
In this example, Excel has chosen h:mm:ss AM/PM, which is the correct time format.
If your time values are in another format, simply click on the appropriate format from the list of options.
We can then click OK.
Next, we can use the following formula to calculate the average time value:
=AVERAGE(A2:A11)
The following screenshot shows how to use this formula in practice:
We can see that the average time is 12:11:51 PM.
Example: Calculate Average Time with Condition in Excel
We can also use an AVERAGEIF function to calculate the average time based on a condition in Excel.
For example, we can use the following formula to calculate the average time only for the times that occur after 12 PM:
=AVERAGEIF(A2:A11, ">12:00:00 PM")
The following screenshot shows how to use this formula in practice:
Excel returns a numerical value, but we can click the Number Format dropdown menu again and click Time to convert this numeric value to a time value:
The average time among the times that occur after 12 PM is 5:18:19 PM.
Additional Resources
The following tutorials explain how to perform other common operations in Excel:
How to Calculate Average If Cell Contains Number in Excel
How to Use AVERAGEIF with Multiple Ranges in Excel
How to Calculate Average Excluding Outliers in Excel
12
Наряду с абсолютными
и относительными величинами в статистике
большое применение находят средние
величины. В
повседневной жизни употребляются
термины «в среднем», «средняя».
Например, средняя цена, средний расход
продуктов, средняя заработная плата,
средняя мощность оборудования, средняя
выработка, средний размер сбережений
и т. д.
В экономическом
анализе часто приходится оперировать
средними величинами в целях лучшего
понимания общей картины, когда нужно
из многих признаков получить величину,
в которой отражались бы свойства всех
признаков, входящих в состав совокупности.
Средняя величина
в С — обобщающий показатель,
характеризующий типичный уровень
явления в конкретных условиях места
и времени, отражающий величину
варьирующего признака в расчете на
единицу качественно однородной
совокупности.
Средняя величина есть обобщающая
количественная характеристика однородных
явлений по какому-либо варьирующему
признаку.
Применение средних
величин позволяет охарактеризовать
определенный признак совокупности
одним числом, несмотря на количественные
различия единиц по данному признаку
внутри совокупности.
Следовательно,
средняя величина есть обобщающая
характеристика совокупности; средняя
величина выражает типичное свойство
совокупности; средняя величина —
величина абстрактная, а не конкретная,
так как в ней сглаживаются отдельные
значения единиц совокупности, имеющие
отклонения в ту и другую сторону;
реальность средней величины достигается,
если она вычисляется из одной совокупности.
Пользуясь средними
величинами при анализе массовых явлений,
необходимо всегда помнить, что часто в
средней величине скрываются отстающие
хозяйствующие субъекты, которые имеют
низкие показатели своей деятельности
и, наоборот, не выявляются фирмы, компании,
предприятия и т. д., которые работают
весьма эффективно. Это возможно, как
уже говорилось выше, в связи со свойством
средней, в которой отклонения отдельных
значений признака от ее величины взаимно
погашаются. (Так, например, при условии
выполнения плана розничного товарооборота
в целом по холдингу, занимающемуся
продажей товаров, часть фирм, входящих
в него, не выполнила план и, наоборот,
другая часть перевыполнила план
товарооборота.) Поэтому, кроме средней,
следует использовать и отдельные
индивидуальные показатели работы фирм,
входящих в холдинг.
В эк. практике
исп.-ся широкий круг показателей,
вычисленных в виде средних величин.
Напр, обобщающим
показателем доходов рабочих АО служит
средний доход одного рабочего, определяемый
отношением фонда з/п и выплат социального
характера за рассматриваемый период
(год, квартал, месяц) к численности
рабочих АО.
Вычисление
среднего – один
из распространенных приемов обобщения;
средний показатель отражает то общее,
что характерно (типично) для всех единиц
изучаемой совокупности, в то же время
он игнорирует различия отдельных
единиц. В каждом явлении и его развитии
имеет место сочетание случайности
и необходимости.
При исчислении средних в силу действия
закона больших чисел случайности
взаимопогашаются, уравновешиваются,
поэтому можно абстрагироваться от
несущественных особенностей явления,
от колич. значений признака в каждом
конкретном случае. В способности
абстрагироваться от случайности
отдельных значений, колебаний и
заключена научная
ценность средних как обобщающих
характеристик совокупностей.
Там, где возникает
потребность обобщения, расчет таких
характеристик приводит к замене множества
различных инд. значений признака средним
показателем, характеризующим всю
совокупность явлений, что позволяет
выявить закономерности, присущие
массовым общ. явлениям, незаметные в
единичных явлениях.
Средняя отражает
характерный, типичный, реальный уровень
изучаемых явлений, характеризует эти
уровни и их изменения во времени и в
пространстве; это сводная характеристика
закономерностей процесса в тех условиях,
в к-рых он протекает.
Выбор
вида средней
определяется эк. содержанием
определенного показателя и исходных
данных.
1)- Класс
степенных средних
— арифметическая,
гармоническая, геометрическая,
квадратическая, кубическая
и т.д. Помимо
степенных средних в с/практике используются
2) Структурные
средние —
применяются для изучения внутреннего
строения и структуры рядов распределения
значений признака. К таким показателям
относятся мода
и медиана..
Средняя хронологическая
Средняя
хронологическая — это средний уровень
ряда динамики, т. е.
средняя,
исчисленная по совокупности значений
показателя в разные моменты или периоды
времени. В
зависимости от вида ряда динамики
применяются различные способы ее
расчета, а именно расчет средней
хронологической интервального ряда и
средней хронологической моментного
ряда.
Средней
хронологической интервального ряда
является средняя величина из уровней
интервального ряда динамики,
которая исчисляется по формуле
где
— средний уровень ряда;
у
— уровень ряда динамики;
n
— число членов ряда.
Средней
хронологической моментного ряда является
средняя величина из уровней моментного
ряда динамики.
Если f(t)
есть функция, выражающая изменение
моментного показателя во времени, то
за время (t)
от а
до b
средняя хронологическая моментyого
ряда равна:
Однако данных
непрерывного наблюдения значения f(t)
в распоряжении статистики, как правило,
нет. Поэтому в зависимости от характера
изменения показателя и имеющихся данных
применяются различные методы расчета.
При равных промежутках времени между
датами, на которые имеются данные, и
равномерном изменении размера показателя
между датами средняя хронологическая
моментного ряда обычно исчисляется
по формуле:
где у
— уровень ряда; n
— число всех
членов ряда;
—
средний уровень.
Если периоды
времени, отделяющие одну дату от другой,
не равны между собой, то расчет средней
хронологической моментного ряда
производится по формуле средней
взвешенной арифметической, в качестве
весов которой принимаются отрезки
времени между датами, т. е. по формуле:
гдеТ—
время, в течение которого данный уровень
ряда (у)
оставался без изменения.
Известно, например,
что в январе 2007 года произошло следующее
изменение численности сотрудников
компании «Бест»: было на 1 января
551 чел., уволился 2 января один сотрудник,
было принято 6 января 24 человека, 16
января— 6 человек, уволилось 25 января—
10 сотрудников. Требуется определить
среднюю численность сотрудников компании
«Бест» в январе 2007 г. Рассчитаем
число календарных дней, в течение которых
численность сотрудников компании «Бест»
оставалась без изменения, и произведение
этих чисел.
Таблица 5
Данные для расчета средней численности сотрудников компании «Бест»
|
Численность |
Число |
Произведение |
|
551 |
1 |
551 |
|
550 |
4 |
2200 |
|
574 |
10 |
5740 |
|
580 |
9 |
5220 |
|
570 |
7 |
3990 |
|
ИТОГО |
31 |
17701 |
Используя данные
произведенных расчетов, получим:
В отличие от первого
способа расчета средней хронологической
моментного ряда второй способ дает
точное значение средней.
Средняя гармоническая (сг).
СГ применяется
в тех случаях, когда частоты (веса) не
приводятся непосредственно, а входят
сомножителями в один из имеющихся
показателей.
Пример. Автомобиль
доставил товары в три магазина фирмы
«Весна», которые удалены от головного
предприятия на одинаковое расстояние.
Так, до первого магазина, расположенного
на шоссейной дороге, автомобиль прошел
путь со скоростью 50 км/ч, до второго, по
проселочной дороге, — 40 км/ч, а в третьем
случае автомобилю пришлось полпути
пройти через лесной массив, и скорость
движения составила только 30 км/ч.
Требуется определить
среднюю скорость движения автомобиля.
На первый взгляд представляется, что
средняя скорость • движения может быть
определена по формуле простой
арифметической:
Однако нетрудно
убедиться, что средняя вычислена
неправильно. В самом деле, производя
расчет средней скорости по простой
арифметической средней, исходим из
того, что автомобиль во всех трех случаях
прошел одинаковое расстояние, пройдя
соответственно 50, 40 и 30 км, т. е. всего
120 км. Если бы условие этой задачи
было сформулировано в такой форме, то
средняя была бы рассчитана правильно
и характеризовала бы пройденное
автомобилем среднее расстояние.
В действительности
же эта средняя рассчитана неверно, так
как «в условия задачи не следует, что
автомобиль на преодоление расстояния
до трех магазинов фирмы «Весна»
проехал 120 км, так как Скорость движения
была различная. Следовательно, он прошел
и разное расстояние.
В тех случаях,
когда вес каждого варианта равен единице
(индивидуальные значения обратного
признака встречаются по одному разу),
применяется СГ
простая,
исчисляемая по формуле:
где x
– отдельные варианты обратного
признака, встречающиеся по одному разу;
n–
число вариантов.
(8)

в сокращенном виде
где
—средняя
гармоническая;
—
числа, обратные заданным вариантам.
Иначе говоря, СГ
простая
отношение числа вариантов к сумме
обратных значений этих вариантов.
Для нашего примера
будем иметь:
В нашем примере
СА (ха)
оказалась
больше средней гармонической
.
При этом абсолютная
ошибка завышения составляет
— 2 км/ч (38 — 40), а относительная —5%
Т.о., неправильное
использование СА привело бы к завышению
средней скорости движения автомобиля
и к неправильному определению объема
перевозок. Это еще раз доказывает, с
какой осторожностью следует решать
вопрос о том, какую среднюю надлежит
применять в экономических расчетах.
В рассмотренном
примере частоты (веса) имели одно значение
и равнялись единице. Если же частоты
(веса) различные, то применяется СГ
взвешенная, которая
вычисляется следующим образом:
Где
—
СГ взвешенная:
Как первая, так и
вторая формулы показывают, что СГ есть
величина обратная СА.
Веса арифметической
средней и гармонической средней
обозначены разными буквами: f
и m.
Это не случайно, так как весами СА служат
частоты рассматриваемого ряда, а весами
СГ будет произведение вариантов на
веса.
Пример.
Рассмотрим данные о реализации товаров
по двум магазинам фирмы «Весна»
(табл. 6). Таблица
.6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
29.05.20153.63 Mб107. Лекц.БУ-анализ.doc
- #
18.12.2018130.46 Кб297.docx
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
- Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
- средняя арифметическая;
- средняя гармоническая;
- средняя геометрическая;
- средняя квадратическая.
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
- Средняя арифметическая простая (невзвешенная) – вычисляется когда каждый вариант совокупности встречается только один раз.
- Средняя арифметическая (взвешенная) – варианты повторяются различное число раз, при этом число повторений вариантов называется частотой, или статистическим весом.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
- Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле (8.8):
(8.8 -формула средней арифметической простой)
- где хi – вариант, а n – количество единиц совокупности.
- Пример вычисления средней арифметической простой. Провели опрос о желаемом размере заработной платы у пяти сотрудников офиса. По результатам опроса выяснили, что желаемый размер заработной платы составляет соответственно для каждого сотрудника: 50000, 100000, 200000, 350000, 500000 рублей человек. Рассчитаем среднюю арифметическую простую по формуле (8.8):
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
- Средняя арифметическая взвешенная формула 8.9.
(8.9 -формула средней арифметической взвешенной)
- где хi – вариант, а fi – частота или статистический вес.
- Пример вычисления средней арифметической взвешенной. Результаты опроса всех работников офиса приведены в табл. 8.2.
Таблица 8.2 – Результаты опроса работников офиса
|
Желаемый размер заработной платы, тыс.руб хi |
Количество работников fi | хifi |
| 1 | 2 | 3 |
|
50 100 200 350 500 |
6
10 20 9 5 |
300
1000 4000 3150 2500 |
| Итого | 50 | 10950 |
Пример. Вычислим (ориентируясь на итоговые строки таблицы) желаемый размер заработной платы, 50 сотрудников офиса (используем формулу 8.9):
Пример вычисления средней арифметической взвешенной
Вывод: в среднем желаемый размер заработной платы по результатам опроса 50 человек составил 219 тысяч рублей.
Среднеарифметическая – всегда обобщающая количественная характеристика варьирующего признака совокупности.
- Средняя гармоническая вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины.
- Средняя гармоническая простая представлена ниже:
(8.10 – формула средней гармонической простой)
Средняя гармоническая взвешенная определяется по формуле
(8.11- формула средней гармонической взвешенной)
где xi – вариант, n – количество вариантов, Vi – веса для обратных значений xi.
Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, чем взвешенная. Для иллюстрации области ее применения воспользуемся упрощенным условным примером.
- Пример (вычисление средней гармонической простой (невзвешенной)).
Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 5 мин., второй – 15 мин.
- Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?
На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. если используем среднюю арифметическую простую получим: (5+15):2=10, мин.
- Проверим обоснованность такого подхода на примере одного часа (60 минут) работы. За этот час первый работник обрабатывает 12 заказов (60:5), второй – 4 заказа (60:15), что в сумме составляет 16 заказов.
Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится: (60/10) + (60/10) = 12 заказов (что не соответствует истине).
- Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов, т.е. используем среднюю гармоническую:
Пример вычисления средней гармонической простой (невзвешенной)
Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится: (60/7,5) + (60/7,5) = 16 заказов
- Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения Wj для единиц совокупности равны (в рассмотренном примере рабочий день у сотрудников одинаковый).
Пример (вычисление средней гармонической взвешенной) В ходе торгов на валютной бирже за первый час работы заключено пять сделок. Данные о сумме продажи рублей и курсе рубля по отношению к доллару США приведены в табл.8.3.
Таблица 8.3 – Данные о ходе торгов на валютной бирже (цифры условные)
Номер сделки Сумма продажи V, млн руб. Курс рубля x, руб. за 1 дол. V/x 1 2 3 4 1
2
3
4
5
455,00
327,50
528,00
266,00
332,50
65,00 65,50
66,00
66,50
66,50
7,00
5,00
8,00
4,00
5,00
итого 1909,00 – 29,00 Для того чтобы определить средний курс рубля по отношению к доллару, нужно найти соотношение между суммой продажи рублей, которые затрачены на покупку долларов в ходе всех сделок, и суммой приобретенных в результате этих сделок долларов.
- Вывод: средний курс за один доллар составил 65,83 руб.;
- Если бы для расчета среднего курса была использована средняя арифметическая простая:
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин как отношение каждого уровня ряда к предыдущему уровню.
- Средняя геометрическая простая рассчитывается по формуле 8.12
(8.12)
- Если использовать частоты m, получим формулу средней геометрической взвешенной
- Средняя геометрическая взвешенная рассчитывается по формуле 8.13
(8.13)
Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.
Для несгруппированных данных используют формулу средней квадратической простой
Средняя квадратическая простая (формула 8.14)
8.14
Для сгруппированных данных используют формулу средней квадратической взвешенной
Средняя квадратическая взвешенная (формула 8.15)
(8.15) – Формула -средняя квадратическая взвешенная
Средние арифметическая, гармоническая, геометрическая и квадратическая, рассчитанные для одного и того же ряда вариантов, отличаются друг от друга. Их численное значение возрастает с ростом показателя степени в формуле степенной средней правило мажорантности средних А.Я. Боярского, т.е.
Мода и Медиана (структурные средние) формулы и примеры вычисления см. по ссылке
Простой пример: Утром вы ведёте машину до работы со скоростью 30 км/ч, потому что вы не хотите на работу, а обратно едете уже со скоростью 60 км/ч, потому что спешите попасть домой. Какова средняя скорость вашего передвижения в этот день?
Подсказка: Нет, не 45 км/ч.
А пока вот вам небольшая табличка.
Но что всё это значит?
Давайте начнём сначала. Что вообще мы понимаем под словом «среднее»? Для большинства из нас это «какое-то число посередине» либо некое сбалансированное по каким-то критериям число.
Можно предложить более универсальную интерпретацию понятия «среднее значение». Среднее значение какого-либо ряда значений — это то, которым можно заменить любую единицу ряда и получить тот же результат. Условно говоря, я могу выбросить все представленные данные, кроме среднего значения, и общий смысл не изменится.
Одна из целей получения среднего значения — это понять суть выборки данных с помощью репрезентативного образца. Но сам процесс вычисления среднего значения зависит от того, каким образом взаимодействуют элементы группы данных. Давайте посмотрим, как это происходит.
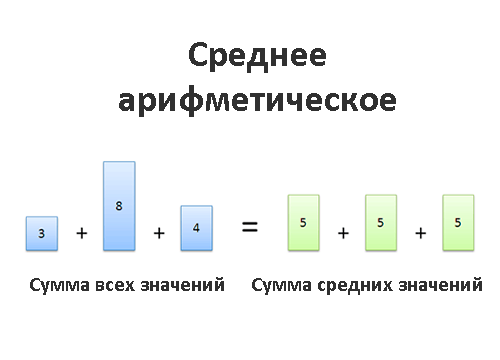
Среднее арифметическое
Среднее арифметическое знакомо нам всем со школы:
среднее арифметическое = сумма всех величин/количество величин
Задачка: вы весите 75 кг и зашли в лифт с подростком весом 50 кг и толстяком весом 175 кг. Каков средний вес вашей группы?
На самом деле вопрос стоит так: Если заменить вашу весёлую компанию тремя клонированными людьми с одинаковым весом, каким весом должен обладать каждый такой клон?
В этом случае мы просто заказываем на фабрике по производству клонов человека трёх экземпляров весом в 100 килограмм каждый (Помним: (75+50+175)/3) и довольно потираем руки.
Преимущества среднего арифметического:
- Отлично работает для совокупностей, значения которых легко складываются;
- Просто вычисляется: складывай, разделяй и властвуй;
- Интуитивно понятно — среднее арифметическое для нас как раз и является «числом где-то в середине» между наибольшим и наименьшим значением.
Недостатки среднего арифметического:
- Среднее арифметическое не работает для числовых рядов с большим разбросом в значениях. Ну, скажем, среднее арифметическое чисел 100, 200 и -300 — это 0, а это уже обескураживает.
Среднее арифметическое срабатывает в 80% случаев. К сожалению, 20% оставшихся случаев и вынуждают нас искать альтернативы для подсчёта среднего значения.
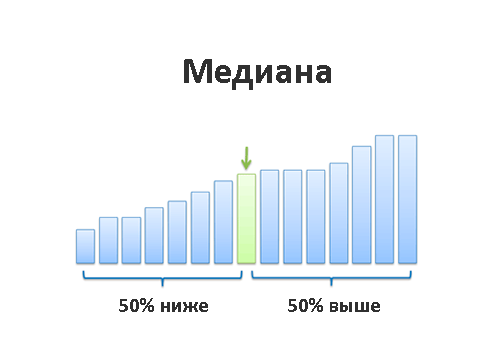
Медиана
Медиана — это та самая грань, которая отделяет наибольшие значения от наименьших. То самое «число посередине». Постойте-постойте, а разве среднее арифметическое делает не то же самое?
Вот вам простой пример. Какое число находится в середине этого ряда?
1, 2, 3, 4, 100
Число «3» находится в середине ряда. И хотя среднее арифметическое (22) является «средним», оно никак не отражает распределения этих чисел. Интуитивно (и абсолютно правильно!) мы считаем, что в середине этого ряда всё-таки 3, а не 22. Здесь среднее значение увеличилось благодаря резко отклоняющемуся от общей массы значению, 100.
Медиана решает эту проблему. Медиана делит наш числовой ряд на две равные части, причём первая половина имеет значения меньше либо равные медиане, а вторая — больше либо равные. Если в середине числового ряда оказывается два числа, мы просто берём среднее арифметическое этих двух чисел, чтобы получить медиану. В числовом ряду 1, 2, 3, 4 медианой станет число 2,5. Именно медиана позволяет выбивающимся из общей массы числам вроде 100 в нашем примере выше не влиять на общее впечатление о числовом ряде.
Преимущества медианы:
- Прекрасно справляется с резко отклоняющимися значениями, поэтому зачастую является самым репрезентативным значением для группы;
- Разбивает данные на две группы, состоящие из одинакового количества элементов.
Недостатки медианы:
- Немного усложняются вычисления: необходимо разбить ряд на две части;
- Медиана менее популярна; если вы скажете «среднее медианное значение», люди запросто могут подумать, что вы говорите о среднем арифметическом. Отсюда возникают недопонимания.
Такие средние значения, как цены на недвижимость или, например, уровень дохода часто вычисляются именно по медиане, потому что нам важна именно средняя стоимость большей части домов в конкретном районе или средний уровень доходов большей части населения. В таком случае Билл Гейтс с годовым доходом в несколько миллиардов не испортит нам всю статистику. Видите, как много зависит от того, как мы работаем с имеющимися данными?
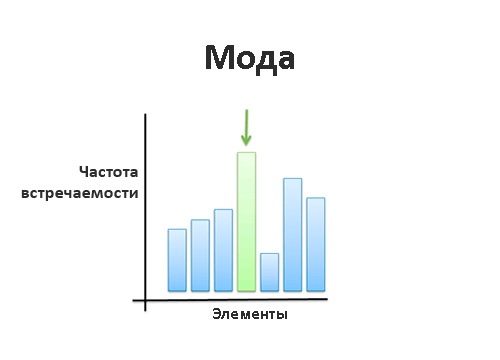
Мода
Само слово может звучать странно, но оно означает всего лишь наиболее часто встречающийся в группе элемент. На практике обычно мода определяется путём опросов и сбора мнений. Да, действительно порой бывают случаи, когда лучшим способом получить наиболее репрезентативный образец данных является сбор откликов.
Ну, скажем, вы планируете вечеринку, и вам нужно выбрать день для её проведения. Дни недели — такой же числовой ряд, что и любой другой. Это всего лишь числа от 1 до 7. Среднее арифметическое и медиана тут не помогут (Лиза и Паша могут в пятницу, а Коля и Петя — в воскресенье; поэтому назначим субботу). Что делать в таком случае? Конечно, выбрать тот день, который выберет большинство.
Как правило, мода используется для получения наиболее репрезентативного значения в нечисловых рядах. Популярные цвета в сезоне, хиты продаж, рейтинги фильмов и музыки, лучшие кафе и закусочные определяются именно по моде.
Преимущества моды: — Прекрасно работает для получения представления об общественном мнении; — Даёт представление о потребностях большой части людей (там, где среднее арифметическое даёт лишь осечку); — Проста для понимания.
Недостатки моды: — Для её вычисления требуется больше усилий (нужно собрать мнения и обработать их); — Победителю достаётся всё: мода выявляет только одного лидера.
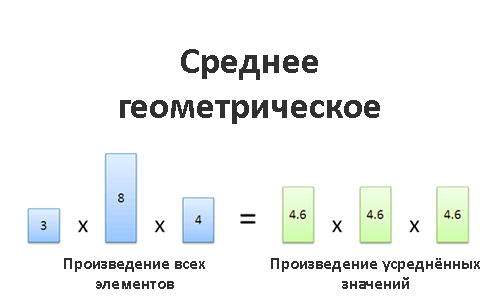
Среднее геометрическое
Наш «усреднённый элемент» зависит от того, что мы делаем с уже существующими элементами группы данных. В большинстве случаев элементы просто складываются, и среднее арифметическое прекрасно работает. Но иногда нам нужно что-то большее. Например, когда мы работаем с инвестициями, площадью и объёмом. В таких случаях данные взаимодействуют между собой именно путём умножения (ожидаемая доходность, объём или площадь фигуры вычисляются с помощью умножения), и это меняет наш подход к выявлению средних значений.
Вот пример. Какой инвестиционный портфель вы предпочтёте? Иными словами, какой из них принесёт большую прибыль в течение типичного года?
- Портфель А: +10%, -10%, +10%, -10%
- Портфель Б: +30%, -30%, +30%, -30%
Выглядят они похоже. Наша повседневная логика, построенная на привычке к среднему арифметическому, говорит нам, что оба портфеля достаточно рискованны, и оба в среднем приведут к убыткам или нулевой прибыли. Поэтому, наверное, мы выберем портфель Б, поскольку в успешный год он принесёт больше прибыли.
И это неверно! На фондовом рынке с таким подходом мы с вами точно бы прогорели. Проценты с инвестиций умножаются, а не складываются. Мы не можем просто взять и использовать среднее арифметическое, нам нужно найти действительный коэффициент окупаемости. Коэффициент окупаемости считается достаточно просто: берём условные 100% нашего текущего капитала в качестве единицы. Далее представляем колебания доходности-убытка, представленные в описании портфелей, добавляя к нашей единице или вычитая из неё процентные показатели. Затем перемножаем полученные колебания и получаем коэффициент. Для расчёта среднегодового значения коэффициента окупаемости делим полученный коэффициент на 4 (поскольку элементов в нашем числовом ряду четыре).
- Портфель А:
Коэффициент окупаемости: 1,1 * 0,9 * 1,1 * 0,9 = 0,98 (2% убытка)
Среднегодовое значение: (0,98)^(1/4) = 0,5% годового убытка
- Портфель Б:
Коэффициент окупаемости: 1,3 * 0,7 * 1,3 * 0,7 = 0,83 (17% убытка)
Среднегодовое значение: (0,83)^(1/4) = 4,6% годового убытка
Выбор между 2% или 17%? Огромная разница! Конечно, разумный человек отказался бы от обоих портфелей, но из двух зол лучше выбрать Портфель А. И именно здесь среднее арифметическое не работает.
Несколько примеров, где работает среднее геометрическое:
- Темпы инфляции: У вас есть показатели в 1%, 2% и 10%. Каков средний показатель инфляции за конкретный период времени? (1,01 * 1,02 * 1,10)^(1/3) = 4,3%.
- Скидки: У вас есть три скидочных купона на 50%, 25% и 35%. Какова средняя скидка? (0,5 * 0,75 * 0,65)^(1/3) = 37.5%.
- Площадь: У вас есть участок земли 40х60 м. Вам нужно вычислить «усреднённую сторону» — иными словами, сторону квадрата примерно той же площади. (40 * 60)^(0.5) = 49 м.
- Объём: У вас есть коробка 12х24х48 см. Вам снова нужна усреднённая сторона, то есть сторона куба примерно того же объёма. (12 * 24 * 48)^(1/3) = 24 см.
Среднее геометрическое помогает найти «типичный элемент» среди группы элементов, взаимодействующих друг с другом путём умножения. И, как видим, у него множество практических применений.
Среднее гармоническое
Среднее гармоническое представить сложнее, чем предыдущих представителей «средних», но оно не менее полезно. Между прочим, само понятие «гармоники» в математике связано с обратными числами (1/2, 1/3 и т.д.). Среднее гармоническое помогает нам вычислить среднее арифметическое в рядах чисел, заданных обратными значениями. Это случается чаще, чем вы можете подумать.
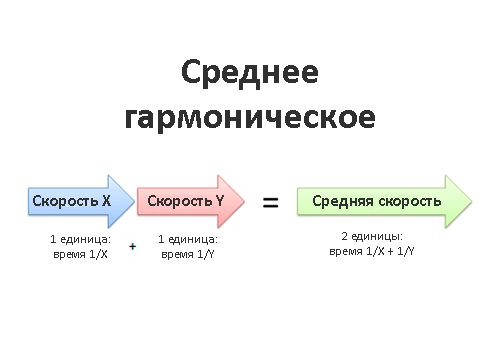
Например, если я еду со скоростью 30 км/ч, это значит, что я получаю определённый результат (30 км) за какую-либо единицу времени (1 час). Когда мы хотим узнать среднее значение для нескольких скоростей (Х и Y), нужно думать о результате и единицах измерения, а не об исходных цифрах.
средняя скорость = общий результат/общая единица измерения
Возьмём двух работников: Х и Y. Оба работают в одном проекте и выполняют одинаковое количество работы, но скорость их работы разная. Какова средняя скорость их работы?
Скажем, работник Х кладёт 30 кирпичей в час, а работник Y — 60 кирпичей в час. Значит, на один кирпич у каждого работника уходит:
- У работника X укладка одного кирпича займёт 1/X времени (1/30);
- У работника Y укладка одного кирпича займёт 1/Y времени (1/60)
Складываем результаты и единицы измерения:
Общий результат: 2 кирпича (Х и Y уложили по одному) Общая единица времени: 1/X + 1/Y (у каждого уходит разное количество времени)
Средней скоростью обоих работников будет:
Если бы у нас было 3 работника (X, Y и Z), их средняя скорость вычислялась бы по формуле:
Здорово же иметь одну формулу вместо того, чтобы каждый раз заниматься долгими вычислениями. Даже вычисляя среднюю скорость 5 нерадивых работников стало бы головной болью. Помните наш первый пример про скорость, с которой вы едете на работу и домой? Чтобы найти среднюю скорость вашего передвижения в тот день, мы просто используем формулу.
При этом нам даже не нужно знать, где находится дом или офис! Теперь вместо X и Y у нас не кирпичи, а количество километров за единицу времени. Вне зависимости от расстояния результат один и тот же: допустим, некое количество километров R мы проходим на скорости X, а другое количество километров R — на скорости Y. Средняя скорость при этом будет вычисляться так же, как вычисляется средняя скорость прохождения 1 км на скорости X и одного километра на скорости Y:
Ключевая идея: Среднее гармоническое используется тогда, когда один и тот же объём работы выполняется на разных скоростях.
Ещё более ключевая идея: Помните, что среднее значение — это один элемент, способный передать суть целой группы элементов. В нашем примере с работой и офисой в среднем туда-обратно мы едем на скорости 40 км/ч (вместо 30 км/ч туда и 60 км/ч обратно). Важно помнить, что средней скоростью мы заменяем каждую «стадию».
Ещё несколько примеров из жизни среднего гармонического:
- Передача данных: Мы передаём данные между клиентом и сервером. Клиент посылает данные за плату 10 Гб/доллар, а сервер получает их за плату 20 Гб/доллар. Каково среднее количество Гб, которые можно передать и получить за один доллар? Мы усредняем значения для клиента и для сервера: 2 / (1/10 + 1/20) = 13,3 Гб/доллар для каждой стороны. Поскольку данные и передаются, и получаются (каждая сторона выполняет свою половину работу), мы делим это значение на 2 и получаем следующее значение: 6,65 Гб за доллар.
- Продуктивность машины: У нас есть производственная установка для подготовки и полировки деталей. За час установка может подготовить 25 деталей; либо за тот же час она может отполировать 10 деталей. Какова средняя производительность установки? Усредняем значения для каждой стадии: 2 / (1/25 + 1/10) = 14,28 деталей/час. Снова делим это значение на два, поскольку нас интересует средняя производительность установки, если она занимается сразу двумя фазами: получаем 7,14 деталей/час.
В чём здесь фокус?
Среднее гармоническое действительно не самая очевидная вещь. Дело в том, что если бы у вас было две разных установки, одна из которых работает со скоростью 10 деталей/час, а другая — 20 деталей/час, конечно, их средняя производительность составляла бы 15 деталей/час. В этом случае вы имеете полное право просто сложить их производительность и вычислить среднее арифметическое, ведь установки работают независимо друг от друга.
Если не верите в среднее гармоническое, можно устроить себе обратную проверку. Мы утверждаем, что наша универсальная установка по заготовке и полировке деталей справляется с 7,14 деталями в час. Проверим: мы знаем, что за час машина либо обрабатывает 25 деталей, либо полирует 10. Получаем:
Подготовка: 7,14/25 = 0,29 часов Полировка: 7,14/10 = 0,71 часов
Да-да, 0,29 + 0,71 = 1, цифры работают: для полного цикла изготовления 7,14 деталей действительно требуется один час.
В качестве заключения
Даже такая простая на первый взгляд идея, как «среднее значение», имеет множество применений. Мы здесь рассмотрели лишь самые основные и не затронули средневзвешенное, центр тяжести, математическое ожидание и многое другое. Но мы поняли главные принципы:
- Среднее значение призвано отразить основную суть всех элементов в группе
- Тип среднего значения зависит от того, как взаимодействуют элементы в группе (складываются? умножаются? становятся обратными величинами? просто выбираются?)
Спасибо прекрасной статье на Better Explained.
Удачных вам статистических изысканий и не забудьте прочитать другие статьи из серии переводов Better Explained: Удивительные применения теоремы Пифагора, Как развить математическую интуицию? и Открытие числа Пи.
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.

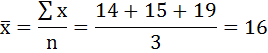
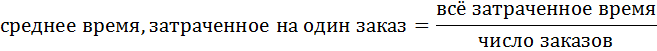
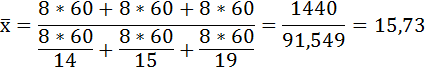
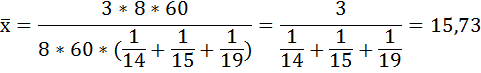
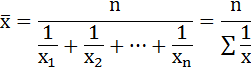







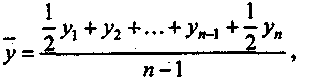





 Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.





 то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.