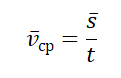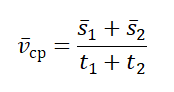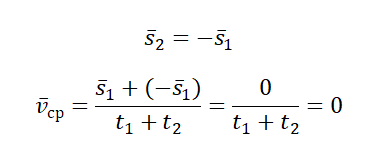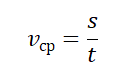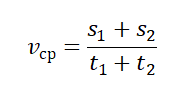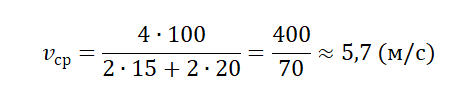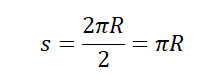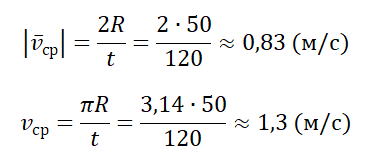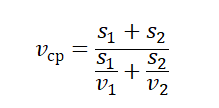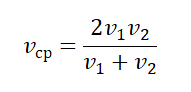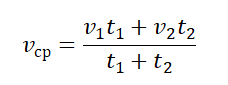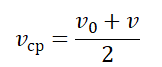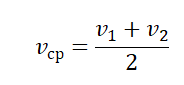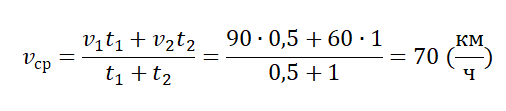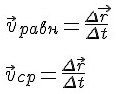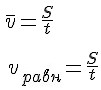Приступая
к изучению движения какого-либо тела,
нужно указать, по отношению к какому
телу мы рассматриваем движение данного
тела. Для измерения времени необходимо
иметь часы. Роль часов может выполнять
любое устройство, совершающее многократно
один и тот же процесс.
Множество
неподвижных относительно друг друга
тел, по отношению к которым рассматривается
движение, и отсчитывающих время часов
образует систему
отсчета.
Совокупность
тел, выделенная для рассмотрения,
называется механической
системой.
Тело,
размерами которого в условиях данной
задачи можно пренебречь, называется
материальной
точкой.
Материальная
точка при своем движении описывает
некоторую линию — траекторию.
В зависимости от формы траектории
различают прямолинейное движение,
движение по окружности, криволинейное
движение и т. д.
Расстояние
между начальным и конечным положением
частицы, отсчитанное вдоль траектории,
называется путем, пройденным частицей.
Обозначается буквой s.
Прямолинейный
отрезок, соединяющий начальное и конечное
положение частицы, называется её
перемещением.
В
обыденной жизни под скоростью
понимают
путь, проходимый частицей за единицу
времени. Если за равные, сколь угодно
малые промежутки времени частица
проходит одинаковые пути, движение
частицы называют равномерным.
В
физике под скоростью
понимают векторную
величину,
характеризующую не только быстроту
перемещения частицы по траектории, но
и направление, в котором движется эта
частица в каждый момент времени.
Радиус-вектор
точки это вектор, проведенный из начала
координат в данную точку. Его проекции
на координатные оси равны координатам
точки:
rх
=х,
rу=у,
rz
= z.
Среднее
значение скорости
за время Δt
это отношение Δ
/Δt.
Если
брать все меньшие промежутки времени
Δt,
то это отношение в пределе даст скорость
в момент времени
t:

Если
брать отрезки пути Δs
и перемещения, соответствующие все
меньшим промежуткам времени Δt,
то их различие будет убывать и их
отношение в пределе станет равным
единице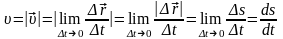
Модуль
скорости
равен производной пути по времени. При
равномерном движении модуль скорости
остается неизменным, а направление
вектора изменяется произвольным
образом. Вектор скорости, можно представить
в виде

Чтобы
вычислить путь,
проходимый частицей с момента времени
t1
до момента t2,
нужно проинтегрировать формулу для
модуля скорости

Пройденный
путь
можно представить как площадь фигуры,
ограниченной кривой u(t),
осью t
и прямыми t
= t1
и t
= t2.
Среднее
значение модуля скорости
за время от t1
до t2
по
определению равно
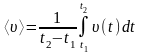
Вопрос № 2 Ускорение. Нормальная и тангенциальная составляющие ускорения. Связь нормального ускорения с радиусом кривизны и скоростью.
Скорость
частицы может изменяться со временем,
как по модулю, так и по направлению.
Быстрота изменения вектора скорости,
определяется производной вектора по
t.
Обозначается буквой a
и
называется — ускорение.

Введём
орт касательной к траектории τ,
направленный также как и вектор скорости.
Следовательно,
вектор
можно представить в виде суммы двух
составляющих. Одна из них коллинеарна
с
, т. е. направлена по касательной к
траектории, и поэтому обозначается at
и называется тангенциальным
ускорением
Если
> 0 (скорость увеличивается), вектор
направлен в ту же сторону, что и
Если
< 0 (скорость со временем уменьшается),
векторы
и
направлены в противоположные стороны.
При равномерном движении ускорение
равно 0 и, следовательно, тангенциального
ускорения нет.
Нормальное
ускорение
—
—
центростремительное ускорение.
Всякий
бесконечно малый участок траектории
FABG
в окрестностях точки А
можно рассматривать как дугу окружности
О радиусом R.
Его называют радиусом кривизны траектории
в точке А,
а центр O
такой окружности — центром кривизны.


При
и
β
=π/2+Δα/2
®π/2.
Следовательно, вектор нормален к вектору
скорости и направлен к центру O
кривизны траектории. Поэтому его называют
нормальным (центростремительным)
ускорением. Итак, вектор ускорения при
движении частицы по плоской кривой
определяется следующим выражением:

Вопрос
№ 3
Вращательное
движение. Угловая скорость, период
обращения, угловое ускорение. Связь
векторов линейной и угловой скорости.
Нормальное и тангенциальное ускорение
– связь с радиусом, угловой скоростью
и угловым ускорением.
При
вращательном движении все точки тела
движутся по окружностям, центры которых
лежат на одной и той же прямой, называемой
осью
вращения
Поворот
тела на некоторый угол φ
можно задать в виде отрезка, длина
которого равна φ,
а направление совпадает с осью, вокруг
которой производится поворот. Для того
чтобы указать, в какую сторону совершается
поворот вокруг данной оси, связывают
направления поворота и изображающего
его отрезка.
Правило
правого винта: направление отрезка
должно быть таким, чтобы, глядя вдоль
него, мы видели поворот совершающимся
по часовой стрелке (вращая головку
правого винта по часовой стрелке, мы
вызовем его перемещение от себя).
Угловой
скоростью
тела называется векторная величина,
модуль которой определяется формулой
.
Угловая скорость ω
направлена вдоль оси, вокруг которой
вращается тело, в сторону, определяемую
правилом правого винта. Вращение с
постоянной угловой скоростью называется
равномерным.
Изменение
вектора угловой скорости со временем
характеризуется величиной которую
называют угловым
ускорением.

Если
ось вращение неподвижна, то: если w
возрастает, то E
и w
сонаправлены, если w
убывает, то E
и w
направлены в противоположные стороны.
О
тдельные
точки вращающегося тела имеют различные
линейные скорости. Скорость каждой из
точек изменяет свое направление. Модуль
скорости определяется скоростью
вращения тела и расстоянием R
рассматриваемой точки от оси вращения.
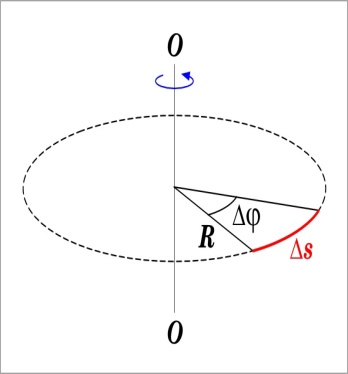
Пусть
за малый промежуток времени тело
повернулось
на
угол Δφ.
Точка, находящаяся на расстоянии R
от оси,
проходит
при этом путь Δs = RΔφ.
Линейная скорость точки
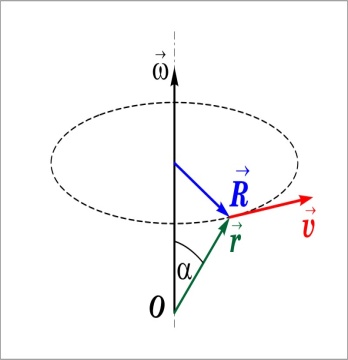
Из
рисунка видно, что векторное произведение
совпадает
по направлению с вектором скорости и
имеет модуль, равный ωrsinα=ωR.

Модуль
нормального ускорения точек вращающегося
тела равен
= υ2/R
= ω2R 
Предположим,
что ось вращения тела не поворачивается
в пространстве. Модуль тангенциального
ускорения равен |dυ/dt|.
Учтем, что расстояние точки тела от оси
вращения R
= const, тогда

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
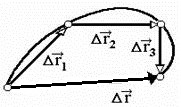
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Определение и формулы
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
vср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Определение и формулы
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
- vср=vср, если путь равен модулю перемещения. Так бывает в случае равномерного прямолинейного движения.
- vср>vср, если путь больше модуля перемещения. Так бывает в случае неравномерного прямолинейного или любого криволинейного движения.
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
Полезные советы и формулы
- Если известны значения отдельных участков пути и скорости на этих участках, средняя скорость равна:
- Если известны скорости на первой и второй половине пути (s1=s2), средняя скорость равна:
- Если известно время прохождения отдельных участков пути и скорости движения на этих участках, средняя скорость равна:
- Если тело движется прямолинейно и равноускорено, его средняя скорость равна половине суммы начальной и конечной скорости:
- Если известны скорости тела за равные промежутки времени, его средняя скорость равна:
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
Алиса Никитина | Просмотров: 5.7k
Векторная величина, то есть она имеет абсолютную величину и направление.
Движение тела можно представить как совокупность мгновенных пребываний его в последовательных точках траектории, поэтому указанную характеристику движения называют мгновенной скоростью.
Вектор скорости нередко выражают в проекциях на координатные оси:
v=vxi+vyj+vzkv={{v}_{x}}i+{{v}_{y}}j+{{v}_{z}}k
или в виде
v=dxdti+dydtj+dzdtkv=frac{dx}{dt}i+frac{dy}{dt}j+frac{dz}{dt}k
а модуль вектора находят по формуле
v=vx2+vy2+vz2v=sqrt{{{v}_{x}}^{2}+{{v}_{y}}^{2}+{{v}_{z}}^{2}}
Такой чисто физический смысл скорости как меры движения отдельного тела.
Средняя скалярная скорость
Наряду с этим на практике в описаниях движений часто удовлетворяются средней скалярной скоростью – характеристикой движения, которая определяется как отношение пути к промежутку времени, за который тело преодолело этот путь:
v=s/Δtv = s/Δt,
где vv – средняя скорость, ss – путь, ΔtΔ t – промежуток времени.
Это определение отличается от определения собственно скорости тем, что скорость является отношением перемещения к промежутку времени, а следовательно векторной величиной.
Например, болид Формулы 1, преодолев круг, и вернувшись на свое место, совершил нулевое перемещение, но прошел путь, равный длине окружности. То есть, можно посчитать среднюю скорость его движения.
Единицы измерения средней скалярной скорости те же, что и для скорости, м/с, км/ч и т.д.
При предельном переходе Δt→0Δt → 0, значение средней скалярной скорости стремится к модулю скорости.
Средне-квадратичная скорость
При определении скорости движения частиц в статистической физике удобнее усреднять не модуль скорости, а квадрат её значения. Тогда средняя скорость определяется как
v=⟨v2⟩v = ⟨v2⟩.
Усреднения проводится по всем частицам и по времени.
При отсутствии упорядоченного движения, то есть течения, среднее перемещение отдельной частицы на достаточно большом промежутке времени равно нулю, поэтому среднее значение векторной скорости тоже равна нулю. Однако среднее значение квадрата скорости отличное от нуля и связано с температурой.
Тангенциальная скорость
Линейная скорость, определяет расстояние пройденное за единицу времени, в то время как тангенциальная скорость это линейная скорость чего-то, что движется вокруг круговой траектории. Точка на внешней части карусели проходит большую дистанцию при одном полном обороте чем точка ближе к центру.
Прохождение большего расстояния за одинаковое время означает, что данная точка будет иметь большую скорость, и поэтому линейная скорость будет больше на внешнем крае вращающегося объекта, чем более близкого к оси вращения. Такую скорость вдоль круговой траектории называют тангенциальной скоростью поскольку направлением движения является прямая, касательная к дуге окружности.
Для кругового движения, тангенциальная скорость и линейная скорость являются взаимозаменяемыми и обе выражаются в м/с, км/ч или т.д.
Тест по теме «Средняя скорость»
§ 17. Переменное
движение. Средняя скорость. Средний
модуль скорости
1. Переменное
движение.
Определение
1. Движение
называется переменным,
если за любые равные промежутки
времени точка совершает различные
перемещения.
Перемещение
— вектор. Он может изменяться по модулю
и направлению. При переменном движении
за любые равные промежутки времени
перемещения могут отличаться либо
модулями, либо направлениями, либо и
модулями и направлениями.
2. Средняя
скорость.
Определение
2а. Средней
скоростью переменного движения
называется отношение перемещения
ко времени, за которое это
перемещение произошло.
Запишем
формулу скорости равномерного
движения и средней скорости
переменного движения.
Если
посмотреть на правые части этих
равенств, заметим, что они одинаковы. В
этом заключается смысл средней
скорости.
Определение
2б. Под средней
скоростью переменного движения
понимают скорость некоторого
воображаемого равномерного
прямолинейного движения, у которого
перемещение и время одинаковы с
переменным движением.
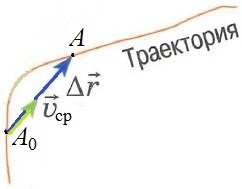
Согласно рисунку, представленному выше,
это понимать надо так. Если бы точка
двигалась не переменно по
криволинейной траектории, а равномерно
и прямолинейно прямо по вектору
перемещения ,
то она за время
попала бы в точку A из точки ,
если бы скорость этого воображаемого
равномерного движения была бы
одинаковой со средней скоростью
переменного движения.
Модуль
вектора средней скорости, или
модуль средней скорости:
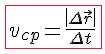
3. Средний
модуль скорости.
На
практике при составлении расписания
движения поездов, автобусов используют
ещё одно понятие средней скорости,
которое называют средним модулем
скорости, то есть средним по времени
модулем всех скоростей, которые имела
точка на различных участках траектории.
Определение
3а. Средним
модулем скорости переменного
движения называется отношение пути S
ко времени t, за которое этот
путь пройден.
—
средний модуль скорости
Не надо
путать средний модуль скорости с
модулем вектора средней скорости.
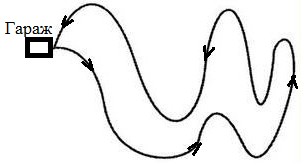
Например, если автобус вышел на маршрут
в начале дня и к концу дня возвратился в
гараж, то перемещение за всё время
движения равно нулю .
Поэтому равны нулю средняя скорость и
её модуль:
,
.
Но
средний модуль скорости отличен от
нуля, так как не равен нулю путь,
пройденный автобусом:
.
Аналогично для бумеранга.
За время
полёта бумеранга средняя скорость его
движения и модуль средней скорости
равны нулю, так как равно нулю
перемещение бумеранга относительно
точки А (см. рис.). Но так как путь,
который проделал бумеранг, не равен
нулю, то и средний модуль скорости
движения бумеранга отличен от нуля.
Если
посмотреть на правые части формул
модуля скорости равномерного движения
и среднего модуля скорости переменного
движения, то увидим, что правые части
равенств одинаковы.
В этом
заключается смысл среднего модуля
скорости.
Определение
3б. Средний
модуль скорости переменного
движения равен модулю скорости
такого воображаемого равномерного
прямолинейного движения, у которого
путь и время одинаковы с переменным
движением.
Содержание:
- Определение и формула средней скорости
- Вектор средней скорости
- Единицы измерения
- Примеры решения задач
Определение и формула средней скорости
Определение
Средней путевой скоростью материальной точки на отрезке времени
$Delta t$называется скалярная физическая величина, равная отношению
длины пути, пройденного точкой к промежутку времени, в течение которого данный путь пройден. Среднюю скорость обозначают:
$$langle vrangle, bar{v}, v_{s r}$$
Математически определение средней скорости можно записать в следующем виде:
$$langle vrangle(t+Delta t)=frac{Delta s}{Delta t}=frac{s(t+Delta t)-s(t)}{Delta t}(1)$$
где $Delta s=s(t+Delta t)-s(t)$ — длина пути, которую прошла точка за время
$Delta t$.
Если перейти к пределу при $Delta t rightarrow 0$ , получим:
$$lim _{Delta t rightarrow 0}langle vrangle=lim _{Delta t rightarrow 0} frac{Delta s}{Delta t}=frac{d s}{d t}=v(t)(2)$$
средняя путевая скорость в пределе совпадает с величиной (модулем) мгновенной скорости точки в момент времени t.
При равномерном движении:
$$langle vrangle=v(3)$$
Вектор средней скорости
Определение
Вектором средней скорости $langlevec{v}rangle$ материальной точки на
отрезке времени $Delta t$называют величину, равную приращению радиус-вектора,
который определяет положение данной точки к промежутку времени $Delta t$:
$$langlebar{v}rangle(t+Delta t)=frac{Delta bar{r}}{Delta t}=frac{bar{r}(t+Delta t)-bar{r}(t)}{Delta t}(4)$$
где $Delta bar{r}$ – приращение радиус-вектора материальной точки.
Вектор средней скорости в пределе при $Delta t rightarrow 0$ совпадает с вектором скорости в момент времени t:
$$lim _{Delta t rightarrow 0}langlebar{v}rangle=lim _{Delta t rightarrow 0} frac{Delta bar{r}}{Delta t}=frac{d bar{r}}{d t}=bar{v}(t)(5)$$
где $bar{v}(t)$ – вектор мгновенной скорости токи.
Если точка совершает равномерное и прямолинейное движение, то выполняется равенство:
$$langlebar{v}rangle=bar{v}(6)$$
Средняя путевая скорость и модуль вектора средней скорости равны
$(langle vrangle=|langlebar{v}rangle|)$ только при прямолинейном движении.
При всех остальных видах движения выполняется неравенство:
$$langle vrangle>|langlebar{v}rangle|(7)$$
Единицы измерения
Основной единицей измерения средней скорости в системе СИ является: м/с
В СГС: см/с
Примеры решения задач
Пример
Задание. Какова средняя скорость материальной точки за время ее движения, если точка прошла первую половину
пути имея скорость v1, остальную часть пути данная точка 1/2 времени двигалась со скоростью v2, последний
участок пути точка двигалась со скоростью v3.
Решение. В качестве основы для решения задачи формулу:
$$langle vrangle=frac{s}{Delta t}(1.1)$$
где время потраченное на путь ($Delta t$) делится на три части:
$$Delta t=t_{1}+t_{2}+t_{3}(1.2)$$
При этом имеют место следующие соотношения между отрезками пути, скоростью их преодоления и временем:
$$left{begin{array}{c}frac{1}{2} s=v_{1} t_{1} rightarrow t_{1}=frac{s}{2 v_{1}} \ frac{1}{2} s=v_{2} t_{2}+v_{3} t_{3} rightarrow t_{3}=frac{s}{2left(v_{2}+v_{3}right)}(1.3) \ t_{2}=t_{3}=frac{1}{2} tend{array}right.$$
$$langle vrangle=frac{2 v_{1}left(v_{2}+v_{3}right)}{v_{2}+v_{3}+2 v_{1}}$$
Ответ. $langle vrangle=frac{2 v_{1}left(v_{2}+v_{3}right)}{v_{2}+v_{3}+2 v_{1}}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
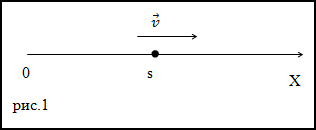
Задание. Какова средняя скорость частицы, движущейся по оси Xза время в течение которого, она пройдет первые
s метров пути, если функция скорости задана уравнением: $v=A sqrt{x}$,
где A=const>0. Считать, что x=0 при t=0.
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для средней путевой скорости, так как движение прямолинейное,
то средняя путевая скорость равна модулю вектора средней скорости. По условию задачи точка движется по оси X, тогда:
$$langle vrangle(t+Delta t)=frac{Delta x}{Delta t}(2.1)$$
По условиям x(t=0)=0, среднюю скорость ищем, когда тело находится в точкеx=sследовательно, выражение (2.1) преобразуем к виду:
$$langle vrangle=frac{s}{t}(2.2)$$
Найдем зависимость скорости от времени, исходя из определения мгновенной скоростидля движения точки по оси X:
$$v=frac{d x}{d t}=A sqrt{x}(2.3)$$
Выразим из (2.2) x:
$$frac{d x}{sqrt{x}}=A d t rightarrow x=frac{A^{2} t^{2}}{4}(2.4)$$
Так как движение происходит по оси X, то $x=s=frac{A^{2} t^{2}}{4}$ . Выразим время, которое точка затратила на путьs :
$$t=frac{2 sqrt{s}}{A}(2.5)$$
Подставим время из (2.4) в формулу (2.2):
$$langle vrangle=frac{A}{2} sqrt{s}$$
Ответ. $langle vrangle=frac{A}{2} sqrt{s}$
Читать дальше: Формула угловой скорости.