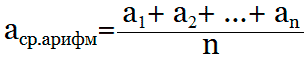Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также
В качестве разделителя использовать:
Пробел
Точка с запятой
С новой строки
Введите числа:
Всего чисел:
Результат:
Решение:
# Теория
Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Среднее арифметическое расчитывается по следующей формуле:
x = dfrac{a_1 + a_2 + … + a_n}{n}
- x — среднее арифметическое
- a1, a2, an — числа
- n — количество чисел
Комментарии 0
Нет комментариев
Войдите чтобы писать комментарии
Понятие среднее арифметическое ряда чисел можно встретить в разных сферах — в математике, статистике, инженерных расчетах и многих других.
Чтобы найти среднее арифметическое чисел надо их сложить и эту сумму разделить на количество чисел.
Мы создали этот калькулятор для упрощения расчетов. Он с легкостью найдет среднее арифметическое 3, 4, 5 и даже 15 чисел. Следует упомянуть, что кроме среднего арифметического есть очень схожие понятия медианы и среднего гармонического.
Калькулятор среднего арифметического
Как найти среднее арифметическое
Допустим, что нам надо найти среднее арифметическое чисел 7 23 9 73 3. Сложим их и получим 7 + 23 + 9 + 73 + 3 = 115. Поделим эту сумму на количество чисел, то есть на 5:
222 / 5 = 23
Значит среднее арифметическое приведенных чисел равно 23.
Ваша оценка
[Оценок: 913 Средняя: 3.5]
Среднее арифметическое чисел Автор admin средний рейтинг 3.5/5 — 913 рейтинги пользователей
Среднее арифметическое
- Главная
- /
- Математика
- /
- Арифметика
- /
- Среднее арифметическое
Чтобы найти среднее арифметическое нескольких чисел воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Среднее арифметическое:
0
Округление ответа:
Просто введите числа и получите среднее арифметическое этих чисел. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой «+».
Теория
Среднее арифметическое x̅ ряда чисел (x1,…,xn) — сумма всех чисел ряда, делённая на их количество n.
Формула
| x̅ | = | x1 + x2 + … + xn |
| n |
Примеры
Среднее арифметическое двух чисел
К примеру, вы периодически покупаете хлеб в двух разных магазинах. В одном он стоит 40 рублей, а в другом — 44 рубля. Давайте выясним сколько в среднем вы платите за буханку хлеба. Для этого найдём среднее арифметическое чисел 40 и 44:
Средняя стоимость хлеба = (40 + 44) / 2 = 42 рубля
Среднее арифметическое трёх чисел
Предположим у нас в разных комнатах в доме есть три градусника и каждый показывает разную температуру: в одной комнате 20°С, во второй 22°С, а в третьей, окна которой выходят на юг, — все 27°С. Давайте определим среднюю температуру в нашем доме:
Средняя температура = (20 +22 + 27) / 3 = 69 / 3 = 23°C
Среднее арифметическое нескольких чисел
Для примера посчитаем среднее арифметическое оценок за четверть среднестатистического школьника. Допустим, у него было 7 предметов, за которые он получил такие оценки: 4,4,3,3,5,3,4.
Средняя оценка = (4+4+3+3+5+3+4) / 7 = 26/7 = 3,71 ≈ 4
См. также
Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.
Смысл коэффициента
Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:
Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.
Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.
Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.
Подсчет среднего арифметического
Формула для вычислений предельно проста:
P = (a1 + a2 + … an) / n,
где an – значение величины, n – общее количество значений.
Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.
К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.
Как считать средние для разнородных данных
В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.
Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.
Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.
Рассмотрим пару примеров
Расчет средней оценки
Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:
(3 + 3 + 5 + 4) / 4 = 3,75
Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.
Расчет съеденных конфет
Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.
Заключение
Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.