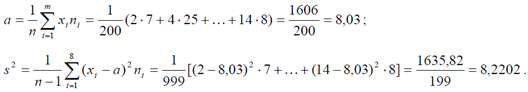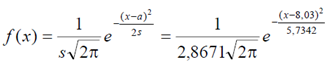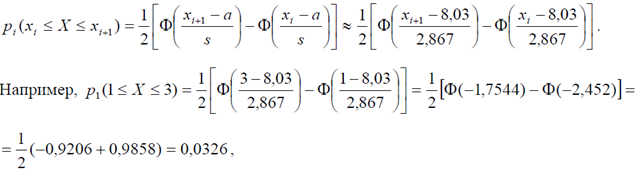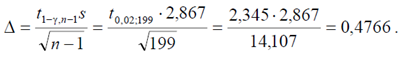Как оценить среднее значение и медиану любой гистограммы
17 авг. 2022 г.
читать 2 мин
Гистограмма — это диаграмма, которая помогает нам визуализировать распределение значений в наборе данных.
По оси X гистограммы отображаются интервалы значений данных, а по оси Y указано, сколько наблюдений в наборе данных приходится на каждый интервал.
Хотя гистограммы полезны для визуализации распределений, не всегда очевидно, что представляют собой средние и медианные значения, просто взглянув на гистограммы.
И хотя невозможно найти точное среднее и срединное значения распределения, просто взглянув на гистограмму, можно оценить оба значения. В этом руководстве объясняется, как это сделать.
Как оценить среднее значение гистограммы
Мы можем использовать следующую формулу, чтобы найти наилучшую оценку среднего значения любой гистограммы:
Наилучшая оценка среднего: Σm i n i / N
куда:
- m i : середина i -го бина
- n i : частота i -го бина
- N: общий размер выборки
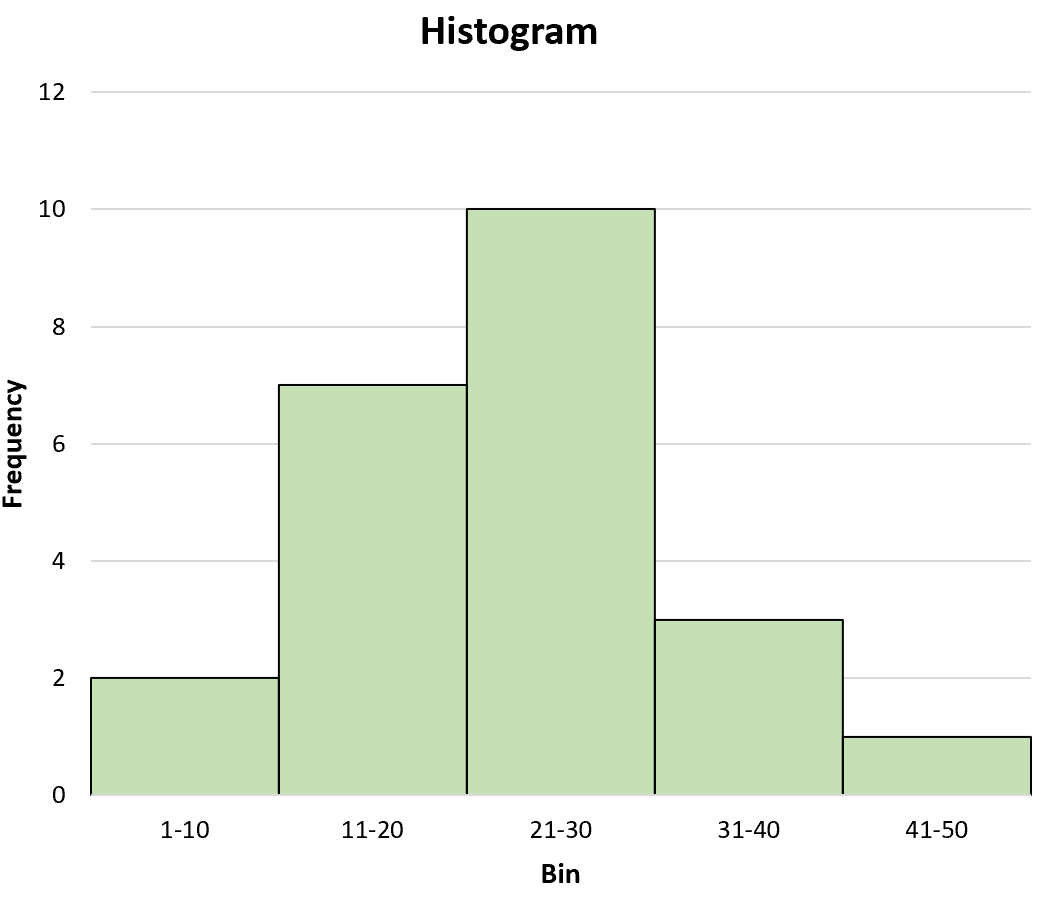
Например, рассмотрим следующую гистограмму:
Наилучшей оценкой среднего значения будет:
Среднее значение = (5,5*2 + 15,5*7 + 25,5*10 + 35,5*3 + 45,5*1) / 23 = 22,89 .
Глядя на гистограмму, это кажется разумной оценкой среднего значения.
Как оценить медиану гистограммы
Мы можем использовать следующую формулу, чтобы найти наилучшую оценку медианы любой гистограммы:
Наилучшая оценка медианы: L + ((n/2 – F)/f) * w
куда:
- L: Нижний предел средней группы
- n: общее количество наблюдений
- F: кумулятивная частота до средней группы
- f: частота срединной группы
- w: ширина срединной группы
Еще раз рассмотрим следующую гистограмму:
Наилучшей оценкой медианы будет:
Медиана = 21 + ((25/2 – 9)/10) * 9 = 24,15 .
Глядя на гистограмму, это также кажется разумной оценкой медианы.
Связанный: Как оценить стандартное отклонение любой гистограммы
Дополнительные ресурсы
Как найти среднее значение, медиану и моду в диаграммах «стебель-и-листья»
Как рассчитать среднее значение из таблиц частот
Когда использовать среднее значение против медианы
Как определить подходящую меру центральной тенденции?
Время на прочтение
6 мин
Количество просмотров 5.1K

Мера центральной тенденции (measure of central tendency) представляет из себя статистическую величину, которая характеризует целый набор данных одним единственным числом. Ее также называют мерой центрального расположения (measure of central location). Она описывает, как выглядит приблизительный центр набора данных.
Но сам по себе термин “центр” может подразумевать немного разные значения в зависимости от конкретной ситуации. Вы можете считать “центром” среднее арифметическое. Вы также можете назвать “центром” данные, которые просто находятся в середине вашей выборки. А еще вы можете рассматривать в качестве “центра” данные, которые повторяются чаще всего. Все эти центры по-своему характеризуют ваши данные.
Поскольку человеческое понимание “центра” может разниться, статистика позаботилась определить каждый вариант. Таким образом мы имеем следующие общепринятые меры центральной тенденции:
-
Среднее арифметическое.
-
Медиана.
-
Мода.
В этой статье я расскажу, каким образом распределение вашего набора данных играет роль в выборе подходящей меры центральной тенденции. А объяснять я буду это на примере реальных наборов данных.
1. Среднее арифметическое
Среднее арифметическое — это среднее значение всех элементов в наборе данных. Оно рассчитывается как сумма всех значений, деленная на общее количество значений.
Среднее арифметическое = сумма всех значений / общее количество значений
Когда следует использовать среднее арифметическое?
Среднее арифметическое лучше всего использовать для описания данных, которые имеют нормальное распределение. Нормальное распределение — это когда построив график по “значениям” и их “частоте” (количеству появлений каждого значения в наборе данных), вы получаете кривую, по форме напоминающую колокол. Центр этой кривой совпадает со средним арифметическим.
Пример — набор данных с длинами крыльев комнатной мухи
В качестве примера я буду использовать реальный набор данных — это набор данных с длинами крыльев комнатной мухи, который естественным образом имеет нормальное распределение.
Источник набора данных: [Sokal, R.R. and F.J. Rohlf, 1968. Biometry, Freeman Publishing Co., p 109. Original data from Sokal, R.R. and P.E. Hunter. 1955. A morphometric analysis of DDT-resistant and non-resistant housefly strains Ann. Entomol. Soc. Amer. 48: 499-507.]
Набор данных содержит длины крыльев комнатной мухи в миллиметрах. В нем 100 элементов.
Я построил гистограмму (по “значениям” и “количествам повторений этих значений”) этих данных, которую вы можете наблюдать ниже. Если мы проведем по внешним краям столбцов плавную линию, то она образует колоколообразную кривую. Вычислив среднее арифметическое значение этих данных, мы получим 45,5. А теперь давайте поищем на приведенном ниже графике полученное значение 45,5. Он находится прямо по середине.
Колоколообразная кривая со средним значением в центре дает нам четкое понимание, что этот набор данных имеет нормальное распределение.
import numpy as np
import matplotlib.pyplot as plt
data_housefly = np.loadtxt("housefly_wing_length.txt")
plt.hist(data_housefly)
plt.xlabel("Wing length")
plt.ylabel("Number of occurences")
plt.title("Histogram - Housefly wing lengths")
plt.show()Это хороший пример, наглядно демонстрирующий, что для нормально распределенных данных имеет смысл использовать “среднее арифметическое” как меру центральной тенденции.
Когда НЕ стоит использовать среднее арифметическое?
Хотя среднее арифметическое является одной из основных мер центральной тенденции, иногда (на самом деле очень часто) оно наоборот может ввести вас в заблуждение. Данные из реального мира не всегда имеют нормальное распределение. В подавляющем большинстве случаев есть вероятность, что ваши данные ассиметричны.
Ассиметричные данные — это данные, в которых несколько элементов у верхнего или нижнего пределов имеют заметно отличающийся паттерн по сравнению с остальной частью набора данных.
Пример — набор данных с зарплатами игроков NBA
Давайте посмотрим на набор данных с зарплатами игроков NBA. Этот набор данных содержит зарплаты в долларах США за период с 2017 по 2018 годы.
Я построил гистограмму столбца c зарплатой (название столбца “season17_18”).
import numpy as np
import matplotlib.pyplot as plt
data_nba = pd.read_csv("NBA_player_salary.csv")
plt.hist(data_nba.season17_18)
plt.xlabel("Salary in US Dollars")
plt.ylabel("Number of occurrences")
plt.title("NBA Player Salary - Histogram")
plt.show()Глядя на приведенное выше распределение, становится очевидным, что данные распределены не нормально. Из 573 игроков более 300 получают зарплату ниже 2,5 миллионов долларов (из графика выше). Но когда мы вычисляем среднее арифметическое заработной платы, оно составляет 5,85 миллиона долларов.
Как вы считаете, годится ли среднее арифметическое в качестве лучшего представления этих данных в целом?
Уж точно нет. Те немногие игроки, которые получали огромные зарплаты, утащили среднее арифметическое далеко от центра. Это называется асимметрией данных.
Не имеет смысла и говорить о том, что среднее арифметическое, которое составляет 5,85 миллиона, является центром, потому что абсолютное большинство из игроков получили зарплату менее 2,5 миллиона долларов.
Таким образом, в случае подобных асимметрий наборов данных среднее арифметическое хорошим выбором для представления данных не является. Здесь нам может помочь медиана.
2. Медиана
Медиана — это значение, которое находится в центре (прямо посередине), если данные расположены в порядке возрастания или убывания.
Если общее количество значений в наборе данных нечетное, то в центральной позиции будет только одно число. Это и будет наша медиана. Если общее количество значений в наборе данных четное, в центральной позиции будет два значения. В этом случае медиана представляет собой среднее значение этих двух значений.
Когда следует использовать медиану?
Если набор данных асимметричен или содержит выбросы, среднее арифметическое — не лучший способ представления данных. В таком случае как меру центральной тенденции можно использовать медиану. Выбросы не портят медиану. Потому что само название “выбросы” означает, что они располагаются снаружи, либо в нижнем, либо в верхнем диапазоне. В таком случае медиана — это среднее значение, не нарушенное выбросами.
Еще раз давайте рассмотрим ассиметричный набор данных с зарплатами игроков NBA. (Который мы рассматривали в предыдущем разделе “Когда НЕ стоит использовать среднее арифметическое?”). Медиана по зарплате составляет 2,38 миллиона долларов.
Это значение находится в первой столбце. Обратите внимание, что ось X это 10^7. Итак, первый столбик представляет зарплату до 2,5 миллионов. Таким образом, медианное значение 2,38 миллиона лучше всего представляет эти данные, потому что большинство игроков получают зарплату, близкую к этому показателю.
Когда НЕ стоит использовать медиану?
Если и среднее арифметическое, и медиана одного и того же набора данных не сильно отклоняются, то можно использовать обе эти меры. В любом случае расчет среднего арифметического предполагает учет всех элементов данных и их усреднение. Таким образом, логичнее, что среднее арифметическое является более точной мерой (когда среднее арифметическое и медиана не сильно отклоняются).
Как определить, является ли ваш набор данных асимметричным или содержит выбросы?
Самый банальный способ определить, является ли ваш набор данных асимметричным или содержит выбросы, — это вычислить среднее арифметическое и медиану. Если обе меры не сильно отклоняются, то с вашим набором данных все в порядке. И вы сэкономили время, которое в противном случае было бы потрачено на очистку и преобразование данных.
Если среднее арифметическое и медиана очень сильно отклоняются, ваш набор данных асимметричен или содержит выбросы. Следующий шаг — провести исследование с целью выявить и удалить выбросы, если таковые имеются. Или применить какое-либо преобразование, чтобы уменьшить асимметрию в ваших данных, если таковая имеется.
3. Мода
Мода — это значение, которое чаще всего встречается в наборе данных. В гистограмме мода — это значение с самым высоким столбцом.
Если набор данных имеет более одного значения с одинаковой максимальной частотой появления, набор данных имеет мультимодальное распределение, поскольку он имеет несколько мод. Если в наборе данных нет повторяющихся значений, то и моды у него тоже нет.
Когда стоит использовать моду?
Моду можно использовать для анализа часто встречающихся значений как числовых, так и категориальных данных.
Мода — единственная мера центральной тенденции, которую можно использовать с категориальными данными. Для категориальных данных вы не можете вычислить среднее арифметическое или медиану. Мода — единственный выбор в таких случаях.
Пример — Простое перечисление
Ниже приведен учебный набор данных, отражающий любимый вид искусства семерых человек. Построим частотный график (гистограмму).
data_art = [‘music’, ‘painting’, ‘pottery’, ‘painting’, ‘dance’, ‘music’, ‘music’]
import matplotlib.pyplot as plt
data_art = ['music', 'painting', 'pottery', 'painting', 'dance', 'music', 'music']
plt.hist(data_art)
plt.xlabel("Favorite art")
plt.ylabel("Number of occurrences")
plt.title("Histogram of favorite art")
plt.show()Во многих областях машинного обучения возникают функции многих переменных и их производные. Такие производные ещё называют «матричными». На открытом уроке мы поговорим про отличие таких производных от обычных, изучаемых в школе, разберём необходимую теорию, научимся такие производные считать, а также посмотрим, где и как матричные производные используются. Регистрация открыта по ссылке для всех желающих.
Гистограмма
Основу
любого исследования составляют данные,
полученные в результате контроля и
измерения одного или нескольких
параметров изделия (характеристики
качества). Во всех отраслях промышленности
требуется проведение анализа точности
и стабильности процесса, наблюдение за
качеством продукции, отслеживание
существенных показателей производства.
Путем измерения соответствующих
параметров необходимыми средствами
получают ряд данных, представляющих
собой неупорядоченную последовательность
значений параметра, на основе которых
невозможно сделать корректные выводы.
Поэтому для осмысления качественных
характеристик изделий, процессов,
производства (статистических данных)
часто строят гистограмму распределения.
Гистограмма
– это инструмент, позволяющий зрительно
оценить распределение статистических
данных, сгруппированных по частоте
попадания данных в определенный (заранее
заданный) интервал.
Гистограмма – это столбиковая диаграмма,
служащая для графического представления
имеющейся количественной информации,
собранная за длительный период времени
(неделя, месяц, год и т.д.), которая дает
важную информацию для оценки проблемы
и нахождения способов ее решения.
Гистограмма
применяется главным образом для анализа
значений измеряемых параметров.
Общий порядок построения гистограмм
следующий:
1. Собираются
данные контролируемого параметра (xi
) за определенный период (месяц, квартал,
год и т.д.). Число данных должно быть не
менее 30-50, оптимальное число порядка
100.
2. Определяются наибольшее Xmax
и наименьшее Хmin
значения из всех полученных данных и
вычисляется размах R:
R= Xmax
— Хmin
Размах характеризует разброс контролируемой
величины, он определяет ширину гистограммы.
3. Полученный диапазон (размах) делится
на несколько интервалов. Число интервалов
k зависит от общего числа
собранных данных n и
некоторых других факторов. Рекомендуется
использовать формулу Стерджесса:
k = 1 + 3,322 · lg
n
Также
можно использовать формулу:
k =
± 2
4. Далее определяют ширину интервала:
R / k = (
xmax
-xmin)
/ k.
Все полученные данные распределяют по
интервалам. Если какое-то значение
попадает на границу, его следует относить
к левому по отношению к ней интервалу.
Подсчитывается число значений, попавших
в каждый интервал mj,
где j-номер интервала.
5
.
Для каждого интервала подсчитывается
относительная частота попадания в него
данных:
-
По
полученным данным строится гистограмма
— столбчатая диаграмма, высота столбиков
которой соответствует частоте или
относительной частоте попадания данных
в каждый из интервалов.
Рассмотрим пример построения гистограммы.
В результате наблюдений получено 90
значений показателя качества (табл.4).
Таблица 4
|
77,2 |
86,4 |
86,0 |
76,3 |
68,4 |
63,9 |
|
77,5 |
93,4 |
75,8 |
91,1 |
74,9 |
61,8 |
|
91,5 |
74,1 |
86,9 |
78,0 |
72,2 |
84,2 |
|
83,5 |
88,5 |
78,6 |
82,4 |
76,6 |
86,3 |
|
61,9 |
71,8 |
69,8 |
77,1 |
82,4 |
76,7 |
|
58,7 |
68,3 |
73,0 |
82,4 |
78,7 |
69,8 |
|
87,9 |
62,4 |
67,7 |
63,8 |
74,8 |
71,3 |
|
80,2 |
77,3 |
76,0 |
91,5 |
51,2 |
74,8 |
|
77,4 |
80,9 |
67,0 |
72,5 |
85,9 |
66,6 |
|
77,8 |
84,1 |
79,2 |
88,4 |
72,3 |
69,4 |
|
91,7 |
79,0 |
101,0 |
74,7 |
71,5 |
97,7 |
|
87,0 |
70,6 |
89,3 |
87,5 |
95,6 |
85,9 |
|
54,5 |
75,6 |
70,9 |
83,7 |
72,9 |
92,6 |
|
93,9 |
77,1 |
76,3 |
94,9 |
78,5 |
82,9 |
|
73,8 |
79,1 |
90,8 |
92,7 |
61,6 |
80,6 |
1. Находим наибольшее
и наименьшее значения:
Xmax
= 101,0; Хmin
= 51,2.
2. Размах равен:
R
= 101,0 — 51,2 = 49,8.
3. Выбираем количество
интервалов равное 9 (k
= 9).
4. Находим ширину
интервала: R/k
= 49,8/ 9 = 5,53. Для удобства построения
выбираем ширину интервала – 5,6.
Границы
интервалов устанавливаем следующими:
левая граница первого интервала 51,0
(меньше Хmin),
правая отстоит на ширину интервала
(5,56) и составляет 56,6. Последующие границы:
62,2; 67,8; 73,8 и т.д. Правая граница последнего
интервала 101,4, что больше наибольшего
из имеющихся значений.
5. Определяем частоту
каждого интервала. В первый интервал
попало два значения, во второй — четыре
и т.д. Результаты сводим в табл. 5.
Таблица 5
-
Номер интервала, i
Границы интервала
Частота, mj
Относительная частота f*(x)
Накопленная частота F*(x)
1
51,056,6
2
0,022
0,02
2
56,662,2
4
0,044
0,07
3
62,267,8
6
0,067
0,13
4
67,873,4
15
0,167
0,30
5
73,479,0
25
0,278
0,58
6
79,084,6
13
0,144
0,72
7
84,690,2
12
0,133
0,86
8
90,295,8
11
0,122
0,98
9
95,8101,4
2
0,022
1,00
(a)Всего
90
1,000
6. Вычисляем относительную
частоту попадания данных в каждый
интервал:
для
первого интервала: f*(x)
= 2 / 90 = 0,022;
для
второго: f*(x)
= 4 / 90 = 0,044;
и т. д.
7. Вычисляем накопленную
относительную частоту, прибавляя каждое
последующее значение относительной
частоты к сумме предыдущих значений.
Строим гистограмму
распределения. Вид полученной гистограммы
приведен на рис.13.
30
25
20
15
10
5
0
51.0
56.6
62.2
67.8
73.4
79
84.6
90.2
95.8
Рис.13 Гистограмма распределения значений
показателя качества
График
накопленной относительной частоты, т.
е. интегральную функцию распределения,
представлен на рис.14.
Полезную
информацию о возможном характере
распределения можно получить, взглянув
на рис.15. Формы, представленные на этом
рисунке, типичны, и ими можно воспользоваться
как образцами при анализе процессов.

Рис.14 Интегральная
функция распределения
а) Обычный тип (симметричный).
Гистограмма с таким распределением
встречается чаще всего. Она указывает
на стабильность процесса.

Рис.15а
б)
Гребенка (мультимодальный тип).
Здесь классы через один имеют более
низкие частоты. Такая форма встречается,
когда число единичных наблюдений,
попадающих в класс, колеблется от класса
к классу или, когда действует определенное
правило округления данных.

Рис.15б
в)
Положительно (отрицательно) скошенное
распределение. Среднее значение
гистограммы локализуется слева (справа)
от центра размаха. Частоты довольно
резко спадают при движении влево (вправо)
и, наоборот, медленно вправо (влево).
Такая (асимметричная) форма встречается,
когда невозможно получить значения
ниже определенного, например для диаметра
деталей и т.д.

Рис.15в
г)
Распределение с обрывом слева
(справа). Это одна из тех форм, которые
часто встречаются при 100%-ном контроле
изделий из-за плохой воспроизводимости
процесса, а также когда, например,
отобраны и исключены из партии все
изделия с параметрами ниже контрольного
нормативы (или выше, или и те и другие).

Рис.15г
д) Плато
(равномерное и прямоугольное распределение).
Такая гистограмма получается в случаях,
когда объединяются несколько распределений,
в которых средние значения имеют
небольшую разницу между собой. Анализ
такой гистограммы целесообразно
проводить, используя метод расслоения.

Рис.15д
е)
Двухпиковый тип (бимодальный тип).
Такая форма встречается, когда смешиваются
два распределения с далеко отстоящими
средними значениями, например, в случае
наличия разницы между двумя видами
материалов, двумя операторами и т.д. В
этом случае можно провести расслоение
по двум видам фактора, исследовать
причины различия и принять соответствующие
меры для его устранения.

Рис.15е
ж)
Распределение с изолированным пиком.
Рядом с распределением обычного типа
появляется маленький изолированный
пик. Это форма появляется при наличии
малых включений данных из другого
распределения, появления ошибки измерения
или просто включения данных из другого
процесса. По результатам анализа
гистограммы дают заключение о необходимости
настройки измерительного прибора или
срочного осуществления контроля
процесса.

Рис.15ж
Если
имеется допуск, то необходимо нанести
на гистограмму границы допуска (SL
– нижняя граница допуска, SU
.- верхняя граница допуска), чтобы
сравнить распределение с этими границами.
Существует пять типичных случаев,
показанных на Рис. 16. Используйте их для
справок при оценивании популяций.
С
лучаи,
в которых гистограмма удовлетворяет
допуску:
Случаи, в которых гистограмма не
удовлетворяет допуску:
Рис. 16 Гистограммы и границы поля допуска
(SL —
нижняя граница поля допуска, Su-
верхняя граница поля допуска)
Если гистограмма удовлетворяет допуску,
то в случаях:
а) поддержание существующего состояния
– это все, что требуется, поскольку
гистограмма вполне соответствует
допускам;
б) допуски удовлетворяются, но нет
никакого запаса, поэтому необходимо
сократить разброс до меньшего значения.
Когда гистограмма не удовлетворяет
допуску, то в случаях:
в) необходимо добиться смещения среднего
ближе к центру поля допуска;
г) требуются действия, направленные на
снижение вариации;
д) одновременно требуются меры, описанные
в пунктах в) и г).
Распределения различных эмпирических
данных чаще всего строятся в виде
гистограмм, а иногда в виде полигона. В
случае полигона ординаты, пропорциональные
частотам интервалов, восстанавливаются
перпендикулярно оси абсцисс в точках
соответствующих серединам данных
интервалов. Вершины ординат соединяются
прямыми линиями. Для замыкания кривой
крайние ординаты соединяются с близлежащей
серединой интервала, в которой частота
равна 0 (Рис. 17).
f*(x)
0,30
0,20
0,10
0
5,4
5,5
5,3
5,1
5,2
5,0
x
Рис. 17 Полигон
Обычно
значения случайных величин не являются
совершенно произвольными. Каждое
значение может появиться с некоторой
вероятностью. Зависимость, связывающая
значения случайной величины с вероятностью
их появления, называется законом
распределения случайной величины. Зная
закон распределения, можно заранее
предсказать, что те или иные значения
этой величины могут появиться с той или
иной вероятностью. Законы распределения
определяются физическим содержанием
случайной величины и для многих случаев
они могут быть найдены в результате
теоретического анализа. Однако при
таком анализе не могут быть учтены
многочисленные факторы, неизбежно
оказывающие влияние на эту величину.
Поэтому реальные законы распределения
всегда несколько отличаются от
теоретических. Знание законов распределения
бывает необходимо для принятия
определенных решений по управлению
процессами.
Закон
распределения может быть представлен
в виде вероятности того, что случайная
величина примет значение не большее,
чем данная величина. Это так называемая
интегральная форма закона. Возможна
также форма дифференциальная,
представляющая собой плотность
вероятности случайной величины —
отношение частоты попадания случайной
величины в некоторый диапазон ее
изменения к величине этого диапазона.
Зависимость плотности распределения
от значений случайной величины, то есть
дифференциальная форма закона более
наглядна и применяется чаще.
Вид закона
распределения может в некоторых случаях
быть представлен теоретически, но часто
это сделать не удается. Кроме того, во
многих случаях на практике имеются
отклонения от теоретического закона.
Как же определить действительный,
реальный закон распределения. Сделать
это можно путем построения диаграммы
распределения частоты появления
случайной величины по результатам
наблюдений, то есть гистограммы.
Всякая гистограмма строится на основе
некоторого числа данных. Но что произойдет
с гистограммой, если мы будем наращивать
число данных? Если интервал класса по
мере роста числа данных будет все меньше
и меньше, то сглаженная кривая распределения
частот получится как предел распределения
относительных частот.
Есть множество видов распределений.
Рассмотрим наиболее широко встречающиеся
теоретические законы распределения
случайных величин.
Нормальному распределению (распределению
Гаусса), самому типичному распределению,
подчиняются случайные величины, на
которые оказывают влияние многочисленные
примерно равные по силе воздействия
факторы.
Наиболее вероятными являются значения
вблизи средней величины. Вероятность
больших отклонений мала. Этому закону
подчиняются размеры деталей, обрабатываемых
в одинаковых условиях, результаты
многократных измерений при отсутствии
систематических погрешностей и многие
другие величины.
Вершина кривой нормального распределения
лежит над абсциссой, соответствующей
математическому ожиданию. Кривая
симметрична, имеет форму колокола и
асимптотически приближается к оси
абсцисс. Колоколообразная кривая имеет
две точки перегиба, расстояние от которых
до ординаты вершины, т. е. до вертикали,
проведенной через математическое
ожидание, равно среднему квадратичному
отклонению. Расстояние между двумя
точками перегиба равно 2сигма. Таким
образом, в случае нормального распределения
среднее квадратичное отклонение можно
представить наглядно (Рис. 18).
68.26%
95.44%
99.73%
-3
-2
-1
+1
+2
+3
Рис.18. Нормальное
распределение.
Когда выяснено, что гистограмма следует
гауссовскому (нормальному) закону
распределения, становится возможным
исследование воспроизводимости процесса,
т.е. определяется неизменность основных
параметров процесса: среднего значения
Х или математического
ожидания М(х) и стандартного отклонения
во времени. Оно важно при оценке процесса
с помощью выборочных данных, когда
требуется выяснить вероятность
пересечения распределения генеральной
совокупности, границ поля допуска и
появления в связи с этим несоответствия
требованиям потребителя (пользователя).
Если процесс имеет нормальное
распределение, то не представляет труда
определить возможность выхода
распределения генеральной совокупности
при заданных значениях М(х) и
исходя из сравнения соответствующих
трехсигмовых пределов и пределов поля
допуска.
Величина
площади под кривой Гаусса при различных
границах изменения
случайной
величины представлены в табл.6.
Таблица 6
|
Границы изменения случайной величины |
Площадь под кривой Гаусса |
|
Односигмовые М(х)-; |
0,6826 |
|
Двухсигмовые М(х)-2; |
0,9544 |
|
Трехсигмовые М(х)-3; |
0,9973 |
Полученные результаты истолковываются
следующим образом. Если 68,26%, т.е. примерно
2/3 значений лежат между границами
— и
+ , то 31,74% всех
наблюдений следует ожидать за этими
границами, а именно: 15,87% — за границей
+ и 15,87% за границей
—
в силу симметричности нормального
распределения.
Границы — 2
и + 2
охватывают 95,44% всех значений, а вне этих
границ находятся по 2,28% значений (за
границей + 2
и — 2),
т.е. всего 4,56%.
Между 3 границами
( — 3;
+ 3)
находится 99,73% всех наблюдений, т.е.
практически все значения. Только 0,27%
значений находятся за границами, а
именно: 0,135% за границей
+ 3 и 0,135% за
— 3.
Таким образом,
теоретически нормальная переменная
может принимать любое значение от -
до +, однако вероятность
попадания в 3 границы
составляет 99,7%. Это означает, что на
практике мы можем пренебречь шансами,
что X окажется за пределами3
границ – это правило служит основанием
для определения контрольных пределов
в контрольных картах (по количественному
признаку).
Равномерное (равновероятное) распределение
наблюдается в случаях, когда на случайную
величину решающее влияние оказывает
величина, также распределенная равномерно,
а так же в случаях, когда ни одно из
значений случайной величины не имеет
преимущества перед другими.
Треугольное распределение (распределение
Симпсона) возникает, если рассматривается
сумма или разность двух равномерно
распределенных случайных величин.
Экспоненциальное распределение
характерно для величины наработки
изделий до отказа, если отказы происходят
с равной вероятностью (одинаковой
интенсивностью) в течении всего срока
службы (например, за счет скрытых дефектов
или случайных отклонений в технологии).
Логарифмически нормальное распределение
характерно для времени простоя некоторых
видов оборудования, для оценки потребности
в различных типоразмерах изделий,
усталостной долговечности деталей.
Биноминальное распределение обобщает
различные случаи оценки доли бракованных
изделий в партии при контроле по
альтернативному признаку (годен — не
годен). Частными случаями его являются
гипергеометрическое и распределение
Пуассона, описывающее вероятность
редких событий.
С нормальным
распределением связан еще ряд специальных
распределений, описывающих поведение
случайных величин различных типов. На
практике часто встречаются комбинации
различных законов, а так же различные
усечения их, обусловленные физической
природой явлений. Однако, хотя в чистом
виде эти законы практически никогда не
проявляются из-за неизбежных отклонений,
называемых действием случайных факторов,
их использование чрезвычайно полезно,
так как позволяет прогнозировать
возможные значения случайной величины,
что необходимо при принятии управленческих
решений.
На практике даже если закон распределения
точно известен, бывают неизвестны его
параметры. Поэтому для определения
закона и его параметров проводятся
статистические наблюдения, по результатам
которых строят эмпирические распределения.
По их виду судят о характере закона
распределения и при необходимости
подбирают параметры теоретического
закона, соответствующие полученным
экспериментальным результатам.
Распределение
случайной величины может быть представлено
не только в виде графика функции или
плотности распределения, но и в виде
чисел, отражающих наиболее существенные
особенности случайной величины. Оценки
случайной величины с помощью чисел
называются точечными оценками.
Наиболее
употребительными точечными оценками
являются: среднее арифметическое, мода,
медиана, размах, среднее квадратичное
отклонение. Они показаны на рис. 19.
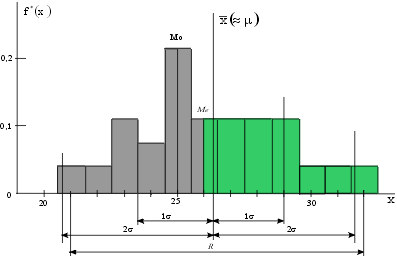
Рис.19 Точечные
характеристики статистического
распределения случайной величины:
среднее арифметическоеХ,
мода М0,
медиана Ме, размах R,
среднее квадратичное отклонение
Среднее
арифметическое (выборочное среднее
арифметическое) — средняя величина,
получаемая из всех имеющихся результатов
по формуле:
n
Х = 1/N*Хi,
где
i=1
i
— порядковый номер значения случайной
величины;
n
— общее число ее значений.
Следует подчеркнуть, что средняя только
в том случае является обобщающей
характеристикой, когда она применяется
к однородной совокупности статистического
материала.
Кроме важнейшей
характеристики положения — средней
арифметической при анализе и контроле
процесса необходимо работать и с другими
характеристиками положения, в частности
с медианой и модой случайной величины.
Медиана — среднее значение в выборке.
Если полученные при измерениях значения
расположить в возрастающем или убывающем
порядке, то медианой будет значение,
занимающее серединное значение в ряду.
Таким образом, медиана — это значение
параметра, которое делит упорядоченный
ряд на две равные по объему группы. То
есть, вероятность того, что случайная
величина может оказаться меньше медианы,
равна вероятности, что она окажется
больше ее. При абсолютной симметрии
правой и левой стороны распределения
медиана и среднее арифметическое
совпадают.
Мода — это наиболее часто встречающееся
значение случайной величины. Возможно,
что среди полученных значений имеется
не одна, а две или более мод. Такое
распределение называют двумодальным
или полимодальным. Возможно, что
распределение не имеет моды, это
равномерное распределение.
Нередко встречаются антимодальные
распределения, имеющие в середине
диапазона полный или частичный провал
плотности распределения. На практике
антимодальные распределения могут
возникнуть, если из выборки извлекается
ее средняя по вероятности часть. Например,
из выборки деталей, размеры которых
распределены по нормальному закону,
извлекаются только детали, имеющие
наименьшие отклонения от среднего
значения, тогда остающиеся детали будут
иметь размеры, определенные по
антимодальному распределению.
Двумодальное распределение может
возникнуть, если рассматривается
смешение двух выборок, имеющих нормальные
распределения.
Размах (R) — это
разность между наибольшим и наименьшим
значениями в выборке. Размах характеризует
разброс случайной величины.
Лучшей, чем размах, более эффективной
оценкой разброса является дисперсия
Dх = x2
и среднее квадратичное отклонение x.
Дисперсия представляет собой среднее
значение квадратов отклонений каждого
значения случайной величины от среднего
арифметического. Вообще говоря, дисперсия
определяется для всей генеральной
совокупности и является понятием
теоретическим. На практике определяется
выборочная дисперсия, которая вычисляется
по следующей формуле:
n
Sx2
= 1/(n-1)(Xi
-X)2
i=1
По мере увеличения числа наблюдений
выборочная дисперсия приближается к
своему теоретическому значению —
дисперсии генеральной совокупности
x2.
Среднее квадратичное отклонение и
выборочное среднее квадратичное
отклонение представляют собой
корень квадратный из соответствующих
дисперсий:
.
Когда выясняется, что гистограмма
следует нормальному распределению,
часто предпринимается исследование
воспроизводимости процесса, т.е.
определяется неизменность основных
параметров процесса: среднего
значения
и стандартного отклонения во времени
. Оно важно при
оценке того, сможет ли процесс пересечь
границы поля допуска или нет и появления
в связи с этим несоответствия требованиям
потребителя. Если допустить, что процесс
имеет нормальное распределение, то
можно сразу же определить процент
дефектов, оказавшихся за данными
границами допуска при данных параметрах
(
,s).
Но более полезно оценить процесс с
помощью СР—индекса
воспроизводимости процесса (индекс
возможностей). Приведем определение
СР.
При двусторонних границах допуска
(SU
или SL
– значения верхней и нижней границ
допуска):
.
При односторонних границах допуска
(SU
или SL):
или
.
Исследование воспроизводимости процесса
с помощью СР позволяет
оценить качество процесса в соответствии
с требованиями потребителя. Чем больше
величина СР, тем выше
качество процесса и тем меньше вероятность
несоответствия его выхода ожиданиям
потребителя.
Точность технологического процесса
оценивают, исходя из следующих критериев:
1. В случае, когда СР1,67,
ширина интервала между контрольными
нормативами не менее чем в 10 раз превышает
стандартное отклонение s;
разброс параметров изделия невелик,
появление брака не угрожает.
2. В случае, когда 1,67СР1,33,
ширина интервала между контрольными
нормативами в 8-10 раз превышает стандартное
отклонение s.
Идеальное состояние процесса.
3. В случае, когда 1,33СР1,00,
ширина интервала между контрольными
нормативами в 6-8 раз превышает стандартное
отклонение s.
Когда показатель СР
близок к 1, вероятность появления
брака составляет 0,27%, поэтому необходимо
усилить контроль процесса, провести
анализ факторов, влияющих на разброс,
и провести мероприятия по улучшению
состояния процесса.
4. В случае, когда 1,00СР0,67,
ширина интервала между нижней и верхней
границами нормы всего лишь в 4-6 раз
превышает стандартное отклонение s.
Когда показатель СР
приближается к 0,67, вероятность появления
брака составляет 4,56%. Это означает, что
контроль процесса не удовлетворителен.
Необходимо наладить строгий контроль
процесса и провести сплошной контроль
выпускаемых изделий с целью недопущения
брака.
5. В случае, когда 0,67СР,
ширина интервала между нижней и верхней
границами нормы не превышает 4s.
Процент брака превышает 4,56%. О таком
процессе можно сказать, что он
неконтролируем. Необходимо провести
сплошной контроль продукции, чтобы
предотвратить выпуск бракованных
изделий.
Выбирать оборудование необходимо так,
чтобы поле допуска на изготавливаемые
изделия составляло 7 или 8 единиц его
стандартного отклонения. Если такого
оборудования нет, то необходимо
пересмотреть нормы на процент брака,
который должен быть установлен более
0,27%.
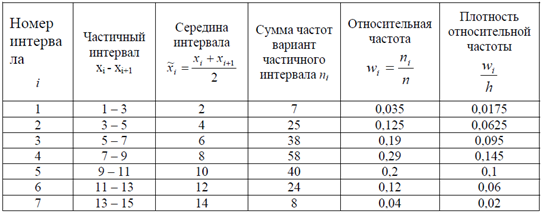
Построить гистограмму частот. Найти несмещенные оценки генеральной средней и генеральной дисперсии.
Дана таблица:
Задание:
1) построить гистограмму частот. Найти несмещенные оценки генеральной средней и генеральной дисперсии;
2) используя результаты пункта 1, обосновать гипотезу о нормальном распределении генеральной совокупности. Записать выражение соответствующего теоретического распределения;
3) вычислить для всех интервалов значений X соответствующие вероятности и теоретические частоты, используя критерий Пирсона (с уровнем значимости α = 0,1). Проверить обоснованную выше гипотезу;
4) в предположении, что выборка извлечена из нормально распределенной генеральной совокупности, найти доверительный интервал, заключающий генеральную среднюю признака с надежностью γ = 0,98.
Решение:
1) Объем выборки Величины всех интервалов одинаковы и равны h = 2 .
Для построения гистограммы частот составим таблицу.
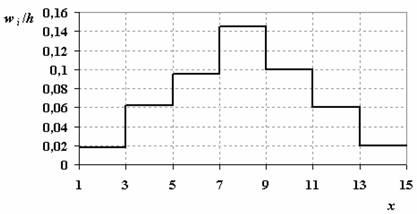
Гистограмма частот имеет следующий вид:
Несмещенные оценки генеральной средней B x и генеральной дисперсии s2 случайной величины Х найдем по формулам: , где где xi – середина i-го интервала; m = 7.
Подставив данные из последней таблицы в расчетные формулы, получим:
Определим также среднеее квадратическое отклонение s случайной величины Х по формуле:
2) Рассмотрение полученной гистограммы частот позволяет предположить гипотезу о нормальном распределении генеральной совокупности. Выражение
плотности соответствующего теоретического распределения имеет вид
3) Проверить предложенную выше гипотезу о нормальности распределения, используя критерий Пирсона (с уровнем значимости α = 0,1).
Для расчета вероятностей pi попадания случайной величины X в интервалы используем функцию Лапласа в соответствии со свойством
нормального распределения:
и, соответствующая первому интервалу теоретическая частота 200 0,0326 6,515 1 np = ⋅ = и т.д.
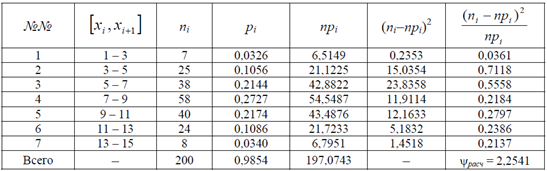
Для определения расчетной статистики удобно составить таблицу:
Итак, расчетное значение статистики = 2,254. Поскольку число интервалов m = 7, а нормальный закон распределения определяется S = 2 параметрами,
то число степеней свободы k = m − S −1 = 7 − 2 −1 = 4 . Соответствующие верхнее и нижнее критические значения статистики определим из статистической
таблицы:
Т.к. , гипотеза о выбранном теоретическом нормальном законе с параметрами a = 8,03 ; s = 2,867 согласуется с опытными данными.
4) Доверительный интервал для генеральной средней равен
Подставив исходные данные, получим:
Отсюда доверительный интервал, заключающий генеральную среднюю признака с надежностью γ = 0,98, равен
Если испытываете трудности в написании контрольной работы по статистике, оформите заявку и Вы узнаете сроки и стоимость работы. Цена — от 99 рублей.
При обработке большого числа экспериментальных данных их предварительно группируют и оформляют в виде так называемого Интервального ряда.
Пример 1. Средняя месячная зарплата за год каждого из пятидесяти случайно отобранных работников хозяйства такова:
317 304 230 285 290 320 262 274 205 180 234 221 241 270 257 290 258 296 301 150 160 210 235 308 240 370 180 244 365 130 170 250 370 267 288 231 253 315 201 256 279 285 226 367 247 252 320 160 215 350.
Здесь переменной величиной X является средняя месячная зарплата. Как видно из приведенных данных, наименьшее значение величины Х равно 130, а наибольшее — 370. Таким образом, диапазон наблюдений представляет собой интервал 130 – 370, длина которого равна 370 – 130 = 240.
Разобьем диапазон наблюдений на части (разряды) Так, чтобы каждый разряд содержал несколько экспериментальных данных. Например, разделим интервал 130 – 370 на 6 равных частей, тогда длина каждого разряда будет 40. Границами разрядов будут числа 130, 170, 210, 250, 290, 330, 370 (рис. 3).
Подсчитаем число значений, попавших в каждый разряд. Например, в первый разряд попадают следующие числа: 150 (1 раз), 160 (2 раза), 130 (1 раз), 170 (1 раз). Поскольку число 170 находится на границе между первым и вторым разрядами, мы включим его и в первый и во второй разряды, но с кратностью 1/2. Сложив кратности, мы получим Абсолютную частоту первого разряда:
M1 = 1 + 2 + 1 + 0,5 = 4,5.
Разделив абсолютную частоту на число П всех наблюдений, получим Относительную частоту Попадания величины Х в первый разряд:
Проделав вычисления для всех разрядов, мы получим следующую таблицу.
Таблица 6
Здесь Mi — абсолютные частоты, — относительные частоты. Табл. 6 называется Интервальным рядом.
Сумма всех абсолютных частот равна числу всех приведенных в табл. 6 значений переменной величины:
4,5 + 5 + 12 + 14,5 + 9 + 5 = 50.
Это свойство используется для проверки правильности вычислений. Из него следует, что сумма всех относительных частот равна единице:
0,09 + 0,10 + 0,24 + 0,29 + 0,18 + 0,10 = 1.
Интервальный ряд изображают графически в виде Гистограммы, которая строится так. Сначала вычисляют плотности частот H1, H2, H3, … , разделив относительную частоту каждого разряда на его длину:
Затем выбирают на плоскости систему координат и откладывают на оси Х значения 40, 80, 120, … , соответствующие границам разрядов. На каждом из отрезков длины 40, как на основании, строят прямоугольник, высота которого равна плотности частоты соответствую щего разряда. Полученная фигура и называется Гистограммой. Она изображена на рис. 4.
Заметьте, что высоты H1, H2, … , H6 прямоугольников, образующих гистограмму, выбраны так, что их площади будут , т. е. равны соответствующим относительным частотам. Отсюда вытекает такое правило:
Для того, чтобы найти долю тех значений величины. X, которые попадают в некоторый интервал, нужно найти площадь той части гистограммы, основанием которой является данный интервал.
Определим, например, долю значений величины X, Принадлежащих интервалу 210 – 300. Для этого вычислим площадь фигуры с основанием 210 – 300 (на рисунке она выделена штриховкой). Площади первых двух прямоугольников, составляющих фигуру, равны соответственно = 0,24 и
= 0,29; площадь третьего равна 10 • 0,0045 = 0,045. Сумма площадей 0,24 + 0,29 + 0,045 = 0,575 и дает нужное число. Иными словами, 57,5% значений величины Х находится в границах от 210 до 300.
Как мы заметили в начале параграфа, интервальный ряд составляют при обработке больших массивов информации. В таких случаях, как правило, отдельные значения величины Х не фиксируются, а подсчитывается количество ее значений, попавших в каждый разряд (т. е. абсолютные частоты). Поэтому исследователь не знает отдельных значений наблюдаемой величины Х и не может воспользоваться формулами (1), (5) и (7) для вычисления среднего арифметического, дисперсии и среднего квадратического отклонения. Но приближенное значение этих числовых характеристик можно найти с помощью интервального ряда. Для этого сначала находят середины разрядов: (здесь K — Число всех разрядов интервального ряда); затем проводят вычисления по следующим формулам:
Результаты расчетов по данным табл. 6 сведены в следующую таблицу:
Таблица 7
В первом столбце записаны номера разрядов, во втором — числа (середины разрядов), в третьем — произведения
, и т. д. Таблица заполняется по столбцам. Середину разряда вычисляем как полусумму его границ:
Согласно формуле (8), сумма чисел третьего столбца дает среднее арифметическое = 256,8. Оно записано в последней строке этого столбца. Сумма чисел последнего столбца равна дисперсии D = 3113,75 [см. формулу (9)]. Наконец, по формуле (10) определяем среднее квадратическое отклонение S =
= 55,80.
Интервальный ряд, гистограмма и числовые характеристики, найденные по формулам (8)—(10), составляют Математическую модель средней заработной платы. Она используется при проведении различных социологических исследований, например, при определении уровня жизни работников какой-либо отрасли.
ТИПОВЫЕ ЗАДАНИЯ
1. Для проведения демографических исследований выбрали 50 семей и получили следующие данные о количестве членов семьи:
2 5 3 4 1 3 6 2 4 3 4 1 3 5 2 3 4 4 3 3 2 5 3 4 4
3 3 4 4 3 2 5 3 1 4 3 4 2 6 3 2 3 1 6 4 3 3 2 1 7.
Укажите переменную величину; составьте табл. 5; найдите числовые характеристики — среднее арифметическое, дисперсию, среднее квадратическое отклонение.
2. Управление сельского хозяйства Дрюковского района представило сводку по пятидесяти хозяйствам. Согласно этой сводке, урожайность ржи в них составила (в центнерах с гектара):
17.5 17.8 18.6 18.3 19.1 19.9 20.6 20.1 22 21.4 17.5 18.5 19 20 22 20.6 19.1 18.6 17.9 19.1 22 19 17.5 22 22.6 21 21.4 19 17.8 18.3 19.9 20.1 21.4 18.5 20 20.6 18.6 21.4 21 20 20 18 18 18 17.5 18.6 19.1 20.6 17.5 18.6 .
Постройте интервальный ряд (табл. 6), гистограмму, составьте табл. 7 и по формулам (8)-(10) найдите числовые характеристики — среднее арифметическое, дисперсию, среднее квадратическое отклонение.
| < Предыдущая | Следующая > |
|---|