Меры центральной тенденции.
До сих пор мы обсуждали методы, которые мы можем использовать для организации и представления финансовых данных с целью того, чтобы они были более понятными.
Например, частотное распределение доходности класса активов показывает характер рисков, с которыми инвесторы могут столкнуться в конкретном классе активов. Гистограмма годовой доходности S&P 500 ясно показывает, что большие положительные и отрицательные значения годовой доходности являются обычной ситуацией.
Хотя таблицы частотных распределений и гистограммы предоставляют собой удобный способ обобщить серии наблюдений, эти методы являются лишь первым шагом к описанию финансовых данных.
В этом разделе мы обсудим использование количественных показателей, которые объясняют характеристики данных. Наше внимание сосредоточено на мерах центральной тенденции и других показателях (или параметрах), характеризующих положение данных.
Показатель или мера центральной тенденции (англ. ‘measure of central tendency’) указывает, насколько центрированы финансовые данные.
Меры центральной тенденции, вероятно, используются более широко, чем любые другие статистические показатели, потому что их легко рассчитать и применить. Меры положения (англ. ‘measures of location’) включают в себя не только меры центральной тенденции, но и другие показатели, которые иллюстрируют местоположение или распространение данных в рамках распределения.
Далее мы рассмотрим общепринятые меры центральной тенденции — среднее арифметическое, медиану, моду, взвешенное среднее и среднее геометрическое. Мы также объясняем другие полезные меры положения, включая квартили, квинтили, децили и процентили.
Среднее арифметическое.
Финансовые аналитики и портфельные менеджеры часто хотят получить одно число, которое репрезентативно описывает возможный исход инвестиционного решения. Среднее арифметическое — безусловно, наиболее часто используемая мера середины или центра данных.
Определение среднего арифметического.
Среднее арифметическое (англ. ‘arithmetic mean’) — это сумма наблюдений, деленная на количество наблюдений.
Мы можем вычислить среднее арифметическое как для совокупностей, так и для выборок. Эти показатели известны как среднее по совокупности и выборочное среднее значение соответственно.
Среднее значение для совокупности.
Среднее значение для совокупности (математическое ожидание или среднее по совокупности, от англ. ‘population mean’) — это среднее арифметическое значение, рассчитанное для совокупности.
Если мы можем адекватно определить совокупность, то мы можем рассчитать среднее значение для совокупности как среднее арифметическое всех наблюдений или значений в совокупности.
Например, аналитики, изучающие годовой рост продаж крупных оптовых клубов в США за 2013 финансовый год, могут определить интересующую совокупность, включив в нее только три компании: BJ’s Wholesale Club (частная компания с 2011 г.), Costco Wholesale Corporation. и Sam’s Club, входящую в группу Wal-Mart.
Оптовый клуб (англ. ‘wholesale club’) — это формат магазина, предназначенного в основном для оптовых продаж в торговых точках размером со склад для клиентов, которые платят членские взносы. По состоянию на начало 2010-х годов эти три оптовых клуба доминировали в данном сегменте в Соединенных Штатах.
В качестве другого примера можно привести портфельного менеджера, специализирующегося на индексе Nikkei 225. Интересующая его совокупность включает 225 акций из первой секции Токийской фондовой биржи, которые формируют индекс Nikkei.
Формула среднего значения для совокупности.
Среднее по совокупности, ( bf mu), является средним арифметическим значением совокупности.
Для конечной совокупности используется следующая формула среднего значения:
(large{ mu = {dsum_{i=1}^{N}X_i over N} }) (Формула 2)
где:
- (N) — количество наблюдений во всей совокупности, а
- (X_i) — (i)-е наблюдение.
Среднее по совокупности является примером статистического параметра. Среднее значение для совокупности уникально; то есть, данная совокупность имеет только одно среднее значение.
Чтобы проиллюстрировать расчеты по приведенной формуле, мы можем найти среднее по совокупности для доли прибыли в выручке американских компаний, управляющих крупными оптовыми клубами за 2012 год.
В течение года прибыль в процентах от выручки для оптовых клубов BJ, Costco Wholesale Corporation, и Wal-Mart Stores составляли 0,9%, 1,6% и 3,5% соответственно, согласно списку Fortune 500 за 2012 год. Таким образом, среднее значение по совокупности для прибыли в процентах от выручки составило:
(mu) = (0,9 + 1,6 + 3,5)/3 = 6/3 = 2%
Выборочное среднее значение.
Среднее значение по выборке (выборочное среднее или выборочное среднее значение, от англ. ‘sample mean’) — это среднее арифметическое значение, вычисленное для выборки.
Очень часто мы не можем наблюдать каждый элемент множества данных; вместо этого мы наблюдаем подмножество или выборку из генеральной совокупности.
Концепция среднего значения может применяться к наблюдениям в выборке с небольшим изменением обозначений.
Формула выборочного среднего значения.
Выборочное среднее, ( overline{X} ) (читается как «X-bar») — это среднее арифметическое значение по выборке:
(large{ overline{X} = {dsum_{i=1}^{n}X_i over n} }) (Формула 3)
где:
- (n) — количество наблюдений в выборке.
Формула 3 предписывает суммировать значения наблюдений (X_i) и делить эту сумму на количество наблюдений. Например, если выборка коэффициентов прибыли на акцию (P/E) для шести публичных компаний содержит значения 35, 30, 22, 18, 15 и 12, то среднее значение P/E для выборки будет 132/6 = 22. Среднее значение выборки также называется средним арифметическим (англ. ‘arithmetic average’).
Статистики предпочитают использовать термин «mean», а на «average» (в русском переводе это одно и то же — «среднее»). Некоторые авторы называют все меры центральной тенденции (включая медиану и моду) термином «average». Термин «mean» позволяет избежать любой путаницы.
Как отмечалось ранее, выборочное среднее значение является статистикой (то есть описательной мерой выборки).
Средние значения можно рассчитывать для отдельных статистических единиц или для временного отрезка.
В качестве примера можно привести рентабельность собственного капитала (ROE) за 2013 год для 100 компаний из FTSE Eurotop 100, индексе 100 крупнейших компаний Европы. В этом случае мы рассчитываем среднее значение ROE за 2013 год в среднем по 100 отдельным статистическим единицам (или элементам множества, от англ. ‘statistical unit’ или просто ‘unit’).
Когда мы изучаем характеристики некоторых статистических единиц в определенный момент времени (например, ROE для FTSE Eurotop 100), мы изучаем перекрестные данные (англ. ‘cross-sectional data’). Среднее этих наблюдений называется перекрестным средним значением (англ. ‘cross-sectional mean’).
[см. также: CFA — Временные ряды и перекрестные данные]
С другой стороны, если наша выборка состоит из исторической месячной доходности по FTSE Eurotop 100 за последние 5 лет, то мы имеем дело с данными временного ряда (англ. ‘time-series data’). Среднее значение этих наблюдений называется средним временного ряда (англ. ‘time-series mean’).
Мы рассмотрим специализированные статистические методы, связанные с поведением временных рядов в следующих разделах, посвященных анализу временных рядов.
Ниже мы покажем пример определения выборочной средней доходности для 16 европейских фондовых рынков за 2012 г. В этом случае среднее значение является перекрестным, поскольку мы усредняем доходность по отдельным странам.
Пример вычисления перекрестного среднего значения.
Индекс MSCI EAFE (Европа, Австралия и Дальний Восток) — это индекс рыночной капитализации, скорректированный с учетом свободного обращения акций, предназначенный для оценки акций в развитых странах, за исключением США и Канады.
Термин «скорректированный с учетом свободного обращения акций» (англ. ‘free float-adjusted’) означает, что веса компаний в индексе отражают стоимость акций, фактически доступных для инвестиций.
По состоянию на сентябрь 2013 года EAFE состояла из 22 индексов стран развитых рынков, включая индексы для 16 европейских рынков, 2 австралийских рынков (Австралия и Новая Зеландия), 3 дальневосточных рынков (Гонконг, Япония и Сингапур) и Израиля.
Предположим, что мы заинтересованы в показателях динамики местной валюты на 16 европейских рынках EAFE в 2012 году. Мы хотим найти примерную среднюю общую доходность за 2012 год по этим 16 рынкам.
Ряды ставок доходности, представленные в Таблице 8, приведены в местной валюте (то есть доходность указана для инвесторов, проживающих в стране). Поскольку эта доходность не указывается в валюте каждого отдельного инвестора, она не является доходностью, которую мог бы получить отдельный инвестор. Это, скорее, средняя доходность для местных валют 16 стран.
|
Рынок |
Общая доходность |
|---|---|
|
Австрия |
20.72 |
|
Бельгия |
33.99 |
|
Дания |
28.09 |
|
Финляндия |
8.27 |
|
Франция |
15.90 |
|
Германия |
25.24 |
|
Греция |
-2.35 |
|
Ирландия |
2.24 |
|
Италия |
6.93 |
|
Нидерланды |
15.36 |
|
Норвегия |
6.05 |
|
Португалия |
-2.22 |
|
Испания |
-4.76 |
|
Швеция |
12.66 |
|
Швейцария |
14.83 |
|
Великобритания |
5.93 |
Источник: www.msci.com.
Используя данные Таблицы 8, рассчитайте выборочную среднюю доходность для 16 фондовых рынков за 2012 год.
Решение:
При расчете к ставкам доходности применяется Формула 3:
(20,72 + 33,99 + 28,09 + 8,27 + 15,90 + 25,24 — 2,35 + 2,24 + 6,93 + 15,36 + 6,05 — 2,22 — 4,76 + 12,66 + 14,83 + 5,93) / 16 = 186,88 / 16 = 11,68%
Мы можем убедиться, что на 8 рынках доходность была меньше среднего, а на других 8 — выше среднего. Мы не должны ожидать, что какие-либо фактические наблюдения будут равны среднему значению, потому что выборочные средние значения предоставляют только сводку анализируемых данных.
Кроме того, хотя в этом примере число значений ниже среднего равно количеству значений выше среднего, это не обязательно так на самом деле. Как финансовому аналитику, вам часто нужно будет находить несколько показателей, которые описывают характеристики распределения.
Среднее значение — это, как правило, статистика, которую вы будете использовать как показатель типичного результата для распределения. Затем вы можете использовать среднее значение для сравнения динамики двух разных рынков.
Например, вам может быть интересно сравнить показатели фондового рынка стран Азиатско-Тихоокеанского региона с показателями фондового рынка европейских стран. Вы можете использовать среднюю доходность этих рынков, чтобы сравнить результаты инвестиций.
Свойства среднего арифметического.
Среднее арифметическое можно сравнить с центром тяжести объекта. Рисунок 5 выражает эту аналогию графически и представляет собой график девять гипотетических наблюдений.
Девять наблюдений: 2, 4, 4, 6, 10, 10, 12, 12 и 12. Среднее арифметическое составляет 72/9 = 8. Наблюдения наносятся на ось как столбцы с различной высотой в зависимости от их частоты (то есть 2 — высота в одну единицу, 4 — высота в две единицы и т. д.).
Когда ось помещается на точку опоры, она сбалансируется только тогда, когда точка опоры совпадает с отметкой на оси, соответствующей среднему арифметическому значению.
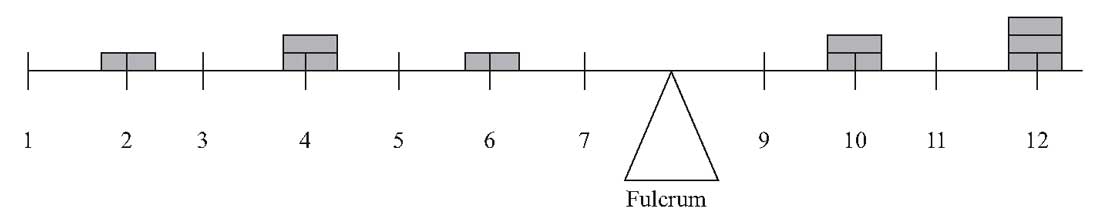
Когда точка опоры установлена на отметку 8, ось идеально сбалансирована.
Как финансовые аналитики, мы часто используем среднюю доходность как меру типичного результата для актива. Однако, как и в приведенном выше примере, некоторые результаты оказываются выше среднего, а некоторые — ниже. Мы можем рассчитать расстояние между средним значением и каждым результатом и назвать его отклонением (англ. ‘deviation’).
Математически всегда верно, что сумма отклонений от среднего равна 0. Мы можем убедиться в этом, взяв среднее арифметическое, приведенное в Формуле 3, и умножив обе части уравнения на (n):
({ noverline{X} = dsum_{i=1}^{n}X_i })
Таким образом, сумма отклонений от среднего значения может быть рассчитана следующим образом:
({ begin{align} & sum_{i=1}^{n} (X_i — overline{X}) = \ & sum_{i=1}^{n}X_i — sum_{i=1}^{n} overline{X} = \ & sum_{i=1}^{n}X_i — noverline{X} = 0 end{align} })
Отклонения от среднего арифметического являются важной информацией, поскольку они указывают на риск. Концепция отклонений от среднего значения формирует основу для более сложных понятий дисперсии, асимметрии и эксцесса, которые мы обсудим в следующих разделах.
Преимущества и недостатки среднего арифметического.
Преимущество среднего арифметического над двумя другими мерами центральной тенденции, — медианой и модой, состоит в том, что среднее использует всю информацию о размере и величине наблюдений. Со средним арифметическим также легко работать математически.
Потенциальный недостаток среднего арифметического — это его чувствительность к экстремальным значениям.
Поскольку для вычисления среднего значения используются все наблюдения, среднее арифметическое может резко увеличиваться или уменьшаться за счет чрезвычайно больших или малых наблюдений, соответственно.
Например, предположим, что мы вычисляем среднее арифметическое следующих семи чисел: 1, 2, 3, 4, 5, 6 и 1000.
Среднее значение равно 1,021 / 7 = 145,86 или приблизительно 146. Поскольку величина среднего, 146, намного больше, чем величина большинства наблюдений (первые 6), мы можем задаться вопросом, насколько хорошо она представляет положение данных в распределении.
На практике, хотя экстремальное значение (или выброс, от англ. ‘outlier’) в финансовых данных может быть редким значением в совокупности, оно также может отражать ошибку, допущенную при записи значения наблюдения или ошибку при формировании выборки из совокупности.
В частности, в последних двух случаях среднее арифметическое может вводить в заблуждение. Наиболее распространенный подход в таких случаях — использовать медиану вместо или в дополнение к среднему значению.
Медиана будет рассмотрена далее.
Другие подходы к обработке экстремальных значений включают применение вариаций среднего арифметического.
Усеченное среднее значение (от англ. ‘trimmed mean’ или ‘truncated mean’) вычисляется путем исключения указанного небольшого процента самых низких и самых высоких значений. Затем вычисляется среднее арифметическое из оставшихся значений.
Например, среднее значение, усеченное на 5%, отбрасывает наименьшие 2,5% и наибольшие 2,5% значений и вычисляет среднее из оставшихся 95% значений.
Усеченное среднее значение часто используется в спортивных соревнованиях, когда самые низкие и самые высокие оценки судей отбрасываются при подсчете оценки участника.
Средняя арифметическая взвешенная и средняя гармоническая
Краткая теория
В процессе обработки и обобщения статистических
данных возникает необходимость определения средних величин. Как правило,
индивидуальные значения одного и того же признака у различных единиц
совокупности неодинаковы. Средняя величина — обобщающая характеристика
изучаемого признака в исследуемой совокупности. Она отражает его типичный
уровень в расчете на единицу совокупности в конкретных условиях места и
времени. Например, при изучении доходов рабочих концерна обобщающей
характеристикой служит средний доход одного рабочего. Для его определения общую
сумму средств, направленных на потребление, в виде заработной платы, социальных
и трудовых льгот, материальной помощи, дивидендов по акциям и процентов по
вкладам в имущество концерна за рассматриваемый период (год, квартал, месяц)
делят на численность рабочих концерна.
Очень важное правило — вычислять средние величины
лишь по однородной совокупности единиц. Только при выполнении этого условия
средняя как обобщающая характеристика отражает общее, типичное, закономерное,
присущее всем единицам исследуемой совокупности. Прежде чем вычислять средние
величины, необходимо произвести группировку единиц исследуемой совокупности,
выделив качественно однородные группы.
Средняя, рассчитанная по совокупности в целом,
называется общей средней, средние, исчисленные для каждой группы, — групповыми
средними. Общая средняя отражает общие черты изучаемого явления, групповая
средняя дает характеристику размера явления, складывающуюся в конкретных
условиях данной группы. Сравнительный анализ групповых и общих средних
используется для характеристики социально-экономических типов изучаемого
общественного явления.
В статистике используются различные виды
средних величии: средняя арифметическая, средняя гармоническая, средняя
геометрическая, средняя квадратическая, средняя хронологическая и т. д. При
использовании средних величин важно правильно выбрать вид средней и способ ее
расчета. Самой распространенной средней, используемой в социально-экономическом
анализе, является средняя арифметическая.
Средние арифметические бывают простые и
взвешенные. Средняя арифметическая простая рассчитывается по формуле:
где
– индивидуальные значения признака, средняя величина
которых находится,
– количество единиц совокупности.
Средняя арифметическая простая
применяется в тех случаях, когда каждое индивидуальное значение признака
встречается один раз или одинаковое количество раз.
Если же варианты (значения признака)
встречаются неодинаковое количество раз, то используется средняя арифметическая взвешенная:
где
– варианты, значения признака,
– частота появления соответствующего значения
признака.
В некоторых случаях средняя
рассчитывается по другому – когда известен ряд вариант
и ряд произведений вариант на частоту
,
а сама частота
неизвестна. В этом случае средняя
рассчитывается по формуле средней гармонической взвешенной:
где
Средняя гармоническая может иметь и
простую форму расчета, которая в практике статистики используется крайне редко
и представляет собой простую среднюю из обратных значений признака.
Величина средних величин зависит как от
индивидуальных значений признака в случае использования простых видов средних величин,
так и от удельного веса этих значений в общей совокупности при использовании
взвешенных видов.
Формулы средних взвешенных применяются во
всех случаях, когда варианты значений признака имеют различный удельный вес, а
формулы простых (не взвешенных) средних — когда варианты имеют равные веса. В первом
случае расчет ведется по уже сгруппированным данным на основании дискретных рядов распределения, а во втором — обычно по несгруппированным, где каждый
признак представлен одним числом или равное число раз. Неправильный выбор
формулы, расчет средних показателей по формуле средней простой вместо средней
взвешенной может привести к серьезным ошибкам.
Средние
величины применяются для оценки достигнутого изучаемого показателя, при анализе
и планировании экономической деятельности предприятий. Средняя величина всегда
величина именованная и имеет ту же размерность что и признак у отдельных единиц
совокупности. Основным условием правильного расчета средней величины
является качественная однородность совокупностей, по которой исчислена средняя.
Примеры решения задач
Задача 1
Имеются
следующие данные о работе автотранспортных предприятий за отчетный период:
| № п/п | Общий грузооборот, млн.т/км |
Выполнено тыс. т/км в среднем на 1 автомобиль |
% выпуска автомобилей на линию |
Средняя грузоподъемность одного автомобиля, т |
В общем грузообороте доля его выполнения за пределы региона (%) |
| 1 | 39 | 130 | 71 | 6.2 | 32 |
| 2 | 57 | 156 | 85 | 5.9 | 45 |
| 3 | 41 | 127 | 79 | 5.5 | 28 |
Определите
по совокупности предприятий средние значения всех признаков, используя
экономически обоснованные формулы расчета. Укажите вид и форму рассчитанных
средних.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Средний
грузооборот вычислим по формуле средней арифметической простой:
Среднее
выполнение на 1 автомобиль тыс.т/км по формуле
средней гармонической, так как определяющим показателем в данном случае
является отсутствующее в условии число
автомобилей:
где
– общий грузооборот
– среднее выполнение на 1 автомобиль тыс.т/км
Средний
процент выпуска автомобилей на линию вычислим по формуле средней арифметической
взвешенной, так как определяющим показателем является численность автомобилей,
которую в свою очередь можно найти делением общего грузооборота на выработку
одного автомобиля.
– процент выпуска автомобилей на линию
– численность автомобилей
Среднюю
грузоподъемность одного автомобиля вычислим по формуле средней арифметической
взвешенной, так как определяющим показателем является численность автомобилей,
которую в свою очередь можно найти делением общего грузооборота на выработку
одного автомобиля.
– грузоподъемность 1 автомобиля
– численность автомобилей
Среднюю
долю выполнения за пределы региона вычислим по формуле средней арифметической
взвешенной, так как определяющим показателем является общий грузооборот.
– доля в общем грузообороте выполнения за
пределы региона
– общий грузооборот
Таким
образом средний грузооборот по предприятиям составил 45,7 млн. т/км, средняя
выработка на 1 автомобиль — 138,6 тыс.
т/км, средний процент выпуска
автомобилей на линию – 78,8%, средняя грузоподъемность одного автомобиля – 5,9
т., а средняя доля в общем грузообороте выполнения за пределы региона составила
36,2%.
Задача 2
Имеются
данные о финансовых показателях предприятий за отчетный период.
| Предприятия | Получено прибыли, тыс.руб. | Акционерный капитал, тыс.р. |
Рентабельность акционерного капитала, % |
| А | 1 | 2 | 3 |
| 1 | 1512 | 5040 | 30 |
| 2 | 528 | 1320 | 40 |
| 3 | 1410 | 5640 | 25 |
Определите
средний процент рентабельности акционерного капитала фирмы, используя
показатели:
- гр. 1
и гр. 2 - гр. 2
и гр. 3 - гр. 1
и гр. 3
Решение
1)
Средний процент рентабельности в этом случае определим напрямую, по формуле
рентабельности:
2)
Средний процент рентабельности в этом случае определим по формуле средней арифметической
взвешенной:
3)
Средний процент рентабельности в этом случае определим по формуле средней
гармонической:
Средний
процент рентабельности по всем предприятиям составил 28.75%
Задача 3
- Рассчитайте средние значения всех признаков, приведенных в условии
задачи. - Укажите формулу расчета средней в обозначениях задачи, расчет полностью,
вид и формулу средней, использованной в расчете, единицы измерения средней.
Имеются
следующие данные (данные условные):
| Страна | Стоимость экспорта РФ, млн.долл.США |
Доля экспорта в стоимости внешнеторгового оборота, % |
Доля морепродуктов в стоимости экспорта, % |
Доля мороженной рыбы в стоимости экспорта морепродуктов, % |
Средняя цена за тонну мороженной рыбы, долл. США |
| S | D | R | M | C | |
| Япония | 2995 | 74.8 | 5.46 | 74.2 | 1843 |
| Корея | 835 | 49.9 | 3.72 | 97.3 | 594 |
| Китай | 3981 | 76.0 | 0.56 | 97.1 | 478 |
| Индия | 2172 | 47.4 | 0.32 | 82.5 | 725 |
Решение
Среднюю
стоимость экспорта вычислим по формуле средней арифметической простой:
Среднюю
долю экспорта в стоимости внешнеторгового оборота вычислим по формуле средней
гармонической:
Среднюю
долю морепродуктов в стоимости экспорта вычислим по формуле средней
арифметической взвешенной:
Долю мороженной рыбы в стоимости экспорта морепродуктов вычислим
по формуле:
Среднюю
цену за тонну мороженной рыбы вычислим по формуле:
Вывод к задаче
Таким
образом средняя стоимость экспорта составила 2495,75 млн.долл.,
средняя доля экспорта в стоимости внешнеторгового оборота 64,4%, средняя доля
морепродуктов в стоимости экспорта 2.2%. Доля мороженной
рыбы в стоимости экспорта морепродуктов составила 79.9%, а средняя цена тонны
мороженной рыбы 1053.1 долл.
-
Сущность
средних в статистике. -
Средняя
арифметическая, ее свойства и техника
исчисления. -
Средняя
гармоническая. -
Мода
и медиана. -
Показатели
вариации.
С
-
Сущность
средних в статистике.
редние величины играют особую роль
в статистическом исследовании. Это
определяется задачей статистики –
выявлением закономерностей массовых
явлений. Закономерности можно выявить,
лишь обобщая однородные явления и давая
обобщенную характеристику единицам
явлений.
Средней
величиной
в статистке называется обобщающая
характеристика совокупности однотипных
явлений по какому-либо варьирующему
признаку, которая показывает уровень
признака, отнесенный к единице
совокупности.
Основополагающим
условием
применения средних величин является
массовость изучаемого явления. Только
при этом условии они покажут общую
тенденцию, лежащую в основе процесса в
целом, и покажут ее типичный для данного
периода уровень проявления.
К
прочим условиям верного и экономически
грамотного использования средних
величин относятся:
-
использование
средней только в том случае, когда
признак изменяется, варьирует у отдельных
единиц совокупности; -
средние
величины могут рассчитываться только
в качественно однородных совокупностях.
Средние величины,
будучи обобщающими показателями, для
совокупности в целом затушевывают
количественные различия изучаемого
признака у отдельных единиц. Поэтому
даже в пределах качественно однородной
совокупности нередко нужно общие средние
дополнять исчислением групповых средних,
так как общие средние величины могут
не раскрыть подлинных закономерностей
изучаемых процессов.
Введем
следующие условные обозначения:
|
Х |
Варианта |
|
F |
Частота |
|
|
Среднее |
Наиболее
часто в практике встречаются средние
арифметические и средние гармонические.
С
-
Средняя
арифметическая, ее свойства и техника
исчисления.
редняя арифметическая
используется в вариационном ряду
распределения, где имеются частоты и
варианты признака. Средняя арифметическая
рассчитывается как:
-
Средняя
арифметическая простая.
Применяется когда частоты вариант
равны между собой или равны единице.
=
—
среднее
значение признака в совокупности;
—
сумма вариант признака;
n
— количество частот.
Пример:
определить среднюю цену на сахар за
год, если средняя цена в первом квартале
составила 2,50; во втором – 2,45; в третьем
– 2,70; в четвертом – 2,60. Так как частоты
равны единице, то используется средняя
арифметическая простая:
грн.
-
Средняя
арифметическая взвешенная.
Используется, в случае, когда варианты
совокупности имеют различную частоту.
=
—
сумма всех частот в совокупности;
—
общий объем значений частот варианты
в совокупности.
Частоты
отдельных вариант могут быть выражены
не только абсолютными величинами, но и
относительными значениями – частностями
(w).
=
Пример:
определить среднюю заработную плату
работников магазина, если 1 человек
получает 500 грн.; 3 – 450; 7 – 350; 2 – 250; 1 –
200. Так как варианты имеют различную
частоту, то необходимо использование
средней арифметической взвешенной:
грн.
В
случае, когда варианты и частоты в
интервальном вариационном ряду имеют
большое численное значение, расчет
среднего значения требует существенных
усилий. Для сокращения трудоемкости
расчетов использует некоторые особенности
средней арифметической, позволяющие
оптимизировать процесс расчета среднего
значения и имеющие название способ
моментов.
При
расчете средней арифметической способом
моментов необходимо:
-
Перейти
от интервального ряда к дискретному
путем нахождения среднего значения
каждого интервала. -
Вычесть
из всех вариант постоянное число (лучше
для этого использовать значение
серединной варианты или варианты с
наибольшей частотой) – A. -
Разделить
варианты на постоянное число, а именно
величину интервала – i. -
Рассчитать
среднюю арифметическую из новых вариант
или так называемый момент первого
порядка.
M1
=
-
Для
определения величины средней
арифметической нужно величину момента
первого порядка умножить на величину
того интервала, на который делили все
варианты, и прибавить к полученному
произведению величину варианты, которую
вычитали.
=
i x M + A
Пример:
на основании приведенных данных о
результатах анализа жирности молока
определить среднее значение.
-
Жирность
молока, %Количество
Жирность
молока, %х
– А (А
= 3)Х1
= (х – А)/i
(i
– 1)0,5
– 1,512
1
—
2—
21,5
– 2,525
2
—
1—
12,5
– 3,538
3
0
0
3,5
– 4,55
4
1
1
М1
=
%
Для
проверки, произведем расчет среднего
процента жирности молока, используя
среднюю арифметическую взвешенную:
-
Средняя
гармоническая.
Учитывая, что статистические средние
всегда выражают качественные свойства
изучаемых общественных процессов и
явлений, важно правильно выбрать формулу
средней исходя из взаимосвязи явлений
и их признаков. Когда статистическая
информация не содержит частот по
отдельным вариантам совокупности, а
представлена как их произведение,
применяется формула средней гармонической,
то есть в этом случае веса приходится
делить на варианты или, что то же самое,
умножать на их обратное значение.
Средняя
гармоническая
– величина, обратная средней арифметической,
из обратных значений признака.
Выбор средней гармонической простой и
взвешенной аналогичен средней
арифметической:
-
в
случае, когда варианты равны между
собой или равны единице, применяется
средняя
гармоническая простая:
-
если
варианты имеют различную частоту,
используется средняя
гармоническая взвешенная:
П
-
Мода
и медиана.
ример: на основании
приведенных данных о цене и объеме
реализации картофеля за месяц на рынках
города определить среднюю цену.
-
Рынки
Цена,
грн.Объем
реализации, тыс. грн.Южный
2,10
1025
Железнодорожный
1,80
1240
Центральный
2,40
890
Калининский
2,25
700
Для
расчета средней цены необходимо
использование средней гармонической
простой, так как объем реализации
выступает как произведение цены
реализации на количество реализованной
продукции.

Модой
в статистике называется величина
признака (варианта), которая чаще всего
встречается в данной совокупности. В
вариационном ряду это будет варианта,
имеющая наибольшую частоту.
В дискретном ряду
модаопределяется визуально, так как
это варианта, имеющая наибольшую частоту.
В случае, если не одна, а две варианты
имеют наибольшую частоту, в ряду будут
две моды и распределение будет бимодальным.
Для
определения моды
в интервальном вариационном ряду
используется следующая формула:
Mo
=
Xmo
+ Imo
x
Xmo
— минимальная граница модального
интервала;
Imo
— величина модального интервала;
Fm0-1
— частота интервала, предшествующего
модальному;
Fm0
— частота модального интервала;
Fm0+1
— частота интервала, следующего за
модальным.
Модальный
интервал – интервал с наибольшей
частотой.
Пример:
на основании ранее рассмотренного
примера определим моду
-
Жирность
молока, %Количество
Жирность
молока, %0,5
– 1,512
1
1,5
– 2,525
2
2,5
– 3,538
3
3,5
– 4,55
4
Для
дискретного ряда распределения модой
будет выступать значение жирности
молока, равное 3%, так именно это значение
наиболее часто встречается в рассмотренной
совокупности – 38 раз.
Определим
значение моды в интервальном ряду
распределения:
Мо
=
Медианой
называется варианта, которая находится
в середине вариационного ряда.
Медиана делит ряд пополам, по обе стороны
от нее находится одинаковое количество
единиц совокупности.
Если
непарное число вариант записано в
порядке возрастания или убывания, то
центральная из них будет медианой
((n+1)/2).
Если число вариант парное, то медиана
рассчитывается как средняя арифметическая
простая двух средних вариант.
Для
нахождения медианы
в интервальном вариационном ряду
используют следующую формулу:
Me
= Xme
+ Ime
x
Xme
— начальное
значение медианного интервала;
Ime
— величина медианного интервала;
—
сумма частот (численность ряда);
S
(me-1)
— сумма накопленных частот в интервалах,
предшествующих медианному;
Fme
— частота медианного интервала.
Медианный интервалэто тот интервал, кумулятивная частота
которого равна или превышает половину
суммы частот.
Пример:
на основании ранее рассмотренного
примера определим медиану.
-
Жирность
молока, %Количество
Жирность
молока, %0,5
– 1,512
1
1,5
– 2,525
2
2,5
– 3,538
3
3,5
– 4,55
4
Для дискретного
ряда распределения с парным числом
вариант медианой будет являться средняя
арифметическая простая двух средних
вариант:
Ме
=
Произведем расчет
медианы для интервального ряда
распределения:
Ме
=
-
Показатели
вариации.
Средние величины
дают обобщающую характеристику
совокупности по варьирующим признакам,
показывают типичный для данных условий
уровень этих признаков. Но, как уже
указывалось, наряду со средними
величинами, большое практическое и
теоретическое значение имеет изучение
отклонений от средних. При этом интересуют
не только крайние отклонения, но и
совокупность всех отклонений. От размера
и распределения отклонений зависит
надежность средних характеристик.
Для
характеристики величин колебания в
статистике рассчитывают целый ряд
показателей. Рассмотрим их на следующем
примере:
Средние
цены на пиво (за 1 литр) по Донецкой
области за ряд лет составили:
-
1997
год – 1,49 грн.; -
1999
год — 1,96 грн.; -
2001
год – 3,10 грн.
-
Размах
вариации –
представляет собой разницу между
наибольшим и наименьшим значением
варьирующего признака.
R
= Xmax
— Xmin
R
= 3,10 – 1,49 = 1,61 грн.
-
Среднее
линейное (арифметическое) отклонение
– характеризует распределение отклонений
фактических значений от среднего.
Используют:
—
простое среднее линейное отклонение:
=
—
взвешенное среднее линейное отклонение:
=
В нашем примере
рассчитывается простое среднее линейное
отклонение. Средняя цена на пиво за
указанный период составила 2,18 грн.
рассчитывается как средняя арифметическая
простая.
грн.
-
Среднее
квадратическое отклонение
– показывает абсолютную меру вариации
и выражается в тех же единицах, в которых
выражены варианта и средняя.
—
простое:
σ
=
—
взвешенное:
σ =
Рассчитаем простое
среднее квадратическое отклонение:
грн.
-
Коэффициент
вариации –
характеризует относительную меру
колебания признаков в вариационном
ряду. Выражается в % или коэффициентах,
что дает возможность сравнивать вариацию
разноименных совокупностей, поэтому
из всех показателей вариации он является
наиболее оптимальным.
V
=
%
Коэффициент
вариации в нашем примере равен: V
=
Соседние файлы в папке Статистика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
- Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
- средняя арифметическая;
- средняя гармоническая;
- средняя геометрическая;
- средняя квадратическая.
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
- Средняя арифметическая простая (невзвешенная) – вычисляется когда каждый вариант совокупности встречается только один раз.
- Средняя арифметическая (взвешенная) – варианты повторяются различное число раз, при этом число повторений вариантов называется частотой, или статистическим весом.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
- Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле (8.8):
(8.8 -формула средней арифметической простой)
- где хi – вариант, а n – количество единиц совокупности.
- Пример вычисления средней арифметической простой. Провели опрос о желаемом размере заработной платы у пяти сотрудников офиса. По результатам опроса выяснили, что желаемый размер заработной платы составляет соответственно для каждого сотрудника: 50000, 100000, 200000, 350000, 500000 рублей человек. Рассчитаем среднюю арифметическую простую по формуле (8.8):
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
- Средняя арифметическая взвешенная формула 8.9.
(8.9 -формула средней арифметической взвешенной)
- где хi – вариант, а fi – частота или статистический вес.
- Пример вычисления средней арифметической взвешенной. Результаты опроса всех работников офиса приведены в табл. 8.2.
Таблица 8.2 – Результаты опроса работников офиса
|
Желаемый размер заработной платы, тыс.руб хi |
Количество работников fi | хifi |
| 1 | 2 | 3 |
|
50 100 200 350 500 |
6
10 20 9 5 |
300
1000 4000 3150 2500 |
| Итого | 50 | 10950 |
Пример. Вычислим (ориентируясь на итоговые строки таблицы) желаемый размер заработной платы, 50 сотрудников офиса (используем формулу 8.9):
Пример вычисления средней арифметической взвешенной
Вывод: в среднем желаемый размер заработной платы по результатам опроса 50 человек составил 219 тысяч рублей.
Среднеарифметическая – всегда обобщающая количественная характеристика варьирующего признака совокупности.
- Средняя гармоническая вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины.
- Средняя гармоническая простая представлена ниже:
(8.10 – формула средней гармонической простой)
Средняя гармоническая взвешенная определяется по формуле
(8.11- формула средней гармонической взвешенной)
где xi – вариант, n – количество вариантов, Vi – веса для обратных значений xi.
Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, чем взвешенная. Для иллюстрации области ее применения воспользуемся упрощенным условным примером.
- Пример (вычисление средней гармонической простой (невзвешенной)).
Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 5 мин., второй – 15 мин.
- Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?
На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. если используем среднюю арифметическую простую получим: (5+15):2=10, мин.
- Проверим обоснованность такого подхода на примере одного часа (60 минут) работы. За этот час первый работник обрабатывает 12 заказов (60:5), второй – 4 заказа (60:15), что в сумме составляет 16 заказов.
Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится: (60/10) + (60/10) = 12 заказов (что не соответствует истине).
- Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов, т.е. используем среднюю гармоническую:
Пример вычисления средней гармонической простой (невзвешенной)
Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится: (60/7,5) + (60/7,5) = 16 заказов
- Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения Wj для единиц совокупности равны (в рассмотренном примере рабочий день у сотрудников одинаковый).
Пример (вычисление средней гармонической взвешенной) В ходе торгов на валютной бирже за первый час работы заключено пять сделок. Данные о сумме продажи рублей и курсе рубля по отношению к доллару США приведены в табл.8.3.
Таблица 8.3 – Данные о ходе торгов на валютной бирже (цифры условные)
Номер сделки Сумма продажи V, млн руб. Курс рубля x, руб. за 1 дол. V/x 1 2 3 4 1
2
3
4
5
455,00
327,50
528,00
266,00
332,50
65,00 65,50
66,00
66,50
66,50
7,00
5,00
8,00
4,00
5,00
итого 1909,00 – 29,00 Для того чтобы определить средний курс рубля по отношению к доллару, нужно найти соотношение между суммой продажи рублей, которые затрачены на покупку долларов в ходе всех сделок, и суммой приобретенных в результате этих сделок долларов.
- Вывод: средний курс за один доллар составил 65,83 руб.;
- Если бы для расчета среднего курса была использована средняя арифметическая простая:
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин как отношение каждого уровня ряда к предыдущему уровню.
- Средняя геометрическая простая рассчитывается по формуле 8.12
(8.12)
- Если использовать частоты m, получим формулу средней геометрической взвешенной
- Средняя геометрическая взвешенная рассчитывается по формуле 8.13
(8.13)
Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.
Для несгруппированных данных используют формулу средней квадратической простой
Средняя квадратическая простая (формула 8.14)
8.14
Для сгруппированных данных используют формулу средней квадратической взвешенной
Средняя квадратическая взвешенная (формула 8.15)
(8.15) – Формула -средняя квадратическая взвешенная
Средние арифметическая, гармоническая, геометрическая и квадратическая, рассчитанные для одного и того же ряда вариантов, отличаются друг от друга. Их численное значение возрастает с ростом показателя степени в формуле степенной средней правило мажорантности средних А.Я. Боярского, т.е.
Мода и Медиана (структурные средние) формулы и примеры вычисления см. по ссылке
Загрузить PDF
Загрузить PDF
Среднее значение, медиана и мода — значения, которые часто используются в статистике и математике. Эти значения найти довольно легко, но их легко и перепутать. Мы расскажем, что они из себя представляют и как их найти.
-
1
Сложите все числа, которые вам даны. Допустим, вам даны числа 2, 3 и 4. Сложим их: 2 + 3 + 4 = 9.
-
2
Сосчитайте количество чисел. У нас есть три цифры.
-
3
Разделите сумму чисел на их количество. Берем 9, делим на 3. 9/3 = 3. Среднее значение в данном случае равно 3. Помните, что не всегда получается целое число.
Реклама
-
1
Запишите все числа, которые вам даны, в порядке возрастания. Например, нам даны числа: 4, 2, 8, 1, 15. Запишите их от меньшего к большему, вот так: 1, 2, 4, 8, 15.
-
2
Найдите два средних числа. Мы расскажем, как это сделать, если у вас имеется четное количество чисел, и как это сделать, если количество чисел нечетное:
- Если у вас нечетное количество чисел, вычеркните левое крайнее число, затем правое крайнее число и так далее. Один оставшийся номер и будет искомой медианой. Если вам дан ряд чисел 4, 7, 8, 11, 21, тогда 8 — медиана, так как 8 стоит посередине.
- Если у вас четное количество чисел, вычеркните по одному числу с каждой стороны, пока у вас не останется два числа посередине. Сложите их и разделите на два. Это и есть значение медианы. Если вам дан ряд чисел 1, 2, 5, 3, 7, 10, то два средних числа — это 5 и 3. Сложим 5 и 3, получим 8, разделим на два, получим 4. Это и есть медиана.
Реклама
-
1
Запишите все числа в ряд. Например, вам даны числа 2, 4, 5, 5, 4 и 5. Запишите их в порядке возрастания.
-
2
Найдите число, которое чаще всего встречается. В данном случае это 5. Если два числа встречаются одинаково часто, то этот ряд двухвершинный или бимодальный, а если больше — то мультимодальный.
Реклама
Советы
- Вам будет легче найти моду и медиану, если вы запишете числа в порядке возрастания.
Реклама
Об этой статье
Эту страницу просматривали 355 010 раз.





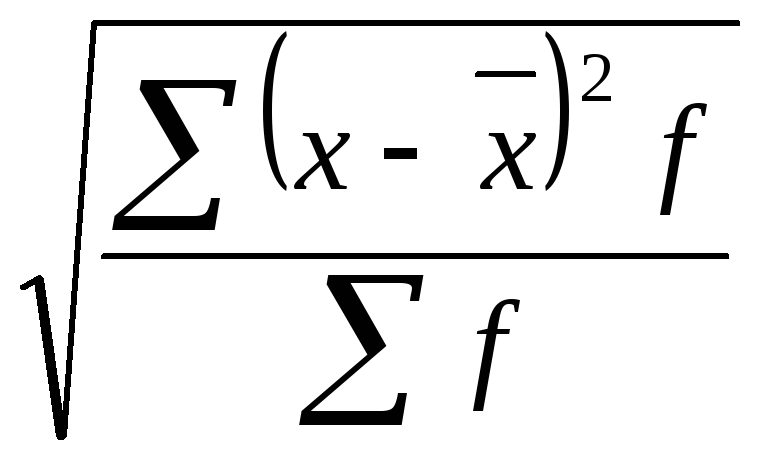


 Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.





 то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.










