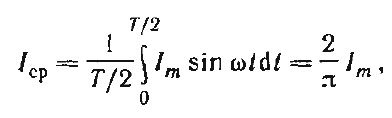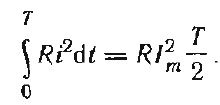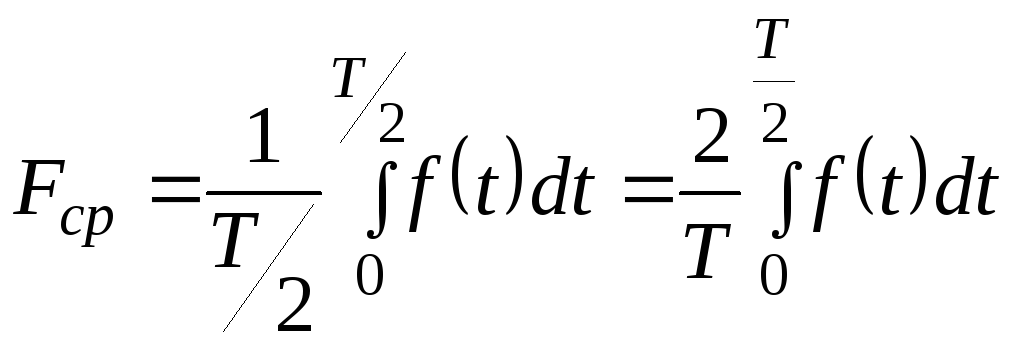Как найти среднее значение синуса

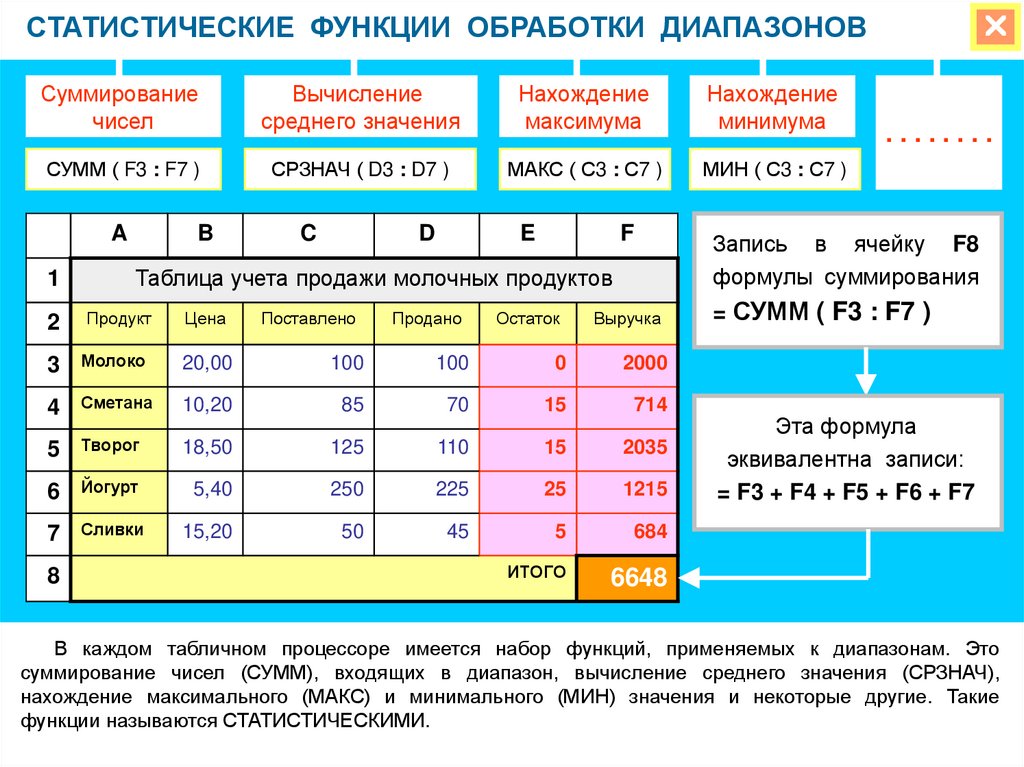
Среднее значение

Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода.

Среднее значение тока:

т. е. среднее значение синусоидального тока составляет 2/π = 0,638 от амплитудного. Аналогично, Eср = 2Ем/π ; Ucp = 2Uм/π.

Действующее значение

Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным).

Действующее значение тока:

Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично 

Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.

Количество теплоты, выделенное за один период синусоидальным током,

Выделенная за то же время постоянным током теплота равна RI^2_пост Т. Приравняем их:

Таким образом, действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.

Большинство измерительных приборов показывает действующее значение измеряемой величины.

Среднее и действующее значение синусоидальных функций

Средним
значением за период любой периодической
функции
называется интеграл

,
где T
—
период

У
любой гармонической функции среднее
значение за период равно нулю, так как
площадь положительной полуволны
компенсируется площа­дью отрицательной.
В этом случае пользуются средним
значением за по­лупериод.

С последним
значением совпадают среднее значение
функции за пе­риод, взятой по абсолютной
величине.

.

Пусть

,
тогда:

Приборы
выпрямительной системы показывают
среднее значение величин.

Приборы
магнитоэлектрической системы,
предназначены для измерения постоянного
напряжения и тока.

Тепловое
действие тока пропорционально квадрату
тока и поэтому часто о величине переменного
тока судят по так называемому средне
квад­ратичному или действующему
значению тока.

,
,
тогда:;

—
действующее значение тока

Действующее
значение показывают приборы
электромагнитной, электродинамической,
ферродинамической, электростатической
систем.

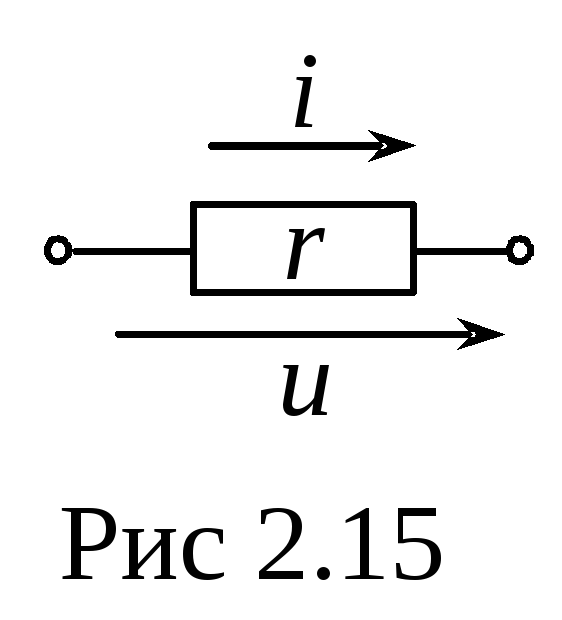
Синусоидальный ток в сопротивлении

Дано:
(рис 2.15).

Найти:

Только в частном
случае сопротивления выпол­няется
закон Ома для мгновенных значений
напряже­ний и тока.

В сопротивлении
напряжение и ток совпадают по фазе (рис
2.16).

Рис. 2.16

Мгновенная мощность
в сопротивлении.

.

Среднее
значение за период мгновенной мощности
называется ак­тивной мощностью.

.

Синусоидальный ток в индуктивности.

Дано:,
(рис.
2.17)

Найти:

;

Напряжение
на индуктивности опережает ток на
.
Обозначим—
реактивное сопротивление индуктивности.

—
реактивная проводимость индуктивности,
тогда

.

О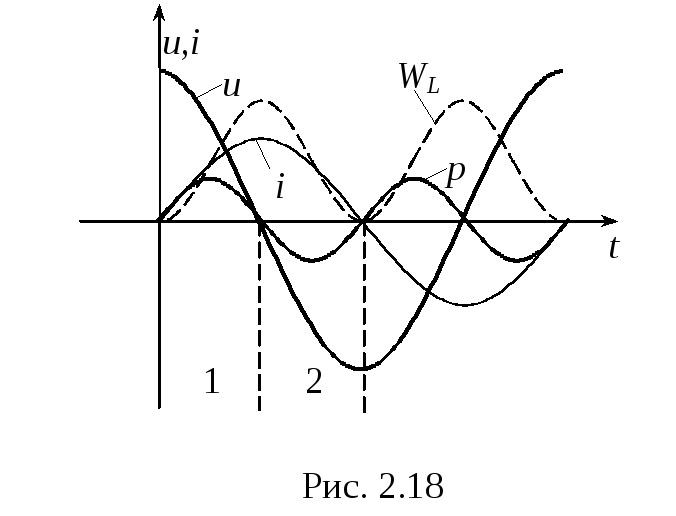тсюда
следует, что амплитуда (действующее
значение) напряжения и тока на индуктивности
связаны соотношением подобным закону
Ома.

;
.

Частное деления
напряжения на ток даёт некоторую функцию
вре­мени не имеющую физического смысла
и практического применения (рис.2.18).

Мгновенная
мощность в индуктивности:

.

Активная
мощность в индуктивности:
.

Энергия магнитного
поля индуктивности:

На первом интервале
энергия поступает в цепь и временно
запаса­ется в магнитном поле
индуктивности. На втором интервале
энергия воз­вращается в источник.
Таким образом, в цепях с индуктивностью
происхо­дит непрерывный колебательный
процесс обмена энергией.

Синусоидальный ток в ёмкости

Д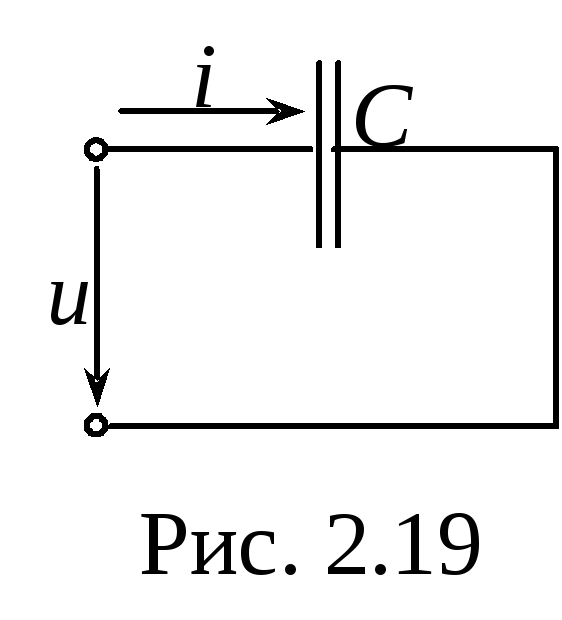ано:(рис.2.19).

Найти:

;

.

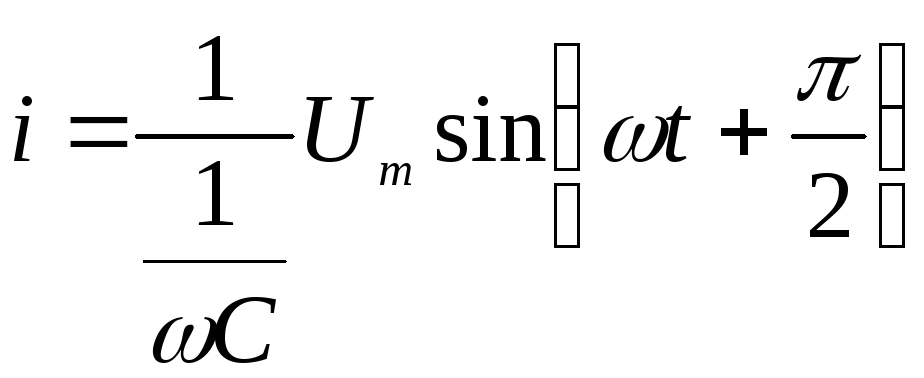
Ток в ёмкости опережает напряжение на 90º (рис. 2.20)

Обозначим
— реак­тивное сопротивление емкости— реактивная проводимость ёмкости.

Тогда:
.

Амплитуды
(действующие значения) напряжения и
тока в ёмкости связаны соотношением
подобным закону Ома.

Мгновенная
мощность
.

Энергия
электрического поля
;

Синусоидальный ток в цепи r, l, c

Дано:

(рис.
2.21).

Найти:

Напряжение будем
искать в виде

,

,,

На основании
второго закона Кирхгофа:

,

.

из тригонометрии:

,

;

Обозначим
— реактивное сопротивление цепи.

,

.

Отсюда
видно, что
.
Обозначим-полное сопротивление цепи, тогда:

-соотношение
подобное закону Ома.

треугольник
сопротивлений (рис. 2.22)

;

Ели
умножить все стороны треугольника
со­противлений на действующее
(амплитудное) значе­ние тока, то мы
получим треугольник напряжений, в
котором катеты – активная и реактивная
составляю­щие входного напряжения
(рис. 2.23).

—
реактивная составляющая

—
активная составляющая

Определение среднего значения функции

Определение среднего значения функции

П. Совертков, Ф.
Дягилев,
г. Нижневартовск

Обсуждая концепцию
математического образования в 12-летней школе [3,
с. 13–18], следует уточнить целеполагание одного
из основных блоков математического образования
– функции. Важным является изучение не столько
свойств функций, сколько развитие умений
применять функции для описания реальных
процессов. Но реальные процессы задаются
сложными функциональными зависимостями.
Математическое моделирование упрощает
зависимости, заменяя одну функцию другой, более
простой.

Основная идея введения
интеграла – аккумуляция (накопление) информации
о функции на отрезке – оказалась незавершенной
не только в школьном курсе математики, но и в
общем образовании учащихся. Нет возврата к более
простой функции, которая порождает такое же
значение интеграла, т. е. накапливает такую же
информацию на отрезке. Другими словами, нет
усреднения заданной функции на отрезке.

В школьных, да и в вузовских
учебниках, пропущено очень важное применение
определенного интеграла для нахождения среднего
значения непрерывной функции на отрезке.
Некоторые авторы программ и учебников много
говорят о развитии функциональной линии, но ни
слова не говорят, как усреднить функцию на
промежутке, хотя среднее значение двух величин
определяется. Следует сказать больше. Мотивация
изучения функциональной линии в общем
образовании учащихся оказалась не полностью
сформулированной и незавершенной.

Моделирование реальных задач
требует усреднения в математических моделях
непрерывных функций (в экологии, в метеосводке
погодных условий и т. д.), усреднения в
компьютерных экспериментах дискретных величин с
малым шагом аргумента – что приближается к
усреднению непрерывных величин.

Среднее значение функции
удобно ввести на примере определения средней
скорости движения, как отношения длины всего
пройденного пути к величине затраченного
времени

Рассмотрим общее определение
среднего значения функции.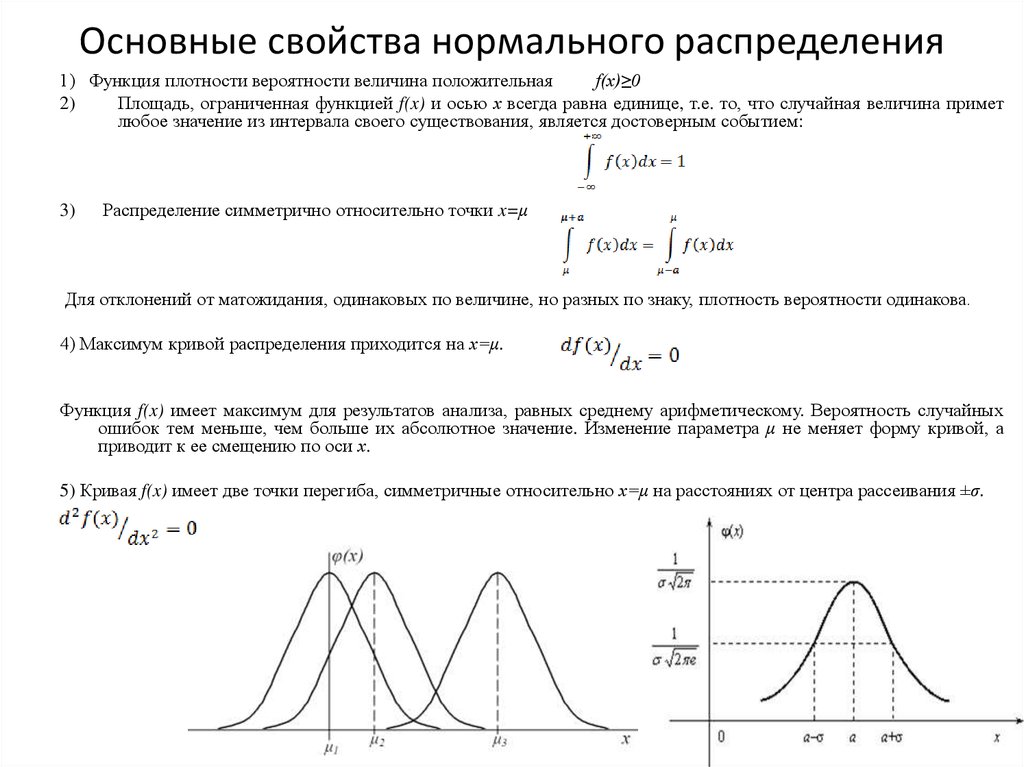

Площадь криволинейной
трапеции, ограниченной графиком непрерывной
функции y = f(x) (пусть f(x)
принимает неотрицательные значения), осью ox и
вертикальными прямыми y = a, y = b,
равна площади некоторого прямоугольника,
построенного на отрезке [a; b]. Высота
этого прямоугольника является средним значением
функции y = f(x) на отрезке [a; b].
В общем случае она определяется по формуле [2, с.
559]

      (1)

В школьных и вузовских
учебниках много внимания уделяется нахождению
интегралов. Это необходимое развитие навыков
нахождения интегралов, но очевидно, что более
важно показать его применения. Из всех учебников
и справочников для школы только в справочниках [1,
с. 497; 2, с. 368, 369] определяется среднее
значение функции на отрезке. Следует отметить,
что пропедевтика введения среднего значения
функции иногда проводится в задачах следующего
типа на вступительных экзаменах в вузы и в
учебниках физики.

1. Катер из
Нижневартовска в Сургут двигался со скоростью v₁,
а в обратном направлении со скоростью v₂.
Найдите среднюю скорость катера на всем пути,
т. е. из Нижневартовска в Сургут и обратно.

Ответ:  

2. Катер вначале двигался
со скоростью v₁ в течение некоторого
промежутка времени, а затем в течение такого же
промежутка времени со скоростью v₂.
Найдите среднюю скорость катера на всем пути.

Ответ:  

3. Первую треть пути между
пунктами велосипедист проехал со скоростью v = 5 м/с,
затем половину оставшегося времени он ехал со
скоростью v = 10 м/с, после чего до
конечного пункта он шел с велосипедом со
скоростью v = 1 м/с. Определите среднюю
скорость движения велосипедиста.

Ответ: 5,3 м/с.

4. Найдите среднюю
скорость тела, если первую четверть времени оно
двигалось со скоростью v = 5 м/с, вторую
четверть времени – со скоростью v = 10 м/с,
оставшуюся часть времени со скоростью v = 15 м/с.

Ответ: 11,25 м/с.

Не каждый учитель видит в этих
задачах функции. Для многих это постоянные
величины. Читатель наверно согласится, что это
требует корректировки.

Рассмотрим другие примеры,
приводящие к пониманию важности изучения
среднего значения. Например, мы иногда не можем
определить значение функции в данный момент
времени и вынуждены пользоваться средними
значениями функции.

Величина переменного тока в
данный момент времени t (мгновенное значение
тока) определяется по формуле

i = I₀ sin wt,

где I₀ –
максимальное (амплитудное) значение тока, w –
частота, – период. Представим себе, что
существует прибор, измеряющий мгновенное
значение тока i. Стрелка прибора в течение 1
секунды будет совершать 50 колебаний, показывая
значения из отрезка [– I₀; I₀].
Зафиксировать информацию практически
невозможно. С другой стороны, почти все приборы
обладают инерционностью, т.  е. требуют для
измерения величины некоторого времени
(быстродействие прибора). Оно, как правило,
значительно больше периода быстрых процессов.
Принцип измерения величин во многих приборах
основан на измерении какого-то действия за
определенный промежуток. Поясним примерами.

Среднее значение переменного
тока за период T равно 0 для синусоидальной
величины и не характеризует величину
переменного тока.

Среднее значение переменного
тока в течение полупериода по формуле (1) равно

Некоторые
электроизмерительные приборы измеряют среднее
значение тока за половину периода, но все они
практически градуируются в действующих
значениях переменного тока, к разъяснению
понятия которого мы переходим.

Действующим (эффективным)
значением I переменного тока называется
значение такого постоянного тока, который
производит такое же действие (тепловое,
электромагнитное, механическое и др.), как и
данный переменный ток.

Работа, совершенная
постоянным током за период T, равна

A = UIT = I²

 RT,

а работа, совершенная
переменным током, равна

Большинство
электроизмерительных приборов в цепях
переменного тока показывают действующее
значение. Для физики и техники большее значение
имеет действующее значение переменного тока, чем
среднее значение переменного тока. В медицине
иногда также выделяется усреднение на отрезке
около наибольшего значения, так как оно может
произвести на пациента большее влияние, чем
средняя величина за период приема лекарства. Эти
примеры показывают, что в некоторых науках
усреднение функций производится по-разному, в
зависимости от воздействия на объект.

Задача. Интервал
движения автобуса a минут, интервал движения
микроавтобуса – m минут, a Э N, m Э N.
Человек приходит на остановку, не зная графика
движения транспорта, т. е. случайным образом.
Сколько времени в среднем ожидает человек на
остановке, если курсируют автобус и
микроавтобус?

Решение. Пусть курсирует
только автобус с интервалом a минут. Введем
отсчет времени от первого уходящего с остановки
автобуса. Если пассажир пришел через t минут (t < a),
то он ждет автобус a – t минут. Если он
пришел через a – t минут, то он ожидает
очередного автобуса t минут, т. е. для
любого ожидания в t минут найдется случай,
когда пассажир будет ожидать a – t минут.
Для этих двух случаев среднее время ожидания
равно минут. Оно не зависит от времени
прихода на остановку. Рассматривая такие случаи
для различных значений t, получим среднее
время ожидания – мин. В этой задаче
среднее время определено элементарным методом с
использованием симметрии относительно середины
промежутка [0; 

a].

Если пассажир пришел на
остановку через t минут, то функция времени
ожидания автобуса имеет вид

f(t) = a –
t.

Найдем среднее значение
времени ожидания автобуса на отрезке [0; a]

Аналогично, если курсирует
только микроавтобус, то среднее время ожидания
равно мин.

Рассмотрим общий случай,
когда курсируют автобус и микроавтобус. Пусть m
является делителем числа a, a = mk, k l 2. Пусть
автобус приходит спустя s (s < m) минут
после отхода микроавтобуса. В течение a минут
человек может попасть в интервалы времени между
транспортами: «микроавтобус – автобус, интервал s
мин», «автобус – микроавтобус, интервал m

– s
мин», «микроавтобус – микроавтобус, интервал m
мин» и т. д.

Если s = 0 или s = m,
т. е. автобус и микроавтобус приходят на
остановку одновременно, то среднее время
ожидания в этом частном случае равно мин.
Пассажир может воспользоваться микроавтобусом
(автобусом он раньше не уедет). Автобус в этом
случае можно исключить из рассмотрения, так как
он приходит одновременно с микроавтобусом.

Пусть пассажир пришел на
остановку через t минут после отхода
микроавтобуса. Если 0 < t m s, то он ждет s
– t минут автобус; если s < t m m,
то он ждет m – t минут микроавтобус; если m < t m 2m,
то он ждет 2m – t минут микроавтобус и
т.  д. функция ожидания равна

Функция ожидания является
кусочно-линейной функцией и состоит из отрезков,
образующих углы в 135° с осью

ox.

Функция ожидания автобуса
является периодической функцией с периодом T = a
мин.

Учитывая геометрический
смысл интеграла, для вычисления среднего
значения функции ожидания достаточно вычислить
площадь равнобедренных треугольников с катетами

При

Условие задачи также требует
уточнения.

Если мы не знаем величины
задержки автобуса относительно микроавтобуса,
т. е. предположим, что она каждый день может
меняться, тогда среднее значение ожидания
следует рассмотреть как функцию t(s) от
параметра s. Величину t(s) следует
проинтегрировать на промежутке [0; m], а
затем поделить на длину этого промежутка. Если s Э [im, (i + 1)m],
i Э N, i < k, то рассуждения
проводятся аналогичные.

Итак, среднее время ожидания
автобуса на отрезке [0; a] вычисляется
следующим образом

Иногда встречается следующая
ошибка.

Если рассматривать все
средние значения только на отрезке [0; m], то
получим следующие результаты

Этот результат получается из
предыдущего при k = 1 и это верно. Но если k > 1,
то эта формула не учитывает интервал
«микроавтобус – микроавтобус, интервал движения
m минут, в течение которого не появляется
автобус».

Некоторые задачи для
самостоятельного решения.

1. Дан отрезок длиной a,
на который произвольным образом бросается точка.
Найдите среднее расстояние до границы отрезка.
2. Рассматриваются всевозможные
треугольники с данными сторонами OA = a,
OB = b и переменным углом g Э [0, p]. Найдите среднее
значение площади треугольников.
3. В окружность радиуса R вписаны
всевозможные прямоугольники с параллельными
сторонами. Найдите среднее значение площади
полученных прямоугольников.

Литература

1. Кожухов И.Б.,
Прокофьев А.А. Справочник по математике. – М.,
Лист, 1999.
2. Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н.
Математика. Алгебра и элементарные функции. – М.,
Агар, 1999.
3. Концепция математического образования в
12-летней школе. – Математика в школе, № 2/2000.
4. Математика. Большой энциклопедический
словарь. – М., БРЭ, 1998.

6. Формула среднего значения для определенного интеграла.

Теорема о среднем.
Если f(x) непрерывна на отрезке [a,b], то
существует точка
,
такая что.
Док-во. Функция, непрерывная на отрезке,
принимает на этом отрезке своё наименьшее
m и наибольшее M значения. Тогда.
Числозаключено
между минимальным и максимальным
значениями функции на отрезке. Одно из
свойств функции, непрерывной на отрезке,
заключается в том, что эта функция
принимает любое значение, расположенное
между m и M. Таким образом, существует
точка,
такая что.
Это свойство имеет простую геометрическую
интерпретацию: еслинепрерывна
на отрезке [a,b], то существует точкатакая,
что площадь криволинейной трапеции
ABCD равна площади прямоугольника с
основанием [a,b] и высотой f(c) (на рисунке
выделен цветом).

Рассмотрим функцию
f (x), интегрируемую по Риману на отрезке
[a, b]. Раз она интегрируема на [a, b], то она
также интегрируема на [a, x] ∀x ∈ [a, b].
Тогда при каждом x ∈ [a, b] имеет смысл
выражение
,
и при каждом x оно равно некоторому
числу.

Таким образом,
каждому x ∈ [a, b] поставлено в соответствие
некоторое число
,

т.е. на [a, b] задана
функция:

(3.1)

Определение:

Функция F (x), заданная
в (3.1), а также само выражение
называется

интегралом с
переменным верхним пределом. Она
определена на всем отрезке [a, b]

интегрируемости
функции f (x).

Теорема:

Условие: f (t)
непрерывна на [a, b], а функция F (x) задана
формулой (3.1).

Утверждение: Функция
F(x) дифференцируема на [a, b], причем F (x)
= f (x).

(В точке a она
дифференцируема справа, а в точке b –
слева.)

Доказательство:

Поскольку для
функции одной переменной F (x)
дифференцируемость равносильна
существованию производной во всех
точках (в точке a справа, а в точке b –
слева), то мы найдем производную F (x).
Рассмотрим разность

Таким образом,

,

при этом точка ξ
лежит на отрезке [x, x + ∆x] (или [x + ∆x, x]
если ∆x < 0).

Теперь вспомним,
что производная функции F(x) в заданной
точке x ∈ [a, b] равна пределу разностного
отношения:
.
Из равенства имеем:

,

Устремляя теперь
∆x → 0, в левой части данного равенства
получим F’(x), a в правой

Вспомним определение
непрерывности функции f (t) в точке x:

Пусть x1 в этом
определении равен ξ. Поскольку ξ ∈ [x +
∆x, x] (ξ ∈ [x, x + ∆x]), а

∆x → 0, то |x − ξ| →
0, и по определению непрерывности, f (ξ)
→ f (x). Отсюда имеем:

F’(x) = f (x).

Следствие:

Условие: f (x)
непрерывна на [a, b].

Утверждение: Любая
первообразная функции f (x) имеет вид

где C
∈ R – некоторая константа.

Доказательство.
По теореме 3.1 функция

является
первообразной для
f(x). Предположим,
что G(x) – другая первообразная f (x).
Тогда G’(x) = f(x) и для функции F(x) − G(x)
имеем: (F
(x) + G(x))’ = F’(x)−G’(x) = f (x)−f(x) ≡ 0. Значит,
производная функции F (x)−G(x)

равна нулю,
следовательно, эта функция есть
постоянная: F(x) − G(x) = const.

Среднее значение функции: метод и формула

Представьте себе, что вам нужно вычислить среднее значение чего-то, что постоянно меняется, например цены на газ. Обычно при расчете среднего набора чисел вы складываете их все и делите на общее количество чисел. Но как это сделать, когда цены меняются каждый месяц, неделю, день или во множестве моментов в течение дня? Как можно выбрать, какие цены будут включены в расчет средней?

Если у вас есть функция для цены газа и ее изменения с течением времени, это ситуация, когда среднее значение функции может быть очень полезным.

Определение среднего значения функции

Возможно, вы знакомы с понятием среднего. Как правило, среднее значение рассчитывается путем сложения чисел и деления на общее количество чисел. Среднее значение функции в исчислении представляет собой аналогичную идею.

Среднее значение функции — это высота прямоугольника, площадь которого эквивалентна площади под кривой функции.

Если вы посмотрите на рисунок ниже, вы уже знаете, что интеграл функции — это вся площадь между функцией и осью (x).

Прямоугольник имеет ту же площадь, что и площадь под кривой

На первый взгляд эта идея может показаться произвольной. Как этот прямоугольник связан со средним? Среднее значение включает в себя деление на количество значений, и как узнать, сколько здесь значений?

Среднее значение функции за интервал

Говоря о среднем значении функции, необходимо указать, за какой интервал. Это происходит по двум причинам:

Чтобы найти среднее значение функции, вместо сложения чисел нужно интегрировать , и вместо деления на количество значений вы делите на длину интервала.

[ begin{align} text{Добавление значений} quad &rightarrow quad text{Интеграция} \ text{Количество значений} quad &rightarrow quad text{Длина интервала } end{align} ]

Использование длины интервала имеет смысл, поскольку интервалы имеют бесконечное число значений, поэтому вместо этого более уместно использовать длину интервала. 9x.]

Здесь (f) измеряется в долларах за галлон, а (x) представляет количество лет, прошедших с 2017 года. Найдите среднюю цену бензина за галлон в период с 2017 по 2022 год.

Ответ :

Чтобы использовать формулу для среднего значения функции, сначала необходимо определить интервал. Поскольку функция измеряет количество лет, прошедших с 2017 г., интервал принимает вид ([0,5],), где 0 представляет 2017 г., а 5 представляет 2022 г.

Далее вам нужно будет найти определенный интеграл 95-1}{ln{1.4}} \ &= 13,012188. end{align} ]

Теперь, когда вы нашли значение определенного интеграла, вы делите его на длину интервала, поэтому

[ begin{align} f_{text{avg}} &= frac{13,012188}{5} \ &= 2,6024376. end{align}]

Это означает, что средняя цена на газ в период с 2017 по 2022 год составляет 2,60 доллара за галлон.

Взгляните на графическое представление проблемы:

Графическое представление среднего значения цены на газ 94 right) \ &= frac{1}{4} — 4 \ &= -frac{15}{4}. end{align} ]

Наконец, разделите значение определенного интеграла на длину интервала, так что

[ begin{align} g_{text{avg}} &= frac{1} {1-(-2)}left(-frac{15}{4} right) \ &= -frac{15}{12} \ &= — frac{5}{4}. end{align}]

Следовательно, среднее значение ( g(x) ) в интервале ( [-2,1] ) равно ( -frac{5}{4}. )

Также возможно, что среднее значение функции равно нулю! 92right) \ &= frac{9}{2}-frac{9}{2} \ &= 0. end{align}]

Поскольку определенный интеграл равен 0, вы также получит 0 после деления на длину интервала, поэтому

[ h_{text{avg}}=0.]

Вы также можете найти среднее значение тригонометрической функции. Пожалуйста, ознакомьтесь с нашей статьей о тригонометрических интегралах, если вам нужно освежить знания.

Найдите среднее значение

[f(x) = sin(x)]

на интервале ( left[ 0, frac{pi}{2} right].) 9{ frac { pi} {2}} sin {x} , mathrm {d} x & = left (- cos { frac { pi} {2}} right) — left ( -cos{0} right) \ &= -0-left( -1 right) \ &= 1. end{align}]

Наконец, разделите на длину интервала, поэтому

[ begin{align} f_{text{avg}} &= frac{1}{frac{pi}{2}}\ &= frac{2}{pi}. end{align}]

Это означает, что среднее значение функции синуса на интервале ( left[ 0, frac{pi}{2} right]) равно (frac{2 }{pi},), что примерно равно (0,63.) 9b f(x), dx.]

Среднее значение функционального уравнения выводится из теоремы о среднем значении для интегралов. Как найти среднее значение с помощью теоремы о среднем значении для интегралов на замкнутом интервале с помощью теоремы о среднем значении для интегралов. Лучший способ понять теорему о среднем значении для интегралов — это использовать диаграмму — посмотрите на следующий рисунок.

На графике слева показан прямоугольник, площадь которого явно на меньше , чем площадь под кривой между 2 и 5 на . Этот прямоугольник имеет высоту, равную самой нижней точке кривой в интервале от 2 до 5.

На среднем графике показан прямоугольник, высота которого равна самой высокой точке кривой. Его площадь явно на 90 198 больше 90 199 90 198, чем 90 199 площади под кривой. К этому моменту вы думаете: «Разве нет прямоугольника, который выше короткого и короче длинного, площадь которого равна 9».0198 то же, что и площадь под кривой?» Конечно. И этот прямоугольник явно пересекает кривую где-то на отрезке. Этот так называемый прямоугольник среднего значения, показанный справа, в основном резюмирует теорему о среднем значении для интегралов.

Это просто здравый смысл. Но вот мубо-юмбо.

Теорема о среднем значении для интегралов: Если f ( x ) является непрерывной функцией на отрезке [ a, b ], то существует число c в замкнутом интервале, таком что

Теорема просто гарантирует существование прямоугольника среднего значения.

Площадь прямоугольника среднего значения, которая совпадает с площадью под кривой, равна длина умножить на ширина или основание умножить на высота , верно?

Эта высота представляет собой среднее значение функции за рассматриваемый интервал.

Вот пример. Какова средняя скорость автомобиля между t = 9 секунд и t = 16 секунд, скорость которых в футах per se cond определяется функцией

Согласно определению среднего значения, эта средняя скорость определяется как

1. Определить площадь под кривой между 9 и 16.

   Этот участок, кстати, представляет собой общее пройденное расстояние от 9 до 16 секунд. Вы понимаете, почему? Рассмотрим прямоугольник среднего значения для этой задачи. Его высота — это скорость (поскольку значения функции или высоты — это скорости), а его основание — количество времени, поэтому его площадь равна 9.0198 скорость раз время что равняется расстоянию .

Функция синуса описывает соотношение между радиусом единичной окружности (или окружности в декартовой плоскости с единичным радиусом) и положением оси Y точки на окружности. Дополнительной функцией является косинус, который описывает то же соотношение, но для положения оси x.

Мощность синусоидальной волны относится к переменному току, при котором ток и, следовательно, напряжение, изменяются со временем как синусоидальная волна. Иногда важно рассчитать средние величины для периодических (или повторяющихся) сигналов, таких как переменный ток, при проектировании или создании цепей.

Что такое функция синуса

Будет полезно определить функцию синуса, чтобы понять ее свойства и, следовательно, как рассчитать среднее значение синуса.

В общем, функция синуса, как она определена, всегда имеет единичную амплитуду, период 2π и отсутствие сдвига фазы. Как уже упоминалось, это отношение между радиусом R и положением оси Y , y , точки на окружности радиуса R. По этой причине амплитуда определяется для единичного круга, но может быть масштабирована на R при необходимости.

Сдвиг фазы будет описывать некоторый угол от оси x, где новая «начальная точка» круга была смещена. Хотя это может быть полезно для некоторых проблем, оно не регулирует среднюю амплитуду или мощность синусоидальной функции.

Расчет среднего значения

Помните, что для цепи уравнение для мощности: P = IV, где V — напряжение, а I — ток. Поскольку V = IR, для цепи с сопротивлением R мы теперь знаем, что P = I ² R.

Сначала рассмотрим изменяющийся во времени ток I (t) в форме I (t) = _I ₀ _sin (ωt). Ток имеет амплитуду I ₀ и период 2π / ω. Если известно, что сопротивление в цепи равно R , то мощность как функция времени равна P (t) = I ₀ ² R sin ² ( * ω * t).

Чтобы рассчитать среднюю мощность, необходимо следовать общей процедуре усреднения: общая мощность в каждый момент в интересующем периоде, деленная на период времени, T.

Поэтому вторым шагом является интеграция P (t) за полный период.

Интеграл от I ₀ ² Rsin ² (ωt) за период T определяется как:

frac {I_0 R (T — Cos (2 pi) Sin (2 pi) / omega)} {2} = frac {I_0RT} {2}

Тогда среднее значение является интегральной или общей мощностью, деленной на период Т:

frac {I_0 R} {2}

Может быть полезно знать, что среднее значение квадрата синусоидальной функции за ее период всегда равно 1/2. Запоминание этого факта может помочь в расчете быстрых оценок.

Как рассчитать среднеквадратичную мощность

Так же, как процедура вычисления среднего значения, среднеквадратичное значение является еще одной полезной величиной. Он рассчитывается (почти) точно так, как он назван: возьмите интересующее вас количество, возведите в квадрат, вычислите среднее (или среднее) и затем возьмите квадратный корень. Это количество часто сокращается как RMS.

Итак, какова среднеквадратичная величина синусоиды? Как и прежде, мы знаем, что среднее значение квадрата синусоидальной волны равно 1/2. Если мы возьмем квадратный корень из 1/2, мы можем определить, что среднеквадратичное значение синусоидальной волны составляет приблизительно 0, 707.

Часто при проектировании схемы требуется среднеквадратичное значение тока или напряжения. Самый быстрый способ определить это — определить пиковый ток или напряжение (или максимальное значение волны), а затем умножить пиковое значение на 1/2, если вам нужно среднее значение, или на 0, 707, если вам нужно среднеквадратичное значение.