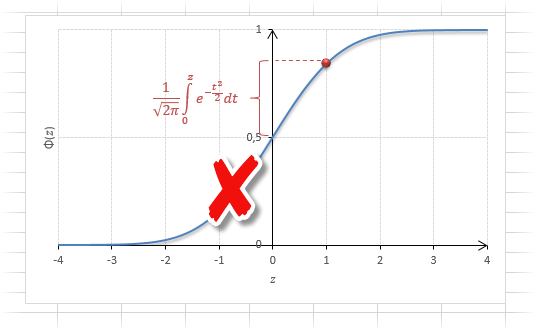
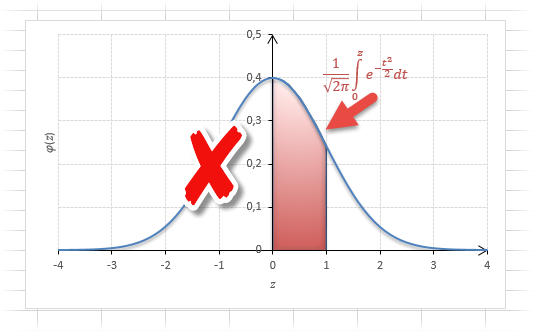
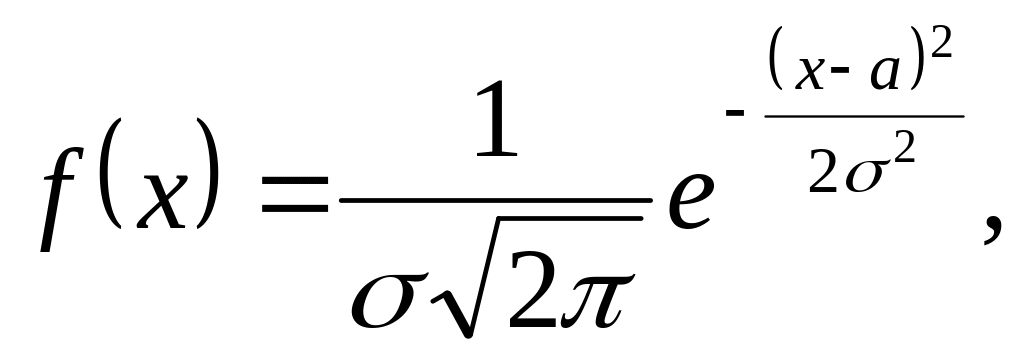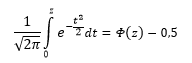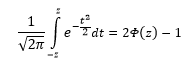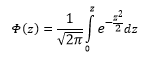Как найти среднее значение в нормальном распределении - Исправление недочетов и поиск решений вместе с Examum.ru

Нормальное распределение

Время на прочтение
7 мин

Количество просмотров 36K

Автор статьи: Виктория Ляликова

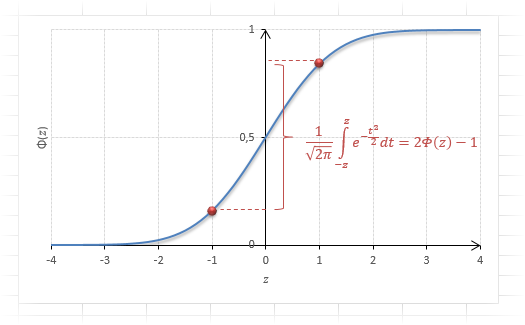
Нормальный закон распределения или закон Гаусса играет важную роль в статистике и занимает особое положение среди других законов. Вспомним как выглядит нормальное распределение

$frac{1}{sigmasqrt{2pi}}e^left(-frac{(x-a)^2)}{2sigma^2}right)$

где a -математическое ожидание, — среднее квадратическое отклонение.

Тестирование данных на нормальность является достаточно частым этапом первичного анализа данных, так как большое количество статистических методов использует тот факт, что данные распределены нормально. Если выборка не подчиняется нормальному закону, тогда предположении о параметрических статистических тестах нарушаются, и должны использоваться непараметрические методы статистики

Нормальное распределение естественным образом возникает практически везде, где речь идет об измерении с ошибками. Например, координаты точки попадания снаряда, рост, вес человека имеют нормальный закон распределения. Более того, центральная предельная теорема вообще утверждает, что сумма большого числа слагаемых сходится к нормальной случайной величине, не зависимо от того, какое было исходное распределение у выборки. Таким образом, данная теорема устанавливает условия, при которых возникает нормальное распределение и нарушение которых ведет к распределению, отличному от нормального.

Можно выделить следующие этапы проверки выборочных значений на нормальность

Подсчет основных характеристик выборки. Выборочное среднее, медиана, коэффициенты асимметрии и эксцесса.
Графический. К этому методу относится построение гистограммы и график квантиль-квантиль или кратко QQ
Статистические методы. Данные методы вычисляют статистику по данным и определяют, какая вероятность того, что данные получены из нормального распределения

При нормальном распределении, которое симметрично, значения медианы и выборочного среднего будут одинаковы, значения эксцесса равно 3, а асимметрии равно нулю. Однако ситуация, когда все указанные выборочные характеристики равны именно таким значениям, практически не встречается. Поэтому после этапа подсчета выборочных характеристик можно переходить к графическому представлению выборочных данных.

Гистограмма позволяет представить выборочные данные в графическом виде – в виде столбчатой диаграммы, где данные делятся на заранее определенное количество групп. Вид гистограммы дает наглядное представление функции плотности вероятности некоторой случайной величины, построенной по выборке.

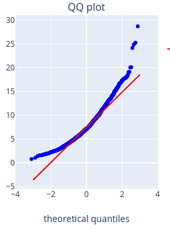
График QQ (квантиль-квантиль) является графиком вероятностей, который представляет собой графический метод сравнения двух распределений путем построения их квантилей. QQ график сравнивает наборы данных теоретических и выборочных (эмпирических) распределений. Если два сравниваемых распределения подобны, тогда точки на графике QQ будут приблизительно лежать на линии y=x. Основным шагом в построении графика QQ является расчет или оценка квантилей.

Существует множество статистических тестов, которые можно использовать для проверки выборочных значений на нормальность. Каждый тест использует разные предположения и рассматривает разные аспекты данных.

Чтобы применять статистические критерии сформулируем задачу. Выдвигаются две гипотезы H0 и H1, которые утверждают

H0 — Выборка подчиняется нормальному закону распределения

H1 — Выборка не подчиняется нормальному распределению

Установи уровень значимости alpha=0,05.

Теперь задача состоит в том, чтобы на основании какого-то критерия отвергнуть или принять основную нулевую гипотезу при уровне значимости

Критерий Шапиро-Уилка

Критерий Шапиро-Уилка основан на отношении оптимальной линейной несмещенной оценки дисперсии к ее обычной оценке методом максимального правдоподобия. Статистика критерия имеет вид

$W=frac{1}{s^2}{sumlimits_{i=1}^n{a_{n-i+1}(x_{n-i+1}-x_{i})}} s^2=sumlimits_{i=1}^n(x_i-overline x^2) overline x=frac{1}{n}sumlimits_{i=1}^n{x}$

Числитель является квадратом оценки среднеквадратического отклонения Ллойда. Коэффициенты ${a_{n-i+1}}$ и критические значения статистики являются табулированными значениями. Если , то нулевая гипотеза нормальности распределения отклоняется на уровне значимости .

В Python функция содержится в библиотеке scipy.stats и возвращает как статистику, рассчитанную тестом, так и значение p. В Python можно использовать выборку до 5000 элементов. Интерпретация вывода осуществляется следующим образом

Если значение , тогда принимается гипотеза H0, в противном случае, т.е. если, , тогда принимается гипотеза H1, т.е. что выборка не подчиняется нормальному закону.

Критерий Д’Агостино

В данном критерии в качестве статистики для проверки нормальности распределения используется отношение оценки Даутона для стандартного отклонения к выборочному стандартному отклонению, оцененному методом максимального правдоподобия

$D=frac{T}{n^2s} T=sumlimits_{i=1}^nbigg(i-frac{n+1}{2}bigg)x_i s^2=sumlimits_{i=1}^n(x_i-overline x^2), {x_1}leq...leq{x_n}$

В качестве статистики критерия Д’Агостино используется величина

$Y=sqrt{n}frac{(D-0,28209479)}{0,02998598}$

значение которой рассчитывается на основе центральной предельной теоремы, которая утверждает, что при

$limlimits_{x to infty}Pbigg(frac{D-M[D]}{sqrt{D[D]}}{<x}bigg)=Phi(x)$

гдестандартная нормальная случайная величина.

Критические значения являются табулированными значениями. Гипотеза нормальности принимается, если значение статистики лежит в интервале критических значений. Данный критерий показывает хорошую мощность против большого спектра альтернатив, по мощности немного уступая критерию Шапиро-Уилка.

В Python функция normaltest() также содержится в библиотеке scipy.stats и возвращает статистику теста и значение p. Интерпретация результата аналогична результатам в критерии Шапиро-Уилка.

Критерий согласия— Пирсона

Данный критерий является одним из наиболее распространенных критериев проверки гипотез о виде закона распределения и позволяет проверить значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Таким образом, данный критерий позволяет проверить гипотезу о принадлежности наблюдаемой выборки некоторому теоретическому закону. Можно сказать, что критерий является универсальным, так как позволяет проверить принадлежность выборочных значений практическому любому закону распределения.

Для решения задачи используется статистика — Пирсона

$G=sumlimits_{k=1}^mfrac{(v_k-np_k)^2}{np_k}$

где — эмпирические частоты (подсчитывается число элементов выборки, попавших в интервал), ${np_k}$ — теоретические частоты. Подсчитывается критическое значение $chi^2_{кр}$ . Если $Ggeq chi^2_{кр}$ , отклоняется гипотеза о принадлежности выборки нормальному распределению и принимается, если $G< chi^2_{кр}$ .

Теперь перейдем к практической части. Для демонстрации функций будем использовать Dataset, взятый с сайта kaggle.com по прогнозированию инсульта по 11 клиническим характеристикам.

Загружаем необходимые библиотеки

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

Загружаем датасет

data_healthcares = pd.read_csv('E:/vika/healthcare-dataset-stroke-data.csv')

Набор состоит из 5110 строк и 12 столбцов.

Посмотрим на основные характеристики, каждого признака.
data_healthcares.describe()

Из данных характеристик можно увидеть, что есть пропущенные значения в показателях индекс массы тела. Посчитаем количество пропущенных значений.

Если бы нам необходимо было делать модель для прогноза, то пропущенные значения bmi являются достаточно большой проблемой, в которой возникает вопрос как их восстановить. Поэтому будем предполагать, что значения столбца bmi (индекс массы тела) подчиняются нормальному закону распределения (предварительно был построен график распределения, поэтому сделано такое предположение). Но так как, на данный момент, у нас нет необходимости в построении модели для прогноза, то удалим все пропущенные значения

new_data=data_healthcares.dropna()

Теперь можем приступать к проверке выборочных значений показателя bmi на нормальность. Вычислим основные выборочные характеристики

Выборочная характеристика	Код в python	Значение характеристики
Выборочное среднее	new_data.bmi.mean()	28,89
Выборочная медиана	new_data.bmi.median()	28,1
Выборочная мода	new_data.bmi.mode()	28,7
Выборочное среднеквадратическое отклонение	new_data.bmi.std()	7.854066729680458
Выборочный коэффициент асиметрии	new_data.bmi.skew()	1.0553402052962928
Выборочный эксцесс	new_data.bmi.kurtosis()	3.362659165623678

После вычислений основных характеристик мы видим, что выборочное среднее и медиана можно сказать принимают одинаковые значения и коэффициент эксцесса равен 3. Но, к сожалению коэффициент асимметрии равен 1, что вводить нас в некоторое замешательство, т.е. мы уже можем предположить, что значения bmi не подчиняются нормальному закону. Продолжим исследования, перейдем к построению графиков.

Строим гистограмму

fig = plt.figure
fig,ax= plt.subplots(figsize=(7,7))
sns.distplot(new_data.bmi,color='red',label='bmi',ax=ax)
plt.show()

Гистограмма достаточно хорошо напоминает нормальное распределение, кроме конечно, небольшого выброса справа, но смотрим дальше. Тут скорее, можно предположить, что значения bmi подчиняются распределению .

Строим QQ график. В python есть отличная функция qqplot(), содержащаяся в библиотеке statsmodel, которая позволяет строить как раз такие графики.

from statsmodels.graphics.gofplots import qqplot
from matplotlib import pyplot
qqplot(new_data.bmi, line=’s’)
Pyplot.show

Что имеем из графика QQ? Наши выборочные значений имеют хвосты слева и справа, и также в правом верхнем углу значения становятся разреженными.

На основе данных графика можно сделать вывод, что значения bmi не подчиняются нормальному закону распределения. Рядом приведен пример QQ графика распределения хи-квадрат с 8 степенями свободы из выборки в 1000 значений.

Для примера построим график QQ для выборки из нормального распределения с такими же показателями стандартного отклонения и среднего, как у bmi.

std=new_data.bmi.std() # вычисляем отклонение
mean=new_data.bmi.mean() #вычисляем среднее
Z=np.random.randn(4909)*std+mean # моделируем нормальное распределение
qqplot(Z,line='s') # строим график
pyplot.show()

Продолжим исследования. Перейдем к статистическим критериям. Будем использовать критерий Шапиро-Уилка и Д’Агостино, чтобы окончательно принять или опровергнуть предположение о нормальном распределении. Для использования критериев подключим библиотеки

from scipy.stats import shapiro
from scipy.stats import normaltest
shapiro(new_data.bmi)
ShapiroResult(statistic=0.9535483717918396, pvalue=6.623218133972133e-37)
Normaltest(new_data.bmi)
NormaltestResult(statistic=1021.1795052962864, pvalue=1.793444363882936e-222)

После применения двух тестов мы имеем, что значение p-value намного меньше заданного критического значения alpha , значит выборочные значения не принадлежат нормальному закону.

Конечно, мы рассмотрели не все тесты на нормальности, которые существуют. Какие можно дать рекомендации по проверке выборочных значений на нормальность. Лучше использовать все возможные варианты, если они уместны.

На этом все. Еще хочу порекомендовать бесплатный вебинар, который 15 июня пройдет на платформе OTUS в рамках запуска курса Математика для Data Science. На вебинаре расскажут про несколько часто используемых подходов в анализе данных, а также разберут, какие математические идеи работают у них под капотом и почему эти подходы вообще работают так, как нам нужно. Регистрация на вебинар доступна по этой ссылке.

Источник

Нормальное распределение

17 авг. 2022 г.
читать 3 мин

Нормальное распределение является наиболее распространенным в статистике распределением вероятностей.

Нормальные распределения имеют следующие особенности:

Форма колокола
Симметричный
Среднее и медиана равны; оба расположены в центре распределения
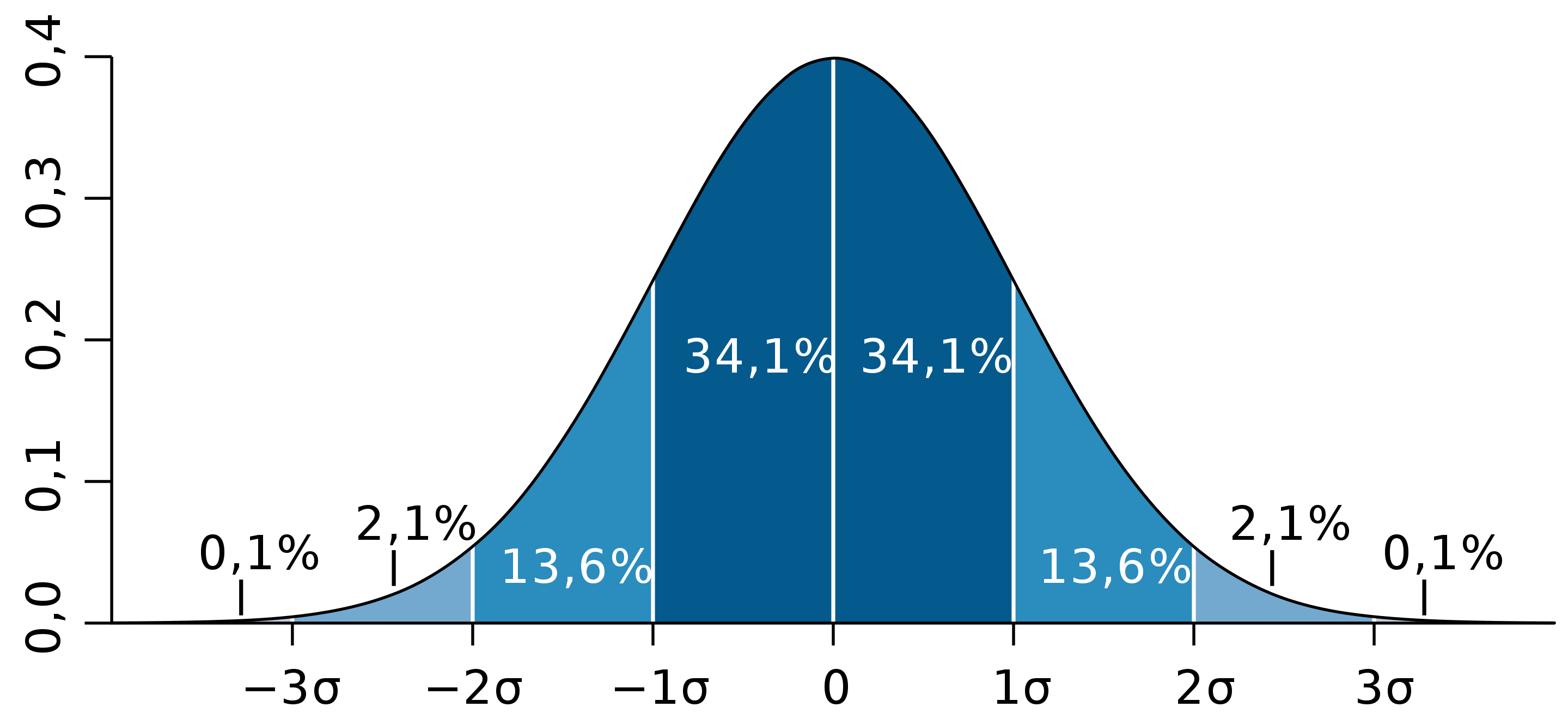
Около 68% данных находятся в пределах одного стандартного отклонения от среднего
Около 95% данных находятся в пределах двух стандартных отклонений от среднего
Около 99,7% данных находятся в пределах трех стандартных отклонений от среднего значения.

Последние три пункта известны как эмпирическое правило , иногда называемое правилом 68-95-99,7 .

Связанный: Эмпирическое правило (практические задачи)

Как нарисовать нормальную кривую

Чтобы нарисовать нормальную кривую, нам нужно знать среднее значение и стандартное отклонение.

Пример 1. Предположим, что рост мальчиков в определенной школе распределен нормально со средним значением μ = 70 дюймов и стандартным отклонением σ = 2 дюйма. Нарисуйте нормальную кривую.

Шаг 1: Нарисуйте нормальную кривую.

Шаг 2: Среднее значение 70 дюймов находится посередине.

Шаг 3: Каждое стандартное отклонение равно расстоянию в 2 дюйма.

Пример 2: Предположим, что вес определенного вида выдр нормально распределен со средним значением μ = 30 фунтов и стандартным отклонением σ = 5 фунтов. Нарисуйте нормальную кривую.

Шаг 1: Нарисуйте нормальную кривую.

Шаг 2: Среднее значение 30 фунтов находится посередине.

Шаг 3: Каждое стандартное отклонение соответствует расстоянию в 5 фунтов.

Как найти проценты, используя нормальное распределение

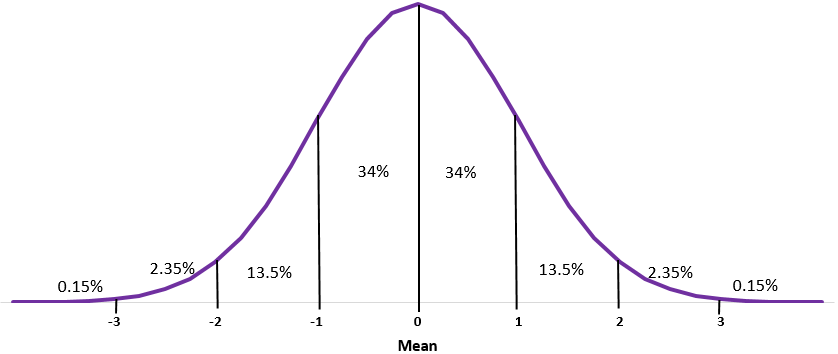
Эмпирическое правило , иногда называемое правилом 68-95-99,7 , гласит, что для случайной величины с нормальным распределением 68 % данных находятся в пределах одного стандартного отклонения от среднего, 95 % — в пределах двух стандартных отклонений от среднего и 99,7% находятся в пределах трех стандартных отклонений от среднего значения.

Используя это правило, мы можем ответить на вопросы о процентах.

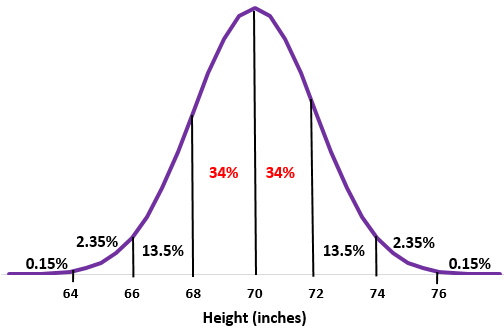
Пример: предположим, что рост мальчиков в определенной школе нормально распределен со средним значением μ = 70 дюймов и стандартным отклонением σ = 2 дюйма.

Приблизительно какой процент мальчиков в этой школе выше 74 дюймов?

Решение:

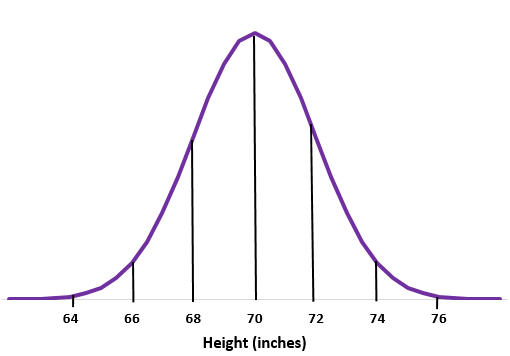
Шаг 1: Нарисуйте нормальное распределение со средним значением μ = 70 дюймов и стандартным отклонением σ = 2 дюйма.

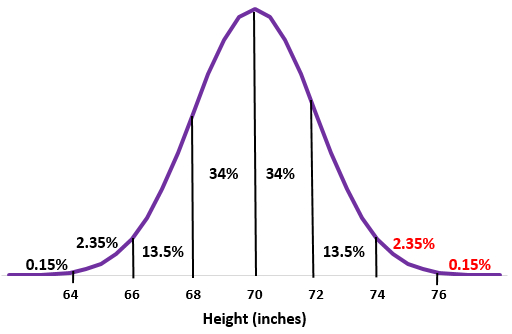
Шаг 2: Рост 74 дюйма на два стандартных отклонения выше среднего. Добавьте проценты выше этой точки в нормальное распределение.

2,35% + 0,15% = 2,5%

Приблизительно 2,5% мальчиков в этой школе выше 74 дюймов.

Приблизительно какой процент мальчиков в этой школе имеет рост от 68 до 72 дюймов?

Решение:

Шаг 2: Высота 68 дюймов и 72 дюйма на одно стандартное отклонение ниже и выше среднего значения соответственно. Просто добавьте проценты между этими двумя точками в нормальном распределении.

34% + 34% = 68%

Приблизительно 68% мальчиков в этой школе имеют рост от 68 до 72 дюймов.

Как найти количество, используя нормальное распределение

Мы также можем использовать эмпирическое правило, чтобы ответить на вопросы о подсчетах.

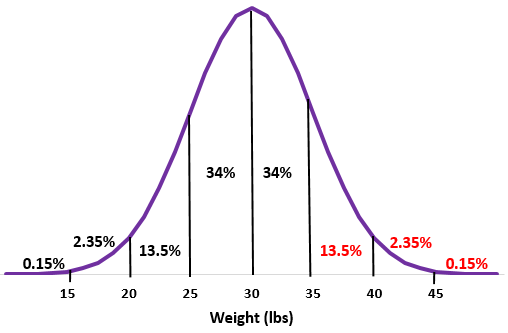
Пример: предположим, что вес определенного вида выдр распределен нормально со средним значением μ = 30 фунтов и стандартным отклонением σ = 5 фунтов.

В одной колонии 200 таких выдр. Примерно сколько из этих выдр весят более 35 фунтов?

Решение:

Шаг 1: Нарисуйте нормальное распределение со средним значением μ = 30 фунтов и стандартным отклонением σ = 5 фунтов.

Шаг 2: Вес 35 фунтов превышает среднее значение на одно стандартное отклонение. Добавьте проценты выше этой точки в нормальное распределение.

13,5% + 2,35% + 0,15% = 16%

Шаг 3: Поскольку в колонии 200 выдр, 16% от 200 = 0,16 * 200 = 32 .

Приблизительно 32 выдры в этой колонии весят более 35 фунтов.

Приблизительно сколько выдр в этой колонии весят менее 30 фунтов?

Вместо того, чтобы проходить все шаги, которые мы только что сделали выше, мы можем признать, что медиана нормального распределения равна среднему значению, которое в данном случае составляет 30 фунтов.

Это означает, что половина выдр весит более 30 фунтов, а половина — менее 30 фунтов. Это означает, что 50% из 200 выдр весят менее 30 фунтов, поэтому 0,5 * 200 = 100 выдр .

Дополнительные ресурсы

Следующие руководства предлагают дополнительную информацию о нормальном распределении:

6 реальных примеров нормального распределения
Нормальное распределение против t-распределения: разница
Как сделать кривую нормального распределения в Excel
Как сделать кривую нормального распределения в Python

Источник

Предлагаю вашему вниманию адаптированный перевод главы книги OnlineStatBook посвященной нормальным распределениям.

Вводный раздел определяет, что значит для распределения быть нормальным и представляет некоторые важные свойства нормального распределения. Интересная история открытия нормального распределения описана во втором разделе. Методы вычисления вероятностей, основанные на нормальном распределении, описаны в разделе «Области нормального распределения». «Разновидности нормального распределения» позволяет вам вводить значения среднего и стандартного отклонения нормального распределения и строить графики получившегося распределения. Часто используемое нормальное распределение, называемое стандартным нормальным распределением, описывается в одноименном разделе. Биномиальное распределение может быть аппроксимировано нормальным. Раздел «Нормальное приближение к биномиальному распределению» показывает это приближение. Демонстрация аппроксимации нормальным распределением позволяет вам исследовать точность этого приближения.

Введение

Нормальное распределение является наиболее важным и широко используемым распределением в статистике. Его иногда называют «колоколообразной кривой», хотя музыкальные качества такого колокола были бы не так приятны. Также его называют «распределением Гаусса» в честь математика Карла Фридриха Гаусса. Как вы увидите в разделе об истории нормального распределения, хотя Гаусс играл в ней важную роль, впервые обнаружил нормальное распределение Абрахам де Муавр.

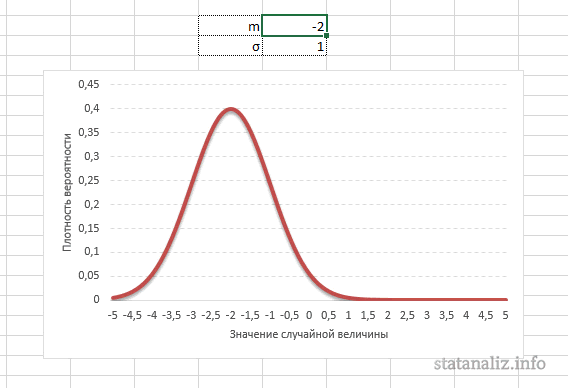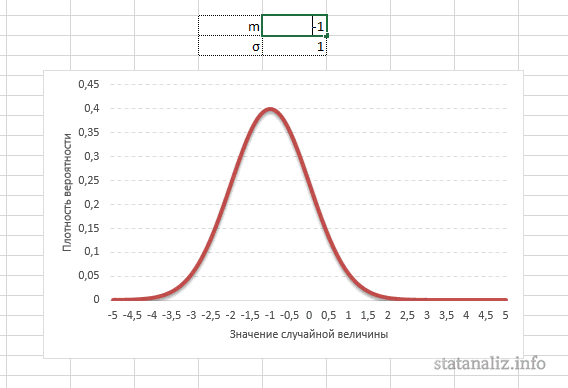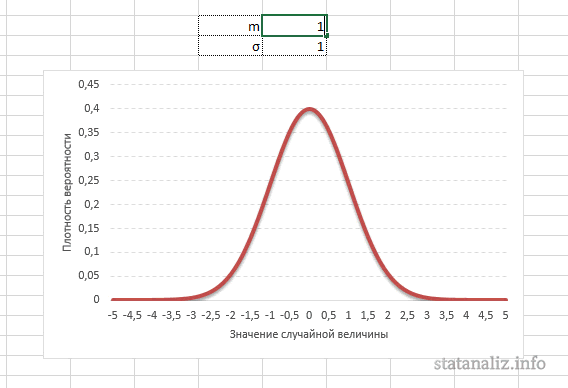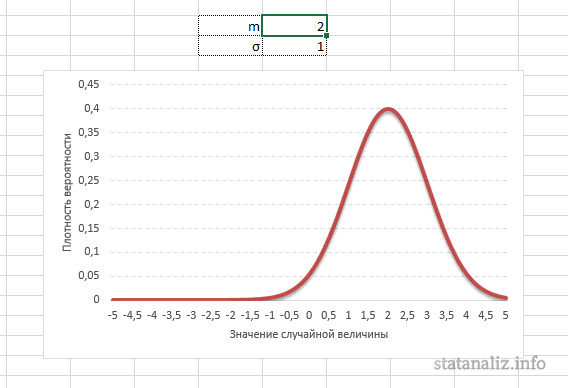
Строго говоря, некорректно говорить о «нормальном распределении» поскольку существует много нормальных распределений. Нормальные распределения могут отличаться своими средними и стандартными отклонениями. На рис. 1 три нормальных распределения. У зеленого (самого левого) среднее равно -3, а стандартное отклонение 0.5, у красного распределения (посередине) среднее равно 0, а стандартное отклонение 1, и у черного распределение (справа) среднее равно 2 а стандартное отклонение 3. Эти, как и все другие нормальные распределения являются симметричными с относительно большими значениями в центре распределения и меньшими значениями в хвостах.

Рисунок 1. Нормальные распределения отличаются средним и стандартным отклонением

Плотность нормального распределения (высота для данного значения на оси x) показана ниже. Нормальное распределение определяется параметрами (mu) и (sigma) являющимися средним и стандартным отклонением соответственно. Символ (e) это основание натурального логарифма, а (pi) это константа пи.

$$
frac{1}{sqrt{2pisigma^2}} e^{frac{-(x-mu)^2}{2sigma^2}}
$$

Поскольку мы не будем углубляться в математическую трактовку статистики, не беспокойтесь, если это выражение вас смущает. Мы не будем возвращаться к нему в следующих разделах.

Семь свойств нормального распределения указаны ниже. Эти свойства будут более подробно проиллюстрированы в следующих разделах этой главы.

Нормальные распределения симметричны относительно своих средних.
Среднее значение, мода и медиана нормального распределения совпадают.
Площадь под нормальным распределением равна 1.
Нормальные распределения плотнее в центре и менее плотны в хвостах.
Нормальные распределения определяются двумя параметрами: среднее (m) и стандартное отклонение (s).
68% площади нормального распределения находится в пределах одного стандартного отклонения от среднего.
Примерно 95% площади нормального распределения находится в пределах двух стандартных отклонений от среднего.

История нормального распределения

В главе посвященной вероятности мы увидели, что биномиальное распределение можно использовать для таких проблем, как: «Если подбросить честную монету 100 раз, какова вероятность выпадения 60 и более орлов?» Вероятность выпадения ровно x орлов за N подбрасываний рассчитывается по формуле:

$$
P(X) = frac{N!}{x!(N-x!)}p^x(1-p)^{N-x}
$$

Где (x) это число орлов (60), (N) – количество подбрасываний монеты (100), а (p) это вероятность выпадения орла (0.5). Таким образом, чтобы решить эту проблему вам нужно вычислить вероятность 60 орлов, затем вероятность 61 орла, 62 и т.д. и сложить эти вероятности. Представьте, сколько времени потребовалось бы для вычисления биномиальных вероятностей до появления калькуляторов и компьютеров.

Абрахам де Муавр, статистик 18-го века и консультант азартных игроков, часто привлекался к проведению этих длительных вычислений. Де Муавр заметил, что, когда число событий (подбрасываний монет) увеличивается, форма биномиального распределения приближается к очень плавной кривой. Биномиальное распределение для 2, 4 и 12 подбрасываний показаны на рис. 2.

Рисунок 2. Примеры биномиальных распределений. Высоты синих столбцов являются вероятностями

Де Муавр рассуждал, что, если бы он мог найти математическое выражение для этой кривой, он мог бы гораздо легче решать такие проблемы, как нахождение вероятности 60 и более орлов из 100 бросков монет. В точности это он и сделал, и кривая, которую он открыл, теперь называется «нормальной кривой».

Рисунок 3. Нормальное приближение биномиального распределения для 12 бросков монет. Гладкая кривая – это нормальное распределение. Обратите внимание, насколько хорошо она аппроксимирует биномиальные вероятности представленные высотой синих линий.

Важность нормальной кривой обусловлена тем, что распределения многих природных явлений, по крайней мере приблизительно, нормально распределены. Одно из первых применений нормального распределения было к анализу ошибок измерений, сделанных при астрономических наблюдениях, ошибок произошедших из-за несовершенства инструментов и наблюдателей. Галилео в 17 веке отметил, что эти ошибки были симметричными и что небольшие ошибки возникали чаще, чем большие. Это привело к нескольким гипотезам о распределении ошибок, но только в начале 19-го века было установлено, что эти ошибки соответствуют нормальному распределению. Независимо друг от друга математики Адрейн в 1808 г. и Гаусс в 1809 г. разработали формулу для нормального распределения и показали, что ошибки хорошо соответствуют этому распределению.

Это же распределение было обнаружено Лапласом в 1778 г., когда он вывел чрезвычайно важную центральную предельную теорему, тему одного из следующих разделов. Лаплас показал, что даже если распределение не является нормальным, средние повторяющихся выборок из распределения будут распределены почти нормально, и чем больше размер выборки, тем ближе к нормальному будет распределение средних.

Большинство статистических процедур для проверки между средними значениями предполагают нормальное распределение. Поскольку распределение средних близко к нормальному, эти тесты работают хорошо даже если само распределение только приблизительно нормально. Кетле был первым, кто применил нормальное распределение к человеческим характеристикам. Он отметил, что такие характеристики, как рост, вес и сила были нормально распределены.

Площади нормального распределения

Площади под кусками нормального распределения могут быть вычислены с использованием математического анализа. Поскольку это нематематический подход к статистике, мы будем полагаться на компьютерные программы и таблицы для определения этих областей. На рис. 4 показано нормальное распределение со средним значением 50 и стандартным отклонением 10. Затененная область между 40 и 60 содержит 68% распределения.

Рисунок 4. Нормальное распределение со средним значением 50 и стандартным отклонением 10. 68% площади находится в пределах одного стандартного отклонения (10) от среднего (50).

На рис. 5 изображено нормальное распределение со средним равным 100 и стандартным отклонением 20. Как и на рис. 4, 68% распределения лежит в пределах одного стандартного отклонения от среднего.

Рисунок 5. Нормальное распределение со средним значением 100 и стандартным отклонением 20. 68% площади находится в пределах одного стандартного отклонения (20) от среднего (100).

Нормальные распределения показанные на рис. 4 и 5 это частные случаи общего правила о том, что 68% площади любого стандартного распределения находится в пределах одного стандартного отклонения от среднего.

На рис. 6 изображено нормальное распределение со средним 75 и стандартным отклонением 10. Закрашенная область содержит 95% площади и находится между 55.4 и 94.6. Для всех нормальных распределений 95% площади находится в пределах 1.96 стандартного отклонения. Для быстрых приближений иногда полезно округлять и использовать 2 вместо 1.96, в качестве числа стандартных отклонений, на которые вам нужно отступить от среднего, чтобы охватить 95% площади.

Рис. 6. Нормальное распределение со средним 75 и стандартным отклонением 10. 95% площади находятся в пределах 1.96 нормального распределения.

Для вычисления площадей под нормальным распределением может быть использован следующий нормальный калькулятор. Например, вы можете использовать его, чтобы найти пропорцию части нормального распределения со средним 90 и стандартным отклонением 12, которая больше 100. Установите среднее равным 90, стандартное отклонение – 12. Затем введите 110 в ячейку справа от кнопки «Above». Внизу экрана вы увидите, что закрашенная область равна 0.0478. Посмотрите сможете ли вы использовать калькулятор, чтобы узнать, что площадь между 115 и 120 равна 0.0124.

Рисунок 7. Изображение калькулятора показывающего площадь над 110.

Скажем, вы хотите найти оценку, соответствующую 75-му перцентилю нормального распределения со средним значением 90 и стандартным отклонением 12. Используя обратный нормальный калькулятор, введите параметры, как показано на рис. 8, и обнаружьте, что площадь ниже 98.09 равна 0.75.

Рисунок 8. Изображение калькулятора показывающего, что 75-ая перцентиль равна 98.09

Стандартное нормальное распределение

Как обсуждалось во вводном разделе, у нормальных распределений не обязательно одинаковые средние и стандартные отклонения. Нормальное распределение со средним равным 0 и стандартным отклонением 1 называется стандартным нормальным распределением.

Области нормального распределения часто представлены таблицами стандартного нормального распределения. Часть таблицы стандартного нормального распределения показана в таблице 9.

Z	Площадь под
-2.5	0.0062
-2.49	0.0064
-2.48	0.0066
-2.47	0.0068
-2.46	0.0069
-2.45	0.0071
-2.44	0.0073
-2.43	0.0075
-2.42	0.0078
-2.41	0.008
-2.4	0.0082
-2.39	0.0084
-2.38	0.0087
-2.37	0.0089
-2.36	0.0091
-2.35	0.0094
-2.34	0.0096
-2.33	0.0099
-2.32	0.0102

Таблица 9. Часть таблицы стандартного нормального распределения.

Первый столбец «Z» содержит значения стандартного нормального отклонения; второй столбец показывает значение площади левее Z. Поскольку среднее распределения равно нулю, а стандартное отклонение 1, в столбец Z равен числу стандартных отклонений левее (или правее) среднего значения. Например, Z равное -2.5 представляет значение равное 2.5 стандартных отклонений левее среднего. Площадь левее Z равна 0.0062.

Ту же информацию можно получить с помощью следующего калькулятора. На рис. 10 показано, как его можно использовать для вычисления площади левее значения -2,5 для стандартного нормального распределения. Обратите внимание, что среднее значение установлено на 0, а стандартное отклонение установлено на 1.

Рисунок 10. Пример работы калькулятора

Значение из любого нормального распределения может быть преобразовано в соответствующее значение в стандартном нормальном распределении при помощи следующей формулы:

$$
Z = frac{(X-mu)}{sigma}
$$

где (Z) это значение стандартного нормального распределения, (X) – значение исходного распределения, (mu) — среднее исходного распределения, а (sigma) — стандартное отклонение исходного распределения.

В качестве простого упражнения, какая часть нормального распределения со средним значением 50 и стандартным отклонением 10 меньше 26? Применяя формулу, получаем:

$$
Z = (26 – 50)/10 = -2.4
$$

Из таблицы 9, мы знаем, что 0.0082 распределения левее -2.4. Нет необходимости преобразовывать значение к (Z) если вы используете апплет как показано на рис. 11.

Рисунок 11. Площадь левее 26 в нормальном распределении со средним 50 и стандартным отклонением 10.

Если все значения распределения преобразовать в (Z) значения, то у распределения будет среднее 0 и стандартное отклонение 1. Процесс преобразования распределения к стандартному со средним 0 и отклонением 1 называется стандартизацией распределения.

Приближение биномиального распределения нормальным

В разделе об истории нормального распределения мы видели, что нормальное распределение можно использовать для аппроксимации биномиального распределения. В этом разделе показывается, как рассчитать эти приближения.

Давайте начнем с примера. Пусть у вас есть честная монета, и вы хотите знать вероятность выпадения 8 орлов за 10 бросков. У биномиального распределения есть среднее равное

(mu = Np = 10*0.5 = 5) и дисперсия (sigma^2 = Np(1-p) = 10*0.5*05 = 2.5). Стандартное отклонение при этом равно 1.5811. Результат 8 орлов равен ((8 — 5)/1.5811 = 1.897) стандартных отклонений правее среднего распределения. «Какова вероятность получения значения в точности равного 1.897 стандартных отклонений правее среднего?» Вы можете удивиться, но ответ равен 0. Вероятность любой отдельной точки равна 0. Проблема в том, что биномиальное распределение является дискретным вероятностным распределением, тогда как нормальное распределение непрерывно.

Решение состоит в том, чтобы округлить и рассмотреть все значения от 7.5 до 8.5, для получения результат 8 орлов. Используя этот подход, мы вычисляем площадь под нормальной кривой от 7.5 до 8.5. Зона зеленого цвета на рис. 12 является приблизительной вероятностью получения 8 орлов.

Рисунок 12. Приближение вероятности 8 орлов нормальным распределением.

Решение состоит в том, чтобы вычислить эту площадь. Сначала мы вычисляем площадь левее 8.5, а затем вычитаем из нее площадь левее 7,5.

Результаты использования калькулятора площади нормального распределения для определения области ниже 8.5 показаны на рисунке 13. Результаты для 7.5 показаны на рисунке 14.

Рисунок 13. Площадь под 8.5

Рисунок 14. Площадь под 7.5

Разница между площадями составляет 0.044, что является приближением биномиальной вероятности. Для этих параметров приближение очень точное.

Если у вас не было калькулятора площади нормального распределения, вы могли бы найти решение с помощью таблицы стандартного нормального распределения (таблица 9) следующим образом:

Найти значение (Z) для 8.5, используя формулу (Z = (8.5 — 5) / 1.5811 = 2.21).
Найти площадь левее (Z) равного 2.21 (= 0,987).
Найти значение (Z) для 7.5, используя формулу (Z = (7.5 — 5) / 1,5811 = 1.58).
Найти площадь левее (Z) 1.58 (= 0.943).
Вычесть значение на шаге 4 из значения на шаге 2, и получить 0.044.

Та же логика применяется при расчете вероятности диапазона результатов. Например, чтобы рассчитать вероятность от 8 до 10 подбрасываний, вычислите площадь от 7.5 до 10.5.

Точность аппроксимации зависит от значений (N) и (p). Эмпирическое правило заключается в том, что аппроксимация хороша, если оба значения (Np) и (N (1-p)) больше 10.

Статистическая грамотность

Анализ рисков часто основан на предположении о нормальном распределении. Критики говорят, что экстремальные явления в действительности происходят чаще, чем можно было бы ожидать, если бы они были нормальными. Предположение даже было названо «большим интеллектуальным мошенничеством».

Недавняя статья, в которой обсуждается, как защитить инвестиции от экстремальных явлений, названных «риск хвоста» и определяемых как «риск хвоста, или экстремальный шок для финансовых рынков, технически определяется как инвестиция, которая двигается на более трех стандартных отклонений от среднего значения нормального распределения возврата инвестиций.»

Риск хвоста можно оценить, предполагая нормальность распределение и вычисляя вероятность такого события. Так ли следует оценивать «риск хвоста»?

События более трех стандартных отклонений от среднего значения очень редки для нормальных распределений. Однако они не так редки для других распределений, например с сильным перекосом. Если нормальное распределение используется для оценки вероятности событий хвоста, определенных таким образом, то «риск хвоста» будет недооценен.

Источник

Нормальное распределение

Нормальное
распределение
– это совокупность объектов, в которой
крайние значения некоторого признака
– наименьшее и наибольшее – появляются
редко; чем ближе значение признака к
математическому ожиданию, тем чаще оно
встречается.

Закон
распределения
вероятностей непрерывной случайной
величины Х
называется нормальным,
если ее дифференциальная функция f(x)
определяется формулой:

где а
совпадает с математическим ожиданием
величины
Х: а=М(Х),
параметр 
совпадает со средним квадратическим
отклонением величины Х:
 =
(Х).
Диаграмма
нормального распределения симметрична
относительно точки а
(математического ожидания). Медиана,
среднее арифметическое нормального
распределения равны тоже а.
При этом в точке а
функция f(x)
достигает своего максимума, который
равен

.

Пример
3:
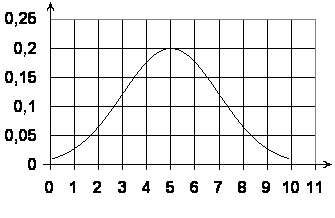
График плотности вероятности нормального
распределения непрерывной величины X
изображен на рисунке. Определите
математическое ожидание, среднее
квадратическое отклонение и максимальное
значение дифференциальной функции
распределения.

Решение.

П
о
графику можно найти максимальное
значение дифференциальной функции
распределения, оно составляет 0,2. Функция
достигает максимума в точке x=5,
следовательно, математическое ожидание
M(X)=5.
В точке максимума функция плотности
вероятности примет вид:

,
следовательно,

В
MS Excel для вычисления значений нормального
распределения используются функция
НОРМРАСП,
которая
вычисляет значения вероятности нормальной
функции распределения для указанного
среднего и стандартного отклонения.

Функция
имеет параметры:

НОРМРАСП
(х;
среднее;
стандартное_откл;
интегральная),

х
– значения выборки, для которых строится
распределение;

среднее
– среднее арифметическое выборки;

стандартное_откл
– стандартное отклонение распределения;

интегральная
– логическое значение, определяющее
форму функции. Если интегральная имеет
значение ИСТИНА(1), то функция НОРМРАСП
возвращает интегральную функцию
распределения; если это аргумент имеет
значение ЛОЖЬ (0), то вычисляется значение
функции плотности распределения.

Если
среднее = 0 и стандартное_откл = 1, то
функция НОРМРАСП
возвращает стандартное нормальное
распределение.

Пример
4:
Составить дифференциальную функцию
распределения непрерывной величины
X,
если известно, что величина распределена
по нормальному закону с параметрами:
математическое ожидание равно -2, а
среднее квадратическое отклонение 2.
Изобразить полученную функцию с помощью
MS Excel.

Решение.

Дифференциальная
функция распределения непрерывной
величины X,
распределенной по нормальному закону,
имеет вид:

где а
– математическое ожидание; 
– среднее квадратическое отклонение.
По условию задачи математическое
ожидание
а=-2;
среднее квадратическое отклонение =2,
следовательно

.

Для
построения графика необходимо выбрать
начальное значение для переменной x.
Серединное значение совпадает с
математическим ожиданием а,
начальное значение отстоит от серединного
не менее чем на ,
поэтому примем начальное значение x=-5.
Запишем в ячейку A1 значение -5, в ячейку
А2 – формулу =А1+0,2 и «протянем» эту
формулу до ячейки А31, в которой получится
значение 1. В ячейку B1 внесем формулу:
=1/(2*КОРЕНЬ(2*ПИ()))*EXP(-((A1+2)^2)/8) и «протянем»
эту формулу до ячейки В31. Выделяем ячейки
в диапазоне А1:В31, выбираем Мастер
диаграмм

Точечная
диаграмма со значениями, соединенными
сглаживающими линиями без маркеров, в
результате получаем график плотности
вероятности нормального распределения.

Пример
5:
Построить график нормальной функции
распределения f(x)
при x,
меняющемся от 19,8 до 28,8 с шагом 0,5, a=24,3
и

=1,5.

Решение.

1.
В ячейку А1 вводим символ случайной
величины х,
а в ячейку B1 – символ функции плотности
вероятности – f(x).

2.
Вводим в диапазон А2:А21 значения х
от 19,8 до 28,8 с шагом 0,5. Для этого
воспользуемся маркером автозаполнения:
в ячейку А2 вводим левую границу диапазона
(19,8), в ячейку A3 левую границу плюс шаг
(20,3). Выделяем блок А2:А3. Затем за правый
нижний угол протягиваем мышью до ячейки
А21 (при нажатой левой кнопке мыши).

3.
Устанавливаем табличный курсор в
ячейку В2 и для получения значения
вероятности воспользуемся специальной
функцией — нажимаем на панели инструментов
кнопку Вставка
функции
f_x.
В появившемся диалоговом окне Мастер
функций – шаг 1 из 2 слева в поле Категория
указаны виды функций. Выбираем
Статистическая.
Справа в поле Функция
выбираем функцию НОРМРАСП.
Нажимаем на кнопку ОК.

4.
Появляется диалоговое окно НОРМРАСП.
В рабочее поле X
вводим адрес ячейки А2 щелчком мыши на
этой ячейке. В рабочее поле Среднее
вводим с клавиатуры значение
математического ожидания (24,3). В
рабочее поле Стандартное_откл
вводим с клавиатуры значение
среднеквадратического отклонения
(1,5). В рабочее поле Интегральная
вводим с клавиатуры вид функции
распределения (0). Нажимаем на кнопку
ОК.

5.
В ячейке В2 появляется вероятность р
= 0,002955. Указателем мыши за правый нижний
угол табличного курсора протягиванием
(при нажатой левой кнопке мыши) из ячейки
В2 до В21 копируем функцию НОРМРАСП
в диапазон В3:В21.

6.
По полученным данным строим искомую
диаграмму нормальной функции
распределения. Щелчком указателя
мыши на кнопке на панели инструментов
вызываем Мастер
диаграмм.
В появившемся диалоговом окне выбираем
тип диаграммы График,
вид – развитие процесса по времени или
по категориям.

После
нажатия кнопки Далее
указываем диапазон данных – В1:В21 (с
помощью мыши). Проверяем, положение
переключателя Ряды в: столбцах. Выбираем
закладку Ряд
и с помощью мыши вводим диапазон подписей
оси X:
А2:А21. Нажав на кнопку Далее,
вводим названия осей Х,
f(x)
и нажимаем на кнопку Готово.

П
олучен
приближенный график нормальной функции
плотности распределения:

Задания
для самостоятельного выполнения

Задание
1.
Закон распределения случайной
величины Х задан таблицей:

Х	0,2	0,4	0,6	0,8	1
Р	0,1	0,2	0,4	р₄	0,1

Найдите
p₄?

Задание
2.
Закон
распределения случайной величины Х
задан таблицей:

Х	3	4	5	6	7
Р	р₁	0,15	р₃	0,25	0,35

Найдите
вероятности
р₁
р₃,
если известно, что р₃
в 4 раза больше р₁?

Задание
3.
Закон
распределения случайной величины
Х
задан таблицей:

Х	2	3	5
р	0,3	0,1	0,6

Найдите
М(Х)
, D(X)
и (Х).

Задание
4.
В
денежной лотерее выпущено 100 билетов.
Разыгрываются 1 выигрыш в 500 руб.
и 10 выигрышей по 100 руб. Найдите закон
распределения случайного выигрыша Х
для владельца одного лотерейного билета.
Определите минимальную стоимость
одного билета

При
некоторых условиях стрельбы вероятность
попадания в цель равна 0,8. Производится
10 выстрелов. Какова вероятность, что
число попаданий в цель будет не менее
двух?
Два
равносильных противника играют в
шахматы. Что вероятнее:

а)
выиграть одну партию из двух или две
партии из четырех?

б)
выиграть не менее двух партий из четырех
или не менее трех партий из пяти?

Задание
7.
Известно,
что непрерывная случайная величина
распределена по нормальному закону,
математическое ожидание равно 4.
Определите значение среднего
квадратического отклонения, если
максимальное значение дифференциальной
функции распределения составляет 0,4.
Постройте график нормального распределения.

Задание
8.
Известно,
что непрерывная случайная величина
распределена по нормированному закону,
где х меняется от 10 до 20. Постройте график
распределения.

Задание
9.
Вероятность
попадания в цель при стрельбе из орудия
р = 0,6. Найдите математическое ожидание
общего числа попаданий, если будет
произведено 10 выстрелов.

Вопросы
для самоконтроля

Чему
равна сумма всех возможных вероятностей
в законе распределения дискретной
случайной величины?

Можно
ли применять формулу Бернулли для
зависимых испытаний?

Какими
должны быть испытания, чтобы можно было
применять формулу Бернулли?
Чему
равно значение непрерывной случайной
величины при котором функция плотности
вероятности этой величины достигает
максимального значения?

Приведите
пример непрерывной случайной величины,
распределенной по нормальному закону?
Как
найти вероятность того, что в n независимых
испытаниях событие A появится хотя бы
один раз?

Математическая
статистика

Основные
умения:
рассчитывать основные статистические
показатели для решения профессиональных
задач; осуществлять самостоятельную
деятельность по сбору, обработке,
группировке, анализу информации;
использовать методы математической
статистики в психолого-педагогических
исследованиях.

Основной
величиной в статистических измерениях
является единица
статистической совокупности (например,
любой из критериев оценки качества
педагога-исследователя). Единица
статистической совокупности характеризуется
набором признаков или параметров.
Значения каждого параметра или признака
могут быть различными и в целом
образовывать ряд случайных значений
x₁,
х₂,
…,
х_n.

Переменная
(variable)
– это параметр измерения, который можно
контролировать или которым можно
манипулировать в исследовании. Так как
значения переменных не постоянны, нужно
научиться описывать их изменчивость.

Для
этого придуманы описательные или
дескриптивные статистики: минимум,
максимум, среднее, дисперсия, стандартное
отклонение, медиана, квартили, мода.

Относительное
значение параметра
– это отношение числа объектов, имеющих
этот показатель, к величине выборки.
Выражается относительным числом или в
процентах (процентное значение).

Пример
1:
Успеваемость в классе = числу положительных
итоговых отметок, деленному на число
всех учащихся класса. Умножение этого
значения на 100 дает успеваемость в
процентах. 25/100=25%

Удельное
значение
данного признака – это расчетная
величина, показывающая количество
объектов с данным показателем, которое
содержалось бы в условной выборке,
состоящей из 10, 100, 1000 и т. д. объектов.

Пример
2:
Для
сравнения уровня правонарушений в
разных регионах берется удельная
величина – количество
правонарушений на 1000 человек
(N).

Минимум
и максимум
– это минимальное и максимальное
значения переменной.

Размах
(R)
–
это
разность между максимальным и минимальным
значением переменной: R= max–min.

Среднее
арифметическое
может вычисляться как по необработанным
первичным данным, так и по результатам
группировки этих данных.

Для
несгруппированных данных:

(1)

где
n
– объем выборки; x_i
– значения выборки.

Для
сгруппированных данных:

(2)

где
n
– объем выборки; k
– число интервалов группировки; n_i–
частоты интервалов; x_i
– срединные значения интервалов.

Пример
3:
Наблюдение посещаемости четырех
внеклассных мероприятий в экспериментальном
(20 учащихся) и контрольном (30) классах
дали значения (соответственно): 18, 20, 20,
18 и 15, 23, 10, 28. Среднее значение посещаемости
в обоих классах получается одинаковое
– 19. Однако видно, что в контрольном
классе этот показатель подчинен
воздействию каких-то специфических
факторов.

Медианой
(Ме)
называется такое значение признака X,
когда одна половина значений
экспериментальных данных меньше ее, а
вторая половина – больше.

Для
вычисления медианы несгруппированных
данных выборку сортируют, находят ранг
R
(порядковый номер) медианы:

(3)

Медианой
будет значение признака, стоящее на R_Ме
месте в ранжированной выборке. Для
нахождения медианы в случае сгруппированных
данных:

(4)

где
х_MeН
– нижняя граница медианного интервала;
h
– ширина интервалов группировки;
n_xMe_–1
– накопленная частота интервала,
предшествующего медианному; n_Me
– частота медианного интервала.

Мода
(Мо)
представляет собой значение признака,
встречающегося в выборке наиболее
часто.

Если
распределение имеет несколько мод, то
говорят, что оно мультимодально
или многомодально
(имеет два или более «пика»). Для
несгруппированных данных мода – это
значение признака с наибольшей
частотой появления.

Для
сгруппированных данных:

(5)

где
x_MoH
– нижняя граница модального интервала,
n_Mo
– частота интервала.

Пример
4:
Найти
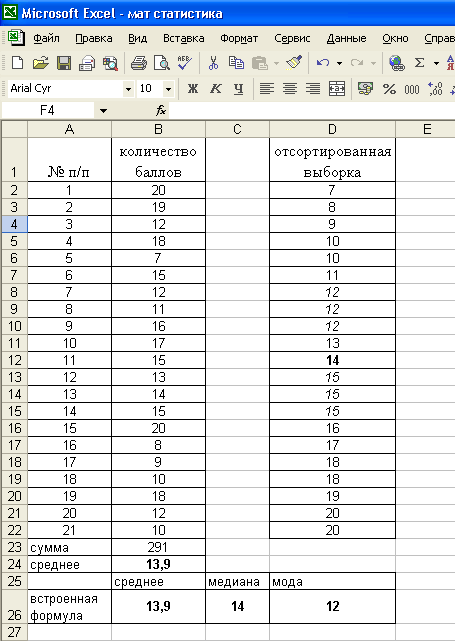
среднее арифметическое, моду и медиану
распределения студентов по числу баллов,
полученных ими на экзамене: 20 19 12 18 7
15 12 11 16 17 15 13 14 15 20 8 9 10 18 12 10.

Решение.

Решим
данную задачу, используя электронные
таблицы MS
Excel.

Внесите
данные задачи в столбец В листа электронных
таблиц, начиная со второй строки. В
столбец А внесите № п/п, проставив
которые получим последний №, соответствующий
объему выборки n=21.

Поставив
курсор в ячейку В23 введем формулу
нахождения среднего значения
=СРЗНАЧ(В2:В22). Можно ввести собственную
формулу: =СУММ(В2:В22)/21.

Для
вычисления медианы, расположим данные
в порядке возрастания: скопируем данные
в столбец D, выделим столбец и отсортируем.
Найдем ранг медианы по формуле (3):

На 11-м месте в ранжированной выборке
стоит значение 14. Ме=14. Используя
встроенную функцию: =МЕДИНА(В2:В22),
получаем то же значение 14.

Для
нахождения моды воспользуемся
ранжированной выборкой, в которой можно
заметить, что наиболее часто (3 раза)
встречаются значения 12 и 15 – значения
несмежные, поэтому выборка имеет 2 моды
и называется бимодальной. Используя
встроенную функцию: =МОДА (В2:В22). Получаем
значение 12 (Excel не рассматривает случаи
бимодальных распределений).

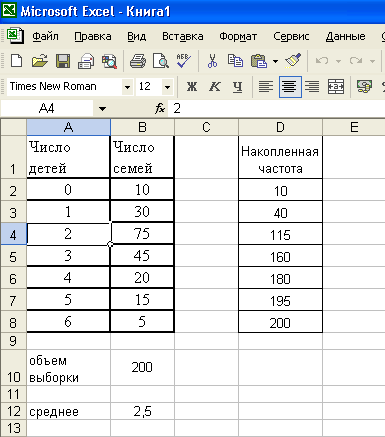
Пример
5:
Дано
распределение семей по числу детей.
Найти моду, медиану и среднее арифметическое.
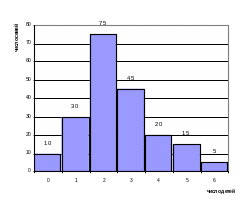
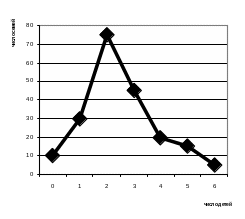
Построить гистограмму и полигон
распределения.

Число детей	0	1	2	3	4	5	6
Число семей	10	30	75	45	20	15	5

Решение.
Значением
признака будет являться число детей, а
частотой – число семей, в которых
содержится такое количество детей.
Найдем среднее арифметическое количества
детей в семье.

Внесем
таблицу на лист электронных таблиц:
число детей – в столбец А; число семей
в столбец В. Данные в таблице являются
сгруппированными.

Н
айдем
общий объем выборки, суммируя данные
столбца числа семей, и занесем в ячейку
В10 формулу =СУММ(В2:В8), получим n=200.
Для нахождения значения среднего
арифметического сгруппированных данных
воспользоваться встроенной функции
невозможно, поэтому применяем формулу
(2) – сумма произведений значений
столбцов А и В =СУММПРОИЗВ(A2:A8;B2:B8)/B10 и
занесем формулу в ячейку В12, получим

.

Для
нахождения медианы необходимо определить
медианный интервал. Медианным
будет
тот интервал, в котором накопленная
частота впервые окажется больше n/2
(n/2=200/2=100).
В столбец D занесем значения накопленных
частот: в D2 – В2, в D3=D2+B3 и т.д. Замечаем,
что накопленная частота больше 100 равная
115 соответствует значению признака 2
ребенка в семье. Ме=2.

Мо=2,
т.к. это значение признака встречается
наиболее часто – 75 раз.

Построим гистограмму:	Построим полигон:

Для
оценки степени разброса (отклонения)
какого-то показателя от его среднего
значения, наряду с максимальным и
минимальным значениями, используются
понятия дисперсии и стандартного
отклонения.

Дисперсия
выборки или выборочная дисперсия
(от
английского variance)
– это
мера изменчивости
переменной.
Термин впервые введен Фишером в 1918
году.

Дисперсия
меняется от нуля до бесконечности.
Крайнее значение 0 означает отсутствие
изменчивости, когда значения переменной
постоянны.

Стандартное
отклонение, среднее квадратическое
отклонение (от
английского standard
deviation) вычисляется
как корень квадратный из дисперсии. Чем
выше дисперсия или стандартное отклонение,
тем сильнее разбросаны значения
переменной относительно среднего.

Пример
7: По данным примера 3,
где приводиится посещаемость четырех
внеклассных мероприятий в экспериментальном
(20 учащихся) и контрольном (30) классах,
рассчитаем дисперсию и стандартное
отклонение:

Классы		D(x)
Экспериментальный	19	1	1
Контрольный	19	48,5	8

Это
означает, что в одном классе посещаемость
высокая, стабильная, а в другом –
отличается непостоянством.

Задания
для самостоятельного выполнения

Задание
1. Найти
среднее арифметическое, моду и медиану
распределения абитуриентов по числу
баллов, полученных ими на экзамене: 80
69 72 44 51 38 62

Задание
2. Рассчитать
описательную статистику для следующего
распределения температуры тела больных
в изоляторе за день: 38 40 37 38 38 40 37 37
38 38 37 39 38 39 38 39 37. Построить дискретный
вариационный ряд и гистограмму, начертить
полигон частот.

Задание
3.

По результатам исследования на вопрос
анкеты: «укажите степень владения
иностранным языком», ответы распределились
следующим образом:

1
– владею свободно – 25

2
– владею в достаточной степени для
общения – 50

3
– владею, но испытываю трудности при
общении – 250

4
– понимаю с трудом – 170

5
– не владею – 10

Найти
среднее значение, медиану и моду выборки.
Постройте гистограмму и полигон частот
по имеющимся данным. Сделайте вывод.

Задание
4.
Педагог-исследователь
провел тестирование интеллекта по тесту
Векслера у 20 школьников и получил
следующие данные: 6, 9, 5, 7, 10, 8, 9, 10, 8, 11, 9,
12, 9, 8, 10, 11, 9, 10, 8, 10. Отсортируйте полученные
данные по убыванию, рассчитайте среднее
значение, моду, медиану, эксцесс и
ассиметрию выборки.

Вопросы
для самоконтроля

В
каких случаях применяется аппарат
математической статистики?

Для
чего предназначен раздел математической
статистики: описательная статистика?

Как
характеризует распределение выборки
стандартное отклонение, ассиметрия и
эксцесс?

В
каких случаях необходим аппарат
математической статистики в деятельности
педагога?

Источник

В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.

Нормальное распределение в статистике

История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.

Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.

Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.

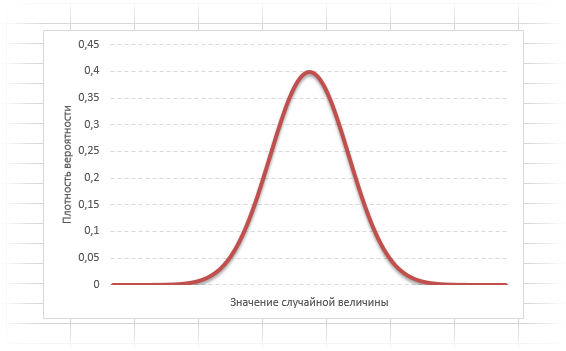
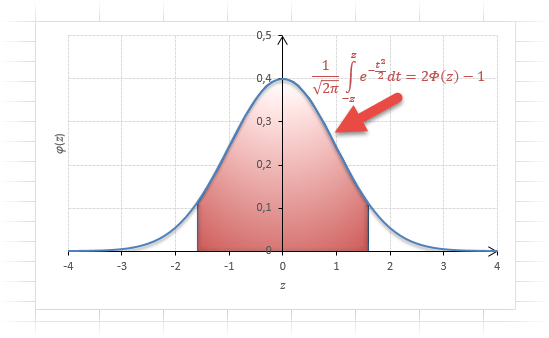
Кривая нормального распределения Гаусса имеет следующий вид.

График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.

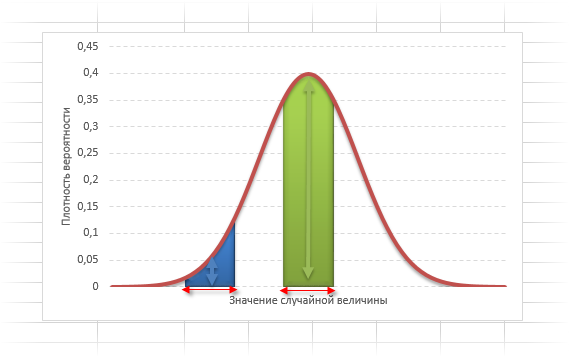
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.

Формула нормального распределения (плотности) следующая.

Формула состоит из двух математических констант:

π – число пи 3,142;

е – основание натурального логарифма 2,718;

двух изменяемых параметров, которые задают форму конкретной кривой:

m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);

σ² – дисперсия;

ну и сама переменная x, для которой высчитывается плотность вероятности.

Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ²). Кратко обозначается N(m, σ²) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ² характеризует размах вариации, то есть «размазанность» данных.

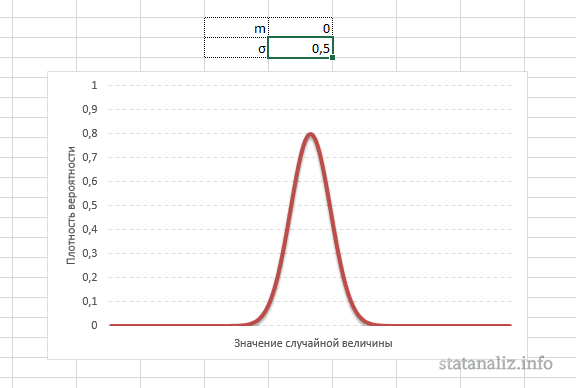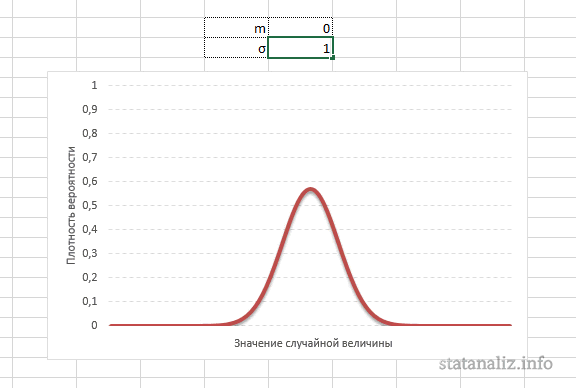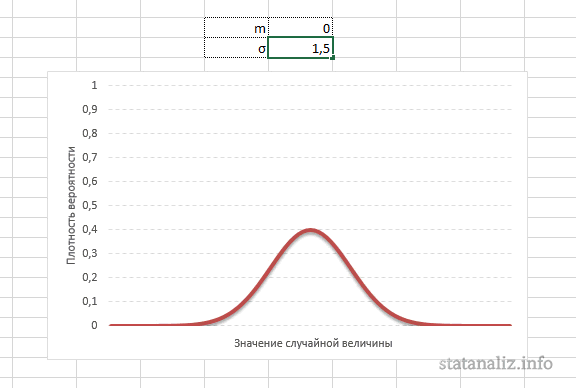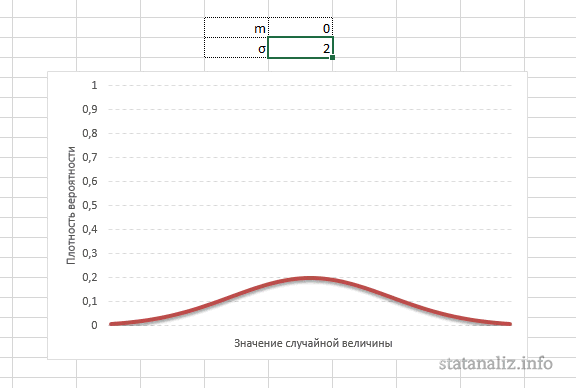
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.

А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.

Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.

Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:

Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как

P(a ≤ X < b) = Ф(b) – Ф(a)

Стандартное нормальное распределение

Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).

Любое нормальное распределение легко превращается в стандартное путем нормирования:

где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.

Для выборочных данных берутся оценки:

Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.

В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.

Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:

Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:

График плотности:

Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e⁰=1 и остается рассчитать только соотношение 1 на корень из 2 пи.

Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.

Функция стандартного нормального распределения позволяет рассчитывать вероятности.

Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.

Таблица нормального распределения

Таблицы нормального распределения встречаются двух типов:

— таблица плотности;

— таблица функции (интеграла от плотности).

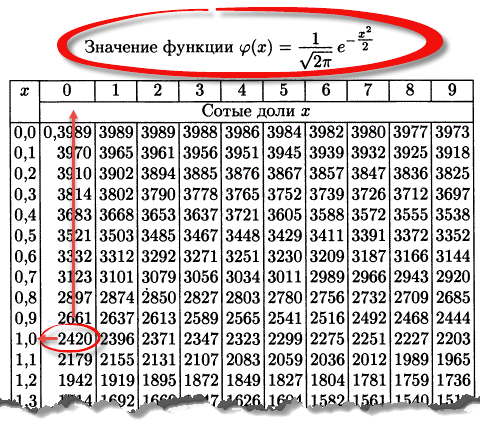
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.

В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).

Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.

Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.

На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.

В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.

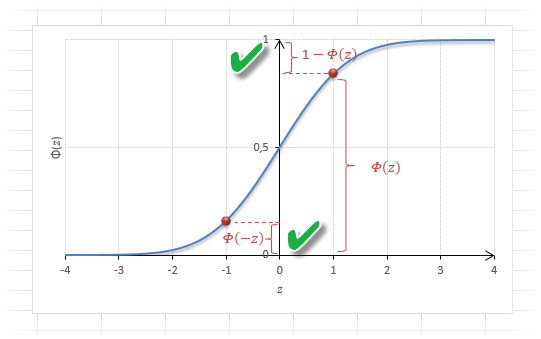
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:

Это факт показан на картинке:

Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.

Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:

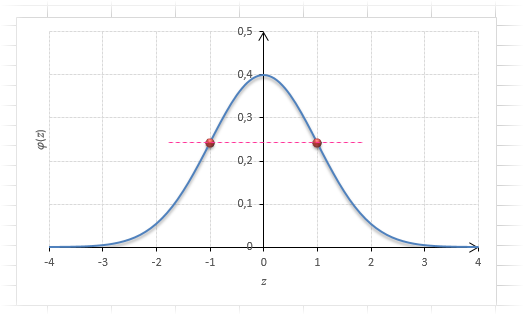
Для наглядности можно взглянуть на рисунок.

На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.

Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:

Рисунок ниже.

Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.

Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.

Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:

Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.

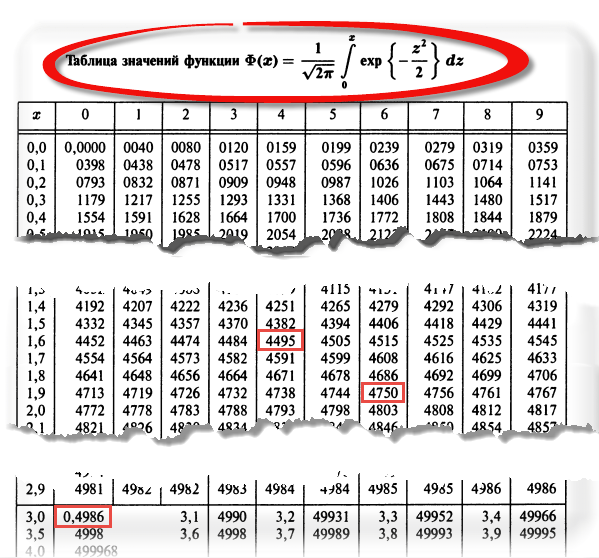
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.

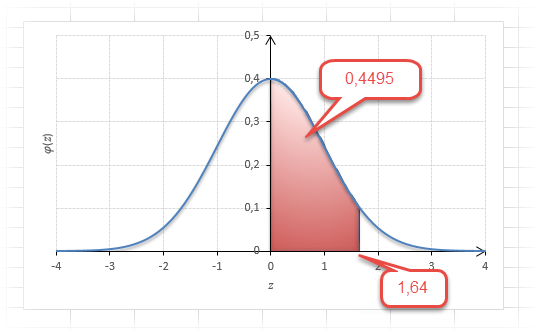
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.

То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.

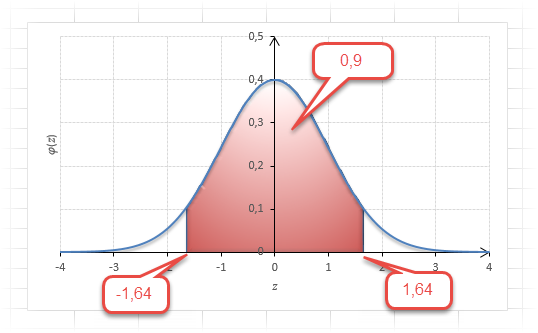
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).

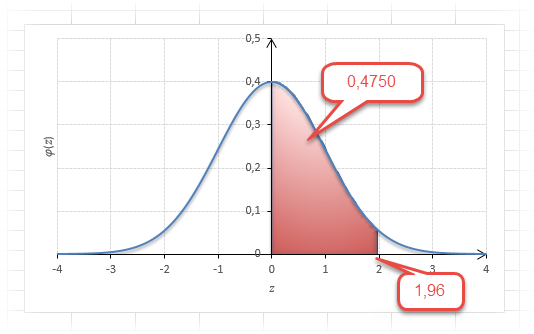
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).

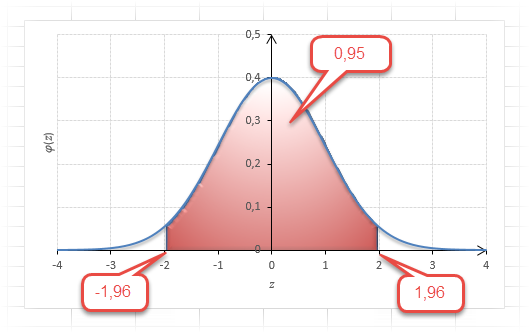
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.

Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.

Так выглядит правило 3 сигм для нормального распределения на диаграмме.

С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.

В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.

Функция НОРМ.СТ.РАСП

Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).

=НОРМ.СТ.РАСП(z;интегральная)

z – значение стандартизованной переменной

интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).

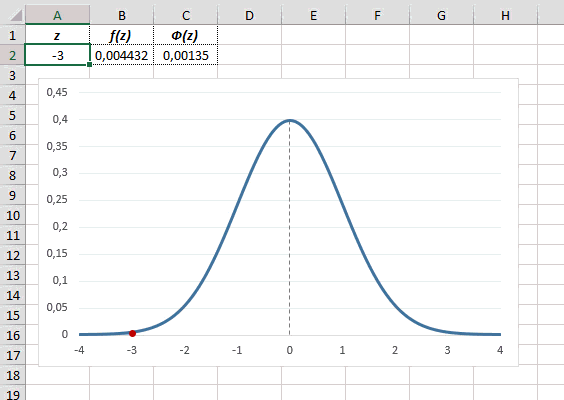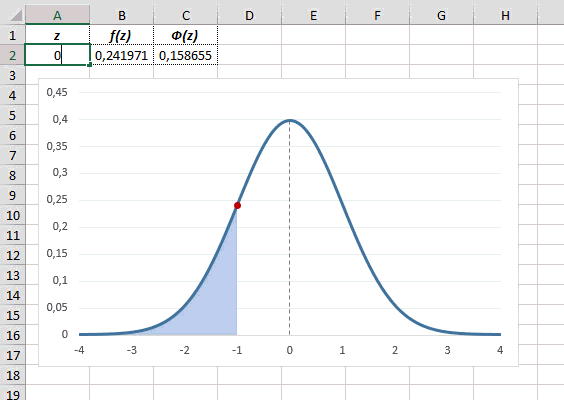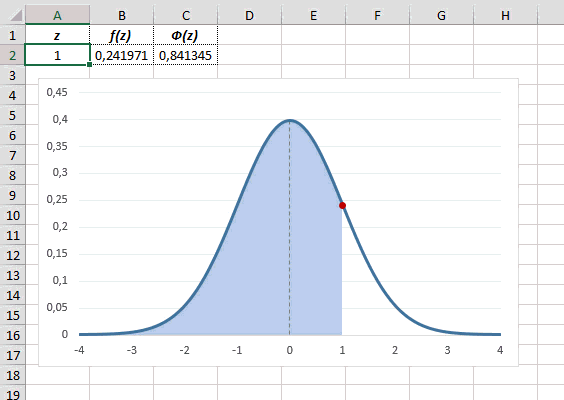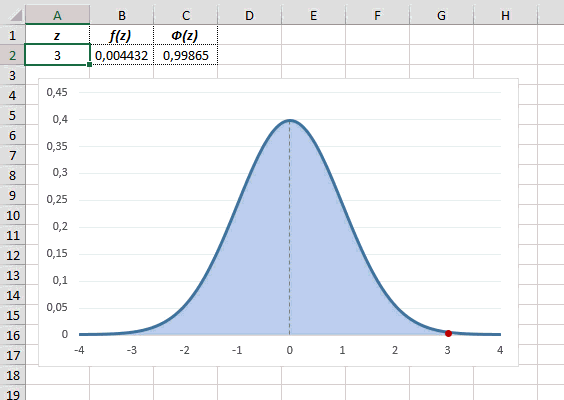
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).

Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.

Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.

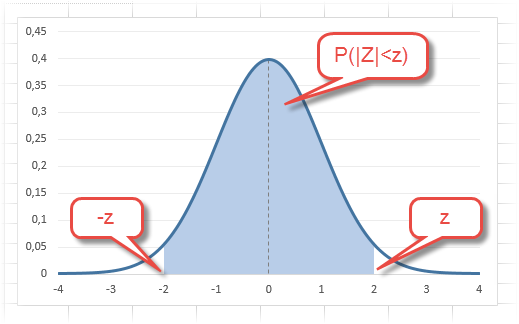
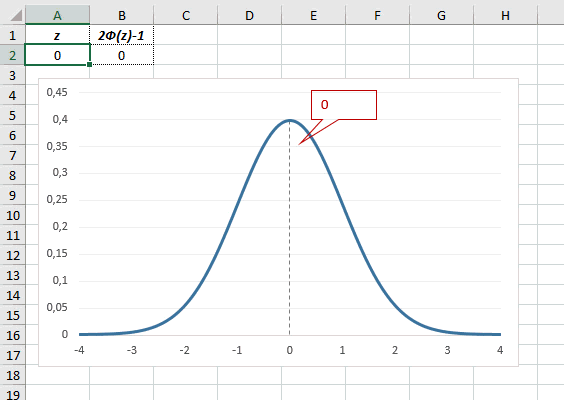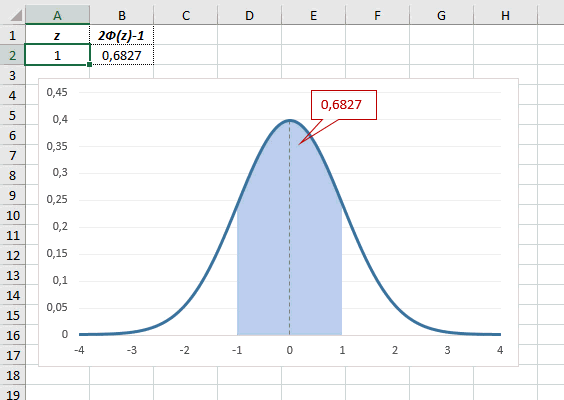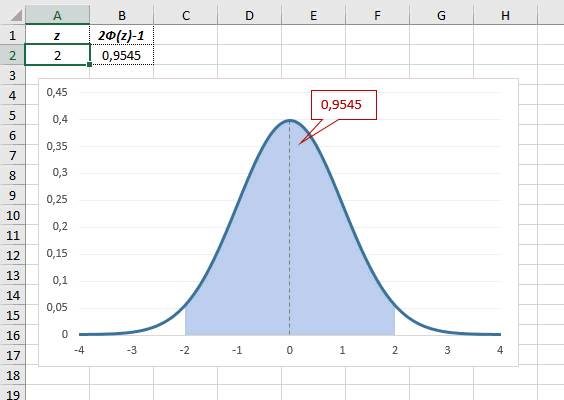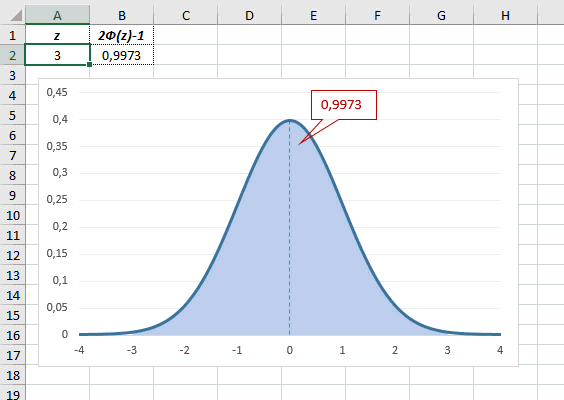
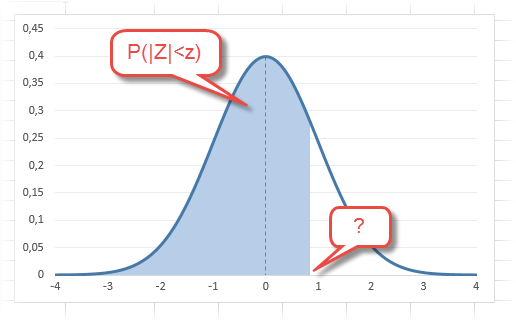
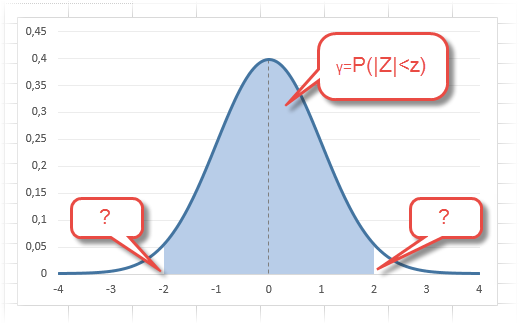
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).

Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.

На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.

Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.

Функция НОРМ.СТ.ОБР

НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:

=НОРМ.СТ.ОБР(вероятность)

вероятность – это вероятность.

Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.

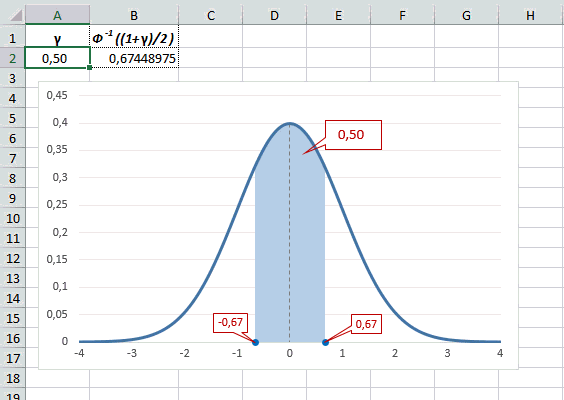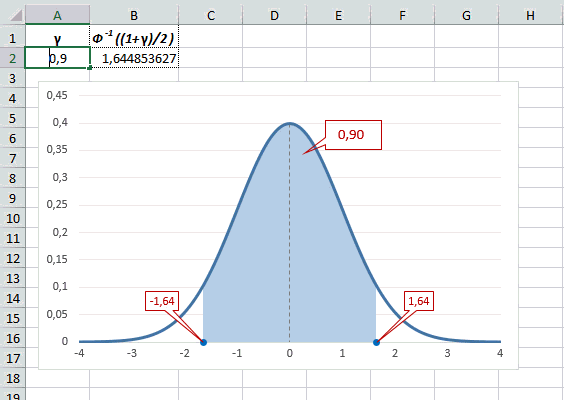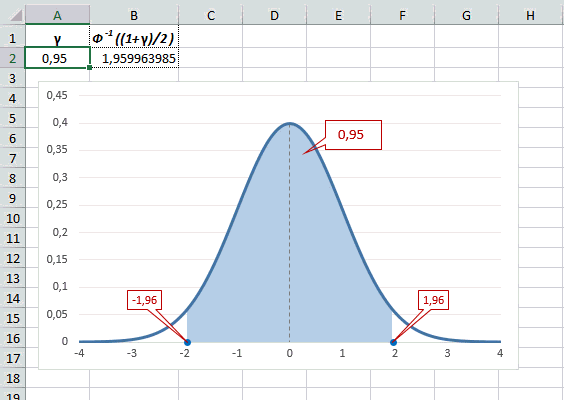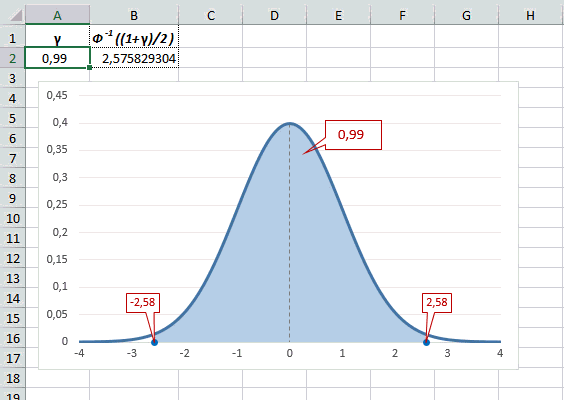
Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.

Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.

Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.

Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.

В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.

Рассмотрим еще пару полезных формул с примерами.

Функция НОРМ.РАСП

Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.

=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)

x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения

среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения

стандартное_откл – среднеквадратичное отклонение – второй параметр модели

интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).

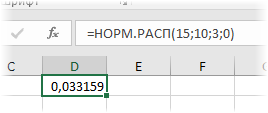
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:

Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.

Функция НОРМ.ОБР

Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.

=НОРМ.ОБР(вероятность;среднее;стандартное_откл)

вероятность – вероятность

среднее – матожидание

стандартное_откл – среднеквадратичное отклонение

Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.

Пример показан в ролике в конце статьи.

Моделирование нормального распределения

Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.

Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.

=НОРМ.ОБР(СЛЧИС();10;3)

Протянем ее на необходимое количество ячеек и нормальная выборка готова.

Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.

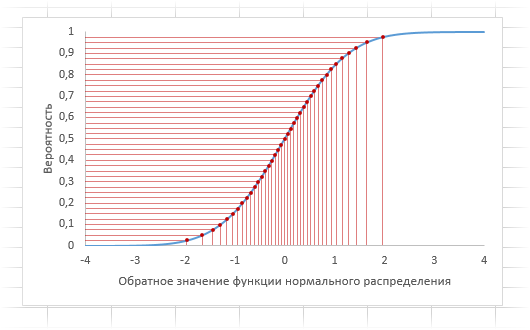
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.

На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.

Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.

Скачать файл с примером.

Поделиться в социальных сетях:

Источник