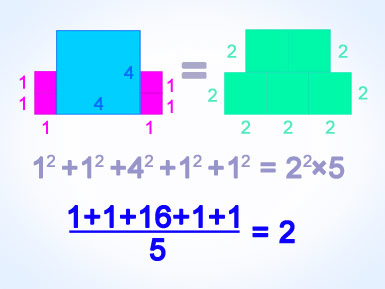Как найти среднеквадратичное число - Исправление недочетов и поиск решений вместе с Examum.ru

From Wikipedia, the free encyclopedia

In mathematics and its applications, the root mean square of a set of numbers $x_{i}$ (abbreviated as RMS, RMS or rms and denoted in formulas as either ${displaystyle x_{mathrm {RMS} }}$ or ${displaystyle mathrm {RMS} _{x}}$ ) is defined as the square root of the mean square (the arithmetic mean of the squares) of the set.^[1]
The RMS is also known as the quadratic mean (denoted $M_{2}$ )^[2]^[3] and is a particular case of the generalized mean. The RMS of a continuously varying function (denoted ${displaystyle f_{mathrm {RMS} }}$ ) can be defined in terms of an integral of the squares of the instantaneous values during a cycle.

For alternating electric current, RMS is equal to the value of the constant direct current that would produce the same power dissipation in a resistive load.^[1]
In estimation theory, the root-mean-square deviation of an estimator is a measure of the imperfection of the fit of the estimator to the data.

Definition[edit]

The RMS value of a set of values (or a continuous-time waveform) is the square root of the arithmetic mean of the squares of the values, or the square of the function that defines the continuous waveform. In physics, the RMS current value can also be defined as the «value of the direct current that dissipates the same power in a resistor.»

In the case of a set of n values ${x_{1},x_{2},dots ,x_{n}}$ , the RMS is

${displaystyle x_{text{RMS}}={sqrt {{frac {1}{n}}left(x_{1}^{2}+x_{2}^{2}+cdots +x_{n}^{2}right)}}.}$

The corresponding formula for a continuous function (or waveform) f(t) defined over the interval $T_{1}leq tleq T_{2}$ is

${displaystyle f_{text{RMS}}={sqrt {{1 over {T_{2}-T_{1}}}{int _{T_{1}}^{T_{2}}{[f(t)]}^{2},{rm {d}}t}}},}$

and the RMS for a function over all time is

${displaystyle f_{text{RMS}}=lim _{Trightarrow infty }{sqrt {{1 over {2T}}{int _{-T}^{T}{[f(t)]}^{2},{rm {d}}t}}}.}$

The RMS over all time of a periodic function is equal to the RMS of one period of the function. The RMS value of a continuous function or signal can be approximated by taking the RMS of a sample consisting of equally spaced observations. Additionally, the RMS value of various waveforms can also be determined without calculus, as shown by Cartwright.^[4]

In the case of the RMS statistic of a random process, the expected value is used instead of the mean.

In common waveforms[edit]

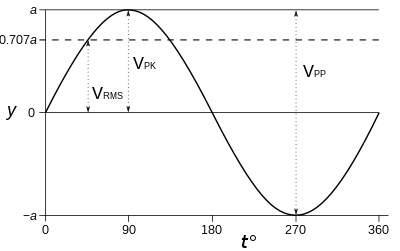
Sine, square, triangle, and sawtooth waveforms. In each, the centerline is at 0, the positive peak is at ${displaystyle y=A_{1}}$ and the negative peak is at ${displaystyle y=-A_{1}}$

A rectangular pulse wave of duty cycle D, the ratio between the pulse duration ( tau ) and the period (T); illustrated here with a = 1.

Graph of a sine wave’s voltage vs. time (in degrees), showing RMS, peak (PK), and peak-to-peak (PP) voltages.

If the waveform is a pure sine wave, the relationships between amplitudes (peak-to-peak, peak) and RMS are fixed and known, as they are for any continuous periodic wave. However, this is not true for an arbitrary waveform, which may not be periodic or continuous. For a zero-mean sine wave, the relationship between RMS and peak-to-peak amplitude is:

Peak-to-peak

{displaystyle =2{sqrt {2}}times {text{RMS}}approx 2.8times {text{RMS}}.}

For other waveforms, the relationships are not the same as they are for sine waves. For example, for either a triangular or sawtooth wave

Peak-to-peak

{displaystyle =2{sqrt {3}}times {text{RMS}}approx 3.5times {text{RMS}}.}

Waveform	Variables and operators	RMS
DC	${displaystyle y=A_{0},}$	${displaystyle A_{0},}$
Sine wave	${displaystyle y=A_{1}sin(2pi ft),}$	${displaystyle {frac {A_{1}}{sqrt {2}}}}$
Square wave	${displaystyle y={begin{cases}A_{1}&operatorname {frac} (ft)<0.5\-A_{1}&operatorname {frac} (ft)>0.5end{cases}}}$	${displaystyle A_{1},}$
DC-shifted square wave	${displaystyle y=A_{0}+{begin{cases}A_{1}&operatorname {frac} (ft)<0.5\-A_{1}&operatorname {frac} (ft)>0.5end{cases}}}$	${displaystyle {sqrt {A_{0}^{2}+A_{1}^{2}}},}$
Modified sine wave	${displaystyle y={begin{cases}0&operatorname {frac} (ft)<0.25\A_{1}&0.25<operatorname {frac} (ft)<0.5\0&0.5<operatorname {frac} (ft)<0.75\-A_{1}&operatorname {frac} (ft)>0.75end{cases}}}$	${displaystyle {frac {A_{1}}{sqrt {2}}}}$
Triangle wave	${displaystyle y=left\|2A_{1}operatorname {frac} (ft)-A_{1}right\|}$	${displaystyle A_{1} over {sqrt {3}}}$
Sawtooth wave	${displaystyle y=2A_{1}operatorname {frac} (ft)-A_{1},}$	${displaystyle A_{1} over {sqrt {3}}}$
Pulse wave	${displaystyle y={begin{cases}A_{1}&operatorname {frac} (ft)<D\0&operatorname {frac} (ft)>Dend{cases}}}$	${displaystyle A_{1}{sqrt {D}}}$
Phase-to-phase voltage	${displaystyle y=A_{1}sin(t)-A_{1}sin left(t-{frac {2pi }{3}}right),}$	${displaystyle A_{1}{sqrt {frac {3}{2}}}}$
where: y is displacement, t is time, f is frequency, A_i is amplitude (peak value), D is the duty cycle or the proportion of the time period (1/f) spent high, frac(r) is the fractional part of r.

In waveform combinations[edit]

Waveforms made by summing known simple waveforms have an RMS value that is the root of the sum of squares of the component RMS values, if the component waveforms are orthogonal (that is, if the average of the product of one simple waveform with another is zero for all pairs other than a waveform times itself).^[5]

${displaystyle {text{RMS}}_{text{Total}}={sqrt {{text{RMS}}_{1}^{2}+{text{RMS}}_{2}^{2}+cdots +{text{RMS}}_{n}^{2}}}}$

Alternatively, for waveforms that are perfectly positively correlated, or «in phase» with each other, their RMS values sum directly.

Uses[edit]

In electrical engineering[edit]

Voltage[edit]

A special case of RMS of waveform combinations is:^[6]

${displaystyle {text{RMS}}_{text{AC+DC}}={sqrt {{text{V}}_{text{DC}}^{2}+{text{RMS}}_{text{AC}}^{2}}}}$

where ${displaystyle {text{V}}_{text{DC}}}$ refers to the direct current (or average) component of the signal, and ${displaystyle {text{RMS}}_{text{AC}}}$ is the alternating current component of the signal.

Average electrical power[edit]

Electrical engineers often need to know the power, P, dissipated by an electrical resistance, R. It is easy to do the calculation when there is a constant current, I, through the resistance. For a load of R ohms, power is defined simply as:

$P=I^{2}R.$

However, if the current is a time-varying function, I(t), this formula must be extended to reflect the fact that the current (and thus the instantaneous power) is varying over time. If the function is periodic (such as household AC power), it is still meaningful to discuss the average power dissipated over time, which is calculated by taking the average power dissipation:

${displaystyle {begin{aligned}P_{av}&=left(I(t)^{2}Rright)_{av}&&{text{where }}left(cdots right)_{av}{text{ denotes the temporal mean of a function}}\[3pt]&=left(I(t)^{2}right)_{av}R&&{text{(as }}R{text{ does not vary over time, it can be factored out)}}\[3pt]&=I_{text{RMS}}^{2}R&&{text{by definition of root-mean-square}}end{aligned}}}$

So, the RMS value, I_RMS, of the function I(t) is the constant current that yields the same power dissipation as the time-averaged power dissipation of the current I(t).

Average power can also be found using the same method that in the case of a time-varying voltage, V(t), with RMS value V_RMS,

${displaystyle P_{text{Avg}}={V_{text{RMS}}^{2} over R}.}$

This equation can be used for any periodic waveform, such as a sinusoidal or sawtooth waveform, allowing us to calculate the mean power delivered into a specified load.

By taking the square root of both these equations and multiplying them together, the power is found to be:

${displaystyle P_{text{Avg}}=V_{text{RMS}}I_{text{RMS}}.}$

Both derivations depend on voltage and current being proportional (that is, the load, R, is purely resistive). Reactive loads (that is, loads capable of not just dissipating energy but also storing it) are discussed under the topic of AC power.

In the common case of alternating current when I(t) is a sinusoidal current, as is approximately true for mains power, the RMS value is easy to calculate from the continuous case equation above. If I_p is defined to be the peak current, then:

${displaystyle I_{text{RMS}}={sqrt {{1 over {T_{2}-T_{1}}}int _{T_{1}}^{T_{2}}left[I_{text{p}}sin(omega t)right]^{2}dt}},}$

where t is time and ω is the angular frequency (ω = 2π/T, where T is the period of the wave).

Since I_p is a positive constant:

${displaystyle I_{text{RMS}}=I_{text{p}}{sqrt {{1 over {T_{2}-T_{1}}}{int _{T_{1}}^{T_{2}}{sin ^{2}(omega t)},dt}}}.}$

Using a trigonometric identity to eliminate squaring of trig function:

${displaystyle {begin{aligned}I_{text{RMS}}&=I_{text{p}}{sqrt {{1 over {T_{2}-T_{1}}}{int _{T_{1}}^{T_{2}}{1-cos(2omega t) over 2},dt}}}\[3pt]&=I_{text{p}}{sqrt {{1 over {T_{2}-T_{1}}}left[{t over 2}-{sin(2omega t) over 4omega }right]_{T_{1}}^{T_{2}}}}end{aligned}}}$

but since the interval is a whole number of complete cycles (per definition of RMS), the sine terms will cancel out, leaving:

${displaystyle I_{text{RMS}}=I_{text{p}}{sqrt {{1 over {T_{2}-T_{1}}}left[{t over 2}right]_{T_{1}}^{T_{2}}}}=I_{text{p}}{sqrt {{1 over {T_{2}-T_{1}}}{{T_{2}-T_{1}} over 2}}}={I_{text{p}} over {sqrt {2}}}.}$

A similar analysis leads to the analogous equation for sinusoidal voltage:

${displaystyle V_{text{RMS}}={V_{text{p}} over {sqrt {2}}},}$

where I_P represents the peak current and V_P represents the peak voltage.

Because of their usefulness in carrying out power calculations, listed voltages for power outlets (for example, 120 V in the US, or 230 V in Europe) are almost always quoted in RMS values, and not peak values. Peak values can be calculated from RMS values from the above formula, which implies V_P = V_RMS × √2, assuming the source is a pure sine wave. Thus the peak value of the mains voltage in the USA is about 120 × √2, or about 170 volts. The peak-to-peak voltage, being double this, is about 340 volts. A similar calculation indicates that the peak mains voltage in Europe is about 325 volts, and the peak-to-peak mains voltage, about 650 volts.

RMS quantities such as electric current are usually calculated over one cycle. However, for some purposes the RMS current over a longer period is required when calculating transmission power losses. The same principle applies, and (for example) a current of 10 amps used for 12 hours each 24-hour day represents an average current of 5 amps, but an RMS current of 7.07 amps, in the long term.

The term RMS power is sometimes erroneously used in the audio industry as a synonym for mean power or average power (it is proportional to the square of the RMS voltage or RMS current in a resistive load). For a discussion of audio power measurements and their shortcomings, see Audio power.

Speed[edit]

In the physics of gas molecules, the root-mean-square speed is defined as the square root of the average squared-speed. The RMS speed of an ideal gas is calculated using the following equation:

${displaystyle v_{text{RMS}}={sqrt {3RT over M}}}$

where R represents the gas constant, 8.314 J/(mol·K), T is the temperature of the gas in kelvins, and M is the molar mass of the gas in kilograms per mole. In physics, speed is defined as the scalar magnitude of velocity. For a stationary gas, the average speed of its molecules can be in the order of thousands of km/hr, even though the average velocity of its molecules is zero.

Error[edit]

When two data sets — one set from theoretical prediction and the other from actual measurement of some physical variable, for instance — are compared, the RMS of the pairwise differences of the two data sets can serve as a measure how far on average the error is from 0. The mean of the absolute values of the pairwise differences could be a useful measure of the variability of the differences. However, the RMS of the differences is usually the preferred measure, probably due to mathematical convention and compatibility with other formulae.

In frequency domain[edit]

The RMS can be computed in the frequency domain, using Parseval’s theorem. For a sampled signal , where is the sampling period,

${displaystyle sum _{n=1}^{N}{x^{2}[n]}={frac {1}{N}}sum _{m=1}^{N}left|X[m]right|^{2},}$

where and N is the sample size, that is, the number of observations in the sample and FFT coefficients.

In this case, the RMS computed in the time domain is the same as in the frequency domain:

${displaystyle {text{RMS}}{x[n]}={sqrt {{frac {1}{N}}sum _{n}{x^{2}[n]}}}={sqrt {{frac {1}{N^{2}}}sum _{m}{{bigl |}X[m]{bigr |}}^{2}}}={sqrt {sum _{m}{left|{frac {X[m]}{N}}right|^{2}}}}.}$

Relationship to other statistics[edit]

If is the arithmetic mean and $sigma _{x}$ is the standard deviation of a population or a waveform, then:^[7]

${displaystyle x_{text{rms}}^{2}={overline {x}}^{2}+sigma _{x}^{2}={overline {x^{2}}}.}$

From this it is clear that the RMS value is always greater than or equal to the average, in that the RMS includes the «error» / square deviation as well.

Physical scientists often use the term root mean square as a synonym for standard deviation when it can be assumed the input signal has zero mean, that is, referring to the square root of the mean squared deviation of a signal from a given baseline or fit.^[8]^[9] This is useful for electrical engineers in calculating the «AC only» RMS of a signal. Standard deviation being the RMS of a signal’s variation about the mean, rather than about 0, the DC component is removed (that is, RMS(signal) = stdev(signal) if the mean signal is 0).

References[edit]

^ ^a ^b «Root-mean-square value». A Dictionary of Physics (6 ed.). Oxford University Press. 2009. ISBN 9780199233991.
^ Thompson, Sylvanus P. (1965). Calculus Made Easy. Macmillan International Higher Education. p. 185. ISBN 9781349004874. Retrieved 5 July 2020.
^ Jones, Alan R. (2018). Probability, Statistics and Other Frightening Stuff. Routledge. p. 48. ISBN 9781351661386. Retrieved 5 July 2020.
^ Cartwright, Kenneth V (Fall 2007). «Determining the Effective or RMS Voltage of Various Waveforms without Calculus» (PDF). Technology Interface. 8 (1): 20 pages.
^
Nastase, Adrian S. «How to Derive the RMS Value of Pulse and Square Waveforms». MasteringElectronicsDesign.com. Retrieved 21 January 2015.
^ «Make Better AC RMS Measurements with your Digital Multimeter» (PDF). Keysight. Keysight. Retrieved 15 January 2019.
^
Chris C. Bissell; David A. Chapman (1992). Digital signal transmission (2nd ed.). Cambridge University Press. p. 64. ISBN 978-0-521-42557-5.
^
Weisstein, Eric W. «Root-Mean-Square». MathWorld.
^ «ROOT, TH1:GetRMS». Archived from the original on 2017-06-30. Retrieved 2013-07-18.

External links[edit]

A case for why RMS is a misnomer when applied to audio power
A Java applet on learning RMS

Cite error: There are <ref group=note> tags on this page, but the references will not show without a {{reflist|group=note}} template (see the help page).

Источник

Что такое среднеквадратичное значение?

Среднеквадратичное значение (RMS) — это квадратный корень из среднего квадрата, который представляет собой среднее арифметическое квадратов набора значений. Это другое название квадратичного среднего. Это частный случай обобщенного среднего, показатель которого равен 2.

Расчетная величина группы чисел представляет собой разницу между двумя наборами данных. Из-за важности больших отклонений среднеквадратичное значение используется чаще, чем среднее арифметическое. Он в основном используется для расчета среднеквадратичного отклонения нескольких значений.

Оглавление

Что такое среднеквадратичное значение?
- Объяснение среднеквадратичного значения
- Приложения RMS
- Формула
- Пример расчета
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи

Формула среднеквадратичного корня дает квадратный корень из всей суммы квадратов каждой точки данных в наблюдении..
Квадратный корень из среднего арифметического квадратов группы значений является их средним квадратом. Он также известен как среднеквадратичное значение.
Его значение больше или равно среднему количеству терминов.
Он имеет множество применений в различных научных, математических и статистических расчетах.

Объяснение среднеквадратичного значения

Среднеквадратичное значение можно определить как изменяющуюся функцию, основанную на интеграле квадратов значений, которые появляются мгновенно в цикле. Другими словами, это квадрат среднего арифметического или квадрат функции. Это метод получения среднего значения набора чисел.

Он рассчитывается путем сложения всех чисел и деления их на общее количество баллов, чтобы получить среднее значение. Можно вычислить среднее значение, если есть набор точек данных, меняющихся вокруг нуля с положительными и n значениями. Однако полученное значение не даст много информации о числах. Таким образом, необходимо вычислить величину.

Для нахождения величины чисел берется среднее абсолютных значений. Это связано с тем, что таким образом легче найти среднюю величину путем нахождения квадратного корня из среднего значения квадратов. В этом методе возведение чисел в квадрат делает их положительными, даже если они отрицательные. В конце концов, чтобы получить значения корней, необходимо извлечь квадратные корни из среднего квадрата.

Среднеквадратичное значение отличается от среднего. Существуют различные способы описания среднего (например, среднее значение, медиана или мода). В нем используется среднее значение, когда оно указано как среднее арифметическое.

Приложения

Среднеквадратичное значение часто используется в различных математических и научных приложениях. Одним из распространенных применений является вычисление среднеквадратичного значения сигнала. Это важно, потому что говорит нам, сколько энергии содержится в волне. Его одно из самых популярных приложений находится в области электротехники.

Например, его часто используют для расчета величины переменного тока или напряжения. Его также можно использовать для определения рассеиваемой мощности резистора. Другое применение — расчет мощности, необходимой для привода определенной нагрузки. Его также можно использовать для измерения изменчивости набора данных. Наконец, в физике его иногда используют для расчета средней кинетической энергии частиц.

Среднеквадратическая ошибка используется для измерения величины дисперсии остатков или ошибок предсказания в расчете. Он обозначает разницу между прогнозируемыми и наблюдаемыми результатами.

Формула

Среднеквадратичное значение заданного набора «n» дискретных наблюдений может быть определено по формуле:

Где x = заданные значения данных

И n = общее количество предметов

Значения сначала возводятся в квадрат, а затем берется среднее значение всех возведенных в квадрат значений. После этого извлекается квадратный корень из среднего.

Для непрерывного набора значений его формула может быть:

Если проводится непрерывный набор наблюдений между временным интервалом T1

Калькулятор среднеквадратичного значения, доступный в Интернете, также можно использовать для легкого расчета.

Пример расчета

Теперь давайте посмотрим, как вычисляется среднеквадратичное значение на примере.

Пусть значения будут 2, 4 и 6,8,10.

Шаг 1:

Берется квадрат этих значений.

22=4

42=8

62=36

82=64,

102=100

Новые полученные значения: 4, 8, 36 и 64 100.

Шаг 2:

Средние квадраты должны быть взяты

Среднее значение=(4+8+36+64, 100)/5= 212/5= 42,4

Шаг 3:

Последним шагом будет извлечение квадратного корня из среднего. Поэтому среднеквадратичное значение будет = 6,5115.

Часто задаваемые вопросы (FAQ)

Как рассчитать среднеквадратичное значение?

Истинное среднеквадратичное значение данного набора наблюдений можно вычислить в три простых шага. Сначала должны быть рассчитаны квадраты для каждого заданного значения. Затем определяется среднее значение полученных площадей. Наконец, на третьем шаге мы можем вычислить квадратный корень из средних значений.

Зачем использовать среднеквадратичное значение вместо среднего?

Среднеквадратичное значение используется, когда переменные, представленные в наборе данных, являются как положительными, так и отрицательными. В то же время среднее как функция используется для определения центральной тенденции конкретного набора данных.

Может ли средний квадрат быть отрицательным?

Приведенные значения возводятся в квадрат, чтобы удалить любые отрицательные числа. Среднеквадратичное значение всегда будет положительным, так как сумма квадратов положительна.

В чем разница между средним квадратом и средним квадратом?

Среднее арифметическое квадратов группы чисел или случайной величины является средним квадратом. Истинное среднеквадратичное значение представляет собой квадратный корень из среднего квадрата и может использоваться для расчета его отклонения.

Среднее квадратическое

Предлагаемая здесь программа, помимо расчета среднего квадратического, умеет еще и приводить исходные данные к стандартному виду, а так же упорядочивать их по возрастанию или убыванию…

Содержание:

Определение среднего квадратического
Свойства среднего квадратического
Расчет среднего квадратического
Прикладное значение среднего квадратического

Среднее квадратическое, как правило, используется тогда, когда смысловое значение имеет квадрат от значений исходной последовательности.
Рассмотрим такую задачу:
Из конверта выпало 2 квадратика со стороной 1 см, затем большой квадратик со стороной 4 см и еще 2 односантиметровых — всего 5 квадратиков.

Какова должна быть сторона у 5 одинаковых квадратиков, занимающих ту же площадь (рисунок на заставке)?
Если предположить, что это будет средняя длина сторон исходных квадратиков

(1+1+4+1+1)/5 = 1,6

то сильно ошибемся: S_{общ ср дл} = (1,6)² × 5 = 12,8.
В то время как

S_{общ кв} = (1)²+(1)²+(4)²+(1)²+(1)²=20; 20 > 12,8

Значит длина стороны одинаковых квадратиков должна быть равна корню квадратному из S_{общ кв}/5, то есть (20/5)^1/2 = (4)^1/2 = 2 (см) — эта длина и есть среднее квадратическое от сторон квадратов!
Прежде чем начать онлайн расчеты будет уместно вспомнить строгое определение предмета счета:

Среднее квадратическое значение множества заданных чисел определяется как число равное квадратному корню от суммы квадратов этих чисел, делённой на их количество:

a_{ср.квадр} =

√

Можно сказать, что среднее квадратическое равно квадратному корню из среднего арифметического^[1] квадратов заданных чисел a₁+ a₂+ …+ a_n и является частным случаем среднего степенного^[2].

Свойства среднего квадратического

1. Среднее квадратическое значение множества заданных неотрицательных чисел лежит между минимальным и максимальным числами из этого множества.

2. Кроме того среднее квадратическое подчиняется неравенству о средних, то есть для любого множества чисел оно не меньше среднего арифметического:

≤

√

Расчет среднего квадратического

Для начала расчета введите исходные числа в одно из полей ввода-вывода данных.
В первое поле можно ввести последовательность чисел, разделенных точкой с запятой (программа попытается так же преобразовать к стандартному виду, например, вставленную копию последовательности чисел с плавающей точкой, разделенных пробелами, запятой или точкой с запятой).
Во второе поле можно вводить числа по одному — они автоматически будут добавляться к данным первого поля, если расчет не запустился автоматически, кликните по зеленой кнопке, показывающей количество чисел в исследуемом массиве:

Введите исходные данные

Введите число

Что-то пошло не так…
Прямое восхождение не может быть больше 24 часов,
минуты и секунды больше 60,
а склонение по абсолютной величине не должно быть больше 90°

Среднее квадратическое, a_{ср.квадр}

Для наглядной демонстрации правила о средних

a_{ср. арифм} ≤ a _{ср.квадр}

выводим так же результат расчета среднего арифметического:

Среднее арифметическое, a_{ср. арифм}

a_{среднее арифметическое} ≤ a _{среднее квадратическое}

Design by Sergey Ov for abc2home.ru

ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:

Сохранить расчет среднего квадратического в истории браузера

Адресную строку с кодом из Ваших данных Вы можете можете переслать на любое устройство и воспроизвести на нем результаты расчетов

После того как будут введены хотя бы два исходных числа цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый и автоматически начнется расчет среднего квадратического и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.

Страницы по теме «Расчет средних значений»

Среднее арифметическое — расчет онлайн, определение, формула
Среднеквадратическое отклонение — расчет онлайн, определение, формула
Среднее геометрическое — расчет онлайн, определение, формула
Среднее гармоническое и среднее степенное — расчет онлайн, определения, формулы
Среднее квадратическое — расчет онлайн, определение, формула

Прикладное значение среднего квадратического

Среднее квадратическое от отклонений значений исследуемых данных находит широкое прикладное применение в метрологии и статистике.
При обработке результатов измерений во многих случаях их окончательные значения определяются как среднее арифметическое от значений, полученных в результате эксперимента, при этом среднеквадратическое отклонение^[3],^[4] величин будет являться оценкой ошибки измерений.
В свою очередь на основе минимизации среднеквадратических отклонений в 19 веке был разработан метод наименьших квадратов, который нашел широкое применение в таких областях как статистический, регрессионный анализ, обработка экспериментальных данных и вычислительная математика.

P.S. На этой странице используется Бета версия программы расчета среднего квадратического, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).

1. Среднее арифметическоезначение (чаще используется термин, просто, «среднее арифметическое» или «среднее») множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:

a_{ср.арифм} =

2. Среднее степенное значение s_d порядка (степени) d от множества заданных чисел a₁+ a₂+ …+ a_n определяется формулой:

s_d =

(

)

1
d

Среднее арифметическое является степенным средним c d = 1, среднее квадратическое — d = 2, среднее гармоническое можно считать степенным средним порядка d = -1.

3. Если вычислено арифметическое среднее заданного множества чисел, то во многих случаях, становится желательной оценка рассеяния значений этих чисел относительно среднего. Оценка расходимости квадратов значений этих чисел от среднего и является оценкой дисперсии.
Вообще термин дисперсия появился в рамках теорий вероятностей. Одной из ее основополагающих характеристик является дисперсия случайной величины как мера разброса значений случайной величины относительно её математического ожидания.
Не углубляясь в дебри Тер-Вера, здесь приводим только используемую для наших расчетов формулу дисперсии:

σ²=

(a₁ — a_cp)² + (a₂ — a_cp)² + …+ (a_n — a_cp)²

4. Среднеквадратическое отклонение σ вычисляется как корень квадратный от дисперсий и возвращает нас в область сопоставимых со средним арифметическим величин:

σ =

√

(a₁ — a_cp)² + (a₂ — a_cp)² + …+ (a_n — a_cp)²

● Главная
▸ Статьи
▸ Блог
▸ Копилка
✔ Среднее квадратическое

Источник

Среднеквадратичное значение

В зарубежной терминологии применяется аббревиатура RMS (rms) — root mean square.
В математике для набора чисел x₁, x₂, …, x_n количеством n среднеквадратичное значение (rms) определяется выражением:

Например, для чисел 2,3 и 6 среднеквадратичным значением будет квадратный корень из (2²+3²+6²)/3. √(49/3) = 4.04

Среднеквадратичным значением двух или нескольких чисел
является квадратный корень из среднеарифметического значения квадратов этих чисел.

Для любой непрерывной функции в интервале T₁ — T₂ среднеквадратичное значение можно рассчитать по формуле:

Среднеквадратичное значение применяется в расчётах, где существует пропорциональная зависимость не самих переменных значений, а их квадратов.

Действующее значение напряжения и тока

В качестве примера можно рассмотреть квадратичную зависимость мощности или работы электрического тока от значений тока или напряжения.

P = I²R; A = I²Rt; P = U²/R; A = U²t/R

Величина постоянного напряжения или тока является его среднеквадратичным значением.
Среднеквадратичное значение переменного тока равно величине постоянного тока,
действие которого произведёт такую же работу в активной (резистивной) нагрузке за время периода.
Определяющим фактором здесь является среднее (среднеарифметическое) значение мощности P_avg
или работы A_avg,
пропорциональное квадрату значения тока.
Так же среднеквадратичное значение переменного напряжения за период равносильно
по своему воздействию на активную нагрузку такому же значению постоянного напряжения.

P = UI = P_avg = U_rmsI_rms

Среднеквадратичное значение переменного напряжения или тока часто называют действующим или эффективным.

Величину переменного напряжения или тока, в большинстве случаев,
выражают его среднеквадратичным значением и измеряют приборами электромагнитного типа или специальными среднеквадратичными измерителями — True RMS.

Примечание:
Электромагнитные приборы используют для измерения переменного тока и напряжения в промышленных установках.
Усилие, создаваемое измерительной катушкой в электромагнитном приборе, пропорционально квадрату тока, поэтому не меняется по направлению.
Угол отклонения стрелки определится некоторым средним усилием F, которое будет пропорционально среднеквадратичному значению тока.

Расчёт действующего значения

В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.

Запишем выражение U_rms с применением интеграла функции
U = U_ampsin(t) для одного периода 2π :

Показать расчёт

Скрыть расчёт

Вынесем U_amp из под знака радикала.
Воспользуемся табличным интегралом ,
перепишем и решим последнее выражение с применением формулы Ньютона-Лейбница:

Так как sin(2π), sin(4π) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:

В результате решения в итоге получим:

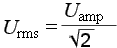
Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T
для функции , представленной на рисунке:

Выразим U_rms искомой функции с помощью определённого интеграла:

Показать расчёт

Скрыть расчёт

Используя табличный интеграл
и формулу Ньютона-Лейбница, получаем:

В итоге преобразований получим:

Ток или напряжение любой сложной формы можно рассмотреть, как набор функций в пределах периода.
Тогда значением RMS будет квадратный корень из среднеарифметического значения интегралов для квадрата каждой функции, ограниченной её интервалом времени в периоде.
Например, для множества функций F₁(t) , F₂(t) , … , F_n(t)
в соответствующих им интервалах времени (0 — T₁), (T₁ — T₂), …, (T_n — T),
составляющих период T, действующее напряжение (RMS) определится выражением:

Для вариантов однополярного или двуполярного напряжения пилообразной и треугольной формы в периоде 2T или 4T, представленных на рисунке ниже,
T и U _amp имеют те же расчётные величины,
что и в рассмотренном случае c функцией ,
а интегралы, определённые в интервалах, равных T, для квадратов используемых функций ,
будут иметь одно и то же значение

Следовательно, вышеуказанные варианты однополярного или двуполярного напряжения пилообразной и треугольной формы будут иметь
среднеквадратичное значение .

В заключении рассмотрим пример вычисления действующего значения положительных прямоугольных импульсов длительностью T_i .

Выразим U_rms одного периода T, как квадратный корень из среднеарифметического значения интегралов,
определённых в интервалах 0 — T_i и T_i — T для квадратов всех значений периода.

В результате получаем значение RMS, равное произведению амплитуды импульсов U_amp на квадратный корень из
коэффициента заполнения (T_i / T).

В качестве дополнительного материала предлагаем рассмотреть расчёт средеквадратичного значения напряжения накала кинескопа цветного телевизора, исходя из амплитуды и формы напряжения.

Замечания и предложения принимаются и приветствуются!

Источник

Загрузить PDF

Вычислив среднеквадратическое отклонение, вы найдете разброс значений в выборке данных.^[1] Но сначала вам придется вычислить некоторые величины: среднее значение и дисперсию выборки. Дисперсия – мера разброса данных вокруг среднего значения.^[2] Среднеквадратическое отклонение равно квадратному корню из дисперсии выборки. Эта статья расскажет вам, как найти среднее значение, дисперсию и среднеквадратическое отклонение.

1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.^[3]
- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
2
Для вычисления среднего значения понадобятся все числа данного набора данных.^[4]
- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
3
Сложите все числа вашего набора данных.^[5]
- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.^[6]
- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Реклама

1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.^[7]
- Эта величина даст вам представление о том, как разбросаны данные выборки.
- Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
- Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
- Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.^[8]
- В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
- 10 — 8 = 2; 8 — 8 = 0, 10 — 2 = 8, 8 — 8 = 0, 8 — 8 = 0, и 4 — 8 = -4.
- Проделайте вычитания еще раз, чтобы проверить каждый ответ. Это очень важно, так как полученные значения понадобятся при вычислениях других величин.
3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.^[9]
- При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
- Возведите эти значения в квадрат: 2², 0², 2², 0², 0², и (-4)² = 4, 0, 4, 0, 0, и 16.
- Проверьте ответы, прежде чем приступить к следующему шагу.
4
Сложите квадраты значений, то есть найдите сумму квадратов.^[10]
- В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
- Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сумма квадратов равна 24.
5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке. Таким образом, вы получите дисперсию.^[11]
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
- n-1 = 5.
- В нашем примере сумма квадратов равна 24.
- 24/5 = 4,8
- Дисперсия данной выборки равна 4,8.
Реклама

1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.^[12]
- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.^[13]
- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.^[14]
- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.
Реклама

Об этой статье

Эту страницу просматривали 64 925 раз.

Была ли эта статья полезной?

Источник

Definition[edit]

In common waveforms[edit]

In waveform combinations[edit]

Uses[edit]

In electrical engineering[edit]

Voltage[edit]

Average electrical power[edit]

Speed[edit]

Error[edit]

In frequency domain[edit]

Relationship to other statistics[edit]

See also[edit]

References[edit]

External links[edit]

Что такое среднеквадратичное значение?

Объяснение среднеквадратичного значения

Приложения

Формула

Пример расчета

Часто задаваемые вопросы (FAQ)

Рекомендуемые статьи

Среднее квадратическое

Свойства среднего квадратического

Расчет среднего квадратического

Что-то пошло не так… Прямое восхождение не может быть больше 24 часов, минуты и секунды больше 60, а склонение по абсолютной величине не должно быть больше 90°

Страницы по теме «Расчет средних значений»

Прикладное значение среднего квадратического

Среднеквадратичное значение

Действующее значение напряжения и тока

Расчёт действующего значения

Об этой статье

Была ли эта статья полезной?

Что-то пошло не так…
Прямое восхождение не может быть больше 24 часов,
минуты и секунды больше 60,
а склонение по абсолютной величине не должно быть больше 90°