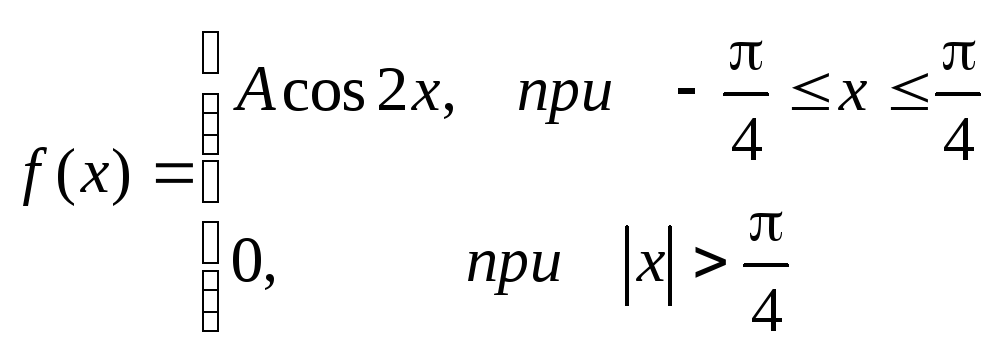Как найти среднеквадратичное отклонение функции - Исправление недочетов и поиск решений вместе с Examum.ru

В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).

Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

Определите среднее (простое среднее арифметическое ряда значений).
Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Порода собаки	Рост в миллиметрах
Ротвейлер	600
Бульдог	470
Такса	170
Пудель	430
Мопс	300

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее $=frac{600+470+170+430+300}{5} = 394$ мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить отклонение роста каждой из собак от среднего:

$[ begin{array}{l} 1: 600-394 = 206 \ 2: 470-394 = 76 \ 3: 170-394 = -224\ 4: 430-394 = 36\ 5: 300-394 = -94 end{array} ]$

Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Дисперсия $= frac{206^2+76^2+(-224)^2+36^2+(-94)^2}{5} = 21704$ мм².

Таким образом, дисперсия составляет 21704 мм².

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

мм (округлено до ближайшего целого значения в мм).

Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть значений, то:

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

Дисперсия выборки = $frac{108520}{4}=27130$ мм².

При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Примечание. Почему именно квадраты разностей?

Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:

$frac{4+4-4-4}{4}=0$ .

Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?

$frac{4+4+|-4|+|-4|}{4} = frac{4+4+4+4}{4}=4$ .

На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:

$frac{7+1+|-6|+|-2|}{4} = frac{7+1+6+2}{4}=4$ .

Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.

А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).

Для первого примера получится:

$sqrt{frac{4^2+4^2+(-4)^2+(-4)^2}{4}}=4$ .

Для второго примера получится:

$sqrt{frac{7^2+1^2+(-6)^2+(-2)^2}{4}}=4.74$ .

Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.

Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.

И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.

О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич

Источник

Загрузить PDF

Вычислив среднеквадратическое отклонение, вы найдете разброс значений в выборке данных.^[1] Но сначала вам придется вычислить некоторые величины: среднее значение и дисперсию выборки. Дисперсия – мера разброса данных вокруг среднего значения.^[2] Среднеквадратическое отклонение равно квадратному корню из дисперсии выборки. Эта статья расскажет вам, как найти среднее значение, дисперсию и среднеквадратическое отклонение.

1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.^[3]
- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
2
Для вычисления среднего значения понадобятся все числа данного набора данных.^[4]
- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
3
Сложите все числа вашего набора данных.^[5]
- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.^[6]
- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Реклама

1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.^[7]
- Эта величина даст вам представление о том, как разбросаны данные выборки.
- Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
- Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
- Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.^[8]
- В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
- 10 — 8 = 2; 8 — 8 = 0, 10 — 2 = 8, 8 — 8 = 0, 8 — 8 = 0, и 4 — 8 = -4.
- Проделайте вычитания еще раз, чтобы проверить каждый ответ. Это очень важно, так как полученные значения понадобятся при вычислениях других величин.
3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.^[9]
- При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
- Возведите эти значения в квадрат: 2², 0², 2², 0², 0², и (-4)² = 4, 0, 4, 0, 0, и 16.
- Проверьте ответы, прежде чем приступить к следующему шагу.
4
Сложите квадраты значений, то есть найдите сумму квадратов.^[10]
- В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
- Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сумма квадратов равна 24.
5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке. Таким образом, вы получите дисперсию.^[11]
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
- n-1 = 5.
- В нашем примере сумма квадратов равна 24.
- 24/5 = 4,8
- Дисперсия данной выборки равна 4,8.
Реклама

1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.^[12]
- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.^[13]
- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.^[14]
- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.
Реклама

Об этой статье

Эту страницу просматривали 64 925 раз.

Была ли эта статья полезной?

Источник

Что такое среднеквадратичное отклонение

Рассматривая какие-либо величины или их изменения, используют такие критерии как среднеарифметическая величина и ее отклонение. Различные понятия позволяют оценить разброс измеряемой величины и ее отклонение. К ним относится абсолютная погрешность, которая показывает насколько каждая конкретная величина отличается от среднего значения. Но так как сумма всех абсолютных погрешностей равна нулю, то этот критерий не позволяет показать разброс измеряемых величин. И для решения этой задачи был введен новый показатель — среднее квадратичное отклонение.

Для того чтобы объяснить его смысл необходимо вспомнить некоторые основные математические понятия.

Определение

Средней величиной или средним арифметическим называется число, полученное в результате деления суммы всех величин на их количество.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Пример

Среднеарифметическое для 3 чисел b₁, b₂ и b₃ определяется как:

(M=frac{b_1+b_2+b_3}3)

Со средней величиной непосредственно связана и другая характеристика — математическое ожидание.

Определение

Значение среднего арифметического некоторого множества при стремлении его членов к бесконечности называется математическим ожиданием (М).

А оценкой математического ожидания является среднее арифметическое определенного числа измерений изучаемой величины.

Определение

Вариантой или абсолютной погрешностью называется разность измеряемой величины со средним значением.

Она обозначается греческой буквой D. Для того чтобы найти варианту единичного измерения ai следует отнять от ее значение среднее арифметическое:

(Da_i=a_i-M)

Также для оценки единичного измерения используется и относительная погрешность, значение которой выражается в процентах. Ее вычисление проводят по формуле:

(sigma=frac{left|triangle a_iright|}Mtimes100%)

Относительная погрешность каждой величины позволяет отбросить из вариации измерений значения с очень большой погрешностью и проводить дальнейший анализ только величин с незначительной относительной погрешностью.

Характеристикой распределения значений некоторой измеряемой величины является дисперсия (D).

Определение

Дисперсией называется среднее арифметическое квадратов всех абсолютных погрешностей.

Теперь можно дать определение и «среднеквадратичному отклонению».

Определение

Значение корня квадратного из дисперсии случайной величины называется среднеквадратичным отклонением и обозначается «ϭ».

Оно вычисляется по формуле:

(sigma=sqrt{D_{left|xright|}})

Единицей измерения среднеквадратического отклонения является единица измерения исследуемой величины. Данный критерий используется при измерении линейной функции, статической проверки гипотезы, расчете стандартной ошибки среднего арифметического, а также при построении доверительных интервалов.

Как найти среднеквадратическое отклонение

Вычисление среднеквадратичного отклонения на первый взгляд может показаться достаточно сложным и запутанным. Но этот процесс можно облегчить, если воспользоваться следующим алгоритмом действий:

Найти среднее арифметическое всех членов множества.
Для каждого элемента вычислить варианту.
Сложить все полученные на предыдущем этапе значения.
Разделить число, полученное при выполнении третьего шага, на количество элементов множества.
Из полученного в предыдущем шаге числа извлечь корень квадратный.

Формула, примеры решения задач

Для четырех измеренных значений величины b формула среднеквадратичного отклонения будет выглядеть следующим образом:

(sigma=sqrt{frac{triangle b_1+triangle b_2+triangle b_3+triangle b_4}4})

где Db₁ — Db₄ являются абсолютными погрешностями каждой исследуемой величины.

Рассмотрим пример решения конкретной задачи.

Задача

При проведении лабораторной работы по физике школьники несколько раз измерили напряжение электрического тока и получили следующие значения:

(U_1=4.22B\U_2=4.30B\U_3=4.27B\U_4=4.23B\U_5=4.20B)

Необходимо рассчитать погрешности (абсолютные и относительные) каждого измерения, дисперсию и среднеквадратическое отклонение.

Решение

Определим среднее арифметическое значение напряжения в данной работе:

(U_c=sqrt{frac{U_1+U_2+U_3+U_4+U_5}5}=frac{4.22+4.30+4.27+4.23+4.20}5=4.244B)

Теперь рассчитаем для каждого полученного измерения абсолютную и относительную погрешности. Так как абсолютная погрешность определяется как разница между средним арифметическим и полученным значением, то

(triangle U_1=0.024\triangle U_2=-0.056\triangle U_3=-0.026\triangle U_4=0.014\triangle U_5=0.044)

Находим относительную погрешность:

(sigma_1=frac{left|U_1right|}{U_c}times100%=0.50%\sigma_2=frac{left|U_2right|}{U_c}times100%=1.06%\sigma_3=frac{left|U_3right|}{U_c}times100%=0.50%\sigma_4=frac{left|U_4right|}{U_c}times100%=0.25%\sigma_5=frac{left|U_5right|}{U_c}times100%=0.84%\)

Зная абсолютные погрешности несложно вычислить дисперсию:

(D=frac{triangle U_1^2+{triangle U_2}^2+{triangle U_3}^2+{triangle U_4}^2+{triangle U_5}^2}5=0.001304\)

Теперь можно вычислить среднеквадратичное отклонение:

(sigma=sqrt D=0.0361\)

Источник

Статистические данные

Слово статистика образовано от латинского status, которое обозначает состояние. От этого корня произошли слова stato (государство), statistica (сумма знаний о государстве). Математическая статистика — наука, которая изучает методы сбора и обработки информации, представленной в численном виде. Эта информация появляется как результат экспериментов. Во многом математическая статистика опирается на теорию вероятностей, которая позволяет оценить точность и надёжность заключений, сделанных на основании изучения ограниченных статистических данных.

Метод не исследует сущность процессов, а формулирует и описывает их количественную сторону. Термином генеральная совокупность обозначается общность всех объектов, относительно которых необходимо сделать выводы при изучении научной проблемы. Выборочная совокупность или выборка — множество объектов, отобранных из генеральной совокупности для исследования. Основные цели математической статистики:

указание способов сбора и систематизации статистических данных;
определение закона распределения случайной величины;
поиск неопределённых параметров;
проверка подлинности выдвинутых гипотез.

Главный метод математической статистики — выборочный метод, состоящий в исследовании представительной выборочной совокупности для получения достоверной характеристики генеральной. Отбор объектов в выборку производится случайно, а исследуемое свойство должно обладать статистической устойчивостью, то есть иметь высокую частоту повторений при многократных испытаниях.

Выборочный метод сокращает время и трудоёмкость исследований, так как изучение всей совокупности оказывается более тяжёлым или невозможным. Математическая статистика выявляет закономерности массовых явлений и предсказывает появление внешних влияний.

Размах вариации

Вариация — это различия значений признака у единиц исследуемой совокупности. Она образуется из-за того, что индивидуальные значения формируются при различных условиях. Выборка должна быть представительной, чтобы по результатам её исследований можно было сделать правильные выводы о характеристиках всей совокупности.

Количественная репрезентативность достигается при использовании достаточного числа наблюдений в выборке, которое может обеспечить получение достоверных результатов. Качественная репрезентативность заключается в одинаковой структуре выборочной и генеральной совокупностей по признакам, имеющим влияние на получение конечного результата. К абсолютным показателям вариации относятся:

размах, R;
среднее линейное отклонение, a;
среднеквадратичное отклонение, σ (сигма);
дисперсия, D.

Размах вариации показывает абсолютную разницу между максимумом и минимумом значений признака:

R = x max — x min, где x — значения признака.

Основным недостатком показателя R можно назвать то обстоятельство, что колебания значений признака могут вызываться случайными причинами и искажать характерный для исследуемой совокупности размах.

Показатели отклонения

Существуют показатели вариации, учитывающие все значения величин, а не только наибольшие или наименьшие. Одним из них можно назвать среднее линейное отклонение — показатель, характеризующий меру разброса значений. Сначала требуется определить точку отсчёта разброса. Как правило, ею становится среднее арифметическое значение, входящее в исследование величин. Потом необходимо измерить, отклонение от среднего для каждого значения. Все отклонения вычисляются по модулю и определяется среднее значение уже среди них. Формула для расчёта отклонения:

a = Σ ⁿ i=1 (x — x̅) / n, где:

a — среднее линейное отклонение;
n — количество значений в исследуемой совокупности;
x — анализируемый показатель;
x̅ — среднее значение показателя.

СКО характеризует разброс значений относительно среднего математического ожидания. Оно измеряется в единицах измерения само́й величины. Существует правило, согласно которому для нормально распределённых данных диапазон разброса 997 значений из 1 тыс. составляет три сигмы от средней арифметической, [x̅ — 3σ; x̅ + 3σ].

Коэффициент вариации

Квадратичное отклонение — это абсолютная оценка меры разброса. Для того чтобы сравнить величину разброса с самими значениями величины, необходимо применить относительный показатель — коэффициент вариации:

V = σ / x̅, где σ — стандартное отклонение из выборки, x̅ — среднее арифметическое.

Коэффициент вариации измеряется в процентах. Показатель полезен для сравнивания однородности разных процессов.

Математическое ожидание — среднее значение случайной величины. Для дискретной выборки оно определяется по формуле:

M (X)= Σ ⁿi=1 xi ⋅ pi, где xi — случайные значения, pi — их вероятность.

Дисперсией называется среднее значение квадрата отклонения случайной величины от её математического ожидания:

D (X) = M (X²) — (M (X))²

Для дискретной случайной величины формула приобретает вид:

D (X) = Σ ⁿi=1 xi² ⋅ pi — M (X)².

Среднеквадратическое отклонение или стандартный разброс — это корень квадратный из дисперсии, формула которого имеет вид:

σ(X) = √ D (X).

Дисперсия и стандартный разброс — взаимозависимые характеристики. Стандартная ошибка среднего — величина, которая характеризует квадратическое отклонение выборочного среднего, рассчитанного по выборке размера из генеральной совокупности. Величина ошибки SDx̅ зависит от дисперсии генеральной совокупности и объёма выборки и рассчитывается по формуле:

SDx̅ = σ / √ n, где σ — величина стандартного разброса генеральной совокупности, а n — объём выборки.

Статистическая закономерность — это количественная форма проявления причинной связи. Она возникает как результат воздействия большого числа причин, действующих либо постоянно, либо только временами. Существует ряд статистических критериев, которые позволяют сравнивать экспериментально полученное распределение с нормальным, полученным в теории. Погрешность измерения — отклонение измеренного значения величины от действительного, являющиеся характеристикой точности измерения. Вместе с полученным результатом должна указываться погрешность измерений.

Пример расчёта

Пример расчёта по формулам для среднеквадратичного отклонения и дисперсии при решении следующей задачи по теории вероятностей: для выполнения ремонтных работ рабочему необходима краска определённого цвета. В городе имеется четыре строительных магазина, в каждом из которых эта краска может находиться в продаже с вероятностью 0,41. Записать закон распределения количества посещаемых магазинов. Рассчитать дисперсию и среднеквадратичное отклонение случайной величины. Обход заканчивается после того, как необходимая краска будет куплена или после посещения всех четырёх магазинов.

x = 1 — краска куплена в первом магазине.

p (1) = 0,41.

x = 2 — краски не нашлось в первом магазине, но она была во втором.

p (2) = (1 — 0,41) · 0,41 = 0,59 · 0,41 = 0,242.

x = 3 — краски не нашлось в двух первых магазинах, но она была в третьем.

p (3) = (1 — 0,41)² · 0,41 = 0,59² · 0,41 = 0,143.

x = 4 — краски не было в первых трёх магазинах, рабочий зашёл в четвёртый магазин, купил краску или просто закончил обход.

p (4) = 0,59³ · 0,41 + 0,59⁴ = 0,205.

Закон распределения:

xi	1	2	3	4
p (X)	0,41	0,242	0,143	0.205

Математическое ожидание: M (X) = 1 · 0,41 + 2 · 0.242 + 3 · 0,143 + 4 · 0,205 = 2,143.

Дисперсия: D (X) = Σ ⁿi=1 xi² ⋅ pi — M (X)² = 1² · 0,41 + 2² · 0,242 + 3² · 0,143 + 4² · 0,205 — 2,143² = 1,353.

Стандартное отклонение: σ(X) = √ D (X) = √1,353 = 1,163.

Ответ: Дисперсия 1,353; квадратическое отклонение 1,163.

Для вычисления среднеквадратичного отклонения в онлайн-калькуляторе достаточно внести в таблицу значения случайной величины xi и их количество.

Среднеквадратичное отклонение применяется для определения погрешности при проведении последовательных измерений. Эта характеристика играет важную роль для сравнения изучаемого процесса с теоретически предсказанным. Если СКО велико, то полученные результаты или метод их получения нужно проверить.

Источник

Математическое ожидание, дисперсия, среднее квадратичное отклонение

Эти величины определяют некоторое
среднее значение, вокруг которого
группируются значения случайной
величины, и степень их разбросанности
вокруг этого среднего значения.

Математическое ожидание Mдискретной случайной величины — это
среднее значение случайной величины,
равное сумме произведений всех возможных
значений случайной величины на их
вероятности.

Свойства математического ожидания:

Математическое ожидание постоянной
величины равно самой постоянной .
Постоянный множитель можно выносить
за знак математического ожидания .
Математическое ожидание произведения
двух независимых случайных величин
равно произведению их математических
ожиданий .
Математическое ожидание суммы двух
случайных величин равно сумме
математических ожиданий слагаемых

Для описания многих практически важных
свойств случайной величины необходимо
знание не только ее математического
ожидания, но и отклонения возможных ее
значений от среднего значения.

Дисперсия случайной величины— мера разброса случайной величины,
равная математическому ожиданию квадрата
отклонения случайной величины от ее
математического ожидания.

Принимая во внимание свойства
математического ожидания, легко показать
что

Казалось бы естественным рассматривать
не квадрат отклонения случайной величины
от ее математического ожидания, а просто
отклонение. Однако математическое
ожидание этого отклонения равно нулю.
Это объясняется тем, что одни возможные
отклонения положительны, другие
отрицательны, и в результате их взаимного
погашения получается ноль. Можно было
бы принять за меру рассеяния математическое
ожидание модуля отклонения случайной
величины от ее математического ожидания,
но как правило, действия связанные с
абсолютными величинами, приводят к
громоздким вычислениям.

Свойства дисперсии:

Дисперсия постоянной равна нулю.
Постоянный множитель можно выносить
за знак дисперсии, возводя его в квадрат.
Если x и y независимые случайные величины
, то дисперсия суммы этих величин равна
сумме их дисперсий.

Средним квадратическим отклонением
случайной величины(иногда применяется
термин «стандартное отклонение случайной
величины») называется число равное.

Среднее квадратическое отклонение,
является, как и дисперсия, мерой рассеяния
распределения, но измеряется, в отличие
от дисперсии, в тех же единицах, которые
используют для измерения значений
случайной величины.

Решение задач:

1)Дана случайная величина Х:

x_i	-3	-2	0	1	2
p_i	0,1	0,2	0,05	0,3	0,35

Найти М(х), D(X).

Решение:

=9=2,31.

2) Известно, что М(Х)=5, М(Y)=2.
Найти математическое ожидание случайной
величиныZ=6X-2Y+9-XY.

Решение:М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.

Пример:Известно, чтоD(Х)=5,D(Y)=2. Найти
математическое ожидание случайной
величиныZ=6X-2Y+9.

Решение:D(Z)=6²D(Х)-2²D(Y)+0=180-8=172.

Тема 7. Непрерывные случайные величины

Задача 14

Случайная
величина, значения которой заполняют
некоторый промежуток, называется
непрерывной.

Плотностью распределениявероятностей непрерывной случайной
величины Х называется функцияf(x)– первая производная от функции
распределенияF(x).

Плотность
распределения также называют
дифференциальной
функцией.
Для описания дискретной случайной
величины плотность распределения
неприемлема.

Зная плотность распределения, можно
вычислить вероятность того, что некоторая
случайная величина Х примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (a,
b), равна определенному
интегралу от плотности распределения,
взятому в пределах от a
до b.