Как найти среднеквадратичное отклонение нормального распределения - Исправление недочетов и поиск решений вместе с Examum.ru

Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.

Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.

Стандартное отклонение обозначается буквой σ (греческая буква сигма).

Стандартное отклонение также называется:

среднеквадратическое отклонение,
среднее квадратическое отклонение,
среднеквадратичное отклонение,
квадратичное отклонение,
стандартный разброс.

Использование и интерпретация величины среднеквадратического отклонения

Стандартное отклонение используется:

в финансах в качестве меры волатильности,
в социологии в опросах общественного мнения — оно помогает в расчёте погрешности.

Пример:

Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.

	День 1	День 2	День 3	День 4
Пред.А	19	21	19	21
Пред.Б	15	26	15	24

В обеих компаниях среднее количество товара составляет 20 единиц:

А -> (19 + 21 + 19+ 21) / 4 = 20
Б -> (15 + 26 + 15+ 24) / 4 = 20

Однако, глядя на цифры, можно заметить:

в компании A количество товара всех четырёх дней очень близко находится к этому среднему значению 20 (колеблется лишь между 19 ед. и 21 ед.),
в компании Б существует большая разница со средним количеством товара (колеблется между 15 ед. и 26 ед.).

Если рассчитать стандартное отклонение каждой компании, оно покажет, что

стандартное отклонение компании A = 1,
стандартное отклонение компании Б ≈ 5.

Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Где:
σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.

стандартное отклонение формула, среднее квадратичное отклонение формула, среднеквадратическое отклонение формула, среднее квадратическое отклонение формула

Где:
S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение «xср» вместо «μ».

Разница между формулами S и σ («n» и «n–1»)

Состоит в том, что мы анализируем — всю выборку или только её часть:

только её часть – используется формула S (с «n–1»),
полностью все данные – используется формула σ (с «n»).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

	День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 — μ = 15 — 20 = -5

x2 — μ = 26 — 20 = 6

x3 — μ = 15 — 20 = -5

x4 — μ = 24 — 20 = 4

3. Каждую полученную разницу возвести в квадрат:

(x1 — μ)² = (-5)² = 25

(x2 — μ)² = 6² = 36

(x3 — μ)² = (-5)² = 25

(x4 — μ)² = 4² = 16

4. Сделать сумму полученных значений:

Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi — μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Дисперсия и стандартное отклонение

Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).

Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:

Вычесть среднее значение из каждого числа
Возвести каждый результат в квадрат (так получатся квадраты разностей)
Найти среднее значение квадратов разностей.

Ещё расчёт дисперсии можно сделать по этой формуле:

Дисперсия и стандартное отклонение расчёт дисперсии формула

Где:
S² — выборочная дисперсия,
Xi — величина отдельного значения выборки,
Xср (может появляться как X̅) — среднее арифметическое выборки,
n — размер выборки.

Правило трёх сигм

Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.

Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:

одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).

Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.

Стандартное отклонение в excel

Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):

1. Занесите все данные в документ Excel.

2. Выберите поле, в котором вы хотите отобразить результат.

3. Введите в этом поле «=СТАНДОТКЛОНА(«

4. Выделите поля, где находятся данные, потом закройте скобки.

5. Нажмите Ввод (Enter).

В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.

Коэффициент вариации

Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.

Стандартное отклонение делится на среднее и умножается на 100%.

Можно классифицировать вариабельность выборки по коэффициенту вариации:

при <10% выборка слабо вариабельна,
при 10% – 20 % — средне вариабельна,
при >20 % — выборка сильно вариабельна.

Узнайте также про:

Корреляции,
Метод Крамера,
Метод наименьших квадратов,
Теорию вероятностей
Интегралы.

Источник

Определение стандартного отклонения

Стандартное отклонение измеряет величину вариации или дисперсии в наборе значений данных относительно его среднего значения (среднего). Это статистический инструмент, используемый для интерпретации надежности данных. Он представлен символом «σ».

Если отклонение меньше, точки данных близки к среднему значению, и данные считаются
надежный. Напротив, если отклонение велико, точки данных разбросаны дальше от среднего значения; такие данные считаются менее надежными. Стандартное отклонение используется при анализе общего риска и доходности портфеля.

Оглавление

Определение стандартного отклонения
- Объяснение стандартного отклонения
- Уравнение стандартного отклонения
- Расчет
- Пример
- Интерпретация
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи

Стандартное отклонение — это статистический инструмент, который измеряет волатильность данных. Он указывает, в какой степени значения выборки отклоняются от средних значений. Он вычисляется как квадратный корень из дисперсии и обозначается символом «σ» (греческая буква).
σ не может быть отрицательным значением и может быть равен 0 только в том случае, если значения в наборе данных равны и не имеют вариаций.
В финансах этот математический инструмент применяется для определения уровня рисков, связанных с конкретными инвестициями или активами. Метод измеряет спред соответствующих цен и доходов. Более высокое отклонение отражает высокую волатильность и наоборот.
Если символ σ обозначает стандартное отклонение, n — общее количество наблюдений в наборе данных, xi — i-е количество наблюдений, а µ — выборочное среднее, то отклонение вычисляется по следующей формуле:

В большинстве случаев минимальное стандартное отклонение считается благоприятным. Если отклонение в предыдущих колебаниях цен для конкретной акции невелико, это считается надежной инвестиционной возможностью.

Этот статистический инструмент помогает исследователям и аналитикам понять распространение данных, чтобы
определить степень разброса данных. Этот математический аппарат показывает
разброс выборочных значений от среднего значения.

Стандартные ошибки подчеркивают точность среднего значения выборки по отношению к генеральной совокупности.
означает, когда данные обширны и широко распространены. На графике отклонение может лежать влево, вправо или в обе стороны — формирование колоколообразной кривойГрафик колоколообразной кривой изображает нормальное распределение, которое является типом непрерывной вероятности. Он получил свое название из-за формы графика, напоминающего колокол. читать далее.

Уравнение стандартного отклонения

Уравнение для определения стандартного отклонения ряда данных выглядит следующим образом:

т.е. σ=√v

Также, µ =∑x/n

Здесь,

σ — это символ, обозначающий стандартное отклонение.
n — количество наблюдений в наборе данных.
xi — i-е количество наблюдений в наборе данных.
µ — среднее значение выборки.
V — дисперсия.
∑x — сумма всех значений в наборе данных.

Расчет

Основные шаги, используемые для поиска и расчета стандартного отклонения, следующие:

Сначала определите среднее значение набора данных.
Затем подготовьте диаграмму со значениями выборки и разницей между выборкой.
значения и средние значения.
В следующем столбце найдите квадрат разностей.
Чтобы получить дисперсию, сложите все квадраты и разделите результат на разницу между общим количеством наблюдений и 1.
Наконец, найдите квадратный корень из дисперсии, чтобы получить стандартное отклонение.

Пример

Давайте рассмотрим несколько примеров, чтобы понять практические последствия:

Найти отклонение цен на сырую нефть за год, когда среднемесячные цены за литр были следующими:

МесяцСредняя цена за литр в долларахЯнварь0,83Февраль0,81Март0,78Апрель0,82Май0,79Июнь0,75Июль0,76Август0,79Сентябрь0,81Октябрь0,77Ноябрь0,76Декабрь0,75

Решение:

Расчет среднего:

µ = ∑x/n

µ = 9,42/12

= 0,785 доллара за литр

С. №МесяцСредняя цена за литр в $ (x)х – 0,785 доллара США(х – 0,785 долл. США)21January0.830.0450.0020252February0.810.0250.0006253March0.78-0.0050.0000254April0.820.0350.0012255May0.790.0050.0000256June0.75-0.0350.0012257July0.76-0.0250.0006258August0.790.0050.0000259September0.810.0250.00062510October0.77-0.0150.00022511November0. 76-0.0250.00062512декабрь0.75-0.0350.00122512–9.42 0,0085

Расчет стандартного отклонения :

σ = √ [0.0085 / (12-1)]
σ = √ (0,00077272727)
σ = 0,0277979724571285 долл. США

Таким образом, стандартное отклонение цен на нефть за литр для данного года равно
0,0277979724571285.

Интерпретация

Стандартное отклонение указывает на волатильность или дисперсию значений конкретного распределения. Он показывает, в какой степени значения выборки отклоняются от средних значений. Таким образом, эта мера облегчает сравнение и анализ.

Ниже приведены различные интерпретации полученного результата:

Если σ велико, то волатильность анализируемых данных также высока.
Точно так же, когда σ низкое, дисперсия между точками данных также незначительна.
В распределении σ может быть равно 0 только тогда, когда разница между точками данных равна нулю. Это также наименьшее значение отклонения, которое можно получить.
Невозможно получить отрицательное значение σ, так как числитель включает квадрат разности между выборочными значениями и средними значениями.
Кроме того, количество наблюдений всегда больше 1; следовательно, знаменатель должен быть положительным значением.
Стандартное отклонение измеряется в тех же единицах, что и значения распределения. Например, в приведенном выше примере σ выражается в долларах.
Выбросы (чрезвычайно высокие или низкие значения) существенно влияют на измерения отклонения.

Часто задаваемые вопросы (FAQ)

Что такое стандартное отклонение?

Стандартное отклонение — это статистический метод, используемый для нахождения разброса данных в распределении с использованием средних значений. Обозначается символом «σ».

Как рассчитать стандартное отклонение?

Стандартное отклонение рассчитывается как квадратный корень из дисперсии. Дисперсия — это сумма квадрата разности между каждым значением в наборе данных и их средними значениями, деленная на значение, полученное путем вычитания единицы из общего числа наблюдений.

Почему стандартное отклонение важно?

Он определяет степень изменчивости значений в выборочном распределении. Это широко используемый статистический инструмент в финансах, инвестициях и бизнесе для интерпретации величины риска, связанного с ценной бумагой или активом. В большинстве случаев минимальное отклонение считается благоприятным. Если отклонение в предыдущих колебаниях цен для конкретной акции невелико, это считается надежной инвестиционной возможностью.

Может ли стандартное отклонение быть равным нулю?

Единственный случай, когда он может быть равен нулю, — это когда все точки данных в распределении одинаковы. Нулевое отклонение указывает на нулевой разброс или изменчивость значений. Для реальных сценариев это практически невозможно.

Нормальное распределение

Время на прочтение
7 мин

Количество просмотров 36K

Автор статьи: Виктория Ляликова

Нормальный закон распределения или закон Гаусса играет важную роль в статистике и занимает особое положение среди других законов. Вспомним как выглядит нормальное распределение

$frac{1}{sigmasqrt{2pi}}e^left(-frac{(x-a)^2)}{2sigma^2}right)$

где a -математическое ожидание, — среднее квадратическое отклонение.

Тестирование данных на нормальность является достаточно частым этапом первичного анализа данных, так как большое количество статистических методов использует тот факт, что данные распределены нормально. Если выборка не подчиняется нормальному закону, тогда предположении о параметрических статистических тестах нарушаются, и должны использоваться непараметрические методы статистики

Нормальное распределение естественным образом возникает практически везде, где речь идет об измерении с ошибками. Например, координаты точки попадания снаряда, рост, вес человека имеют нормальный закон распределения. Более того, центральная предельная теорема вообще утверждает, что сумма большого числа слагаемых сходится к нормальной случайной величине, не зависимо от того, какое было исходное распределение у выборки. Таким образом, данная теорема устанавливает условия, при которых возникает нормальное распределение и нарушение которых ведет к распределению, отличному от нормального.

Можно выделить следующие этапы проверки выборочных значений на нормальность

Подсчет основных характеристик выборки. Выборочное среднее, медиана, коэффициенты асимметрии и эксцесса.
Графический. К этому методу относится построение гистограммы и график квантиль-квантиль или кратко QQ
Статистические методы. Данные методы вычисляют статистику по данным и определяют, какая вероятность того, что данные получены из нормального распределения

При нормальном распределении, которое симметрично, значения медианы и выборочного среднего будут одинаковы, значения эксцесса равно 3, а асимметрии равно нулю. Однако ситуация, когда все указанные выборочные характеристики равны именно таким значениям, практически не встречается. Поэтому после этапа подсчета выборочных характеристик можно переходить к графическому представлению выборочных данных.

Гистограмма позволяет представить выборочные данные в графическом виде – в виде столбчатой диаграммы, где данные делятся на заранее определенное количество групп. Вид гистограммы дает наглядное представление функции плотности вероятности некоторой случайной величины, построенной по выборке.

График QQ (квантиль-квантиль) является графиком вероятностей, который представляет собой графический метод сравнения двух распределений путем построения их квантилей. QQ график сравнивает наборы данных теоретических и выборочных (эмпирических) распределений. Если два сравниваемых распределения подобны, тогда точки на графике QQ будут приблизительно лежать на линии y=x. Основным шагом в построении графика QQ является расчет или оценка квантилей.

Существует множество статистических тестов, которые можно использовать для проверки выборочных значений на нормальность. Каждый тест использует разные предположения и рассматривает разные аспекты данных.

Чтобы применять статистические критерии сформулируем задачу. Выдвигаются две гипотезы H0 и H1, которые утверждают

H0 — Выборка подчиняется нормальному закону распределения

H1 — Выборка не подчиняется нормальному распределению

Установи уровень значимости alpha=0,05.

Теперь задача состоит в том, чтобы на основании какого-то критерия отвергнуть или принять основную нулевую гипотезу при уровне значимости

Критерий Шапиро-Уилка

Критерий Шапиро-Уилка основан на отношении оптимальной линейной несмещенной оценки дисперсии к ее обычной оценке методом максимального правдоподобия. Статистика критерия имеет вид

$W=frac{1}{s^2}{sumlimits_{i=1}^n{a_{n-i+1}(x_{n-i+1}-x_{i})}} s^2=sumlimits_{i=1}^n(x_i-overline x^2) overline x=frac{1}{n}sumlimits_{i=1}^n{x}$

Числитель является квадратом оценки среднеквадратического отклонения Ллойда. Коэффициенты ${a_{n-i+1}}$ и критические значения статистики являются табулированными значениями. Если , то нулевая гипотеза нормальности распределения отклоняется на уровне значимости .

В Python функция содержится в библиотеке scipy.stats и возвращает как статистику, рассчитанную тестом, так и значение p. В Python можно использовать выборку до 5000 элементов. Интерпретация вывода осуществляется следующим образом

Если значение , тогда принимается гипотеза H0, в противном случае, т.е. если, , тогда принимается гипотеза H1, т.е. что выборка не подчиняется нормальному закону.

Критерий Д’Агостино

В данном критерии в качестве статистики для проверки нормальности распределения используется отношение оценки Даутона для стандартного отклонения к выборочному стандартному отклонению, оцененному методом максимального правдоподобия

$D=frac{T}{n^2s} T=sumlimits_{i=1}^nbigg(i-frac{n+1}{2}bigg)x_i s^2=sumlimits_{i=1}^n(x_i-overline x^2), {x_1}leq...leq{x_n}$

В качестве статистики критерия Д’Агостино используется величина

$Y=sqrt{n}frac{(D-0,28209479)}{0,02998598}$

значение которой рассчитывается на основе центральной предельной теоремы, которая утверждает, что при

$limlimits_{x to infty}Pbigg(frac{D-M[D]}{sqrt{D[D]}}{<x}bigg)=Phi(x)$

гдестандартная нормальная случайная величина.

Критические значения являются табулированными значениями. Гипотеза нормальности принимается, если значение статистики лежит в интервале критических значений. Данный критерий показывает хорошую мощность против большого спектра альтернатив, по мощности немного уступая критерию Шапиро-Уилка.

В Python функция normaltest() также содержится в библиотеке scipy.stats и возвращает статистику теста и значение p. Интерпретация результата аналогична результатам в критерии Шапиро-Уилка.

Критерий согласия— Пирсона

Данный критерий является одним из наиболее распространенных критериев проверки гипотез о виде закона распределения и позволяет проверить значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Таким образом, данный критерий позволяет проверить гипотезу о принадлежности наблюдаемой выборки некоторому теоретическому закону. Можно сказать, что критерий является универсальным, так как позволяет проверить принадлежность выборочных значений практическому любому закону распределения.

Для решения задачи используется статистика — Пирсона

$G=sumlimits_{k=1}^mfrac{(v_k-np_k)^2}{np_k}$

где — эмпирические частоты (подсчитывается число элементов выборки, попавших в интервал), ${np_k}$ — теоретические частоты. Подсчитывается критическое значение $chi^2_{кр}$ . Если $Ggeq chi^2_{кр}$ , отклоняется гипотеза о принадлежности выборки нормальному распределению и принимается, если $G< chi^2_{кр}$ .

Теперь перейдем к практической части. Для демонстрации функций будем использовать Dataset, взятый с сайта kaggle.com по прогнозированию инсульта по 11 клиническим характеристикам.

Загружаем необходимые библиотеки

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

Загружаем датасет

data_healthcares = pd.read_csv('E:/vika/healthcare-dataset-stroke-data.csv')

Набор состоит из 5110 строк и 12 столбцов.

Посмотрим на основные характеристики, каждого признака.
data_healthcares.describe()

Из данных характеристик можно увидеть, что есть пропущенные значения в показателях индекс массы тела. Посчитаем количество пропущенных значений.

Если бы нам необходимо было делать модель для прогноза, то пропущенные значения bmi являются достаточно большой проблемой, в которой возникает вопрос как их восстановить. Поэтому будем предполагать, что значения столбца bmi (индекс массы тела) подчиняются нормальному закону распределения (предварительно был построен график распределения, поэтому сделано такое предположение). Но так как, на данный момент, у нас нет необходимости в построении модели для прогноза, то удалим все пропущенные значения

new_data=data_healthcares.dropna()

Теперь можем приступать к проверке выборочных значений показателя bmi на нормальность. Вычислим основные выборочные характеристики

Выборочная характеристика	Код в python	Значение характеристики
Выборочное среднее	new_data.bmi.mean()	28,89
Выборочная медиана	new_data.bmi.median()	28,1
Выборочная мода	new_data.bmi.mode()	28,7
Выборочное среднеквадратическое отклонение	new_data.bmi.std()	7.854066729680458
Выборочный коэффициент асиметрии	new_data.bmi.skew()	1.0553402052962928
Выборочный эксцесс	new_data.bmi.kurtosis()	3.362659165623678

После вычислений основных характеристик мы видим, что выборочное среднее и медиана можно сказать принимают одинаковые значения и коэффициент эксцесса равен 3. Но, к сожалению коэффициент асимметрии равен 1, что вводить нас в некоторое замешательство, т.е. мы уже можем предположить, что значения bmi не подчиняются нормальному закону. Продолжим исследования, перейдем к построению графиков.

Строим гистограмму

fig = plt.figure
fig,ax= plt.subplots(figsize=(7,7))
sns.distplot(new_data.bmi,color='red',label='bmi',ax=ax)
plt.show()

Гистограмма достаточно хорошо напоминает нормальное распределение, кроме конечно, небольшого выброса справа, но смотрим дальше. Тут скорее, можно предположить, что значения bmi подчиняются распределению .

Строим QQ график. В python есть отличная функция qqplot(), содержащаяся в библиотеке statsmodel, которая позволяет строить как раз такие графики.

from statsmodels.graphics.gofplots import qqplot
from matplotlib import pyplot
qqplot(new_data.bmi, line=’s’)
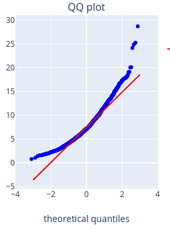
Pyplot.show

Что имеем из графика QQ? Наши выборочные значений имеют хвосты слева и справа, и также в правом верхнем углу значения становятся разреженными.

На основе данных графика можно сделать вывод, что значения bmi не подчиняются нормальному закону распределения. Рядом приведен пример QQ графика распределения хи-квадрат с 8 степенями свободы из выборки в 1000 значений.

Для примера построим график QQ для выборки из нормального распределения с такими же показателями стандартного отклонения и среднего, как у bmi.

std=new_data.bmi.std() # вычисляем отклонение
mean=new_data.bmi.mean() #вычисляем среднее
Z=np.random.randn(4909)*std+mean # моделируем нормальное распределение
qqplot(Z,line='s') # строим график
pyplot.show()

Продолжим исследования. Перейдем к статистическим критериям. Будем использовать критерий Шапиро-Уилка и Д’Агостино, чтобы окончательно принять или опровергнуть предположение о нормальном распределении. Для использования критериев подключим библиотеки

from scipy.stats import shapiro
from scipy.stats import normaltest
shapiro(new_data.bmi)
ShapiroResult(statistic=0.9535483717918396, pvalue=6.623218133972133e-37)
Normaltest(new_data.bmi)
NormaltestResult(statistic=1021.1795052962864, pvalue=1.793444363882936e-222)

После применения двух тестов мы имеем, что значение p-value намного меньше заданного критического значения alpha , значит выборочные значения не принадлежат нормальному закону.

Конечно, мы рассмотрели не все тесты на нормальности, которые существуют. Какие можно дать рекомендации по проверке выборочных значений на нормальность. Лучше использовать все возможные варианты, если они уместны.

На этом все. Еще хочу порекомендовать бесплатный вебинар, который 15 июня пройдет на платформе OTUS в рамках запуска курса Математика для Data Science. На вебинаре расскажут про несколько часто используемых подходов в анализе данных, а также разберут, какие математические идеи работают у них под капотом и почему эти подходы вообще работают так, как нам нужно. Регистрация на вебинар доступна по этой ссылке.

Источник

Загрузить PDF

Вычислив среднеквадратическое отклонение, вы найдете разброс значений в выборке данных.^[1] Но сначала вам придется вычислить некоторые величины: среднее значение и дисперсию выборки. Дисперсия – мера разброса данных вокруг среднего значения.^[2] Среднеквадратическое отклонение равно квадратному корню из дисперсии выборки. Эта статья расскажет вам, как найти среднее значение, дисперсию и среднеквадратическое отклонение.

1
Возьмите наборе данных. Среднее значение – это важная величина в статистических расчетах.^[3]
- Определите количество чисел в наборе данных.
- Числа в наборе сильно отличаются друг от друга или они очень близки (отличаются на дробные доли)?
- Что представляют числа в наборе данных? Тестовые оценки, показания пульса, роста, веса и так далее.
- Например, набор тестовых оценок: 10, 8, 10, 8, 8, 4.
2
Для вычисления среднего значения понадобятся все числа данного набора данных.^[4]
- Среднее значение – это усредненное значение всех чисел в наборе данных.
- Для вычисления среднего значения сложите все числа вашего набора данных и разделите полученное значение на общее количество чисел в наборе (n).
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
3
Сложите все числа вашего набора данных.^[5]
- В нашем примере даны числа: 10, 8, 10, 8, 8 и 4.
- 10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных.
- Сложите числа еще раз, чтобы проверить ответ.
4
Разделите сумму чисел на количество чисел (n) в выборке. Вы найдете среднее значение.^[6]
- В нашем примере (10, 8, 10, 8, 8 и 4) n = 6.
- В нашем примере сумма чисел равна 48. Таким образом, разделите 48 на n.
- 48/6 = 8
- Среднее значение данной выборки равно 8.
Реклама

1
Вычислите дисперсию. Это мера разброса данных вокруг среднего значения.^[7]
- Эта величина даст вам представление о том, как разбросаны данные выборки.
- Выборка с малой дисперсией включает данные, которые ненамного отличаются от среднего значения.
- Выборка с высокой дисперсией включает данные, которые сильно отличаются от среднего значения.
- Дисперсию часто используют для того, чтобы сравнить распределение двух наборов данных.
2
Вычтите среднее значение из каждого числа в наборе данных. Вы узнаете, насколько каждая величина в наборе данных отличается от среднего значения.^[8]
- В нашем примере (10, 8, 10, 8, 8, 4) среднее значение равно 8.
- 10 — 8 = 2; 8 — 8 = 0, 10 — 2 = 8, 8 — 8 = 0, 8 — 8 = 0, и 4 — 8 = -4.
- Проделайте вычитания еще раз, чтобы проверить каждый ответ. Это очень важно, так как полученные значения понадобятся при вычислениях других величин.
3
Возведите в квадрат каждое значение, полученное вами в предыдущем шаге.^[9]
- При вычитании среднего значения (8) из каждого числа данной выборки (10, 8, 10, 8, 8 и 4) вы получили следующие значения: 2, 0, 2, 0, 0 и -4.
- Возведите эти значения в квадрат: 2², 0², 2², 0², 0², и (-4)² = 4, 0, 4, 0, 0, и 16.
- Проверьте ответы, прежде чем приступить к следующему шагу.
4
Сложите квадраты значений, то есть найдите сумму квадратов.^[10]
- В нашем примере квадраты значений: 4, 0, 4, 0, 0 и 16.
- Напомним, что значения получены путем вычитания среднего значения из каждого числа выборки: (10-8)^2 + (8-8)^2 + (10-2)^2 + (8-8)^2 + (8-8)^2 + (4-8)^2
- 4 + 0 + 4 + 0 + 0 + 16 = 24.
- Сумма квадратов равна 24.
5
Разделите сумму квадратов на (n-1). Помните, что n – это количество данных (чисел) в вашей выборке. Таким образом, вы получите дисперсию.^[11]
- В нашем примере (10, 8, 10, 8, 8, 4) n = 6.
- n-1 = 5.
- В нашем примере сумма квадратов равна 24.
- 24/5 = 4,8
- Дисперсия данной выборки равна 4,8.
Реклама

1
Найдите дисперсию, чтобы вычислить среднеквадратическое отклонение.^[12]
- Помните, что дисперсия – это мера разброса данных вокруг среднего значения.
- Среднеквадратическое отклонение – это аналогичная величина, описывающая характер распределения данных в выборке.
- В нашем примере дисперсия равна 4,8.
2
Извлеките квадратный корень из дисперсии, чтобы найти среднеквадратическое отклонение.^[13]
- Как правило, 68% всех данных расположены в пределах одного среднеквадратического отклонения от среднего значения.
- В нашем примере дисперсия равна 4,8.
- √4,8 = 2,19. Среднеквадратическое отклонение данной выборки равно 2,19.
- 5 из 6 чисел (83%) данной выборки (10, 8, 10, 8, 8, 4) находится в пределах одного среднеквадратического отклонения (2,19) от среднего значения (8).
3
Проверьте правильность вычисления среднего значения, дисперсии и среднеквадратического отклонения. Это позволит вам проверить ваш ответ.^[14]
- Обязательно записывайте вычисления.
- Если в процессе проверки вычислений вы получили другое значение, проверьте все вычисления с самого начала.
- Если вы не можете найти, где сделали ошибку, проделайте вычисления с самого начала.
Реклама

Об этой статье

Эту страницу просматривали 65 043 раза.

Была ли эта статья полезной?

Источник

В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.

Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).

Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

Определите среднее (простое среднее арифметическое ряда значений).
Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Порода собаки	Рост в миллиметрах
Ротвейлер	600
Бульдог	470
Такса	170
Пудель	430
Мопс	300

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее $=frac{600+470+170+430+300}{5} = 394$ мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить отклонение роста каждой из собак от среднего:

$[ begin{array}{l} 1: 600-394 = 206 \ 2: 470-394 = 76 \ 3: 170-394 = -224\ 4: 430-394 = 36\ 5: 300-394 = -94 end{array} ]$

Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Дисперсия $= frac{206^2+76^2+(-224)^2+36^2+(-94)^2}{5} = 21704$ мм².

Таким образом, дисперсия составляет 21704 мм².

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

мм (округлено до ближайшего целого значения в мм).

Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Что такое стандартное отклонение

Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.

Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.

Если есть значений, то:

Все остальные расчеты производятся аналогично, в том числе и определение среднего.

Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:

Дисперсия выборки = $frac{108520}{4}=27130$ мм².

При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).

Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.

Примечание. Почему именно квадраты разностей?

Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:

$frac{4+4-4-4}{4}=0$ .

Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?

$frac{4+4+|-4|+|-4|}{4} = frac{4+4+4+4}{4}=4$ .

На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:

$frac{7+1+|-6|+|-2|}{4} = frac{7+1+6+2}{4}=4$ .

Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.

А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).

Для первого примера получится:

$sqrt{frac{4^2+4^2+(-4)^2+(-4)^2}{4}}=4$ .

Для второго примера получится:

$sqrt{frac{7^2+1^2+(-6)^2+(-2)^2}{4}}=4.74$ .

Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.

Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.

И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.

О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич

Источник

Использование и интерпретация величины среднеквадратического отклонения

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Разница между формулами S и σ («n» и «n–1»)

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Пример 2 (с S)

Дисперсия и стандартное отклонение

Правило трёх сигм

Стандартное отклонение в excel

Коэффициент вариации

Определение стандартного отклонения

Уравнение стандартного отклонения

Расчет

Пример

Интерпретация

Часто задаваемые вопросы (FAQ)

Рекомендуемые статьи

Нормальное распределение

Об этой статье

Была ли эта статья полезной?

Что такое дисперсия

Что такое стандартное отклонение

Примечание. Почему именно квадраты разностей?