| Таблица 1.1 Различные определения среднего диаметра частиц | 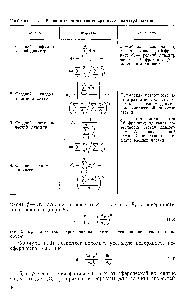 |
Для определения среднего диаметра частиц рекомендуется следующая формула [c.66]
Геометрическая удельная поверхность — это абсолютная величина, которая может быть подсчитана по значению среднего диаметра частиц сажи, определенного с помощью электронного микроскопа. Так как, однако, форма сажевых частиц не идеально сферическая, а поверхность их не гладкая, то 5г является несколько условной величиной. [c.216]
Физические методы исследования морфологии поверхности и пористости электродов являются наиболее старыми и прямыми. Эти методы обычно позволяют быстро получить воспроизводимые результаты, но они не обладают точностью адсорбционных и химических методов. Многие физические методы определения поверхности (или ее шероховатости), такие, как седиментационный анализ, требуют некоторых предположений относительно размеров частиц. Например, приходится использовать величину среднего диаметра частиц. Поскольку электроды редко состоят из частиц одинаковых размеров, эти методы не позволяют определить поверхность с большой точностью и поэтому ниже они либо не рассматриваются вообще, либо описываются очень кратко. [c.366]
Если, как это бывает в промышленных условиях, псевдоожиженный слой состоит из частиц различного размера, расчеты по определению Шк и Шп следует проводить, подставляя в приведенные выше формулы значения среднего диаметра частиц, найден-ны ,, например, по уравнениям (6,88) или (6.89). [c.527]
Средний диаметр частиц 8, может быть определен различными способами. При достаточно узком гранулометрическом составе частиц, по форме близкой к сферической, если их размер меняется от до (1 , [c.20]
Зная средний диаметр частиц определенной плотности (например, частиц кварца), выносимых в слив классификатора, и коэффициент равнопадаемости, можно [c.40]
Зная средний диаметр частиц определенной плотности (например, частиц кварца), выносимых в слив классификатора, и коэффициент равнопадаемости /, можно рассчитать размер частиц любой плотности, выносимых в слив, по формуле [c.160]
В экспериментальной практике значение 5у определяют применительно к сравнительной большой порции сыпучего материала, состоящей из множества частиц. В этом случае формула (5.6) позволяет рассчитать средний диаметр частиц исследуемой порции сыпучего материала. Параметр определяют на специальном приборе принцип его действия основан на измерении сопротивления, которое оказывает слой определенной порции сыпучего материала потоку прокачиваемого через него газа. Параметр 5 , используют для характеристики свойств сыпучего материала в случаях, когда они зависят от площади поверхности его частиц например, теплопроводность, звукопроницаемость, растворимость, химическая активность во многом зависят от Значения 5у меняются в большом диапазоне (от нескольких сотен тысяч до нескольких миллионов см ) в зависимости от степени дисперсности частиц. [c.147]
Очевидно, что для определения удельной поверхности сажи, зависящей только от среднего диаметра частиц, измерение оптической плотности следует проводить при постоянных значениях концентрации, толщины поглощающего слоя и при определенной длине волны падающего света. [c.221]
Эта зависимость имеет большое практическое значение, так как позволяет по экспериментально определенным величинам Ох при нескольких значениях определить размеры частиц золя. Для этого достаточно построить прямую в координатах 1 /)х =/(lg ) тангенс угла наклона прямой равен коэффициенту а (это легко показать, прологарифмировав основное уравнение IgD), = — ilgЯ,). Далее по калибровочной кривой Геллера для латексов, построенной в координатах а = /( ), и находят средний диаметр частиц исследуемой системы. [c.41]
Для фракций, содержащих более крупные частицы (порядка 60—75. чк), расчетные уравнения и коэффициенты, принятые в методике, неточны. Из данных, приведенных в табл. 2, следует также, что длительность определения среднего диаметра частиц предложенным методом в большинстве случаев не превышает 20—30 мин. [c.418]
В химической технике мы обычно встречаемся со смесью частиц различных размеров. Рассмотрим сперва N частиц одинаковой формы, но с разными диаметрами Введем понятие среднего диаметра частиц. В приложениях приходится встречаться с различными определениями этого понятия. [c.633]
Ход определения. Порошковую краску П-ЭП-45 в количестве I г нась[пают на часовое стекло н помещают под окуляр микроскопа, измеряя величину изображения одной частицы в делениях микроскопа. Условно принимают число частиц и-ного размера и по полученным данным визуальных наблюдений рассчитывают средний диаметр частиц иэ 10 определений при проведении трех испытаний. [c.70]
Результаты измерения статистического распределения частиц дисперсной фазы по размерам (на примере мазута тюменской нефти) были обработаны на ЭВМ с определением среднего диаметра частиц, среднестатистического отклонения, коэффициента асимметрии Кд, эксцесса 3 и кумулятивного объема по ( юрмулам [84]. Полу- [c.44]
Остановимся на некоторых способах определения среднего диаметра частиц, наиболее часто применяемых в расчетной практике [63, 65, 99]. [c.9]
Число фракций при определении гранулометрического состава твердой фазы практически не должно быть больше 10 при отношении средних диаметров частиц соседних фракций 1,2. [c.133]
Для определения индекса смешения необходимо подсчитать число частиц в пробе. По данным работы [20], средний диаметр частиц серы составляет 4—5 мкм. Поскольку сажекаучуковая смесь представляет собой дисперсионную среду, число частиц в пробе равно [c.207]
Таким образом, имеется ряд способов определения среднего диаметра частиц, и выбор того или иного метода зависит от того, какой параметр измеряется. Наиболее важные способы определения среднего размера частиц приведены в табл. 6. Если частицы образца имеют неправильную форму, величина а неизвестна. Обычно принимают, что форма частиц эквивалентна сфере, и выбирают соответствующие значения а (табл. 6). [c.363]
Не следует переоценивать абсолютную точность определения среднего диаметра частиц методом уширения линий. Влияние формы частиц и характера кривой распределения частиц по размерам ограничивают эту точность примерно 30%. [c.373]
Комплексное изучение одних и тех же объектов несколькими независимыми методами позволяет, с одной стороны, установить достоверность результатов, получаемых этими методами, а с другой — определить границы применимости каждого из методов, преимущества и их недостатки. Одним из таких методов, результаты которого непосредственно связаны с геометрическими характеристиками высокодисперсных непористых тел, является метод электронной микроскопии. Суть данного метода заключается в замере большого числа частиц (несколько сотен) и определении их среднего диаметра. При наличии большого разброса частиц по дисперсности их, как правило, подразделяют на несколько групп, более или менее близких по размерам, и для каждой из групп по формуле (4.44) находят средний диаметр частицы [108, 109] [c.135]
У большинства сыпучих материалов твердые частицы имеют неодинаковые размеры, характеризующиеся определенным интервалом. Распределение частиц по размерам описывается дифференциальной или интегральной кривой распределения [5, с. 15]. Эти кривые обычно строят на основе результатов ситового анализа, определяющего доли частиц в определенных интервалах (фракциях) размеров. По данным такого ступенчатого анализа можно построить гистограмму, которую затем по известным законам спрямляют и превращают в непрерывную кривую. Чем уже интервал для измерения каждой фракции, тем точнее гистограмма и построенная по ней кривая распределения. На рис. 1.3 и 1.4 представлены примерные виды дифференциальной и интегральной кривых распределения. Каждая фракция, получаемая при ситовом анализе, характеризуется средним диаметром, для определения которого существует несколько методов. [c.21]
Дпя практических целей, вероятно, можно ограничиться выражением, предложенным [5] для определения среднего диаметра частиц адсорбента idp) . [c.25]
Для опытов использовали три фракции угля со средним диаметром частиц 0,35 0,53 и 0,71 мм, полученных путем классификации угля на виброфракцион-ной установке. Уголь предварительно отмывался от пыли и в виде суспензии загружался в колонки с целью предотвращения попадания воздуха м жду гранулами угля. Б процессе опыта отбирались пробы сточных вод, цветность которых определялась на лабораторном фотоэлектрическом нефелометре (по калибровочной кривой, выражающей зависимость оптической плотности от концентрации пла-тино-кобальтового раствора нри определенной длине волны) и выражалась в ПКШ. [c.486]
Для отработки прибора и методики ходового анализа катализаторов потребовалось уточнить конструкцию и размер гильзы под ручную запрессовку образца (вместо предусмотренной в приборе запрессовки копром), выбрать целесообразную высоту запрессованного слоя и объем пропускаемого через него воздуха, подобрать ниппель и дополнительный груз. В результате были выбраны условия испытания, позволяющие оценивать средний диаметр частиц тонкой фракции катализаторов по ходу определения их гранулометрического состава, используя для этого одну и ту же навеску порощка (25 г). Затрата дополнительного времени при анализе обычных промышленных катализаторов не превышает 30—60 мин, и испытание ведется в приборе, уже выпускаемом отечественной промышленностью, с простыми дополнительными приспособлениями. [c.408]
При широком гранулометрическом составе путем рассева Еыде-[яют узкие фракции и рассчитывают средний диаметр частиц по юрмуле (5.9) и долю частиц А с этим размером. Средний диаметр астиц всех фракций катализатора может быть определен по юрмуле [c.241]
I) Исходный материал — древесная или хлопковая целлюлоза. Вязкость растворов нитратов, полученньк из хлопкового материала, значительно превышает вязкость нитратов клетчатки яа древесного материала. Объяснение этому следует искать в различных размерах коллоидных частиц. Средний диаметр их, определенный по измерению скорости диффузии в ацетонкыхрастворах, оказывается для хлопка равным 340,10 см э то время [c.107]
Для ультратонкнх пленок со средним диаметром частиц не более 5,0 нм сведения о структуре этих частиц можно получить, только сравнивая результаты определений с данными, полученными при наблюдении более крупных частиц (ср. гл. 5). Тщательное исследование электронно-микроскопических снимков темного поля (подобных приведенному на рис. 18) подтверждает присутствие значительного количества пятиугольных частиц многократного двойникования, а также показывает, что большинство частиц ориентировано гранью (Ш) параллельно поверхности подложки. О вероятной структуре ультратонких пленок таких металлов, как платина, частицы которых слишком малы для детального исследования, можно сказать следующее [c.227]
Водород на серебре не хемосорбируется, в то время как на меди хемосорбция водорода — активированный процесс, степень покрытия обычно мала. Поэтому водород для определения удельной поверхности этих металлов не пригоден. Кислород легко хемосорбируется на меди даже при 77 К, но трудно быть уверенным, что Хт — 2 из-за тенденции к сверхмонослойному поглощению. Схолтен и др. [106] разработали способ определения удельной поверхности меди, основанный на разложении на ней закиси азота. Реакция протекает при 360—370 К и примерно 27 кПа ( 200 мм рт. ст.) с образованием поверхностного кислорода в соотношении один атом кислорода на один атом меди и с выделением азота в газовую фазу. Результаты определения удельной поверхности указанным методом удовлетворительно согласуются с данными определения среднего диаметра частиц меди по уширению рентгеновских дифракционных линий. [c.328]
Между тем существует метод, который позволяет сказать, действительно ли кислород хемосорбируется на никеле и отличается ли эта хемосорбция от образования пленки окиси никеля. Ранее уже неоднократно говорилось, что магнитные свойства частиц никеля, имеющих диаметр 80—100Л, отличаются от свойств истинных сверхпарамагнетиков и что газы, адсорбированные в определенных условиях на таких частицах, дают увеличение намагничивания. Хотя причины, обусловливающие этот эффект, не ясны, его можно использовать для доказательства существования истинной хемосорбции кислорода. Если взять образец обычного катализатора N /Al20з и подвергнуть его спеканию при 600° в течение часа, то это приведет к увеличению среднего диаметра частиц до желаемого размера. После этого на образец подается кислород прн —78°С. Кислород следует подавать при низком давлении или в смеси с гелием (можно и в виде N0). Во всех этих случаях намагничивание никеля будет увеличиваться. Однако если кислород пускается быстро и при заметном давлении, то окисление никеля будет вызывать уменьшение намагничивания. Таким образом, имеется по крайней мере два способа связывания кислорода, однако следует вновь подчеркнуть, что эти результаты не обязательно указывают на отдачу никелем -электронов кислороду [17]. [c.25]
В работе [14] на основе экспериментальных исследований вертикального пневмотранспорта частиц бронзы [средние кубические диаметры частиц, определенные по уравнению (1.30), равны 830 к 270 мкм], стекла (1040 мкм) и полистирола (1040 мкм) в трубах диаметром 83 и 53 мм получены эмпирические выражения для перепада давления, определяемого ударами частиц о стенку вертикального пневмоподъемннка [c.172]
В критическом обзоре метода проницаемости Салливан и Гертель[ 2] отмечают Из чрезвычайно обширного материала, приводимого различными лицами, работавшими в этой области, явствует, что при тщательном экспериментировании определение удельной поверхности, поверхности на грамм, или среднего диаметра частиц из измерений проницаемости может быть произведено с прекрасной воспроизводимостью и большой точностью на порошках, песках, текстильных волокнах и других слабо связанных пористых телах. Если же эти тела консолидированы (как, [c.414]

где fsi ni di2 / nidi2 – поверхностная доля i-ой фракции.
i
Среднемассовый (или среднеобъемный) диаметр dw соответствует диамет-
ру частиц в такой монодисперсной системе, в которой суммарная масса (или объем) частиц такие же, как и в данной полидисперсной системе:
|
n d 3 |
|||||||||||
|
dw |
fwi di , |
(11) |
|||||||||
|
3 di |
|||||||||||
|
i i |
|||||||||||
|
i |
ni di |
i |
|||||||||
|
i |
|||||||||||
|
где fwi ni di3 / nidi3 – массовая (объемная) доля i-ой фракции. |
|||||||||||
|
i |
|||||||||||
|
Среднемассовый диаметр частиц рассчитывают, например, по данным се- |
|||||||||||
|
диментационного анализа. Значения dw |
могут быть найдены также методами |
||||||||||
|
ситового анализа и рассеяния света. Среднеповерхностный диаметр ds |
опреде- |
ляют, изучая адсорбцию на частицах дисперсной фазы. Среднечисленный диаметр dn , чаще всего, находят методами оптической и электронной микроскопии.
Усредненные размеры частиц dn , ds и dw одинаковы лишь для монодис-
персных систем, а в полидисперсных системах они различны. При этом всегда dw > ds > dn и чем более полидисперсна система, тем в большей степени разли-
чаются их значения. Поэтому степень полидисперсности систем часто характе-
|
ризуют параметром: |
||||||
|
П = |
d |
n |
. |
(12) |
||
|
dw |
Очевидно, что для монодисперсных систем П = 1, а для полидисперсных систем П 1.
В отсутствии данных о средних размерах частиц, найденных с использованием разных методов усреднения, для характеристики степени полидисперсности исследуемой системы может использоваться коэффициент вариации:
|
Kn |
100%, |
(13) |
||
|
d n |
||||
где – стандартное отклонение, которое характеризует широту распределения частиц по размерам.
Стандартное отклонение может быть определено на основе тех же исходных данных, что и средний размер частиц. Например, стандартное отклонение для среднечисленного диаметра рассчитывается по следующему соотношению:
|
1/ 2 |
1/ 2 |
||||||||||||||
|
n |
2 |
2 |
|||||||||||||
|
i |
di dn |
fni di |
dn |
. |
(14) |
||||||||||
|
ni |
|||||||||||||||
|
i |
i |
||||||||||||||
|
i |
Обычно система рассматривается как монодисперсная, если коэффициент вариации составляет менее 5 % (или, как максимум, 10 %).
13
2. ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ИХ ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
Помимо наибольшего, наименьшего и среднего размеров частиц более полно полидисперсность материала характеризуется дисперсным (гранулометрическим, зерновым) составом. Данная характеристика позволяет определить не только перечисленные параметры, но и установить процентное содержание частиц с определенным интервалом размеров.
С точки зрения математической статистики, диаметр частиц можно рассматривать как одномерную случайную величину. В этом случае свойства полидисперсного материала описывают функцией распределения числа (массы, площади и пр.) частиц от их размера.
Как правило, процентное содержание отдельных фракций представляют в виде гистограммы – ступенчатого графика зависимости относительного содержания фракций частиц от их размера.
Гистограмму строят в виде диаграммы, состоящей из нескольких прямоугольников (их число соответствует числу фракций), основания которых находятся между значениями диаметра от di– di/2 до di+ di/2 (рис. 4). Такие гистограммы дают наглядное представление о степени полидисперсности анализируемых систем и содержании в них каждой фракции, поскольку интервалы диаметров во фракциях берутся одинаковыми.
При построении дифференциальных кривых распределения частиц по размерам по оси абсцисс также отсчитываются значения их диаметров, а по оси ординат – отношение процентного содержания частиц в каком-то интервале размеров Qi к этому интервалу di, т.е. плотность распределения. Здесь величины интервалов размеров di могут быть неодинаковыми. Дифференциальную кривую распределения частиц по размерам получают, построив на графике отдельные для каждого интервала от di– di/2 до di+ di/2 прямоугольники и соединив средние точки их верхних оснований плавной кривой (рис. 5).
Для получения дифференциальной кривой численного распределения по оси ординат откладывают отношения Qni/ di. Значение численного содержания каждой фракции в процентах вычисляют по формуле:
|
Qni |
ni |
100 fni |
100. |
(15) |
|
|
ni |
|||||
i
Для построения дифференциальных кривых массового и поверхностного распределения по размерам по оси ординат наносят, соответственно, Qwi/ di иQsi/ di. Значения массового и поверхностного содержания фракций в процентах рассчитывают как
|
Qwi |
n d |
3 |
100 fwi |
100; |
||
|
i |
i |
|||||
|
ni di3 |
||||||
|
i |
||||||
|
Qsi |
n d 2 |
100 fsi |
100. |
|||
|
i |
i |
|||||
|
ni di2 |
i
14

Рис. 4. Гистограмма распределения частиц по размерам
Рис. 5 Дифференциальная кривая распределения частиц по размерам
Дифференциальные кривые численного, поверхностного и массового распределения частиц по размерам для одной и той же полидисперсной системы имеют вид, показанный на рис 6. С уменьшением степени полидисперсности
15

систем ширина дифференциальных кривых распределения становится уже, а их максимум увеличивается.
В пределе, при бесконечном числе фракций, имеем:
|
Q |
dQ |
F di , |
(18) |
|||
|
lim |
i |
|||||
|
di 0 |
di |
dd |
где F(di) – функция распределения (а точнее, численное значение функции распределения в i-ой точке).
Рис. 6. Дифференциальные кривые численного (1), поверхностного (2) и массового (3) распределения частиц по размерам
В соответствии со свойствами функции распределения можем записать:
|
dfi F di ddi |
(19) |
|
|
и |
||
|
d2 |
||
|
f12 F di |
ddi , |
(20) |
|
d1 |
||
|
где dfi – доля частиц (в процентах) с размерами от di до di ddi ; |
f12 – доля час- |
|
|
тиц (в процентах) с размерами от d1 до d2 . |
Графически эта доля частиц f12 равна площади под кривой функции распределения, ограниченной с двух сторон диаметрами d1 и d2
16

F d
3. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ ДЛЯ ОПИСАНИЯ ДИСПЕРСНОГО СОСТАВА
Для полного описания дифференциальной кривой и расчета основных параметров распределения удобнее использовать непрерывную функцию распределения в аналитическом виде. Были предложены различные функции
F d для описания дифференциальных кривых распределения, получаемых
при дисперсионном анализе реальных систем. Вид кривых распределения может быть различным в зависимости от физико-химических свойств порошка и, в основном, от способа его получения.
Для аналитического описания кривых распределения существуют различные формулы. Используемые формулы могут быть одно-, двух- и трех параметрическими и подразделяются на теоретические и эмпирические. Теоретические формулы выведены на основе некоторых физических представлений о закономерностях распределения частиц дисперсных материалов. Эмпирические получены на основе описания экспериментальных результатов дисперсионного анализа.
Среди теоретических наиболее часто используется нормальное (распределение Гаусса) и логарифмическое нормальное (логнормальное) распределения.
Принимая общее содержание частиц за 100%, уравнение нормального распределения может быть записано как
|
2 |
|||||||||||||
|
100 |
1 |
d d |
|||||||||||
|
FG d |
(21) |
||||||||||||
|
exp |
, |
||||||||||||
|
2 |
2 |
||||||||||||
где d – средний диаметр частиц, величина которого, как это отмечалось ранее, зависит от метода усреднения; – стандартное отклонение распределения вокруг среднего.
Для построения кумулятивной (интегральной) кривой распределения уравнение (21) должно быть проинтегрировано:
|
di |
2 |
ti |
2 |
||||||||||||||||||||
|
100 |
1 |
d d |
100 |
t |
|||||||||||||||||||
|
Q d di |
(22) |
||||||||||||||||||||||
|
exp |
dd |
exp |
dt, |
||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||
|
/ ; Q d di |
– доля частиц (в процентах) с размерами от до di . |
||||||||||||||||||||||
|
где t d d |
Для расчета доли частиц Q d di интегрирование должно быть проведено в пределах от di до .
Логарифмическое нормальное распределение получается, если в нормальную Гауссову функцию распределения подставить в качестве аргумента не диаметр частиц, а логарифм диаметра. В таком случае функция F имеет вид:
|
2 |
||||||||||||||||
|
100 |
1 |
ln d ln dg |
||||||||||||||
|
FL ln d |
||||||||||||||||
|
exp |
, |
(23) |
||||||||||||||
|
d ln g 2 |
2 |
ln g |
||||||||||||||
|
где g – |
геометрическое стандартное отклонение (логарифм величины g ра- |
|||||||||||||||
|
17 |

d de
вен стандартному отклонению величины ln d ); dg – средний геометрический
диаметр частиц, логарифм которого равен значению среднего логарифма диаметров ln dg ln d .
Следует отметить, что применимость того или иного распределения для описания состава конкретной дисперсной системы определяется главным образом способом получения этой системы. Так, в частности, распределение частиц по размерам, получаемых помолом, очень близко к логарифмически нормальному.
Из эмпирических уравнений распределения часто используются формулы Годена и Розина–Раммлера [3].
Формула Годена, выведенная на основе обобщения результатов ситового анализа минералов, измельченных различными методами, имеет вид:
где dmin – минимальный диаметр для данной фракции частиц (нижняя граница диапазона диаметров частиц данной фракции), А и l – константы уравнения.
Из формулы (24) следует, что она не предназначена для описания интегральных кривых распределения частиц по размерам, у которых есть точка перегиба, соответствующая, например, максимуму на дифференциальной кривой распределения. Это означает, что она может быть использована для описания только какой-то части полной интегральной кривой распределения.
Для описания интегральных кривых распределения по данным ситовых анализов может быть использована формула Розина–Раммлера:
|
d |
a |
|||||
|
Q 100 exp |
, |
|||||
|
(25) |
||||||
|
de |
||||||
где a – постоянная этого уравнения, характеризующая ширину распределения, de – такой диаметр, при котором масса частиц с диаметрами составляет
36,8 %.
Следует отметить, что как формула Годена, так и Розина–Раммлера в основном хорошо описывают характеристики порошков, полученных измельчением с помощью определенного оборудования [3]. Так, например, было установлено, что формула Годена описывает данные для порощков, полученных при использовании валковых и щековых дробилок, а также стержневой мельницы. Те же самые материалы, но измельченные в шаровой мельнице, описывались данным уравнением лишь в ограниченном интервале размеров.
18
4. ОПТИЧЕСКАЯ МИКРОСКОПИЯ
Оптический или световой микроскоп представляет собой оптическую систему с двумя ступенями увеличения – объективом и окуляром. Объектив представляет собой первую ступень увеличения.
Принципиальная схема микроскопа приведена на рис. 7. Объект освещается источником света через оптическую систему коллектор-конденсор. Конденсор представляет собой короткофокусную линзу или систему линз, используемую в оптическом приборе для освещения рассматриваемого или проецируемого предмета. Конденсор собирает, усиливает и превращает поток света в пучок равномерных параллельных лучей в границах всей площади конденсора, который рассчитывается для освещения площади исследуемого предмета. Конденсор направляет на предмет лучи от источника света, в том числе и такие, которые в его отсутствие проходят сквозь предмет. В результате такого уплотнения светового потока резко возрастает освещенность предмета. Объектив создает действительное перевернутое и увеличенное изображение объекта, которое рассматривается через окуляр. Окуляр предназначен для создания дополнительного увеличения и создает мнимое изображение [3].
Существует большое количество разнообразных объективов, их классификация основана на степени исправления оптических искажений – хроматических и сферических аберраций. Хроматические аберрации обусловлены тем, что световые волны с разной длиной фокусируются в разных точках на оптической оси. В результате изображение оказывается окрашенным. Сферические аберрации связаны с тем, что свет, проходящий через центр объектива, и свет, идущий через его периферийную часть, фокусируются в разных точках на оси. В результате изображение оказывается нечетким. Ахроматические объективы являются наиболее распространенными на данный момент. В них хроматические аберрации подавляются при помощи стеклянных элементов с разной дисперсией, обеспечивающих схождение крайних лучей видимого спектра – синих и красных – в одном фокусе. Небольшая окрашенность изображения остается и видна иногда в виде слабых зеленых полос вокруг объекта. Сферическая аберрация может быть скорректирована только для одного цвета. Во флюоритовых объективах при помощи добавок к стеклу, улучшающих цветовую коррекцию, окрашенность изображения почти полностью устраняется. Апохроматические объективы – это объективы с самой сложной цветовой коррекцией. В них не только почти полностью устранены хроматические аберрации, но и коррекция сферических аберраций выполнена не для одного, а для двух цветов.
Общее увеличение микроскопа определяется как произведение увеличения объектива на увеличение окуляра. Наиболее распространены объективы с увеличением от 3Х до 90Х и окуляры от 5Х до 20Х, таким образом, общее увеличение микроскопа в видимой области спектра можно изменять в пределах от 15Х до 1800Х. Разрешающая способность оптического микроскопа составляет порядка 0,2–0,3 мкм.
19

Рис. 7. Схематичное изображение оптического микроскопа: окуляр (1), объектив (2), исследуемый объект (3), конденсор (4), предметный столик (5), осветительное зеркало (6) [4]
Для наблюдения частиц меньших размеров необходимо увеличить разрешающую способность микроскопа. Это возможно осуществить двумя способами: применяя свет с меньшей длиной волны и увеличивая апертуру объектива. Апертура представляет собой действующее отверстие оптической системы, определяемое размерами линз или диафрагмами. Апертура определяется апертурным углом и показателем преломления среды между объектом и фронтальной линзой объектива.
Разрешающая способность микроскопа определяется выражением:
|
dмикр |
, |
(26) |
|||
|
2Ас |
2nD sin |
||||
где λ – длина волны света, Ас – численная апертура объектива, nD – показатель преломления среды, заполняющей пространство между объектом и фронтальной линзой объектива, α – половина угла между двумя крайними лучами.
Для увеличения апертуры пространство между линзой объектива и объектом заполняется иммерсионной жидкостью (рис. 8).
20

Рис. 8. Схема действия сухой и иммерсионной систем [5]
Вкачестве иммерсионной жидкости применяется кедровое масло, показа-
тель преломления которого равен показателю преломления стекла (nD = 1,52), вода (nD = 1,33), глицерин (nD = 1,45), бромнафталин (nD = 1,66).
Так как показатели преломления иммерсионных жидкостей больше пока-
зателя преломления воздуха (nD = 1), то в таком случае в объектив будут попадать лучи, составляющие с осью оптической системы больший угол, чем в случае сухой системы.
Минимальные размеры частиц, которые можно наблюдать при белом свете для средней длины волны видимого диапазона (λ = 550 нм), составляют: для сухой системы 0,28 мкм, при водной иммерсии – 0,2 мкм и при масляной – 0,18 мкм.
Разрешающую способность микроскопа можно также значительно повысить, применяя для освещения свет с более короткой длиной волны. Для этого используются светофильтры с различным спектральным пропусканием (зеленый λ = 520 нм, синий λ = 455 нм и др.). При использовании ультрафиолетового света можно добиться разрешающей способности до 0,1 мкм.
Взависимости от оптических свойств объекта оптической микроскопии применяются различные методы освещения [6]. Основной целью данного выбора является получение наиболее контрастного изображения.
Метод светлого поля в проходящем свете позволяет получать равномерно освещенное поле в плоскости изображения. При этом свет из конденсора проходит через объект и объектив. Изображение объекта становится видимым вследствие частичного поглощения и отклонения отдельными его элементами падающего на них света.
Метод светлого поля в отраженном свете основан на освещении объекта сверху через объектив, который одновременно выполняет роль конденсора. Как разновидность данного метода можно выделить метод косого освещения. Отличие между ними состоит в том, что свет на объект направляют под большим углом. Такой способ освещения придает изображению объекта высокую контрастность, а также иногда позволяет оценить рельеф исследуемого образца.
Метод темного поля в проходящем свете дает возможность точно опреде-
21

лить контуры рассматриваемых объектов, так как на темном фоне образуются светлые изображения объекта. При использовании метода темного поля в проходящем свете свет от осветителя и зеркала направляется на объект конденсором специальной конструкции. Основная часть лучей образует пучок в виде полого конуса и не попадает в объектив. Изображение в объективе формируется при помощи небольшой части лучей, рассеянных частицами внутрь конуса и прошедших в объектив.
Метод темного поля в отраженном свете основан на освещении объекта сверху с помощью специальной кольцевой системы, называемой эпиконденсором. В таком случае изображение образуется только рассеянными лучами, имеющими слабую интенсивность. Поэтому для освещения объекта используются яркие источники света. В этом случае изображение частиц имеет вид ярко светящихся тел на совершенно темном фоне. На рис. 9 приведены изображения частиц МоО3·nH2O, полученных методом светлого (а) и темного (б) поля.
Рис. 9. Изображения частиц МоО3·nH2O, полученных методом: светлого поля в проходящем свете (а) и темного поля в отраженном свете (б).
Увеличение 900Х
Метод исследования в поляризованном свете применяют для изучения объектов, элементы которого имеют неодинаковые оптические свойства по различным направлениям. Использование поляризационного света дает возможность исследовать структуру и оптические свойства частиц.
Метод фазового контраста основан на том, что при прохождении через элементы объекта с различными показателями преломления световая волна претерпевает изменения, приобретая так называемый фазовый рельеф. Это значительно увеличивает контрастность изображения. Фазовые изменения световой волны преобразуются с помощью специального устройства в изменение амплитуды волны, что приводит к изменению интенсивности света, которая и воспринимается наблюдателем.
Флюоресцентная микроскопия позволяет в объекте сложного состава рассмотреть частицы различных веществ. Вследствие освещения объекта снизу или сверху сине-фиолетовыми или ультрафиолетовыми лучами возбуждается флюоресценция объекта. При этом вещество испускает видимый свет с харак-
22
D[1,0] это средний диаметр частиц, каким же образом он рассчитывается?
Представим к примеру, что у нас есть три частицы с диаметрами 2,3 и 4 мкм. Суммируем диаметры всех частиц:
Далее делим на количество частиц, в нашем случае n=3 и получаем :
D[1,0] = 3 мкм — средний диаметр частиц
Основной целью компьютерного моделирования упаковок дискретных сред является получение статистически адекватных закономерностей, численно описывающих процесс структурообразования реальных сыпучих материалов. Следовательно, для построения компьютерной модели дискретной среды необходимо знать морфологические и размерные параметры частиц, из которых состоит дискретная среда.
В таблице 1 перечислены основные методы определения размеров частиц в зависимости от диапазона измеряемых частиц.
Таблица 1 – Экспериментальные методы определения размеров частиц в зависимости от диапазона измеряемых частиц

Для определения распределения частиц по размерам необходимо использовать методы, позволяющие собрать данные о размерах большого количества частиц (обычно не менее 200 частиц) либо массе фракций, а затем обработать эти данные согласно законам статистики. Такими методами являются: оптическая и электронная микроскопия, седиментация в гравитационном и центробежном поле, ситовой анализ, и некоторые другие.
Результаты дисперсионных анализов могут быть изображены графически в виде интегральных и дифференциальных кривых распределения частиц по размерам. На гранулометрическом графике по оси абсцисс откладывается линейный размер (d) измеряемых частиц. В случае интегрального графика распределения (рисунок 1) размеров частиц по оси ординат откладываются объемные доли (Q) частиц, размер которых меньше текущего. Таким образом, интегральная кривая распределения представляет собой некую функцию Q=f(d).

Рисунок 1 – Интегральная кривая распределения частиц по размерам
К примеру, если нас интересует объемная доля частиц порошка, размер которых меньше d1, то для этого необходимо найти на нижней шкале размер d1, провести вертикальную прямую из этой точки до пересечения с интегральной кривой распределения. Ордината полученной точки пересечения и покажет ту объемную долю, которую занимают частицы порошка, размер которых меньше d1, в данном случае это Q1. Интервалу размеров частиц от d1 до d2 соответствует интервал объемных долей от Q1 до Q2.
Если разбить интегральную кривую на интервалы по оси абсцисс (рисунок 2), отложив соответствующие ординаты точек пересечения вертикальных линий с интегральной кривой, то для каждого интервала Δdi мы получим ряд интервалов ΔQi, причем:

где N – количество выделенных интервалов (фракций) размеров частиц.

Рисунок 2 – Разбивка интегральной кривой распределения размеров частиц на интервалы
Интервалы объемных долей можно представить в виде столбиков с высотой Fi=ΔQi, в таком случае мы получим дифференциальную гистограмму распределения частиц по размерам (рисунок 3).

Рисунок 3 – Дифференциальная гистограмма распределения частиц по размерам
Соединив середины верхних оснований столбиков дифференциальной гистограммы распределения, мы получим плавную дифференциальную кривую. Она означает, что частицы со средними размерами, заключенными между правым и левым краем одного столбика (diср), занимают Fi, % по объему в измеряемом материале.
Часто при построении дифференциальной кривой распределения, на оси ординат откладывают не интервалы объемных долей Fi, а отношения ΔQi/Δdi. В полученной гистограмме площадь каждого прямоугольника представляет собой содержание фракции материала в пределах выбранного интервала размеров Δdi. Соединив плавной кривой середины верхних оснований прямоугольников, также получают дифференциальную кривую распределения, по которой можно определить dн.в. – наиболее вероятный диаметр частиц в данной дисперсной системе (рисунок 4).

Рисунок 4 – Дифференциальная кривая распределения частиц по размерам и наиболее вероятный диаметр частиц
Основными статистическими характеристиками дифференциальных кри-вых распределения частиц по размерам являются: среднее значение, медиана и мода распределения (рисунок 5).

Рисунок 5 – Основные статистические характеристики при нормальном или гауссовом распределении (а) и бимодальном распределении (б) частиц по размерам
Среднее значение – средний размер частиц, результат усредненных данных. Средние значения вычисляют для определенного набора частиц, например, d[1…4]. Для конкретного распределения средним является математическое ожидание/среднее арифметическое.
Медиана – это значение размера частиц, которое делит популяцию на две равные части, т.е. точка на дифференциальной кривой распределения, слева и справа от которой находится по 50 % распределения.
Мода – положение максимума дифференциальной кривой распределения, или наиболее вероятный в популяции размер частиц.
Для нормального распределения среднее, медиана и мода совпадают (рисунок 5.а). Однако, например, для бимодального распределения (рисунок 5.б) среднее находится в точности между двумя интервалами распределения. При этом частицы с диаметром, равным среднему отсутствуют. Медианный диаметр сдвинут в правую часть распределения. Дифференциальная кривая имеет два выраженных максимума (две моды). Наибольшая мода соответствует положению максимума правой части распределения. Данный пример демонстрирует, что среднее, мода и медиана – совершенно разные параметры, которые совпадают или близки лишь в исключительных случаях [1].
Библиографические ссылки:
[1] – Роул, А. Основные принципы анализа размеров частиц / А. Роул // Техническая аннотация Malvern Instruments Limited. 2009. 12 c.
Определение — средний диаметр — частица
Cтраница 1
Определение среднего диаметра частиц на основании опытных данных является весьма трудоемкой операцией. Для облегчения таких расчетов целесообразно пользоваться уравнениями характеристик распределения.
[1]
Для определения среднего диаметра частиц проводят рассев на наборе сит порции катализатора. Сита имеют размер отверстий 40 мкм и выше.
[3]
Для определения среднего диаметра частиц проводят рассев порции катализатора на наборе сит. Сита имеют размер отверстий 40 мкм и более.
[4]
Не следует переоценивать абсолютную точность определения среднего диаметра частиц методом уширения линий.
[5]
Таким образом, имеется ряд способов определения среднего диаметра частиц, и выбор того или иного метода зависит от того, какой параметр измеряется. Если частицы образца имеют неправильную форму, величина а неизвестна.
[6]
Все это свидетельствует о том, что определение среднего диаметра единичной частицы, а тем более некоторой смеси частиц является далеко не однозначным. Отсюда следует, что практически невозможно дать однозначное и точное числовое значение размера одной или группы частиц, образующих даже узкую фракцию.
[7]
Наиболее вероятная причина наблюдаемых расхождений в 20 — 30 % — недостаточная точность уравнения (2.28), вызванная ненадежностью определения среднего диаметра частиц, заметным присутствием в ионите мелких фракций, а также отклонением зерен ионита от шарообразной формы, приводящим к не учтенному нами увеличению удельной поверхности ионита.
[8]
Однако для практических целей например, для проектирования технологических аппаратов, газоходов-вентиляционных устройств, а также для сопоставления результатов анализов, выполненных различными — методами, удобно выражать распределение частиц по массе. Расчет распределения-по массе частиц правильной геометрической формы и известной плотности несложно выполнить, определив объем частицы. Однако для частиц неправильной формы такой расчет вызывает серьезные затруднения — связанные как с надежностью определения среднего диаметра частиц, так и их плотности.
[9]
С другой стороны, Хаппель [37] получил эмпирическую связь между модифицированным коэффициентом трения и модифицированным числом Рейнольдса для движущихся слоев. Такие слои соответствуют условиям рыхлой упаковки, так что изменение падения давления с порозностью отражает изменение дисперсности слоя. Хаппель и Эпштейн предположили [42], что для изучения влияния консолидации слоя в направлении наиболее плотной укладки, которое может встретиться в стационарных упакованных слоях, можно использовать функцию порозности в уравнении Кармана — Козени. Все эмпирические формулы такого типа сложны, потому что невозможно на основе теоретических или экспериментальных соображений независимо предложить правильный метод определения среднего диаметра частиц и порозности.
[10]
Водород на серебре не хемосорбируется, в то время как на меди хемосорбция водорода — активированный процесс, степень покрытия обычно мала. Поэтому водород для определения удельной поверхности этих металлов не пригоден. Кислород легко хемосорбируется на меди даже при 77 К, но трудно быть уверенным, что Хт2 из-за тенденции к сверхмоиослойному поглощению. Схолтен и др. [106] разработали способ определения удельной поверхности меди, основанный на разложении на ней закиси азота. Реакция протекает при 360 — 370 К и примерно 27 кПа ( — 200 мм рт. ст.) с образованием поверхностного кислорода в соотношении один атом кислорода на один атом меди и с выделением азота в газовую фазу. Результаты определения удельной поверхности указанным методом удовлетворительно согласуются с данными определения среднего диаметра частиц меди по уширению рентгеновских дифракционных линий.
[11]
Страницы:
1
