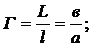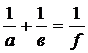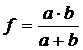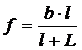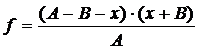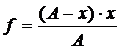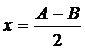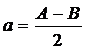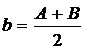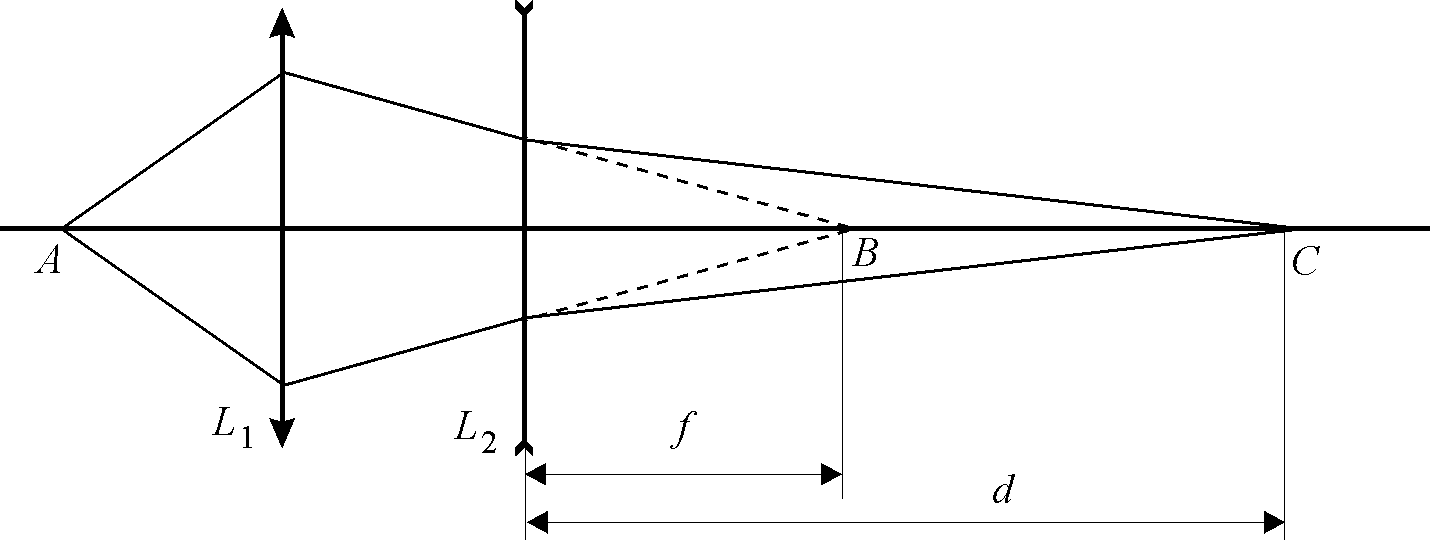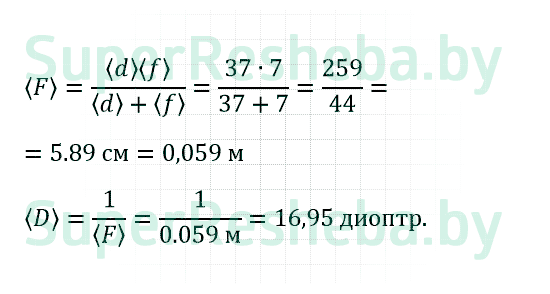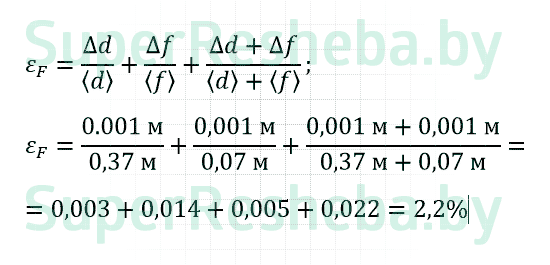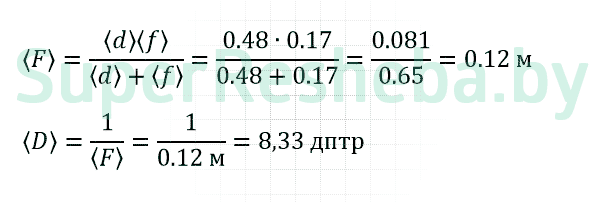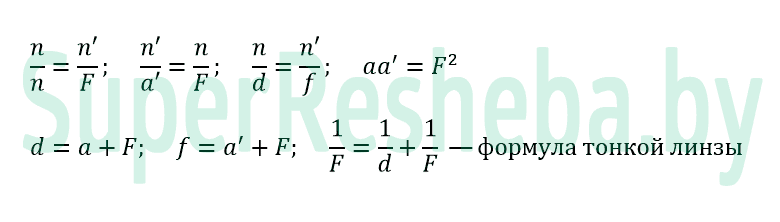Определение фокусного расстояния
рассеивающей линзы затрудняется тем,
что изображение предмета получается
мнимым и поэтому расстояния, входящие
в формулу линзы не могут быть непосредственно
измеряны.. Эту трудность легко обойти
с помощью вспомогательной собирающей
линзы. В начале опыта на оптическую
скамью помещают только одну собирающую
линзу и получают на экране действительное
изображение предмета А (см рис.6). По
линейке расположенной у основания
оптической скамьи, отмечают положение
D этого изображения
рис.6.
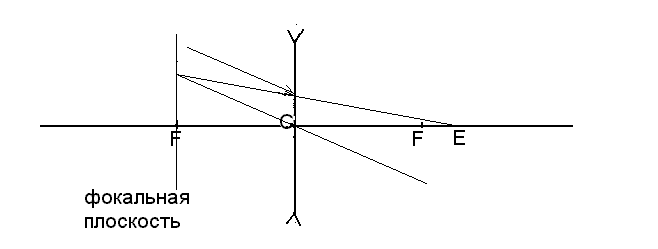
Если на пути лучей,
выходящих из точки А и сходящихся в
точке D после преломления их в собирающей
линзе B (рис. 6), поставить рассеивающую
линзу С так, чтобы расстояние CD было
меньше её фокусного расстояния, то
изображение точки А удалится от линзы
В. Пусть оно переместится в точку Е (рис.
7).
.
рис.
7.
На
рис. 7 показан ход лучей через рассеивающую
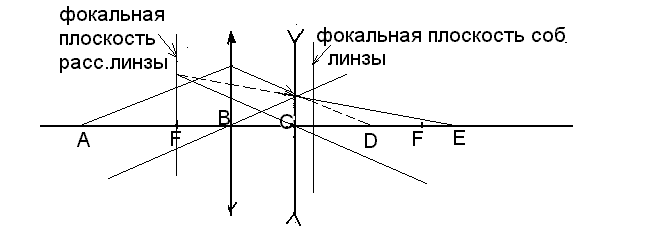
линзу С. Совместим рисунки 6 и 7
. рис. 8.
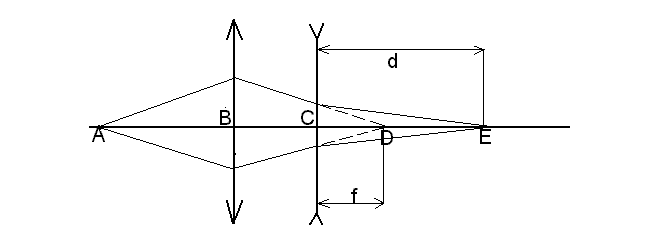
или схематично это будет выглядеть так
как показано на рис. 9.
рис. 9.
В силу оптического
принципа взаимности ( обратимость
световых лучей) можно мысленно рассмотреть
лучи, распространяющиеся из точки
E в обратную сторону. Тогда точка D будет
мнимым изображением точки E, расстояние
EC — расстоянием от линзы до объекта d, а
ДС — расстоянием от линзы до изображения
f. Учитывая правило знаков отметим, что
f- отрицательно, тогда можно записать
.
(8)
Или
.
(9)
Порядок выполнения работы
В работе используется
оптическая скамья, на которой имеется
шкала, позволяющая отмечать положение
линз, экрана и объекта, перемещаемых по
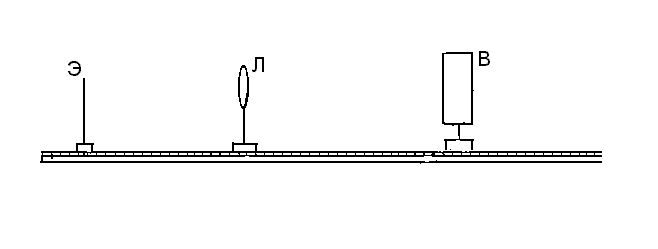
скамье, показанной на рис. 10.
рис.10.
На рис. 10: В — источник
света, Л — собирающая линза, Э — экран.
Установку на оптической скамье экрана,
линз и объекта (нити лампы) необходимо
производить так, чтобы их центры лежали
на одной прямой параллельной оптической
скамье, оптическая ось линзы должна
совпадать с этой прямой, а плоскость
экрана должна быть перпендикулярна
ей.
1 ОПРЕДЕЛЕНИЕ ГЛАВНОГО ФОКУСНОГО
РАССТОЯНИЯ СОБИРАЮЩЕЙ ЛИНЗЫ ПО ПОЛОЖЕНИЮ
ОБЪЕКТА И ЕГО ИЗОБРАЖЕНИЯ
1. Поместив экран на
достаточно большом расстоянии от объекта
ставят между ними линзу и передвигают
её до тех пор, пока не получат на экране
отчетливое увеличенное изображение
объекта.
2. По шкале на оптической скамье отсчитывают
расстояние d от объекта до линзы и
расстояние f от линзы до изображения.
3. Полученные данные заносятся в таблицу
1.
4. Ввиду неточности визуальной оценки
резкости изображения измерения (п.1-3)
рекомендуется повторить не менее трех
раз при разных положениях экрана.
5. Поместив экран на достаточно большом
расстоянии от объекта, ставят между
ними линзу и передвигают ее до тех пор,
пока не получат на экране отчетливое
уменьшенное изображение.
6. Повторяют пункты 2-4.
7. Из каждого отдельного
измерения по формуле (3) определяют
фокусное расстояние и из полученных
результатов находят среднее арифметическое.
8. Определяют оптическую силу линзы D.
5. Рассчитывают погрешность измерения.
Таблица 1
|
Номер опыта |
d |
f |
F |
D=1/F |
Примечание |
|
1
2 2 3 … |
Увеличенное изображение
Уменьшенное |
II.
ОПРЕДЕЛЕНИЕ ГЛАВНОГО ФОКУСНОГО РАССТОЯНИЯ
СОБИРАЮЩЕЙ ЛИНЗЫ ПО ВЕЛИЧИНЕ ПЕРЕМЕЩЕНИЯ
ЛИНЗЫ
.1. Передвигая линзу по оптической скамье
при неизменном положении экрана и
источника света, получают на экране
резкое уменьшенное изображение нити
лампы. Записывают в таблицу 2 деление
шкалы х1, указывающее положения линзы
на скамье. Настройку и измерения
производят не менее трех раз.
2. Не изменяя расстояния между осветителем
и экраном передвигают линзу на скамье
так, чтобы получить на экране увеличенное
изображение нити лампы. Записывают
деление шкалы х2, соответствующее новому
положению линзы. Измерения также
повторяют не менее трех раз.
3. Определяют расстояние L между экраном
и объектом по шкале оптической скамьи.
4. По данным таблицы
2 находят среднее значение величины
перемещения линзы и рассчитывают
фокусное расстояние линзы по формуле
(7).
5. Рассчитывают погрешность измерения.
Таблица 2
|
Номер опыта. Положение линзы на скамье |
l = x2-x1 (м) |
L (м) |
F |
|
|
При уменьшенном |
При увеличенном |
|||
|
1 2 3 и т.д. |
||||
|
Среднее значение х1 |
Среднее значение х2 |
Ш. ОПРЕДЕЛЕНИЕ ГЛАВНОГО ФОКУСНОГО
РАССТОЯНИЯ РАССЕИВАЮЩЕЙ ЛИНЗЫ
1. Помещают между
экраном и объектом собирающую линзу.
Перемещая экран, добиваются резкого
изображения объект и записывают в
таблицу 3 деление шкалы, соответствующее
данному положению экрана ХD.
2. Экран отодвигают
от линзы, между собирающей линзой и
первым положением экрана устанавливают
рассеивающую линзу (рис .7)
3. Перемещая экран, получают на нем резкое
изображение объекта. В таблицу 3 записывают
деление шкалы ХE, соответствующее новому
положению экрана.
4. Записывают деление шкалы ХC, где на
скамье установлена рассеивающая линза.
5. Пункты 1-3 повторяют
не менее трех раз. Для каждого из опытов
находят значения величин d = ХC — ХE и f =
ХC — ХD по формуле (8) подсчитывают фокусное
расстояние F, а затем находят его среднее
значение.
6. Рассчитывают погрешность измерения.
Таблица 3
|
Номер опыта |
XC (м) |
ХD (М) |
ХЕ (м) |
d = XC-XE (м) |
f = ХС-ХD (м) |
F (м) |
|
1 2 3 и т.д. |
||||||
|
Fср. |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется фокусом линзы ?
2. Что такое фокусное расстояние ?
3. Как располагается фокальная плоскость
?
4. Что называется
оптической силой линзы ? В каких единицах
она измеряется?
5. Как построить изображение в собирающей
линзе ?
7. В чем заключается метод определения
фокусного расстояния по величине
перемещения линзы ?
8. Почему нельзя использовать методы
определения фокусного расстояния
собирающих линз для рассеивающих линз?
9. Почему фокусное
расстояние собирающей линзы должно
быть меньше, чем у рассеивающей, если
мы хотим с помощью собирающей линзы
определить фокусное расстояние
рассеивающей линзы?
10. Как рассчитываются погрешности
измерения фокусных расстояний линз ?
Соседние файлы в папке Физика лекции
- #
- #
- #
- #
- #
- #
- #
Содержание
- ОПРЕДЕЛЕНИЕ ФОКУСНЫХ РАССТОЯНИЙ ЛИНЗ
- Определение фокусных расстояний линз.
- Определение фокусных расстояний собирающей и рассеивающей линз
- 391005, Рязань, ул. Гагарина, 59/1.
ОПРЕДЕЛЕНИЕ ФОКУСНЫХ РАССТОЯНИЙ ЛИНЗ

Прямая, проходящая через центры кривизны сферических поверхностей линзы, называется главной оптической осью (рис. 1). Если одна из поверхностей линзы плоская, то оптическая ось проходит перпендикулярно к ней. Точки пересечения поверхностей линзы с главной оптической осью (рис. 1, точки O1, О2) называются вершинами. Расстояние между вершинами называется толщиной линзы.
Линза называется тонкой, если ее толщина значительно меньше радиусов кривизны ее поверхностей. Точка тонкой линзы, через которую лучи проходят без изменения своего направления, называется оптическим центром линзы. Главная оптическая ось проходит через оптический центр. Любая другая прямая, проходящая через оптический центр линзы, называется побочной осью линзы.
Линза называется собирающей, если она преобразует падающий на нее параксиальный пучок лучей, параллельный главной оптической оси, в сходящийся гомоцентрический пучок. В противном случае линза называется рассеивающей.

У любой линзы имеется два фокуса. Расстояние от оптического центра тонкой линзы до фокуса называется фокусным расстоянием. Плоскости, проходящие через фокусы перпендикулярно главной оптической оси, называются фокальными плоскостями. Если среда по обе стороны линзы одна и та же, то модули ее фокусных расстояний равны.
Для параксиальных пучков лучей, которые преобразуются тонкой линзой, выполняется соотношение

где a1 — расстояние от линзы до предмета, a2 — расстояние от линзы до изображения, f — фокусное расстояние линзы, R1 и R2 — радиусы кривизны сферических поверхностей, ограничивающих линзу, n — относительный показатель преломления вещества, из которого изготовлена линза. Соотношение (1) называется формулой тонкой линзы.
Правило знаков.При расчетах по формуле (1) значения a1 или а2 подставляются со знаком плюс, если направления их отсчета от оптического центра линзы совпадают с направлением распространения света (см. рис. 2). Значения R1 и R2 также подставляются со знаком плюс, если их направления отсчета от вершин сферических поверхностей совпадают с направлением распространения света, в противном случае эти значения подставляются со знаками минус. Радиус кривизны R1 относится к той поверхности линзы, которая первой пересекается светом. Значения фокусного расстояния f собирающей линзы подставляются со знаком плюс, рассеивающей — со знаком минус.
Отношение показателя преломления окружающей линзу среды к ее фокусному расстоянию называется оптической силой:

Единица оптической силы — диоптрия (дптр). 1 диоптрия — это оптическая сила линзы, расположенной в воздухе, с фокусным расстоянием 1 м. Оптическая сила — величина алгебраическая: собирающая линза имеет положительную оптическую силу, рассеивающая — отрицательную.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Для определения фокусных расстояний используется оптическая скамья, на которой с помощью рейтеров устанавливаются освещённое матовое стекло с прямоугольной сеткой, белый экран и соответствующие линзы.
Определение фокусного расстояния собирающей линзы

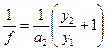
2-й способ. Если расстояние A между сеткой и экраном будет больше 4f, то посредством перемещения линзы при данном расстоянии A можно получить два изображения предмета — увеличенное и уменьшенное — (рис. 3). В этом случае уравнение (1) можно представить в следующем виде:
Два корня этого уравнения a ′ 1 и a ′′ 1 соответствуют двум возможным положениям линзы относительно сетки. На рис. 3 указаны эти положения линзы и соответствующие построения изображений, большему значению a1 (по модулю) соответствуют штриховые линии. Если обозначить разность 

ЗАДАНИЕ. Измерить двумя способами фокусное расстояние собирающей линзы.
Источник
Определение фокусных расстояний линз.



Лабораторная работа №5
Определение фокусных
Расстояний линз.
Определение фокусных расстояний линз.
Цель работы: экспериментальное определение фокусных расстояний тонких линз.
Принадлежности: оптическая скамья, двояковогнутая и двояковыпуклая линзы, экран, светящийся предмет, линейка.
Оптическая система называется идеальной, если в ней сохраняется гомоцентричность пучка и изображение получается строго геометрически подобно предмету. Гомоцентрически пучок, имеющий центр, т.е. все лучи или их продолжения выходят из одной точки или сходятся в одной точке. Идеальная оптическая система обладает осью симметрии, которая называется главной оптической осью. Лучи параллельные главной оптической оси, проходят через идеальную оптическую систему, пересекаются в одной точке, называется фокусом оптической системы. Всякая оптическая система имеет два фокуса. В тонкой линзе за фокусное расстояние можно принять расстояние от фокуса до линзы, по главной оптической оси. Лучи, проходящие через фокусы линзы, и оптический центр, удобно использовать для построения изображения в линзах.
Экспериментальное определение фокусных расстояний линзы основано на измерении расстояний от предмета до линзы, от изображения до линзы, комбинации этих расстояний согласно формуле линзы:
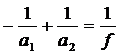
где а1 – расстояние от предмета до линзы,
а2 – расстояние от линзы до изображения,
f – фокусное расстояние.
В формуле (1) все расстояния являются алгебраическими величинами. При расчете по формуле (1) необходимо пользоваться следующими правилами знаков: 1) расстояния отсчитываются от оптического центра линзы Р (рис.1), 2)отрезки которые откладываются против хода луча, записываются со знаком »+», 3) численные значения фокусного расстояния подставляют со знаком »+», если линза имеет положительную оптическую силу, для линзы с отрицательной оптической силой- подставляется »-».
Отношение линейных размеров изображения (L) и предмета (1) называется увеличением линзы:
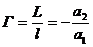
Для собирающей линзы имеем:
Здесь а и в арифметические величины. В нашем эксперименте l=1,5см (сторона предмета).
Опыт 1.Определение фокусного расстояния двояковыпуклой линзы по расстоянию от предмета до линзы и от линзы до изображения.
Из формулы (2) имеем:
Ввиду неточности визуальной оценки резкости изображения, измерения нужно проводить не менее трех раз. Часть измерений нужно провести при увеличенном, а часть при уменьшенном изображении.
Опыт 2.Определение фокусного расстояния по величине предмета, по величине его изображения L и расстояния от линзы до изображения.
Комбинируя формулу (2) получим:
Эта формула является рабочей формулой для этого эксперимента. Все три измерения в данном опыте нужно проводить при увеличенном изображении.
Опыт 3.Определение фокусного расстояния положительной линзы по способу Бресселя.
Если расстояние от предмета до изображения, которое обозначим через А, более 4f, то всегда найдется два таких положения линзы, при которых на экране получится отчетливое изображение предмета: в одном случае уменьшенное, а в другом – увеличенное (рис.2).
Воспользовавшись уравнением (2), можно записать для первого и второго положения линзы:
Приравнивая правые части этих уравнений, найдем:
Чтобы получить выражение для фокусного расстояния, рассмотрим одно из положений линзы, например:
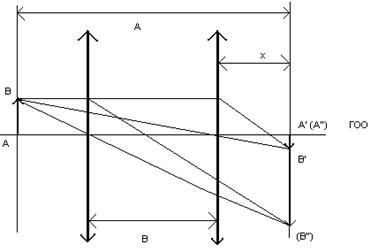
а расстояние от линзы до изображения:
Подставляя эти величины в формулу (1), найдем:
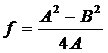
Для проведения эксперимента предмет и экран установить на расстоянии А > 4f. Грубое значение будет из предыдущих опытов. Передвигая линзу между предметом и экраном, находят положения линзы, при которых получается увеличенное и уменьшенное изображения предмета. По шкале на оптической скамье проводят необходимые измерения. По среднему значению В, используя формулу (3), вычисляют фокусное расстояние. Измерения проводят для трех различных А.
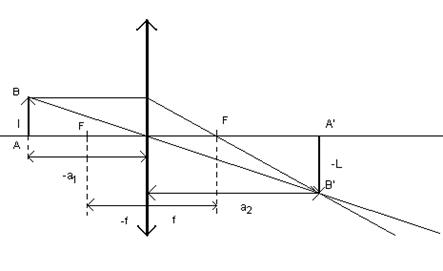
Опыт 4.Определение фокусного расстояния рассеивающей линзы.

Изображение реального объекта в рассеивающей линзе является мнимым и поэтому не может быть получено на экране непосредственно. Для определения фокусного расстояния рассеивающей линзы удобно воспользоваться мнимым источником, создаваемым собирающей линзой. Такое расположение линз показано на рис.3.

где а – расстояние между точками Д и С, b— расстояние СЕ.
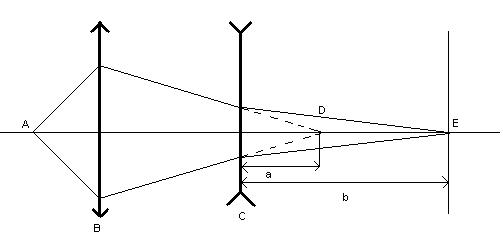
Источник
Определение фокусных расстояний собирающей и рассеивающей линз
к лабораторной работе
Определение фокусных расстояний собирающей и рассеивающей линз: Методические указания к лабораторной работе / Рязан. гос. радиотехн. акад.; Сост. А.Е. Малютин; Под ред. А.П. Соколова. Рязань, 2003. 8 с.
Описывается процесс прохождения света через линзу, кратко изложены теория и методы экспериментального определения фокусных расстояний, даны описание экспериментальной установки и рекомендации по выполнению лабораторной работы.
Лабораторная работа поставлена с участием студента гр. 131 Буханова А.И.
Предназначены для студентов всех специальностей дневной и вечерней форм обучения.
Ил. 6. Библиогр.: 2 назв.
Оптическая система, линза, фокусное расстояние
Печатается по решению методического совета Рязанской государственной радиотехнической академии.
Рецензент: кафедра общей и экспериментальной физики РГРТА
(зав. кафедрой проф. Э.П.Шеретов)
Определение фокусных расстояний собирающей и рассеивающей линз
Составитель М а л ю т и н Александр Евгеньевич
Редактор М.Е. Цветкова
Корректор Н.Ф. Богданова
Подписано в печать . Формат бумаги 60´84 1/16.
Бумага газетная. Печать трафаретная. Усл. печ. л. 0,5.
Уч.-изд. л. 0,5. Тираж 200 экз. Заказ .
Рязанская государственная радиотехническая академия.
391005, Рязань, ул. Гагарина, 59/1.
Редакционно-издательский центр РГРТА.
Цель работы: изучить методы определения фокусных расстояний собирающей и рассеивающей линз.
Приборы и принадлежности: оптическая скамья, собирающая и рассеивающая линзы, лампа накаливания, щелевая диафрагма с сеткой, экран.
Оптическая система представляет собой совокупность отражающих и преломляющих поверхностей, отделяющих друг от друга однородные среды. Оптическая система, образованная сферическими (в частности, плоскими) поверхностями, называется центрированной, если центры всех поверхностей лежат на одной прямой. Эту прямую называют главной оптической осью системы.
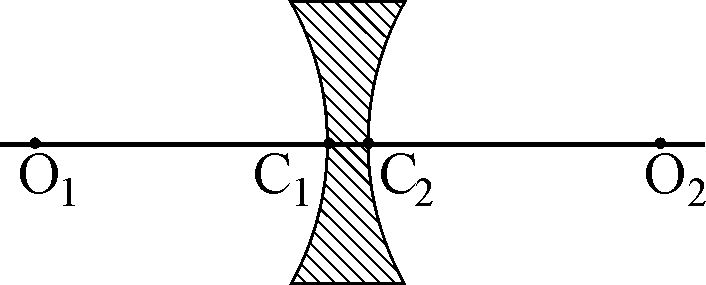
Простейшей центрированной оптической системой является линза. Она представляет собой прозрачное тело, ограниченное двумя сферическими поверхностями. В частном случае одна из поверхностей может быть плоской. Центры кривизны поверхностей О1 и О2 лежат на главной оптической оси (рис. 1,а,б). Точки пересечения поверхностей с главной оптической осью С1 и С2 называются вершинами линзы. Расстояние между вершинами именуется толщиной линзы. Линза называется тонкой, если ее толщиной С1С2 можно пренебречь по сравнению с меньшим из радиусов кривизны О1С1 или О2С2. Для таких линз можно считать, что вершины С1 и С2 сливаются в одну точку, называемую оптическим центром линзы. Прямая, проходящая через оптический центр линзы, называется побочной оптической осью.
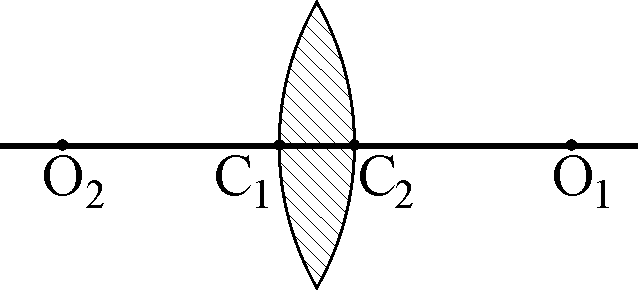
Рис. 1. Формы линз: а – двояковыпуклая, б – двояковогнутая
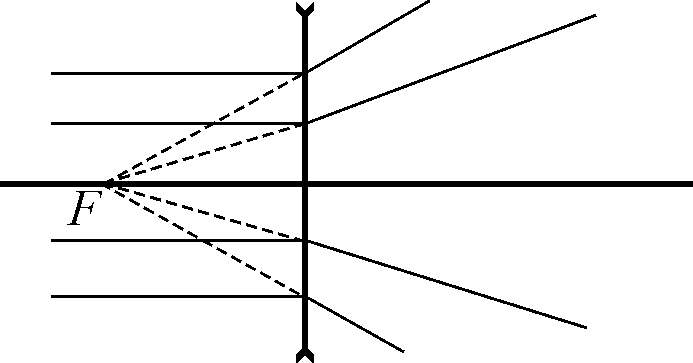
Луч света, идущий вдоль главной или побочной оптической оси тонкой линзы, не испытывает преломления. Если на линзу падает пучок лучей, параллельных главной оптической оси, то после линзы он будет сходящимся или расходящимся. В первом случае линза называется собирающей, а во втором рассеивающей. Условные обозначения собирающей и рассеивающей линз и ход лучей в них приведены на рис. 2,а,б. Пучок лучей, параллельных главной оптической оси, прошедший собирающую линзу, собирается в точке на главной оптической оси, называемой главным фокусом. Продолжения параллельных главной оптической оси лучей, прошедших рассеивающую линзу, пересекаются в лежащей перед линзой точке главной оптической оси, которая также называется главным фокусом.
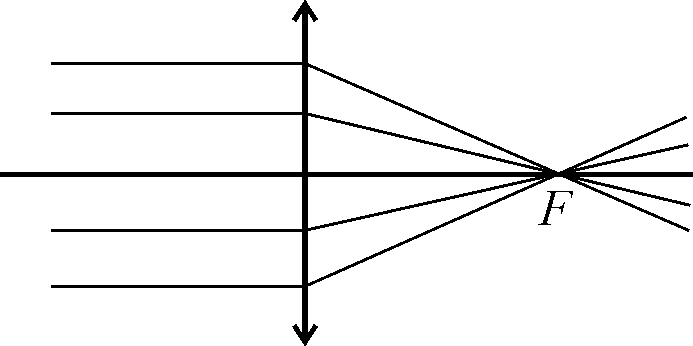
Рис. 2. Ход лучей в собирающей (а) и рассеивающей (б) линзах
Расстояние между оптическим центром линзы и главным фокусом называется фокусным расстоянием линзы. Для собирающей линзы оно считается положительным, а для рассеивающей – отрицательным. Фокусное расстояние тонкой линзы может быть найдено по формуле:

где n – показатель преломления линзы, n0 – показатель преломления среды, окружающей линзу, R1 и R2 – радиусы кривизны поверхностей линзы. Для выпуклой поверхности, то есть когда центр кривизны О лежит справа от вершины С (О1 на рис. 1,а и О2 на рис. 1,б), радиус кривизны нужно считать положительным. Для вогнутой поверхности, то есть когда центр кривизны О лежит слева от вершины С (О2 на рис. 1,а и О1 на рис. 1,б), радиус кривизны нужно считать отрицательным.
Плоскость, перпендикулярная к главной оптической оси и проходящая через главный фокус, называется фокальной плоскостью линзы. Любой параллельный пучок лучей после прохождения собирающей линзы соберется в точке, лежащей на пересечении фокальной плоскости и побочной оптической оси, параллельной пучку.
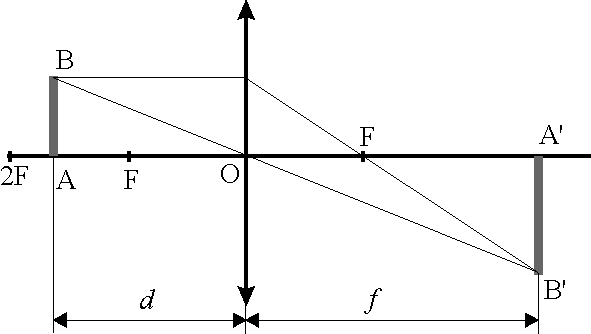
Рис. 3. Построение изображения предмета в собирающей линзе
Если светящийся предмет поместить на расстоянии d от оптического центра линзы, то его изображение получится на расстоянии f от него (рис. 3). Эти два расстояния связаны между собой соотношением:
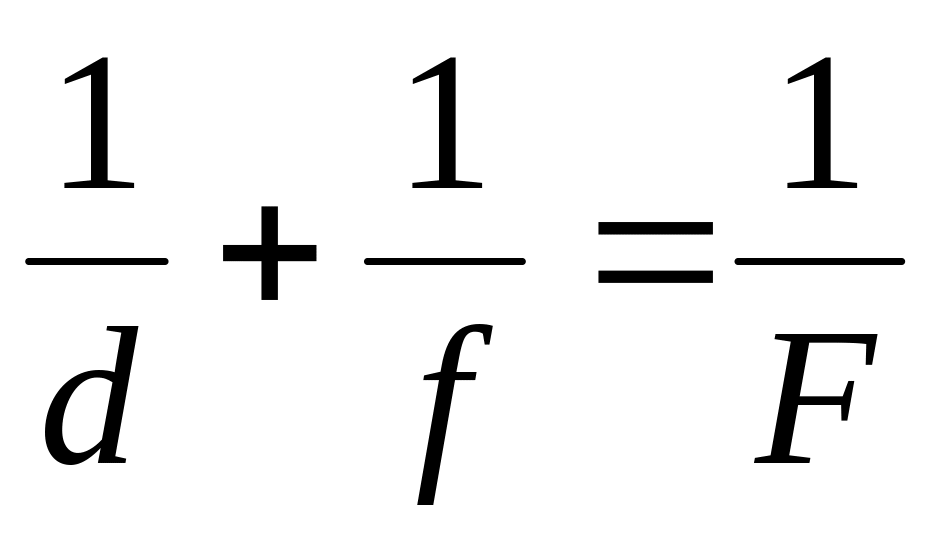
Если предмет поместить на расстояние f от оптического центра линзы, то изображение получится на расстоянии d от него. Поэтому расстояния d и f называют сопряженными.
Определение фокусного расстояния собирающей линзы
Формула (2) может быть использована для определения фокусного расстояния собирающей линзы. Измерив расстояния d и f, можно найти фокусное расстояние:
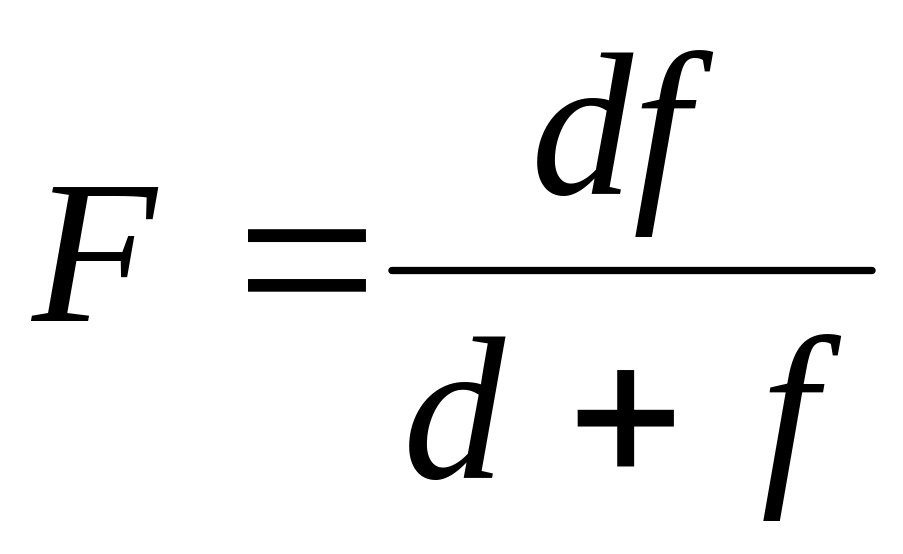
Определить фокусное расстояние можно и другим способом. Так как лучи, проходящие через центр линзы, не испытывают преломления, треугольники OAB и OA‘B‘ будут подобными (рис. 3). Следовательно:
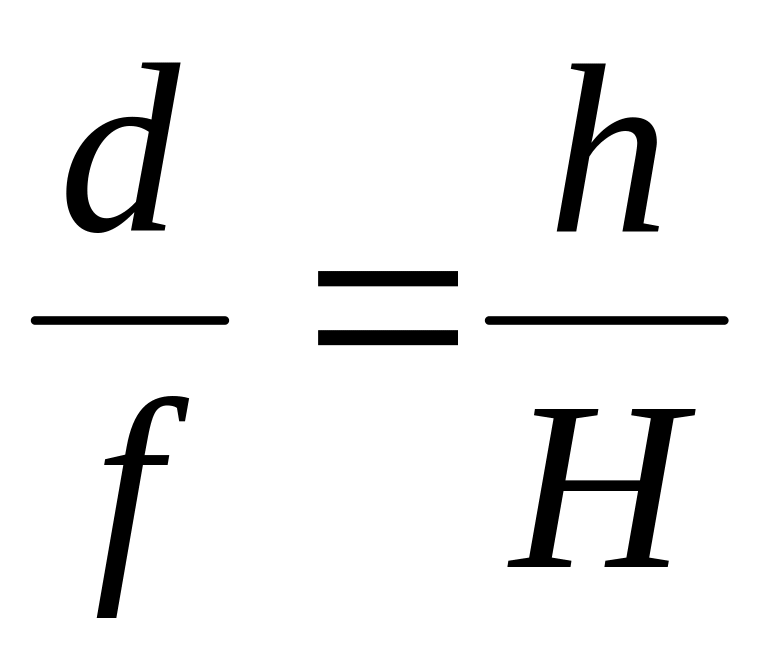
где h – величина предмета |AB|, H – величина изображения |A‘B‘|. Выражая отсюда d и подставляя его в формулу (3), получаем:
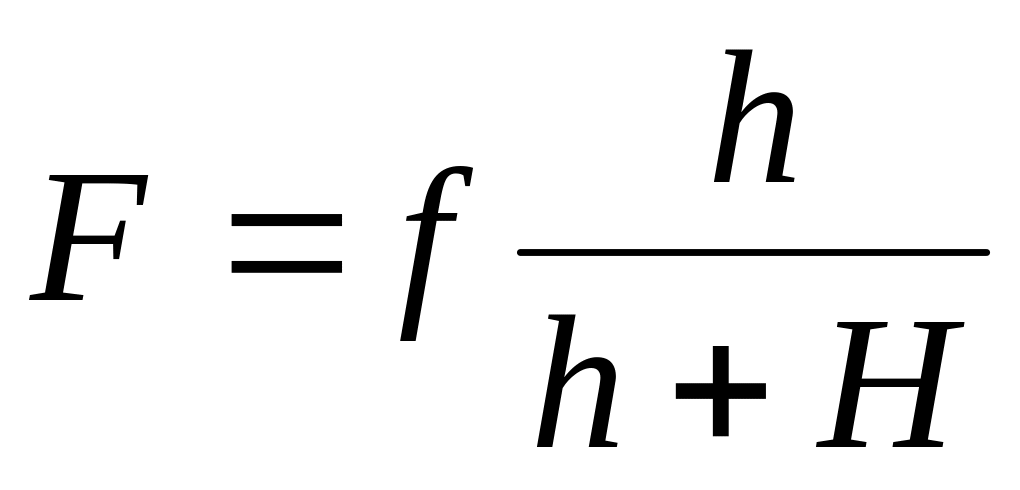
Оба описанных выше способа не лишены недостатков. Реальные линзы имеют конечную толщину. Принимая середину линзы за оптический центр и измеряя расстояния от нее, мы допускаем ошибку. На самом деле расстояния d и f нужно измерять от соответствующих главных плоскостей линзы, положение которых должно быть известно. Определить фокусное расстояние при неизвестном положении главных плоскостей можно методом Бесселя, в котором измеряются не расстояния до линзы, а ее перемещение l.
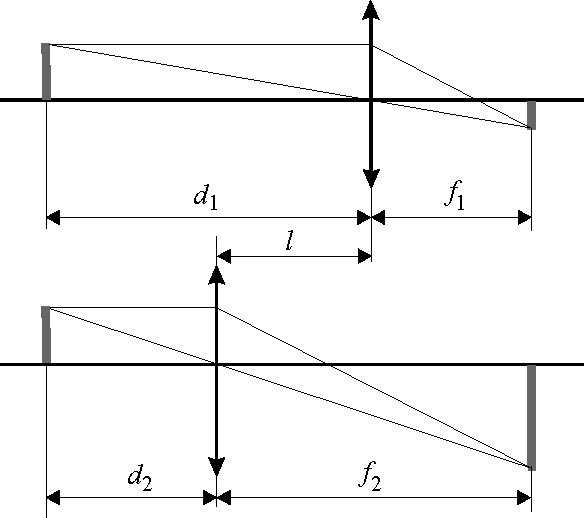
Если расстояние L между предметом и экраном больше, чем 4F, то всегда найдутся два таких положения линзы, при которых на экране получается отчетливое изображение предмета: в одном случае уменьшенное, в другом – увеличенное (рис. 4). Нетрудно увидеть, что формула (3) может быть записана в виде:
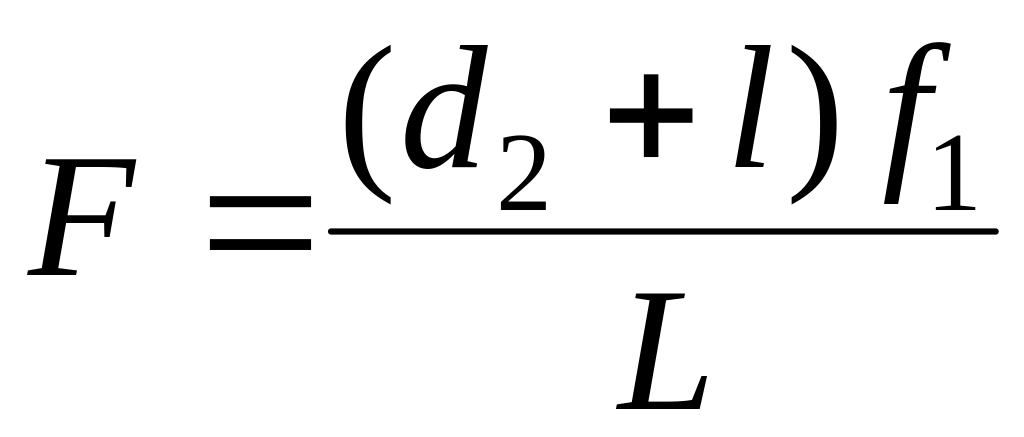
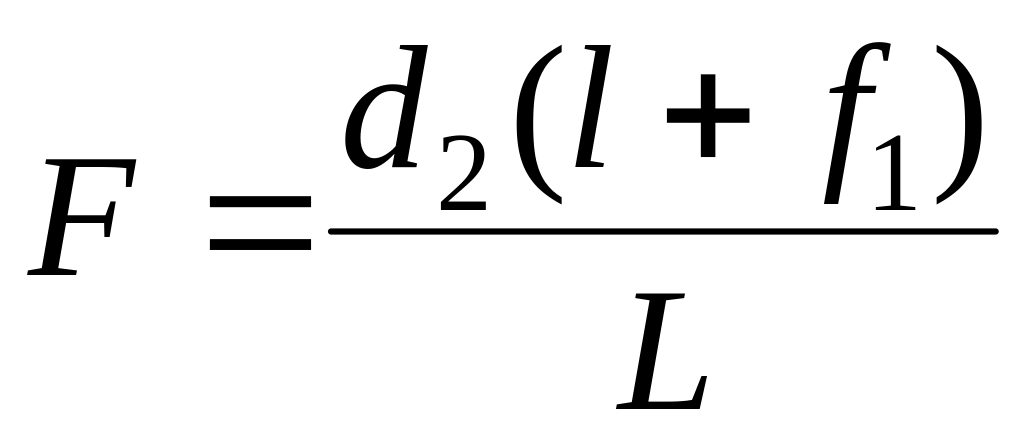
Приравнивая правые части равенств, получаем d2=f1. Так как
Рис. 4. Определение фокусного расстояния методом Бесселя
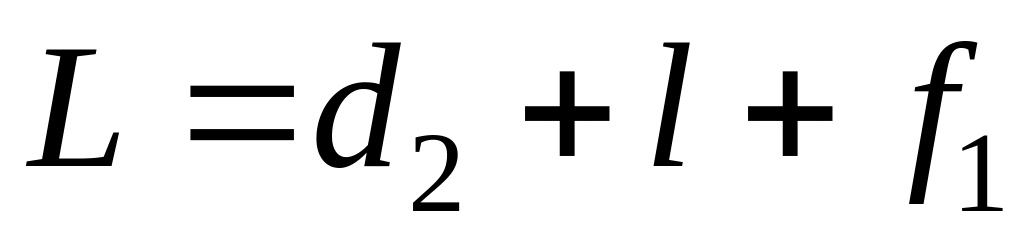
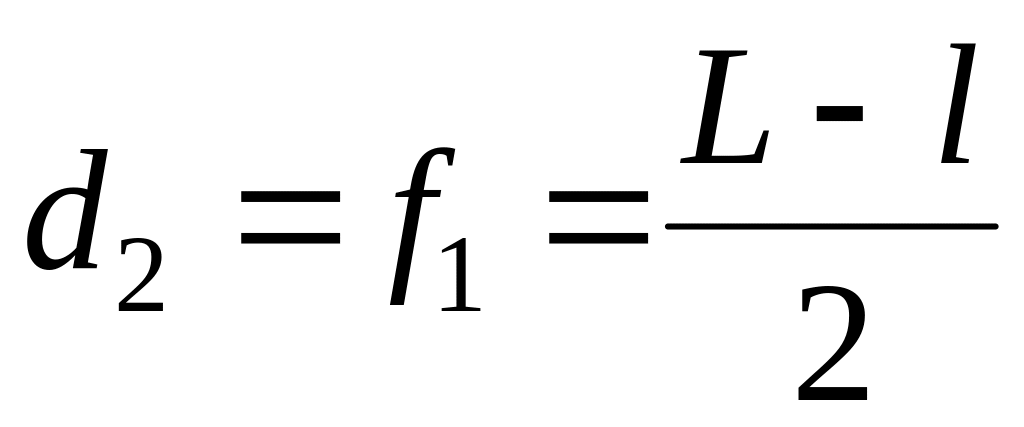
Подставляя эти значения в формулу (6), окончательно получаем:
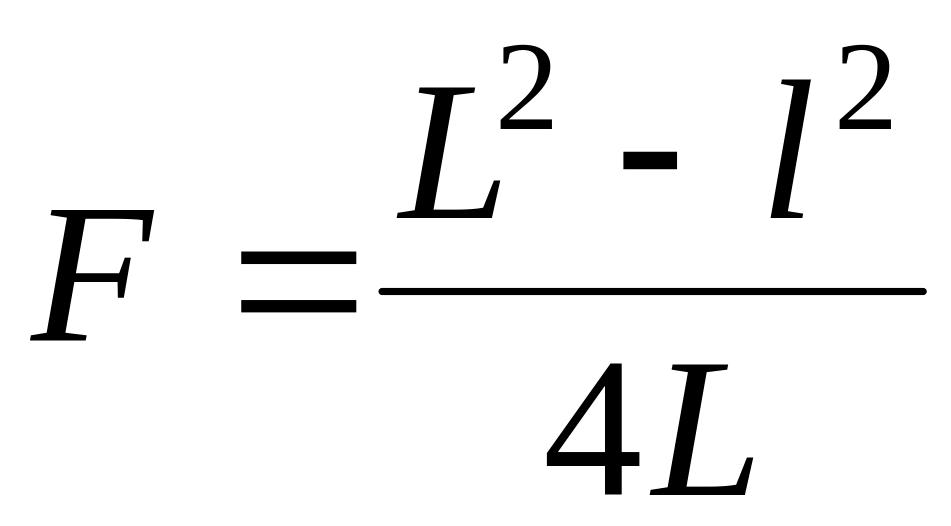
Определение фокусного расстояния рассеивающей линзы
Определить описанными выше способами фокусное расстояние рассеивающей линзы невозможно, так как она не дает действительного изображения. Методы, применяемые в этом случае, обычно используют совокупное действие собирающей и рассеивающей линз.
Пусть точка B есть изображение светящейся точки A, полученное при помощи собирающей линзы L1 (рис. 5). Если между линзой L1 и точкой B поместить рассеивающую линзу L2, то изображение светящейся точки A переместится в точку C. Вследствие принципа обратимости лучей света можно считать, что светящейся точкой является точка C, а точка B является ее мнимым изображением. Принимая во внимание, что f и F в данном случае отрицательные (мнимые), формула (3) для их абсолютных значений принимает вид:
Рис. 5. Определение фокусного расстояния рассеивающей линзы
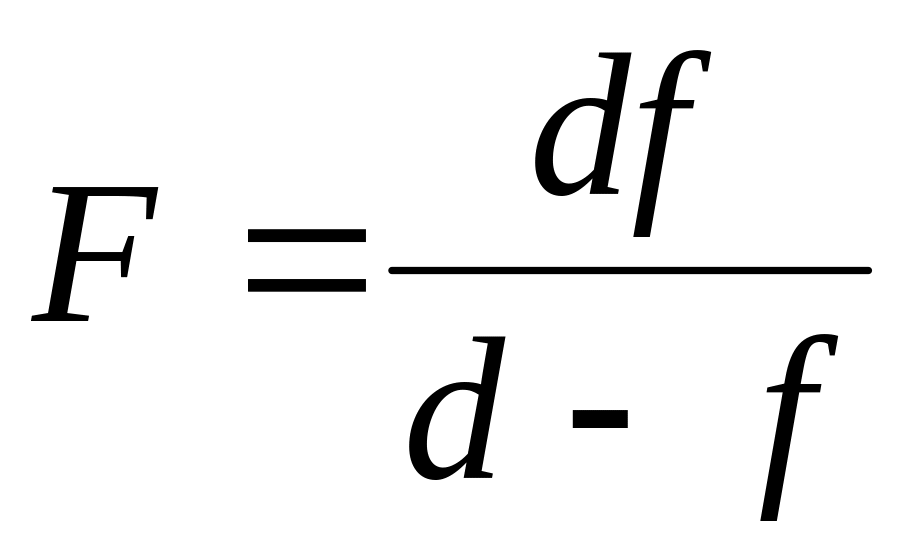
Рис. 6. Схема лабораторной установки
Установка для измерения фокусных расстояний собирающей и рассеивающей линз приведена на рис. 6. На одном конце оптической скамьи 1 помещена щелевая диафрагма с сеткой 2, освещаемая электрической лампой 3. Вдоль скамьи на ползунках могут перемещаться собирающая линза 4 и экран 5. При измерении фокусного расстояния рассеивающей линзы 6 она помещается между собирающей линзой и экраном. Положения диафрагмы, линз и экрана определяется по линейке в нижней части оптической скамьи соответственно указателям на ползунках. Щелевое отверстие диафрагмы, центры линз и середина экрана должны находиться на одной горизонтальной прямой.
Источник
Прозрачные тела, у которых хотя бы одна поверхность искривлена, называются линзами. Чаще всего бывают линзы, симметричные относительно оптической оси. Оптические особенности линзы зависят от радиуса и вида искривления.
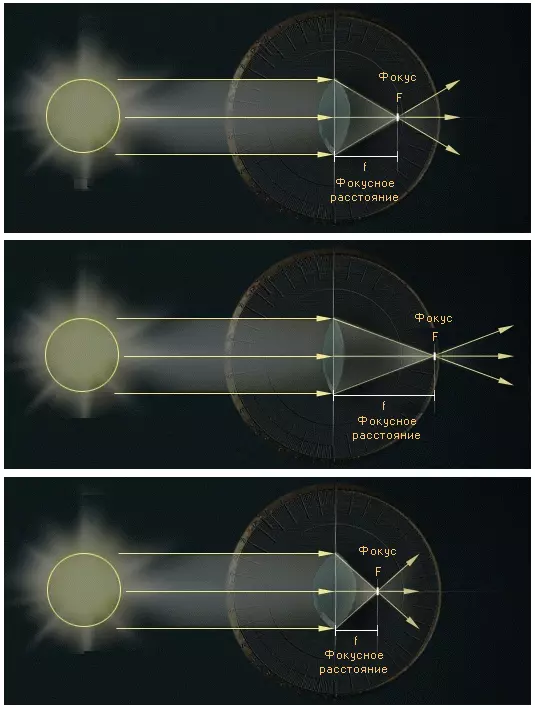
Собирающая линза
У выпуклых, или собирающих, линз середина толще, чем края. Параллельный пучок света, например, солнечный луч, падает на выпуклую линзу. Линза собирает пучок света в фокусе F. Расстояние от средней плоскости до фокуса называется фокусным расстоянием линзы f. Чем оно короче, тем больше оптическая сила линзы. Эта сила измеряется в диоптриях.
Возьмем линзу с фокусным расстоянием 0.5 метра. Тогда оптическая сила линзы равна единице, деленной на фокусное расстояние: 1/0.5 м = 2 диоптрии.
Рассеивающая линза
Вогнутые или рассеивающие линзы — это такие линзы, у которых толщина краев больше, чем толщина посередине.
В этом случае, параллельный пучок света будет рассеиваться. При этом будет казаться, что луч света выходит из одной точки, которая называется мнимым фокусом. Фокусное расстояние в данном случае будет отрицательно и соответственно оптическая сила рассеивающей линзы тоже будет отрицательна.
Возьмем линзу с фокусным расстоянием -0.25 метра. Тогда оптическая сила будет равна: 1/-0.25 = -4 диоптрии.
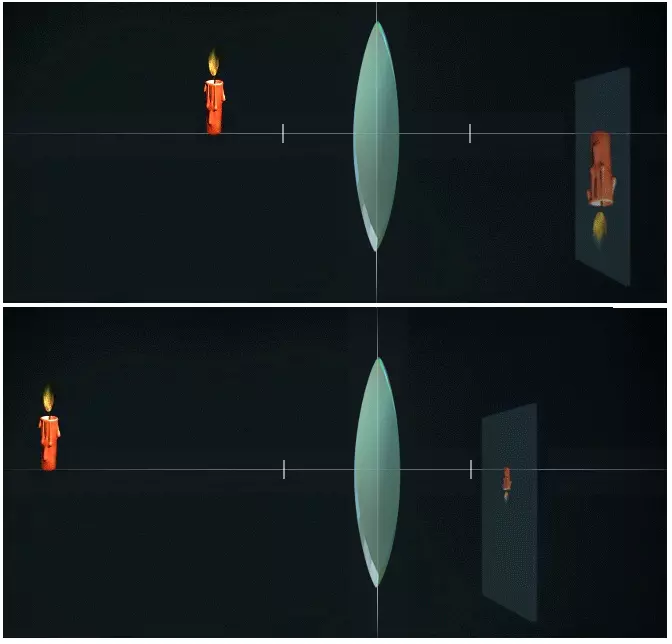
Принцип построения изображения собирающей линзой
Собирающая линза дает действительное изображение. Только оно будет перевернуто вверх ногами.
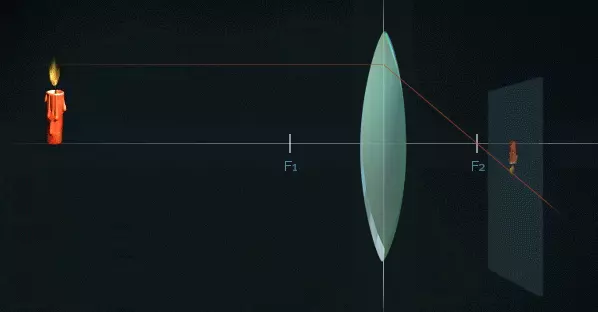
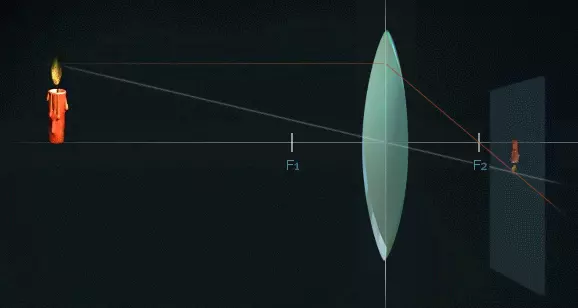
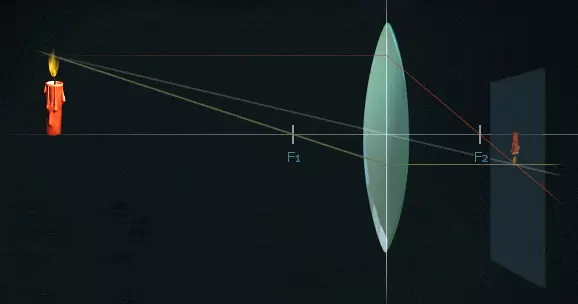
Если мы хотим получить более точное изображение, то, зная длину фокуса, мы можем построить это изображение. Для этого нам необходимы три луча.
Луч, распространяющийся параллельно оптической оси, преломляющийся в линзе и проходящий через фокус, называется параллельным лучом.
Луч, проходящий через центр линзы, называется основным лучом. Он не преломляется.
Луч, который проходит перед линзой через фокус и затем распространяется параллельно оптической оси, называется фокусным лучом. В той точке, где пересекаются все три луча, будет наиболее четкое изображение.
Если расстояние от предмета до линзы очень велико, то расстояние от изображения этого предмета до линзы будет намного меньше, т.е. изображение будет уменьшенным.
Если расстояние от предмета в два раза больше фокусного расстояния, то изображение будет такого же размера, как и сам предмет, и находится оно будет на двойном фокусном расстоянии за линзой.
Если приблизить предмет к фокусу, то мы получим увеличенное изображение, находящееся на большом расстоянии по другую сторону линзы.
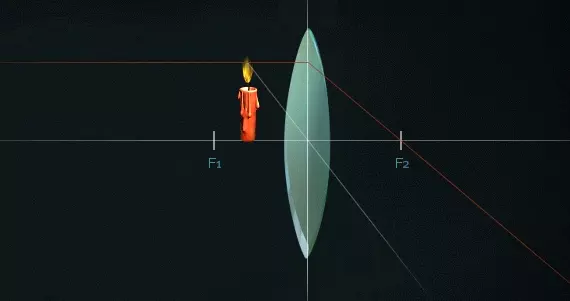
Если предмет находится прямо в фокусе или еще ближе к линзе, то мы получим нечеткое изображение.
Почему вы должны знать, что такое фокусное расстояние?
Знать, что такое фокусное расстояние и в чем заключаются особенности, особенно важно при покупке объективов. Этот урок даст вам информацию о том, как работают объективы с различным фокусным расстоянием, как использовать их творчески и выбрать те, которые подходят именно вам.
Шаг 1 – Что это на самом деле означает?
Фокусное расстояние вашего объектива в основном определяет, какой масштаб изображения будет в ваших фотографиях: чем больше число, тем больше будет эффект увеличения и приближения.
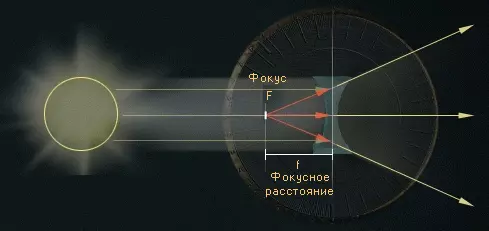
Очень часто неправильно понимают фокусное расстояние, говоря что оно измеряется от передней или задней линзы. В действительности это расстояние от точки конвергенции до сенсора или пленки в фотоаппарате. Посмотрите на диаграмму ниже, где это объясняется
Шаг 2 – Различные фокусные расстояния и как они используются
Сверхширокоугольный 12-24 мм
Эти объективы считаются узкоспециализированными и не часто входят в комплект объективов обычного фотографа. Они создают столь широкий угол обзора, что изображение может выглядеть искаженным, так как наши глаза не привыкли к такого рода диапазонам. Они часто используются в событийной и архитектурной фотографии, для съемки в ограниченном пространстве. Широкоугольные объективы как бы помещают фотографа в центр событий, делая его уже не наблюдателем, а участником, создают эффект присутствия. Они не очень подходят для портретной съемки, так как увеличивают перспективу настолько, что черты лица могут искажаться и выглядеть неестественно.
Широкоугольный 24-35 мм
Здесь вы найдете много комплектных объективов для полнокадровых камер, они начинаются с фокусного расстояния 24 мм, когда угол широкий, но искажения еще не столь выражены. Эти объективы широко применяются для репортажной фотографии, фотожурналистами для документальных съемок, поскольку они обладают достаточно широким углом, чтобы включить большое количество объектов, и при этом искажения не столь значительны.
Стандартный 35-70 мм
Именно в этом диапазоне фокусных расстояний 45-50 мм угол зрения объектива будет примерно соответствовать тому, как видят наши глаза (исключая боковое зрение). Я лично хотел бы использовать этот диапазон при съемке на улице или на встречах с друзьями в пабе или за обеденным столом. Стандартный объектив, такой как 50 мм f/1.8 – отличный недорогой и дает отличные результаты. Объектив с фиксированным фокусным расстоянием всегда даст лучшее качество изображения, чем зум. Это потому, что он построен с единственной целью. Он делает одну работу хорошо, а несколько заданий плохо.
Начальное телефото 70-105 мм
Этот диапазон обычно является крайним для комплектных объективов. С него начинаются телеобъективы и фикс-объективы для портретной съемки (около 85 мм). Это хороший выбор для портретной съемки, так как им можно снимать крупноплановые портреты без искажений, а также получать отделение объекта от фона.
Теле 105-300 мм
Объективы в этом диапазоне часто используются для далеких сцен, таких как здания, горы. Они не подходят для пейзажей, так как сжимают перспективу. Линзы более длиннофокусного диапазона в основном используются для съемки спорта или диких животных.
Шаг 3 – Как фокусное расстояние влияет на перспективу?
Об этом я уже говорил в предыдущем разделе, но чтобы дать вам более полное представление о влиянии фокусного расстояния на перспективу, я сделал 4 фото одних и тех же предметов на разных фокусных расстояниях и сравнил их. Три предмета (банки с супом) находились в одном и том же положении на расстоянии 10 см друг от друга на каждой фотографии. Стоит отметить, что снимки сделаны на кроп-камеру, поэтому фокусное расстояние будет несколько больше.
Теперь поговорим о том, что такое кроп-фактор. В сущности это означает, что если любую линзу для полного кадра (EF, FX и т.д.) поставить на тушку с кроп-фактором, то часть изображения обрежется. Коэффициент обрезки будет составлять примерно 1.6. В реальном выражении это означает, что если вы снимаете объективом 35 мм, получите результат, как будто снимали объективом 50 мм.
Как это работает – показано на рисунках ниже. Это фактически зуммированое изображение, сужение угла зрения объектива.
Даже на объективах, которые сконструированы для кроп-камер (EF-S, DX), будет наблюдаться подобный эффект, так как фокусные расстояния всегда указывается для полного кадра. Просто эти объективы на полном кадре дадут сильный эффект виньетирования, так как изображение проецируется не на всю площадь кадра.
Вот и все! И еще два совершенно разных снимка, сделанных на разных фокусных расстояниях. Первый на 24 мм, второй на 300 мм (оба на камере с кроп-сенсором).
Еще уроки из рубрики «Все основы»
Покупка аккумуляторов: что нужно знать?
Доводилось ли вам использовать свою камеру с объективами от стороннего производителя? Предполагаю, что большинство ответит да. Причина этого в том, что на рынке есть много…
Читать дальше →
09/03/2020.
Основы — Все основы.
Перевод: Алексей Шаповал
9 784
1
Правило эквивалентной экспозиции
Фотоаппарат – восхитительный инструмент. Просто поразительно как одним щелчком затвора можно остановить текущий миг и сохранить его на будущее. Принцип работы фотоаппарата…
Читать дальше →
29/02/2020.
Основы — Все основы.
Перевод: Алексей Шаповал
18 239
2
Оцифровка фотографий и негативов
У каждой семьи есть своя история, а у каждой истории есть свои фотографии: старые цветные распечатки, винтажные черно-белые фотокарточки, негативы и пленки.
Читать дальше →
17/02/2020.
Основы — Все основы.
Перевод: Алексей Шаповал
32 730
4
Как развить профессиональный взгляд
Фотография – мощный инструмент визуальной коммуникации. Объектив в какой-то мере можно считать вашим третьим глазом, который позволяет поделиться с миром тем, что видите вы…
Читать дальше →
10/02/2020.
Основы — Все основы.
Перевод: Алексей Шаповал
14 132
0
Как избежать клише в фотографии
Мир современной пейзажной фотографии весьма сложный. Кажется, будто достаточно иметь камеру, несколько объективов, штатив, фильтры, карту и отличную идею в голове, но в реальности все…
Читать дальше →
05/09/2019.
Основы — Все основы.
Перевод: Алексей Шаповал
13 012
1
Как подзаработать фотографу (не профи)
Существует миф, будто фотографы разделяются на две категории – те, для кого это просто хобби и профессионалы, которые зарабатывают деньги. На самом деле многие находятся в…
Читать дальше →
12/08/2019.
Основы — Все основы.
Перевод: Алексей Шаповал
16 752
2

вкл. 01 Декабрь 2016.
Лабораторная работа №4 (решеба, ответы) по физике 11 класс — Определение фокусных расстояний тонких линз
3. Нарисуйте ход лучей в вашей линзе, указав на рисунке расстояния d, f и F.
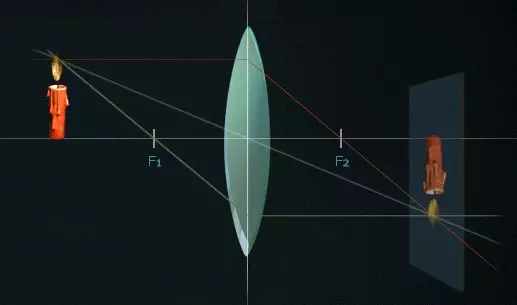
Построения в тонкой собирательной линзе. Изображения действительное, обратное, уменьшенное.
5. Вычислите средние значения <d> и <f>. Результаты вычислений запишите в таблицу 1.
<d> = 37 см = 0.37 м
<f> = 7 см = 0.07 м
6. Вычислите фокусное расстояние <F> и оптическую силу <D> линзы.
7. Нарисуйте ход лучей в данном эксперименте.
Построения в тонкой собирающей линзе. Изображение действительное, отражённое.
8. Рассчитайте абсолютные погрешности прямых измерений.
Δd = 0.0005 м + 0.0005 м = 0,001 м
Δf = 0.001 м
9. Вычислите относительную погрешность косвенных измерений фокусного расстояния собирающей линзы.
10. Вычислите абсолютную погрешность косвенных измерений фокуного расстояния собирающей линзы.
ΔF = ε · <F> = 0.022 · 0.059 м = 0,0013 м
11. Запишите значения фокусного расстояния собирающей линзы и относительной погрешности его измерения.
F = (0.059 ± 0.0013) м; ε = 2,2%
| № | d | Δd | f | Δf | F | D | ε | ΔF |
| 1 | 0,37 | 0,001 | 0,07 | 0,001 | 0,059 | 16,95 | 2,2 | 0,0013 |
| 2 | 0,37 | 0,001 | 0,07 | 0,001 | ||||
| 3 | 0,37 | 0,001 | 0,07 | 0,001 | ||||
| 4 | 0,37 | 0,001 | 0,07 | 0,001 | ||||
| 5 | 0,37 | 0,001 | 0,07 | 0,001 | ||||
| Ср. | 0,37 | 0,001 | 0,07 | 0,001 | 0,059 | 16,95 | 2,2 | 0,0013 |
12. Поверните линзу к окну и получите на экране изображение удалённого предметы за окном. Измерьте расстояние от линзы до экрана и сравните его с полученными ранее значениями фокусного расстояния линзы. Сделайте выводы.
f ≈ F; F = 0.06 м
f = 0.07 м
Если предмет находится далеко от линзы.
Порядок выполнения работы
3. Вычислите среднее значение <f>.
<f> = 17 см = 0,17 м
5. Вычислите среднее значение <d>.
<d> = 48 см = 0,48 м
6. Вычислите средние значения фокусного расстояния <F> и оптической силы <D>рассеивающей линзы.
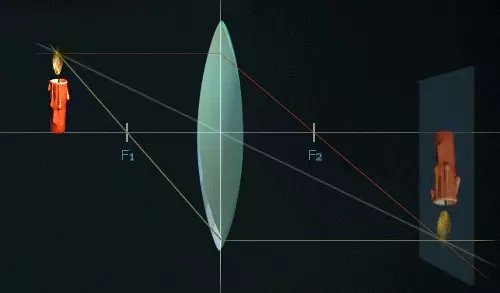
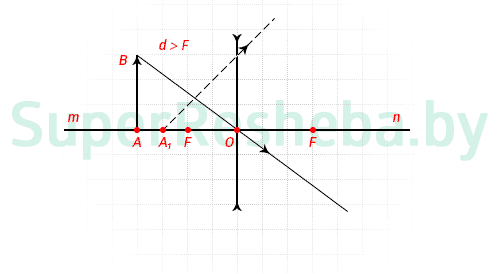
7. Нарисуйте ход лучей в данном эксперименте.
Построение в тонкой рассеивающей линзе, изображение мнимое.
8. Рассчитайте абсолютные погрешности прямых измерений.
Δd = 0,0005 + 0,0005 = 0,001 м
Δf = 0,001 м
9. Вычислите относительную погрешностью косвенных измерений фокусного расстояния рассеивающей линзы.
ε = 0,001/0,48 + 0,001/0,17 + (0,001 + 0,001)/(0,48 + 0,17) = 0,002 + 0,006 + 0,003 = 0,011 => 1,1%
10. Вычислите абсолютную погрешность косвенных измерений фокусного расстояния рассеивающей линзы.
ΔF = 0,001 м
11. Запишите значения фокусного расстояния рассеивающей линзы и относительной погрешности его измерений.
F = (0.120 ± 0.001) м; ε = 1,1%
| № | d | Δd | f | Δf | F | D | ε | ΔF |
| 1 | 0,48 | 0,001 | 0,17 | 0,001 | 0,12 | 8,33 | 1,1 | 0,001 |
| 2 | 0,48 | 0,001 | 0,17 | 0,001 | ||||
| 3 | 0,48 | 0,001 | 0,17 | 0,001 | ||||
| 4 | 0,48 | 0,001 | 0,17 | 0,001 | ||||
| 5 | 0,48 | 0,001 | 0,17 | 0,001 | ||||
| Ср. | 0,48 | 0,001 | 0,17 | 0,001 | 0,12 | 8,33 | 1,1 | 0,001 |
Ответы на контрольные вопросы
1. В каком случае линзу можно считать тонкой? Ответ обоснуйте.
Если она имеет два симметрично расположенных фокуса, через которые проходят параллельные пучки лучей (или их продолжений) после преломления в линзе.
2. Как можно получить формулу тонкой линзы?
Пусть F — расстояние от предмета до тонкой линзы, d — от линзы до изображения, f — фокусное расстояние линзы, расстояние от предмета до переднего главного фокуса — a, от заднего главного фокуса до изображения — a’. Тогда:
3. Сформулируйте правило знаков для тонкой линзы.
- Для собирающей линзы, действительных источника и изображения величины F, d и f считают положительными;
- для рассеивающей линзы, мнимых источника и изображения величины считают отрицательными
Выводы: Линза с F > 0 является собирающей, а линза с F < 0 — рассеивающей.