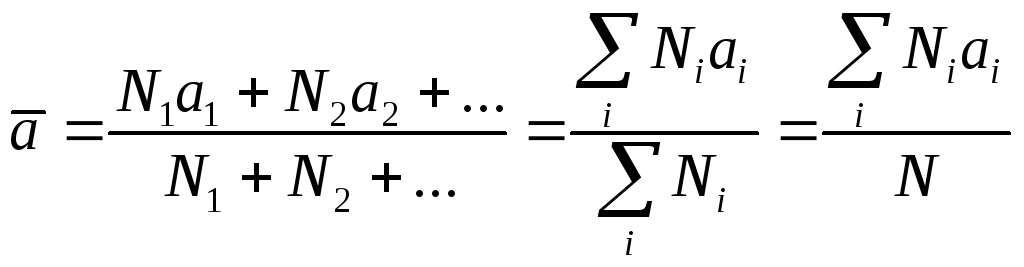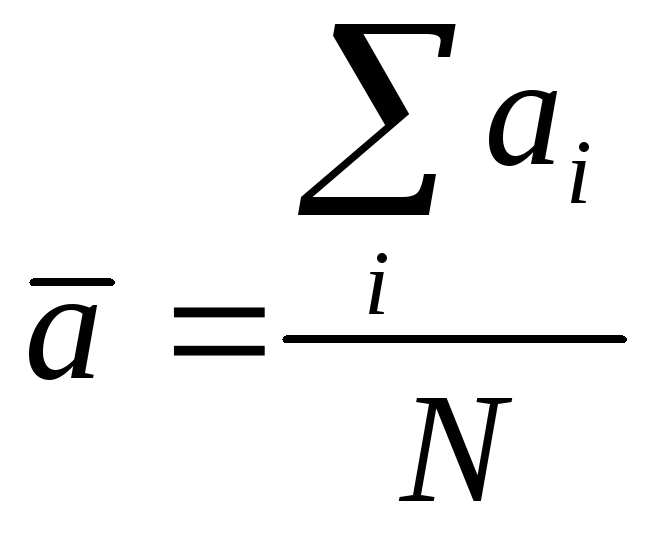Как найти средний объем физика

Продолжим
рассмотрение основных положений ТВ,
акцентируя внимание на термодинамических
процессах. Из-за беспорядочности движения
система молекул за большой промежуток
времени проходит через многочисленный
ряд состояний, в каждом из которых она
побывает не один, а много раз. Пусть
состояние газа характеризуется некоторой
величиной а,
которая принимает дискретный ряд
значений (число молекул в выделенном
объеме). Проделаем (мысленно) множество
наблюдений над системой в ее различных
состояниях. Окажется, что в N₁
наблюдениях из N
система имеет значение а₁,
в N₂
— значение а₂
и т.д. Среднее значение (арифметическое)
дискретной физической величины определяют
по формуле

(7),

или,
с учетом (1), запишем

(7^/).

Бытовой
пример. В группе из 19 человек 3 человека
17-ти летних, 10 человек 18-ти летних, и
шестеро 19-ти летних. Средний возраст
студентов в группе: а_ср= (3^.17
+ 10^.18 +6^.19)/19 = 18,16 лет.

В
том случае, когда величина N_i
близка к единице, можно воспользоваться
более простой формулой для нахождения
среднего значения

(7^//),

где
i
– полное число испытаний от 1 до N.

Покажем,
как поступать с величиной x,
принимающей в определенном интервале
непрерывный ряд значений (скорость
молекул), число которых бесконечно
велико. В этом случае вероятность,
определяемая формулой 1, теряет смысл,
поскольку в состоянии с фиксированным
значением x,
система проводит бесконечно малое
время, и соответствующая вероятность
оказывается практически равной нулю.
Следует рассматривать вероятность
того, что данная величина лежит в
интервале от x
до x
+ dx.
Время, которое система проводит в
состояниях из выбранного интервала,
пропорционально ширине интервала dx.
Тогда вероятность того, что данная
величина находится в пределах от x
до x
+ dx,
равна

dP_x
= (x)dx
(8),

где
(x)
– плотность
вероятности
или вероятность, отнесенная к ширине
интервала dx.
Тогда среднее значение непрерывно
меняющейся величины (подобно 7^/)
будет

(9),

здесь
интегрирование ведется по всем возможным
значениям x.
По аналогии определяют среднее
квадратичные значения дискретной a
и непрерывной x
величин:

(10),

(11).

1. Средняя
   квадратичная флуктуация

Важно
также знать, насколько велики отклонения
рассматриваемой величины от ее среднего
значения. Воспользоваться для оценки
отклонением а
= а_i
— а_ср
(линейной флуктуацией) не удается,
поскольку отклонения от а_ср
в большую и меньшую стороны происходят
одинаково часто, и в среднем а
оказывается равным нулю. Используя
правила вычисления средних величин,
находим

Для
того, чтобы отклонения не “гасили”
друг друга, в качестве меры отклонения
используют квадрат величины а.
Воспользуемся выражением (10) и введем
среднюю
квадратичную флуктуацию
величины а

(12),

которую
называют также дисперсией
и обозначают ²,
то есть:

(12^/).

Дисперсия
служит мерой разброса данной величины
(а),
она тем больше, чем больше вероятность
отклонения величины (а_i)
от среднего. Линейной мерой разброса
служит корень квадратный из дисперсии
или среднеквадратичное
отклонение
(величины а
от ее среднего арифметического значения)

(13).

Погрешность,
которую мы совершаем, заменив а
на а_ср,
оценивают с помощью относительной
флуктуации а

(14).

Основные
свойства дисперсии или квадрата
среднеквадратичного отклонения:

а)
дисперсия независимых величин равна
сумме их дисперсий (без доказательства);

б)
дисперсия
величины а равна среднеквадратичному
минус квадрат среднего этой величины,
используя формулу (10) получим

или
окончательно математическая запись
свойства б):

(15).

Применим
полученные формулы к объему с газом.
Среднее число молекул в выделенном
объеме V
составит

(16),

здесь
N
–полное число молекул в объеме V,
n
— концентрация молекул газа. Найдем
отклонение от среднего или дисперсию
числа молекул в объеме V.

Сопоставим
каждой молекуле случайную величинуа,
которая принимает значения а
= 1, если молекула в объеме V,
и а
= 0, если молекула вне этого объема.
Тогда согласно (10) среднеквадратичное
значение а
будет

,

асреднее значение составит: .
Найдем дисперсию с помощью формулы 15:

Дисперсия

общего числа частиц в объеме V
с учетом свойства а) составит

(17)*.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как найти среднее значение чисел?

Среднее значение Это арифметическое и вычисляется путем с добавления группы чисел и деления на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6. Медиана Среднее число числа.

Что такое среднее значение в физике?

В теории вероятностей и статистике

среднее значение случайной величины — то же, что математическое ожидание случайной величины. По сути — среднее значение её функции распределения.

Как рассчитать среднее значение между двумя числами?

Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.

Как рассчитать среднее значение в Excel?

Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула.

Как найти среднее значение за месяц?

Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.

1. x – среднее арифметическое;
2. xn – конкретное значение;
3. n – количество значений .

Как найти среднее значение в ворде?

Чтобы вычислить среднее арифметическое в строке или столбце, ставим курсор в их последнюю ячейку, открываем окно «Формула» («Работа с таблицами» — вкладка «Макет» — раздел «Данные» — кнопка «Формула»).

Как посчитать медиану?

Медианой (серединой) набора чисел называется число стоящее посередине упорядоченного по возрастанию ряда чисел. Если количество чисел в ряду чётное, то медианой ряда является полусумма двух стоящих посередине чисел.

Как вывести среднее значение?

Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество.

Как найти среднее значение показателя?

В математике среднее арифметическое — это среднее число, которое получается, если сложить несколько чисел и разделить результат на количество этих чисел. Это не единственный способ вычисления среднего числа, но именно о нем большинство людей думает, когда речь идет о среднем.

Как найти среднее значение скорости?

Чтобы найти среднюю скорость, нужно разделить весь путь, пройденный объектом, на все время его движения.

Что такое среднее значение величины?

Среднее значение — Среднее значение числовая характеристика множества чисел или функций; некоторое число, заключённое между наименьшим и наибольшим из их значений.

Что такое среднее значение в математике пример?

Среднее арифметическое – это частное от деления суммы чисел на их количество. Пример 1. Найти среднее арифметическое двух чисел: 4 и 6.

Что такое среднее арифметическое значение?

Средним арифметическим нескольких чисел называют сумму этих чисел, делённую на количество слагаемых. Среднее арифметическое = сумма всех чисел количество слагаемых .

Целью данной работы
является проверка навыков по определению объёма тела с помощью измерительного
цилиндра (мензурки).

Для выполнения этой работы нам предлагают использовать
комплект оборудования № 1 в составе: мензурка, цилиндр, номер которого будет
указан в работе, стакан с водой и весы (это могут быть как электронные весы,
так и рычажные весы с разновесом).

Теперь давайте с вами вспомним, что же такое плотность
вещества. Плотность вещества — это масса вещества, содержащаяся в
единице его объёма:

Единицей измерения плотности в СИ:

Хотя при выполнении этой работы допускается
использование внесистемной единицы измерения плотности.

Анализ формулы плотности и оборудования, которое нам
предоставлено, показывает, что массу цилиндра мы можем найти прямыми
измерениями. А вот его объём придётся находить косвенными измерениями.

Для начала определим с вами массу предложенного
цилиндра. Если в комплекте оборудования идут электронные весы, то мы просто
ставим тело на весы и снимаем показания электронного циферблата. При этом не
забываем, что результаты мы должны записать с учётом погрешности измерения (её
значение дано в задании):

Если же в комплекте будут идти рычажные весы, то перед
взвешиванием необходимо убедиться, что весы уравновешены. При необходимости для
установления равновесия на более лёгкую чашку нужно положить полоски бумаги,
картона и тому подобного. Затем нужно на левую чашу весов аккуратно поставить
взвешиваемое тело, а на правую — гири. Масса гирь подбирается таким образом,
чтобы плечи весов находились в равновесии.

Теперь определим объём цилиндра. Для этого мы должны
взять мензурку и определить её цену деления.

Затем в мензурку необходимо налить столько воды, чтобы
тело могло полностью погрузиться в воду, и измерить начальный объём воды
(обозначим его через V₁).

После этого мы аккуратно на нитке опускаем цилиндр в
мензурку так, чтобы он смог полностью погрузиться в воду. И вновь измеряем
объём воды в мензурке (его мы обозначим V₂).

Теперь, чтобы определить объём цилиндра, мы должны
найти разницу объёмов воды после погружения цилиндра и до него (эту формулу мы
записываем рядом с формулой плотности):

Подставив в формулу числа найдём, что объём данного
нам цилиндра, с учётом погрешности измерений, равен (26 ± 2) см³.

Вернёмся к пункту «один» и схематически изобразим нашу
экспериментальную установку для определения объёма цилиндра.

Наконец можно найти числовое значение плотности
материала цилиндра, подставив в формулу значения массы и объёма цилиндра. После
несложных вычислений получаем 7,5 см³.

В конце работы можно написать вывод: плотность вещества, из которого изготовлен цилиндр, равна семи с
половиной граммам на кубический сантиметр.

Объем — это измерение того, сколько места занимает вещество. Среднее значение — это математическое среднее для набора чисел, которое вы можете найти, сложив числа и разделив итоговое число на количество измерений. От вас может потребоваться найти средний объем как часть математики средней школы или средней школы или класса науки. Этот тип расчета может быть полезен при записи измерений объема, которые подвержены изменениям, например, в случае дождемера или лабораторного стакана.

Запишите несколько измерений объема.

Добавьте измерения. Например, вы могли бы записать следующие измерения в миллилитрах: 25, 40, 30 и 35. Вы бы добавили эти цифры в общей сложности 130 миллилитров.

Разделите итоги второго этапа на количество использованных измерений. В этом примере вы разделите 130 на 4, чтобы получить средний объем 32, 5 миллилитра.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.