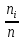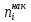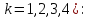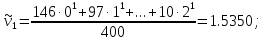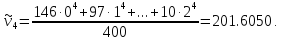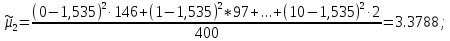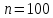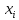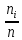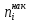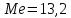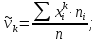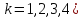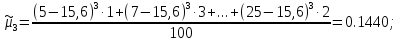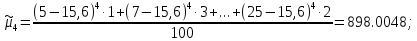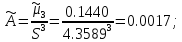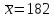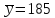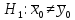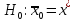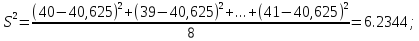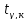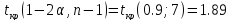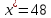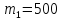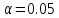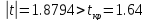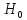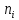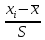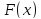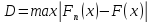Определить предельные отклонения, размеры и зазоры допуски отверстия, вала, посадки и зазоры средние отклонения и зазоры начертить схему полей допусков. [c.29]
Основной предпосылкой взаимозаменяемости является выполнение сопрягаемых размеров деталей в заранее установленных пределах, определяемых допусками. Величина допуска и расположение поля допуска на неточность изготовления непосредственно связаны с характером соединения (посадкой), с предельными и средними значениями возможных зазоров или натягов и, таким образом, с конструктивными требованиями, предъявляемыми к работе данного узла и всего механизма. Конструктивные требования вызывают в ряде случаев необходимость возможного приближения зазоров и натягов к расчётным величинам, к сужению пределов их колебаний и тем самым к уменьшению величины допуска. Эти конструктивные требования ограничиваются технологическими возможностями, поскольку уменьшение допуска связано в большинстве случаев с увеличением трудоёмкости и стоимости изготовления деталей. [c.1]
За расчетные размеры детали принимают средние от предельных размеров с учетом допусков Д на их изготовление. Предельные размеры обозначены индексом max и min. [c.602]
Расчетные данные занесем в табл. 6.3. В графе «Характеристики размеров» запишем номинальные значения размеров 7/, их предельные отклонения esj и е/ средние отклонения ети, и допуски Причем в графе «Известные» укажем характеристики размеров, заданные стандартами (в данном случае ГОСТ Р 50894-96, ГОСТ Р 50891-96, ГОСТ 8592-79), а в графе «Расчетные» — характеристики предварительно назначенных размеров. [c.524]
Расчет средней величины допуска или средней степени точности размеров составляющих звеньев Корректировка допусков и проверка правильности назначения допусков Назначение допускаемых отклонений на размеры составляющих звеньев цепи Проверка правильности назначения предельных отклонений [c.29]
При прочих равных условиях значение крутящего момента зависит от метода определения величины натяга когда натяг определяется как разность средних диаметров резьбы шпильки и гнезда крутящий момент примерно в 1,5 раза больше (при одинаковой величине натяга) крутящего момента, определенного как разность приведенных средних диаметров резьбы. Поэтому в основу классификации точности резьбы с гарантированным натягом положена величина допуска по средним диаметрам резьбы соединяемых деталей. В ГОСТе 4608—65 даны предельные отклонения средних диаметров резьбы гнезда и шпильки, которые используются при их сортировке на группы для селективной сборки. Одновременно для устранения возможности выхода действительного значения с1 резьбы за установленные размеры вследствие отклонений формы шпильки и гнезда и обеспечения большей надежности соединений в стандарте указано, что нижнее предельное отклонение резьбы гнезда и верхнее предельное отклонение резьбы шпильки ограничивают приведенные средние диаметры резьбы гнезда и шпильки. Это указание обязывает контролировать резьбы шпилек и гнезд после их изготовления (до сортировки) производить предельными калибрами или измерительными приборами, но по приведенному диаметру. Установлены следующие четыре посадки (сочетание полей допусков резьбового гнезда А [c.151]
Нормы точности монтажа силовых нерегулируемых червячных передач включают требования к пятну контакта, к предельному отклонению межосевого расстояния передачи АдЛ и А Л, к предельному смещению средней плоскости колеса A ,g и А и к допуску иа перекос осей бу. Требования, предъявляемые к межосевому расстоянию передачи, не относятся к конструкциям передач, в которых межосевое расстояние регулируется. То же следует указать и о смещении средней плоскости колеса, если колесо регулируется при сборке. В конструкциях, не предусматривающих осевой установки колеса по отношению к оси червяка, выполнение требований, предъявляемых к допустимому смещению средней плоскости колеса, должно быть обеспечено допусками на составляющие размеры размерной цепи, определяющей расположение средней плоскости колеса относительно оси червяка. [c.232]
Основной предпосылкой взаимозаменяемости является выполнение сопрягаемых размеров деталей в заранее установленных пределах, определяемых допусками. Величина допуска и расположение поля допуска на неточность изготовления непосредственно связаны с характером соединения — посадкой, а также с предельными и средними значениями зазоров или натягов, которые определяются конструктивными требованиями, предъявляемыми к работе данного узла или механизма. [c.1]
Нетрудно видеть, что для предотвращения брака (для охватываемых размеров) необходимо исключить возможность отклонения групповых средних размеров от рабочего настроечного размера в направлении нижней границы поля допуска. С этой целью можно, например, использовать методику определения предельных значений групповых средних размеров, разработанную А. Б. Яхиным [32], при которых с требуемой степенью надежности обеспечивается правильность настройки. [c.252]
Для облегчения настройки можно воспользоваться вероятностными расчетами для установления предельных групповых средних размеров в зависимости от принимаемого процента риска выхода некоторой части размера за пределы поля допуска. [c.255]
Чтобы при пользовании предельными калибрами средние размеры всегда находились в установленных пределах допуска, необходимо размеры предельных калибров рассчитывать по предельным отклонениям, установленным для среднего диаметра. Следовательно, допускаемые стандартом предельные отклонения наибольшего и наименьшего диаметров при этом уже не могут быть использованы при изготовлении колец подшипников. Таким образом, применение предельных калибров вызывает необходимость суш,ественного сокращения допусков размеров подшипников. Обнаруженные в результате критического анализа отмеченные выше и другие недостатки ГОСТ 520-45 были устранены в новом стандарте на подшип—ники. [c.378]
Комплексный метод контроля точности всех цилиндрических резьб осуществляется предельными калибрами, а резьб малых размеров также и с помощью проекторов, путем сравнения действительного контура проверяемой резьбы с предельными на всей длине свинчивания. Этот метод применяется для проверки резьбовых деталей, допуск среднего диаметра которых является суммарным. При этом методе проходными резьбовыми калибрами проверяют у болта размеры с/г и ь а у гайки — г и й. Одновременно с помощью этих калибров проверяют наличие диаметральной компенсации погрешностей шага и половины угла профиля. Проходной калибр должен свободно свинчиваться с проверяемой резьбой. Таким образом, проходные калибры дают возможность установить приведенный средний диаметр резьбы. С помощью непроходных резьбовых калибров проверяют только собственно средний диаметр резьбы. Непроходной калибр не должен свинчиваться с проверяемой резьбой (допускается свинчивание непроходного калибра до двух оборотов [1, 2, 7, 129]. [c.444]
За расчетные размеры изделия принимают средние от предельных размеров с учетом допусков на изготовление. Московский инструментальный завод рекомендует брать следующие размеры [c.1003]
На изображении червячного колеса, согласно ГОСТ 2.406—68, указывают диаметр окружности выступов в средней плоскости зубчатого венца и при необходимости предельное значение радиального биения поверхности выступов в средней плоскости наибольший диаметр зубчатого венца по выступам ширину зубчатого венца и при необходимости биение базового торца расстояние от средней плоскости зубчатого венца до базового торца и предельное смещение средней плоскости зубчатого венца в обработке (для червячных колес, не регулируемых при монтаже в осевом направлении, предельные значения смещений назначают из соответствующего стандарта на допуски червячных передач) данные, определяющие внешний контур зубчатого венца (например, радиус выточки на поверхности выступов, размеры фасок или радиусы закруглений торцовых кромок) данные о специальной форме зубьев. [c.103]
У калибров-колец имеется проходное кольцо. Если проходное кольцо навинчивается на резьбу, то это означает, что размер среднего диаметра не больше его предельного размера, а все остальные элементы такл<е лежат в пределах допусков на них. Следовательно, средний диаметр резьбового проходного кольца равен номинальному среднему диаметру резьбы изделия. Такой калибр обозначается ПР. [c.285]
В графе Характеристики размеров записывают номинальные значения размера с предельными отклонениями, средние отклонения и допуски на размеры, причем в графе- Известные указывают характеристики размеров, заданные стандартами или заимствованные из других расчетных схем или изделий в графе Расчетные записывают характеристики размеров, полученные расчетом. [c.115]
Непроходное резьбовое кольцо б проверяет только средний диаметр резьбы. Его размеры выполняются по наименьшему предельному размеру среднего диаметра резьбы (т. е. для метрической резьбы со скользящей посадкой по размеру 2—6), и оно не должно навинчиваться (допускается навинчивание не более [c.316]
Формулы (1.21)—(1.29) соответствуют методу расчета посадки на максим м — минимум. Более точное представление о посадке дают вероятностные значения предельных и средних зазоров или натягов и допуска посадки, определенные с учетом характеристик рассеяния размеров деталей. [c.19]
Для больших размеров предпочтительные поля допусков не выделены, так как набор полей допусков и без того ограничен по сравнению с диапазоном средних размеров, а размерный инструмент и предельные калибры применяют крайне редко. [c.77]
При решении прямой задачи (формулировку задачи см. с. 560) известны предельные значения исходного звена (или эквивалентные им величины номинальный размер среднее отклонение поля допуска [Г ,]). Требуется распределить допуск исходного звена между составляющими звеньями и назначить предельные отклонения размеров составляющих звеньев. [c.626]
На рабочих чертежах деталей, в технологических картах и другой технической документации геометрические параметры, т. е. размеры, указывают в виде номинального значения и допустимых отклонений, например, Dl . Здесь D — номинальное значение размера а — верхнее предельное отклонение Ь — нижнее предельное отклонение. Пользуясь отклонениями, допуск можно определить как разность верхнего и нижнего отклонений 6 = а—(—Ь). Среднее арифметическое между верхним и нижним отклонениями называется средним отклонением бср= (а + Ь)/2. [c.123]
О1о о2о- Рассчитать посадку с зазором определить номинальные и предельные размеры предельные и средние отклонения, предельные зазоры, допуски отверстия, вала и посадки. Построить схемы полей допусков по предельным размерам и упрощенную. [c.23]
Верхнее отклонение наружного диаметра гайки и иижнее отклонение внутреннего диаметра белта стандартом не нормируюач я. Зазоры в резьбовых соединениях по этим диаметрам обеспечиваются размерами резьбообразующего инструмента. Допуски на диаметры резьбы назначаются по классам точности 2а, 3 и 4. Предельные отклонения для резьбы классов точности 2а и 3 соответствуют ГОСТу 9253—59. Дяя резьбы с крупными шагами нижние отклонения на средние диаметры болта класса точности 2а соответствуют ГОСТу 10191—62. [c.200]
Ряды полей допусков по ЕСДП для валов и отверстий при размерах свыше 500 до 3150 мм приведешь в табл. 1.18 и 1.25, а при размерах свыше 3150 до 10 ООО мм — в табл. 1.19 и 1.26. Для больших размеров предпочтительные поля допусков не выделены, так как набор полей допусков и без того ограашчен по сравнению с диапазоном средних размеров, а размерный инструмент и предельные калибры применяют крайне редко. Поля допусков и посадки для размеров свыше 10 ООО до 40 ООО мм в ГОСТ 26179—84 не предусмотрены. [c.88]
Для трубной конической резьбы установлено осевое смещение основной плоскости Aj/j а (табл, 4,56). Осевое смещение является суммарным, т. е. включает отклонения среднего диаметра, шага, угла наклона боковой стороны профиля и угла конуса. Установлены также предельные отклонения среднего диаметра внутренней цилиндрической резьбы (см. табл. 4.56), со.единяемой с наружной конической резьбой. Допускается соединение наружной конической резьбы с внутренней цилиндрической резьбой класса точности А по ГОСТ 6357—81 (см. табл. 4.52). Даны предельные отклонения для тех параметров резьбы, которые являются исходными при проектировании резьбообразующего инструмента и расче ге резьбовых калибров. К ним относятся (табл. 4.57) отклонения среза веришн и впадик (размера С, рис. к [c.252]
Тогда предельные размеры среднего диаметра резьбы будут равны наибольший 14,701 — 0,038 = 14,663 мм, наименьший 14,701 — 0,198 = 14,503 мм, допуск среднего диаметра. 14,663 — 14,503 = 0,16 мм. Размер 25 показывает длину резьбы-с полным профилем, т. е. без сбега. Размеры резьбы нужно знать, когда резьба нарезается резцом, резьбовой фрезой или ее получают резьбошлифованием, а не мерным резьбонарезным инструментом (метчик или плашка). Но так как для стандартных резьб в чертеже размеры резьбы не указьшают, то их берут из карт технологического процесса. [c.17]
Степень точности и поле допуска 6g определяют точность резьбы по ее среднему диаметру. Из таблиц (ГОСТ 16093-81) находим, что средний диаметр резьбы М16Х2 равен 14,701 мм, а его предельные отклонения для поля допуска вg составляют 18 91 мм. Тогда предельные размеры среднего диаметра резьбы будут равны наибольший 14,701—0,038=14,663 мм, наименьший 14,701—0,198 = 14,503 мм, допуск среднего диаметра 14,663-14,503= 0,16 мм. Размер 25 мм показывает длину резьбы с полным профилем, т. е. без сбега. Размеры среднего диаметра резьбы нужно знать, когда резьбу нарезают резцом, резьбовой фрезой или ее получают резьбошлифованием, а не мерным резьбонарезным инструментом (метчик или плашка). Но так как для стандартных резьб в чертеже размеры резьбы не указывают, то их берут из карт технологического процесса или других документов. [c.18]
В некоторых чертежах неуказанные предельные отклонения остальных размеров могут нормироваться по 1Т14/2 вместо /2, по классу точности средний (или допусками квалитетов 12, 16 или 17). [c.23]
Для сопряжённых размеров указывают поля допусков- в соответствии с посадками, показанными на чертеже общего виДа изделия. Для цепочных размеров задают предельные отклонения на основании результатов расчета допусков соответствующих расчетных схем. Предельные отклонения свободных размеров чаще всего соответствуют среднему классу тотаостц, т. е. — -4. — /2. [c.214]
При указанных условиях отклонения формы и расположения первой группы в предельном случае могут достигнуть значения, определяемого полным допуском размера (подробнее см. п. 2.2 и 2.3) Эти предельные значения должны учитываться конструктором, который решает, допустимы ли они для обеспечения правильной работы детали или следует указать в чертеже более жесткие допуски формы и расположения. Однако и при отсутствии в чертежах допусков формы и расположения первой группы технолог должен ограничить их в технологической документации некоторой частью допуска размера (обычно в пределах от 40 до 60%). Без таких ограничений нельзя обеспечить нормальный ход технологического процесса, так как не остается запаса на другие составляющие погрешности размера (погрешность настройки на размер, разброс размеров в деталях партии, износ инструмента и др.), и неизбежно забракование части деталей по размеру. Например, отклонение от параллельности для детали, показанной на рис. 2.5, о, может достигнуть полной величины допуска размера (Апар = в) в том случае, если средний размер детали Ва будет находиться точно в середине поля допуска. Если же из-за воздействия других погрешностей обработки размер Вс будет выше середины поля допуска (рис. 2.5, б) или ниже его (рис. 2.5, в), то допустимое отклонение от параллельности для данных деталей будет меньше допуска размера, а при Дпар = Тв (на рис. 2.5, бив показано штриховой линией) будет нарушен допуск размера на участках, заштрихованных в клетку. При выполнении размера В на верхнем или нижнем пределе поля допуска размера отклонение от параллельности недопустимо, так как в любом случае приведет к нарушению допуска размера. Контроль технологических допусков формы и расположения при приемке изделий не является обязательным. [c.375]
Если соединить два таких звена, как показано на рис. 21, а и б, то зазор, равный нулю, может быть только в одном случае, когда отверстие выполнено по наименьщему, а вал — по наибольшему предельному размеру. Зазор, равный сумме допусков (10 мк), может быть также только в одном случае, когда отверстие выполнено по наибольщему, а вал — по наименьщему предельному размеру. Средний зазор, равный 6 мк, может иметь место в шести случаях, например при соединении вала, имеющего действительное отклонение —0,003 мм, с отверстием, имеющим действительное отклонение -f 0,003 мм, или, что то же, при составлении двух звеньев линейной цепи (рис. 21,6), имеющих отклонения по —0,003 мм. Распределение зазоров будет характеризоваться законом треугольника (рис. 21,в). [c.36]
Федеральное
государственное бюджетное образовательное
учреждение высшего профессионального
образования «Чувашский государственный
университет им И.Н. Ульянова»
Дополнительные
главы математики.
Типовой
расчет.
Выполнил:
ст. гр. МЭЭ-03-13
Нестерин
А.А.
Проверила:
Картузова Т.В.
Чебоксары
2014 г.
Дано
распределение признака X
(случайной величины X),
полученной по наблюдениям. Необходимо:
-
построить
полигон (гистограмму), кумуляту и
эмпирическую функцию распределения; -
найти
среднюю арифметическую
;
медиану
и моду
;
дисперсию
,
среднее квадратическое отклонение
и коэффициент вариации
;
начальные
и центральные
моменты
— го порядка ();
коэффициент асимметрии
и эксцесс
.
1.
X
– число сделок на фондовой бирже за
квартал;
(инвесторов).
|
|
Частота |
Частотность |
Наклон |
Накопленная |
|
0 |
146 |
0.3650 |
146 |
0.3650 |
|
1 |
97 |
0.2425 |
243 |
0.6075 |
|
2 |
73 |
0.1825 |
316 |
0.7900 |
|
3 |
34 |
0.0850 |
350 |
0.8750 |
|
4 |
23 |
0.0575 |
373 |
0.9325 |
|
5 |
10 |
0.0250 |
383 |
0.9575 |
|
6 |
6 |
0.0150 |
389 |
0.9725 |
|
7 |
3 |
0.0075 |
392 |
0.9800 |
|
8 |
4 |
0.0100 |
396 |
0.9900 |
|
9 |
2 |
0.0050 |
398 |
0.9950 |
|
10 |
2 |
0.0050 |
400 |
1.0000 |
Средняя
арифметическая вариационного ряда:
Медиана
вариационного ряда (значение признака,
которое приходится на середину
ранжированного ряда):

Мода
вариационного ряда (варианта, которой
соответствует наибольшая частота):
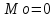
Дисперсия
вариационного ряда:
Среднее
квадратическое отклонение:

Коэффициент
вариации:
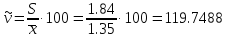
Начальные
моменты
— го порядка (
Центральные
моменты
— го порядка (
Коэффициент
асимметрии:
Эксцесс

2.
X
– удой коров на молочной ферме за
лактационный период (в ц.);
(коров).
|
Интервалы |
Середины |
Частота |
Частотность |
Наклон |
Накопленная |
|
4-6 |
5 |
1 |
0.0100 |
1 |
0.0100 |
|
6-8 |
7 |
3 |
0.0300 |
4 |
0.0400 |
|
8-10 |
9 |
6 |
0.0600 |
10 |
0.1000 |
|
10-12 |
11 |
11 |
0.1100 |
21 |
0.2100 |
|
12-14 |
13 |
15 |
0.1500 |
36 |
0.3600 |
|
14-16 |
15 |
20 |
0.2000 |
56 |
0.5600 |
|
16-18 |
17 |
14 |
0.1400 |
70 |
0.7000 |
|
18-20 |
19 |
12 |
0.1200 |
82 |
0.8200 |
|
20-22 |
21 |
10 |
0.1000 |
92 |
0.9200 |
|
22-24 |
23 |
6 |
0.0600 |
98 |
0.9800 |
|
24-26 |
25 |
2 |
0.0200 |
100 |
1.0000 |
Среднее
арифметическое вариационного ряда:
Медиана
вариационного ряда (определим по
кумуляте):
Моду
определим по гистограмме:
Дисперсия:
Среднее
квадратическое отклонение:
Коэффициент
вариации:
Начальные
моменты
— го порядка (
Центральные
моменты
— го порядка (
:
Коэффициент
асимметрии:
Эксцесс:
3.
По выборкам объемом
и
найдены средние размеры деталей
соответственно
и
мм. Установлено, что размер детали,
изготовленный каждым автоматом, имеет
нормальный закон распределения. Известны
дисперсии
и
для первого и второго автоматов. На
уровне значимости
выявить влияние на средний размер детали
автомата, на котором она изготовлена.
Рассмотреть два случая: а)

б)

Нулевая
гипотеза
При
справедливости
статистика рассчитывается следующим
образом:
а)
в данном случае средний размер детали
зависит от выбора автомата — двусторонняя
критическая область
по таблице II
(Значения функции Лапласа) находим
значение
Получим:
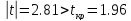
Нулевая
гипотеза отвергается, значит средний
размер детали зависит от выбора автомата.
б)
в данном случае влияние второго автомата
больше) — односторонняя критическая
область

таблице II
(Значения функции Лапласа) находим
значение
Получим:

Нулевая
гипотеза отвергается, значит влияние
второго автомата больше.
4.
Имеются следующие данные о качестве
детского питания, изготовленного
различными фирмами (в баллах): 40, 39, 42
,37, 38, 43, 45, 41, 48. Есть основание полагать,
что показатель качества продукции
последней фирмы зарегистрирован неверно.
Является ли это значение аномальным
(резко выделяющимся) на 5% уровне
значимости?
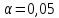
Нулевая
гипотеза
(т.е значение
принадлежит к остальным наблюдениям).
Значение
исключаем, а для остальных найдем среднее
арифметическое и среднее квадратическое
отклонение (
Рассчитаем
значение статистики, имеющий распределение
Стьюдента
По
таблице IV
(Значения
— критерия Стьюдента) находим
Получили:
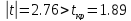
Нулевая
гипотеза отвергается, т.о. значение
является аномальным.
5.
Вступительный экзамен проводился на
двух факультетах института. На
экономическом факультет из
абитуриентов выдержали экзамен
человек, а на финансово-кредитном из
абитуриентов —

На уровне значимости
проверить гипотезу об отсутствии
существенных различий в уровне подготовки
абитуриентов двух факультетов. Рассмотреть
два случая: а)
б)
Нулевая
гипотеза:
(т.е. уровни подготовки абитуриентов
одинаковы)
Найдем
выборочные доли
и
Рассчитаем
выборочную долю признака:
Рассчитаем
значение статистики:
а)
(уровни подготовки абитуриентов
отличаются) – одностороння критическая
область:
По
таблице II
(значения функции Лапласа):
Получили:
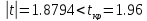
Нулевая
гипотеза принимается, т.е. полученные
данные не противоречат гипотезе об
одинаковом уровне подготовки абитуриентов.
б)
(уровень подготовки абитуриентов
экономического факультета лучше уровня
подготовки студентов финансово —
кредитного) – одностороння критическая
область:
По
таблице II
(значения функции Лапласа):
Получили:
Нулевая
гипотеза отвергается, т.е. полученные
данные противоречат гипотезе о лучшем
уровне подготовки абитуриентов
экономического факультета.
6.
На уровне значимости 0.05 проверить
гипотезу о нормальном законе распределения
признака (случайной величины)

используя критерий согласия: а)
– Пирсона; б) Колмогорова (по данным
таблицы задания 2).

из задания 2 имеем

n=100;
|
Интервалы |
Частота |
Вероятность |
Теоретические |
|
|
|
4-6 |
1 |
0.01 |
1 |
0 |
0 |
|
6-8 |
3 |
0.027 |
2.7 |
0.0900 |
0.0333 |
|
8-10 |
6 |
0.058 |
5.8 |
0.0400 |
0.0069 |
|
10-12 |
11 |
0.105 |
10.5 |
0.2500 |
0.0238 |
|
12-14 |
15 |
0.153 |
15.3 |
0.0900 |
0.0059 |
|
14-16 |
20 |
0.18 |
18 |
4.0000 |
0.2222 |
|
16-18 |
14 |
0.173 |
17.3 |
10.8900 |
0.6295 |
|
18-20 |
12 |
0.135 |
13.5 |
2.2500 |
0.1667 |
|
20-22 |
10 |
0.086 |
8.6 |
1.9600 |
0.2279 |
|
22-24 |
6 |
0.044 |
4.4 |
2.5600 |
0.5818 |
|
24-26 |
2 |
0.019 |
1.9 |
0.0100 |
0.0053 |
Нулевая
гипотеза
— случайная величина
распределена нормально
а)
Критерий согласия Пирсона (
Рассчитываем
вероятности

По
данным примера 2 имеем

Рассчитаем
значения вероятностей. Значения Ф(х)
находим по таблице II
(значения функции Лапласа):
Все
остальные значения вероятностей
рассчитываются подобным образом. Найдем
последнее из них:
Определим
меру расхождения эмпирических и
теоретических частот:
Число
степеней свободы:
где
— число интервалов эмпирического
распределения
— число параметров теории распределения
По
таблице V
(значения критерия Пирсона) находим:
Получили:
Т.о.
гипотеза о выбранном теоретическом
нормальном законе распределения
согласуется с опытными данными.
б)
Критерий согласия Колмогорова:
|
|
Частота |
Накопленная |
|
|
|
|
|
6 |
1 |
0.0100 |
-2.2024 |
-0.9566 |
0.0217 |
0.0039 |
|
8 |
3 |
0.0400 |
-1.7436 |
-0.9181 |
0.0409 |
0.0009 |
|
10 |
6 |
0.1000 |
-1.2847 |
-0.7984 |
0.1008 |
0.0014 |
|
12 |
11 |
0.2100 |
-0.8259 |
-0.5935 |
0.2032 |
0.0068 |
|
14 |
15 |
0.3600 |
-0.3671 |
-0.2886 |
0.3557 |
0.0043 |
|
16 |
20 |
0.5600 |
0.0918 |
0.0717 |
0.5359 |
0.0241 |
|
18 |
14 |
0.7000 |
0.5506 |
0.4245 |
0.7123 |
0.0088 |
|
20 |
12 |
0.8200 |
1.0094 |
0.6827 |
0.8414 |
0.0238 |
|
22 |
10 |
0.9200 |
1.4683 |
0.8584 |
0.9292 |
0.0092 |
|
24 |
6 |
0.9800 |
1.9271 |
0.9464 |
0.9732 |
0.0064 |
|
26 |
2 |
1.0000 |
2.3859 |
0.9832 |
0.9916 |
0.0084 |
Значения
это накопленные частости
(они соответствуют значениям полученным
в задании 2).
Для
построения
в случае нормального закона воспользуемся
формулой:
Получим:
При
и
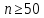
Получили:
Т.о.
гипотеза о выбранном теоретическом
нормальном законе распределения
согласуется с опытными данными.
Соседние файлы в папке Типовой расчет
- #
- #
06.02.20153.93 Кб23matanm.m
- #
06.02.2015792 б10matanm2.m
Средний размер — деталь
Cтраница 1
Средний размер деталей постепенно увеличивается из-за износа круга и влияния других факторов. Настройка первого контакта ( команды) датчика производится по настроечному размеру детали, соответствующему значению подналадочной границы / — /, которая смещена внутрь поля допуска на расчетную величину с относительно верхнего предела.
[2]
Средний размер деталей уменьшается на величину подналадочного импульса г. Начинается новый цикл подналадки. В случае выхода размера детали за пределы поля допуска срабатывает второй контакт ( команда) датчика: бракованная деталь направляется в сборник 8 брака, зажигается сигнал брака, и станок останавливается.
[3]
Получив значения среднего размера детали и величину средне-квадратического отклонения, можно сделать вывод о точности обработки деталей на данной операции. Если средний размер детали не совпадает с серединой допуска, это значит, что имеются систематические погрешности, которые необходимо выявить и устранить. Если среднеквадратическая погрешность не превышает ] / 6 допуска на изготовление, то точность выполнения данной операции соответствует требованиям. Если же окажется, что среднеквадратическое отклонение значительно превышает VB часть допуска, то это означает, что точность выполнения данной операции не соответствует требованиям. Случайные погрешности, имеющиеся при выполнении данной операции, слишком велики и необходимо или изменить метод обработки, или перенести выполнение данной операции на более точный станок.
[4]
Получив значения среднего размера детали и величину среднеквадратического отклонения, можно сделать вывод о точности обработки деталей на данной операции. Если средний размер детали не совпадает с серединой поля допуска, это значит, что имеются систематические погрешности, которые необходимо выявить и устранить. Если среднеквадратическая погрешность не превышает Ve поля допуска на изготовление, то точность выполнения данной операции соответствует требованиям. Если же окажется, что среднеквадратическое отклонение значительно превышает / в поля допуска, то это означает, что точность выполнения данной операции не соответствует требованиям. Случайные погрешности, имеющиеся при выполнении данной операции, слишком велики и необходимо или изменить метод обработки, или перенести выполнение данной операции на более точный станок.
[5]
По этой системе постоянно поддерживается средний размер детали. Каждая деталь после обработки автоматически проверяется непосредственно на станке на встроенных в нем приборах. В случае обнаружения отклонений автоматически подается команда на перемещение резца в радиальном направлении, осуществляя тем самым восстановление размера обработки. Система автоматического регулирования размеров деталей посредством малых импульсов осуществлена в специальном автомате конструкции ВНИИ для тонкой расточки отверстий в поршне под поршневой палец. Величина регулировочных импульсов в этом станке предусмотрена 0 2 мк на радиус обработки.
[6]
Если откладывать на графике по горизонтальной оси средние размеры деталей, а по вертикали — количество деталей, соответствующих этим размерам, то получим так называемую кривую распределения ( фиг.
[7]
Апар ТВ) в том случае, если средний размер детали Вс будет находиться точно в середине поля допуска.
[8]
Подналадка производится только по нескольким подряд идущим импульсам или по среднему размеру деталей. Если обрабатываемая деталь имеет сложную форму и непосредственное ее измерение затруднено, то измеряют величину размерного износа режущего инструмента, по результатам которого производится подналадка станка.
[9]
Таким образом, координата середины поля допуска, по существу, характеризует геометрически средний размер детали.
[10]
На основе приведенных выше соображений нами была разработана и испытана система автоматического регулирования текущего среднего размера детали, обрабатываемой на токарном гидрокопировальном полуавтомате мод.
[11]
Поднастройка размерных и кинематических цепей системы СПИД обычно осуществляется в те моменты, когда групповой средний размер детали подходит к одной из контрольных границ, или когда отклонения размера хотя бы одной детали из группы ( выборки) выходит за пределы допуска.
[12]
Номинальный размер отливки следует принимать равным номинальному размеру детали для необрабатываемых поверхностей и сумме среднего размера детали и общего припуска на обработку — для обрабатываемых поверхностей. У наклонных, конических и фасонных поверхностей за номинальный размер принимают наибольший.
[13]
Наиболее распространены автоматические регулирующие устройства, использующие статистический контроль, когда под-наладка ведется по среднему размеру детали.
[14]
При малых, во сложных по конфигурации вырубаемых деталях матрицы вырубных штампов делают составными, для средних размеров деталей независимо от их конфигурации и для простых по форме и малых по размеру — цельные и для крупных по размеру деталей — секционные.
[15]
Страницы:
1
2
средний размер детали
- средний размер детали
-
3.2 средний размер детали: Размер детали, соответствующий середине поля его допуска.
(Измененная редакция, title=»Изменение № 2, ИУС 06-2013″).
Словарь-справочник терминов нормативно-технической документации.
.
2015.
Смотреть что такое «средний размер детали» в других словарях:
-
ГОСТ Р 52134-2003: Трубы напорные из термопластов и соединительные детали к ним для систем водоснабжения и отопления. Общие технические условия — Терминология ГОСТ Р 52134 2003: Трубы напорные из термопластов и соединительные детали к ним для систем водоснабжения и отопления. Общие технические условия оригинал документа: коэффициент запаса прочности С: Безразмерная величина, имеющая… … Словарь-справочник терминов нормативно-технической документации
-
ГОСТ Р 53464-2009: Отливки из металлов и сплавов. Допуски размеров, массы и припуски на механическую обработку — Терминология ГОСТ Р 53464 2009: Отливки из металлов и сплавов. Допуски размеров, массы и припуски на механическую обработку оригинал документа: 3.3 вид размеров отливки: Совокупность размеров отливки, характеризующихся подобными конструктивными и … Словарь-справочник терминов нормативно-технической документации
-
Заработная плата — (Wages) Важнейшее средство повышения заинтересованности работников Участие трудящихся в доле вновь созданных материальных и духовных благ Содержание Содержание. > заработная плата – это важнейшее средство повышения заинтересованности… … Энциклопедия инвестора
-
ГОСТ 520-2002: Подшипники качения. Общие технические условия — Терминология ГОСТ 520 2002: Подшипники качения. Общие технические условия оригинал документа: 3.6.1.3 асинхронное радиальное биение внутреннего кольца собранного радиального подшипника Kiaa: Разность между наибольшим и наименьшим расстояниями в… … Словарь-справочник терминов нормативно-технической документации
-
Личные доходы — (Personal income) Личные доходы это денежные средства, полученные физическим лицом Что такое личный располагаемый доход, его источники, распределение, расчет и учет Содержание >>>>>>>>>>>> … Энциклопедия инвестора
-
Аналитик — (Analyst) Специалист, работник фирмы, банка Информация о сфере деятельности аналитиков, финансовая и бизнес аналитика, аналитика валютного и фондового рынка Содержание >>>>>>>> Аналитик это, оределение История Аналитика появилась тогда, когда… … Энциклопедия инвестора
-
ГОЛОВНЫЕ УБОРЫ — бывают мужские, женские и детские. Зимние и осенние головные уборы должны защищать голову от холода (обладать хорошими теплозащитными свойствами), летние и весенние от солнца и жары (обладать солнцезащитными свойствами и воздухопроницаемостью).… … Краткая энциклопедия домашнего хозяйства
-
Синий кит — Синий кит … Википедия
-
Нанотехнология — (Nanotechnology) Содержание Содержание 1. Определения и терминология 2. : история возникновения и развития 3. Фундаментальные положения Сканирующая зондовая микроскопия Наноматериалы Наночастицы Самоорганизация наночастиц Проблема образования… … Энциклопедия инвестора
-
Белорусская Советская Социалистическая Республика — (Беларуская Савецкая Сацыялicтычная Рэспублiкa) Белоруссия (Беларусь). I. Общие сведения БССР образована 1 января 1919. С созданием Союза ССР 30 декабря 1922 вошла в его состав как союзная республика. Граничит на З. с… … Большая советская энциклопедия

 ;
;
 ;
; ,
,
 ;
;


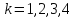 );
);
 .
.