Мода и медиана
Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
Обратимся снова к нашему примеру со сборной по футболу:
Чему в данном примере равна мода? Какое число наиболее часто встречается в этой выборке?
Все верно, это число ( displaystyle 181), так как два игрока имеют рост ( displaystyle 181) см; рост же остальных игроков не повторяется.
Тут все должно быть ясно и понятно, да и слово знакомое, правда?
Перейдем к медиане, ты ее должен знать из курса геометрии. Но мне не сложно напомнить, что в геометрии медиана (в переводе с латинского- «средняя») — отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.
Ключевое слово – СЕРЕДИНА. Если ты знал это определение, то тебе легко будет запомнить, что такое медиана в статистике.
Медианой ряда чисел с нечетным числом членов называется число, которое окажется посередине, если этот ряд упорядочить (проранжировать, т.е. расположить значения в порядке убывания или возрастания).
Медианой ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине, если этот ряд упорядочить.
Ну что, вернемся к нашей выборке футболистов?
Ты заметил в определении медианы важный момент, который нам еще здесь не встречался? Конечно, «если этот ряд упорядочить»!
Для того, чтобы в ряду чисел был порядок, можно расположить значения роста футболистов как в порядке убывания, так и в порядке возрастания. Мне удобней выстроить этот ряд в порядке возрастания (от самого маленького к самому большому).
Вот, что у меня получилось:
Так, ряд упорядочили, какой еще есть важный момент в определении медианы? Правильно, четное и нечетное количество членов в выборке.
Заметил, что для четного и нечетного количества даже определения отличаются? Да, ты прав, не заметить – сложно. А раз так, то нам надо определиться, четное у нас количество игроков в нашей выборке или нечетное?
Все верно – игроков ( displaystyle 11), значит, количество нечетное! Теперь можем применять к нашей выборке менее заковыристое определение медианы для нечетного количества членов в выборке.
Ищем число, которое оказалось посередине в нашем упорядоченном ряду:
Ну вот, чисел у нас ( displaystyle 11), значит, по краям остается по пять чисел, а рост ( displaystyle 183) см будет медианой в нашей выборке.
Не так уж и сложно, правда?
Частота и относительная частота
Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.
То есть частота определяет то, как часто повторяется та или иная величина в выборке.
Разберемся на нашем примере с футболистами. Перед нами вот такой вот упорядоченный ряд:
Частота – это число повторений какой-либо величины параметра. В нашем случае, это можно считать вот так. Сколько игроков имеет рост ( 176)?
Все верно, один игрок. Таким образом, частота встречи игрока с ростом ( 176) в нашей выборке равна ( 1).
Сколько игроков имеет рост ( 178)? Да, опять же один игрок. Частота встречи игрока с ростом ( 178) в нашей выборке равна ( 1).
Задавая такие вопросы и отвечая на них, можно составить вот такую табличку:
Ну вот, все довольно просто. Помни, что сумма частот должна равняться количеству элементов в выборке (объему выборки).
То есть в нашем примере: ( 1+1+1+2+1+1+1+1+1+1=11)
Перейдем к следующей характеристике – относительная частота.
Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах.
Обратимся опять к нашему примеру с футболистами. Частоты для каждого значения мы рассчитали, общее количество данных в ряду мы тоже знаем ( left( n=11 right)) .
Рассчитываем относительную частоту для каждого значения роста и получаем вот такую табличку:
А теперь сам составь таблицы частот и относительных частот для примера с 9-классниками, решающими задачи.
|
0 / 0 / 0 Регистрация: 30.11.2019 Сообщений: 8 |
|
|
1 |
|
Найти средний рост среди учащихся класса02.01.2020, 15:28. Показов 8134. Ответов 3
Дан целочисленный массив из 15 элементов.
0 |
|
ValentinNemo 2373 / 775 / 561 Регистрация: 15.01.2019 Сообщений: 2,394 |
||||
|
02.01.2020, 15:54 |
2 |
|||
0 |
|
0 / 0 / 0 Регистрация: 30.11.2019 Сообщений: 8 |
|
|
02.01.2020, 16:07 [ТС] |
3 |
|
Можно использовать только три переменные и массив
0 |
|
2373 / 775 / 561 Регистрация: 15.01.2019 Сообщений: 2,394 |
|
|
04.01.2020, 07:55 |
4 |
|
Конечно можно. Разрешаю вам удалить переменную n и заменить ее в программе числом 15!
0 |
В футбольной команде игроки ростом 120 см; 135 см; 171 см; 142 см; 116 см.
Найдем средний рост команды.
Для того, чтобы найти средний рост команды, нужно найти сумму роста игроков и разделить на количество игроков.
Получаем:
(120 см + 135 см + 171 см + 142 см + 4116 см)/5 = (120 + 135 + 171 + 142 + 116)/5 см = 684/5 см = 136,8 см.
Отсюда получаем, что средний рост игроков команды равна 136,8 см.
Рост хоккеистов: анализируем данные всех чемпионатов мира в текущем веке
Время на прочтение
15 мин
Количество просмотров 47K
На днях завершился очередной чемпионат мира по хоккею.
За просмотром матчей родилась идея. Когда в перерывах телевизионная камера показывает уходящих в раздевалку игроков, трудно не заметить, насколько они огромные. На фоне тренеров, функционеров команд, сотрудников ледовой арены, журналистов или просто фанатов они, как правило, выглядят очень внушительно.
Вот, к примеру, восходящие звезды финского хоккея, Патрик Лайне и Александр Барков, вместе с преданными поклонниками
И я задался вопросами. Действительно ли хоккеисты выше обычных людей? Как изменяется рост хоккеистов со временем в сравнении с обычными людьми? Есть ли устойчивые межстрановые различия?
Данные
IIHF, организация, проводящая чемпионаты мира по хоккею, каждый год публикует составы участвующих команд с информацией о росте и весе каждого игрока. Архив этих данных тут.
Я собрал вместе данные всех чемпионатов мира с 2001 по 2016 годы. От года к году формат предоставления данных слегка меняется, что требует некоторых усилий по их очистке. Не представляя, как грамотно автоматизировать процесс, все данные копировал вручную, что заняло чуть больше 3 часов. Объединенный датасет выложил в открытый доступ.
R code. Подготовка к работе, загрузка данных
# load required packages
require(dplyr) # data manipulation
require(lubridate) # easy manipulations with dates
require(ggplot2) # visualization
require(ggthemes) # themes for ggplot2
require(cowplot) # nice alignment of the ggplots
require(RColorBrewer) # generate color palettes
require(texreg) # easy export of regression tables
require(xtable) # export a data frame into an html table
# download the IIHF data set; if there are some problems, you can download manually
# using the stable URL (https://dx.doi.org/10.6084/m9.figshare.3394735.v2)
df <- read.csv('https://ndownloader.figshare.com/files/5303173')
# color palette
brbg11 <- brewer.pal(11,'BrBG')Растут ли хоккеисты? Грубое (периодное) сравнение
Для начала сравним средний рост игроков на всех 16 чемпионатах мира.
R code. Рисунок 1. Изменение среднего роста хоккеистов на чемпионатах мира, 2001-2016 гг.
# mean height by championship
df_per <- df %>% group_by(year) %>%
summarise(height=mean(height))
gg_period_mean <- ggplot(df_per, aes(x=year,y=height))+
geom_point(size=3,color=brbg11[9])+
stat_smooth(method='lm',size=1,color=brbg11[11])+
ylab('height, cm')+
xlab('year of competition')+
scale_x_continuous(breaks=seq(2005,2015,5),labels=seq(2005,2015,5))+
theme_few(base_size = 15)+
theme(panel.grid=element_line(colour = 'grey75',size=.25))
gg_period_jitter <- ggplot(df, aes(x=year,y=height))+
geom_jitter(size=2,color=brbg11[9],alpha=.25,width = .75)+
stat_smooth(method='lm',size=1,se=F,color=brbg11[11])+
ylab('height, cm')+
xlab('year of competition')+
scale_x_continuous(breaks=seq(2005,2015,5),labels=seq(2005,2015,5))+
theme_few(base_size = 15)+
theme(panel.grid=element_line(colour = 'grey75',size=.25))
gg_period <- plot_grid(gg_period_mean,gg_period_jitter)Положительный тренд очевиден. За полтора десятилетия средний рост хоккеиста на чемпионате мира увеличился почти на 2 сантиметра (левая панель). Как будто бы незначительный прирост на фоне довольно большой вариации (правая панель). Много это или мало? Чтобы ответить на вопрос, надо корректно сравнить с населением (но об этом ближе к концу статьи).
Когортный анализ
Более корректный способ изучения изменения в росте подразумевает сравнение по когортам рождения. Тут мы сталкиваемся с любопытным нюансом — некоторые хоккеисты участвовали не в одном чемпионате мира. Вопрос: вычищать ли повторные записи для одних и тех же людей? Если нам интересен средний рост хоккеиста на чемпионате (как на картинке выше), пожалуй, не имеет смысла зачищать. Но если мы хотим проследить изменение роста хоккеистов как таковое, на мой взгляд, было бы неправильно присваивать больший вес тем игрокам, которые регулярнее попадали на чемпионаты мира. Поэтому для дальнейшего анализа я очистил данные от повторных записей одних и тех же игроков.
R code. Подготовка данных к когортному анализу
# remove double counts
dfu_h <- df %>% select(year,name,country,position,birth,cohort,height) %>%
spread(year,height)
dfu_h$av.height <- apply(dfu_h[,6:21],1,mean,na.rm=T)
dfu_h$times_participated <- apply(!is.na(dfu_h[,6:21]),1,sum)
dfu_w <- df %>% select(year,name,country,position,birth,cohort,weight) %>%
spread(year,weight)
dfu_w$av.weight <- apply(dfu_w[,6:21],1,mean,na.rm=T)
dfu <- left_join(dfu_h %>% select(name,country,position,birth,cohort,av.height,times_participated),
dfu_w %>% select(name,country,position,birth,cohort,av.weight),
by = c('name','country','position','birth','cohort')) %>%
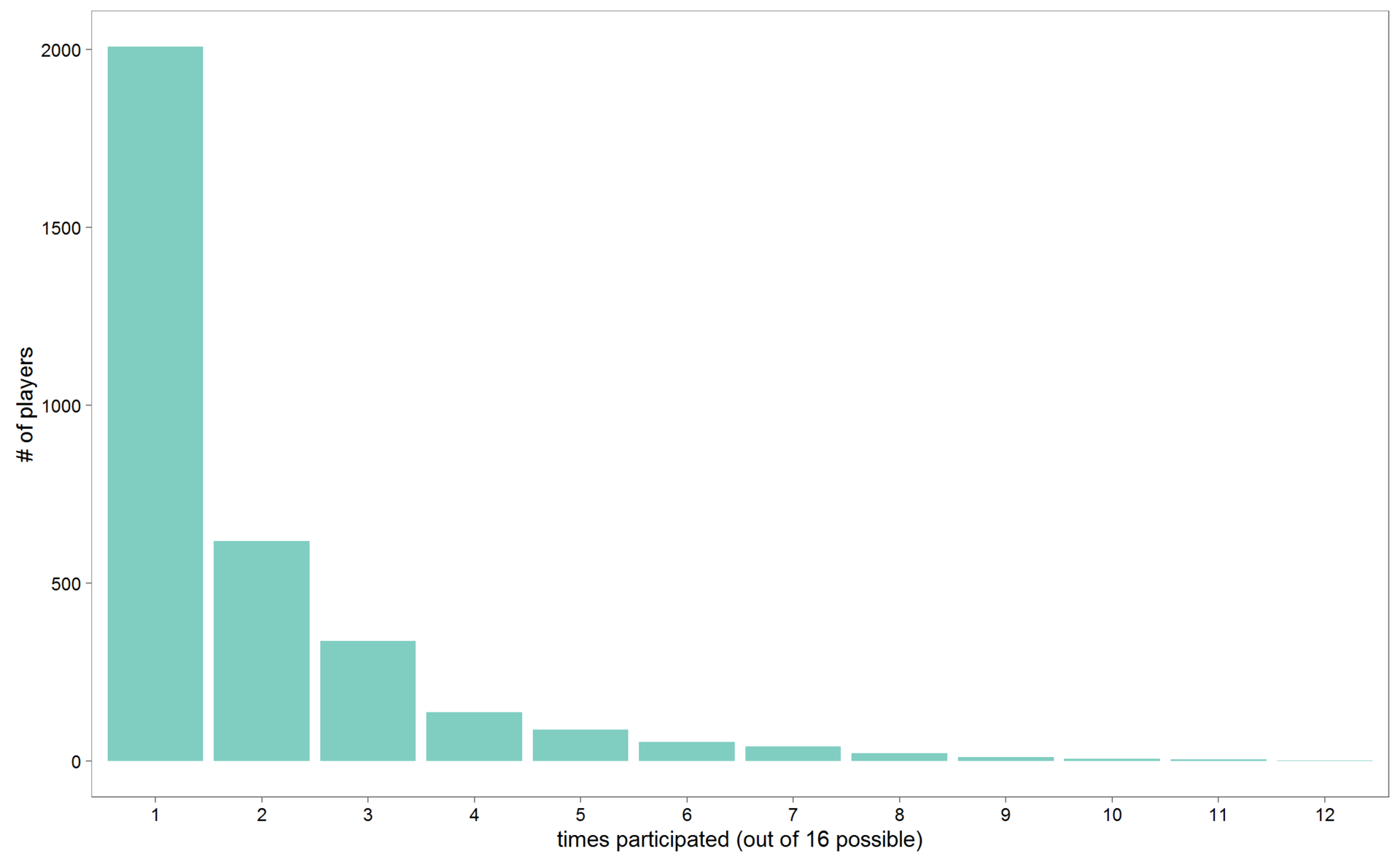
mutate(bmi = av.weight/(av.height/100)^2)Общее количество наблюдений сократилось с 6292 до 3333. Если хоккеист участвовал более чем в одном чемпионате мира, данные о росте и весе я усреднял, поскольку рост и (в особенности) вес отдельно взятого хоккеиста мог меняться со временем. Сколько же раз хоккеисты удостаиваются чести сыграть за национальные сборные на чемпионатах мира? В среднем чуть менее 2 раз.
R code. Рисунок 2. Гистограмма распределения хоккеистов по количеству участий в ЧМ
# frequencies of participation in world championships
mean(dfu$times_participated)
df_part <- as.data.frame(table(dfu$times_participated))
gg_times_part <- ggplot(df_part,aes(y=Freq,x=Var1))+
geom_bar(stat='identity',fill=brbg11[9])+
ylab('# of players')+
xlab('times participated (out of 16 possible)')+
theme_few(base_size = 15)Но есть и уникумы. Посмотрим, кто из игроков принял участие как минимум в 10 чемпионатах мира. Таких игроков оказалось 14.
R code. Таблица 1. Лидеры участия в чемпионатах мира
# the leaders of participation in world championships
# save the table to html
leaders <- dfu %>% filter(times_participated > 9)
View(leaders)
print(xtable(leaders), type="html", file="table_leaders.html")| name | country | position | birth | cohort | av.height | times_participated | av.weight | bmi | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | ovechkin alexander | RUS | F | 1985-09-17 | 1985 | 188.45 | 11 | 98.36 | 27.70 |
| 2 | nielsen daniel | DEN | D | 1980-10-31 | 1980 | 182.27 | 11 | 79.73 | 24.00 |
| 3 | staal kim | DEN | F | 1978-03-10 | 1978 | 182.00 | 10 | 87.80 | 26.51 |
| 4 | green morten | DEN | F | 1981-03-19 | 1981 | 183.00 | 12 | 85.83 | 25.63 |
| 5 | masalskis edgars | LAT | G | 1980-03-31 | 1980 | 176.00 | 12 | 79.17 | 25.56 |
| 6 | ambuhl andres | SUI | F | 1983-09-14 | 1983 | 176.80 | 10 | 83.70 | 26.78 |
| 7 | granak dominik | SVK | D | 1983-06-11 | 1983 | 182.00 | 10 | 79.50 | 24.00 |
| 8 | madsen morten | DEN | F | 1987-01-16 | 1987 | 189.82 | 11 | 86.00 | 23.87 |
| 9 | redlihs mikelis | LAT | F | 1984-07-01 | 1984 | 180.00 | 10 | 80.40 | 24.81 |
| 10 | cipulis martins | LAT | F | 1980-11-29 | 1980 | 180.70 | 10 | 82.10 | 25.14 |
| 11 | holos jonas | NOR | D | 1987-08-27 | 1987 | 180.18 | 11 | 91.36 | 28.14 |
| 12 | bastiansen anders | NOR | F | 1980-10-31 | 1980 | 190.00 | 11 | 93.64 | 25.94 |
| 13 | ask morten | NOR | F | 1980-05-14 | 1980 | 185.00 | 10 | 88.30 | 25.80 |
| 14 | forsberg kristian | NOR | F | 1986-05-05 | 1986 | 184.50 | 10 | 87.50 | 25.70 |
Александр Овечкин, 11 раз! Но тут надо отметить, что не для всех хоккеистов в принципе возможно было поучаствовать во всех 16 чемпионатах: зависит когорты рождения (насколько игровая карьера пересеклась именно с этим периодом наблюдения), от того, участвовала ли сборная игрока во всех чемпионатах мира (см. рисунок 3) и попадал ли игрок стабильно в сборную; наконец есть еще НХЛ, стабильно отвлекающий лучших из лучших от участия в чемпионатах мира.
R code. Рисунок 3. Участие сборных в чемпионатах мира по хоккею в 2001-2016 гг.
# countries times participated
df_cnt_part <- df %>% select(year,country,no) %>%
mutate(country=factor(paste(country))) %>%
group_by(country,year) %>%
summarise(value=sum(as.numeric(no))) %>%
mutate(value=1) %>%
ungroup() %>%
mutate(country=factor(country, levels = rev(levels(country))),
year=factor(year))
d_cnt_n <- df_cnt_part %>% group_by(country) %>%
summarise(n=sum(value))
gg_cnt_part <- ggplot(data = df_cnt_part, aes(x=year,y=country))+
geom_point(color=brbg11[11],size=7)+
geom_text(data=d_cnt_n,aes(y=country,x=17.5,label=n,color=n),size=7,fontface=2)+
geom_text(data=d_cnt_n,aes(y=country,x=18.5,label=' '),size=7)+
scale_color_gradientn(colours = brbg11[7:11])+
xlab(NULL)+
ylab(NULL)+
theme_bw(base_size = 25)+
theme(legend.position='none',
axis.text.x = element_text(angle = 90, hjust = 1,vjust=0.5))Растут ли хоккеисты? Регрессионный анализ
Регрессионный анализ позволяет более корректно ответить на вопрос об изменении роста игроков. В данном случаем с помощью мультиноминальной линейной регрессии предсказыватся рост хоккеиста в зависимость от когорты рождения. Включая в спецификацию регресиионной модели различные дополнительные (контрольные) переменные, мы получаем значение наиболее интересующего нас коэффициента «при прочих равных». Например, добавляя к объясняющим переменным помимо когорты рождения позицию игрока на поле, мы получаем взаимосвязь роста и когорты, очищенную от эффекта различий в зависимости от позиции; добавляя в контрольны переменные страны, получаем результат, очищенный от межстрановых различий. Разумеется, если контрольные переменные сами оказываются значимыми, на это тоже стоит обратить внимание.
Регрессионные модели (особенно линейные регрессии) очень чувствительны к выбросам (см., например, эту статью). Не вдаваясь глубоко в эту обширную тему, я лишь убрал из анализа когорты, для которых мы имеем слишком небольшое количество представителей.
R code. Убираем маленькие когорты
# remove small cohorts
table(dfu$cohort)
dfuc <- dfu %>% filter(cohort<1997,cohort>1963)Не желая резать данные сильно, я убрал только когорты 1963, 1997 и 1998 годов рождения, для которых у нас есть менее 10 игроков.
Итак, результаты рагрессионного анализа. В каждой следующей модели я добавляю одну переменную.
Зависимая переменная: рост хоккеиста.
Объясняющие перемеенные: 1) когорта рождения; 2) + позиция на поле (сравнение с защитниками); 3) + страна (сравнение с Россией).
R code. Таблица 2. Результаты регрессионного анализа
# relevel counrty variable to compare with Russia
dfuc$country <- relevel(dfuc$country,ref = 'RUS')
# regression models
m1 <- lm(data = dfuc,av.height~cohort)
m2 <- lm(data = dfuc,av.height~cohort+position)
m3 <- lm(data = dfuc,av.height~cohort+position+country)
# export the models to html
htmlreg(list(m1,m2,m3),file = 'models_height.html',single.row = T)| Model 1 | Model 2 | Model 3 | |
|---|---|---|---|
| (Intercept) | -10.17 (27.67) | -18.64 (27.01) | 32.59 (27.00) |
| cohort | 0.10 (0.01)*** | 0.10 (0.01)*** | 0.08 (0.01)*** |
| positionF | -2.59 (0.20)*** | -2.59 (0.20)*** | |
| positionG | -1.96 (0.31)*** | -1.93 (0.30)*** | |
| countryAUT | -0.94 (0.55) | ||
| countryBLR | -0.95 (0.53) | ||
| countryCAN | 1.13 (0.46)* | ||
| countryCZE | 0.56 (0.49) | ||
| countryDEN | -0.10 (0.56) | ||
| countryFIN | 0.20 (0.50) | ||
| countryFRA | -2.19 (0.69)** | ||
| countryGER | -0.61 (0.51) | ||
| countryHUN | -0.61 (0.86) | ||
| countryITA | -3.58 (0.61)*** | ||
| countryJPN | -5.24 (0.71)*** | ||
| countryKAZ | -1.16 (0.57)* | ||
| countryLAT | -1.38 (0.55)* | ||
| countryNOR | -1.61 (0.62)** | ||
| countryPOL | 0.06 (1.12) | ||
| countrySLO | -1.55 (0.58)** | ||
| countrySUI | -1.80 (0.53)*** | ||
| countrySVK | 1.44 (0.50)** | ||
| countrySWE | 1.18 (0.48)* | ||
| countryUKR | -1.82 (0.59)** | ||
| countryUSA | 0.54 (0.45) | ||
| R2 | 0.01 | 0.06 | 0.13 |
| Adj. R2 | 0.01 | 0.06 | 0.12 |
| Num. obs. | 3319 | 3319 | 3319 |
| RMSE | 5.40 | 5.27 | 5.10 |
| ***p < 0.001, **p < 0.01, *p < 0.05 |
Интерпретация моделей
Модель 1. Увеличение когорты на один год соответсвует увеличению роста хоккеистов на 0.1 см. Коэффициент статистически значим, но при этом модель объясняет лишь 1% вариации зависимой переменной. В принципе это не проблема, поскольку моделирование носит объясняющий характер, задача предсказания не ставится. Тем не менее, низкий коэффициент детерминации показывает, что должны быть другие переменные, гораздо лучше объясняющие различия между хоккеистами в росте.
Модель 2. Защитники — самые высокие игроки в хоккее. Вратари ниже на 2 см, нападающие — на 2.6 см. Все коэффициенты статистически значимы. Объясненная вариация зависимой переменной возрастает до 6%. При этом коэффициент при переменной когорта рождения не изменяется.
Модель 3. Добавление контрольных переменных для стран любопытно по двум причинам. Во-первых, некоторые различия статистически значимы и интересны сами по себе. Так, например, шведы, словаки и канадцы статистически значимо выше наших игроков. Большинство же наций значительно ниже нас, японцы аж на 5.2 см, итальянцы — на 3.6 см, французы — на 2.2 см (см. также рисунок 4). Во-вторых, введение контрольных переменных для стран значительно уменьшает коэффициент при переменной когорта рождения — до 0.08. Это значит, что межстрановые различия объясняют часть различий по когортам рождения. Коэффициент детерминации модели возрастает до 13%.
R code. Рисунок 4. Рост хоккеистов по странам
# players' height by country
gg_av.h_country <- ggplot(dfuc ,aes(x=factor(cohort),y=av.height))+
geom_point(color='grey50',alpha=.25)+
stat_summary(aes(group=country),geom='line',fun.y = mean,size=.5,color='grey50')+
stat_smooth(aes(group=country,color=country),geom='line',size=1)+
#geom_hline(yintercept = mean(height),color='red',size=.5)+
facet_wrap(~country,ncol=4)+
coord_cartesian(ylim = c(170,195))+
scale_x_discrete(labels=paste(seq(1965,1995,10)),breaks=paste(seq(1965,1995,10)))+
theme_few(base_size = 15)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))Наиболее полная модель показывает, что увеличение роста хоккеистов происходит со скоростью 0.08 см в год. Это означает прирост 0.8 см за десятилетие или на 2.56 см за 32 года с 1964 по 1996. Обратите внимание, что при учете контрольных переменных скорость увеличения роста хоккеистов оказывается примерно в полтора раза ниже, чем при более грубом анализе средних значений (рисунок 1): 0.8 см за десятилетие против примерно 1.2 см.
Прежде чем мы, наконец, постараемся понять, насколько значительным оказывается увеличение роста, хочу обратить внимание еще на один любопытный момент. Введение контрольных переменных подразумевает фиксацию различий между категориями при едином наклоне регрессионной линии (единый коэффициент при главной объясняющей переменной). Это не всегда хорошо и может замаскировать значительные различия в тесноте связи между исследуемыми переменными в подвыборках. Так, например, раздельное моделирование зависимости роста игроков от амплуа (рисунок 5) показывает, что взаимосвязь наиболее ярко выражена для вратарей и наименее заметна для защитников.
R code. Рисунок 5. Корреляция между ростом и когортой раздельно для защитников, форвардов и вратарей
dfuc_pos <- dfuc
levels(dfuc_pos$position) <- c('Defenders','Forwards','Goalkeeprs')
gg_pos <- ggplot(dfuc_pos ,aes(x=cohort,y=av.height))+
geom_jitter(aes(color=position),alpha=.5)+
stat_smooth(method = 'lm', se = T,color=brbg11[11],size=1)+
scale_x_continuous(labels=seq(1965,1995,5),breaks=seq(1965,1995,5))+
scale_color_manual(values = brbg11[c(8,4,10)])+
facet_wrap(~position,ncol=3)+
xlab('birth cohort')+
ylab('height, cm')+
theme_few(base_size = 20)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))R code. Таблица 3. Модель 3 раздельно для подвыборок защитников, форвардов и вратарей
# separate models for positions
m3d <- lm(data = dfuc %>% filter(position=='D'),av.height~cohort+country)
m3f <- lm(data = dfuc %>% filter(position=='F'),av.height~cohort+country)
m3g <- lm(data = dfuc %>% filter(position=='G'),av.height~cohort+country)
htmlreg(list(m3d,m3f,m3g),file = '2016/160500 Hockey players/models_height_pos.html',single.row = T,
custom.model.names = c('Model 3 D','Model 3 F','Model 3 G'))| Model 3 D | Model 3 F | Model 3 G | |
|---|---|---|---|
| (Intercept) | 108.45 (46.46)* | 49.32 (36.73) | -295.76 (74.61)*** |
| cohort | 0.04 (0.02) | 0.07 (0.02)*** | 0.24 (0.04)*** |
| countryAUT | 0.14 (0.96) | -2.01 (0.75)** | 0.47 (1.47) |
| countryBLR | 0.30 (0.87) | -1.53 (0.73)* | -2.73 (1.55) |
| countryCAN | 1.55 (0.78)* | 0.39 (0.62) | 3.45 (1.26)** |
| countryCZE | 0.87 (0.84) | 0.30 (0.67) | 0.63 (1.36) |
| countryDEN | -0.60 (0.95) | 0.10 (0.75) | -0.19 (1.62) |
| countryFIN | -0.55 (0.89) | -0.04 (0.67) | 2.40 (1.32) |
| countryFRA | -3.34 (1.15)** | -2.06 (0.93)* | 1.39 (2.07) |
| countryGER | 0.48 (0.85) | -1.40 (0.72) | -0.65 (1.33) |
| countryHUN | -1.32 (1.47) | -0.70 (1.16) | 0.65 (2.39) |
| countryITA | -2.08 (1.08) | -4.78 (0.82)*** | -2.02 (1.62) |
| countryJPN | -4.13 (1.26)** | -6.52 (0.94)*** | -2.27 (1.98) |
| countryKAZ | -1.23 (0.95) | -1.82 (0.79)* | 1.79 (1.58) |
| countryLAT | -0.73 (0.95) | -1.39 (0.75) | -3.42 (1.49)* |
| countryNOR | -3.25 (1.07)** | -1.06 (0.85) | -0.10 (1.66) |
| countryPOL | 0.82 (1.89) | -0.58 (1.55) | 0.37 (2.97) |
| countrySLO | -1.57 (0.99) | -1.54 (0.79) | -2.25 (1.66) |
| countrySUI | -1.98 (0.91)* | -2.36 (0.71)*** | 1.12 (1.47) |
| countrySVK | 2.94 (0.87)*** | 0.81 (0.67) | -0.70 (1.50) |
| countrySWE | 0.75 (0.81) | 1.24 (0.65) | 1.37 (1.33) |
| countryUKR | -1.37 (1.01) | -1.77 (0.80)* | -3.71 (1.66)* |
| countryUSA | 0.76 (0.78) | -0.08 (0.62) | 2.58 (1.26)* |
| R2 | 0.09 | 0.10 | 0.24 |
| Adj. R2 | 0.07 | 0.09 | 0.20 |
| Num. obs. | 1094 | 1824 | 401 |
| RMSE | 5.08 | 5.08 | 4.87 |
| ***p < 0.001, **p < 0.01, *p < 0.05 |
Раздельное моделирование показывает, что в когортах 1964-1996 годов рождения, средний рост хоккеистов, участвовавших в чемпионатах мира в 2001-2016 годах, увеличивался со скоростью 0.4 см за десятиление для защитников, 0.7 см — для нападающих и (!) 2.4 см — для вратарей. За три десятиления средний рост вратарей увеличился на 7 см!
Пришло время сравнить эти изменения со средними значениями для населения.
Сравнение с населением
Результаты регрессионного анализа фиксируют значительные межстрановые различия. Поэтому сравнивать имеет смысл по странам: хоккеистов определенной страны с мужским населением этой же страны.
Для сравнения роста хоккеистов со средними показателями мужского населения я использовал данные из релевантной научной статьи (PDF). Данные я скопировал из статьи (использовав замечательную программку tabula) и тоже разместил в открытом доступе.
R code. Загрузка данных Hatton, T. J., & Bray, B. E. (2010) и подготовка к анализу
# download the data from Hatton, T. J., & Bray, B. E. (2010).
# Long run trends in the heights of European men, 19th–20th centuries.
# Economics & Human Biology, 8(3), 405–413.
# http://doi.org/10.1016/j.ehb.2010.03.001
# stable URL, copied data (https://dx.doi.org/10.6084/m9.figshare.3394795.v1)
df_hb <- read.csv('https://ndownloader.figshare.com/files/5303878')
df_hb <- df_hb %>%
gather('country','h_pop',2:16) %>%
mutate(period=paste(period)) %>%
separate(period,c('t1','t2'),sep = '/')%>%
transmute(cohort=(as.numeric(t1)+as.numeric(t2))/2,country,h_pop)
# calculate hockey players' cohort height averages for each country
df_hoc <- dfu %>% group_by(country,cohort) %>%
summarise(h_hp=mean(av.height)) %>%
ungroup()К сожалению, данные о динамике роста населения пересекаются лишь с 8 странами из моего хоккейного датасета: Австрия, Дания, Финляндия, Франция, Германия, Италия, Норвегия, Швеция.
R code. Пересекающиеся данные
# countries in both data sets
both_cnt <- levels(factor(df_hb$country))[which(levels(factor(df_hb$country)) %in% levels(df_hoc$country))]
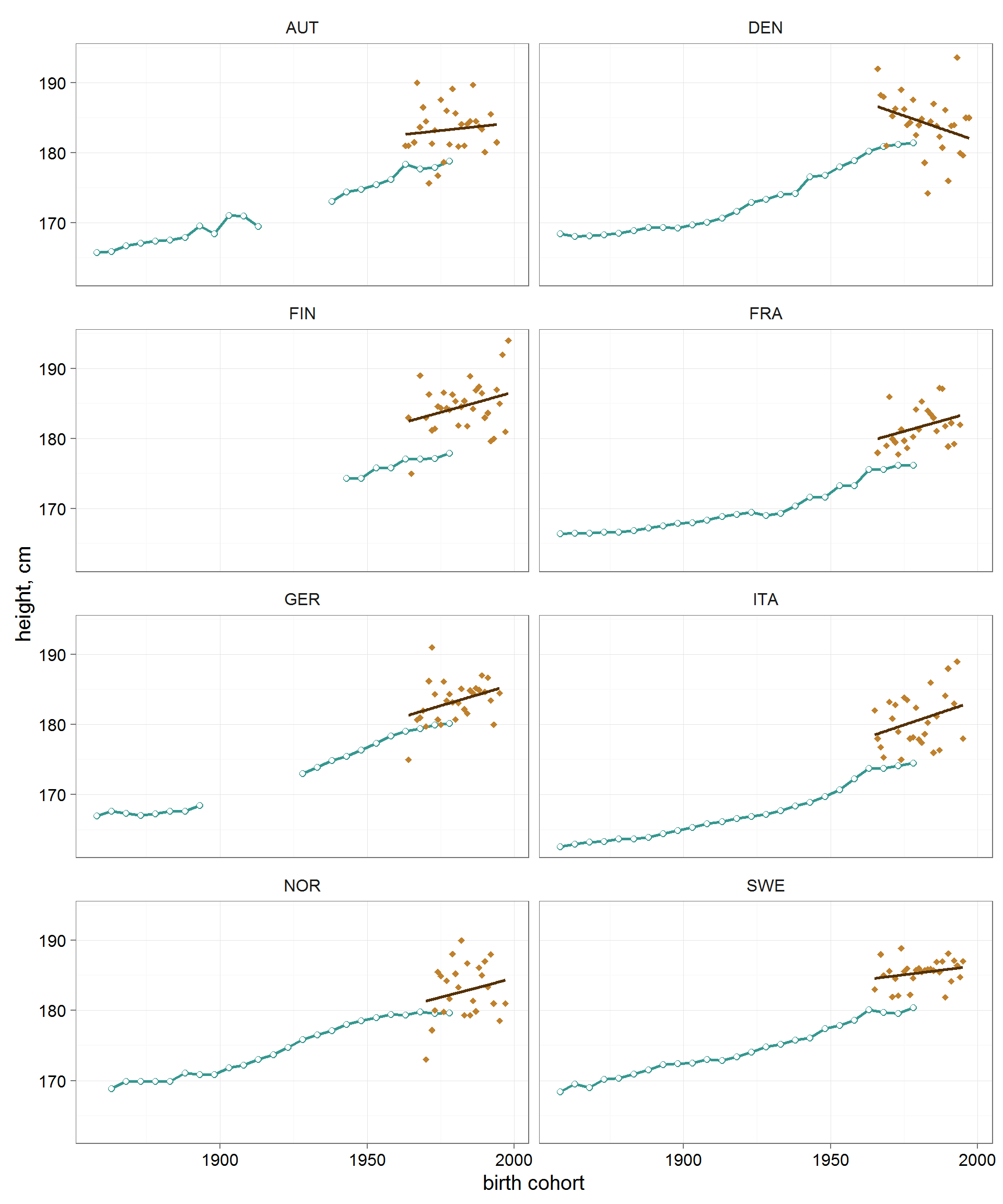
both_cntR code. Рисунок 6. Сравнение динамики увеличения роста мужского населения и хоккеистов. Примечание: зеленый цвет — мужское население; коричневый цвет — хоккеисты.
gg_hoc_vs_pop <- ggplot()+
geom_path(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop),
color=brbg11[9],size=1)+
geom_point(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop),
color=brbg11[9],size=2)+
geom_point(data = df_hb %>% filter(country %in% both_cnt), aes(x=cohort,y=h_pop),
color='white',size=1.5)+
geom_point(data = df_hoc %>% filter(country %in% both_cnt), aes(x=cohort,y=h_hp),
color=brbg11[3],size=2,pch=18)+
stat_smooth(data = df_hoc %>% filter(country %in% both_cnt), aes(x=cohort,y=h_hp),
method='lm',se=F,color=brbg11[1],size=1)+
facet_wrap(~country,ncol=2)+
ylab('height, cm')+
xlab('birth cohort')+
theme_few(base_size = 15)+
theme(panel.grid=element_line(colour = 'grey75',size=.25))Во всех проанализировнных странах хоккеисты выше стеднестатистических мужчин на 2-5 см. Но это не удивительно — в спорте значительная селекция.
Примечательно другое. В развитых странах мира особенно бурное увеличение роста мужского населения происходило в первой середине 20 века. В когортах примерно 1960-х годов рождения рост мужчин приблизился к плато и пеерстал бурно увеличиваться. Тренд среднего роста хоккеистов во всех странах (кроме почему-то Дании) как будто бы продолжил приостановившийся многолетний тренд всего мужского населения.
Для когорт европейцев, родившихся в первой половине 20 века, темпы увеличения среднего роста варьировались от 1.18 до 1.74 см за десятилетие в зависимости от страны (рисунок 7). Начиная с 1960-х годов этот показатель опустился до уровня 0.15-0.80 за 10 лет.
R code. Рисунок 7. Средняя динамика роста мужского населения
# growth in population
df_hb_w <- df_hb %>% spread(cohort,h_pop)
names(df_hb_w)[2:26] <- paste('y',names(df_hb_w)[2:26])
diffs <- df_hb_w[,3:26]-df_hb_w[,2:25]
df_hb_gr<- df_hb_w %>%
transmute(country,
gr_1961_1980 = unname(apply(diffs[,22:24],1,mean,na.rm=T))*2,
gr_1901_1960 = unname(apply(diffs[,9:21],1,mean,na.rm=T))*2,
gr_1856_1900 = unname(apply(diffs[,1:8],1,mean,na.rm=T))*2) %>%
gather('period','average_growth',2:4) %>%
filter(country %in% both_cnt) %>%
mutate(country=factor(country,levels = rev(levels(factor(country)))),
period=factor(period,labels = c('1856-1900','1901-1960','1961-1980')))
gg_hb_growth <- ggplot(df_hb_gr, aes(x=average_growth,y=country))+
geom_point(aes(color=period),size=3)+
scale_color_manual(values = brbg11[c(8,3,10)])+
scale_x_continuous(limits=c(0,2))+
facet_wrap(~period)+
theme_few()+
xlab("average growth in men's height over 10 years, cm")+
ylab(NULL)+
theme_few(base_size = 20)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))На фоне стагнирующего тренда в населении увеличение роста хоккеистов выглядит весьма внушительным. А акселерация среди вратарей вообще беспрецедентна.
Не стоит забывать и про селекцию. Расхождение трендов в населении и среди хоккеистов, вероятно, свидетельствует об усиливающейся селекции — хоккей требует все большего роста для успешной карьеры.
Селекция в спорте
Проглядывая научную литературу по теме я наткнулся на примечательный результат. Оказывается, в профессиональном спорте преобладают люди, рожденные в первой половине года. Объясняется это тем, что спортивные секции, как правило, формируют детские команды по когортам рождения. Таким образом, рожденные в начале года, всегда имеют чуть больше прожитого времени за плечами, что зачастую прямо выражается в физическом превосходстве над сверстниками, рожденными под конец года. Нетрудно проверить этот результат на нашем датасете.
R code. Рисунок 8. Распределение хоккеистов по месяцам рождения
# check if there are more players born in earlier months
df_month <- df %>% mutate(month=month(birth)) %>%
mutate(month=factor(month,levels = rev(levels(factor(month)))))
gg_month <- ggplot(df_month,aes(x=factor(month)))+
geom_bar(stat='count',fill=brbg11[8])+
scale_x_discrete(breaks=1:12,labels=month.name)+
xlab('month of birth')+
coord_flip()+
theme_few(base_size = 20)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))Действительно, респределение довольно сильно смещено в сторону ранних месяцев. Если разбить данные по декадам рождения, то невооруженным глазом видно, что эффект усиливается со временем (рисунок 9). Косвенно это свидетельствует о том, что селекция в хоккее становится жестче.
R code. Рисунок 9. Распределение хоккеистов по месяцам рождения, раздельно по декадам рождения
# facet by decades
df_month_dec <- df_month %>%
mutate(dec=factor(substr(paste(cohort),3,3),labels = paste('born in',c('1960s','1970s','1980s','1990s'))))
gg_month_dec <- ggplot(df_month_dec,aes(x=factor(month)))+
geom_bar(stat='count',fill=brbg11[8])+
scale_x_discrete(breaks=1:12,labels=month.abb)+
xlab('month of birth')+
facet_wrap(~dec,ncol=2,scales = 'free')+
theme_few(base_size = 20)+
theme(legend.position='none',
panel.grid=element_line(colour = 'grey75',size=.25))На будущее
Любопытно будет посмотреть, влияют ли физические данные на игровую статистику хоккеистов. Наткнулся на занимательную статью, опубликованную в очень приличном научном журнале, в которой авторы нашли корреляцию между соотношением пропорций лица хоккеиста и средним количеством штрафных минут за игру.
График из указанной статьи
Reproducibility
Полный R скрипт, воспроизводящий результаты моей статьи, тут.
Использована версия R-3.2.4
Все пакеты по состоянию на 2016-03-14. В случае пакетных несовместимостей, данный код будет гарантированно воспроизведен при использовании пакета checkpoint с указанием соответствующей даты.
Среднее значение, медиана и мода являются фундаментальными темами статистики. Вы можете легко вычислить их в Python, с использованием внешних библиотек и без них.
Эти три меры являются основными Главная тенденция. Центральная тенденция позволяет нам узнать «нормальные» или «средние» значения набора данных. Если вы только начинаете заниматься наукой о данных, это руководство для вас.
К концу этого урока вы:
- Понимание понятия среднего, медианы и моды
- Уметь создавать свои собственные функции среднего, медианы и режима в Python.
- Используйте модуль статистики Python, чтобы быстро начать использовать эти измерения.
Если вам нужна загружаемая версия следующих упражнений, не стесняйтесь проверить Репозиторий GitHub.
Давайте рассмотрим различные способы вычисления среднего значения, медианы и моды.
иметь в виду или среднее арифметическое является наиболее часто используемой мерой центральной тенденции.
Помните, что центральная тенденция является типичным значением набора данных.
Набор данных — это набор данных, поэтому набор данных в Python может быть любой из следующих встроенных структур данных:
- Списки, кортежи и наборы: коллекция объектов
- Строки: набор символов
- Словарь: набор пар ключ-значение
Примечание. Хотя в Python есть и другие структуры данных, такие как очереди или стеки, мы будем использовать только встроенные.
Мы можем вычислить среднее значение, добавив все значения набора данных и разделив результат на количество значений. Например, если у нас есть следующий список чисел:
[1, 2, 3, 4, 5, 6]
Среднее значение будет 3,5, потому что сумма списка равна 21, а его длина равна 6. Двадцать один разделить на шесть равно 3,5. Вы можете выполнить этот расчет с помощью следующего расчета:
(1 + 2 + 3 + 4 + 5 + 6) / 6 = 21
В этом уроке мы будем использовать игроков баскетбольной команды в качестве примера данных.
Создание пользовательской функции среднего
Начнем с расчета среднего (среднего) возраста игроков баскетбольной команды. Название команды будет «Pythonic Machines».
pythonic_machine_ages = [19, 22, 34, 26, 32, 30, 24, 24]
def mean(dataset):
return sum(dataset) / len(dataset)
print(mean(pythonic_machine_ages))
Разбираем этот код:
- «pythonic_machine_ages» — это список возрастов баскетболистов.
- Мы определяем функцию mean(), которая возвращает сумму данного набора данных, деленную на его длину.
- Функция sum() возвращает общую сумму (по иронии судьбы) значений итерируемого объекта, в данном случае списка. Попробуйте передать набор данных в качестве аргумента, он вернет 211
- Функция len() возвращает длину итерации, если вы передадите ей набор данных, вы получите 8
- Мы передаем возраст баскетбольной команды в функцию mean() и печатаем результат.
Если вы проверите вывод, вы получите:
26.375 # Because 211 / 8 = 26.375
Этот результат представляет собой средний возраст игроков баскетбольной команды. Обратите внимание, что число не появляется в наборе данных, но точно описывает возраст большинства игроков.
Использование mean() из статистического модуля Python
Вычисление показателей центральной тенденции является обычной операцией для большинства разработчиков. Это потому что Статистика Python модуль предоставляет различные функции для их расчета, а также другие основные темы статистики.
Поскольку это часть Стандартная библиотека Python вам не нужно будет устанавливать какой-либо внешний пакет с PIP.
Вот как вы используете этот модуль:
from statistics import mean pythonic_machine_ages = [19, 22, 34, 26, 32, 30, 24, 24] print(mean(pythonic_machine_ages))
В приведенном выше коде вам просто нужно импортировать функцию mean() из модуля статистики и передать ей набор данных в качестве аргумента. Это вернет тот же результат, что и пользовательская функция, которую мы определили в предыдущем разделе:
26.375
Теперь у вас есть кристально ясное понятие среднего, давайте продолжим измерение медианы.
Нахождение медианы в Python
медиана является средним значением отсортированного набора данных. Он используется — опять же — для предоставления «типичного» значения определенного Население.
В программировании мы можем определить медиану как значение, которое разделяет последовательность на две части — нижнюю половину и верхнюю половину.
Чтобы вычислить медиану, сначала нам нужно отсортировать набор данных. Мы могли бы сделать это с помощью алгоритмов сортировки или с помощью встроенной функции sorted(). Второй шаг — определить, является ли длина набора данных четной или нечетной. В зависимости от этого некоторые из следующих процессов:
- Нечетный: медиана — это среднее значение набора данных.
- Четное: медиана представляет собой сумму двух средних значений, деленную на два.
Продолжая работу с набором данных нашей баскетбольной команды, давайте рассчитаем средний рост игроков в сантиметрах:
[181, 187, 196, 196, 198, 203, 207, 211, 215] # Since the dataset is odd, we select the middle value median = 198
Как видите, поскольку длина набора данных нечетная, мы можем взять среднее значение в качестве медианы. Однако что произойдет, если игрок только что вышел на пенсию?
Нам нужно будет вычислить медиану, взяв два средних значения набора данных.
[181, 187, 196, 198, 203, 207, 211, 215] # We select the two middle values, and divide them by 2 median = (198 + 203) / 2 median = 200.5
Создание пользовательской медианной функции
Давайте реализуем описанную выше концепцию в функции Python.
Помните три шага, которые нам нужно выполнить, чтобы получить медиану набора данных:
- Сортировка набора данных: мы можем сделать это с помощью функции sorted()
- Определите, является ли он нечетным или четным: мы можем сделать это, получив длину набора данных и используя оператор по модулю (%)
- Верните медиану на основе каждого случая:
- Нечетный: вернуть среднее значение
- Даже: возвращает среднее значение двух средних значений.
Это приведет к следующей функции:
pythonic_machines_heights = [181, 187, 196, 196, 198, 203, 207, 211, 215]
after_retirement = [181, 187, 196, 198, 203, 207, 211, 215]
def median(dataset):
data = sorted(dataset)
index = len(data) // 2
# If the dataset is odd
if len(dataset) % 2 != 0:
return data[index]
# If the dataset is even
return (data[index - 1] + data[index]) / 2
Печать результата наших наборов данных:
print(median(pythonic_machines_heights)) print(median(after_retirement))
Выход:
198 200.5
Обратите внимание, как мы создаем переменную данных, которая указывает на отсортированную базу данных в начале функции. Хотя приведенные выше списки отсортированы, мы хотим создать повторно используемую функцию, поэтому набор данных будет сортироваться при каждом вызове функции.
Индекс сохраняет среднее значение — или верхне-среднее значение — набора данных с помощью оператора целочисленного деления. Например, если бы мы передавали список «pythonic_machine_heights», он имел бы значение 4.
Помните, что в Python индексы последовательности начинаются с нуля, потому что мы можем вернуть средний индекс списка с целочисленным делением.
Затем мы проверяем, является ли длина набора данных нечетной, сравнивая результат операции по модулю с любым значением, отличным от нуля. Если условие истинно, мы возвращаем средний элемент, например, со списком «pythonic_machine_heights»:
>>> pythonic_machine_heights[4] # 198
С другой стороны, если набор данных четный, мы возвращаем сумму средних значений, деленную на два. Обратите внимание, что данные[index -1] дает нам нижнюю среднюю точку набора данных, а данные[index] дает нам верхнюю среднюю точку.
Использование median() из статистического модуля Python
Этот способ намного проще, потому что мы используем уже существующую функцию из модуля статистики.
Лично для меня, если бы что-то уже было определено, я бы использовал это из-за принципа DRY — Don’t Repeat Yourself (в данном случае — не повторять чужой код).
Вы можете вычислить медиану предыдущих наборов данных с помощью следующего кода:
from statistics import median pythonic_machines_heights = [181, 187, 196, 196, 198, 203, 207, 211, 215] after_retirement = [181, 187, 196, 198, 203, 207, 211, 215] print(median(pythonic_machines_heights)) print(median(after_retirement))
Выход:
198 200.5
Вычисление режима в Python
Режим является наиболее часто встречающимся значением в наборе данных. Мы можем думать об этом как о «популярной» группе школы, которая может представлять собой стандарт для всех учащихся.
Примером режима могут быть ежедневные продажи в магазине техники. Режим этого набора данных будет самым продаваемым продуктом за определенный день.
['laptop', 'desktop', 'smartphone', 'laptop', 'laptop', 'headphones']
Как вы понимаете, режим приведенного выше набора данных — «ноутбук», потому что это наиболее часто встречающееся значение в списке.
Преимущество режима в том, что набор данных не должен быть числовым. Например, мы можем работать со строками.
Проанализируем продажи другого дня:
['mouse', 'camera', 'headphones', 'usb', 'headphones', 'mouse']
Приведенный выше набор данных имеет два режима: «мышь» и «наушники», потому что оба имеют частоту, равную двум. Это означает, что это мультимодальный набор данных.
Что, если мы не сможем найти моду в наборе данных, как показано ниже?
['usb', 'camera', 'smartphone', 'laptop', 'TV']
Это называется равномерное распределениепо сути, это означает, что в наборе данных нет моды.
Теперь, когда вы быстро разобрались с концепцией режима, давайте посчитаем его в Python.
Создание функции пользовательского режима
Мы можем думать о частоте значения как о паре ключ-значение, другими словами, как о словаре Python.
Повторяя аналогию с баскетболом, мы можем использовать два набора данных для работы: количество очков за игру и спонсорство кроссовок некоторых игроков.
Чтобы сначала найти моду, нам нужно создать словарь частот с каждым из значений, присутствующих в наборе данных, затем получить максимальную частоту и вернуть все элементы с этой частотой.
Переведем это в код:
points_per_game = [3, 15, 23, 42, 30, 10, 10, 12]
sponsorship = ['nike', 'adidas', 'nike', 'jordan',
'jordan', 'rebook', 'under-armour', 'adidas']
def mode(dataset):
frequency = {}
for value in dataset:
frequency[value] = frequency.get(value, 0) + 1
most_frequent = max(frequency.values())
modes = [key for key, value in frequency.items()
if value == most_frequent]
return modes
Проверка результата с передачей двух списков в качестве аргументов:
print(mode(points_per_game)) print(mode(sponsorship))
Выход:
[10] ['nike', 'adidas', 'jordan']
Как видите, первый оператор печати дал нам один режим, а второй вернул несколько режимов.
Объяснение более глубокого кода выше:
- Объявляем частотный словарь
- Мы перебираем набор данных, чтобы создать гистограмма — статистический термин для набора счетчиков (или частот) —
- Если ключ найден в словаре, то он добавляет единицу к значению
- Если он не найден, мы создаем пару ключ-значение со значением один
- Переменная most_frequent хранит, по иронии судьбы, самое большое значение (не ключ) частотного словаря.
- Мы возвращаем переменную режимов, которая состоит из всех ключей в частотном словаре с наибольшей частотой.
Обратите внимание, как важно именовать переменные для написания читаемого кода.
Использование режима() и мультимода() из статистического модуля Python
И снова модуль статистики предоставляет нам быстрый способ выполнения основных операций со статистикой.
Мы можем использовать две функции: Режим() а также многомодовый().
from statistics import mode, multimode
points_per_game = [3, 15, 23, 42, 30, 10, 10, 12]
sponsorship = ['nike', 'adidas', 'nike', 'jordan',
'jordan', 'rebook', 'under-armour', 'adidas']
Приведенный выше код импортирует обе функции и определяет наборы данных, с которыми мы работали.
Вот небольшое отличие: функция mode() возвращает первый обнаруженный режим, а multimode() возвращает список с наиболее часто встречающимися значениями в наборе данных.
Следовательно, мы можем сказать, что пользовательская функция, которую мы определили, на самом деле является функцией multimode().
print(mode(points_per_game)) print(mode(sponsorship))
Выход:
10 nike
Примечание. В Python 3.8 и более поздних версиях функция mode() возвращает первый найденный режим. Если у вас более старая версия, вы получите СтатистикаОшибка.
Использование функции multimode():
print(multimode(points_per_game)) print(multimode(sponsorship))
Выход:
[10] ['nike', 'adidas', 'jordan']
Подводить итоги
Поздравляем! Если вы дочитали до этого момента, вы научились вычислять среднее значение, медиану и моду, основные измерения центральной тенденции.
Хотя вы можете определить свои пользовательские функции для поиска среднего значения, медианы и моды, рекомендуется использовать модуль статистики, так как он является частью стандартной библиотеки, и вам не нужно ничего устанавливать, чтобы начать его использовать.
Затем прочитайте дружественное введение в анализ данных в Python.