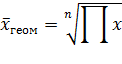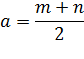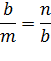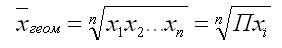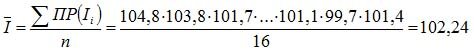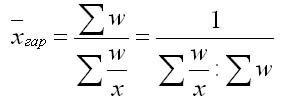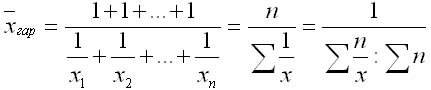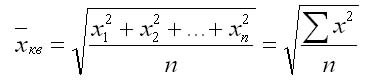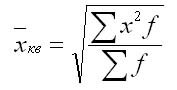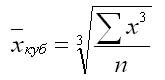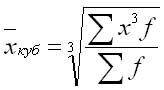Средние величины в статистике дают обобщающую характеристику анализируемого явления. Самая распространенная из них – среднее арифметическое. Она применяется, когда агрегатный показатель образуется с помощью суммы элементов. Например, масса нескольких яблок, суммарная выручка за каждый день продаж и т.д. Но так бывает не всегда. Иногда агрегатный показатель образуется не в результате суммирования, а в результате умножения.
Такой пример. Месячная инфляция – это изменение уровня цен одного месяца по сравнению с предыдущим. Если известны показатели инфляции за каждый месяц, то как получить годовое значение? С точки зрения статистики – это цепной индекс, поэтому правильный ответ: с помощью перемножения месячных показателей инфляции. То есть общий показатель инфляции – это не сумма, а произведение. А как теперь узнать среднюю инфляцию за месяц, если имеется годовое значение? Нет, не разделить на 12, а извлечь корень 12-й степени (степень зависит от количества множителей). В общем случае среднее геометрическое рассчитывается по формуле:
То есть корень из произведения исходных данных, где степень определяется количеством множителей. Например, среднее геометрическое двух чисел – это квадратный корень из их произведения
Среднее геометрическое трех чисел – кубический корень из произведения
и т.д.
Если каждое исходное число заменить на их среднее геометрическое, то произведение даст тот же результат.
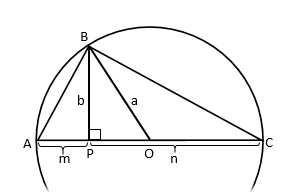
Чтобы лучше разобраться, чем отличаются среднее арифметическое и среднее геометрическое, рассмотрим следующий рисунок. Имеется прямоугольный треугольник, вписанный в круг.
Из прямого угла опущена медиана a (на середину гипотенузы). Также из прямого угла опущена высота b, которая в точке P делит гипотенузу на две части m и n. Т.к. гипотенуза – это диаметр описанного круга, а медиана – радиус, то очевидно, что длина медианы a – это среднее арифметическое из m и n.
Рассчитаем, чему равна высота b. В силу подобия треугольников АВP и BCP справедливо равенство
Откуда
Значит, высота прямоугольного треугольника – это среднее геометрическое из отрезков, на которые она разбивает гипотенузу. Такое наглядное отличие.
В MS Excel среднюю геометрическую можно найти с помощью функции СРГЕОМ.
Все очень просто: вызвали функцию, указали диапазон и готово.
На практике этот показатель используют не так часто, как среднее арифметическое, но все же встречается. Например, есть такой индекс развития человеческого потенциала, с помощью которого сравнивают уровень жизни в разных странах. Он рассчитывается, как среднее геометрическое из нескольких индексов.
Ниже видео, как найти среднее геометрическое чисел в Excel.
Поделиться в социальных сетях:
Download Article
Download Article
The geometric mean is another way to find the average value of a number set, but instead of adding the values and dividing like you would to find the arithmetic mean, you multiply them together before taking the root. The geometric mean can be used to calculate average rates of return in finances or show how much something has grown over a specific period of time. In order to find the geometric mean, multiply all of the values together before taking the nth root, where n equals the total number of values in the set. You can also use the logarithmic functions on your calculator to solve the geometric mean if you want.
Geometric Mean Help
-
1
Multiply the values you want to find the geometric mean for. You can either use a calculator or do the math by hand when you find the product. Multiply all of the numbers in the set you’re calculating so you can find the product. Write down the product so you don’t forget it.[1]
- For example, if the value set is 3, 5, and 12, then you would write: (3 x 5 x 12) = 180.
- For another example, if you want to find the geometric mean for the set 2 and 18, then write: (2 x 18) = 36.
-
2
Find the nth root of the product where n is the number of values. Count how many values are in the set you’re calculating the geometric mean for the value n. Use the n value to determine which root you need to take of the product. For example, take the square root if you have 2 values, cube root if you have 3 values, and so on. Use your calculator to solve the equation and write down your answer.[2]
- For example, for the set of 3, 5, and 12, write: ∛(180) ≈ 5.65.
- In the second example with a set of 2 and 18, write: √(36) = 6.
Variation: You can also write the value as an exponent 1/n if it’s easier to type in your calculator. For example, for the set 3, 5, and 12, you can write (180)1/3 instead of ∛(180).
Advertisement
-
3
Convert percentages to their decimal multiplier equivalents. If the number set is written out as increases or decreases in percentages, avoid using the percent value in the geometric mean since it will skew your results. If the percent is an increase, move the decimal point 2 spaces to the left and add 1 to it. If there’s a percent decrease, then move the decimal point 2 places to the left and subtract it from 1.[3]
- For example, say you want to find the geometric mean of the value of an object that increases by 10%, and then falls by 3%.
- Convert 10% to a decimal and add 1 to it to get 1.10.
- Then convert 3% to a decimal and subtract it from 1 to get 0.97.
- Use the 2 decimal values to find the geometric mean: √(1.10 x 0.97) ≈ 1.03.
- Convert the number back to a percent by moving the decimal point 2 places to the right and subtracting 1 from it to find a total of a 3% increase in value.
Advertisement
-
1
Add the logarithmic values for each number in the set. The LOG function takes a value out of base-10 and determines how many times you need to multiply 10 together to equal that value. Locate the LOG function on your calculator, which usually is on the left side of the keypad. Click the LOG button and enter the first value in the set. Type in a “+” before putting in LOG for your second value. Continue separating the LOG functions for each value with a plus sign before finding the sum.[4]
- For example, with a set of 7, 9, and 12, you would type in log(7) + log(9) + log(12) before hitting “=” on your calculator. When you solve the functions, your sum will be about 2.878521796.
- You may also calculate each of the logarithms separately before adding the answers together.
-
2
Divide the sum of the logarithmic values by the number of values in the set. Count the number of values in your set and then divide the sum you just found by that number. The answer you get will be the logarithmic value of the geometric mean.[5]
- In this example, there’s a set of 3 numbers, so type in: 2.878521796 / 3 ≈ 0.959507265.
-
3
Take the antilog of the quotient to determine the geometric mean. The antilog function is the inverse of the LOG function on your calculator and it converts the value back to base-10. Look for the symbol “10x” on your calculator, which is usually a secondary function of the LOG button. Press the “2nd” button in the top left corner of the calculator followed by the LOG button to activate the antilog. Type in the quotient you found in the last step before solving the equation.[6]
- For this example, your calculator will read: 10(0.959507265) ≈ 9.11.
Advertisement
Add New Question
-
Question
How do I identify average numbers geometric mean, arithmetic mean and harmonic mean?
See wikiHow’s articles on each of those subjects.
-
Question
What is the geometric mean of 2, 4, 16, and 32?
To make this trivially easy, use logarithms Base 2. Then the logarithms are 1, 2, 4, and 5. The simple average of those logarithms is 3, so the geometric mean of 2, 4, 16, and 32 is 2^3 = 8.
-
Question
How do I find the geometric mean of 3 and 7?
3 x 7 = 21. √21 = 4.58.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
You cannot find the geometric mean of negative numbers.[7]
-
Any set that has 0 in it will have a geometric mean of 0.
Thanks for submitting a tip for review!
Advertisement
Things You’ll Need
- Calculator
References
About This Article
Article SummaryX
To calculate the geometric mean of 2 numbers, multiply those 2 numbers together, then calculate the square root of the resulting product. If you have 3 or more numbers, multiply all of the numbers together, then raise them to the power of 1 divided by n, where n is the total number of entries in the data set. To learn how to calculate the geometric mean of a data set using logarithms, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 858,811 times.
Did this article help you?
Средняя геометрическая
Средняя геометрическая
применяется в тех случаях, когда
индивидуальные значения признака
представляют собой, как правило,
относительные величины динамики,
построенные в виде цепных величин, как
отношение к предыдущему уровню каждого
уровня в ряду динамики, то есть
характеризует средний коэффициент
роста.
Средняя
геометрическая
исчисляется извлечением корня степени
n
из произведений отдельных значений –
вариантов признака х.
(5.11)
где n
– число вариантов;
П – знак произведения.
Наиболее широкое
применение средняя геометрическая
получила для определения средних темпов
изменения в рядах динамики, а также в
рядах распределения.
Средняя квадратическая и средняя кубическая
В ряде случаев в
экономической практике возникает
потребность расчета среднего размера
признака, выраженного в квадратных или
кубических единицах измерения. Тогда
применяется средняя
квадратическая
(например, для вычисления средней
величины стороны n
квадратных участков, средних диаметров
труб, стволов и т.п.) и средняя
кубическая
(например, при определении средней длины
стороны n
кубов).
Формулы для расчета
средней квадратической:
-
Средняя
квадратическая простая
является квадратным корнем из частного
от деления суммы квадратов отдельных
значений признака на их число:
(5.12)
-
Средняя
квадратическая взвешенная
(5.13)
где f
– веса.
Формулы для расчета
средней кубической аналогичны:
-
Средняя кубическая
простая
(5.14)
-
Средняя кубическая
взвешенная
(5.15)
Средние квадратическая
и кубическая имеют ограниченное
применение в практике статистики. Широко
пользуется статистика средней
квадратической, но не из самих вариантов
х, и из их отклонений от средней ()
при расчете показателей вариации.
Средняя может быть
вычислена не для всех, а для какой-либо
части единиц совокупности. Примером
такой средней может быть средняя
прогрессивная
как одна из частных средних, вычисляемая
не для всех, а только для «лучших»
(например, для показателей выше или ниже
средних индивидуальных).
5.5. Структурные средние.
Для изучения
структуры исследуемой совокупности
применяют так называемые структурные
средние: моду и медиану.
Модой в
статистике называют наиболее часто
встречающиеся в исследуемой совокупности
значение признака.
В дискретном
вариационном ряду моду определяют по
наибольшей частоте. По
следующим данным дискретного ряда
распределении определим моду:
Дневная выработка
рабочего, шт 10 12 15
25 25 30
Число рабочих,
имеющих
данную выработку,
чел. 5 10 8
12 9 7
Просматривая
частоты ряда (число рабочих), видим, что
наибольшая частота-12. Она соответствует
дневной выработке 20 шт. Таким образом,
мода показывает, что в данной совокупности
наибольшее число рабочих имеют выработку
20 шт. деталей в день.
В интервальном
ряду мода определяется по формуле:
,
(
где x0—
нижняя граница модального интервала
(модальным называется интервал, имеющий
наибольшую частоту);
i
— величина
модального интервала;
fmo
— частота
модального интервала;
fmo-1
—
частота
интервала, предшествующего модальному;
fmo
+1 —
частота
интервала, следующая за модальным.
Несколько иначе
определяется мода для интервального
вариационного ряда. В качестве примера
воспользуемся данными табл. 16.
Сначала найдем
модальный интервал, на который должна
приходиться наибольшая частота; по
условию задачи это будет интервал
100-105, так как ему соответствует наибольшая
частота – 16 чел. Подставив соответствующие
значения в формулу, получим:
M0=
100 + 5 *(16-3 / (16 – 3) + (16 – 8)) = 103 %/
Наибольшее число
рабочих выполняют месячное задание на
103 %.
Медианой в
статистике называют такое значение
признака, которое расположено в середине
упорядоченного ряда.
Медиана определяется
по – разному для дискретного и
интервального вариационного рядов.
Медиана
дискретного вариационного ряда,
расположенного в ранжированном порядке,
имеет серединное
значение.
Если дискретный ряд включает четное
число единиц, то медиана (Ме) определяется
как средняя из двух центральных значений.
Медиана в интервальном ряду определяется
по формуле:
где xМе
— нижняя
граница медианного интервала ( медианным
называется первый интервал, накопленная
частота которого превышает половину
общей суммы частот);
i
— величина
медианного интервала;
∑ f
—
сумма
частот;
Sme-1
– накопленная
частота интервала, предшествующего
медианному
fme
– частота
медианного интервала.
По следующим данным
дискретного ряда распределения,
расположенного в ранжированном порядке
(в порядке возрастания) определим
медиану:
Номер по порядку
рабочего….1 2 3 4 5
Стаж работы, лет
…………… .7 8 9 10 11
Так как медиана
имеет значение признака, находящееся
в середине упорядоченного ряда, то для
данного ряда распределения она составит
9 лет. Это значит, что половина совокупности
рабочих имеет стаж работы до 9 лет,
половина – более 9 лет.
Несколько сложнее
определяется сложнее определяется
медиана для интервального вариационного
ряда (табл.16)
Таблица 16
Распределение
рабочих по проценту выполнения месячного
задания
|
Выполнение месячного |
Число рабочих, чел. |
Накопленные от |
|
95 |
3 |
3 |
|
100 |
16 |
19 |
|
105 |
8 |
27 |
|
110 |
7 |
34 |
|
115 |
6 |
40 |
Прежде находится
медианный интервал, на который должно
приходиться 50% накопленных частот
данного ряда, что по условию задачи
40/2=20. Сумма частот первых двух интервалов
равна 19, что меньше 20. Следовательно,
медианный интервал будет находиться
не во второй группе, а в третьей, т.е. в
пределах границ 105 — 110.
Подставим
соответствующие значения в формулу:
Ме
= 105 + 5 * (
(40 + 2) — 19/8 ) =
105,6 %.
Таким образом, 50%
всех рабочих выполняют производственное
задание менее чем на 105,6%, 50% — более чем
на 105,6%.
Моду и медиану в
интервальном ряду можно определить
графически. Мода определяется по
гистограмме
распределения.
Для этого выберем
самый высокий прямоугольник,
который является модальным. Затем правую
вершину модального прямоугольника
соединяем с правым верхним углом
предыдущего прямоугольника, а левую
вершину модального прямоугольника
соединяем с правым верхним углом
последующего прямоугольника. Из точки
пересечения отпускаем перпендикуляр
на ось абсцисс. Абсцисса точки пересечения
этих прямых и будет модой распределения.
Медиана рассчитывается
на кумуляте.
Для ее определения из точки на шкале
накопленных частот, соответствующей
50 %, проводится прямая, параллельная оси
абсцисс, до пересечения с кумулятой.
Затем из точки пересечения указанной
прямой с кумулятой опускается
перпендикуляр на ось абсцисс. Абсцисса
точки пересечения является медианой.
Аналогично с
нахождением медианы в вариационных
рядах распределения можно найти значение
признака у любой по порядку единицы
ранжированного ряда. Можно найти значение
признака у единиц, делящих ряд на четыре
равные части, на десять, сто частей. Эти
величины называются квартили, децили,
перцентили.
Квартили
представляют
собой значения признака, делящие
ранжированную совокупность на четыре
равные части. Различают квартиль нижний
(Q1),
отделяющий ¼ часть совокупности с
наименьшими значениями признака, и
квартиль верхний (Q3),
отделяющий ¼ с наибольшими значениями
признака. Это означает, что 25 % единиц
совокупности будут по величине меньше
Q1;
25 % будут заключены между Q1
и Q2,
25 % между Q2
и Q3,
а остальные 25 % превосходят Q3.
Средним квартилем Q2
является медиана.
Для расчета
квартилей по интервальному вариационному
ряду используются формулы:
¼
∑ f – SQ1-1
Q1
=
xq1 + i
*———————
;
f
Q1
¾
∑ f – SQ3-1
Q3
= xQ3
+ i
*———————
;
f
Q3
где xq1
– нижняя граница интервала, содержащая
нижний квартиль (интервал определяется
по накопленной частоте, первой превышающей
25 %);
xQ3
— нижняя граница интервала, содержащая
верхний квартиль (интервал определяется
по накопленной частоте, первой превышающей
75 %);
i
– величина интервала;
SQ1-1
– накопленная частота интервала,
предшествующего интервалу, содержащему
нижний квартиль;
SQ3
– 1 – то же для верхнего квартиля;
f
Q1
– частота интервала, содержащего нижний
квартиль;
f
Q3
– то же для верхнего квартиля;
Рассмотрим на
примере (табл. 17).
Таблица 17
Распределение
семей города по размеру среднедушевого
дохода в январе 2007 г.
|
Группы |
Число |
Накопленные частоты |
Накопленные частоты, |
|
До 5000 5000-6000 6000-7000 7000-8000 8000-9000 9000-10000 свыше |
600 700 1700 2500 2200 1500 800 |
600 1300 3000 5500 7700 9200 10000 |
6 13 30 55 77 92 100 |
|
Итого |
10000 |
— |
— |
Нижний квартиль
находится в интервале 6000-7000, накопленная
частота которого равна 30 %. Верхний
квартиль лежит в интервале 8000-9000 с
накопленной частотой 77 %. Поэтому
получаем:
Q1=
6000 + 100*((1/4 10000 – 1300) / 1700) = 6710 руб.
Q3
=8000 + 100 * ((3/4 10000 – 5500) / 2200) = 8910 руб.
Итак, 25 % семей
имеют среднедушевой доход менее 6710
руб., 255 семей – свыше 8910 руб., а остальные
имеют доход в пределах 6710 — 8910 руб.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Средняя геометрическая в статистике
Понятие средней геометрической
Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т. е. характеризует средний коэффициент роста.
В контрольных по статистике она исчисляется извлечением корня степени n из произведений отдельных значений — вариантов признака Х по формуле:
где П — оператор умножения, знак произведения;
n — число вариантов.
Средняя геометрическая в частности рассчитывается тогда, когда данные даны в процентах.
Рассчитаем среднюю величину инфляции
Исходные данные взяты из справочника «Краткосрочные экономические показатели Российской Федерации за 2012 г.». Сайт www.gks.ru
| год | квартал | Индекс потребительских цен, y |
| 2008 | 1 | 104,8 |
| 2 | 103,8 | |
| 3 | 101,7 | |
| 4 | 102,5 | |
| 2009 | 1 | 105,4 |
| 2 | 101,9 | |
| 3 | 100,6 | |
| 4 | 100,7 | |
| 2010 | 1 | 103,2 |
| 2 | 101,2 | |
| 3 | 101,8 | |
| 4 | 102,4 | |
| 2011 | 1 | 103,8 |
| 2 | 101,1 | |
| 3 | 99,7 | |
| 4 | 101,4 |
Среднемесячный индекс потребительских цен определяется по формуле средней геометрической, т.к. в основе расчета лежит индекс. Перемножим данные и разделим на число кварталов за 4 года:
Вывод: в период с 2008 по 2011 года средний квартальный прирост инфляции составил 2,24%
Средняя гармоническая
Определяющее свойство средней гармонической заключается в том, чтобы при осреднении оставалась неизменной сумма величин, обратных осредняемым.
Формула средней геометрической взвешенной применяется в тех случаях, когда статистическая информация не содержит частот f по отдельным вариантам х совокупности и представлена как их произведение xf. Для того чтобы исчислить среднюю геометрическую, необходимо обозначить: xf = w, откуда f = w/x.
Преобразуем формулу средней арифметической так, чтобы по имеющимся данным х и w можно было вычислить среднюю. В формулу средней арифметической взвешенной вместо xn подставим w, а вместо n — отношение w/x и таким образом получим формулу средней гармонической взвешенной:
Средняя гармоническая простая применяется в тогда, когда вес каждого варианта равен единице. Она вычисляется по формуле:
где 1/x — отдельные варианты обратного признака, встречающиеся по одному разу;
n — число вариантов.
Средняя квадратичная
Средняя квадратичная применяется, например, для вычисления средней величины сторон n квадратных участков, средних диаметров стволов, труб и т. д. Она подразделяется на два вида.
Средняя квадратичная простая. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратичной средней величиной.
Она является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:
Средняя квадратичная взвешенная вычисляется по формуле:
где f — признак веса.
Средняя кубическая
Средняя кубическая применяется, например, при определении средней длины стороны и кубов. Она подразделяется на два вида.
Средняя кубическая простая:
Средняя кубическая взвешенная:
Средняя квадратическая и средняя кубическая имеют неширокое применение в практической статистике. Часто в статистике используют среднюю квадратическую, но не из самих факторов х, и из их отклонений от средней при расчете показателей вариации.
Средняя может быть рассчитана не для всей, а для какой-либо части данных совокупности. Примером может быть средняя прогрессивная как одна из частных средних, рассчитанная не для всех, а только для «лучших» (например, для показателей выше или ниже средних индивидуальных).
Структурные средние
Для характеристики центральной тенденции в статистических распределениях рационально вместе со средней арифметической использовать некое значение признака X, которое в силу определенных особенностей расположения в ряду распределения может характеризовать его уровень.
Это особенно важно тогда, когда в ряду распределения крайние значения признака имеют нечеткие границы. В связи с этим точное определение средней арифметической, как правило, невозможно, либо очень сложно. В таких случаях средний уровень можно определить, взяв, например, значение признака, которое расположено в середине ряда частот или которое чаще всего встречается в текущем ряду.
Такие значения зависят только от характера частот т. е. от структуры распределения. Они типичны по месту расположения в ряду частот, поэтому такие значения рассматриваются в качестве характеристик центра распределения и поэтому получили определение структурных средних.
Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.
Мода и медиана очень часто рассчитывают в задачах статистики и они являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа типа рядов распределения, которое может нормальным, асимметричным, симметричным и т.д.
Также как и медиану вычисляются значения признака, делящего совокупность на четыре равные части — квартели, на пять частей — квинтели, на десять равных частей — децели, на сто равных частей — перцентели. Использование при анализе вариационных рядов распределения рассмотренных характеристик в статистике позволяет более глубоко и детально охарактеризовать изучаемую совокупность.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
В данной публикации мы рассмотрим, с помощью какой формулы можно найти среднее геометрическое чисел, а также разберем примеры задач для ее демонстрации на практике.
- Расчет среднего геометрического
- Пример задачи
Расчет среднего геометрического
Чтобы вычислить среднее геометрическое двух или более чисел, требуется их перемножить, а затем из полученного результата извлечь корень, степень которого равняется их количеству.
Допустим, у нас есть числа a1, a2, … , an. Среднее геометрическое находится по формуле:
Частные случаи формулы:
Пример задачи
Задание 1
Найдем среднее геометрическое чисел 3, 6 и 12.
Решение:
Воспользуемся соответствующей формулой для трех чисел:
Задание 2
Среднее геометрическое четырех чисел равняется 4, а также известны три из них – 2, 2 и 4. Найдем четвертое.
Решение:
Обозначим число, которое требуется найти буквой x. Формула выглядит следующим образом:
Помещаем число 4 под знак корня, сохранив равенство (для этого возводим его в четвертую степень, т.е. 44 = 256):
Следовательно, x = 256 : 16 = 16.