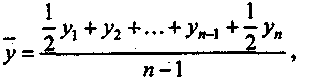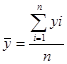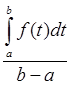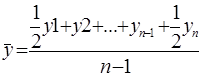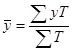Средняя хронологическая
Краткая теория
Средняя хронологическая — это средний
уровень ряда динамики, т. е. средняя, исчисленная по совокупности значений
показателя в разные моменты или периоды времени. В зависимости от вида ряда
динамики применяются различные способы ее расчета, а именно расчет средней
хронологической интервального ряда и средней хронологической моментного ряда.
Ряды динамики состоят из числовых значений двух показателей:
моментов или периодов времени t, к которым относятся приводимые данные, и
соответствующих им статистических данных у, которые называются уровнями
динамического ряда. В зависимости от того, к моментам или периодам времени
привязываются статистические данные, различают два вида рядов динамики:
моментные и интервальные.
Когда уровни ряда динамики характеризуют размеры общественных
явлений за определенные интервалы (периоды) времени (за сутки, месяц, квартал,
год и т. п.), то такие ряды называются интервальными (или периодическими). В
отличие от моментного ряда динамики уровни интервального ряда динамики могут
быть суммированы. Например, сложив данные выпуска станков за четыре квартала,
можно получить показатель их выпуска за год.
Для интервальных рядов с равноотстоящими уровнями средняя
хронологическая имеет вид средней арифметической простой:
где
– уровни интервального ряда
— количество равных периодов времени
В интервальных рядах с неравноотстоящими
уровнями средняя хронологическая имеет вид средней
арифметической взвешенной:
где
– периоды времени, отделяющие один уровень
ряда от другого
Если уровни ряда динамики выражают состояние явления на
определенные моменты времени или даты, то такие ряды называют моментными рядами
динамики. Особенность моментного ряда динамики в том, что некоторые его уровни
содержат элементы повторного счета, т. е. каждый последующий уровень полностью
или частично включает в себя предыдущий уровень. Поэтому суммирование уровней
моментного динамического ряда не имеет смысла, но разность уровней имеет
определенное значение.
В моментном ряду динамики с равноотстоящими уровнями средняя хронологическая
имеет вид:
Средний уровень моментного ряда динамики с неравноотстоящими
уровнями характеризует средняя хронологическая взвешенная, которая исчисляется
по формуле:
где
и
– значение уровня моментного ряда динамики и
уровня, следующего за ним;
–
промежуток времени между датами.
Примеры решения задач
Задача 1
Остатки
готовой продукции на складе составили, тыс.руб.:
| Дата |
Остатки готовой продукции, тыс.руб. |
| 01.04.2011 | 506 |
| 01.05.2011 | 519 |
| 01.06.2011 | 587 |
| 01.07.2011 | 624 |
| 01.08.2011 | 624 |
| 01.09.2011 | 545 |
| 01.10.2011 | 580 |
| 01.11.2011 | 542 |
| 01.12.2011 | 576 |
| 01.01.2012 | 606 |
Требуется:
Определить средние остатки готовой
продукции на складе за II квартал, за III квартал, за IV квартал, за второе
полугодие 2011 года.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Средние
остатки продукции можно вычислить по формуле средней хронологической, так как
нам дан динамический моментный ряд с
равноотстоящими интервалами.
Средние
остатки за 2-й квартал:
Средние
остатки за 3-й квартал:
Средние
остатки за 4-й квартал:
Средние
остатки готовой продукции за второе полугодие:
Вывод
Таким
образом средние остатки готовой продукции за 2-й
квартал составили 557 тыс.р., за 3-й квартал 590,3 тыс.р., а за 4-й квартал 570,3 тыс.р.
Средние остатки готовой продукции за 2-е полугодие составили 580,3 тыс.р.
Задача 2
Известны
следующие данные об изменениях в списочном составе работников банка за январь,
человек.
| Число сотрудников | |
| Состояло по списку на 1 января | 205 |
| на 9 января | 200 |
| на 12 января | 198 |
| на 16 января | 201 |
| на 19 января | 197 |
| на 27 января | 199 |
| Состояло по списку на 1 февраля | 199 |
Определите
среднюю списочную численность работников банка в январе.
Решение
Данный
динамический ряд моментный, с неравноотстоящими датами.
Средняя
хронологическая взвешенная:
Вывод
Среднесписочная
численность работников банка в январе составила 200,2 чел.
Задача 3
Имеются
следующие данные о производстве молока в России за 1995-2000 годы (млн.т.)
| 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
| 39.2 | 35.8 | 34.1 | 33.3 | 32.3 | 32.3 |
Для
анализа ряда динамики определите средний уровень ряда динамики.
Решение
Так
как данный динамический ряд интервальный,
с равноотстоящими уровнями, то средний уровень исследуемого динамического
ряда найдем по формуле средней арифметической:
Вывод
Среднегодовое
производство молока в исследуемом периоде составило 34,5 млн. тонн.
Задача 4
Имеются
следующие данные о производстве продукции на заводе (млн. руб.)
| 2005 | 2008 | 2010 | 2011 | 2013 | 2014 |
| 45,4 | 48,3 | 41,5 | 39,6 | 42,5 | 46,8 |
Для
анализа ряда динамики определите средний уровень ряда динамики.
Решение
Так
как данный динамический ряд интервальный,
с неравноотстоящими уровнями, то средний уровень
исследуемого динамического ряда найдем по формуле средней арифметической
взвешенной:
Вывод
Среднегодовое производство продукции на предприятии в исследуемом
периоде составило 44,8 млн. рублей.
ПОИСКСтраницы«Назад | Вперед » Партнеры сайта_________________________________
|
Средняя хронологическая
Средняя арифметическая
| Средняя гармоническая | Средняя квадратическая | Средняя хронологическая | Средняя геометрическая Формулой средней хронологической пользуются
Пример:
Средняя численность рабочих за первый квартал:
|
меню пользователяНе зарегистрирован Вход Забыли пароль? Регистрация Новости
|
12
Наряду с абсолютными
и относительными величинами в статистике
большое применение находят средние
величины. В
повседневной жизни употребляются
термины «в среднем», «средняя».
Например, средняя цена, средний расход
продуктов, средняя заработная плата,
средняя мощность оборудования, средняя
выработка, средний размер сбережений
и т. д.
В экономическом
анализе часто приходится оперировать
средними величинами в целях лучшего
понимания общей картины, когда нужно
из многих признаков получить величину,
в которой отражались бы свойства всех
признаков, входящих в состав совокупности.
Средняя величина
в С — обобщающий показатель,
характеризующий типичный уровень
явления в конкретных условиях места
и времени, отражающий величину
варьирующего признака в расчете на
единицу качественно однородной
совокупности.
Средняя величина есть обобщающая
количественная характеристика однородных
явлений по какому-либо варьирующему
признаку.
Применение средних
величин позволяет охарактеризовать
определенный признак совокупности
одним числом, несмотря на количественные
различия единиц по данному признаку
внутри совокупности.
Следовательно,
средняя величина есть обобщающая
характеристика совокупности; средняя
величина выражает типичное свойство
совокупности; средняя величина —
величина абстрактная, а не конкретная,
так как в ней сглаживаются отдельные
значения единиц совокупности, имеющие
отклонения в ту и другую сторону;
реальность средней величины достигается,
если она вычисляется из одной совокупности.
Пользуясь средними
величинами при анализе массовых явлений,
необходимо всегда помнить, что часто в
средней величине скрываются отстающие
хозяйствующие субъекты, которые имеют
низкие показатели своей деятельности
и, наоборот, не выявляются фирмы, компании,
предприятия и т. д., которые работают
весьма эффективно. Это возможно, как
уже говорилось выше, в связи со свойством
средней, в которой отклонения отдельных
значений признака от ее величины взаимно
погашаются. (Так, например, при условии
выполнения плана розничного товарооборота
в целом по холдингу, занимающемуся
продажей товаров, часть фирм, входящих
в него, не выполнила план и, наоборот,
другая часть перевыполнила план
товарооборота.) Поэтому, кроме средней,
следует использовать и отдельные
индивидуальные показатели работы фирм,
входящих в холдинг.
В эк. практике
исп.-ся широкий круг показателей,
вычисленных в виде средних величин.
Напр, обобщающим
показателем доходов рабочих АО служит
средний доход одного рабочего, определяемый
отношением фонда з/п и выплат социального
характера за рассматриваемый период
(год, квартал, месяц) к численности
рабочих АО.
Вычисление
среднего – один
из распространенных приемов обобщения;
средний показатель отражает то общее,
что характерно (типично) для всех единиц
изучаемой совокупности, в то же время
он игнорирует различия отдельных
единиц. В каждом явлении и его развитии
имеет место сочетание случайности
и необходимости.
При исчислении средних в силу действия
закона больших чисел случайности
взаимопогашаются, уравновешиваются,
поэтому можно абстрагироваться от
несущественных особенностей явления,
от колич. значений признака в каждом
конкретном случае. В способности
абстрагироваться от случайности
отдельных значений, колебаний и
заключена научная
ценность средних как обобщающих
характеристик совокупностей.
Там, где возникает
потребность обобщения, расчет таких
характеристик приводит к замене множества
различных инд. значений признака средним
показателем, характеризующим всю
совокупность явлений, что позволяет
выявить закономерности, присущие
массовым общ. явлениям, незаметные в
единичных явлениях.
Средняя отражает
характерный, типичный, реальный уровень
изучаемых явлений, характеризует эти
уровни и их изменения во времени и в
пространстве; это сводная характеристика
закономерностей процесса в тех условиях,
в к-рых он протекает.
Выбор
вида средней
определяется эк. содержанием
определенного показателя и исходных
данных.
1)- Класс
степенных средних
— арифметическая,
гармоническая, геометрическая,
квадратическая, кубическая
и т.д. Помимо
степенных средних в с/практике используются
2) Структурные
средние —
применяются для изучения внутреннего
строения и структуры рядов распределения
значений признака. К таким показателям
относятся мода
и медиана..
Средняя хронологическая
Средняя
хронологическая — это средний уровень
ряда динамики, т. е.
средняя,
исчисленная по совокупности значений
показателя в разные моменты или периоды
времени. В
зависимости от вида ряда динамики
применяются различные способы ее
расчета, а именно расчет средней
хронологической интервального ряда и
средней хронологической моментного
ряда.
С
редней
хронологической интервального ряда
является средняя величина из уровней
интервального ряда динамики,
которая исчисляется по формуле
где
— средний уровень ряда;
у
— уровень ряда динамики;
n
— число членов ряда.
Средней
хронологической моментного ряда является
средняя величина из уровней моментного
ряда динамики.
Если f(t)
есть функция, выражающая изменение
моментного показателя во времени, то
за время (t)
от а
до b
средняя хронологическая моментyого
ряда равна:
Однако данных
непрерывного наблюдения значения f(t)
в распоряжении статистики, как правило,
нет. Поэтому в зависимости от характера
изменения показателя и имеющихся данных
применяются различные методы расчета.
При равных промежутках времени между
датами, на которые имеются данные, и
равномерном изменении размера показателя
между датами средняя хронологическая
моментного ряда обычно исчисляется
по формуле:
где у
— уровень ряда; n
— число всех
членов ряда;
—
средний уровень.
Если периоды
времени, отделяющие одну дату от другой,
не равны между собой, то расчет средней
хронологической моментного ряда
производится по формуле средней
взвешенной арифметической, в качестве
весов которой принимаются отрезки
времени между датами, т. е. по формуле:
г
деТ—
время, в течение которого данный уровень
ряда (у)
оставался без изменения.
Известно, например,
что в январе 2007 года произошло следующее
изменение численности сотрудников
компании «Бест»: было на 1 января
551 чел., уволился 2 января один сотрудник,
было принято 6 января 24 человека, 16
января— 6 человек, уволилось 25 января—
10 сотрудников. Требуется определить
среднюю численность сотрудников компании
«Бест» в январе 2007 г. Рассчитаем
число календарных дней, в течение которых
численность сотрудников компании «Бест»
оставалась без изменения, и произведение
этих чисел.
Таблица 5
Данные для расчета средней численности сотрудников компании «Бест»
|
Численность |
Число |
Произведение |
|
551 |
1 |
551 |
|
550 |
4 |
2200 |
|
574 |
10 |
5740 |
|
580 |
9 |
5220 |
|
570 |
7 |
3990 |
|
ИТОГО |
31 |
17701 |
Используя данные
произведенных расчетов, получим:
В отличие от первого
способа расчета средней хронологической
моментного ряда второй способ дает
точное значение средней.
Средняя гармоническая (сг).
СГ применяется
в тех случаях, когда частоты (веса) не
приводятся непосредственно, а входят
сомножителями в один из имеющихся
показателей.
Пример. Автомобиль
доставил товары в три магазина фирмы
«Весна», которые удалены от головного
предприятия на одинаковое расстояние.
Так, до первого магазина, расположенного
на шоссейной дороге, автомобиль прошел
путь со скоростью 50 км/ч, до второго, по
проселочной дороге, — 40 км/ч, а в третьем
случае автомобилю пришлось полпути
пройти через лесной массив, и скорость
движения составила только 30 км/ч.
Требуется определить
среднюю скорость движения автомобиля.
На первый взгляд представляется, что
средняя скорость • движения может быть
определена по формуле простой
арифметической:
Однако нетрудно
убедиться, что средняя вычислена
неправильно. В самом деле, производя
расчет средней скорости по простой
арифметической средней, исходим из
того, что автомобиль во всех трех случаях
прошел одинаковое расстояние, пройдя
соответственно 50, 40 и 30 км, т. е. всего
120 км. Если бы условие этой задачи
было сформулировано в такой форме, то
средняя была бы рассчитана правильно
и характеризовала бы пройденное
автомобилем среднее расстояние.
В действительности
же эта средняя рассчитана неверно, так
как «в условия задачи не следует, что
автомобиль на преодоление расстояния
до трех магазинов фирмы «Весна»
проехал 120 км, так как Скорость движения
была различная. Следовательно, он прошел
и разное расстояние.
В тех случаях,
когда вес каждого варианта равен единице
(индивидуальные значения обратного
признака встречаются по одному разу),
применяется СГ
простая,
исчисляемая по формуле:
где x
– отдельные варианты обратного
признака, встречающиеся по одному разу;
n–
число вариантов.
(8)
или
в сокращенном виде
где
—средняя
гармоническая;
—
числа, обратные заданным вариантам.
Иначе говоря, СГ
простая
отношение числа вариантов к сумме
обратных значений этих вариантов.
Для нашего примера
будем иметь:
В нашем примере
СА (ха)
оказалась
больше средней гармонической
.
При этом абсолютная
ошибка завышения составляет
— 2 км/ч (38 — 40), а относительная —5%
Т.о., неправильное
использование СА привело бы к завышению
средней скорости движения автомобиля
и к неправильному определению объема
перевозок. Это еще раз доказывает, с
какой осторожностью следует решать
вопрос о том, какую среднюю надлежит
применять в экономических расчетах.
В рассмотренном
примере частоты (веса) имели одно значение
и равнялись единице. Если же частоты
(веса) различные, то применяется СГ
взвешенная, которая
вычисляется следующим образом:
Где
—
СГ взвешенная:
Как первая, так и
вторая формулы показывают, что СГ есть
величина обратная СА.
Веса арифметической
средней и гармонической средней
обозначены разными буквами: f
и m.
Это не случайно, так как весами СА служат
частоты рассматриваемого ряда, а весами
СГ будет произведение вариантов на
веса.
Пример.
Рассмотрим данные о реализации товаров
по двум магазинам фирмы «Весна»
(табл. 6). Таблица
.6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
29.05.20153.63 Mб107. Лекц.БУ-анализ.doc
- #
18.12.2018130.46 Кб297.docx
Средняя хронологическая
(chronological mean)
— средняя, рассчитанная из значений, изменяющихся во времени. Используется для расчета среднего уровня моментного ряда. В том случае, если имеющиеся данные относятся к фиксированным моментам времени c равными интервалами, то используется следующая формула:
Х – значение уровней ряда,
n – число имеющихся показателей.
Пример. Предположим, что на счете фирмы в банке были зафиксированы остатки средств на следующие даты в млн. руб.:
| 1.01.2010 | 1.02.2010 | 1.03.2010 | 1.04.2010 | 1.05.2010 | 1.06.2010 | 1.07.2010 |
| 128 | 144 | 155 | 161 | 147 | 154 | 158 |
Средний остаток средств на счете фирмы за рассматриваемый период составит:
Средний уровень моментных рядов динамики с неравноотстоящими датами определяется по формуле средней хронологической взвешенной:
уровни рядов динамики
— длительность интервала времени между уровнями
Пример. Известна списочная численность рабочих организации на некоторые даты (человек) на:
| 01.01.2010 | 01.03.2010 | 01.06.2010 | 01.09.2010 | 01.01.2011 |
| 1100 | 1000 | 1150 | 1400 | 1250 |
Среднегодовая численность работников составит:
Содержание
- Средняя хронологическая
- Еще статьи по экономике
- Средняя хронологическая
- Данные для расчета средней численности сотрудников компании «Бест»
- Способ расчета хронологической средней
Средняя хронологическая
Средняя хронологическая — это средний уровень ряда динамики, т. е. средняя, исчисленная по совокупности значений показателя в разные моменты или периоды времени.
В зависимости от вида ряда динамики применяются различные способы ее расчета, а именно расчет средней хронологической интервального ряда и средней хронологической моментного ряда.
Средней хронологической интервального (более распространённого) ряда является средняя величина из уровней интервального ряда динамики, которая исчисляется по формуле:
где 
— средний уровень ряда;
— уровень ряда динамики;
— число членов ряда
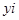
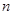
Для примера рассмотрим данные о детских оздоровительных учреждениях в Пскове и области.
Таблица. Детские оздоровительные учреждения
Число летних оздоровительных лагерей
Исследуемый ряд является интервальным, используя формулу средней хронологической можем высчитать среднее количество оздоровительных учреждений:
учреждений.
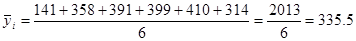
Средней хронологической моментного ряда является средняя величина из уровней моментного ряда динамики. Если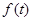 
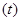
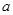
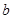
есть функция, выражающая изменение моментного показателя во времени, то за время 
от 
до 
средняя хронологическая моментного ряда равна:
Однако данных непрерывного наблюдения значения 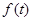в распоряжении статистики, как правило, нет. Поэтому в зависимости от характера изменения показателя и имеющихся данных применяются различные методы расчета.
При равных промежутках времени между датами, на которые имеются данные, и равномерном изменении размера показателя между датами средняя хронологическая моментного ряда обычно исчисляется по формуле:
где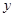 
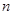
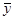
— уровень ряда;
— число всех членов ряда;
— средний уровень.
Если периоды времени, отделяющие одну дату от другой, не равны между собой, то расчет средней хронологической моментного ряда производится по формуле средней взвешенной арифметической, в качестве весов которой принимаются отрезки времени между датами, т. е. по формуле:
где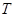 
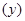
— время, в течение которого данный уровень ряда 
оставался без изменения. [2 c.149]
Еще статьи по экономике
Финансовый анализ деятельности предприятия на примере ОАО ГОЗСА
рыночная экономика В условиях современной конкурентной рыночной среды и финансовой неопределенности в долгосрочном периоде из-за рисков возникновения кризисных явлений, финансов .
Инвестиционная политика Республики Казахстан
Из послания следует, что Н.А.Назарбаев ставит целью привлечение инвестиций в Казахстан: «Одними из основных вопросов в ходе моих международных поездок были вопросы инвестиций в Казахст .
Комплексный анализ хозяйственной деятельности предприятия на примере ООО ОПТ-Сервис КМВ
Переход к рыночной экономике требует от предприятия торговли повышения эффективности деятельности, конкурентоспособности реализуемых товаров и услуг на основе внедрения достиж .
Источник
Средняя хронологическая
Средняя хронологическая — это средний уровень ряда динамики, т. е. средняя, исчисленная по совокупности значений показателя в разные моменты или периоды времени. В зависимости от вида ряда динамики применяются различные способы ее расчета, а именно расчет средней хронологической интервального ряда и средней хронологической моментного ряда.
Средней хронологической интервального ряда является средняя величина из уровней интервального ряда динамики, которая исчисляется по формуле
где — средний уровень ряда;
у — уровень ряда динамики;
n — число членов ряда.
Средней хронологической моментного ряда является средняя величина из уровней моментного ряда динамики. Если f(t) есть функция, выражающая изменение моментного показателя во времени, то за время (t) от а до b средняя хронологическая моментyого ряда равна:
Однако данных непрерывного наблюдения значения f(t) в распоряжении статистики, как правило, нет. Поэтому в зависимости от характера изменения показателя и имеющихся данных применяются различные методы расчета. При равных промежутках времени между датами, на которые имеются данные, и равномерном изменении размера показателя между датами средняя хронологическая моментного ряда обычно исчисляется по формуле:
где у — уровень ряда; n — число всех членов ряда; — средний уровень.
Если периоды времени, отделяющие одну дату от другой, не равны между собой, то расчет средней хронологической моментного ряда производится по формуле средней взвешенной арифметической, в качестве весов которой принимаются отрезки времени между датами, т. е. по формуле:
гдеТ— время, в течение которого данный уровень ряда (у) оставался без изменения.
Известно, например, что в январе 2007 года произошло следующее изменение численности сотрудников компании «Бест»: было на 1 января 551 чел., уволился 2 января один сотрудник, было принято 6 января 24 человека, 16 января— 6 человек, уволилось 25 января— 10 сотрудников. Требуется определить среднюю численность сотрудников компании «Бест» в январе 2007 г. Рассчитаем число календарных дней, в течение которых численность сотрудников компании «Бест» оставалась без изменения, и произведение этих чисел.
Данные для расчета средней численности сотрудников компании «Бест»
Численность сотрудников компании «Бест», чел.(y)
Число календарных дней, в течение которых данная численность сотрудников оставалась безизменения (T)
Произведение численности сотрудников на число календарных дней(yT)
Источник
Способ расчета хронологической средней
Среднегодовое количество буровых установок определяется по формуле средней хронологической [c.28]
Средняя сумма оборотных средств рассчитывается по средней арифметической или средней хронологической. Если оборачиваемость рассчитывается за год, то берется наличие оборотных средств на начало каждого месяца. [c.232]
В аналитических расчетах применяют, исходя из необходимости, различные формы средних — средняя арифметическая, средняя гармоническая взвешенная, средняя хронологическая моментного ряда, мода, медиана. [c.48]
Товарные запасы в абсолютном выражении характеризуют лишь товарные остатки в торговом предприятии на определенный момент (на начало и конец отчетного периода или какую-либо промежуточную дату). Использовать данные об остатках товаров на какие-либо отдельные даты для оценки товарных запасов за весь отчетный период нельзя. Для такой оценки необходимо исчислить показатели среднего запаса. Этот запас определяется по данным об остатках товаров на отдельные даты. Исчисление среднего товарного запаса за отчетный год можно произвести двумя способами 1) по формуле среднеарифметической с привлечением двух слагаемых — остатка товаров на начало и остатка товаров на конец отчетного периода 2) по формуле средней хронологической моментного ряда. [c.310]
Формула средней хронологической моментного ряда, как известно, такова [c.310]
Среднегодовая стоимость рассчитывается по формуле средней хронологической на основе данных о стоимости имущества, включаемого в налогооблагаемую базу на 1-е число первого месяца каждого квартала года за соответствующий налогооблагаемый период. [c.129]
Средние остатки всего капитала и его составных частей рассчитываются по средней хронологической 1/2 суммы на начало периода плюс остатки на начало каждого следующего месяца плюс 1 /2 остатка на конец периода и результат делится на количество месяцев в отчетном периоде. Необходимая информация для расчета показателей оборачиваемости имеется в бухгалтерском балансе и отчете о финансовых результатах. [c.314]
Вообще статистические методы используются в экономическом анализе наиболее часто. Это расчеты средних величин простых средних арифметических, взвешенных средних, хронологических средних. [c.25]
Остатки кредита в статистической отчетности показываются на дату, т.е. представляют собой моментный динамический ряд. Поэтому расчет среднего остатка ссуд выполняется по формуле средней хронологической [c.303]
Потребительские настроения все время меняются, поэтому денежная масса может быть исчислена только на определенный момент времени, т.е. является моментным показателем и характеризует количество денег в экономической системе на определенный момент времени — чаще всего на начало периода (месяца, года). Говоря о величине денежной массы в некотором временном периоде, мы должны определить среднее значение этой величины по формулам исчисления средней в моментном динамическом ряду средней хронологической или средневзвешенной по величине интервала, в течение которого денежная масса сохраняла свое значение. [c.446]
Среднее сальдо определяется по формуле средней хронологической из возможно большего числа сальдо. Если мы рассчитываем оборачиваемость за месяц, то минимальное число сальдо равно двум (на начало и конец месяца), а максимальное — 30 (на каждый день месяца). Чем большее число сальдо мы возьмем, тем будет точнее среднее сальдо, а значит, и оборачиваемость. [c.305]
Средний остаток оборотных средств в целом или какого-нибудь их вида исчисляют по формуле средней хронологической [c.326]
В анализе финансово-хозяйственной деятельности широко используется средняя хронологическая. Дело в том, что одна из основных классификаций экономических показателей подразумевает их подразделение на интервальные и моментные. Примерами первых являются товарооборот, прибыль, объем поступления за некоторый период примерами вторых — данные о запасах, основных средствах, численности на определенную дату. Для усреднения интервальных показателей чаще всего используется формула средней арифметической что касается усреднения моментных показателей, то здесь как раз и применяется формула средней хронологической. [c.108]
Если дан ряд моментных показателей х/,. . х , то средняя хронологическая S h для этого ряда рассчитывается по формуле [c.108]
Именно формула средней хронологической применяется для расчета средних товарных запасов, средней дебиторской задолженности, средней численности и др. Примеры использования средних будут приведены при изложении методики анализа финансового состояния предприятия. [c.109]
Унифицированного подхода к расчету фондоотдачи нет. Различия возникают, в частности, в зависимости от выбранной стоимостной характеристики основных средств, приведенной в знаменателе дроби. В качестве ее могут выступать первоначальная или остаточная стоимости, причем в отечественной практике традиционно используется первоначальная стоимость, в западной — остаточная. Средняя стоимость рассчитывается по формуле средней хронологической за тот период, к которому относится выручка от продаж. [c.351]
Экономическая интерпретация алгоритма в формуле (8.5) достаточно очевидна. Числитель показывает общую сумму средств, потребленных для производства продукции, а знаменатель — величину запаса в среднем, рассчитываемую по формуле средней хронологической. Чем меньшим запасом обходилось предприятие в отчетном периоде, тем более эффективно использовались выделенные для инвестирования в оборотные активы денежные средства. В зависимости от вида оцениваемых активов, отраслевой принадлежности предприятия и имеющегося в распоряжении аналитика информационного обеспечения исходные параметры в формуле (8.5) могут меняться. Кроме того, известны и другие показатели эффективности. Приведем их характеристику. [c.352]
Собственные оборотные средства — 306,313,316 Спекулирование — 455 Средняя хронологическая — 108 Средства-217, 301 [c.548]
Средний остаток оборотных средств определяется как средняя хронологическая моментного ряда, исчисляемая по совокупности значений показателя в разные моменты времени [c.217]
Примечай и я 1 С применением стандартных норм амортизации, установленных постановлением Совмина СССР № 1072 от 22.10.1990 г., и коэффициента ускорения, равного 2, в соответствии с Постановлением Правительства РФ № 967 от 19.08.1994 г. (для машин и оборудования предприятий, производящих строительные материалы, Минстроем РФ утвержден их перечень для ускоренной амортизации). Методические указания по учету основных средств не предусматривают применение коэффициента ускорения к линейному способу, однако возможность его применения здесь установлена вышеуказанным постановлением № 967. 2 Допустим, по коэффициенту, равному 0,1. 3 Допустим, срок полезного использования равен десяти годам. В аналогичном порядке, но с учетом особенностей его применения рассчитывается влияние начисления амортизации по способу уменьшаемого остатка. 4 Для граф 5 и 6. 5 Для графы 7. Здесь и далее данные базового варианта обозначаются индексом О , а вариантов возможных индексом I . 7 Расчет средней балансовой стоимости производится по формуле средней хронологической, применение которой к расчетным балансовым остаткам основных средств по состоянию на 1.01, 1.04, 1.07, 1.10, 1.01 следующего года позволило, допустим, определить (О ), т.е. среднегодовую стоимость основных средств при применении линейного способа — 900 ед. способа замедленной амортизации 995 ед. способа начисления амортизации по сумме чисел лет срока полезного использования 909 ед.. » Для граф 5 и 6. 9 Увеличение прибыли в целях ее налогообложения на сумму ускорения амортизации. » Для графы 7. [c.121]
Средний балансовый остаток материалов ш/i Средняя хронологическая 2875 3240 [c.127]
При расчете коэффициентов прибыльности берутся средние показатели инвестиций. Они рассчитываются по методу средней хронологической. [c.82]
Средние остатки всех и отдельных видов оборотных средств рассчитываются по средней хронологической 1/2 остатка на начало периода, плюс остатки на начало каждого месяца, плюс 1/2 остатка на конец периода полученная сумма делится на число месяцев в изучаемом периоде, например на 12. [c.88]
Е — средняя (хронологическая) величина оборотного капитала [c.32]
Помимо степенных средних в статистической практике используются также средние структурные, среди которых наиболее распространены мода и медиана. При осреднении уровней динамических рядов применяются различные виды средней хронологической. [c.54]
Что касается средней хронологической, то она рассчитывается в том случае, если имеются данные на определенные даты (обычно на начало месяца, квартала, года). Простая средняя хронологическая определяется по формуле [c.58]
Эта формула применяется в случае наличия одинаковых интервалов между данными. Если интервалы не равны, то используется взвешенная средняя хронологическая [c.58]
Для иллюстрации расчета средней хронологической возьмем следующие данные о численности работников сельскохозяйственного предприятия и ее изменении в течение года. [c.59]
Поскольку интервалы не равны, расчет средней хронологической проводится по взвешенной формуле [c.59]
Средний уровень ряда динамики (у) рассчитывается по средней хронологической. Средней хронологической называется средняя, исчисленная из значений, изменяющихся во времени. Такие средние обобщают хронологическую вариацию. В хронологической средней отражается совокупность тех условий, в которых развивалось изучаемое явление в данном промежутке времени. [c.75]
Средний уровень моментного равноотстоящего ряда динамики находится по формуле средней хронологической [c.76]
Определить среднегодовую численность трудовых ресурсов по формуле средней арифметической по формуле средней хронологической [c.193]
Однако этот метод не учитывает колебания численности внутри периода. Более точный расчет дает использование формулы средней хронологической, которая применяется тогда, когда исходные сведения о численности трудовых ресурсов и экономически активного населения имеются на начало каждого месяца, квартала, т.е. за равные промежутки времени. Если интервалы между наблюдениями равны, то применяется формула [c.210]
Если имеются данные за неравные интервалы времени, то применяется формула средней хронологической взвешенной [c.210]
Проиллюстрируем расчет среднегодовой численности трудовых ресурсов при наличии данных за неравные интервалы времени по формуле средней хронологической взвешенной на следующем условном примере. [c.211]
Средние показатели, используемые для расчета сети, штатов и контингентов, определяются по формуле средней хронологической простой, если данные представлены рядом динамики с равностоящим уровнем. Например, среднее количество штатов, групп, койко-мест, а также штатных работников, педагогического персонала, медицинского персонала, воспитателей, студентов, учащихся, детей определяется по формуле средней хронологической, так как данные об их численности представляются на первое число каждого месяца (на 1 января, 1 февраля и т.д.). Если в течение учебного года число классов, групп и учащихся не изменилось, то среднегодовое количество, например, классов (комплектов) будет определяться по формуле средней арифметической взвешенной. [c.231]
Этот расчет приблизителен. Более точные оценки могут быть получены по внугригодовым данным. В частности, при использовании квартальных балансов расчет осуществляется по формуле средней хронологической [c.286]
Средний уровень моментных рядов динамики с неравноотстоящими уровнями определяется по формуле средней хронологической взвешенной [c.76]
Источник