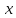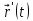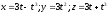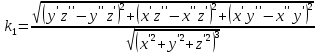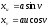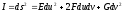Как найти среднюю кривизну - Исправление недочетов и поиск решений вместе с Examum.ru

Рассматриваем
регулярную поверхность

в окрестности точки
.
Дифференциалы
,

из (3.7.1) подставим в выражение (3.6.4) для
нормальной кривизны поверхности. После
сокращение на

приходим к равенству

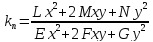
Отсюда
получаем

Дифференцируем
это равенство по

и по
:

Главные
направления в касательной плоскости
определяются этой системой уравнений,
если она имеет ненулевые решения, т.е.
в случае
.

Значение
определителя

Главные
кривизны
,

есть корни выписанного уравнения.
Воспользуемся теоремой Виетта:

,
.

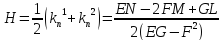
Полная
и средняя кривизны поверхности найдены
без вычисления главных кривизн.

Практическая
часть.

4.Кривая.

Кривая
задана следующим образом:

Найдем
производные первого, второго и третьего
порядков.

4.1.Найдем
уравнение касательной по формуле:

Возьмем
=0;

Найдем
производную

При
подставлении

в

получим точку Р =(0,0,0);

При
подставлении

в

получим точку
=(3,0,3);

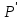
Составим
уравнение касательной для кривой
:

4.2.Найдем
уравнение нормальной плоскости для
кривой

по формуле:

Подставляя
уже найденные ранее данные, получаем:

4.3.Найдем
уравнение соприкасающейся плоскости
по формуле:

Раскроем
определитель по первой строке

—+=0;

Примем

Подставим
значения в уравнение соприкасающейся
плоскости:

Уравнение
соприкасающейся плоскости имеет вид:

8x+6y-3z-1=0.

4.4.Сосчитаем
кривизну кривой

по следующей формуле:

Подставляя
ранее полученные значения производных
первого и второго порядков в основную
формулу нахождения кривизны кривой в
координатах, получим нужную нам кривизну.
Из-за сложности в подсчетах разделим
вычисление на несколько этапов:

Вычисление
числителя без извлечения корня

Приведем
подобные слагаемые и извлечем корень
из получившегося выражения:

2)Вычисление
знаменателя без извлечения корня.

Извлечем
корень

Подставим
все в итоговую формулу

4.5.Вычислим кручение кривой :

Примем
t=0;

Получим
.

4. 6. Изображение кривой.

5. Поверхность.

Поверхность
задана следующим образом:

Вычислим
производные:

5.1. Найдем уравнение касательной плоскости, используя формулу:

Подставляя
в нее значения производных, получим:

Раскроем
определители и получим общее уравнение
искомой поверхности:

Найдем
уравнение касательной плоскости в
конкретной точке:

Выберем
произвольную точку Р(1,2,1).

Зададим
u=1,v=;

Примем
a=2,k=;

Подставляя
в формулу, получим:

5.2. Найдем уравнение нормали для искомой поверхности.

Раскроем
определители:

Подставляя
уже найденные ранее производные и
приводя подобные слагаемые, получим:

Найдем
уравнение нормали в конкретной точке:

Выберем
произвольную точку Р (1,1,2).

Зададим
a=2
,k=,
u=1,v=
;

Подставим
заданные значения в уравнение:

5.3.Вычисление
первой квадратичной формы.

Найдем
частные производные:

Вычисляем
коэффициенты первой квадратичной формы
поверхности:

Детерминант
первой квадратичной формы:

Корень
из детерминанта первой квадратичной
формы:

Первая
квадратичная форма имеет вид:

Подставим
получившиеся значения в эту формулу и
получим

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

оксана николаевна кузнецова

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Основная формула для вычисления кривизны плоской кривой

Кривизна представляет собой количественную характеристику степени изогнутости плоской кривой.

Построим касательную к кривой в точке $M$. При переходе по кривой из точки $M$ в некоторую соседнюю точку $N$, касательная в текущей точке поворачивается на угол $Delta phi $.

Определение

Отношение угла $Delta phi $ к длине дуги $Delta s$ между точками $M$ и $N$ называется средней кривизной дуги $K_{A@} =frac{Delta phi }{Delta s} $.

Средняя кривизна характеризует среднюю изогнутость на всей дуге. Но на отдельных участках кривой значения кривизны могут испытывать значительные отклонения от среднего значения. Здравый смысл подсказывает, что чем короче дуга, тем лучше она характеризуется средней кривизной. А точнее всего характеризовать изогнутость кривой непосредственно в самой точке $M$.

Кривизной $K$ данной кривой в данной точке $M$ называется предел средней кривизны дуги $cup MN$ при неограниченном приближении точки $N$ к точке $M$, то есть $K=mathop{lim }limits_{Delta sto 0} frac{Delta phi }{Delta s} =frac{dphi }{ds} $. Поскольку считается, что кривизна кривой — величина положительная, то $K=left|frac{dphi }{ds} right|$.

Вычисление кривизны плоской кривой

При произвольном параметрическом задании кривой $x=xleft(tright)$ и $y=yleft(tright)$ имеет место выражение $s’_{t} =sqrt{left(x’_{t} right)^{2} +left(y’_{t} right)^{2} } $.

Теперь для выражения $K = frac {d phi}{ds} = frac {d phi / dt}{ds/dt}= frac{phi ‘_{t} }{s’_{t} } $ необходимо вычислить $phi ‘_{t} $.

Так как по определению производной $tgphi =frac{y’_{t} }{x’_{t} } $, то $phi =arctgfrac{y’_{t} }{x’_{t} } $, откуда $phi ‘_{t} =frac{1}{1+left(frac{y’_{t} }{x’_{t} } right)^{2} } cdot frac{left(y’_{t} right)^{{‘} } _{t} cdot x’_{t} -left(x’_{t} right)^{{‘} } _{t} cdot y’_{t} }{left(x’_{t} right)^{2} } $.

После преобразований получаем: $phi ‘_{t} =frac{left(y’_{t} right)^{{‘} } _{t} cdot x’_{t} -left(x’_{t} right)^{{‘} } _{t} cdot y’_{t} }{left(x’_{t} right)^{2} +left(y’_{t} right)^{2} } $.

Теперь формула для кривизны кривой приобретает окончательный вид: $K=frac{left(y’_{t} right)^{{‘} } _{t} cdot x’_{t} -left(x’_{t} right)^{{‘} } _{t} cdot y’_{t} }{sqrt{left(left(x’_{t} right)^{2} +left(y’_{t} right)^{2} right)^{3} } } $.

Если кривая задана в явном виде $y=fleft(xright)$, то выбирая в качестве параметра $t=x$, получаем $K=frac{left(y’_{x} right)^{{‘} } _{x} }{sqrt{left(1+left(y’_{x} right)^{2} right)^{3} } } $.

Если кривая задана в полярных координатах $rho =rho left(phi right)$, то принимая в качестве параметра $t=phi $ и учитывая формулы $x=rho cdot cos phi $ и $y=rho cdot sin phi $, получаем:

[x’_{phi } =left(rho cdot cos phi right)^{{‘} } _{phi } =rho ‘_{phi } cdot cos phi -rho cdot sin phi ;]

[left(x’_{phi } right)^{{‘} } _{phi } =left(rho ‘_{phi } cdot cos phi -rho cdot sin phi right)^{{‘} } _{phi } =left(rho ‘_{phi } right)^{{‘} } _{phi } cdot cos phi -2cdot rho ‘_{phi } cdot sin phi -rho cdot cos phi ;]

[y’_{phi } =left(rho cdot sin phi right)^{{‘} } _{phi } =rho ‘_{phi } cdot sin phi +rho cdot cos phi ;]

[left(y’_{phi } right)^{{‘} } _{phi } =left(rho ‘_{phi } cdot sin phi +rho cdot cos phi right)^{{‘} } _{phi } =left(rho ‘_{phi } right)^{{‘} } _{phi } cdot sin phi +2cdot rho ‘_{phi } cdot cos phi -rho cdot sin phi .]

После подстановки имеем: $K=frac{rho ^{2} +2cdot left(rho ‘_{phi } right)^{2} -rho cdot left(rho ‘_{phi } right)^{{‘} } _{phi } }{sqrt{left(rho ^{2} +left(rho ‘_{phi } right)^{2} right)^{3} } } $.

Задачи вычисления кривизны плоской кривой.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Задача 1

Определить кривизну параболы $y=2cdot x^{2} $ в её произвольной точке $Mleft(x,yright)$, а также в точке $M_{1} left(0,0right)$.

Вычисляем первую и вторую производные функции $y=2cdot x^{2} $:

[y’=left(2cdot x^{2} right)^{{‘} } =4cdot x; y»=left(4cdot xright)^{{‘} } =4. ]

Подставляем полученные выражения в формулу для кривизны:

[K=frac{y»}{sqrt{left(1+left(y’right)^{2} right)^{3} } } =frac{4}{sqrt{left(1+left(4cdot xright)^{2} right)^{3} } } =frac{4}{sqrt{left(1+16cdot x^{2} right)^{3} } } .]

В точке $M_{1} left(0,0right)$ имеем $K=4$.

Задача 2

Определить кривизну параболы $y^{2} =frac{1}{2} cdot x$ в её произвольной точке $Mleft(x,yright)$, а также в точке $M_{1} left(0,0right)$. Сравнить результат решения с результатом, полученным в задаче 1.

Вычисляем первую и вторую производные функции $y^{2} =frac{1}{2} cdot x$:

$left(y^{2} right)^{{‘} } =left(frac{1}{2} cdot xright)^{{‘} } $; $2cdot ycdot y’=frac{1}{2} $, откуда $y’=frac{1}{4cdot y} $;

$left(2cdot ycdot y’right)^{{‘} } =left(frac{1}{2} right)^{{‘} } $; $y’cdot y’+ycdot y»=0$, откуда $y»=-frac{1}{16cdot y^{3} } $.

Подставляем полученные выражения в формулу для кривизны:

[K=frac{y»}{sqrt{left(1+left(y’right)^{2} right)^{3} } } =frac{frac{1}{16cdot y^{3} } }{sqrt{left(1+frac{1}{16cdot y^{2} } right)^{3} } } =frac{4}{sqrt{left(1+16cdot y^{2} right)^{3} } } .]

В точке $M_{1} left(0,0right)$ имеем $K=4$.

Полученный результат по форме и численно совпадает с результатом, полученным в задаче 1. Действительно, кривые обеих задач совпадут, если систему координат второй задачи повернуть на $frac{pi }{2} $ против часовой стрелки. Естественно, что кривизна кривой не меняется при преобразованиях её системы координат.

«Кривизна и её вычисление» 👇

Задача 3

Найти кривизну параметрически заданной линии $left{begin{array}{c} {x=2cdot cos left(3cdot tright)} \ {y=3cdot sin left(2cdot tright)} end{array}right. $ в точке $t=frac{pi }{6} $.

Находим производные:

[x’_{t} =left(2cdot cos left(3cdot tright)right)^{{‘} } _{t} =-6cdot sin left(3cdot tright);]

[x»_{tt} =left(-6cdot sin left(3cdot tright)right)^{{‘} } _{t} =-18cdot cos left(3cdot tright);]

[y’_{t} =left(3cdot sin left(2cdot tright)right)^{{‘} } _{t} =6cdot cos left(2cdot tright);]

[y»_{tt} =left(6cdot cos left(2cdot tright)right)^{{‘} } _{t} =-12cdot sin left(2cdot tright).]

Вычисляем значения производных в заданной точке $t=frac{pi }{6} $:

[x’_{t} left(frac{pi }{6} right)=-6cdot sin left(3cdot frac{pi }{6} right)=-6;]

[x»_{tt} left(frac{pi }{6} right)=-18cdot cos left(3cdot frac{pi }{6} right)=0;]

[y’_{t} left(frac{pi }{6} right)=6cdot cos left(2cdot frac{pi }{6} right)=3;]

[y»_{tt} left(frac{pi }{6} right)=-12cdot sin left(2cdot frac{pi }{6} right)=-6cdot sqrt{3} .]

Полученные значения подставляем в формулу для кривизны:

[K=frac{y»_{tt} cdot x’_{t} -x»_{tt} cdot y’_{t} }{sqrt{left(left(x’_{t} right)^{2} +left(y’_{t} right)^{2} right)^{3} } } =frac{-6cdot sqrt{3} cdot left(-6right)-0cdot 3}{sqrt{left(left(-6right)^{2} +left(3right)^{2} right)^{3} } } =frac{36cdot sqrt{3} }{45cdot sqrt{45} } =frac{4}{5cdot sqrt{15} } .]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

From Wikipedia, the free encyclopedia

In mathematics, the mean curvature of a surface is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space.

The concept was used by Sophie Germain in her work on elasticity theory.^[1]^[2] Jean Baptiste Marie Meusnier used it in 1776, in his studies of minimal surfaces. It is important in the analysis of minimal surfaces, which have mean curvature zero, and in the analysis of physical interfaces between fluids (such as soap films) which, for example, have constant mean curvature in static flows, by the Young-Laplace equation.

Definition[edit]

Let be a point on the surface inside the three dimensional Euclidean space R³. Each plane through containing the normal line to cuts in a (plane) curve. Fixing a choice of unit normal gives a signed curvature to that curve. As the plane is rotated by an angle theta (always containing the normal line) that curvature can vary. The maximal curvature kappa_1 and minimal curvature kappa_2 are known as the principal curvatures of .

The mean curvature at pin S is then the average of the signed curvature over all angles theta :

${displaystyle H={frac {1}{2pi }}int _{0}^{2pi }kappa (theta );dtheta }$

By applying Euler’s theorem, this is equal to the average of the principal curvatures (Spivak 1999, Volume 3, Chapter 2):

$H = {1 over 2} (kappa_1 + kappa_2).$

More generally (Spivak 1999, Volume 4, Chapter 7), for a hypersurface the mean curvature is given as

$H=frac{1}{n}sum_{i=1}^{n} kappa_{i}.$

More abstractly, the mean curvature is the trace of the second fundamental form divided by n (or equivalently, the shape operator).

Additionally, the mean curvature may be written in terms of the covariant derivative nabla as

$Hvec{n} = g^{ij}nabla_inabla_j X,$

using the Gauss-Weingarten relations, where X(x) is a smoothly embedded hypersurface, vec{n} a unit normal vector, and $g_{ij}$ the metric tensor.

A surface is a minimal surface if and only if the mean curvature is zero. Furthermore, a surface which evolves under the mean curvature of the surface , is said to obey a heat-type equation called the mean curvature flow equation.

The sphere is the only embedded surface of constant positive mean curvature without boundary or singularities. However, the result is not true when the condition «embedded surface» is weakened to «immersed surface».^[3]

Surfaces in 3D space[edit]

For a surface defined in 3D space, the mean curvature is related to a unit normal of the surface:

where the normal chosen affects the sign of the curvature. The sign of the curvature depends on the choice of normal: the curvature is positive if the surface curves «towards» the normal. The formula above holds for surfaces in 3D space defined in any manner, as long as the divergence of the unit normal may be calculated. Mean Curvature may also be calculated

${displaystyle 2H={text{Trace}}((mathrm {II} )(mathrm {I} ^{-1}))}$

where I and II denote first and second quadratic form matrices, respectively.

If is a parametrization of the surface and u,v are two linearly independent vectors in parameter space then the mean curvature can be written in terms of the first and second fundamental forms as

${displaystyle {frac {lG-2mF+nE}{2(EG-F^{2})}}}$

where , , , , , .^[4]

For the special case of a surface defined as a function of two coordinates, e.g. , and using the upward pointing normal the (doubled) mean curvature expression is

${displaystyle {begin{aligned}2H&=-nabla cdot left({frac {nabla (z-S)}{|nabla (z-S)|}}right)\&=nabla cdot left({frac {nabla S-nabla z}{sqrt {1+|nabla S|^{2}}}}right)\&={frac {left(1+left({frac {partial S}{partial x}}right)^{2}right){frac {partial ^{2}S}{partial y^{2}}}-2{frac {partial S}{partial x}}{frac {partial S}{partial y}}{frac {partial ^{2}S}{partial xpartial y}}+left(1+left({frac {partial S}{partial y}}right)^{2}right){frac {partial ^{2}S}{partial x^{2}}}}{left(1+left({frac {partial S}{partial x}}right)^{2}+left({frac {partial S}{partial y}}right)^{2}right)^{3/2}}}.end{aligned}}}$

In particular at a point where , the mean curvature is half the trace of the Hessian matrix of .

If the surface is additionally known to be axisymmetric with ,

$2 H = frac{frac{partial^2 S}{partial r^2}}{left(1 + left(frac{partial S}{partial r}right)^2right)^{3/2}} + {frac{partial S}{partial r}}frac{1}{r left(1 + left(frac{partial S}{partial r}right)^2right)^{1/2}},$

where ${displaystyle {frac {partial S}{partial r}}{frac {1}{r}}}$ comes from the derivative of ${textstyle z=S(r)=Sleft({sqrt {x^{2}+y^{2}}}right)}$ .

Implicit form of mean curvature[edit]

The mean curvature of a surface specified by an equation can be calculated by using the gradient $nabla F=left({frac {partial F}{partial x}},{frac {partial F}{partial y}},{frac {partial F}{partial z}}right)$ and the Hessian matrix

${displaystyle textstyle {mbox{Hess}}(F)={begin{pmatrix}{frac {partial ^{2}F}{partial x^{2}}}&{frac {partial ^{2}F}{partial xpartial y}}&{frac {partial ^{2}F}{partial xpartial z}}\{frac {partial ^{2}F}{partial ypartial x}}&{frac {partial ^{2}F}{partial y^{2}}}&{frac {partial ^{2}F}{partial ypartial z}}\{frac {partial ^{2}F}{partial zpartial x}}&{frac {partial ^{2}F}{partial zpartial y}}&{frac {partial ^{2}F}{partial z^{2}}}end{pmatrix}}.}$

The mean curvature is given by:^[5]^[6]

$H={frac {nabla F {mbox{Hess}}(F) nabla F^{{{mathsf {T}}}}-|nabla F|^{2},{text{Trace}}({mbox{Hess}}(F))}{2|nabla F|^{3}}}$

Another form is as the divergence of the unit normal. A unit normal is given by ${frac {nabla F}{|nabla F|}}$ and the mean curvature is

$H = -{frac{1}{2}}nablacdot left(frac{nabla F}{|nabla F|}right).$

Mean curvature in fluid mechanics[edit]

An alternate definition is occasionally used in fluid mechanics to avoid factors of two:

This results in the pressure according to the Young-Laplace equation inside an equilibrium spherical droplet being surface tension times $H_{f}$ ; the two curvatures are equal to the reciprocal of the droplet’s radius

$kappa_1 = kappa_2 = r^{-1} ,$

Minimal surfaces[edit]

A rendering of Costa’s minimal surface.

A minimal surface is a surface which has zero mean curvature at all points. Classic examples include the catenoid, helicoid and Enneper surface. Recent discoveries include Costa’s minimal surface and the Gyroid.

CMC surfaces[edit]

An extension of the idea of a minimal surface are surfaces of constant mean curvature. The surfaces of unit constant mean curvature in hyperbolic space are called Bryant surfaces.^[7]

Notes[edit]

^ Marie-Louise Dubreil-Jacotin on Sophie Germain Archived 2008-02-23 at the Wayback Machine
^ Lodder, J. (2003). «Curvature in the Calculus Curriculum». The American Mathematical Monthly. 110 (7): 593–605. doi:10.2307/3647744. JSTOR 3647744.
^ Wente, Henry C. (1986). «Counterexample to a conjecture of H. Hopf». Pacific Journal of Mathematics. 121 (1): 193–243. doi:10.2140/pjm.1986.121.193. MR 0815044. Zbl 0586.53003.
^ Do Carmo, Manfredo (2016). Differential Geometry of Curves and Surfaces (Second ed.). Dover. p. 158. ISBN 978-0-486-80699-0.
^ Goldman, R. (2005). «Curvature formulas for implicit curves and surfaces». Computer Aided Geometric Design. 22 (7): 632–658. doi:10.1016/j.cagd.2005.06.005.
^ Spivak, M (1975). A Comprehensive Introduction to Differential Geometry. Vol. 3. Publish or Perish, Boston.
^ Rosenberg, Harold (2002), «Bryant surfaces», The global theory of minimal surfaces in flat spaces (Martina Franca, 1999), Lecture Notes in Math., vol. 1775, Berlin: Springer, pp. 67–111, doi:10.1007/978-3-540-45609-4_3, ISBN 978-3-540-43120-6, MR 1901614.

References[edit]

Spivak, Michael (1999), A comprehensive introduction to differential geometry (Volumes 3-4) (3rd ed.), Publish or Perish Press, ISBN 978-0-914098-72-0, (Volume 3), (Volume 4).
P.Grinfeld (2014). Introduction to Tensor Analysis and the Calculus of Moving Surfaces. Springer. ISBN 978-1-4614-7866-9.

Источник

Содержание

Вторая квадратичная форма

Краткие теоретические сведения

begin{gather*}
I_2 = -dvec{r}cdot dvec{n}=d^2vec{r}cdot vec{n}.
end{gather*}
Равенство $-dvec{r}cdot dvec{n}=d^2vec{r}cdot vec{n}$ можно доказать:
begin{equation*}
dvec{r}cdot vec{n}=0,, Rightarrow ,, d(dvec{r}cdot vec{n})=(d^2vec{r}cdot vec{n})+(dvec{r}cdot dvec{n})=0
end{equation*}
Так как
begin{equation*}
I_2 = d^2vec{r}cdot vec{n}
end{equation*}
и
begin{equation*}
vec{n}=frac{vec{r}_utimes vec{r}_v}{|vec{r}_utimes vec{r}_v|}, ,, |vec{r}_utimes vec{r}_v|=sqrt{EG-F^2},
end{equation*}
то коэффициенты для второй квадратичной формы можно записать через смешанное произведение:
begin{align*}
I_2&=L,du^2+2M,du,dv+N,dv^2,\
L&=frac{(vec{r}_{u u},vec{r}_u, vec{r}_v)}{sqrt{EG-F^2}},\
M&=frac{(vec{r}_{u v},vec{r}_u, vec{r}_v)}{sqrt{EG-F^2}},\
N&=frac{(vec{r}_{v v},vec{r}_u, vec{r}_v)}{sqrt{EG-F^2}}.
end{align*}

Решение задач

Задание 1 (Феденко 717)

Найти вторую квадратичную форму сферы:
begin{align*}
x&=R,mbox{cos},u,mbox{cos},v,\
y&=R,mbox{cos},u,mbox{sin},v,\
z&=R,mbox{sin},u.
end{align*}

begin{equation*}
E=R^2, ,, F=0, ,, G= R^2,mbox{cos}^2u.
end{equation*}
begin{equation*}
sqrt{EG-F^2}=R^2mbox{cos},u.
end{equation*}
begin{equation*}
L=R, ,, M=0, ,, N= R,mbox{cos}^2u.
end{equation*}
begin{equation*}
I_2=R,du^2+R,mbox{cos}^2u,dv^2.
end{equation*}

Кривизны

Краткие теоретические сведения

Нормальным сечением поверхности в точке $P$ называют линию пересечения поверхности с плоскостью, проходящей через нормаль поверхности в этой точке.

Кривизну нормального сечения поверхности в направлении $du:dv$ называют нормальной кривизной поверхности в данной точке и в данном направлении. Она вычисляется по формуле:
begin{equation*}
k_n=frac{L,du^2+2M,du,dv+N,dv^2}{E,du^2+2F,du,dv+G,dv^2}=frac{I_2}{I_1}
end{equation*}

Направление $du:dv$ называется главным, если нормальная кривизна поверхности в этом направлении достигает экстремального значения. В каждой точке поверхности имеются два главных направления. Нормальные кривизны соответствующих главных направлений называют главными кривизнами $k_1$ и $k_2$.

Необходимое и достаточное условие, чтобы направление $du:dv$ было главным:
begin{equation*}
left|
begin{array}{ccc}
dv^2 & -du,dv & du^2 \
E & F & G \
L & M & N \
end{array}
right|=0.
end{equation*}

Главные кривизны $k_1$ и $k_2$ можно найти из уравнения:
begin{equation*}
k^2(EG-F^2)-k(LG-2MF+NE)+(LN-M^2)=0.
end{equation*}

Полная (гауссова) кривизна:
begin{equation*}
K=k_1k_2=frac{LN-M^2}{EG-F^2}.
end{equation*}

Средняя кривизна:
begin{equation*}
H=frac{k_1+k_2}{2}=frac{EN+GL-2FM}{2(EG-F^2)}.
end{equation*}

begin{align*}
& K>0 ,, Rightarrow mbox{ точка поверхности называется эллиптической},\
& K<0 ,, Rightarrow mbox{ точка поверхности называется гиперболической},\
& K=0 ,, Rightarrow mbox{ точка поверхности называется /параболической}.
end{align*}

Решение задач

Задание 1

Записать выражение для нормальной кривизны в случае параметризации поверхности: $z=z(x,y)$.

begin{equation*}
k_n=frac{L,du^2+2M,du,dv+N,dv^2}{E,du^2+2F,du,dv+G,dv^2}=frac{I_2}{I_1}.
end{equation*}
begin{align*}
&I_1=(1+z_x^2)dx^2+2z_xz_ydxdy+(1+z_y^2)dy^2,\
&I_2=L,du^2+2M,du,dv+N,dv^2,\
&L=frac{z_{xx}}{sqrt{1+z_x^2+z_y^2}},\
&M=frac{z_{xy}}{sqrt{1+z_x^2+z_y^2}},\
&N=frac{z_{yy}}{sqrt{1+z_x^2+z_y^2}}.
end{align*}

Задание 2

Найти нормальную кривизну гиперболического параболоида $z=x^2-y^2$ в точке $M(x=0, y=0)$ в направлении $frac{dy}{dx}=frac12$.
begin{align*}
&E=1+4x^2=1, ,, F=-4xy=0, ,, G=1+4y^2=1.\
&L=frac{2}{sqrt{1+4x^2+4y^2}}=2,\
&M=0,\
&N=frac{-2}{sqrt{1+4x^2+4y^2}}=-2.\
end{align*}
Учитывая направление $dx=2dy$, запишем нормальную кривизну:
begin{equation*}
k_n=frac{2dx^2-2dy^2}{dx^2+dy^2}=frac65.
end{equation*}

Задание 3 (Феденко 733)

Найти главные направления и главные кривизны прямого геликоида
begin{equation*}
x=u,mbox{cos}v, ,, y=u,mbox{sin},v, ,, z=av.
end{equation*}

begin{align*}
&E=1, ,, F=0, ,, G=u^2+a^2.\
&L=0, ,, M=frac{-a}{sqrt{u^2+a^2}}, ,, N=0.\
end{align*}
begin{align*}
&EG-F^2=u^2+a^2,\
&LG-2MF+NE=0,\
&LN-M^2=-frac{a^2}{u^2+a^2}.
end{align*}

Получили уравнение для нахождения $k_1$ и $k_2$:
begin{equation*}
(u^2+a^2)k^2-frac{a^2}{u^2+a^2}=0 ,, Rightarrow
end{equation*}
главные кривизны:
begin{equation*}
k_{1,2}=pmfrac{a}{u^2+a^2}.
end{equation*}

Условие для главных направлений:
begin{equation*}
left|
begin{array}{ccc}
dv^2 & -du,dv & du^2 \
1 & 0 & u^2+a^2 \
0 & frac{-a}{sqrt{u^2+a^2}} & 0 \
end{array}
right|=0 ,, Rightarrow
end{equation*}
главные направления:
begin{equation*}
frac{du}{dv}=pmsqrt{u^2+a^2}
end{equation*}

Задание 4 (Феденко 756)

Найти полную и среднюю кривизны прямого геликоида
begin{equation*}
x=u,mbox{cos}v, ,, y=u,mbox{sin},v, ,, z=av.
end{equation*}
На каких линиях полная кривизна постоянна?

Полная кривизна:
begin{equation*}
K=k_1k_2=-frac{a^2}{(u^2+a^2)^2}.
end{equation*}
Средняя кривизна:
begin{equation*}
H=frac{k_1+k_2}{2}=0.
end{equation*}
$K$ постоянна на винтовых линиях:
begin{equation*}
K=mbox{const} ,, Rightarrow ,, u=u_0=mbox{const} ,, Rightarrow ,, x=u_0mbox{cos},v,,, y=u_0mbox{sin},v,,,z=a,v.
end{equation*}

Источник

4.Кривая.

4.5.Вычислим кручение кривой :

4. 6. Изображение кривой.

5. Поверхность.

5.1. Найдем уравнение касательной плоскости, используя формулу:

5.2. Найдем уравнение нормали для искомой поверхности.

Основная формула для вычисления кривизны плоской кривой

Вычисление кривизны плоской кривой

Definition[edit]

Surfaces in 3D space[edit]

Implicit form of mean curvature[edit]

Mean curvature in fluid mechanics[edit]

Minimal surfaces[edit]

CMC surfaces[edit]

See also[edit]

Notes[edit]

References[edit]

Содержание

Вторая квадратичная форма

Краткие теоретические сведения

Решение задач

Задание 1 (Феденко 717)

Кривизны

Краткие теоретические сведения

Решение задач

Задание 1

Задание 2

Задание 3 (Феденко 733)

Задание 4 (Феденко 756)