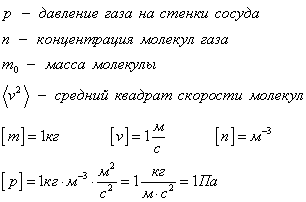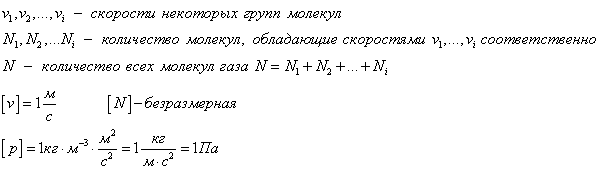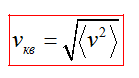Как найти среднюю квадратичную скорость через температуру

II. Молекулярная физика

Тестирование онлайн

Идеальный газ

Это несуществующая физическая модель газа, который состоит из большого числа молекул, размеры которых ничтожно малы по сравнению со средними расстояниями между ними. Молекулы такого газа можно считать материальными точками, это означает, что их вращательное и колебательное движения не принимаются во внимание. Движение молекул происходит без столкновений с другими молекулами, подчиняется законам Ньютона. Соударения молекул со стенками сосуда являются абсолютно упругими.

Параметры состояния газа

Давление, температура и объем — параметры состояния газа. Или их называют макропараметрами. Температура — внешняя характеристика скоростей частиц газа. Давление — внешняя характеристика соударений со стенками, например, сосуда. Объем — место, куда заключены частицы газа. Газ занимает весь предоставленный ему объем. Существуют еще внешние параметры, например тела или поля, действующие на газ из вне.

Микропараметры (маленькие, внутренние характеристики) газа — это параметры, которые мы не можем оценить без специальных экспериментов, например, скорость и направление движения каждой молекулы газа.

Состояние термодинамической системы, когда все ее параметры при неизменных внешних условиях не изменяются со временем, называют равновесным.

Основное уравнение молекулярно-кинетической теории

Уравнение связывает микропараметры и макропараметры (давление, объем и температуру) идеального газа.

Рассмотрим идеальный газ, который находится в кубическом сосуде. Каждая молекула упруго сталкивается со стенкой сосуда, при этом изменятся ее импульс. Столкновение всех молекул со стенкой на макроуровне ощущается как давление газа на сосуд. В формулах будут присутствовать средние значения, потому что какая-то молекула движется быстрее, какая-то помедленнее, для того, чтобы оценить примерную скорость, будем брать средние значения.

Основное уравнение мкт имеет вид

Средний квадрат скорости молекул

Средняя квадратичная скорость v_кв молекул это квадратный корень из среднего квадрата скорости

Средняя кинетическая энергия молекул

Можно вывести формулы

Температура

Это макропараметр, который характеризует способность тел к теплопередаче. Если два тела разной температуры контактируют, то произойдет переход энергии или передача теплоты от более горячего к холодному. Установится тепловое равновесие, все части будут одинаковой температуры.

Температура характеризует интенсивность движения частиц, поэтому связана со средней кинетической энергией частиц. Из опыта известно, что средняя кинетическая энергия молекул не зависит от вида газа и определяется температурой.

Связь между температурами по шкале Цельсия и по шкале Кельвина

Молекулы и атомы газа движутся хаотически во всех направлениях с разными скоростями, распределение которых подчиняется статистике Максвелла-Больцмана. Вероятность столкновения между частицами крайне низка, из-за их пренебрежимо малых размеров и больших расстояний между ними.

Несмотря на то, что индивидуальные скорости газовых частиц сильно отличаются друг от друга, среднее значение этой величины сохраняется постоянным во времени, если отсутствуют внешние воздействия на систему. Формулу средней квадратичной скорости молекул газа можно получить, если рассмотреть связь между кинетической энергией и температурой. Займемся этим вопросом в следующем пункте статьи.

Вывод формулы квадратичной средней скорости молекул газа идеального

Каждый школьник знает из общего курса физики, что кинетическая энергия поступательного движения тела массой m рассчитывается так:

Где v — линейная скорость. С другой стороны, кинетическую энергию частицы также можно определить через абсолютную температуру T, используя переводной множитель kB (постоянная Больцмана). Поскольку наше пространство является трехмерным, то Ek рассчитывается так:

Приравнивая оба равенства и выражая из них v, получим формулу средней скорости квадратичной газа идеального:

В этой формуле m — является массой газовой частицы. Ее значение неудобно использовать в практических расчетах, поскольку оно невелико (≈ 10-27 кг). Чтобы избежать этого неудобство вспомним об универсальной газовой постоянной R и молярной массе M. Постоянная R с kB связана равенством:

Величина M определяется так:

Принимая во внимание оба равенства, получаем следующее выражение для средней квадратичной скорости молекул:

Таким образом, средняя квадратичная скорость газовых частиц оказывается прямо пропорциональной квадратному корню из абсолютной температуры и обратно пропорциональна корню квадратному из молярной массы.

Пример решения задачи

Каждый знает, что воздух, которым мы дышим, на 99% состоит из азота и кислорода. Необходимо определить разницы в средних скоростях молекул N2 и O2 при температуре 15 oC.

Эту задачу будет решать последовательно. Сначала переведем температуру в абсолютные единицы, имеем:

T = 273,15 + 15 = 288,15 К.

Теперь выпишем молярные массы для каждой рассматриваемой молекулы:

MN2 = 0,028 кг/моль;

MO2 = 0,032 кг/моль.

Поскольку значения молярных масс отличаются между собой незначительно, то средние их скорости при одинаковой температуре тоже должны быть близки. Пользуясь формулой для v, получаем следующие значения для молекул азота и кислорода:

v (N2) = √(3*8,314*288,15/0,028) = 506,6 м/с;

v (O2) = √(3*8,314*288,15/0,032) = 473,9 м/с.

Поскольку молекулы азота немного легче, чем молекулы кислорода, то движутся они быстрее. Разница средних скоростей составляет:

v (N2) — v (O2) = 506,6 — 473,9 = 32,7 м/с.

Полученное значение составляет всего 6,5 % от средней скорости молекул азота. Обращаем внимание на большие значения скоростей молекул в газах даже при невысоких температурах.

Средняя скорость молекул

В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.

Средняя скорость движения молекул

Средняя скорость движения молекул называется также скоростью теплового движения молекул.

Формула средней относительной скорости молекул в физике представлена следующим выражением:

» open=» υ o t n = 2 8 k T πm 0 = 2 » open=» υ .

Средняя квадратичная скорость

Средняя квадратичная скорость движения молекул газа это следующая величина:

» open=» υ k υ = 1 N ∑ i = 1 N υ i 2

Формулу средней квадратичной скорости можно переписать так:

» open=» υ k υ 2 = ∫ 0 ∞ υ 2 F υ d υ .

Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:

» open=» υ k υ = 3 k T m 0 = 3 R T μ

Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:

p = 1 3 n m 0 » open=» υ k υ ,

где n = N V – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.

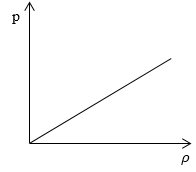
Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1 ).

Запишем выражение для средней скорости движения молекул газа следующим образом:

» open=» υ = 8 k T πm 0

Из графика видно, что p

ρ или p = C ρ , где C – это некоторая константа.

m 0 = ρ n , p = n k T = C ρ → k T = C ρ n

Подставив m 0 = ρ n , p = n k T = C ρ → k T = C ρ n в » open=» υ = 8 k T πm 0 , получаем:

» open=» υ = 8 k T πm 0 = 8 C ρ π n n ρ = 8 C π

Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.

Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа ( p ) , молярная масса газа ( μ ) , а также концентрация молекул газа ( n ) ?

Применим выражение для » open=» υ k υ :

» open=» υ k υ = 3 R T μ

Помимо этого, из уравнения Менделеева-Клайперона и зная, что m μ = N N A :

p V = m μ R T = N N A R T .

Поделим правую и левую части p V = m μ R T = N N A R T на V , и зная N V = n , получаем:

p = n N A R T → R T = p N A n

Подставляем p = n N A R T → R T = p N A n в выражение для среднеквадратичной скорости » open=» υ k υ = 3 R T μ , получаем:

» open=» υ k υ = 3 p N A μ n

Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы » open=» υ k υ = 3 p N A μ n .

Идеальный газ. Средняя квадратичная скорость

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы введём понятие идеального газа, то есть газа, в котором молекулы не взаимодействуют между собой и не обладают объёмом. Также мы узнаем, что такое средняя квадратичная скорость молекул, микро- и макропараметры, и рассмотрим применение модели идеального газа.

Молекулярно-кинетическая теория позволяет, анализируя микроскопическое поведение системы и используя методы статистической механики, получить важные макроскопические характеристики термодинамической системы. Одной из микроскопических характеристик, которая связана с температурой системы, является средняя квадратичная скорость молекул газа. Формулу для нее приведем и рассмотрим в статье.

Газ идеальный

Сразу отметим, что формула квадратичной средней скорости молекул газа будет приведена именно для газа идеального. Под ним в физике полагают такую многочастичную систему, в которой частицы (атомы, молекулы) не взаимодействуют друг с другом (их кинетическая энергия на несколько порядков превышает потенциальную энергию взаимодействия) и не имеют размеров, то есть являются точками с конечной массой (расстояние между частицами на несколько порядков превышает их размеры линейные).

Вам будет интересно:Экранирование магнитного поля: принципы и материалы. Относительная магнитная проницаемость материалов

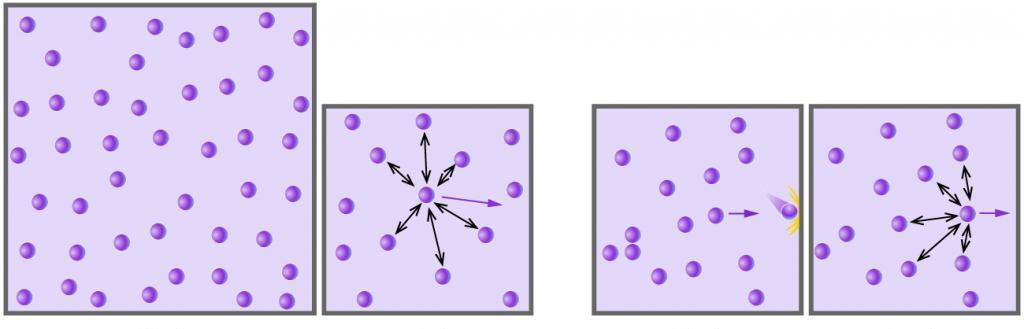
Любой газ, который состоит из химически нейтральных молекул или атомов, и что находится под небольшим давлением и имеет высокую температуру, может считаться идеальным. Например, воздух — это идеальный газ, а водяной пар таковым уже не является (между молекулами воды действуют сильные водородные связи).

Теория молекулярно-кинетическая (МКТ)

Изучая идеальный газ в рамках МКТ, следует обратить внимание на два важных процесса:

Газ создает давление за счет передачи стенкам сосуда, который его содержит, количества движения при столкновении с ними молекул и атомов. Такие столкновения являются абсолютно упругими.

Молекулы и атомы газа движутся хаотически во всех направлениях с разными скоростями, распределение которых подчиняется статистике Максвелла-Больцмана. Вероятность столкновения между частицами крайне низка, из-за их пренебрежимо малых размеров и больших расстояний между ними.

Несмотря на то, что индивидуальные скорости газовых частиц сильно отличаются друг от друга, среднее значение этой величины сохраняется постоянным во времени, если отсутствуют внешние воздействия на систему. Формулу средней квадратичной скорости молекул газа можно получить, если рассмотреть связь между кинетической энергией и температурой. Займемся этим вопросом в следующем пункте статьи.

Вывод формулы квадратичной средней скорости молекул газа идеального

Каждый школьник знает из общего курса физики, что кинетическая энергия поступательного движения тела массой m рассчитывается так:

Ek = m*v2/2

Где v — линейная скорость. С другой стороны, кинетическую энергию частицы также можно определить через абсолютную температуру T, используя переводной множитель kB (постоянная Больцмана). Поскольку наше пространство является трехмерным, то Ek рассчитывается так:

Ek = 3/2*kB*T.

Приравнивая оба равенства и выражая из них v, получим формулу средней скорости квадратичной газа идеального:

m*v2/2 = 3/2*kB*T =>

v = √(3*kB*T/m).

В этой формуле m — является массой газовой частицы. Ее значение неудобно использовать в практических расчетах, поскольку оно невелико (≈ 10-27 кг). Чтобы избежать этого неудобство вспомним об универсальной газовой постоянной R и молярной массе M. Постоянная R с kB связана равенством:

kB = R/NA.

Величина M определяется так:

M = m*NA.

Принимая во внимание оба равенства, получаем следующее выражение для средней квадратичной скорости молекул:

v = √(3*R*T/M).

Таким образом, средняя квадратичная скорость газовых частиц оказывается прямо пропорциональной квадратному корню из абсолютной температуры и обратно пропорциональна корню квадратному из молярной массы.

Пример решения задачи

Каждый знает, что воздух, которым мы дышим, на 99% состоит из азота и кислорода. Необходимо определить разницы в средних скоростях молекул N2 и O2 при температуре 15 oC.

Эту задачу будет решать последовательно. Сначала переведем температуру в абсолютные единицы, имеем:

T = 273,15 + 15 = 288,15 К.

Теперь выпишем молярные массы для каждой рассматриваемой молекулы:

MN2 = 0,028 кг/моль;

MO2 = 0,032 кг/моль.

Поскольку значения молярных масс отличаются между собой незначительно, то средние их скорости при одинаковой температуре тоже должны быть близки. Пользуясь формулой для v, получаем следующие значения для молекул азота и кислорода:

v (N2) = √(3*8,314*288,15/0,028) = 506,6 м/с;

v (O2) = √(3*8,314*288,15/0,032) = 473,9 м/с.

Поскольку молекулы азота немного легче, чем молекулы кислорода, то движутся они быстрее. Разница средних скоростей составляет:

v (N2) — v (O2) = 506,6 — 473,9 = 32,7 м/с.

Полученное значение составляет всего 6,5 % от средней скорости молекул азота. Обращаем внимание на большие значения скоростей молекул в газах даже при невысоких температурах.

Жду ваши вопросы и мнения в комментариях

Основное уравнение мкт

,
где k является постоянной
Больцмана (отношение универсальной
газовой постоянной R к числу
Авогадро N_A), i
— число степеней свободы молекул (i
= 3 в большинстве задач про идеальные
газы, где молекулы предполагаются
сферами малого радиуса, физическим
аналогом которых могут служить инертные
газы), а T — абсолютная температура.

Основное
уравнение МКТ связывает макроскопические
параметры (давление,
объём,
температура)
газовой системы с микроскопическими
(масса молекул, средняя скорость их
движения).

Вывод основного уравнения мкт

Пусть
имеется кубический сосуд с ребром длиной
l и одна частица массой m в нём.

Обозначим
скорость движения v_x, тогда
перед столкновением со стенкой сосуда
импульс
частицы равен mv_x, а после —
− mv_x, поэтому стенке
передается импульс p = 2mv_x.
Время, через которое частица сталкивается
с одной и той же стенкой, равно

.

Отсюда
следует:

Так
как давление

,
следовательно сила F = p * S

Подставив,
получим:

Преобразовав:

Так
как рассматривается кубический сосуд,
то V = Sl

Отсюда:

.

Соответственно,

и

.

Таким
образом, для большого числа частиц верно
следующее:

,
аналогично для осей y и z.

Поскольку

,
то

.
Это следует из того, что все направления
движения молекул
в хаотичной среде равновероятны.

Отсюда

или

.

Пусть

 —
среднее значение кинетической энергии
всех молекул, тогда:

,
откуда

.

Для
одного моля выражение примет вид

Уравнение среднеквадратичной скорости молекулы

Уравнение
среднеквадратичной скорости молекулы
легко выводится из основного уравнения
МКТ для одного моля газа.

,
для 1 моля N = N_a, где N_a —
постоянная
Авогадро

N_am
= M_r, где M_r —
молярная
масса газа

Отсюда
окончательно

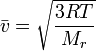
43

Асчёт скорости движения молекул. Введение. Температура, как мера средней кинетической энергии молекул

Попробуем
получить нетривиальные результаты,
используя уравнение Клайперона-Менделеева
и основное уравнение МКТ.

Введем
понятие средней кинетической энергии
молекул:

(1)

Преобразуем
основное уравнение МКТ с учетом формулы
(1):

т.е.
основное уравнение МКТ запишем так

(2)

Воспользуемся
уравнением К.-М. в таком виде:

(3)

Сравним
уравнения (2) и (3) и получим, что

или

(4)

Как
понимать формулу (4)?

Мы
выяснили, что от температуры зависит
величина средней кинетической энергии
молекул. Поэтому говорят, что температура
— мера средней кинетической энергии
молекул. Это утверждение мы доказали
на для идеального газа, но оказывается
оно справедливо и для других агрегатных
сосятояний вещества.

Среднеквадратичная скорость движения молекул.

Интересен
вопрос о скорости движения молекул
газа. В газен царит полный хаос, молекулы
движутся по всем направлениям с самыми
разными скоростями.

Оказывается,
что

1. в газе есть молекулы с очень маленькими
   скоростями и с очень большими, но их
   сравнительно мало.

2. Средняя
   проекция скорости на любое направление
   для всего газа равна 0 (иначе, в газе
   существовали бы потоки).

3. Оказывается
   у молекул есть средняя скорость (по
   модулю), которая зависит от температуры,
   и основная часть молекул имеет модуль
   скорости близкий к ней. Эту скорость
   мы не можем вычислить, но можем легко
   посчитать среднеквадратичную скорость
   движения молекул газа, которая отличается
   от средней скорости коэффициентом
   порядка 1.

Определение.
Среднеквадратичная скорость молекул
равна квадратному корню из среднего
квадрата скорости молекул:

(5)

Вычислим
среднеквадратичную скорость из средней
кинетической энергии молекул, которую
мы легко можем сосчитать:

(6)

С
учетом уравнения (4) получим:

(7)

Посчитаем,
например, среднюю скорость молекул газа
в классной комнате:

T=300K,
m_o=M/N_a, М=0,029 г/моль. С учетом
этого имеем:

44
Распределение энергии по степеням
свободы молекулы

Молекулы
можно рассматривать как системы
материальных точек (атомов) совершающих
как поступательное, так и вращательное
движения. При исследовании движения
тела необходимо знать его положение
относительно выбранной системы координат.
Для этого вводится понятие о степенях
свободы тела. Число независимых
координат, которые полностью определяют
положение тела в пространстве, называется
числом степеней свободы тела.

При
движении точки по прямой линии для
оценки ее положения необходимо знать
одну координату, т.е. точка имеет одну
степень свободы. Если точка движения
по плоскости, ее положение характеризуется
двумя координатами; при этом точка
обладает двумя степенями свободы.
Положение точки в пространстве
определяется 3 координатами. Число
степеней свободы обычно обозначают
буквой i. Молекулы, которые состоят из
обычного атома, считаются материальными
точками и имеют три степени свободы
(аргон, гелий).

Двухатомные
жесткие молекулы, например молекулы
водорода, азота и др., обладают пятью
степенями свободы: они имеют 3 степени
свободы поступательного движения и 2
степени свободы вращения вокруг осей
ОХ и OZ. Вращением вокруг оси OY можно
пренебречь, т.к. момент инерции ее
относительно этой оси пренебрежимо
мал. Поэтому вклад энергии вращательного
движения вокруг оси OY в суммарную энергию
двухатомной молекулы можно не учитывать.

Молекулы,
состоящие из трех и более жестко связанных
атомов, не лежащих на одной прямой, имеют
число степеней свободы i = 6: три степени
свободы поступательного движения и 3
степени свободы вращения вокруг осей
ОХ, OY и OZ.

В
этом случае, если расстояние между
атомами может изменяться (нежесткие
молекулы), появляются дополнительные
степени свободы .

Согласно
молекулярно-кинетической теории газов
движение молекул носит беспорядочный
характер; эта беспорядочность относится
ко всем видам движения молекулы. Ни один
из видов движения не имеет преимущества
перед другим. При статистическом
равновесии движений энергия в среднем
распределяется равномерно между всеми
видами движения. Закон равномерного
распределения энергии по степеням
свободы молекул можно сформулировать
следующим образом: статистически в
среднем на каждую степень свободы
молекул приходится одинаковая энергия.
Поступательное движение молекул
характеризуется средней кинетической
энергией, равной

.
Так как поступательному движению
соответствует 3 степени свободы, то в
среднем на одну степень свободы движения
молекул приходится энергия

В
однородном газе, молекулы которого
имеют любое число степеней свободы i,
каждая молекула в среднем обладает
энергией движения, равной

(10.11)

45

Если
в результате теплообмена телу передается
некоторое количество теплоты, то
внутренняя энергия тела и его температура
изменяются. Количество теплоты Q,
необходимое для нагревания 1 кг
вещества на 1 К называют удельной
теплоемкостью вещества
c.

c = Q / (mΔT).

  Во
многих случаях удобно использовать
молярную
теплоемкость
C:

C = M · c,

где
M – молярная масса вещества. 
Определенная таким образом теплоемкость
не
является однозначной
характеристикой вещества. Согласно
первому закону термодинамики изменение
внутренней энергии тела зависит не
только от полученного количества
теплоты, но и от работы, совершенной
телом.

В
зависимости от условий, при которых
осуществлялся процесс теплопередачи,
тело могло совершать различную работу.
Поэтому одинаковое количество теплоты,
переданное телу, могло вызвать различные
изменения его внутренней энергии и,
следовательно, температуры. Такая
неоднозначность определения теплоемкости
характерна только для газообразного
вещества.

При
нагревании жидких и твердых тел их объем
практически не изменяется, и работа
расширения оказывается равной нулю.
Поэтому все количество теплоты, полученное
телом, идет на изменение его внутренней
энергии. В отличие от жидкостей и твердых
тел, газ в процессе теплопередачи может
сильно изменять свой объем и совершать
работу. Поэтому теплоемкость газообразного
вещества зависит от характера
термодинамического процесса. Обычно
рассматриваются два значения теплоемкости
газов: CV – молярная
теплоемкость в изохорном процессе
(V = const)
и Cp – молярная
теплоемкость в изобарном процессе
(p = const). В процессе при постоянном
объеме газ работы не совершает: A = 0.
Из первого закона термодинамики для
1 моля газа следует

QV = CVΔT = ΔU.

  Изменение
ΔU внутренней энергии газа прямо
пропорционально изменению ΔT его
температуры. Для процесса при постоянном
давлении первый закон термодинамики
дает:

Qp = ΔU + p(V2 – V1) = CVΔT + pΔV,

где
ΔV – изменение объема 1 моля идеального
газа при изменении его температуры на
ΔT. Отсюда следует:

  Отношение
ΔV / ΔT может быть найдено из уравнения
состояния идеального газа, записанного
для 1 моля:

pV = RT,

где
R – универсальная газовая постоянная.
При p = const

  Таким
образом, соотношение, выражающее связь
между молярными теплоемкостями Cp и CV,
имеет вид (формула
Майера):

Cp = CV + R.

  Молярная
теплоемкость Cp газа в процессе с
постоянным давлением всегда больше
молярной теплоемкости CV в процессе с
постоянным объемом (рис. 3.10.1).

1

Рисунок 3.10.1. Два возможных процесса нагревания газа на ΔT = T2 – T1. При p = const газ совершает работу A = p1(V2 – V1). Поэтому Cp > CV.

Отношение
теплоемкостей в процессах с постоянным
давлением и постоянным объемом играет
важную роль в термодинамике. Оно
обозначается греческой буквой γ.

  В
частности, это отношение входит в формулу
для адиабатического процесса (см. §3.9).
Между двумя изотермами с температурами
T1 и T2 на диаграмме (p, V) возможны
различные пути перехода. Поскольку для
всех таких переходов изменение температуры
ΔT = T2 – T1 одинаково,
следовательно, одинаково изменение ΔU
внутренней энергии. Однако, совершенные
при этом работы A и полученные в результате
теплообмена количества теплоты Q окажутся
различными для разных путей перехода.

Отсюда
следует, что у газа имеется бесчисленное
количество теплоемкостей. Теплоемкости
Cp и CV – это лишь частные (и очень важные
для теории газов) значения теплоемкостей.
Термодинамические процессы, в которых
теплоемкость газа остается неизменной,
называются политропическими.

Все
изопроцессы являются политропическими.
В случае изотермического процесса
ΔT = 0, поэтому CT = ∞. В
адиабатическом процессе ΔQ = 0,
следовательно, Cад = 0. Следует
отметить, что «теплоемкость», как и
«количество теплоты» – крайне неудачные
термины.

Они
достались современной науке в наследство
от теории теплорода,
господствовавшей в XVIII веке. Эта
теория рассматривала теплоту как особое
невесомое вещество, содержащееся в
телах. Оно не может быть ни создано, ни
уничтожено. Нагревание тел объяснялось
увеличением, а охлаждение – уменьшением
содержащегося внутри них теплорода.
Теория теплорода несостоятельна.

Она
не может объяснить, почему одно и то же
изменение внутренней энергии тела можно
получить, передавая ему разное количество
теплоты в зависимости от работы, которую
совершает тело. Поэтому лишено физического
смысла утверждение, что «в данном теле
содержится такой-то запас теплоты». В
молекулярно-кинетической теории
устанавливается следующее соотношение
между средней кинетической энергией

поступательного
движения
молекул и абсолютной температурой T:

  Внутренняя
энергия 1 моля идеального газа равна
произведению

на
число Авогадро NА:

  При
изменении температуры на ΔT внутренняя
энергия изменяется на величину

  Коэффициент
пропорциональности между ΔU и ΔT равен
теплоемкости CV при постоянном давлении:

  Это
соотношение хорошо подтверждается в
экспериментах с газами, состоящими из
одноатомных молекул (гелий, неон, аргон).
Однако, для двухатомных (водород, азот)
и многоатомных (углекислый газ) газов
это соотношение не согласуется с
экспериментальными данными. Причина
такого расхождения состоит в том, что
для двух- и многоатомных молекул средняя
кинетическая энергия должна включать
не только энергию поступательного
движения, но и энергию вращательного
движения молекул.

На
рис. 3.10.2 изображена модель двухатомной
молекулы. Молекула может совершать пять
независимых движений: три поступательных
движения вдоль осей X, Y, Z и два вращения
относительно осей X и Y. Опыт показывает,
что вращение относительно оси Z, на
которой лежат центры обоих атомов, может
быть возбуждено только при очень высоких
температурах. При обычных температурах
вращение около оси Z не происходит, так
же как не вращается одноатомная молекула.

Каждое
независимое движение называется степенью
свободы. Таким образом, одноатомная
молекула имеет 3 поступательные степени
свободы, «жесткая» двухатомная молекула
имеет 5 степеней (3 поступательные и 2
вращательные), а многоатомная молекула
– 6 степеней свободы (3 поступательные
и 3 вращательные). В классической
статистической физике доказывается
так называемая теорема
о равномерном распределении энергии
по степеням свободы:
Если
система молекул находится в тепловом
равновесии при температуре T, то средняя
кинетическая энергия равномерно
распределена между всеми степенями
свободы и для каждой степени свободы
молекулы она равна

Из
этой теоремы следует, что молярные
теплоемкости газа Cp и CV и их отношение
γ могут быть записаны в виде

где
i – число степеней свободы газа.  Для
газа, состоящего из одноатомных
молекул
(i = 3)

  Для
газа, состоящего из двухатомных
молекул
(i = 5)

  Для
газа, состоящего из многоатомных
молекул
(i = 6)

  Экспериментально
измеренные теплоемкости многих газов
при обычных условиях достаточно хорошо
согласуются с приведенными выражениями.
Однако, в целом классическая теория
теплоемкости газов не может считаться
вполне удовлетворительной. Существует
много примеров значительных расхождений
между теорией и экспериментом. Это
объясняется тем, что классическая теория
не в состоянии полностью учесть энергию,
связанную с внутренними движениями в
молекуле. Теорему о равномерном
распределении энергии по степеням
свободы можно применить и к тепловому
движению частиц в твердом теле.

Атомы,
входящие в состав кристаллической
решетки, совершают колебания около
положений равновесия. Энергия этих
колебаний и представляет собой внутреннюю
энергию твердого тела. Каждый атом в
кристаллической решетке может колебаться
в трех взаимно перпендикулярных
направлениях. Следовательно, каждый
атом имеет 3 колебательные степени.

При
гармонических колебаниях средняя
кинетическая энергия равна средней
потенциальной энергии. Поэтому в
соответствии с теоремой о равномерном
распределении на каждую колебательную
степень свободы приходится средняя
энергия kT, а на один атом – 3kT. Внутренняя
энергия 1 моля
твердого вещества равна:

U = 3NAkT = 3RT.

  Поэтому
молярная теплоемкость вещества в твердом
состоянии равна:

C = 3R = 25,12 Дж/моль·К.

  Это
соотношение называется законом
Дюлонга–Пти.
Для твердых тел практически не существует
различия между Cp и CV из-за ничтожно малой
работы при расширении или сжатии. Опыт
показывает, что у многих твердых тел
(химических элементов) молярная
теплоемкость при обычных температурах
действительно близка к 3R. Однако, при
низких температурах наблюдаются
значительные расхождения между теорией
и экспериментом. Это показывает, что
гипотеза о равномерном распределении
энергии по степеням свободы является
приближением. Наблюдаемая на опыте
зависимость теплоемкости от температуры
может быть объяснена только на основе
квантовых представлений.  

46

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Перейти к контенту