Определение средней квадратичной скорости молекул газа
Содержание:
- Средняя квадратичная скорость молекул газа — что это за параметр
- От каких величин зависит в идеальном газе
-
Формула средней квадратичной скорости молекул
- Как посчитать в зависимости от природы газа и температуры?
Средняя квадратичная скорость молекул газа — что это за параметр
Молекулы любого газа пребывают в постоянном движении. Его можно охарактеризовать с точки зрения средней их скорости или средней квадратичной скорости. Первое понятие имеет специальный термин — скорость теплового движения. Второе — средняя квадратичная скорость — величина, для которой существует специальная формула.
Для того, чтобы полностью разобраться в понятии средней квадратичной скорости молекул газа, вводится условный участник процесса — идеальный газ.
Определение
Идеальный газ — это математическая модель, потенциальную энергию которой принимают за ноль, а кинетическую характеризуют в полном объеме. Идеальный газ подходит в качестве модели окружающих нас газов, например, обычного воздуха.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Средняя квадратичная скорость — физическая величина, отличная от средней арифметической скорости молекул, определяемая по формуле: корень квадратный из средней арифметической квадратов скоростей различных молекул.
Кинетическая энергия определяется скоростью движения молекул, поэтому зависит от температуры. Скорости молекул одного газа не одинаковы. Часть молекул движутся очень быстро, часть — с незначительной скоростью. Однако для большинства существует некое среднее значение. Если изобразить это на графике в виде параболы, такие молекулы со средней скоростью будут составлять ее верхнюю часть.
В единице объема газа содержится огромное число молекул. Поэтому, например, его давление на стенки сосуда — величина постоянная. В ином случае, если бы в единицу времени о стенку ударялось различное количество молекул, давление бы «скакало».
Из изложенного можно сделать вывод: скорость — свойство отдельной молекулы газа, а давление — характеристика их совокупности.
От каких величин зависит в идеальном газе
Для идеального газа средняя квадратичная скорость прямо пропорциональна его температуре и обратно пропорциональна молярной массе газа.
В математическом выражении данная зависимость выражается через корень квадратный:
(V=surd(3RT/mu)
)
где R — универсальная постоянная величина, Т — температура газа, μ — молярная масса.
Из формулы видно, что искомая величина (средняя квадратичная скорость) зависит от природных свойств газа и его температуры.
Формула средней квадратичной скорости молекул
Математическое выражение формулы выглядит следующим образом:
(V_{ср;кв}=surd(V_{12}+V_{22}+V_{n2})/N)
В формуле присутствуют следующие условные обозначения: V1, V2, Vn — скорости молекул, а N — их количество.
Формула может иметь и другой вид:
(V_{ср;кв}=surd1/Nastsum V_2)
или
(V_{ср;кв}=int V_2F(V)dV)
Как посчитать в зависимости от природы газа и температуры?
Проведенное интегрирование формулы, цель которого определить зависимость искомой единицы от природных свойств иттемпературы газа, приводит расчеты к формуле:
(V_{ср;кв}=surd(3kT/mo))
или
(V_{ср;кв}=surd(3RT/mu))
При поступательном движении молекул газа Vср кв — составляющая уравнения для молекулярно-кинетической теории.
Если n=N/V, где N — число частиц, а V — объем, то концентрация частиц n получает следующее формульное выражение:
(p=1/3ast nmo(V_{ср;кв})^2)
Насколько полезной была для вас статья?
Рейтинг: 2.33 (Голосов: 3)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Молекулярно-кинетическая теория позволяет, анализируя микроскопическое поведение системы и используя методы статистической механики, получить важные макроскопические характеристики термодинамической системы. Одной из микроскопических характеристик, которая связана с температурой системы, является средняя квадратичная скорость молекул газа. Формулу для нее приведем и рассмотрим в статье.
Газ идеальный
Сразу отметим, что формула квадратичной средней скорости молекул газа будет приведена именно для газа идеального. Под ним в физике полагают такую многочастичную систему, в которой частицы (атомы, молекулы) не взаимодействуют друг с другом (их кинетическая энергия на несколько порядков превышает потенциальную энергию взаимодействия) и не имеют размеров, то есть являются точками с конечной массой (расстояние между частицами на несколько порядков превышает их размеры линейные).
Любой газ, который состоит из химически нейтральных молекул или атомов, и что находится под небольшим давлением и имеет высокую температуру, может считаться идеальным. Например, воздух — это идеальный газ, а водяной пар таковым уже не является (между молекулами воды действуют сильные водородные связи).
Теория молекулярно-кинетическая (МКТ)

Изучая идеальный газ в рамках МКТ, следует обратить внимание на два важных процесса:
Несмотря на то, что индивидуальные скорости газовых частиц сильно отличаются друг от друга, среднее значение этой величины сохраняется постоянным во времени, если отсутствуют внешние воздействия на систему. Формулу средней квадратичной скорости молекул газа можно получить, если рассмотреть связь между кинетической энергией и температурой. Займемся этим вопросом в следующем пункте статьи.
Вывод формулы квадратичной средней скорости молекул газа идеального
Каждый школьник знает из общего курса физики, что кинетическая энергия поступательного движения тела массой m рассчитывается так:
Ek = m*v2/2
Где v — линейная скорость. С другой стороны, кинетическую энергию частицы также можно определить через абсолютную температуру T, используя переводной множитель kB (постоянная Больцмана). Поскольку наше пространство является трехмерным, то Ek рассчитывается так:
Ek = 3/2*kB*T.
Приравнивая оба равенства и выражая из них v, получим формулу средней скорости квадратичной газа идеального:
m*v2/2 = 3/2*kB*T =>
v = √(3*kB*T/m).
В этой формуле m — является массой газовой частицы. Ее значение неудобно использовать в практических расчетах, поскольку оно невелико (≈ 10-27 кг). Чтобы избежать этого неудобство вспомним об универсальной газовой постоянной R и молярной массе M. Постоянная R с kB связана равенством:
kB = R/NA.
Величина M определяется так:
M = m*NA.
Принимая во внимание оба равенства, получаем следующее выражение для средней квадратичной скорости молекул:
v = √(3*R*T/M).
Таким образом, средняя квадратичная скорость газовых частиц оказывается прямо пропорциональной квадратному корню из абсолютной температуры и обратно пропорциональна корню квадратному из молярной массы.
Пример решения задачи
Каждый знает, что воздух, которым мы дышим, на 99% состоит из азота и кислорода. Необходимо определить разницы в средних скоростях молекул N2 и O2 при температуре 15 oC.

Эту задачу будет решать последовательно. Сначала переведем температуру в абсолютные единицы, имеем:
T = 273,15 + 15 = 288,15 К.
Теперь выпишем молярные массы для каждой рассматриваемой молекулы:
MN2 = 0,028 кг/моль;
MO2 = 0,032 кг/моль.
Поскольку значения молярных масс отличаются между собой незначительно, то средние их скорости при одинаковой температуре тоже должны быть близки. Пользуясь формулой для v, получаем следующие значения для молекул азота и кислорода:
v (N2) = √(3*8,314*288,15/0,028) = 506,6 м/с;
v (O2) = √(3*8,314*288,15/0,032) = 473,9 м/с.
Поскольку молекулы азота немного легче, чем молекулы кислорода, то движутся они быстрее. Разница средних скоростей составляет:
v (N2) — v (O2) = 506,6 — 473,9 = 32,7 м/с.
Полученное значение составляет всего 6,5 % от средней скорости молекул азота. Обращаем внимание на большие значения скоростей молекул в газах даже при невысоких температурах.
Автор:
16-01-2019 19:51
Жду ваши вопросы и мнения в комментариях
Введение
Мы начинаем изучение молекулярно-кинетической теории (свойства тел с точки зрения их атомно-молекулярного строения). Тела находятся в жидком, твёрдом и газообразном состоянии. На этом уроке мы рассмотрим наиболее простую модель, то есть описание свойств газов, так как в газах потенциальная энергия взаимодействия между молекулами настолько мала, что ею часто пренебрегают, превращая реальный газ в идеальный.
Идеальный газ
Идеальный газ – математическая модель газа, в которой предполагается, что:
- потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией;
- суммарный объём молекул газа пренебрежимо мал. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.
Модель идеального газа вполне эффективно описывает окружающие нас газы (в частности, воздух).
Скорости движения молекул. Средняя квадратичная скорость
Кинетической энергией (в отличие от потенциальной) молекул газа не пренебрегают. Кинетическая энергия – это энергия движения, то есть она зависит от скорости, поэтому рассмотрим скорости теплового движения молекул.
Несмотря на то что молекулы одного и того же газа являются одинаковыми, скорости у них разные. Этот факт экспериментально доказал французский физик Жан-Батист Перрен.
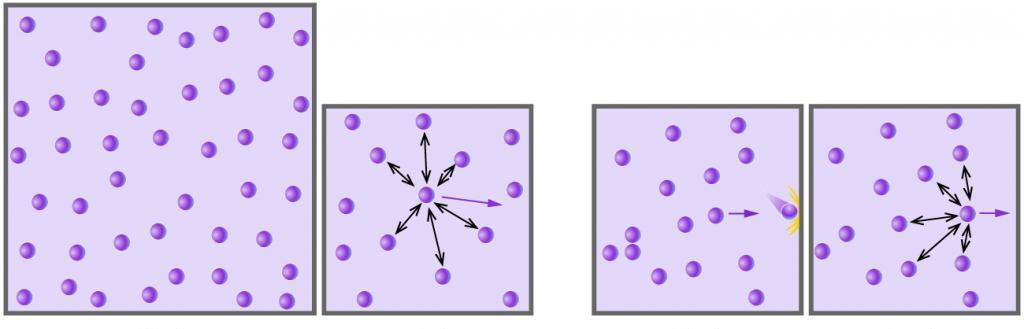
На рисунке 1 изображено распределение молекул по скоростям, так называемое распределение Максвелла. На нём видно, что существуют очень быстрые молекулы и очень медленные, но большинство молекул двигаются со средним значением скорости (выделено жёлтым).
Рис. 1. Распределение молекул воздуха по скоростям
Принято считать, что все молекулы идеального газа двигаются с одинаковой скоростью, которую назвали средней квадратичной.
Средняя квадратичная скорость – это скорость, равная корню квадратному из средней арифметической величины квадратов скоростей отдельных молекул; она несколько отличается от средней арифметической скорости молекул.
,
где ,
,
– скорости отдельных молекул, N – количество молекул.
К чему приводит наличие скорости у молекул газа, можно увидеть из эксперимента, для которого понадобится песок (моделирует молекулы газа) и пластинка из бумаги (моделирует сосуд, в котором находится газ). При высыпании песка пластинка под давлением песчинок отклоняется (см. рис. 2). Точно так же и молекулы газа оказывают давление на стенки сосуда, в котором они находятся.
Рис. 2. Отклонение пластинки под действием давления песка
Рассмотрим график зависимости давления газа на стенки сосуда от времени (см. рис. 3). На нём видно, что если молекул было бы мало, то наблюдались бы отклонения, так как в какой-то момент в стенку могло бы ударить разное количество молекул, и это ощутимо поменяло бы давление. Но так как в реальности молекул огромное количество, то давление всё время остаётся постоянным.
Рис. 3. График зависимости давления газа на стенки сосуда от времени
Можно сделать вывод, что скорость – это величина, которая характеризует отдельную молекулу, а давление имеет смысл только для большого числа молекул (понятие «давление одной молекулы» совершенно бессмысленно).
Микропараметры и макропараметры
Параметры, которые характеризуют каждую молекулу по отдельности, принято называть микропараметрами. К ним относятся:
а) – скорость отдельной молекулы;
б) – масса молекулы;
в) – размеры молекулы;
г) – импульс.
Параметры, которые характеризуют газ в целом, без детализации на отдельные молекулы, называют макропараметрами. К ним относятся:
а) p – давление;
б) n – концентрация (число частиц в единице объёма);
в) V – объём газа;
г) – средняя квадратичная скорость;
д) T – температура.
Именно макропараметры измеряются измерительными приборами.
Применение модели идеального газа
Модель идеального газа оказалась настолько универсальной, что физики применяют её не только для газов, подобных воздуху, но и для электронного газа в металле, для излучения электромагнитных волн и даже для звуковых колебаний в кристаллах. Теория идеального газа позволяет оценить давление и температуру внутри звёзд, результаты таких оценок близки к полученным строгими расчётами.
Список литературы
- Мякишев Г. Я., Синяков А. З. Молекулярная физика. Термодинамика. – М.: Дрофа, 2010.
- Генденштейн Л. Э., Дик Ю. И. Физика 10 класс. – М.: Илекса, 2005.
- Касьянов В. А. Физика 10 класс. – М.: Дрофа, 2010.
Домашнее задание
- Идеальным газом называется…
- Объясните своими словами содержания понятия «идеальный газ».
- Какие макропараметры, характеризующие газ, Вы знаете?
- Что такое средняя квадратичная скорость?
- Каким ещё способом можно продемонстрировать наличие скорости у молекул газа?
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «clck.ru» (Источник)
- Интернет-портал «clck.ru» (Источник)
- Интернет-портал «clck.ru» (Источник)
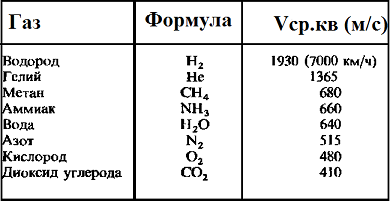
Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа
Таблица значений средней квадратичной скорости молекул некоторых газов
Для того чтоб понять, откуда же у нас получается эта формула, мы выведем среднюю квадратичную скорость молекул. Вывод формулы начинается с основного уравнения молекулярно кинетический теории (МКТ):
Где у нас количество вещества, для более легкого доказательства, возьмем на рассмотрение 1 моль вещества, тогда у нас получается:
Если посмотреть, то PV это две третьих средней кинетической энергии всех молекул (а у нас взят 1 моль молекул):
Тогда, если приравнять правые части, у нас получается, что для 1 моля газа средняя кинетическая энергия будет равняться:
Но средняя кинетическая энергия, так же находится, как :
А вот теперь, если мы приравняем правые части и выразим из них скорость и возьмем квадрат,Число Авогадро на массу молекулы , получается Молярная масса то у нас и получится формула для средней квадратичной скорости молекулы газа:
А если расписать универсальную газовую постоянную, как , и за одно молярную массу
, то у нас получится?
В Формуле мы использовали :
— Средняя квадратичная скорость молекул
— Постоянная Больцмана
— Температура
— Масса одной молекулы
— Универсальная газовая постоянная
— Молярная масса
— Количество вещества
— Средняя кинетическая энергия молекул
— Число Авогадро
Для характеристики движения молекул в физике используют две скорости: среднюю и среднюю квадратичную скорость молекул.
Важно. Следует обязательно понимать, что в реальных условиях мы не можем точно знать ни конкретное число молекул в системе, ни тем более скорость каждой из них в конкретный момент времени. Это обусловлено неимоверно гигантским числом частиц в реальных и даже сколько-нибудь приближенных к ним системах. Например, в 1 см3 при давлении 200 мм. рт. ст. содержится 4,18*1018 молекул водорода. Говоря более понятными категориями, это более чем 4 миллиарда миллиардов. Заметим, что указанное давление меньше атмосферного почти в 4 раза. Последнее в среднем равняется 760 мм. рт. ст. Разрежённый водород по своим свойствам наиболее близок к идеальному газу. В данном случае физика вынуждена иметь дело с распределениями скоростей и энергий частиц.
Что такое средняя скорость движения молекул
Среднюю скорость движения молекул часто именуют скоростью их теплового движения.
Определение 1
Вид формулы средней относительной скорости молекул в физике можно представить выражением:
[text { Vотн }=sqrt{2} sqrt{frac{8 R T}{pi m_{0}}}]
Выражение под корнем – средняя скорость молекул идеального газа.
Как определить среднюю квадратичную скорость движения молекул
Определение 2
Средней квадратичной скоростью молекул идеального газа называют величину равную квадратному корню из среднего арифметического величины квадратов скоростей каждой из молекул.
Средняя скорость молекул равна:
[leftlanglemathrm{V}_{mathrm{KB}}rightrangle=sqrt{frac{1}{N} sum_{i=1}^{N} v_{i}^{2}}]
Если обе её части возвести в квадрат и проинтегрировать, то получим выражение:
[langlemathrm{VKB}rangle^{2}=int_{0}^{infty} v^{2} F(v) d v]
Ещё одно выражение для среднеквадратичной скорости:
[leftlangle V_{K B}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]
Именно она присутствует в уравнении, именуемом основным уравнением молекулярно-кинетической теории
P = (1/3)nm*<Vкв>
Где n – концентрация молекул, которая вычисляется делением их общего числа на объём.
Пример. 1.
Рассмотрим простейший случай, чтобы использование интегрирования не затруднило понимание сути явления и помогло лучше понять материал. Вычислим как меняется средняя скорость движения молекул в идеальном газе при линейном увеличении его давления. График следующий:
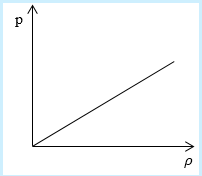
Напомним, что средняя скорость частиц:
[mathrm{Vcp}=sqrt{frac{8 R T}{pi m_{0}}}]
Если присмотреться к представленному графику, то можно заметить, что P приблизительно равно ρ. Эти две величины можно связать соотношением
P=C*ρ
Где С – некоторая постоянная величина, константа.
Далее считаем m0= ρ/n, p = n*k*T = C* ρ. Отсюда следует, что k*T = (C*ρ)/n.
Нужно лишь подставить эти значения в формулу для средней скорости:
[V c p=sqrt{8 mathrm{kT} / pi mathrm{m}}=sqrt{(8 mathrm{C} rho / pi mathrm{n})(mathrm{n} / rho)}=sqrt{8 mathrm{C} / pi}]
В полученном выражении нет ни одной переменной величины, т. е. при увеличении давления, вопреки ожиданиям, скорость оказалась неизменной.
Ответ: В процессе, который был дан нам на графике, при увеличении давления средняя скорость молекул никак не меняется.
Нет времени решать самому?
Наши эксперты помогут!
Пример. 2.
Определим среднюю квадратичную скорость молекул газа при условии, что нам известны его давление (P), молярная масса (M) и концентрация частиц (n).
Воспользуемся формулой:
[leftlanglemathrm{V}_{kappa в}rightrangle=sqrt{frac{3 k T}{m_{0}}}=sqrt{frac{3 R T}{mu}}]
Также нам потребуется уравнение Менделеева-Клайперона
Здесь мы воспользовались тем, что:
m/μ = N/Na
PV = (m/μ)*RT = (N/Na)*RT
Если обе части этого уравнения поделить на V и принять во внимание, что
(N/V) = n, то можно получить
P = (n/Na)*RT. Отсюда находим, что RT = (p*N)/n
Если мы это подставим в выражение для среднеквадратичной скорости [leftlangle V_{K B}rightrangle=sqrt{3 mathrm{kT} / mathrm{m}_{0}}=sqrt{3 mathrm{RT} / mu}], получим, что средняя квадратичная скорость движения молекул газа: [leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]
Ответ: Формула средней квадратичной скорости молекул исходя из данный нам условий следующая:
[leftlangle V_{K B}rightrangle=sqrt{left(3 rho N_{a}right) /(mu mathrm{n})}]