Как найти среднюю квадратичную скорость плотность - Исправление недочетов и поиск решений вместе с Examum.ru

Условие задачи:

Найти среднюю квадратичную скорость молекул газа, имеющего плотность 1,8 кг/м³ при давлении 152 кПа.

Задача №4.1.44 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(rho=1,8) кг/м³, (p=152) кПа, (upsilon_{кв}-?)

Решение задачи:

Запишем для начала основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

[p = frac{1}{3}n{m_0}upsilon _{кв}^2]

Распишем в этой формуле концентрацию молекул (n) как отношение числа молекул (N) к объему газа (V):

[p = frac{1}{3}frac{{{m_0}N}}{V}upsilon _{кв}^2]

Произведение массы одной молекулы (m_0) на число молекул (N) равна массе газа (m), поэтому:

[p = frac{1}{3}frac{m}{V}upsilon _{кв}^2]

Отношение массы газа (m) к его объему (V) есть плотность газа (rho), значит:

[p = frac{1}{3}rho upsilon _{кв}^2]

Выразим отсюда искомую среднюю квадратичную скорость молекул (upsilon_{кв}):

[{upsilon _{кв}} = sqrt {frac{{3p}}{rho }} ]

Численное значение этой скорости равно:

[{upsilon _{кв}} = sqrt {frac{{3 cdot 152 cdot {{10}^3}}}{{1,8}}} = 503,3;м/с = 1812;км/ч]

Ответ: 1812 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

4.1.43 Найдите отношение средних скоростей молекул O2 и H2 при одинаковой температуре
4.1.45 В баллоне находится кислород при давлении 4 МПа и температуре 42 C. Определить
4.1.46 В баллоне объемом 0,01 м3 находится газ, кинетическая энергия поступательного движения

Источник

Основное уравнение молекулярно-кинетической теории:

где

– давление
газа,

– концентрация
молекул,
–
масса одной молекулы,

–
средняя квадратичная скорость одной
молекулы,
—
плотность газа,
–абсолютная
температура,

–
постоянная
Больцмана.

Средняя
кинетическая энергия поступательного
движения одной молекулы:

Изопроцессы
(газовые законы) –
для
:

1)
— изотермический:;

2)
—
изобарный:;

3)
—
изохорный:

Уравнение
Менделеева-Клапейрона:

где

–
объём газа,

– масса газа,

– молярная масса;
)
– универсальная
газовая постоянная.

Количество
вещества:

где

– общее число молекул;

– постоянная Авогадро.

Скорости
молекул:

—
средняя квадратичная,

—
средняя арифметическая,

—
наиболее вероятная.

Нормальные
условия:

—
объём
одного моля газа.

Примеры решения задач

Задача
1.
Смесь кислорода и азота при температуре
t=27⁰С
находится под давлением Р=2,3·10²Па.
Масса кислорода составляет 75% от общей
массы смеси. Определите концентрацию
молекул каждого из газов.

Дано:

Т=300
К;

Р=2,3·10²Па;

m₁=0,75
m;

М₁=0,032
кг/моль;

М₂=0,028
кг/моль.

Решение:

Смесь
газов принимаем за идеальный газ,
описываемый уравнением Менделеева–
Клапейрона:

,

(1)

где

—

(2) концентрация смеси газов;

–
концентрациямолекул
кислорода,
–
концентрация молекул

азота;–
постоянная Больцмана.

n₁— ?n₂— ?

Из
выражений (1) и (2) имеем:

.

(3)

Выразим
концентрацию n₁
через концентрацию n₂.

По
условию задачи масса кислорода:

m₁
= 0,75 m
,
(4)

где
m
– масса смеси.

Массу
кислорода можно выразить также через
концентрацию n₁
и объем газа:

m₁
=
,
(5)

где
М₁
–
молярная масса кислорода;
N_A
– число Авогадро;
V
– объем газа.

Приравняв
правые части выражений (4) и (5), получим:

.
(6)

Масса
азота m₂=0,25m,
или иначе
.
Приравняв значенияm₂
из последних двух формул, найдем:

.
(7)

Из
выражений (6) и (7) имеем:

.
(8)

Подставив
в формулу (3) значение n₂из
последнего выражения, получим n₁
=.
После подстановки значений и вычисленияn₁=
0,40·10²³
1/м³,
n₂=
0,15·10²³(1/м³).

Ответ:
n₁=
0,40·10²³
1/м³,
n₂=
0,15·10²³(1/м³).

Задача
2.
В
закрытом сосуде объемом V=1
м³находится
m₁=1кг
азота и m₂=1,5
кг воды. Определите давление в сосуде
при температуре t=600⁰С,
зная, что при этой температуре вся вода
превратится в пар.

Дано:

V=1
м³;

m₁=1
кг;

m₂=1,5
кг;

Т=873К;

M₁=0,028
кг/моль;

M₂=0,018
кг/моль.

Решение:

По
закону Дальтона давление в сосуде
после превращения воды в пар:

Р=Р₁+Р₂
, (1)

где
Р₁
— давление азота, Р₂
– давление водяного пара. Состояние
азота в сосуде определяется уравнением
Менделеева — Клапейрона:

(2)

где
M₁
– молярная масса азота, R
–
универсальная газовая постоянная.
Аналогично для водяного пара:

,
(3)

где
M₂
– молярная масса водяного пара.

Р
— ?

Из
уравнений (2) и (3) имеем:
,.
После подстановки давленийР₁
и
Р₂
в
выражение
(1)
имеем
Используя числовые значения, получим:

Р
=
8,62·10⁵Па.

Ответ:
Р =
8,62·10⁵Па.

Задача
3.
Определите
число молекул воздуха в аудитории
объемом V=180
м³
при температуре t=22⁰С
и давлении Р=0,98·10⁵
Па. Какова концентрация молекул воздуха
при этих условиях?

Дано:

V=180
м³;

Т=295
К;

Р=0,98·
10⁵
Па;

Решение:

Число
молей воздуха в аудитории:

(1)

где
– N_A
—
число Авогадро, m
– масса воздуха в аудитории, М
–
молярная масса воздуха.

Из
выражения (1):

N
=
.
(2)

N
— ? , n — ?

Число
молей воздуха в аудитории можно выразить,
используя уравнение Клапейрона-Менделеева

откудаПосле
подстановки
из последней формулы в выражение (2)
получим:

.
(3)

Используя
числовые значения, определим N
=
0,43·10²⁸.
Проверим единицы измерения правой части
выражения (3)
. Концентрацию (число молекул в единице
объема) определим по формуле:

.
После
подстановки:
n=0,24·10²⁶.

Ответ:
N =
0,43·10²⁸,
n=0,24·10²⁶.

Задача
4.
Определите
среднюю квадратичную скорость молекул
некоторого газа, плотность которого
при давлении Р=1,1·10⁵Па
равна ρ=0,024.
Какова масса одного моля этого газа,
если значениеплотности
дано для температуры 27⁰С?

Дано:

=
1,1·10
⁵
Па;

=
0,024
;

=
300 К.

Решение:

Для
определения средней квадратичной
скорости движения молекул используем
основное уравнение молекулярно-кинетической
теории в таком виде:

,
(1)

где
m₀
– масса одной молекулы газа, n
–
концентрация молекул.

Так
как m₀n
= ρ,
то уравнение (1) можно записать

—
?

в
таком виде:
,
откуда,после
подстановки числовых значений и
вычисления получим:

Для
определения массы одного моля газа
используем уравнение Клапейрона-Менделеева
—

откуда.
Так как,
то,
или.
После подстановки числовых значений и
вычисления:

Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Агата Ильина
15 сентября, 10:52

Данные задачи: ρ (плотность газа) = 1,8 кг/м³; P (давление газа) = 152 кПа (152 * 10³ Па).

Среднюю квадратичную скорость молекул газа можно вычислить из формулы: Р = 1/3 * ρ * Vср², откуда Vср = √ (3 Р / ρ).

Выполним расчет: Vср = √ (3 * 152 * 10³ / 1,8) = 503,3 м/с.

Ответ: Средняя квадратичная скорость молекул газа составляет 503,3 м/с.

Комментировать
Жалоба
Ссылка

Источник

Газ находится под давлением 2 атм и имеет плотность 1,2 кг/м3 Определить среднюю квадратичную скорость молекул газа.

Оцените сложность задачи:

0 голосов, средняя сложность: 0.0000

Решения задачи

Данные задачи: газ находится под давлением

Давление газа	P	2	атм
Плотность		1,2	$frac{кг}{м^{3}}$
Средняя квадратичная скорость молекул газа	$υ$	?

Средняя квадратичная скорость

$ υ = sqrt{frac{3RT}{μ}} $

Уравнение Менделеева-Клайпейрона

$ PV = frac{m}{μ}RT $

Или

$ P =ρfrac{RT}{μ} $

Откуда находим

$ frac{P}{ρ} = frac{RT}{μ} $

и тогда

$ υ = sqrt{3frac{RT}{μ}}=sqrt{3frac{P}{ρ}}=sqrt{3frac{2×1,01×10^{5}}{1,2}}=711 frac{м}{с} $

Ответ:

$ Средняя квадратичная скорость молекул газа 711 frac{м}{с} $

Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь

Источник

Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа

$Large vecupsilon =sqrt{frac{3kT}{m}}=sqrt{frac{3RT}{M}}$

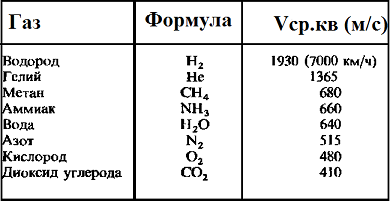
Таблица значений средней квадратичной скорости молекул некоторых газов

Для того чтоб понять, откуда же у нас получается эта формула, мы выведем среднюю квадратичную скорость молекул. Вывод формулы начинается с основного уравнения молекулярно кинетический теории (МКТ):

Где у нас количество вещества, для более легкого доказательства, возьмем на рассмотрение 1 моль вещества, тогда у нас получается:

Если посмотреть, то PV это две третьих средней кинетической энергии всех молекул (а у нас взят 1 моль молекул):

$large PV=frac{2}{3}vec E_k$

Тогда, если приравнять правые части, у нас получается, что для 1 моля газа средняя кинетическая энергия будет равняться:

$large vec E_k =frac{3}{2}RT$

Но средняя кинетическая энергия, так же находится, как :

$large vec E_k =frac{1}{2}N_a m vecupsilon^2$

А вот теперь, если мы приравняем правые части и выразим из них скорость и возьмем квадрат,Число Авогадро на массу молекулы , получается Молярная масса то у нас и получится формула для средней квадратичной скорости молекулы газа: