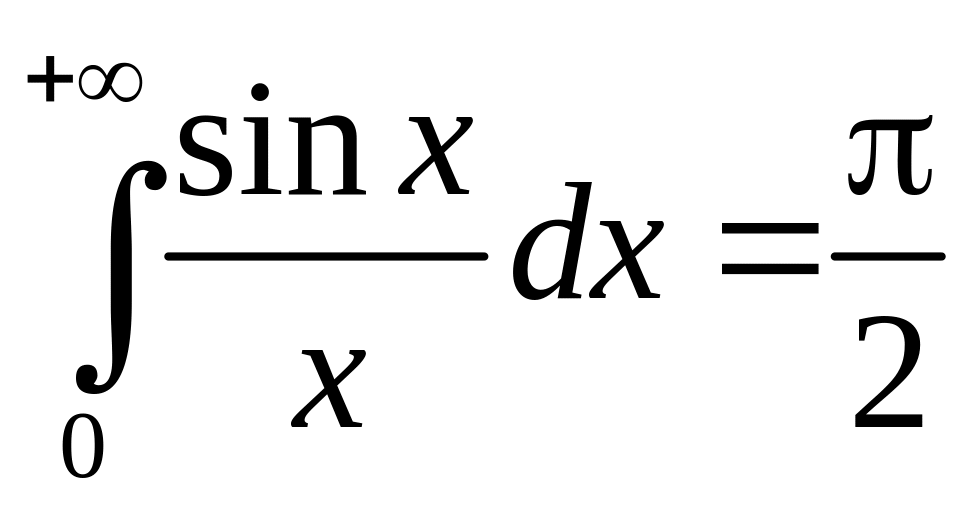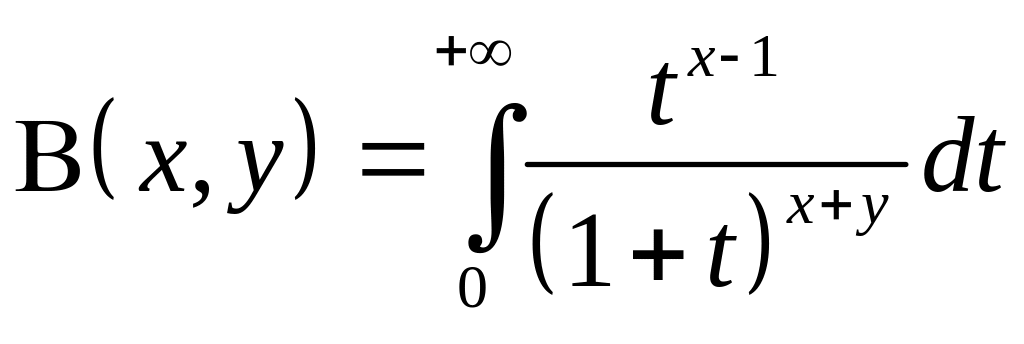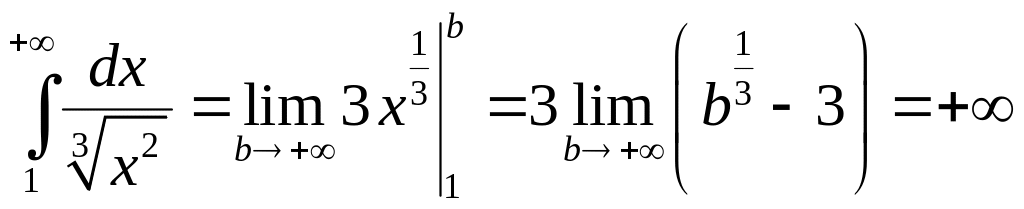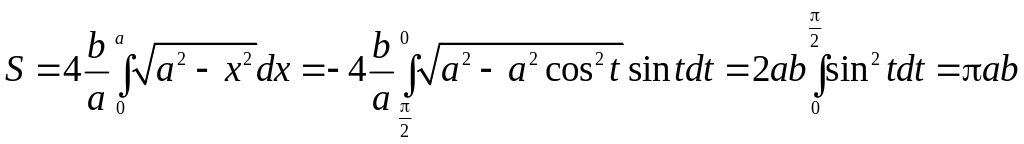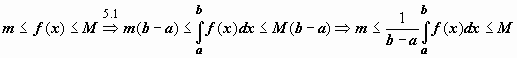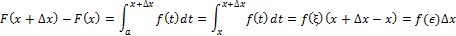Contents
- 1 Calculus Concept
- 2 Problem
- 3 Solution
- 4 Additional Remark
Calculus Concept
The mean value theorem states that for a given planar curve defined by a function 
![{displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



.
Problem
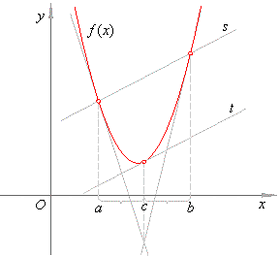
Figure 1. Illustration of the mean value of a parabola
Consider the parabola 
Part 1: Determine the slope of the secant line between two points 


Part 2: Determine the value 
Solution
Part 1
Evaluate the function at 

.
Next, calculate the slope of the secant line:
Part 2
The slope of the tangent line of the function 
.
Equating the slope of the tangent to the slope of the secant in Part 1 gives
.
Solving for 


.
Additional Remark
The triangle with its vertices on 


Пусть
интегрируема и ограничена на
и
,
— соответственно, верхняя и нижняя
грани
на отрезке
.
Тогда, существует такое число
,
что:
и
.
Число
называется средним значением функции
на отрезке
.
Примеры:
4.1. Вычислить
среднее значение функции
на отрезке
.
По формуле
среднего значения функции на интервале,
получаем
.◄
4.2. Вычислить
среднее значение функции
на отрезке
.
По формуле
среднего значения функции на интервале,
получаем
.◄
4.3. Вычислить
среднее значение функции
на отрезке
.
По формуле
среднего значения функции на интервале,
получаем
.◄
5. Несобственные интегралы
5. 1. Интегралы с бесконечными пределами
Если
непрерывна на интервале
,
то интеграл

называется
несобственным интегралом от
.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если
при
,
то при
интеграл сходится, при
интеграл расходится.
Отметим важные
примеры несобственных интегралов:
— интеграл Пуассона,
— интеграл Дирихле,
— Бета-функция
(эйлеров интеграл 1 рода),
— Гамма-функция
(эйлеров интеграл 2 рода).
Примеры:
5.1.1. Вычислить
интеграл
Найдём
.
Предел существует
и конечен. Значит, интеграл сходится. ◄
5.1.2. Вычислить
интеграл
Найдём
.
Предел не существует.
Несобственный интеграл расходится. ◄
5.1.3. Вычислить
интеграл
.
Подынтегральная
функция чётная, поэтому
.
Вычислим интеграл:
.
Получили
.
Интеграл сходится. ◄
5.1.4. Доказать
расходимость интеграла
.
Так как при
,
,
то вычисляя
интеграл
.
Этот интеграл
расходится. Следовательно, по признаку
сравнения исходный интеграл
тоже расходится.
5.2. Интегралы от функций с бесконечными разрывами
Если
непрерывна на
и неограниченна в любой окрестности
точки
,
то интеграл

называется
несобственным интегралом от
.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если
при
,
то при
интеграл сходится, при
интеграл расходится.
Примеры:
5.2.1. Исследовать
на сходимость интеграл
.
Так как
подынтегральная функция
терпит
разрыв в точке
,
то получим:
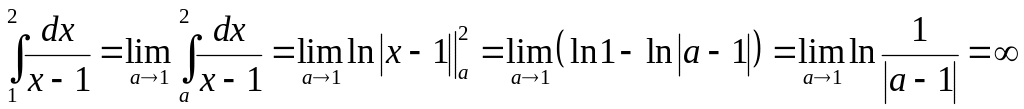
Конечного предела
не существует, значит, интеграл расходится.
◄
5.2.2.
Исследовать на сходимость интеграл
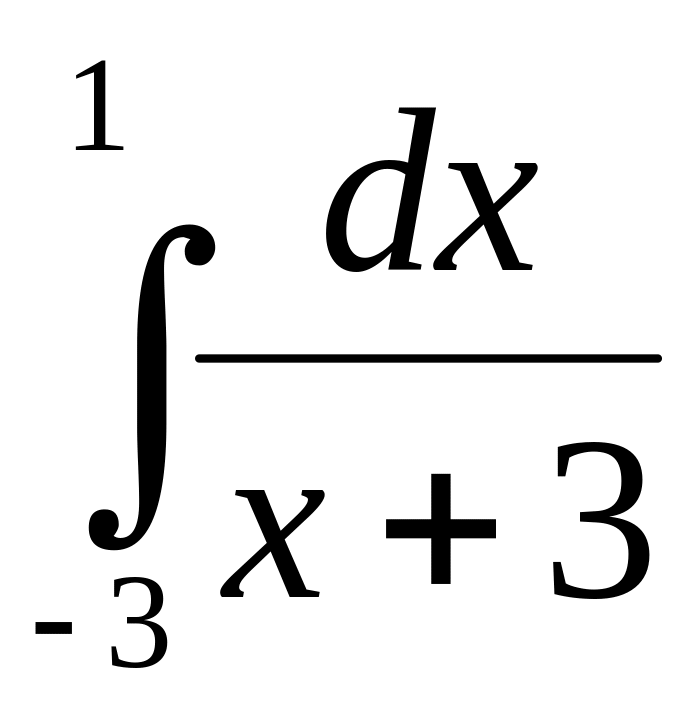
Так как
подынтегральная функция
терпит
разрыв в точке
,
то получим:
.
Конечный предел
равен бесконечности. Значит, интеграл
расходится. ◄
5.2.3. Исследовать
на сходимость интеграл

Так как
подынтегральная функция
терпит
разрыв в точке
,
получим:
.
Применим
интегрирование по частям. Пусть
Тогда
.
И первоначальный
интеграл примет вид:
.
Предел конечен.
Поэтому интеграл сходится.
◄
5.2.4. Исследовать
на сходимость интеграл
Имеем
.
Предел бесконечен.
Следовательно, интеграл расходится.
◄
6. Геометрические и физические приложения определенного интеграла
6.1. Вычисление площади криволинейной трапеции
Площадь плоской
области
стандартной относительно оси
,
ограниченной прямыми
и
и кривыми
,
такими, что для любых
выполнено
(т.е.
)
вычисляется
.
Аналогично площадь
плоской области стандартной относительно
оси
,
ограниченной прямыми
и
и кривыми
,
такими, что для любых
выполнено
(т.е.
)
вычисляется
.
Если область
ограничена непрерывной замкнутой
кривой, заданной параметрически
,
то её площадь можно
вычислить по одной из трёх формул
,
,
.
Какую из них удобнее
применять, зависит от конкретного вида
функций
и
.
Площадь области
:
,
называемой
криволинейным сектором, ограниченной
графиком
и двумя лучами, составляющими с полярной
осью углы
и
имеет площадь
.
Примеры:
6.1.1.
Вычислить площадь области, ограниченной
линиями:
и
.
Изобразим фигуру
в декартовой системе координат:
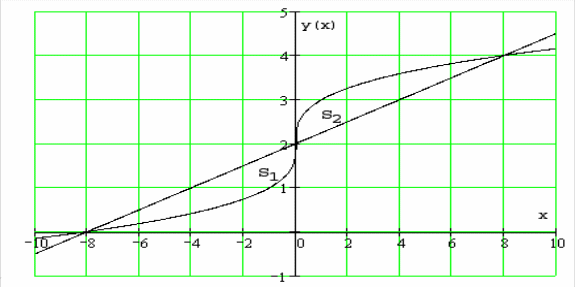
Из условия симметрии
фигуры относительно точки с координатами
,
площади
и
равны. Так как данная область является
стандартной как относительно оси
так и относительно оси
,
то ее площадь можно вычислить одним из
двух способов.
1) Выразим зависимости
в явном виде:
и
,
а стандартная
относительно оси
область
.
Тогда получаем
.
2) Заметим, что для
вычисления площади можно было
воспользоваться исходным видом
зависимостей:
.
6.1.2.
Вычислить площадь области, ограниченной
параболами
и
.
Изобразим фигуру
в декартовой системе координат

Очевидно, область
симметрична относительно оси
,
кроме того, она не является стандартной
относительно оси
и стандартной относительно оси
,
а ее площадь можно вычислить одним из
двух способов.
-
Данная область
не является стандартной относительно
оси.
Её можно разбить на две стандартные
относительно осиобласти:
,
.
Из симметрии
областей
и
относительно оси
следует, что

.
-
Относительно оси
данная область
является стандартной:
.
Снова, используя
симметрию области, получаем
.
6.1.3.
Вычислить площадь эллипса, заданного
уравнением
(
,
).
Искомую площадь
можно вычислить, используя как явное
представление линии, так и параметрическое.
-
Выразив уравнение
в явном виде
,
получим,
применив подстановку
,
,
приходим к
.
2) С другой стороны,
используя параметрическое представление
,
при изменении параметра
в пределах от
до
,
получаем:
.
6.1.4.
Вычислить площадь астроиды, заданной
уравнением
(
,
)
Изобразим кривую
в декартовых координатах:

Используя
параметрическое представление
,
при изменении параметра
в пределах от
до
,
получаем:

.
6.1.5.
Найти площадь фигуры, ограниченной
кардиоидой
,
.
Изобразим кривую
в декартовых координатах:
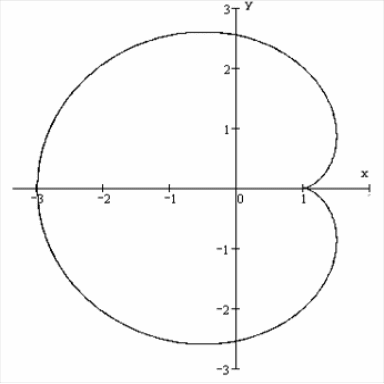
Так как кардиоида
симметрична относительно оси
,
то, используя параметрическое
представление, будем менять параметр
в пределах от
до
.
Так как
и
,
получаем по любой
из трех формул


,


,

.
Отметим, что площадь
кардиоиды задаваемой уравнением в
полярных координатах
равна
.
6.1.6.
Найти площадь области, ограниченной
кривой
.
Кривая образует
три симметричные петли, каждая из которых
ограничивает криволинейный сектор.
Изобразим ее в полярных координатах.

Рассмотрим сектор,
лежащий в первой четверти:
.
Площадь его,
очевидно, равна 1/3 площади всей области,
ограниченной данной кривой. Следовательно,
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Быстрая математика для графиков, на примере вычисления среднего
Рассмотрим, в качестве примера, формулу для вычисления среднего значения. На ней я постараюсь рассказать и показать какие подходы к реализации можно применять и чем они эффективны или не эффективны.
Это сумма всех значений за выбранный период, делённая на период. Иными словами -среднее значение за последние n значений.
Классический подход
Как ни странно, большинство решений в сети выглядит, как последовательный перебор всех групп размером n (например 4) и вычисление среднего для каждой:
Безусловно, это решение работает, но оно очень плохое. Здесь происходит огромное количество повторных вычислений и лишних операций. Разберем весь код по порядку и посмотрим, строка за строкой, что происходит «под капотом».
Создание массива в JavaScript, выделяет определенную область памяти для хранения данных. Размер массива не определенный и он наполняется по мере работы цикла, в какой-то момент может наступить заполнение выделенной области памяти и модуль управления памятью будет вынужден выделить новоую, более широкую область, затем осуществить перенос в нее диапазона всех значений памяти из предыдущей области, в разных движках это может работать по разному, но в любом случае необходимо, как минимум, выделение новой области памяти. И вот, как выглядит график замера времени на операцию push, в зависимости от длинны массива.
На картинке видны космические, по местным масштабам выбросы. Это происходит по причине тех самых накладных работ в памяти движка на перенос всей области, либо на выделение новой области и связывание со старой.
Из этого можно сделать два вывода:
Для работы с большими массивами лучше использовать создание массива через конструктор как: new Array(size) . Это позволит вам задать размер массива и движок выделит столько памяти, сколько нужно.
А зачем тут этот массив вообще. (Позже мы к этому вернемся)
Для начала, ремарка про цикл. Я бы не стал так подробно мусолить цикл и перешел бы к следующей части, тк в целом оптимизация цикла не дала бы нужный эффект производительности, но это просто крик души, ода к безграмотности современных разработчиков, щепетильно пишущих бенчмарки налево и направо.
Погуглив «Самый быстрый способ итерации в JavaScript» не трудно наткнуться на кучу разных бенчмарков, которые написаны не правильно. Почему не правильно? .
В теории самый самый быстрый способ итерации в JavaScript - while(i > 0) , но все тесты в лучшем случае предлагают такой вариант условия остановки: while(i++) , в котором добавляется дополнительная нагрузка в виде приведения типа числа из Number в Boolean . Даже такой вариант выхода из цикла не совсем правильный: while(i потому, что сравнение с 0 является одной из самых быстрых операций и отличается от сравнения с любыми другими видами чисел.
Бытует мнение, что это миф, однако это не так. Доказательство очень простое, взглянем как процессор обрабатывает сравнение с 0 и с 1
Обратите внимание на 5ую строку. Там используется сравнение LdaZero. Которое вежливо отмечено вторым в порядке быстродействия самими разработчиками v8.
Сравнение с нулем или нет — разница есть!
Не верьте бенчмаркам, если они написаны не правильно
Все эти вычисления можно сделать без цикла, об этом позже.
Теперь очередь этой строки. Оператор slice создает новый массив, для которого выделяется память, заполняет его данными из предыдущего массива (иммутабильно) и присваивается в переменную chunk. Это с ума сойти сколько операций на пустом месте. И тут все можно описать столь же подробно, но я не стану, потому что больше нет сил разбираться в рубрике «По колено в коде» (Олды тут?). Выше, я все обещал позже рассказать о том, как сделать эти вычисления эффективнее. Приступим!
Потоковая обработка
В основе идеи потоковой обработки, лежит архитектура последовательных вычислений, с последующим переиспользованием (по возможности) результатов предыдущих вычислений. Такой подход хорош всегда и везде (где он применим), он применяется в парсинге текста, вычислениях, поисках в математических абстракциях и прочее.
Реализация вычислений SMA в этом подходе выглядит так:
Преимущества подхода в сравнении с классической реализацией:
Массив фиксированной длинны, который заполняется значениями и очищается при переполнении, поддерживая константную размерность. Тем самым позволяет не хранить в памяти лишнюю информацию.
Повторное использование вычислений, позволяет вообще отказаться от итераций по какому-либо массиву, мы просто записываем сумму всех входящих значений, и вычитаем сумму уходящих значений (при переполнении массива)
Но проблемные места все же есть:
Проблема 1 - это постоянное условие проверки переполненности массива, даже оптимизированное в this.filled , все еще вызвыается в холостую на каждую итерацию.
Проблема 2 -Мы все еще вынуждены хранить массив длинной 4 и постоянно выполнять операции shift и push , и если push нам не так страшен, то shift , вызывает последовательное смещение индексов, что дорого.
В остальном, даже в таком виде это решение будет работать быстрее в разы, чем классический подход.
Решаем проблему под номером один. Для этого при заполнении массива переопределим метод
Это позволит избежать в дальнейших расчетах дополнительных проверок на заполненность массива. Такой «лайфхак» имеет мелкое негативное воздействие на так называемые Shape структуры браузера, которые применяются для оптимизации доступа к свойствам объекта в реальном режиме времени. Прочитать про это можно здесь. Однако это воздействие будет разовым и на дальнейших вычисления не скажется. Такой подход дает в итоге даст значительное ускорение.
Мы сегодня с вами разобрали два подхода к вычислениям среднего значения, но это все легко переносится и на любые другие вычисления, поддающиеся потоковому анализу. Я постарался сделать статью интересной затронув глубинный уровень языка и работу с памятью.
SMA и многие другие аналитические функции (технические индикаторы) можно найти в моем репозитории.
Домашнее задание
В статье решается только одна из двух проблем потоковой реализации. Можно ли избавиться от проблемы номер два? Пишите ваши предложения в комментариях.
Определение среднего значения функции
Обсуждая концепцию математического образования в 12-летней школе [3, с. 13–18], следует уточнить целеполагание одного из основных блоков математического образования – функции. Важным является изучение не столько свойств функций, сколько развитие умений применять функции для описания реальных процессов. Но реальные процессы задаются сложными функциональными зависимостями. Математическое моделирование упрощает зависимости, заменяя одну функцию другой, более простой.
Основная идея введения интеграла – аккумуляция (накопление) информации о функции на отрезке – оказалась незавершенной не только в школьном курсе математики, но и в общем образовании учащихся. Нет возврата к более простой функции, которая порождает такое же значение интеграла, т. е. накапливает такую же информацию на отрезке. Другими словами, нет усреднения заданной функции на отрезке.
В школьных, да и в вузовских учебниках, пропущено очень важное применение определенного интеграла для нахождения среднего значения непрерывной функции на отрезке. Некоторые авторы программ и учебников много говорят о развитии функциональной линии, но ни слова не говорят, как усреднить функцию на промежутке, хотя среднее значение двух величин определяется. Следует сказать больше. Мотивация изучения функциональной линии в общем образовании учащихся оказалась не полностью сформулированной и незавершенной.
Моделирование реальных задач требует усреднения в математических моделях непрерывных функций (в экологии, в метеосводке погодных условий и т. д.), усреднения в компьютерных экспериментах дискретных величин с малым шагом аргумента – что приближается к усреднению непрерывных величин.
Среднее значение функции удобно ввести на примере определения средней скорости движения, как отношения длины всего пройденного пути к величине затраченного времени
Рассмотрим общее определение среднего значения функции.
Площадь криволинейной трапеции, ограниченной графиком непрерывной функции y = f(x) (пусть f(x) принимает неотрицательные значения), осью ox и вертикальными прямыми y = a, y = b, равна площади некоторого прямоугольника, построенного на отрезке [a; b]. Высота этого прямоугольника является средним значением функции y = f(x) на отрезке [a; b]. В общем случае она определяется по формуле [2, с. 559]
(1)
В школьных и вузовских учебниках много внимания уделяется нахождению интегралов. Это необходимое развитие навыков нахождения интегралов, но очевидно, что более важно показать его применения. Из всех учебников и справочников для школы только в справочниках [1, с. 497; 2, с. 368, 369] определяется среднее значение функции на отрезке. Следует отметить, что пропедевтика введения среднего значения функции иногда проводится в задачах следующего типа на вступительных экзаменах в вузы и в учебниках физики.
1. Катер из Нижневартовска в Сургут двигался со скоростью v1, а в обратном направлении со скоростью v2. Найдите среднюю скорость катера на всем пути, т. е. из Нижневартовска в Сургут и обратно.
Ответ:
2. Катер вначале двигался со скоростью v1 в течение некоторого промежутка времени, а затем в течение такого же промежутка времени со скоростью v2. Найдите среднюю скорость катера на всем пути.
Ответ:
3. Первую треть пути между пунктами велосипедист проехал со скоростью v = 5 м/с, затем половину оставшегося времени он ехал со скоростью v = 10 м/с, после чего до конечного пункта он шел с велосипедом со скоростью v = 1 м/с. Определите среднюю скорость движения велосипедиста.
4. Найдите среднюю скорость тела, если первую четверть времени оно двигалось со скоростью v = 5 м/с, вторую четверть времени – со скоростью v = 10 м/с, оставшуюся часть времени со скоростью v = 15 м/с.
Не каждый учитель видит в этих задачах функции. Для многих это постоянные величины. Читатель наверно согласится, что это требует корректировки.
Рассмотрим другие примеры, приводящие к пониманию важности изучения среднего значения. Например, мы иногда не можем определить значение функции в данный момент времени и вынуждены пользоваться средними значениями функции.
Величина переменного тока в данный момент времени t (мгновенное значение тока) определяется по формуле
где I0 – максимальное (амплитудное) значение тока, w – частота, – период. Представим себе, что существует прибор, измеряющий мгновенное значение тока i. Стрелка прибора в течение 1 секунды будет совершать 50 колебаний, показывая значения из отрезка [– I0; I0]. Зафиксировать информацию практически невозможно. С другой стороны, почти все приборы обладают инерционностью, т. е. требуют для измерения величины некоторого времени (быстродействие прибора). Оно, как правило, значительно больше периода быстрых процессов. Принцип измерения величин во многих приборах основан на измерении какого-то действия за определенный промежуток. Поясним примерами.
Среднее значение переменного тока за период T равно 0 для синусоидальной величины и не характеризует величину переменного тока.
Среднее значение переменного тока в течение полупериода по формуле (1) равно
Некоторые электроизмерительные приборы измеряют среднее значение тока за половину периода, но все они практически градуируются в действующих значениях переменного тока, к разъяснению понятия которого мы переходим.
Действующим (эффективным) значением I переменного тока называется значение такого постоянного тока, который производит такое же действие (тепловое, электромагнитное, механическое и др.), как и данный переменный ток.
Работа, совершенная постоянным током за период T, равна
а работа, совершенная переменным током, равна
Большинство электроизмерительных приборов в цепях переменного тока показывают действующее значение. Для физики и техники большее значение имеет действующее значение переменного тока, чем среднее значение переменного тока. В медицине иногда также выделяется усреднение на отрезке около наибольшего значения, так как оно может произвести на пациента большее влияние, чем средняя величина за период приема лекарства. Эти примеры показывают, что в некоторых науках усреднение функций производится по-разному, в зависимости от воздействия на объект.
Задача. Интервал движения автобуса a минут, интервал движения микроавтобуса – m минут, a Э N, m Э N. Человек приходит на остановку, не зная графика движения транспорта, т. е. случайным образом. Сколько времени в среднем ожидает человек на остановке, если курсируют автобус и микроавтобус?
Решение. Пусть курсирует только автобус с интервалом a минут. Введем отсчет времени от первого уходящего с остановки автобуса. Если пассажир пришел через t минут (t минут. Оно не зависит от времени прихода на остановку. Рассматривая такие случаи для различных значений t, получим среднее время ожидания – мин. В этой задаче среднее время определено элементарным методом с использованием симметрии относительно середины промежутка [0; a].
Если пассажир пришел на остановку через t минут, то функция времени ожидания автобуса имеет вид
Найдем среднее значение времени ожидания автобуса на отрезке [0; a]
Аналогично, если курсирует только микроавтобус, то среднее время ожидания равно мин.
Рассмотрим общий случай, когда курсируют автобус и микроавтобус. Пусть m является делителем числа a, a = mk, k l 2. Пусть автобус приходит спустя s (s
Если s = 0 или s = m, т. е. автобус и микроавтобус приходят на остановку одновременно, то среднее время ожидания в этом частном случае равно мин. Пассажир может воспользоваться микроавтобусом (автобусом он раньше не уедет). Автобус в этом случае можно исключить из рассмотрения, так как он приходит одновременно с микроавтобусом.
Пусть пассажир пришел на остановку через t минут после отхода микроавтобуса. Если 0
Функция ожидания является кусочно-линейной функцией и состоит из отрезков, образующих углы в 135° с осью ox.
Функция ожидания автобуса является периодической функцией с периодом T = a мин.
Учитывая геометрический смысл интеграла, для вычисления среднего значения функции ожидания достаточно вычислить площадь равнобедренных треугольников с катетами
При
Условие задачи также требует уточнения.
Если мы не знаем величины задержки автобуса относительно микроавтобуса, т. е. предположим, что она каждый день может меняться, тогда среднее значение ожидания следует рассмотреть как функцию t(s) от параметра s. Величину t(s) следует проинтегрировать на промежутке [0; m], а затем поделить на длину этого промежутка. Если s Э [im, (i + 1)m], i Э N, i
Итак, среднее время ожидания автобуса на отрезке [0; a] вычисляется следующим образом
Иногда встречается следующая ошибка.
Если рассматривать все средние значения только на отрезке [0; m], то получим следующие результаты
Этот результат получается из предыдущего при k = 1 и это верно. Но если k > 1, то эта формула не учитывает интервал «микроавтобус – микроавтобус, интервал движения m минут, в течение которого не появляется автобус».
Некоторые задачи для самостоятельного решения.
1. Дан отрезок длиной a, на который произвольным образом бросается точка. Найдите среднее расстояние до границы отрезка.
2. Рассматриваются всевозможные треугольники с данными сторонами OA = a, OB = b и переменным углом g Э [0, p ]. Найдите среднее значение площади треугольников.
3. В окружность радиуса R вписаны всевозможные прямоугольники с параллельными сторонами. Найдите среднее значение площади полученных прямоугольников.
Как найти среднее значение функции на отрезке
«Вы, профессор, воля ваша, что-то нескладное придумали! Оно, может, и умно, но больно непонятно. Над вами потешаться будут»
«Мастер и Маргарита», Булгаков М. А.
Жизнь у всех разная и проявляется это ещё и в том, что источники информации, с которыми мы имеем дело, тоже у всех различны. Кроме этого, далеко не каждые сведения оставляют нас равнодушными, не вызывая совершенно никаких эмоций или мыслей. При этом иногда сочетание данных из двух источников может побуждать к весьма своеобразным умозаключениям.
Есть у меня одна книга – пособие для учителя информатики [1] . Не помню, как она у меня появилась – может купил, а может мне её кто-то подарил – однако в школе она мне как-то пригодилась в освоении языка Basic, программы на котором мы тогда собственноручно набивали на болгарских машинах «Правец 8A». Именно из этой книги я когда-то впервые узнал, что помимо так называемого среднего арифметического для нескольких чисел бывает, например, ещё и среднее квадратическое.
На первом курсе (1999-2000 гг.) университета, на лекциях по высшей математике, когда мы проходили определённые интегралы, была упомянута так называемая «теорема о среднем» [2, с. 353] . И вот это-то, в комбинации с сидящими в памяти сведениями из упомянутой книги, почему-то отозвалось в мозгах вопросом: «А какое именно среднее имеется в виду в теореме: арифметическое, кубическое или какое-нибудь другое?». Ну а раз возник вопрос – можно попытаться найти и ответ. Поиск сей вскоре привёл меня к тому, что, собственно, и составляет основу материала данной заметки. Свои измышления я условно назвал «теорией средних» и достаточно долгое время они хранились у меня в виде конспекта. Теперь же результаты этой «мозговой гимнастики» я выложил в сеть по следующим соображениям. Во-первых, если на этот материал наткнётся математик, то, думается, это сможет его повеселить. Во-вторых, мне слабо верится, что никто из профессиональных математиков в своих работах не додумался до чего-то подобному тому, что изложено здесь. В связи с этим мне особенно интересно было бы узнать, чьи это результаты мной, вероятно, «переоткрыты» – к сожалению, я не располагаю возможностью и временем это выяснить самостоятельно, но буду очень благодарен за сведения об этом.
I. Типы средних (введение)
Пусть у нас имеется множество из n чисел x 1, x 2. xn .
а) Среднее арифметическое этих чисел:
б) Среднее квадратическое:
в) Среднее кубическое:
г) Если ни одно из чисел рассматриваемого множества не равно нулю, то для них можно вычислить среднее гармоническое [1, с. 132] :
II. Средние значения функции на замкнутом числовом промежутке
Рассмотрим непрерывную функцию y = f ( x ), определённую на отрезке [ a ; b ]. Разобьём [ a ; b ] на n равных частей величиной Δ xi =( b – a )/ n . Теперь внутри каждого отрезка разбиения Δ xi произвольно выберем точку Ci () и вычислим значение функции y = f ( x ) в точке Ci : yi = f ( Ci ) (Рисунок 1).
Для полученного таким образом множества значений по формулам (1), (2), (3) можно вычислить средние арифметическое, квадратическое и кубическое:
В случае, если f ( x ) на [ a ; b ] ни в одной точке не обращается в ноль, то по (4) можно вычислить и среднее гармоническое:
Будем теперь увеличивать неограниченно n и найдём пределы выражений (5), (6), (7) и (8) при n →∞. Если эти пределы существуют для рассматриваемой функции y = f ( x ) на отрезке [ a ; b ], то назовём их, соответственно, средним арифметическим, средним квадратическим, средним кубическим и средним гармоническим значениями функции y = f ( x ) на отрезке [ a ; b ]. Введём обозначения:
Для удобства операторы
, , ,
назовём арифией, квадрией, кубинией и гармонией соответственно.
III. Вычисление арифии функции на замкнутом числовом промежутке
Вернёмся к Рисунку 1. Составим для функции f ( x ) интегральную сумму Римана:
Эта сумма при неограниченном возрастании n имеет предел, равный интегралу:
Величина ( b – a ) – длина отрезка [ a ; b ] – число постоянное, поэтому
Подставим (9) в (13):
Из (14) как раз и следует ответ на возникший у меня вопрос: в теореме о среднем фигурирует именно среднее арифметическое значение функции на отрезке (придуманная мной «арифия»).
IV. Свойства арифии функции на отрезке
Свойство 1 (свойство линейности оператора арифии):
( C 1 и C 2 – постоянные числа, f ( x ) и g ( x ) – непрерывные и определённые на [ a ; b ] функции).
Свойство 2. Если C =const, то
Свойство 3. Если a c b , то
Свойство 4. Если f ( x ) – чётная функция и a > 0, то
Так как f ( x ) – чётная, то
, .
Свойство 5. Если f ( x ) – нечётная функция, то
Так как f ( x ) – нечётная, то
,
Домножим обе части этого неравенства на ( b – a ) ( b – a > 0):
V. Вычисление квадрии, кубинии и гармонии функции на отрезке
Пусть g 1( x )=[ f ( x )] 2 , тогда
Пусть теперь g 2( x )=[ f ( x )] 3 , тогда
Пусть теперь функция y = f ( x ) на [ a ; b ] ни в одной точке не принимает нулевого значения. Обозначим .
6*. Формула среднего значения для определенного интеграла.
Теорема о среднем. Если f(x) непрерывна на отрезке [a,b], то существует точка 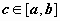


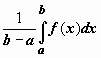

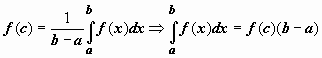


7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость.
Рассмотрим функцию f (x), интегрируемую по Риману на отрезке [a, b]. Раз она интегрируема на [a, b], то она также интегрируема на [a, x] ∀x ∈ [a, b]. Тогда при каждом x ∈ [a, b] имеет смысл выражение 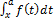
Таким образом, каждому x ∈ [a, b] поставлено в соответствие некоторое число 
т.е. на [a, b] задана функция:

Функция F (x), заданная в (3.1), а также само выражение 
интегралом с переменным верхним пределом. Она определена на всем отрезке [a, b]
интегрируемости функции f (x).
Условие: f (t) непрерывна на [a, b], а функция F (x) задана формулой (3.1).
Утверждение: Функция F(x) дифференцируема на [a, b], причем F (x) = f (x).
(В точке a она дифференцируема справа, а в точке b – слева.)
Поскольку для функции одной переменной F (x) дифференцируемость равносильна существованию производной во всех точках (в точке a справа, а в точке b – слева), то мы найдем производную F (x). Рассмотрим разность

при этом точка ξ лежит на отрезке [x, x + ∆x] (или [x + ∆x, x] если ∆x c=F(a), и
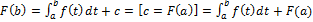
Перенесем F(a) в последнем равенстве в левую часть, переобозначим переменную интегрирования снова через x и получим формулу Ньютона – Лейбница:
Среднее значение функции через интеграл
Теорема 1 (об оценке определенного интеграла)
Если m и M ¾ соответственно наименьшее и наибольшее значения непрерывной функции f(x) на отрезке [ a, b], то
. (5)
Теорема 2 (о среднем значении)
Если функция f(x) непрерывна на отрезке [ a, b], то на этом отрезке существует точка С такая, что
. (6)
Величина
называется средним значением функции f(x) на отрезке [a, b].
Замечание 1 . Теорема 2 имеет четкий геометрический смысл: величина определенного интеграла при f(x) ≥ 0 равна площади прямоугольника, имеющего высоту f(C) и основание b – a (рис. 2).
Имеют место более общие теоремы об оценке и среднем: если функции f( x) и φ( x) непрерывны на отрезке [ a, b] и φ( x) > 0, m – наименьшее, M – наибольшее значения функции f( x) , то
, (7)
. (7 ¢ )
Из соотношений (7) и (7′) следуют соотношения (5) и (6), если принять φ(x) ≡ 1 .
Для непрерывных на отрезке [ a, b] функций f( x) и φ( x) имеет место неравенство Коши – Буняковского:
.
П р и м е р 1. Используя теорему об оценке, найти, какому интервалу принадлежит значение интеграла .
Решение. На отрезке [16, 32] наименьшее значение функции
,
,
длина промежутка интегрирования b – a = 32 – 16 = 16. Согласно неравенству (1) имеем
.
Как известно, среднее значение функции f(x), заданной на отрезке [a, b] равно:
Но это только теория, вас же интересует скорее всего практическая сторона, а именно, вам задана какая-то конкретная функция и для неё необходимо найти среднее значение.
Лучше всего рассмотреть как получить среднее значение функции с помощью примера.
Например, вам дана функция:
f(x) = x*sin(x) и надо найти её среднее значение на отрезке [0, π/2]
Для того, чтобы найти ср. значение функции f(x) онлайн, надо воспользоваться тремя двумя шагами:
1. Получить подробное решение определённого интеграла (который стоит в числителе) здесь
Ввести, x*sin(x) как на рисунке ниже:
После этого нажать на кнопку «Найти интеграл».
Тем самым вы вычислите числитель дроби, который входит в формулу для среднего значения функции.
В нашем примере это значение интеграла будет равно 1, значит числитель будет равен 1.
2. Вычисляем знаменатель. Он равен b – a = π/2 – 0 = π/2
3. Делим числитель на знаменатель и получим необходимое нам среднее значение функции:
В итоге вы получите ответ и подробное решение в придачу.
Опубликовано: Октябрь 30, 2013
Тэги: функция
© Контрольная работа РУ – примеры решения задач
Здравствуйте!
Как найти среднее значение функции на отрезке? Может формулы есть?
Спасибо!
Рассмотрим вопрос о том, как находить среднее значение функции на отрезке.
По этому поводу существует теорема, которая называется теоремой о среднем. В ней говорится, что если на определенном отрезке заданная функция непрерывна, то на этом промежутке найдется такая точка, для которой будет выполняться условие:
Здесь a и b — концы отрезка, f(x) — заданная функция, а с — выше упоминаемая точка.
Значение функции в точке с называют средним ее значением на отрезке от а до b и находят по формуле:
Формулой очень удобно пользоваться, если функция на отрезке задана не линейная, а квадратичная, логарифмическая, тригонометрическая или какая-либо еще.
Рассмотрим пример.
Задание.
Найти среднее значение функции на отрезке [2; 13].
Решение.
Воспользуемся выше упомянутой формулой и подставим в нее известные значения:
Используем формулу Ньютона-Лейбница и найдем значение полученного выражения:
Упростим выражение и вычислим его результат:
Получили среднее значение функции на отрезке [2; 13] равным 35,8.
http://fobosworld.ru/opredelenie-srednego-znacheniya-funktsii/
http://4systems.ru/inf/srednee-znachenie-funkcii-cherez-integral/