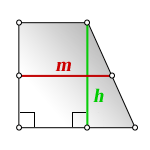
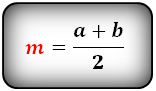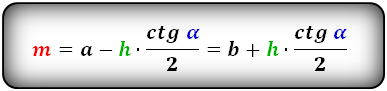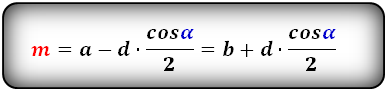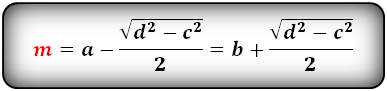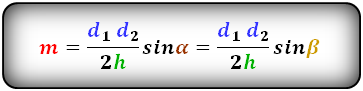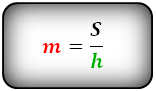Как найти среднюю линию прямой трапеции - Исправление недочетов и поиск решений вместе с Examum.ru

1. Формула средней линии трапеции через основания (для всех видов трапеции)

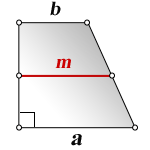
a — нижнее основание

b — верхнее основание

m — средняя линия

Формула средней линии, (m ):

2. Формулы средней линии через основания, высоту и угол при нижнем основании

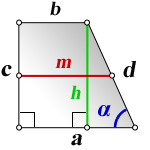
a, b — основания трапеции

c — боковая сторона под прямым углом к основаниям

d — боковая сторона

α — угол при основании

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции, (m ):

3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

d₁ , d₂— диагонали трапеции

α , β — углы между диагоналями

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции, (m ):

4. Формула средней линии трапеции через площадь и высоту (для всех видов трапеции)

S — площадь трапеции

h — высота трапеции

m — средняя линия

Формула средней линии трапеции, (m ):

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

Подробности

Опубликовано: 19 октября 2013

Обновлено: 13 августа 2021

Источник

Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции

Определение.

Прямоугольная трапеция — это трапеция у котрой одна из боковых стороны перпендикулярна основам.

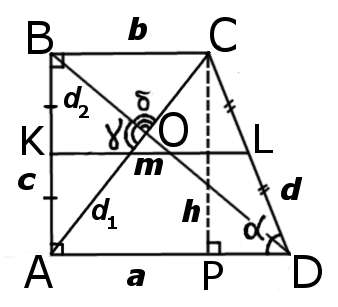Изображение прямоугольной трапеции с обозначениями

Рис.1

Признаки прямоугольной трапеции

Трапеция будет прямоугольной если выполняется одно из этих условий:

1. В тапеции есть два смежных прямых угла:

∠BAD = 90° и ∠ABC = 90°

2. Одна боковая сторона перпендикулярна основам:

AB ┴ BC, AB ┴ AD

Основные свойства прямоугольной трапеции

1. В трапеции есть два смежных прямых угла:

∠BAD = ∠ABC = 90°

2. Одна боковая сторона перпендикулярна основам:

AB ┴ BC ┴ AD

3. Высота равна меньшей боковой стороне:

h = AB

Стороны прямоугольной трапеции

Формулы длин сторон прямоугольной трапеции:

1. Формулы длины оснований через стороны и угол при нижнем основании:

a = b + d cos α = b + c ctg α = b + √d ² — c²

b = a — d cos α = a — c ctg α = a — √d ² — c²

2. Формулы длины оснований через стороны, диагонали и угол между ними:

a =	d₁d₂	· sin γ — b =	d₁d₂	· sin δ — b
c	c

b =	d₁d₂	· sin γ — a =	d₁d₂	· sin δ — a
c	c

3. Формулы длины оснований трапеции через площадь и другие стороны:

a =	2S	— b b =	2S	— a
c	c

4. Формула боковой стороны через другие стороны и угол при нижнем основании:

c = √d ² — (a — b)² = (a — b) tg α = d sin α

5. Формулы боковой стороны через основы, диагонали и угол между ними:

c =	d₁d₂	· sin γ =	d₁d₂	· sin δ
a + b	a + b

6. Формулы боковой стороны через площадь, основы и угол при нижнем основании:

d =	S	=	2S
m sin α	(a + b) sin α

7. Формула боковой стороны через другие стороны, высоту и угол при нижнем основании:

d =	a — b	=	c	=	h	= √c² + (a — b)²
cos α	sin α	sin α

Средняя линия прямоугольной трапеции

Формулы длины средней линии прямоугольной трапеции:

1. Формулы средней линии через основание, высоту (она же равна стороне c ) и угол α при нижнем основании:

m =	a — h ·	ctg α	=	b + h ·	ctg α
2	2

2. Формулы средней линии через основания и боковые стороны сторону:

m =	a —	√d ² — c²	=	b +	√d ² — c²
2	2

Источник

Все формулы средней линии прямоугольной трапеции

1. Формула средней линии трапеции через основания (для всех видов трапеции)

a — нижнее основание

b — верхнее основание

m — средняя линия

Формула средней линии, ( m ):

2. Формулы средней линии через основания, высоту и угол при нижнем основании

a, b — основания трапеции

c — боковая сторона под прямым углом к основаниям

d — боковая сторона

α — угол при основании

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции , ( m ):

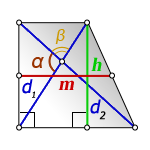
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

d ₁ , d ₂ — диагонали трапеции

α , β — углы между диагоналями

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции , ( m ):

4. Формула средней линии трапеции через площадь и высоту (для всех видов трапеции)

S — площадь трапеции

h — высота трапеции

m — средняя линия

Трапеция. Формулы, признаки и свойства трапеции

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Основы трапеции — параллельные стороны
Боковые стороны — две другие стороны
Средняя линия — отрезок, соединяющий середины боковых сторон.

Равнобедренная трапеция — трапеция, у которой боковые стороны равны
Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам

Основные свойства трапеции

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

BC : AD = OC : AO = OB : DO

d ₁ 2 + d ₂ 2 = 2 a b + c 2 + d 2

Сторона трапеции

Формулы определения длин сторон трапеции:

a = b + h · ( ctg α + ctg β )

b = a — h · ( ctg α + ctg β )

a = b + c· cos α + d· cos β

b = a — c· cos α — d· cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

Средняя линия трапеции

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

2. Формула определения длины средней линии через площадь и высоту:

Высота трапеции

Формулы определения длины высоты трапеции:

h = c· sin α = d· sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d ₁ d ₂	=	sin δ ·	d ₁ d ₂
a + b	a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d ₁ d ₂	=	sin δ ·	d ₁ d ₂
2 m	2 m

4. Формула высоты трапеции через площадь и длины оснований:

5. Формула высоты трапеции через площадь и длину средней линии:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

d ₁ = √ a 2 + d 2 — 2 ad· cos β

d ₂ = √ a 2 + c 2 — 2 ac· cos β

2. Формулы диагоналей через четыре стороны:

d ₁ =	√	d 2 + ab —	a ( d 2 — c 2 )
a — b

d ₂ =	√	c 2 + ab —	a ( c 2 — d 2 )
a — b

d ₁ = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2

d ₂ = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2

d ₁ = √ c 2 + d 2 + 2 ab — d ₂ 2

d ₂ = √ c 2 + d 2 + 2 ab — d ₁ 2

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

3. Формула площади через диагонали и угол между ними:

S =	d ₁ d ₂	· sin γ	=	d ₁ d ₂	· sin δ
2	2

4. Формула площади через четыре стороны:

S =	a + b	√	c 2 —	(	( a — b ) 2 + c 2 — d 2	)	2
2	2( a — b )

5. Формула Герона для трапеции

S =	a + b	√ ( p — a )( p — b )( p — a — c )( p — a — d )
\| a — b \|

где

p =	a + b + c + d	— полупериметр трапеции.
2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d ₁
4√ p ( p — a )( p — c )( p — d ₁)

где

a — большее основание

Окружность вписанная в трапецию

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
2	2	a + b

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Свойства прямоугольной трапеции

В данной статье мы расскажем Вам о свойствах прямоугольной трапеции, как обычной, так и той, в которую вписана окружность.

Для начала напомним некоторые основные определения.

Трапеция – это четырехугольник, имеющий 2 параллельные друг другу стороны, причем 2 другие стороны параллельными не являются.

Прямоугольная трапеция — это такая трапеция, одна из боковых сторон которой перпендикулярна ее основаниям (изображена на рис.).

Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон фигуры (на рис. EF).

Основные свойства прямоугольной трапеции

Средняя линия EF равна половине суммы ее оснований BC и AD.

Средняя линия EF параллельна основаниям трапеции BC и AD.

На одной прямой размещаются:

точка пересечения (H) диагоналей прямоугольной трапеции AC и BD;
точка пересечения (E) продолжений боковых сторон трапеции AB и CD;
середины (F и G) оснований трапеции BC и AD.

Данным свойством обладает как прямоугольная, так и равносторонняя трапеция.

Свойства прямоугольной трапеции, в которую вписана окружность

S_ABCD = BC * AD

Узнать подробнее о свойствах трапеции с прямым углом, в которую вписана окружность, а также ознакомиться с доказательствами этих свойств, можно на сайте uznateshe.ru.

Понравилась статья, расскажите о ней друзьям:

источники:

http://ru.onlinemschool.com/math/formula/trapezium/

http://people-ask.ru/nauki/geometriya/svojstva-pryamougolnoj-trapecii

Источник

Средняя линия прямоугольной трапеции

Средняя линия прямоугольной трапеции — это отрезок, который соединяет средины двух боковых сторон фигуры и является параллельным ее основаниям (MK).

Свойство средней линии

Средняя линия трапеции (косоугольной и прямоугольной) параллельна основаниям фигуры и равна половине их суммы.

Пример задачи

Условие:

Средняя линия трапеции (прямоугольной) равна 9 см. Одно основание в 2 раза больше другого. Острый угол при основании а равен 45 градусов. Нужно найти площадь трапеции.

Решение:

Средняя линия равняется полусумме оснований, таким образом, сумма оснований: 2*9 = 18 см.
Примем размер меньшего основания как х, тогда размер большего – 2х. Исходя из этого:

18 = х+2х -> 18=3х -> х = 6 см
Второе основание: 2*6 = 12 см.
Опустим на большее основание высоту. Она отсечет от фигуры равнобедренный прямоугольный треугольник (так как оба угла будут равны 45 градусам), один катет которого будет высотой, а второй — частью большего основания.
Второй катет находится как разница между большим основанием и меньшим: 12 — 6 = 6 см.
Так как треугольник равнобедренный, то высота равняется 6 см.
Площадь прямоугольной трапеции равняется произведению средней линии на высоту:
S = 9*6=54 см²

Существует также понятие второй средней линии – это отрезок, который соединяет средины оснований трапеции.

Источник

Трапеция и ее свойства

Т. А. Унегова

Определения:

Трапеция — это называется четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.

Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами трапеции.

Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

Если боковые стороны равны, трапеция называется равнобедренной.

Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание.

Трапеция называется вписанной в окружность, если каждая ее вершина принадлежит окружности.

Трапеция называется описанной вокруг окружности, если каждая ее сторона касается окружности.

Трапеция называется равнобедренной (равнобокой, равнобочной), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Теоремы о средней линии и диагоналях трапеции

Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме: $m=displaystyle frac{a+b}{2}$ .

Теорема 2. Диагонали трапеции делят среднюю линию трапеции на три отрезка. Средний из них равен полуразности оснований, а два крайних равны между собой: $EF=GH, ; FG=displaystyle frac{a-b}{2}$ .

Теорема 3. Средняя линия треугольника, составленного из диагоналей и суммы оснований трапеции, равна средней линии трапеции: PQ=MN .

Теорема 4. Четыре точки: середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон — лежат на одной прямой.

Эта теорема называется также «Замечательное свойство трапеции».

Теорема 5. Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.

Теоремы о площади трапеции

Теорема 6. Площадь трапеции равна произведению полусуммы ее оснований на высоту: $S=displaystyle frac{a+b}{2}cdot h$ .

Теорема 7. Площадь трапеции равна произведению ее средней линии на высоту: S=mh .

Теорема 8. Площадь трапеции (как и всякого выпуклого четырехугольника) равна половине произведения ее диагоналей на синус угла между ними: $S=displaystyle frac{1}{2}d_1d_2{sin alpha }$ , где d_1=AC, d_2=BD, (Вместо можно брать

Теорема 9. Если в трапецию можно вписать окружность, то (как и для всякого описанного многоугольника) площадь трапеции равна произведению ее полупериметра на радиус вписанной окружности: S=pr . Таким образом, $S=displaystyle frac{a+b+c+d}{2}cdot r$ .

Теорема 10. Площадь трапеции равна площади треугольника, составленного из диагоналей и суммы оснований этой трапеции. (Сравни эту теорему и теорему 3.)

Теоремы о вписанных и описанных трапециях

Теорема 11. Если трапеция вписана в окружность, то она равнобедренная. И наоборот, если трапеция равнобедренная, то около нее можно описать окружность.

Теорема 12. Если трапеция описана около окружности, то сумма оснований трапеции равна сумме ее боковых сторон.

Задачи ЕГЭ и ОГЭ по теме: Трапеция

Задача 1.

Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны sqrt{2} .

Решение:

Высота трапеции— это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины . Так как сторона квадратной клетки равна sqrt{2} , то по теореме Пифагора получаем, что h=2 .

Ответ: 2.

Задача 2.

Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол ${150}^{{}^circ }$ . Найдите площадь трапеции.

Решение:

Углы angle ABC и angle BAH — односторонние, их сумма равна ${180}^{{}^circ }$ , и тогда angle BAH $=30{}^circ .$

Из ABH найдем высоту BH. Катет, лежащий против угла в ${30}^{{}^circ }$ , равен половине гипотенузы. Получаем, что BH = 3,5.

Площадь трапеции равна $S=displaystyle frac{6+18}{2}cdot 3,5=42$ .

Ответ: 42.

Задача 3.

Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.

Решение:

Что можно увидеть на чертеже? Можно сказать, что изображена трапеция ABCD, и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, ABC и ACD, в которых проведены средние линии.

Напомним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны. Из ACD находим, что x=5.

Ответ: 5.

Задача 4.

Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Решение:

Проведем PQ — среднюю линию трапеции, PQ = 2,5 и . Отсюда получаем, что середина отрезка AC, то есть PM — средняя линия треугольника ABC и PM = 1. Аналогично, NQ = 1.

Ответ: 0,5.

Задача 5.

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Решение:

Периметр треугольника равен сумме его сторон, то есть

Периметр трапеции равен

Ответ: 23.

Задача 6.

В равнобедренной трапеции ABCD диагональ AC является биссектрисой острого угла трапеции и образует со стороной CD угол $63{}^circ$ . Найдите углы трапеции.

Решение:

Пусть angle CAD =alpha , тогда angle CAB =alpha и angle BAD =2alpha , так как трапеция равнобедренная.

Сумма углов $vartriangle ACD=3alpha +63{}^circ =180{}^circ$ , откуда
$alpha =39{}^circ .$
Итак, $angle D=78{}^circ$ , а $angle BCD=180{}^circ -78{}^circ =102{}^circ$ .

Ответ: $78{}^circ , 102{}^circ$ .

Задача 7.

В равнобедренной трапеции основания равны 10 м и 24 м, боковая сторона 25 м. Найдите высоту трапеции.

Решение:

В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и $h^2={25}^2-7^2=left(25-7right)left(25+7right)=18cdot 32.$ Отсюда,

Ответ: 24.

Задача 8.

Тупой угол равнобедренной трапеции равен ${135}^circ$ , а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.

Решение:

Проведем две высоты. Они разделят трапецию на три части: прямоугольник и два равных прямоугольных треугольника с острым углом $45{}^circ$ .

Каждый треугольник равнобедренный, поэтому h = 1,4.

Нетрудно видеть, что верхнее основание трапеции равно 2, а нижнее — 4,8. Отсюда площадь трапеции равна $displaystyle frac{2+4,8}{2}cdot 1,4=4,76$ .

Ответ: 4,76.

Задача 9.

Площадь трапеции равна 60м ^2, а основания 8 м и 12 м. Найдите высоту трапеции.

Решение:

Так как площадь трапеции $S=displaystyle frac{a+b}{2}cdot h$ , то $60=displaystyle frac{8+12}{2}cdot h$ , откуда h = 6.

Ответ: 6.

Задача 10.

В равнобедренной трапеции диагонали перпендикулярны и равны Найдите площадь трапеции.

Решение:

Проведем CE BD и DE — продолжение AD.

Так как BCDE — параллелограмм, то CE = a.

По теореме 10 получим, что $S_{ABCD}=S_{ACE}=displaystyle frac{1}{2}a^2$ .

Ответ: $displaystyle frac{1}{2}a^2$

Задач 11.

В трапеции ABCD с большим основанием AD диагональ AC перпендикулярна к боковой стороне CD и является биссектрисой угла A.

Найдите AD, если периметр трапеции равен 20, а угол D равен $60{}^circ$ .

Решение:

По условию задачи в прямоугольном ACD

angle D $=60{}^circ$ , следовательно, angle CAD $=30{}^circ$ .

Так как AC — биссектриса, то angle CAB $=30{}^circ$ , откуда angle DAB $=60{}^circ$ , то есть, трапеция равнобедренная. angle BCA =angle CAD $=30{}^circ$ как накрест лежащие, поэтому ABC — равнобедренный.

Обозначим длины боковых сторон ABC буквой x.

Тогда AB = BC = CD = x, и AD = 2x, так как в прямоугольном ACD против угла в $30{}^circ$ лежит катет, равный половине гипотенузы.

Таким образом, периметр трапеции, равный 20, составляет 5x, отсюда

x = 4 и AD = 8.

Ответ: 8.

Задача 12.

В равнобедренной трапеции ABCD с острым углом $60{}^circ$ меньшее основание BC равно 2, а боковая сторона AB равна 10. Продолжения боковых сторон трапеции пересекаются в точке M. Во сколько раз площадь трапеции больше площади треугольника BCM?

Решение:

Нетрудно видеть, что BCM равносторонний и BM = 2, тогда AM = 12 и BCM подобен ADM c коэффициентом .

Пусть $S_{BCM}$ =S_1 , $S_{ADM}=S_2$ , тогда

$S_2=k^2cdot S_1=36{cdot S}_1.$

Площадь трапеции будет равна

$S_{ABCD}=S_2-S_1=36 S_1-S_1=35 S_1=35 S_{BCM}.$

Ответ: 35.

Задача 13.

Сумма углов при одном из оснований трапеции равна $90{}^circ$ . Найдите длину отрезка, соединяющего середины оснований, если основания равны 6 и 10.

Решение:

Продолжим боковые стороны до пересечения в точке E и отметим точки F и G — середины оснований трапеции.

Так как сумма углов при основании трапеции равна $90{}^circ$ , то $angle BEC=90{}^circ$ , поэтому EF и EG — медианы в прямоугольных треугольниках BEC и AED соответственно.

Известно, что медиана, проведенная к гипотенузе, равна ее половине, значит

Ответ: 2.

Задача 14.

Найдите радиус окружности, вписанной в равнобочную трапецию, если средняя линия трапеции равна 10, а ее площадь 24.

Решение:

Так как площадь трапеции равна S=mh , а высота трапеции равна диаметру вписанной окружности, то есть h=2r, то , откуда r=1,2 .

Ответ: 1,2.

Задача 15.

Периметр прямоугольной трапеции равен 32, а большая боковая сторона равна 10. Найдите радиус r вписанной в трапецию окружности.

Решение:

По свойствам описанной трапеции сумма ее боковых сторон равна сумме оснований, поэтому

откуда

Сторона AB равна диаметру окружности, поэтому r=3 .

Ответ: 3.

Задача 16.

Около окружности описана трапеция, сумма боковых сторон которой равна 40. Найдите длину ее средней линии.

Решение:

Длина средней линии трапеции равна полусумме оснований. Если трапеция описана вокруг окружности, то в ней сумма оснований равна сумме боковых сторон, поэтому

$m=displaystyle frac{a+b}{2}=displaystyle frac{c+d}{2}=displaystyle frac{40}{2}=20.$

Ответ: 20.

Задача 17.

В окружность вписана трапеция так, что диаметр окружности служит основанием трапеции, а вершины другого основания делят полуокружность на три равные части. Найдите тупые углы трапеции. Ответ выразите в градусах.

Решение:

Так как AD — диаметр окружности, то дуга ABCD равна $180{}^circ$ . Она делится на три равные части по $60{}^circ .$

Вписанный угол D опирается на дугу ABC, которая равна $120{}^circ$ , отсюда $angle ADC=60{}^circ$ и, стало быть, $angle C=120{}^circ =angle B.$

Ответ: 120.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Трапеция и ее свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции

Признаки прямоугольной трапеции

Основные свойства прямоугольной трапеции

Стороны прямоугольной трапеции

Формулы длин сторон прямоугольной трапеции:

Средняя линия прямоугольной трапеции

Формулы длины средней линии прямоугольной трапеции:

Все формулы средней линии прямоугольной трапеции

Трапеция. Формулы, признаки и свойства трапеции

Основные свойства трапеции

Сторона трапеции

Формулы определения длин сторон трапеции:

Средняя линия трапеции

Формулы определения длины средней линии трапеции:

Высота трапеции

Формулы определения длины высоты трапеции:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

Площадь трапеции

Формулы определения площади трапеции:

Периметр трапеции

Формула определения периметра трапеции:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

Окружность вписанная в трапецию

Формула определения радиуса вписанной в трапецию окружности

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

Свойства прямоугольной трапеции

Основные свойства прямоугольной трапеции

Свойства прямоугольной трапеции, в которую вписана окружность

SABCD = BC * AD

Средняя линия прямоугольной трапеции

Свойство средней линии

Пример задачи

Трапеция и ее свойства

Теоремы о средней линии и диагоналях трапеции

Теоремы о площади трапеции

Теоремы о вписанных и описанных трапециях

Задачи ЕГЭ и ОГЭ по теме: Трапеция

S_ABCD = BC * AD