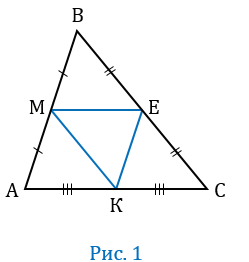
Для определения средней линии, и ее длины, вам нужно взять и разделить ту линию которой она параллельна, на два, на картинке как вы видите этой линией является АС. А средней линией МК, которая и есть по своей длине, не что иное, как половина линии АС.
автор вопроса выбрал этот ответ лучшим
Krisonerrr
[647]
8 лет назад
Для этого существует теорема о средней линии треугольника: средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. То есть, тебе будет достаточно знать длину третьей стороны, что бы найти среднюю линию треугольника.
-Irinka-
[282K]
4 года назад
Средняя линия треугольника — это линия, отрезок, который соединяет две стороны треугольника в их серединах.
При этом средняя линия треугольника всегда параллельна третьей стороне и равна 1/2 её длины.
Для того, чтобы найти длину средней линии нужно знать длину 3-ей параллельной линии и разделить её пополам.
moreljuba
[62.5K]
6 лет назад
Средняя линия треугольника по определению выступает в роли прямой, которая параллельна одной из его сторон и в свою же очередь равно половине той стороны, которой она и параллельна. Чтобы определить среднюю линию вам надо поделить параллельную сторону треугольника на 2.
Alexgroovy
[14.6K]
5 лет назад
По определению средняя линия является отрезком, соединяющим 2 стороны треугольника. При этом она параллельна третьей стороне и ее длина равняется ее половине.
Для треугольника ABC:
Длина средней линии MN находится так:
Птичка2014
[25.4K]
6 лет назад
Средняя длина треугольника найти очень легко. Она равна половине основания, которому параллельна. Так что рассчитать ее очень легко — надо основание поделить на два и это получится средняя длина треугольника.
Nelli4ka
[114K]
5 лет назад
Поможет в решении задачи свойство самой средней линии.
Так, она соединяет середины двух сторон, при этом являясь параллельным отрезком по отношению к третьей стороне. Но и это еще не все: средняя линия по длине равна половине третьей стороны, которой она параллельна.
Для этой теории есть свое доказательство:
Нам же останется только узнать, чему равна третья сторона, и поделить найденное значение пополам.
Кстати, за третью сторону по умолчанию берут основание треугольника.
FantomeRU
[13.3K]
5 лет назад
Средняя линия треугольника по определению — это отрезок, соединяющий середины двух сторон треугольника. В геометрии существует теорема, согласно которой средняя линия всегда будет параллельна основанию треугольника. А для того, чтобы высчитать её длину, нужно длину этого основания поделить пополам.
Алиса в Стране
[364K]
6 лет назад
Есть специальная теорема, которая очень просто и доходчиво объясняет и что такое средняя линия треугольника, и как вычислить ее длину.
Средняя линия, это линия параллельная основанию треугольника, а длина ее равна 1/2 этого основания.
Galina7v7
[120K]
7 лет назад
Пусть дан треугольник АВС, MN- средняя линия треугольника АВС,причём:
AM = MB, BN = NC,тогда средняя линия равна половине стороны,против которой она лежит , и которой она параллельна,то есть MN =AC2.
AHTOXA89
[5K]
5 лет назад
Средняя линия треугольника-Это отрезок соединяющий середины двух его сторон.Зная свойства средней линии,а также длины сторон треугольника и его углы,можно найти длину средней линии.На рисунки показано как найти длину средней линии:
Антон75
[206]
8 лет назад
средняя линия треугольника равна 1/2 основания
Знаете ответ?
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Средняя линия треугольника
Средняя линия треугольника — отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 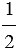




Теорема
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Доказательство
Дано: 
Доказать: МЕ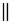
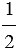
Доказательство:
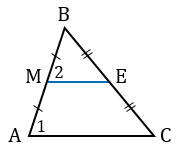
В треугольниках МВЕ и АВС:
Следовательно, треугольники МВЕ и АВС подобны (по 2 признаку подобия треугольников), поэтому 

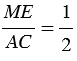
Прямые МЕ и АС пересечены секущей АВ, углы 1 и 2 — соответственные, при этом 

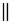
Из равенства 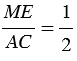
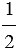
Задача:
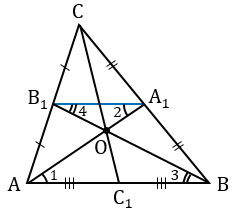
Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Дано: 
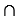
Доказать: АА1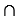
Доказательство:
Проведем среднюю линию В1А1 треугольника 
А1В1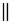








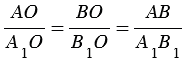
Так как А1В1 — средняя линия, А1В1 = 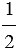
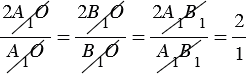
Следовательно, точка О, в которой пересекаются медианы АА1 и ВВ1 делит каждую из них в отношении 2 : 1, считая от вершины.
Аналогично доказывается, что точка пересечения медиан ВВ1 и СС1 делит каждую из них в отношении 2 : 1, считая от вершины, и, значит, совпадает с точкой О.
Итак, все три медианы 
Советуем посмотреть:
Пропорциональные отрезки
Определение подобных треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 570,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 733,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 794,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 797,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 857,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 858,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 861,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 866,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 910,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1278,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Треугольник — геометрическая фигура, составленная из трёх отрезков. Они объединены тремя точками, не
лежащие в единственной прямой. Такие отрезки обычно именуют сторонами, а заданные точки — вершинами.
Средняя линия такого многоугольника — отрезок, объединяющий средины двух сторон.
Во всяком
треугольнике можно проложить три средних линии. В прямоугольном многоугольнике такой отрезок
равняется половине основания. Средняя линия прямоугольного треугольника разделяет его на четыре
прямоугольных треугольника. Существует и признак срединного отрезка треугольника: если отрезок в
многоугольнике пролегает через средину одной из его сторон, пересекает вторую и параллелен ей, тогда
такой отрезок называется средней линией.
Выделяют свойства срединного отрезка:
- Средняя линия равняется половине длины основания и параллельна ему;
- Этот отрезок отделяет треугольник, подобный заданному с коэффициентом 0.5, а его площадь
равняется четверти площади заданной фигуры; - Три средние линии дробят заданный многоугольник на четыре других, эквивалентных друг другу.
Находящуюся по центру фигуру именуют дополнительной.
- Средняя линия треугольника через сторону
- Средняя линия равностороннего треугольника через высоту
- Средняя линия равностороннего треугольника через радиус
вписанной окружности - Средняя линия равностороннего треугольника через радиус
описанной окружности - Средняя линия треугольника через площадь и высоту
- Средняя линия равнобедренного треугольника через боковую
сторону и высоту - Средняя линия равностороннего треугольника через
площадь
Через сторону
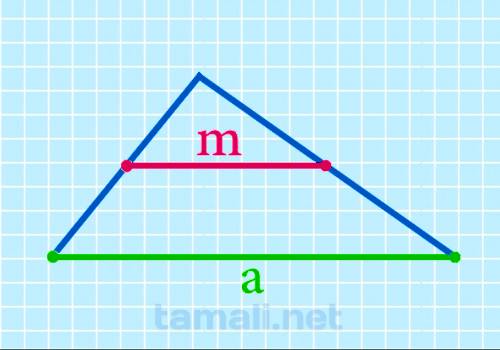
Срединный отрезок равняется половине противолежащей стороны. Следовательно, формула выглядит так:
m = a/2
где a — противолежащая сторона.
Цифр после
запятой:
Результат в:
Следовательно, если такая сторона будет равна 50, то срединный отрезок будет равен m = 50/2 = 25. Если же сторона будет равна 20, тогда срединный отрезок
будет рассчитываться так: m = 20/2 = 10.
Средняя линия равностороннего треугольника через радиус вписанной окружности
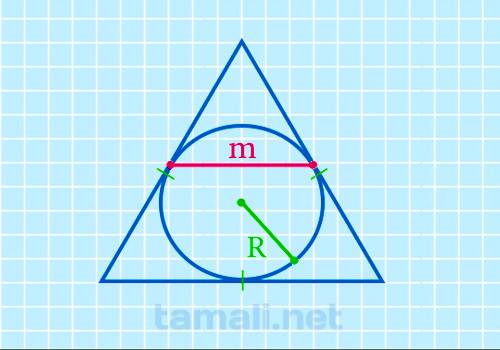
Срединный отрезок равностороннего многоугольника через радиус вписанной окружности высчитывается
так:
m = r√3
где r — радиус вписанной окружности.
Цифр после
запятой:
Результат в:
Таким образом, если радиус такой окружности равняется 5, тогда m= 5√3 ≈ 8,66. Если же радиус будет равен, допустим, 9, в таком случае
m = 9√3 ≈ 15,59.
Средняя линия треугольника через площадь и высоту
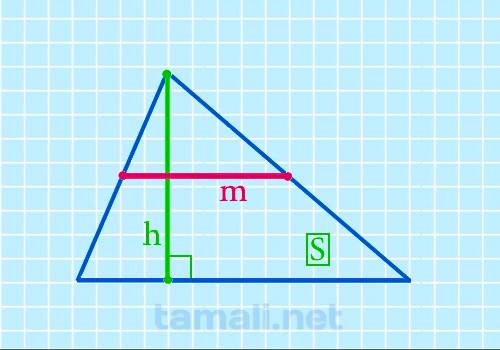
Срединный отрезок многоугольника равен частному площади и высоты, перпендикулярной этой средней
линии. Таким образом, тождество имеет такой вид:
m = S/h
где S — это площадь, а h — перпендикуляр, ортогональный срединному отрезку.
Цифр после
запятой:
Результат в:
Если площадь некоторого многоугольника будет равна 25, а перпендикуляр — 5, тогда m = 25/5 = 5. Если
же в качестве площади взять число 60, а в качестве перпендикуляра — 3, получится следующий срединный
отрезок: m = 60/3 = 20.
Средняя линия равностороннего треугольника через высоту
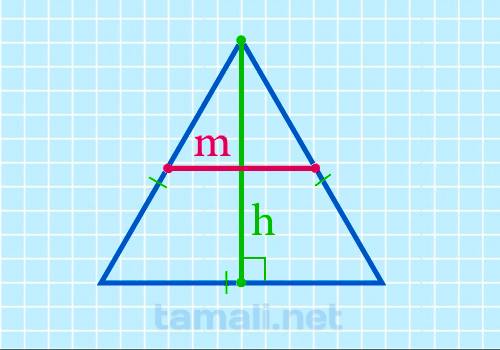
Срединный отрезок равностороннего многоугольника через перпендикуляр высчитывается следующим
образом:
m = h/√3
где h — перпендикуляр равностороннего многоугольника.
Цифр после
запятой:
Результат в:
К примеру, если перпендикуляр равностороннего многоугольника равен 5, тогда срединный отрезок будет
такой: m = 5/√3 ≈ 2,89.
Если же перпендикуляр будет равен 10, тогда
срединный отрезок будет около m = 10/√3 ≈ 5,77.
Средняя линия равнобедренного треугольника через боковую сторону и высоту
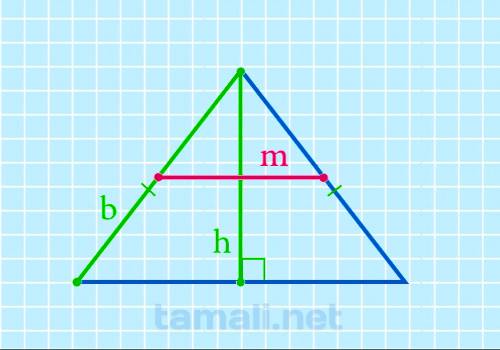
Срединный отрезок равнобедренного многоугольника через боковую сторону и высоту вычисляется следующим
образом:
m = a2 – h2
где a — боковая сторона, а h — перпендикуляр.
Цифр после
запятой:
Результат в:
Допустим, если боковая сторона многоугольника равна 5, а перпендикуляр — 3, тогда m = 25 – 9 = 16.
Если же в качестве боковой стороны взять число 8, а в качестве перпендикуляра равнобедренного
многоугольника — 2, в таком случае m = 64 – 4 = 60.
Средняя линия равностороннего треугольника через площадь
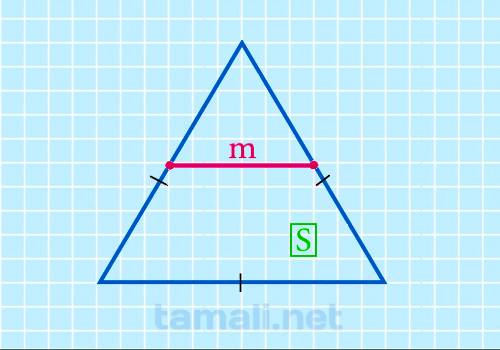
Срединный отрезок равнобедренного многоугольника через площадь находится по следующей формуле:
m = 1/4 √(√3/S)
где S — это площадь равностороннего многоугольника.
Цифр после
запятой:
Результат в:
Допустим, если площадь равностороннего многоугольника будет равна 5, тогда m = 1/4 √(√3/5) ≈ 0,15.
Если выбрать равносторонний многоугольник побольше, к примеру, с площадью 25, в таком случае m = 1/4 √(√3/25) ≈ 0,065.
Средняя линия равностороннего треугольника через радиус описанной окружности
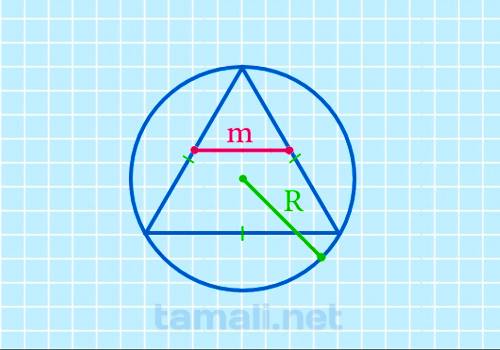
Срединный отрезок равностороннего многоугольника через радиус описанной окружности высчитывается
так:
m = R√3/2
где R — радиус описанной окружности.
Цифр после
запятой:
Результат в:
Следовательно, если радиус такой окружности будет равен 15, тогда m = 15√3/2 =12,99. Если в качестве
радиуса взять число 24, в таком случае m = 24√3/2 = 20,78.
Средняя линия фигур в планиметрии — отрезок, который объединяет средины двух сторон представленной
фигуры. Такой термин используется при описании треугольников, четырёхугольников и трапеций. В
некоторых случаях рассматривается вырожденный треугольник, три вершины которого пролегают на
единственной прямой. Треугольник считается одной из основных геометрических фигур, повсюду
применяемых в науке и технике, потому изучение его качеств велось с давних времён.
Средняя линия треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией этого треугольника.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
В каждом треугольнике — три средних линии.
Средние линии (DE), (EF), (DF).
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией этой трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
У трапеции — только одна средняя линия.
Источники:
Рис. 1-3. Треугольник, трапеция, © ЯКласс.
В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.
- Определение средней линии треугольника
-
Свойства средней линии треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Признак средней линии треугольника
- Пример задачи
Определение средней линии треугольника
Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.
- KL – средняя линия треугольника ABC
- K – середина стороны AB: AK = KB
- L – середина стороны BC: BL = LC
Свойства средней линии треугольника
Свойство 1
Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.
На рисунке выше:
- KL параллельна AC
- KL = 1/2 ⋅ AC
Свойство 2
Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.
На рисунке выше:
- △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
- Стороны △KBL в два раза меньше соответствующих сторон △ABC:
AB = 2KB, BC = 2BL, AC = 2KL. - S△ABC = 4 ⋅ S△KBL
Свойство 3
В любом треугольнике можно провести три средние линии.
KL, KM и ML – средние линии треугольника ABC.
- KL || AC, KL = 1/2 ⋅ AC
- KM || BC, KM = 1/2 ⋅ BC
- ML || AB, ML = 1/2 ⋅ AB
Свойство 4
Три средние линии треугольника делят его на 4 равных по площади треугольника.
S1 = S2 = S3 = S4
Признак средней линии треугольника
Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.
Пример задачи
Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.
Решение
Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.
Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.
BC2 = AB2 + AC2 = 62 + 82 = 100.
BC = 10.
Таким образом, средняя линия LM = 1/2 ⋅ BC = 1/2 ⋅ 10 = 5.