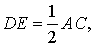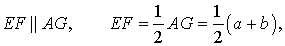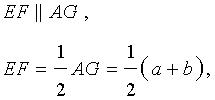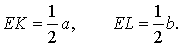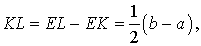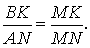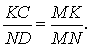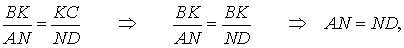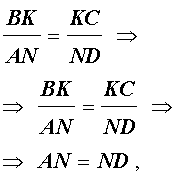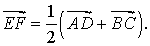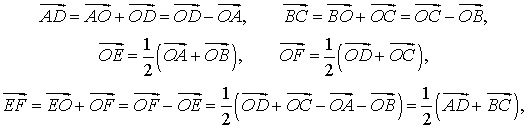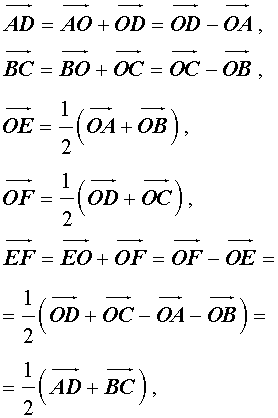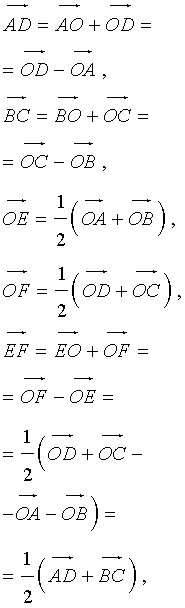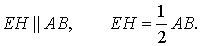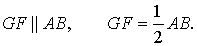Как найти среднюю линию треугольника по точкам - Исправление недочетов и поиск решений вместе с Examum.ru

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Средние линии

Средние линии треугольника

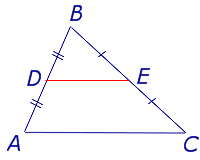
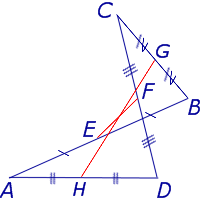
Определение . Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

На рисунке 1 средней линией является отрезок DE .

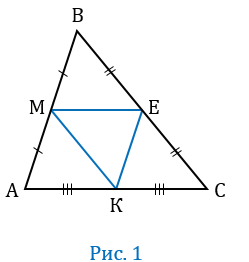
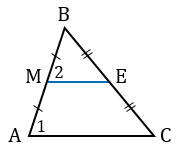
Утверждение 1 . Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.

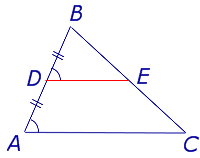
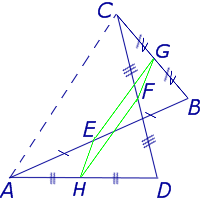
Доказательство . Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .

Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.

Первую часть утверждения 1 мы доказали.

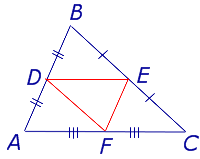
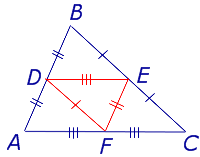
Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).

Но поскольку AF = FC , то отсюда вытекает равенство

что и требуется доказать.

Доказательство утверждения 1 закончено.

Три средних линии делят треугольник на 4 равных треугольника ADF , DBE , ECF , DEF (рис. 4).
Каждый из четырёх треугольников ADF , DBE , ECF , DEF подобен треугольнику ABC с коэффициентом подобия 0,5 .

Средняя линия трапеции

Напомним, что трапецией трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.

Параллельные стороны трапеции называют основаниями , а непараллельные стороны – боковыми сторонами трапеции.

Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.

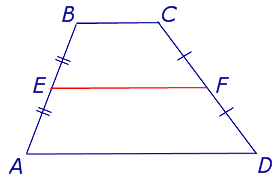
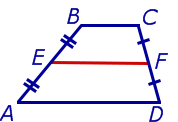
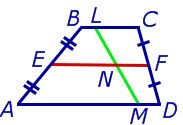
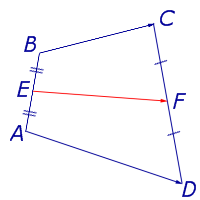
Определение . Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).

На рисунке 5 средней линией трапеции является отрезок EF .

Утверждение 2 . Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.

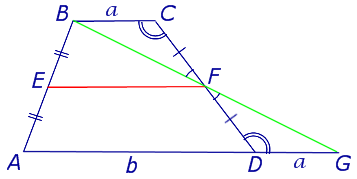
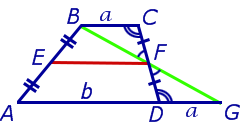
Доказательство . Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому

что и требовалось доказать.

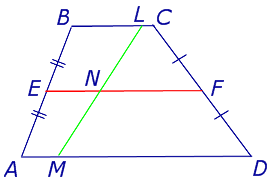
Задача 1 . Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.

Решение . Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.

Задача 2 . Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.

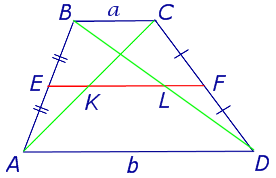
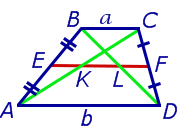
Решение . Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:

что и требовалось доказать.

Утверждение 3 . Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

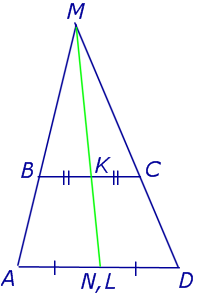
Доказательство . Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:

Из этих соотношений получаем:

откуда вытекает, что точки N и L совпадают. Доказательство завершено.

Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.

Утверждение 4 . Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.

Следствие . Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.

Средние линии четырехугольника. Теорема Вариньона

Определение . Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.

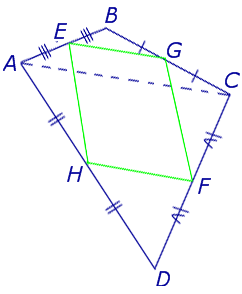
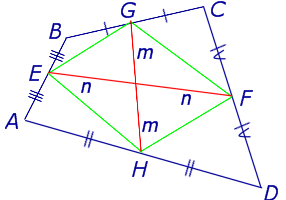
Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).

На рисунке 10 средние линии – это отрезки EF и GH .

Замечание 1 . Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.

На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .

Замечание 2 . Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.

Замечание 3 . В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.

Теорема Вариньона . Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограмма параллелограмма .

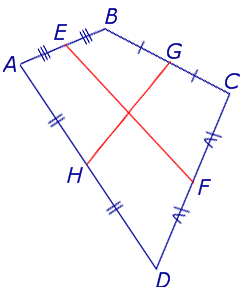
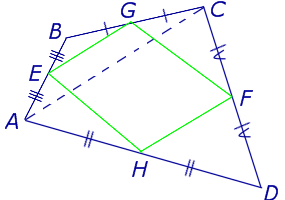
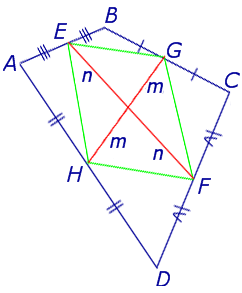
Доказательство . Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.

Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограмма признака параллелограмма признака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.

Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).

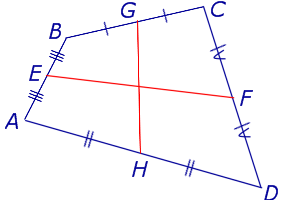
Утверждение 5 . Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).

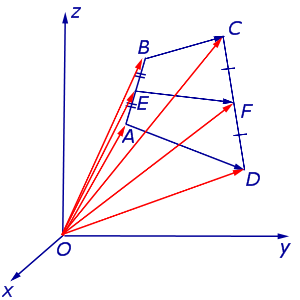
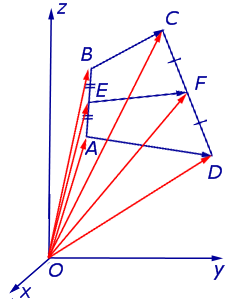
Утверждение 6 . Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:

что и требовалось доказать.

Следствие . Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.

Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапецией трапецией , а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.

Средние линии тетраэдра

Тетраэдром называют произвольную треугольную пирамиду (рис.17).

У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер . На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых .

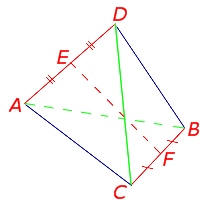
Определение . Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.

У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.

Утверждение 7 . Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.

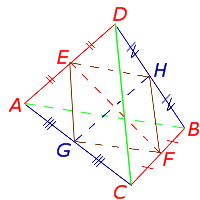
Доказательство . Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).

Заметим, что отрезок EH является средней линией треугольника ADB , поэтому

Определение . Точку пересечения средних линий тетраэдра называют центроидом тетраэдра .

Утверждение 8 . Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:

источники:

http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik

http://www.resolventa.ru/spr/planimetry/mline.htm

Источник

Как составить уравнение средней линии треугольника по координатам его вершин? Как записать уравнение средней линии трапеции?

Для решения этих задач используем свойства средней линии треугольника и средней линии трапеции.

1 способ

Найти координаты середин двух сторон и составить уравнение прямой, проходящей через две найденные точки.

Пример.

1) Написать уравнение прямой, содержащей среднюю линию треугольника с вершинами в точках A(-2;-4), B(1;6), C(7;0), пересекающей стороны AB и BC в точках M и N.

Решение:

М — середина отрезка AB, N — середина BC.

По формулам координат середины отрезка

$[x_M = frac{{x_A + x_B }}{2} = frac{{ - 2 + 1}}{2} = - frac{1}{2};]$

$[y_M = frac{{y_A + y_B }}{2} = frac{{ - 4 + 6}}{2} = 1;]$

$[x_N = frac{{x_B + x_C }}{2} = frac{{1 + 7}}{2} = 4;]$

$[y_N = frac{{y_B + y_C }}{2} = frac{{6 + 0}}{2} = 3.]$

Таким образом,

$[M( - frac{1}{2};1),N(4;3).]$

Составим уравнение прямой MN, например, в виде y=kx+b:

$[left{ begin{array}{l} 1 = k cdot ( - frac{1}{2}) + b; \ 3 = k cdot 4 + b; \ end{array} right.]$

Отсюда

$[k = frac{4}{9},b = frac{{11}}{9},]$

$[y = frac{4}{9}x + frac{{11}}{9},9y = 4x + 11,4x - 9y + 11 = 0.]$

2 способ

Найти координату одной из точек средней линии и составить уравнение прямой, параллельной стороне треугольника.

Решение:

$[M( - frac{1}{2};1)]$

— середина отрезка AB. Составим уравнение прямой AC:

$[left{ begin{array}{l} - 4 = k cdot ( - 2) + b; \ 0 = k cdot 7 + b; \ end{array} right.]$

$[k = frac{4}{9},b = - frac{{28}}{9}, Rightarrow y = frac{4}{9}x - frac{{28}}{9}.]$

Составим уравнение прямой MN как уравнение прямой, проходящей через точку M и параллельной прямой AC.

Угловой коэффициент прямой MN равен угловому коэффициенту прямой AC:

$[k_{MN} = k_{AC} = frac{4}{9},]$

то есть уравнение прямой MN ищем в виде

$[y = frac{4}{9}x + b.]$

Поскольку точка M принадлежит прямой, её координаты удовлетворяют этому уравнению. Отсюда находим значение b:

$[1 = frac{4}{9} cdot ( - frac{1}{2}) + b, Rightarrow b = 1 + frac{2}{9} = frac{{11}}{9}.]$

Таким образом, уравнение прямой MN

$[y = frac{4}{9}x + frac{{11}}{9}]$

или

Аналогичные рассуждения применимы и при составлении уравнения средней линии трапеции.

Написать уравнение прямой, содержащей среднюю линию трапеции с вершинами в точках A(-2;1), B(1;5), C(4;-1), D(0;-3).

Решение:

1 способ

Сначала следует определить основания данной трапеции.

Составим уравнения сторон AD и BC. Если эти прямые параллельны, то AD и BC — основания трапеции. Если эти прямые не параллельны, то основания трапеции — AB и CD.

A(-2;1), D(0;-3), отсюда

$[left{ begin{array}{l} 1 = k cdot ( - 2) + b; \ - 3 = k cdot 0 + b; \ end{array} right. Rightarrow k = - 2,b = - 3.]$

Значит, уравнение прямой AD: y= -2k-3.
B(1;5), C(4;-1),

$[left{ begin{array}{l} 5 = k cdot 1 + b; \ - 1 = k cdot 4 + b; \ end{array} right. Rightarrow k = - 2,b = 7.]$

Уравнение прямой BC: y= -2k+7.

Поскольку угловые коэффициенты прямых равны:

$[k_{AD} = k_{BC} = - 2,]$

то AD ∥BC, то есть AD и BC являются основаниями трапеции ABCD. Значит AB и CD — боковые стороны. Найдём координаты точек M и N — середины AB и CD соответственно.

$[x_M = frac{{x_A + x_B }}{2} = frac{{ - 2 + 1}}{2} = - frac{1}{2},]$

$[y_M = frac{{y_A + y_B }}{2} = frac{{1 + 5}}{2} = 3,]$

$[x_N = frac{{x_C + x_D }}{2} = frac{{4 + 0}}{2} = 2,]$

$[y_N = frac{{y_C + y_D }}{2} = frac{{ - 1 + ( - 3)}}{2} = - 2.]$

Составим уравнение прямой MN, M(-1/2;3), N(2;-2):

$[left{ begin{array}{l} 3 = k cdot ( - frac{1}{2}) + b; \ - 2 = k cdot 2 + b; \ end{array} right. Rightarrow k = - 2,b = 2,]$

то есть y=-2k+2.

2 способ

Уравнение AD — y= -2k-3, середина AB — M(-1/2;3). Составляем уравнение прямой MN, параллельной прямой AD.

$[k_{MN} = k_{AD} = - 2.]$

Значит уравнение MN ищем в виде y= -2x+b.

Так как прямая проходит через точку M, её координаты удовлетворяют уравнению прямой:

$[3 = - 2 cdot ( - frac{1}{2}) + b, Rightarrow b = 2.]$

Следовательно, уравнение средней линии трапеции ABCD имеет вид y=-2x+2 или 2x+y-2=0.

Источник

Треугольник — геометрическая фигура, составленная из трёх отрезков. Они объединены тремя точками, не
лежащие в единственной прямой. Такие отрезки обычно именуют сторонами, а заданные точки — вершинами.
Средняя линия такого многоугольника — отрезок, объединяющий средины двух сторон.

Во всяком
треугольнике можно проложить три средних линии. В прямоугольном многоугольнике такой отрезок
равняется половине основания. Средняя линия прямоугольного треугольника разделяет его на четыре
прямоугольных треугольника. Существует и признак срединного отрезка треугольника: если отрезок в
многоугольнике пролегает через средину одной из его сторон, пересекает вторую и параллелен ей, тогда
такой отрезок называется средней линией.

Выделяют свойства срединного отрезка:

Средняя линия равняется половине длины основания и параллельна ему;
Этот отрезок отделяет треугольник, подобный заданному с коэффициентом 0.5, а его площадь
равняется четверти площади заданной фигуры;
Три средние линии дробят заданный многоугольник на четыре других, эквивалентных друг другу.
Находящуюся по центру фигуру именуют дополнительной.

Средняя линия треугольника через сторону
Средняя линия равностороннего треугольника через высоту
Средняя линия равностороннего треугольника через радиус
вписанной окружности
Средняя линия равностороннего треугольника через радиус
описанной окружности
Средняя линия треугольника через площадь и высоту
Средняя линия равнобедренного треугольника через боковую
сторону и высоту
Средняя линия равностороннего треугольника через
площадь

Через сторону

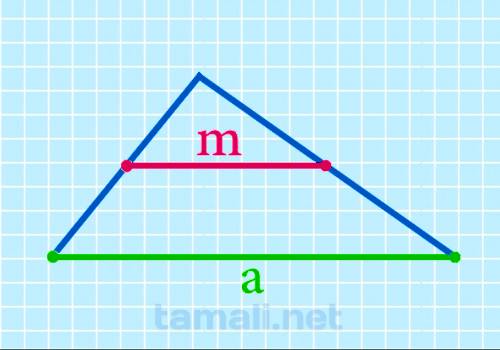
Срединный отрезок равняется половине противолежащей стороны. Следовательно, формула выглядит так:

m = a/2

где a — противолежащая сторона.

Цифр после
запятой:

Результат в:

Следовательно, если такая сторона будет равна 50, то срединный отрезок будет равен m = 50/2 = 25. Если же сторона будет равна 20, тогда срединный отрезок
будет рассчитываться так: m = 20/2 = 10.

Средняя линия равностороннего треугольника через радиус вписанной окружности

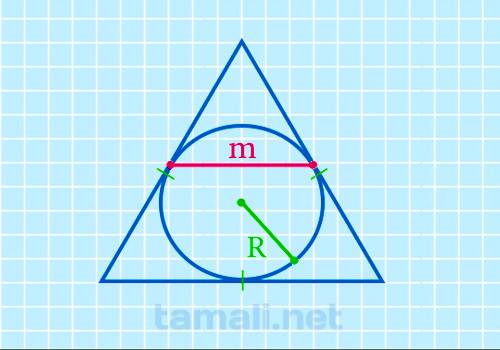
Срединный отрезок равностороннего многоугольника через радиус вписанной окружности высчитывается
так:

m = r√3

где r — радиус вписанной окружности.

Цифр после
запятой:

Результат в:

Таким образом, если радиус такой окружности равняется 5, тогда m= 5√3 ≈ 8,66. Если же радиус будет равен, допустим, 9, в таком случае
m = 9√3 ≈ 15,59.

Средняя линия треугольника через площадь и высоту

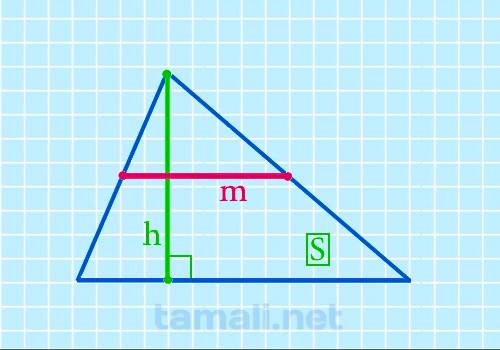
Срединный отрезок многоугольника равен частному площади и высоты, перпендикулярной этой средней
линии. Таким образом, тождество имеет такой вид:

m = S/h

где S — это площадь, а h — перпендикуляр, ортогональный срединному отрезку.

Цифр после
запятой:

Результат в:

Если площадь некоторого многоугольника будет равна 25, а перпендикуляр — 5, тогда m = 25/5 = 5. Если
же в качестве площади взять число 60, а в качестве перпендикуляра — 3, получится следующий срединный
отрезок: m = 60/3 = 20.

Средняя линия равностороннего треугольника через высоту

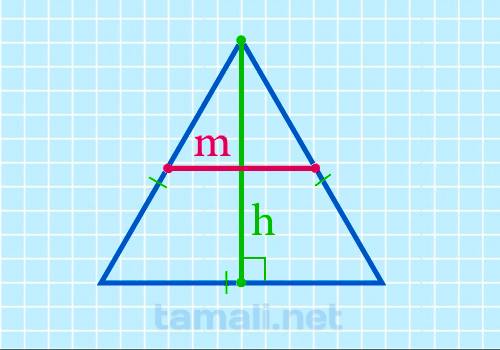
Срединный отрезок равностороннего многоугольника через перпендикуляр высчитывается следующим
образом:

m = h/√3

где h — перпендикуляр равностороннего многоугольника.

Цифр после
запятой:

Результат в:

К примеру, если перпендикуляр равностороннего многоугольника равен 5, тогда срединный отрезок будет
такой: m = 5/√3 ≈ 2,89.
Если же перпендикуляр будет равен 10, тогда
срединный отрезок будет около m = 10/√3 ≈ 5,77.

Средняя линия равнобедренного треугольника через боковую сторону и высоту

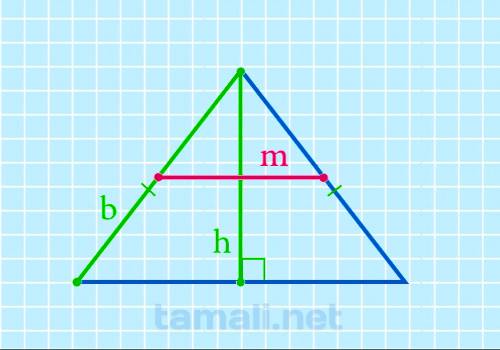
Срединный отрезок равнобедренного многоугольника через боковую сторону и высоту вычисляется следующим
образом:

m = a² – h²

где a — боковая сторона, а h — перпендикуляр.

Цифр после
запятой:

Результат в:

Допустим, если боковая сторона многоугольника равна 5, а перпендикуляр — 3, тогда m = 25 – 9 = 16.
Если же в качестве боковой стороны взять число 8, а в качестве перпендикуляра равнобедренного
многоугольника — 2, в таком случае m = 64 – 4 = 60.

Средняя линия равностороннего треугольника через площадь

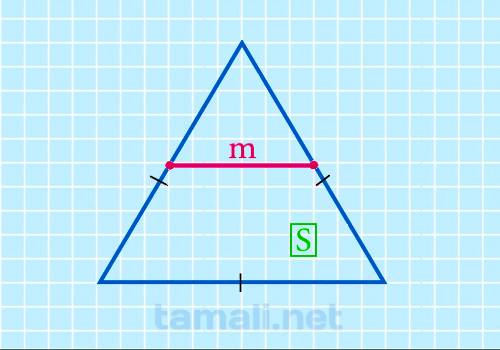
Срединный отрезок равнобедренного многоугольника через площадь находится по следующей формуле:

m = 1/4 √(√3/S)

где S — это площадь равностороннего многоугольника.

Цифр после
запятой:

Результат в:

Допустим, если площадь равностороннего многоугольника будет равна 5, тогда m = 1/4 √(√3/5) ≈ 0,15.
Если выбрать равносторонний многоугольник побольше, к примеру, с площадью 25, в таком случае m = 1/4 √(√3/25) ≈ 0,065.

Средняя линия равностороннего треугольника через радиус описанной окружности

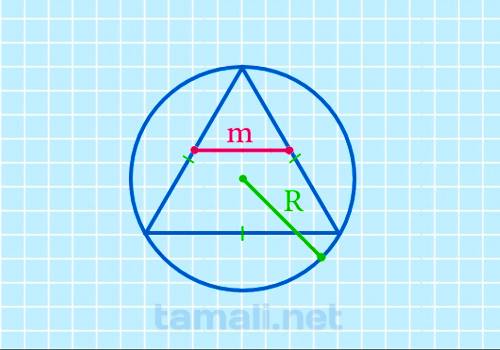
Срединный отрезок равностороннего многоугольника через радиус описанной окружности высчитывается
так:

m = R√3/2

где R — радиус описанной окружности.

Цифр после
запятой:

Результат в:

Следовательно, если радиус такой окружности будет равен 15, тогда m = 15√3/2 =12,99. Если в качестве
радиуса взять число 24, в таком случае m = 24√3/2 = 20,78.

Средняя линия фигур в планиметрии — отрезок, который объединяет средины двух сторон представленной
фигуры. Такой термин используется при описании треугольников, четырёхугольников и трапеций. В
некоторых случаях рассматривается вырожденный треугольник, три вершины которого пролегают на
единственной прямой. Треугольник считается одной из основных геометрических фигур, повсюду
применяемых в науке и технике, потому изучение его качеств велось с давних времён.

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Подобные треугольники
Средняя линия треугольника

Средняя линия треугольника — отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 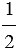. На рисунке 1 изображен треугольник АВС, отрезки МЕ, МК и КЕ являются средними линиями данного треугольника, ВМЕ =АМК =СЕК =МЕК.

Теорема

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Доказательство

Дано: АВС, МЕ — средняя линия.

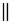
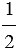
Доказать: МЕАС, МЕ = АС.

Доказательство:

В треугольниках МВЕ и АВС:

Следовательно, треугольники МВЕ и АВС подобны (по 2 признаку подобия треугольников), поэтому 1 =2 и .

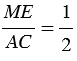
Прямые МЕ и АС пересечены секущей АВ, углы 1 и 2 — соответственные, при этом 1 =2, следовательно, МЕАС (по признаку параллельности двух прямых).

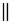
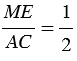
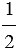
Из равенства следует, что МЕ = АС. Теорема доказана.

Задача:

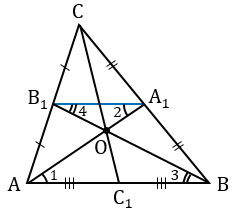
Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.

Дано: АВС, АА₁ и ВВ₁, СС₁ — медианы, АА₁ВВ₁ = О.

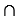
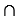
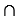
Доказать: АА₁ВВ₁СС₁ = О, АО : ОА₁ = ВО : ОВ₁ = СО : ОС₁ = 2 : 1.

Доказательство:

Проведем среднюю линию В₁А₁ треугольника АВС (В₁А₁ — средняя линия, т.к. по условию АА₁ и ВВ₁ — медианы, значит точки А₁ и В₁ — середины сторон АС и СВ).

А₁В₁АВ (по теореме, доказанной выше), АА₁ и ВВ₁— секущие, 1 и 2, 3 и 4 — накрест лежащие, значит, 1 =2, 3 =4 (по теореме о накрест лежащих углах). Следовательно, треугольники АОВ и А₁ОВ₁ подобны (по 1 признаку подобия), тогда сходственные стороны данных треугольников пропорциональны:

. (1)

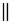
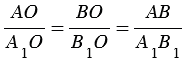
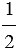
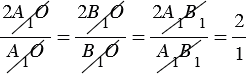
Так как А₁В₁ — средняя линия, А₁В₁ = АВ, откуда АВ = 2А₁В₁, поэтому АО = 2А₁О и ВО = 2В₁О. Подставляя три последних равенства в (1), получим:

Следовательно, точка О, в которой пересекаются медианы АА₁ и ВВ₁ делит каждую из них в отношении 2 : 1, считая от вершины.

Аналогично доказывается, что точка пересечения медиан ВВ₁ и СС₁ делит каждую из них в отношении 2 : 1, считая от вершины, и, значит, совпадает с точкой О.

Итак, все три медианы АВС пересекаются в точке О и делятся ею в отношении 2 : 1, считая от вершины. Что и требовалось доказать.

Советуем посмотреть:

Пропорциональные отрезки

Определение подобных треугольников

Отношение площадей подобных треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Пропорциональные отрезки в прямоугольном треугольнике

Практические приложения подобия треугольников

О подобии произвольных фигур

Синус, косинус и тангенс острого угла прямоугольного треугольника

Значение синуса, косинуса и тангенса для углов 30, 45 и 60

Подобные треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 564,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 565,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 570,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 616,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 618,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 858,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 861,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 866,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 996,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1286,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Содержание материала

Средняя линия треугольника + Задачи по теме
ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ
Видео
Понятие средней линии прямоугольного треугольника
Средняя линия
Важные свойства
Решение задачи
Формула для расчета
Примеры решения задач

Средняя линия треугольника + Задачи по теме

Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

Свойства средней линии треугольника: 1. Средняя линия параллельна третьей стороне и равна ее половине. 2. Средняя линия трeугольника отсекает от него треугольник, подобный данному (с коэффициентом подобия 1/2 ). 3. Три средние линии треугольника делят его на 4 равных треугольника, подобных данному, с коэффициентом подобия 1/2.

Свойство средней линии треугольника является следствием теоремы Фалеса.

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

Задача № 1. Дано: ΔABC; AB = 8 см; BC = 10 см; AC = 12 см; M — середина AB; N — середина BC; L — середина AC. Найти: MN, NL, ML.

Задача № 2.

Задача № 3. ΔABC; K — середина AB; O — середина BC; P — середина AC; P_ABC= 52 см. Найти: P_КOР

Задача № 4.

Это конспект по теме «Средняя линия треугольника + Задачи по теме». Выберите дальнейшие действия:

Перейти к следующему конспекту:
Вернуться к Списку конспектов по геометрии

Видео

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Важное свойство

Средняя линия прямоугольного треугольника делит его на четыре прямоугольных треугольника.

Средняя линия

Чтобы понять, как найти середину треугольника, можно воспользоваться обычной линейкой. Для этого необходимо выбрать произвольные две стороны фигуры. Затем отметить на каждой из них точки, отстоящие на одинаковом расстоянии от соответствующих вершин, которые ограничивают данную сторону. Полученные две точки следует соединить, чтобы начертить средний отрезок. Его название является интуитивно понятным каждому, поскольку он соединяет середины двух сторон.

Важные свойства

Существует три основных свойства, которыми обладает рассматриваемый отрезок. Пусть имеется треугольник произвольного типа ABC, в котором точки P и Q лежат на серединах сторон AB и AC соответственно. При таком обозначении отрезок PQ будет средней линией треугольника ABC. Справедливы следующие геометрические свойства:

Полученный треугольник APQ является подобным исходной фигуре ABC. Доказать это утверждение несложно, если обратить внимание на два факта: во-первых, угол A у обеих фигур является общим, во-вторых, отношение AB/AP равно величине AC/AQ и составляет 2 согласно выполненным геометрическим построениям. Таким образом, выполняется один из признаков подобия.
Длина средней линии PQ оказывается в два раза меньше, чем сторона BC. Кроме того, оба отрезка параллельны друг другу. Утверждение о равенстве PQ = ½*BC следует из факта подобия треугольников APQ и ABC, коэффициент которых составляет 2. Это равенство также можно доказать, если воспользоваться координатным методом.
Треугольник APQ имеет в 4 раза меньшую площадь, чем исходная фигура ABC.

Утверждение № 3 из списка справедливо для произвольного треугольника. Для его доказательства следует воспользоваться формулой Герона. Согласно ей, площадь рассматриваемой фигуры может быть вычислена следующим образом:

S = (p*(p-a)*(p-b)*(p-c))^0,5.

Здесь p = (a+b+c)/2 — полупериметр фигуры. Буквами a, b и c обозначены длины ее сторон. Пусть таким же образом обозначаются стороны для треугольника ABC. Тогда для фигуры APQ они будут иметь длины a/2, b/2 и c/2. Полупериметр для APQ составит величину p1 = (a+b+c)/4 = ½*p. Теперь необходимо подставить все известные величины в формулу Герона, получается площадь S1:

S1 = (p1*(p1-a/2)*(p1-b/2)*(p1-c/2))^0,5 = (½*p*(½*p-a/2)*(½*p-b/2)*(½*p-c/2))^0,5 = ¼*S.

Иными словами, площадь треугольника APQ составляет четвертую часть от этой величины для ABC.

Решение задачи

В треугольнике ABC проведен средний отрезок PQ, граничные точки которой P и Q находятся на сторонах AB и AC соответственно. Необходимо с использованием метода координат доказать, что эта линия имеет в два раза меньшую длину, чем сторона BC.

Прежде чем находить решение этой задачи, следует обозначить координаты вершин исходной фигуры. Они будут следующие:

A (x1, y1);
B (x2, y2);
C (x3, y3).

Поскольку точка P делит ровно пополам сторону AB, то для нахождения ее координат необходимо провести следующие вычисления:

P = ((x1+x2)/2, (y1+y2)/2).

Аналогичным образом рассчитываются координаты точки Q:

Q = ((x1+x3)/2, (y1+y3)/2).

Вспоминая формулу для длины вектора, координаты конца и начала которого известны, для средней линии PQ можно произвести следующие вычисления:

PQ = (((x1+x3)/2 — (x1+x2)/2)^2 + ((y1+y3)/2 — (y1+y2)/2)^2)^0,5 = ½*((x3-x2)^2 + (y3-y2)^2)^0,5.

В свою очередь, длина стороны BC равна:

BC = ((x3-x2)^2 + (y3-y2)^2)^0,5.

Из сопоставления этих двух равенств следует искомая формула, которую требовалось доказать:

PQ = ½*BC.

Поскольку в процессе доказательства были использованы произвольные координаты для вершин треугольника, полученный вывод является общим и универсальным для любого типа рассматриваемых фигур.

Формула для расчета

Теорема

Средняя линия треугольника параллельна основанию и равна её половине.

(A_1C_1=frac12AC)

Доказательство

Дано:

(triangle ABC)

(A_1C_1)— средняя линия

Доказать:

(A_1C_1parallel AC)

(A_1C_1=frac12AC)

Рассмотрим (triangle BA_1C_1) и (triangle BAC):

(left{begin{array}{l}angle B;-;общий\frac{BA_1}{BA}=frac{BC_1}{BC}=frac12end{array}right.)

Из этого следует, что треугольники подобны по двум пропорциональным сторонам и углу между ними.

Следовательно, (angle BA_1C_1=angle BAC) , как соответственные элементы подобных треугольников. Следовательно (A_1C_1parallel AC) по признаку параллельности.

Кроме того, из подобия следует, что (frac{A_1C_1}{AC}=frac12)

Следовательно, (A_1C_1=frac12AC)

Утверждение доказано.

Примечание

Данная формула одинаково работает для любого треугольника: равнобедренного, равностороннего (правильного).

Примеры решения задач

ПРИМЕР 1

Задание В треугольнике провели среднюю линию , параллельную. Найти площадь треугольника , если известно, что см, а высота , опущенная на сторону , равна 5 см. Решение В треугольнике (см. рис. 1) средняя линия равна половине стороны , поэтому

Найдем площадь треугольника :

Так как средняя линия отсекает треугольник , площадь которого равна одной четвёртой площади исходного треугольника , то площадь треугольника равна:

Ответ см.

ПРИМЕР 2

Задание В треугольнике провели средние линии см, см и см. Найти периметр треугольника . Решение Так как средняя линия равна половине стороны, которой она параллельна, то можем найти длины всех сторон треугольника :

см см см

Теперь можно найти периметр треугольника как сумму длин всех его сторон:

см Ответ см.

Средние линии

Средние линии треугольника

Средняя линия трапеции

Средние линии четырехугольника. Теорема Вариньона

Средние линии тетраэдра

Через сторону

Средняя линия равностороннего треугольника через радиус вписанной окружности

Средняя линия треугольника через площадь и высоту

Средняя линия равностороннего треугольника через высоту

Средняя линия равнобедренного треугольника через боковую сторону и высоту

Средняя линия равностороннего треугольника через площадь

Средняя линия равностороннего треугольника через радиус описанной окружности

Доказательство

Задача:

Советуем посмотреть:

Правило встречается в следующих упражнениях:

Средняя линия треугольника + Задачи по теме

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

Видео

Понятие средней линии прямоугольного треугольника

Средняя линия

Важные свойства

Решение задачи

Формула для расчета

Примеры решения задач

Теги