Всего: 132 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Тип 25 № 78 
i
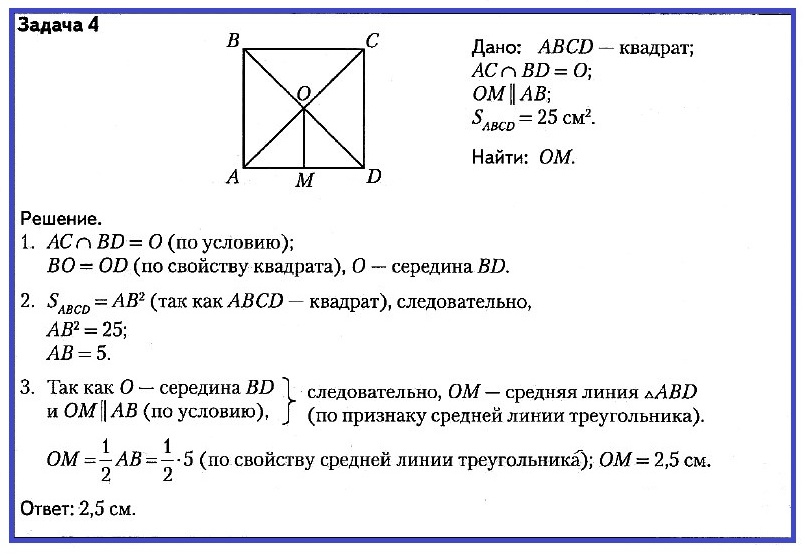
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
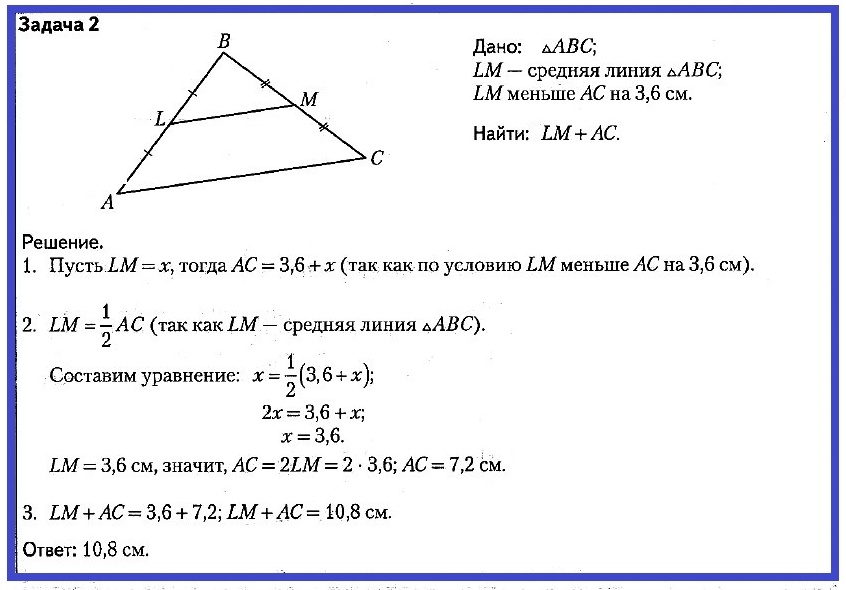
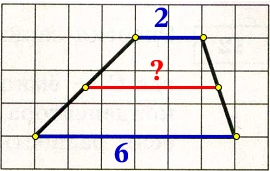
В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.
Источники:
Банк заданий ФИПИ.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
Какие из следующих утверждений верны?
1) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
2) Площадь трапеции равна произведению суммы оснований на высоту.
3) Площадь трапеции не превосходит произведения средней линии на высоту.
4) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.
Какие из следующих утверждений верны?
1) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.
2) В равнобедренном треугольнике имеется не менее двух равных углов.
3) Площадь трапеции не превосходит произведения средней линии на высоту.
4) Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.
Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
Источник: ГИА-2013. Математика. Тренировочная работа № 1 (1 вар.)
Диагональ трапеции делит её среднюю линию на отрезки, равные 4 см и 3 см. Найдите меньшее основание трапеции.
Источник: ГИА-2013. Математика. Тренировочная работа № 1(2 вар)
Найдите площадь выпуклого четырёхугольника с диагоналями 3 и 4, если отрезки, соединяющие середины его противоположных сторон, равны.
Источник: Тренировочные работы. Иркутск — 2013, вариант 1.
В выпуклом четырёхугольнике ABCD длина отрезка, соединяющего середины сторон AB и CD, равна одному метру. Прямые BC и AD перпендикулярны. Найдите длину отрезка, соединяющего середины диагоналей AC и BD.
Источник: Тренировочные работы. Иркутск — 2013, вариант 2.
Найдите площадь выпуклого четырёхугольника с диагоналями 8 и 5, если отрезки, соединяющие середины его противоположных сторон, равны.
Источник: Тренировочные работы. Иркутск — 2013, вариант 3.
Источник: Пробный экзамен. Санкт-Петербург — 2013, вариант 1.
Источник: Пробный экзамен. Санкт-Петербург — 2013, вариант 2.
В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 16. Найдите её среднюю линию.
Основания трапеции равны 16 и 34. Найдите отрезок, соединяющий середины диагоналей трапеции.
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
Если утверждений несколько, запишите их номера в порядке возрастания.
Источник: Банк заданий ФИПИ
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
Источник: Банк заданий ФИПИ
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
Источник: Банк заданий ФИПИ
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
Источник: Банк заданий ФИПИ
Всего: 132 1–20 | 21–40 | 41–60 | 61–80 …
Средняя линия треугольника огэ
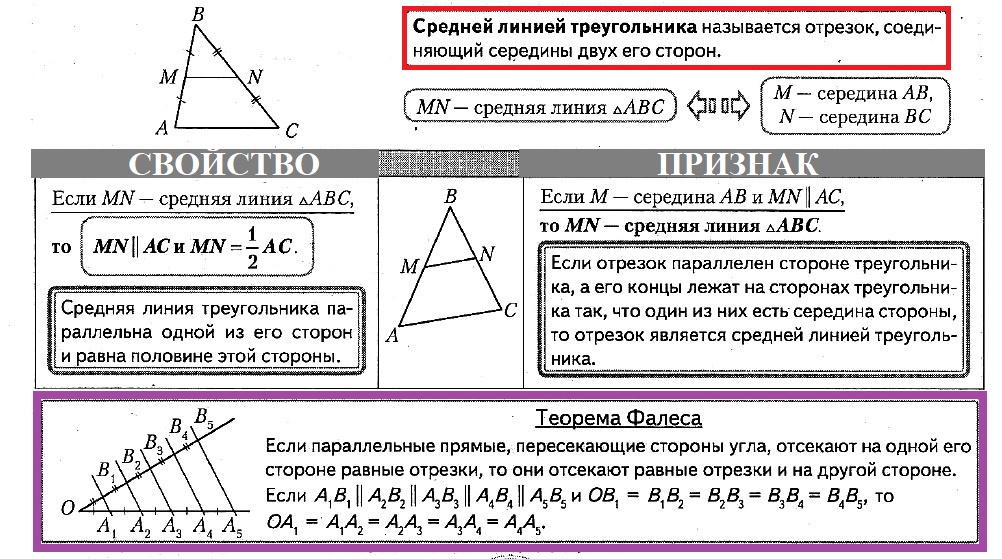
Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника:
1. Средняя линия параллельна третьей стороне и равна ее половине.
2. Средняя линия трeугольника отсекает от него треугольник, подобный данному (с коэффициентом подобия 1/2 ).
3. Три средние линии треугольника делят его на 4 равных треугольника, подобных данному, с коэффициентом подобия 1/2.
Свойство средней линии треугольника является следствием теоремы Фалеса.
ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ
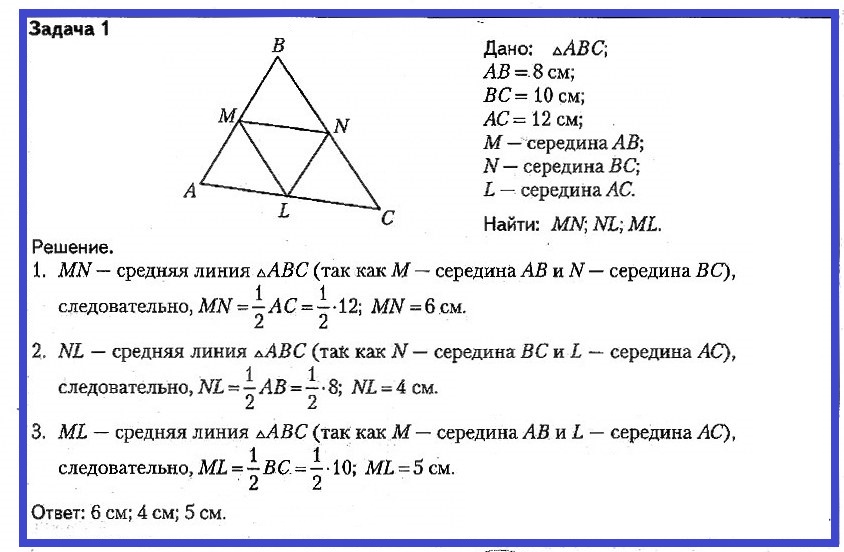
Задача № 1. Дано: ΔABC; AB = 8 см; BC = 10 см; AC = 12 см; M — середина AB; N — середина BC; L — середина AC. Найти: MN, NL, ML.
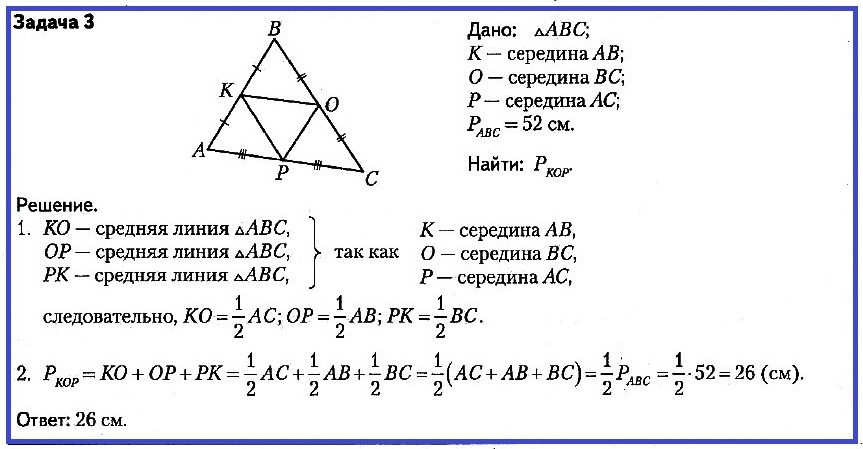
Задача № 3. ΔABC; K — середина AB; O — середина BC; P — середина AC; PABC = 52 см. Найти: PКOР
Это конспект по теме «Средняя линия треугольника + Задачи по теме». Выберите дальнейшие действия:
Задачи по теме:»Средняя линия треугольника» 8 класс
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
1.Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.
2. В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC. Найти периметр треугольника ABC, если MN=12, MK=10, KN=8.
3.В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
4.Периметр равностороннего треугольника АВС равен 24 см. Найдите длину средней линии этого треугольника.
5.Стороны треугольника равны 2 см, 3 см и 4 см. Его вершины являются серединами сторон второго треугольника. Найдите периметр второго треугольника.
6.Периметр треугольника равен 12 см, середины сторон соединены отрезками. Найдите периметр получившегося треугольника.
7.Периметр равностороннего треугольника равен 72 см. Найдите его среднюю линию.
8.Периметр треугольника равен 12 см. Найдите периметр треугольника, отсекаемого от данного какой-нибудь его средней линией.
9.Средняя линия равнобедренного треугольника, параллельная основанию, равна 3 см. Найдите стороны треугольника, если его периметр равен 16 см.
10.Через вершины треугольника проведены прямые, параллельные его противоположным сторонам. Найдите периметр треугольника, ограниченного этими прямыми, если периметр исходного треугольника равен 6 см.
11.В треугольнике ABC DE — средняя линия. Площадь треугольника CDE равна 9. Найдите площадь треугольника ABC.
12.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 45. Найдите площадь треугольника ABC.
13.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 94. Найдите площадь треугольника ABC.
14.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 7. Найдите площадь треугольника ABC.
15.В треугольнике ABC отрезок DE — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.
16.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 24. Найдите площадь треугольника ABC.
17.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.
18.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 21. Найдите площадь треугольника ABC.
19.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 89. Найдите площадь треугольника ABC.
20.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 8. Найдите площадь треугольника ABC.
21.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 96. Найдите площадь треугольника ABC.
22.В треугольнике ABC известно, что DE — средняя линия. Площадь треугольника CDE равна 57. Найдите площадь треугольника ABC.
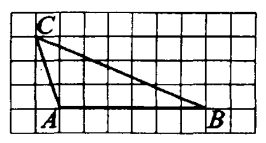
23.На клетчатой бумаге с размером клетки 1х1 изображён треугольник . Найдите длину его средней линии, параллельной стороне .
Презентация «Подготовка к ОГЭ. Модуль «Геометрия». Средняя линия треугольника. Средняя линия трапеции.»
Презентация «Подготовка к ОГЭ. Модуль «Геометрия». Средняя линия треугольника. Средняя линия трапеции.» позволяет повторить основные понятия тем и вспомнить решения ключевых задач. В презентации предусмотрены небольшие тестовые работы. Все рассматриваемые задания взяты из открытого банка заданий ОГЭ.
Просмотр содержимого документа
«Презентация «Подготовка к ОГЭ. Модуль «Геометрия». Средняя линия треугольника. Средняя линия трапеции.»»
Средняя линия треугольника.
Средняя линия трапеции.
МБОУ СОШ № 43 г. Новосибирска
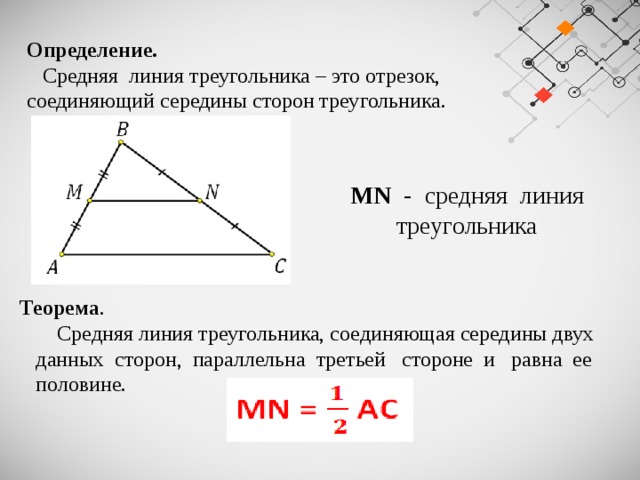
Средняя линия треугольника – это отрезок, соединяющий середины сторон треугольника.
MN — средняя линия треугольника
Средняя линия треугольника, соединяющая середины двух
данных сторон, параллельна третьей стороне и равна ее
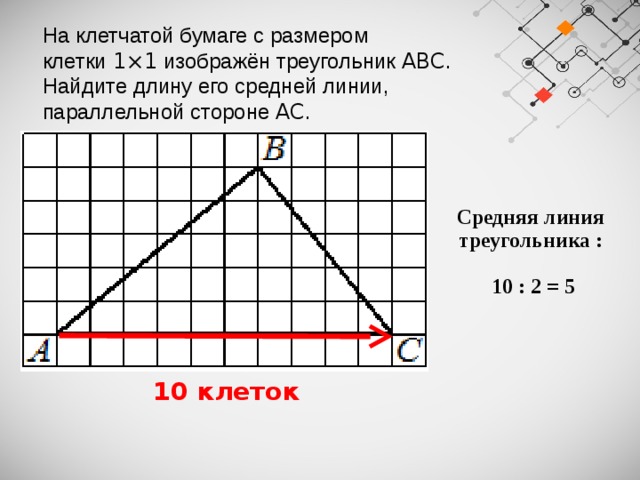
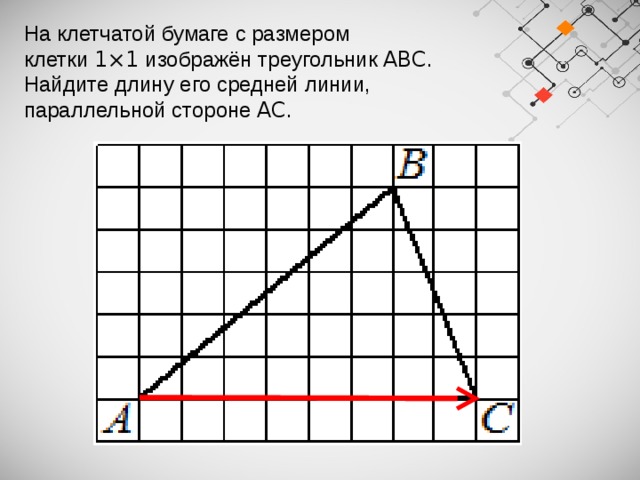
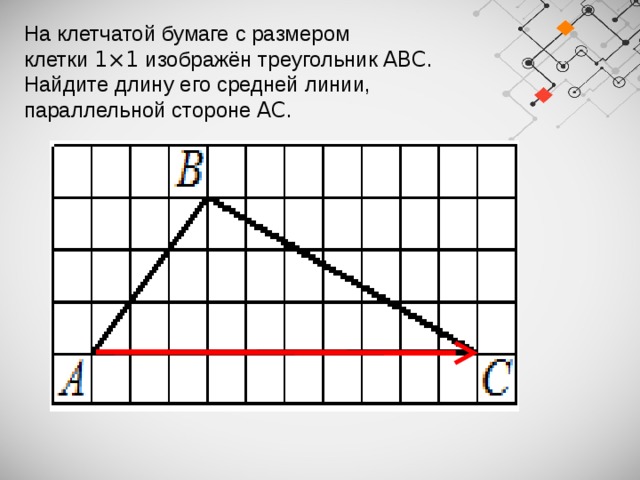
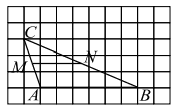
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC .
Найдите длину его средней линии,
параллельной стороне AC .
Средняя линия треугольника :
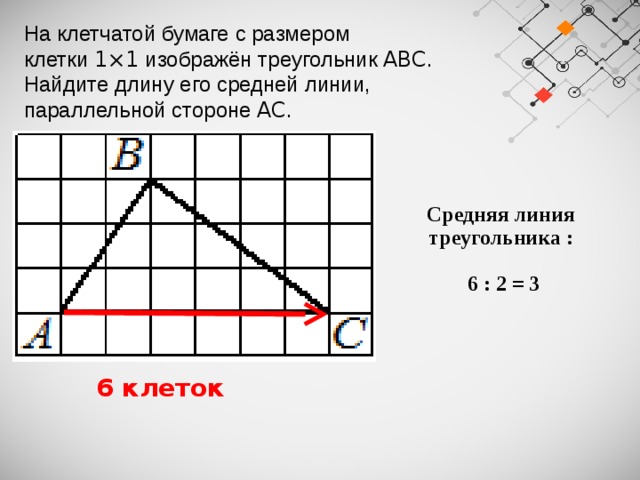
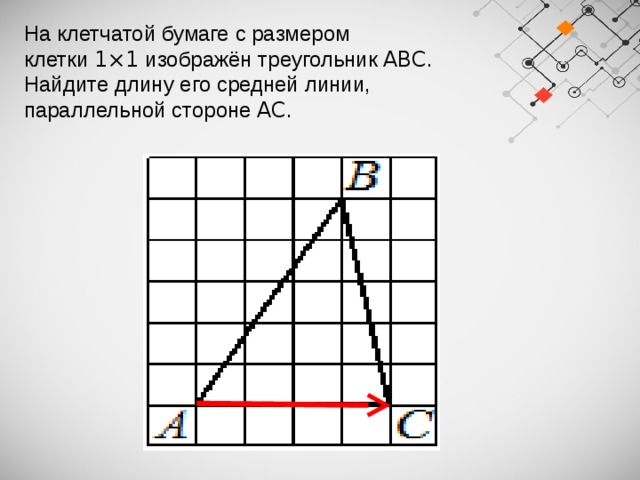
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его средней линии, параллельной стороне AC .
Средняя линия треугольника :
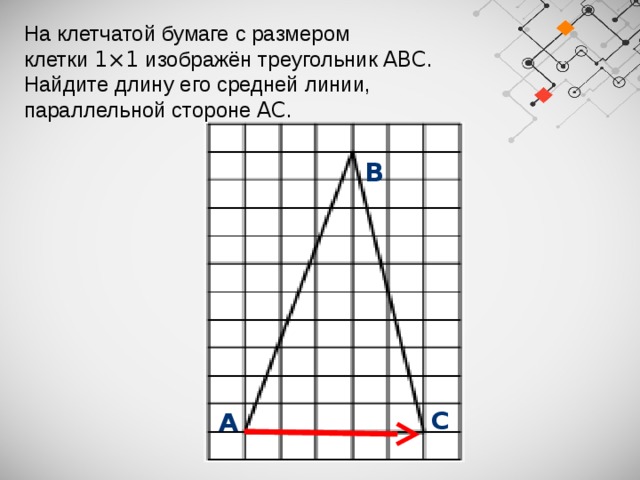
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его средней линии, параллельной стороне AC .
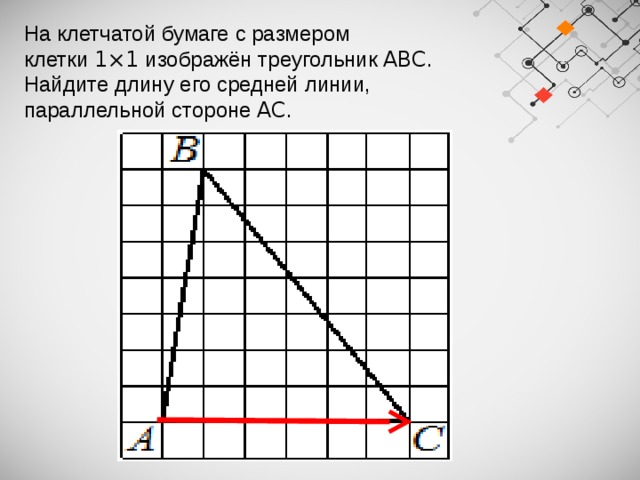
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его средней линии, параллельной стороне AC .
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его средней линии, параллельной стороне AC .
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его средней линии, параллельной стороне AC .
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC . Найдите длину его средней линии, параллельной стороне AC .
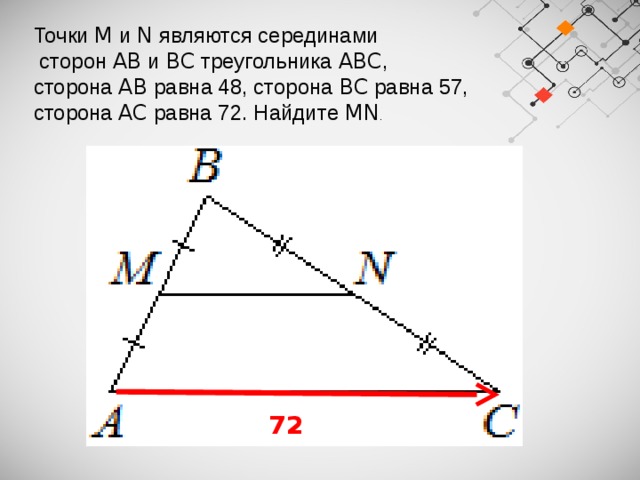
Точки M и N являются серединами
сторон AB и BC треугольника ABC ,
сторона AB равна 48, сторона BC равна 57,
сторона AC равна 72. Найдите MN .
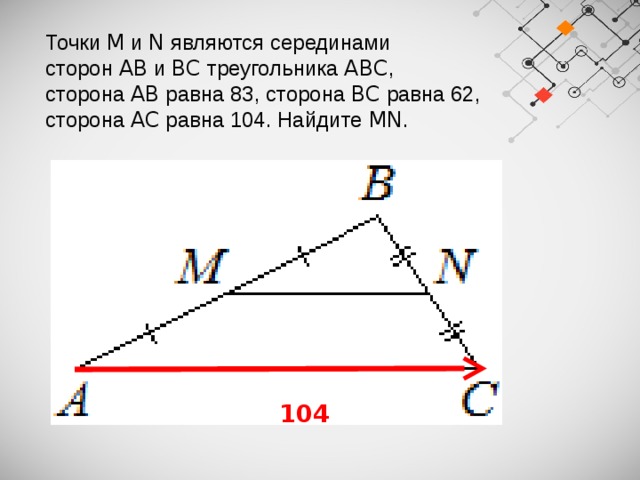
Точки M и N являются серединами сторон AB и BC треугольника ABC ,
сторона AB равна 83, сторона BC равна 62, сторона AC равна 104. Найдите MN .
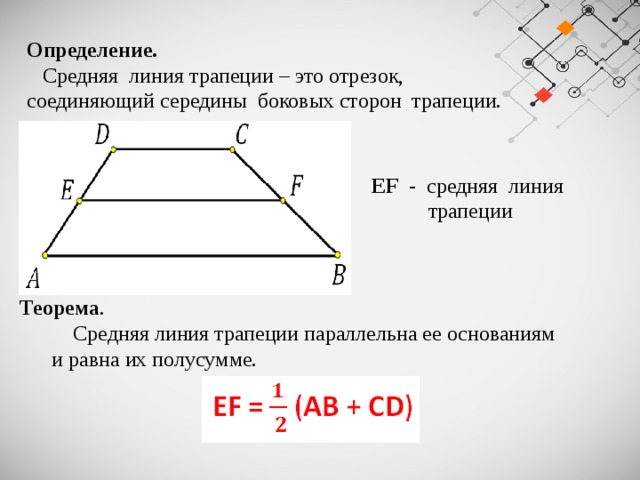
Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон трапеции.
EF — средняя линия
Средняя линия трапеции параллельна ее основаниям
и равна их полусумме.
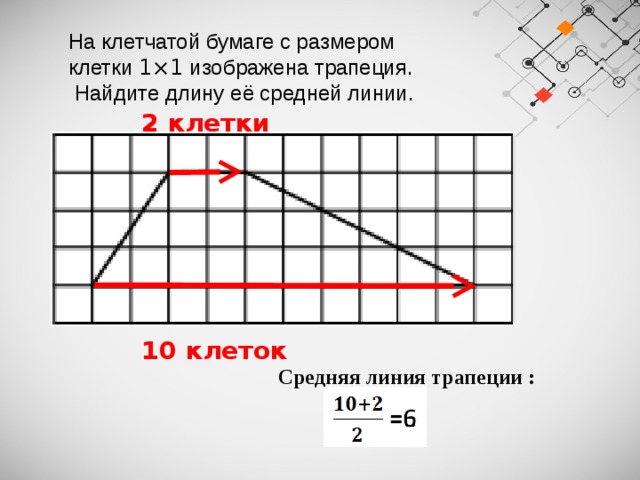
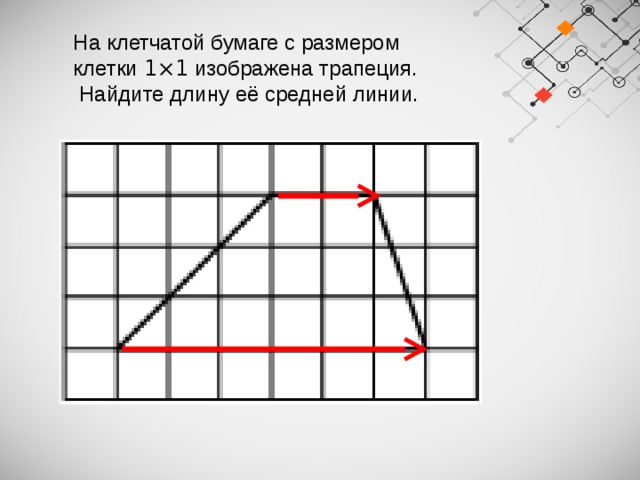
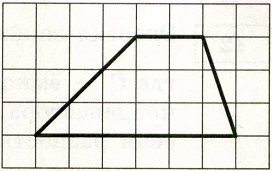
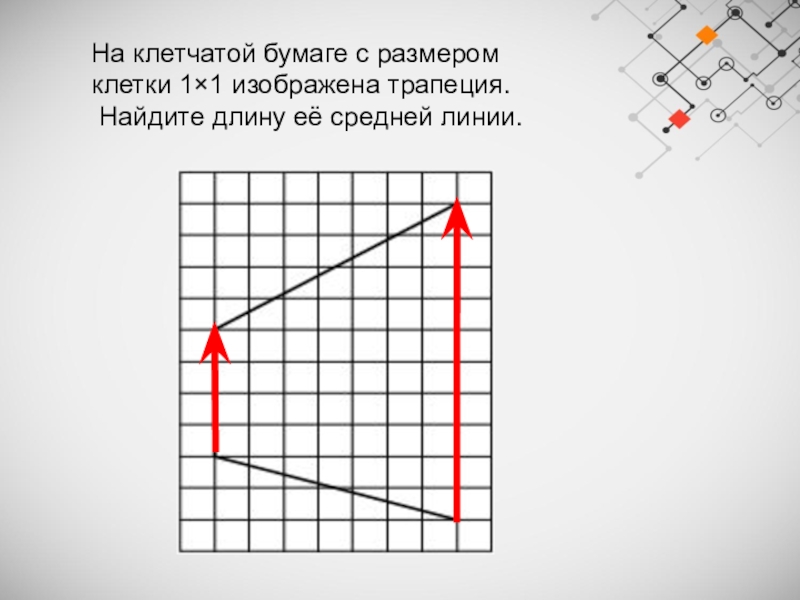
На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её средней линии.
Средняя линия трапеции :
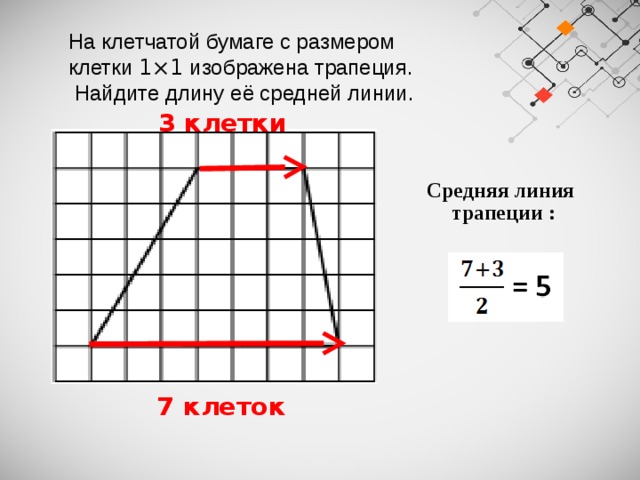
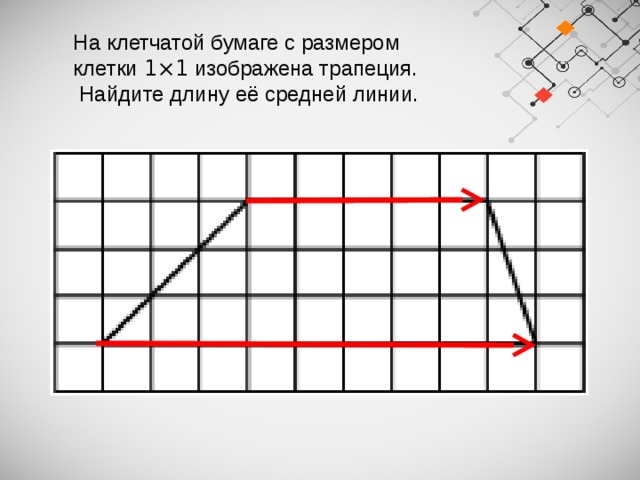
На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её средней линии.
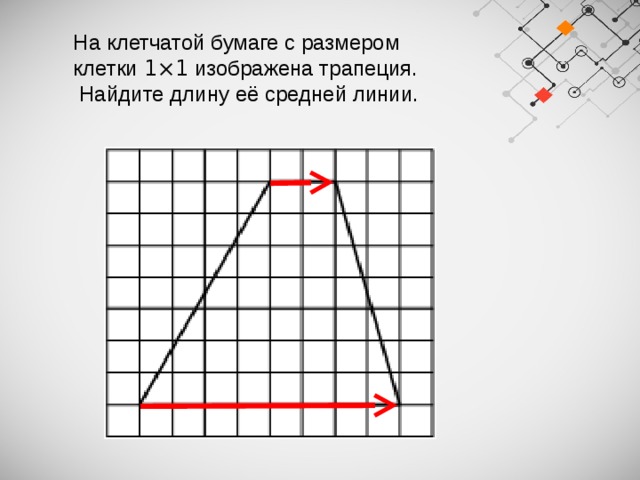
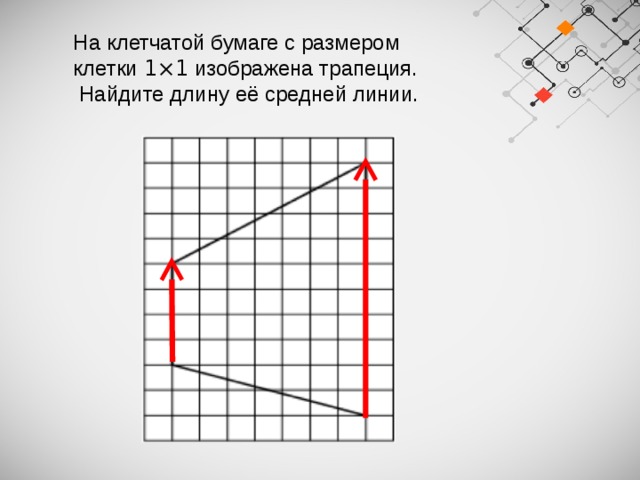
На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её средней линии.
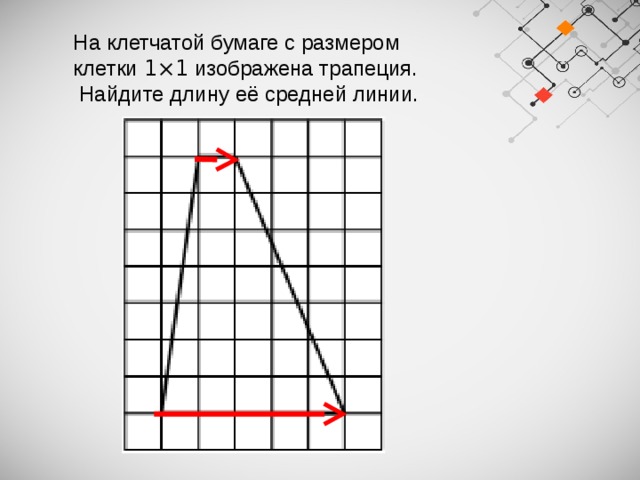
На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её средней линии.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её средней линии.
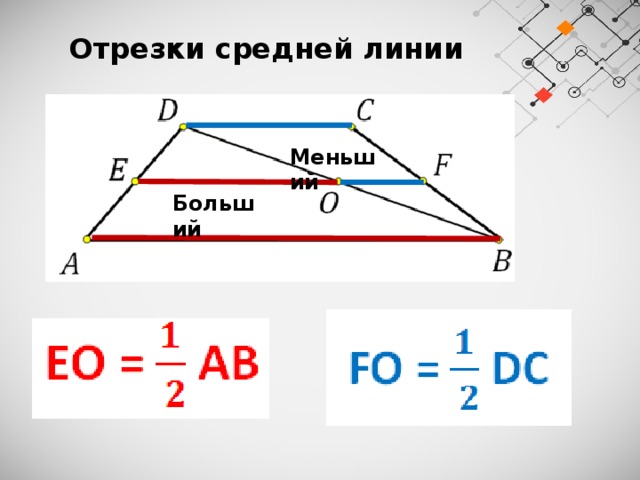
Отрезки средней линии
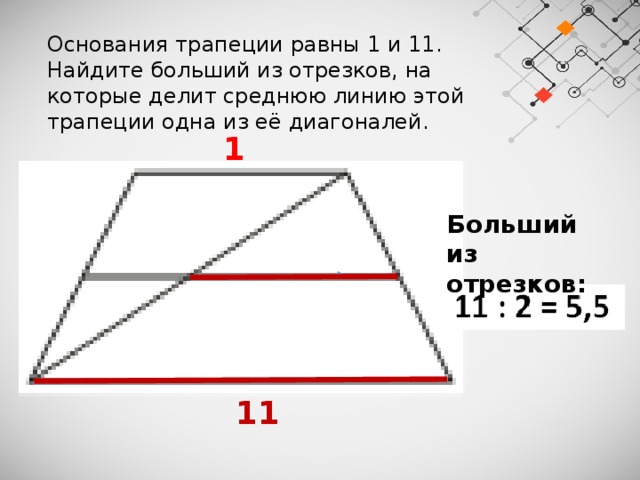
Основания трапеции равны 1 и 11.
Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
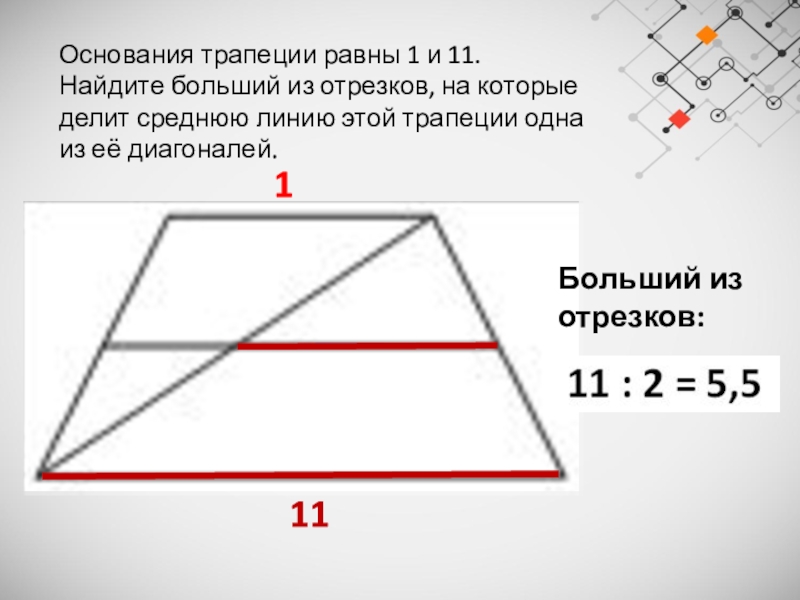
Больший из отрезков:
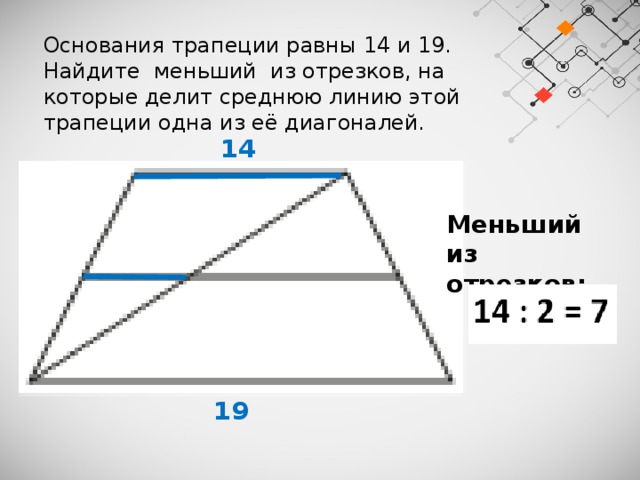
Основания трапеции равны 14 и 19.
Найдите меньший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
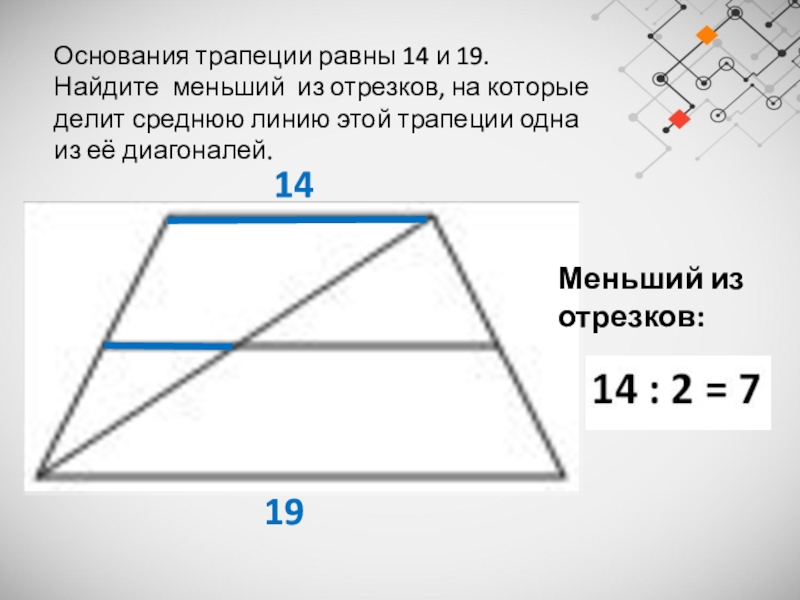
Меньший из отрезков:
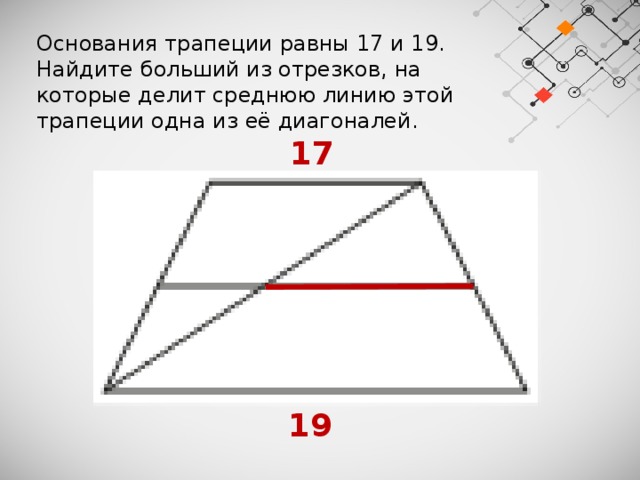
Основания трапеции равны 17 и 19.
Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
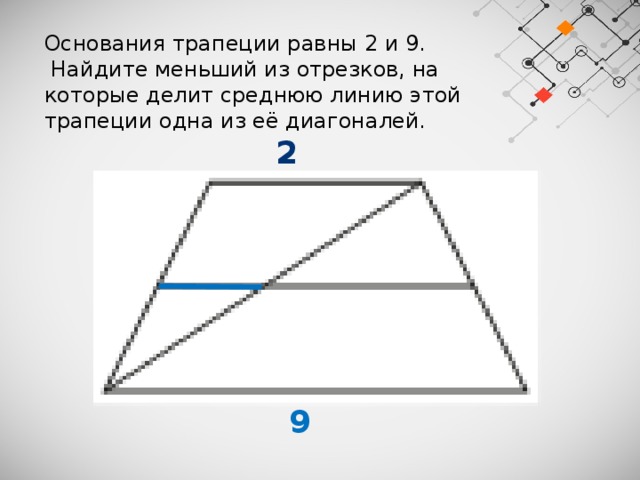
Основания трапеции равны 2 и 9.
Найдите меньший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
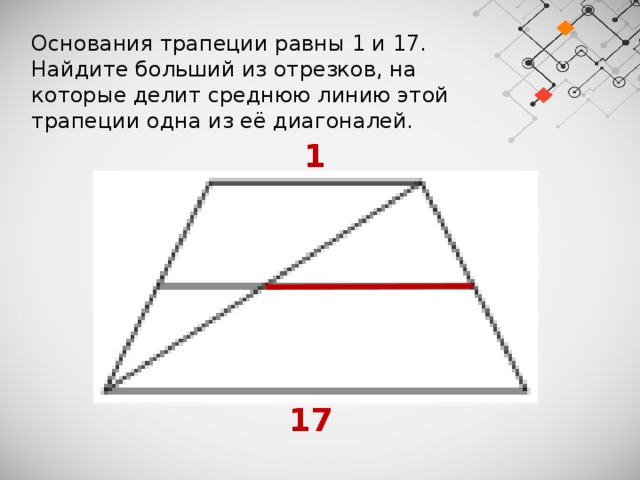
Основания трапеции равны 1 и 17.
Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
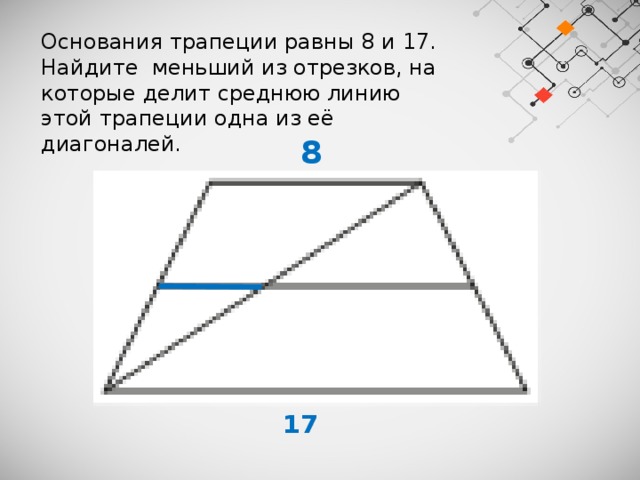
Основания трапеции равны 8 и 17.
Найдите меньший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
http://infourok.ru/zadachi-po-temesrednyaya-liniya-treugolnika-klass-1901755.html
http://kopilkaurokov.ru/matematika/presentacii/priezientatsiia_podghotovka_k_oge_modul_gieomietriia_sriedniaia_liniia_trieughol
Описание презентации по отдельным слайдам:
-
1 слайд
Подготовка к ОГЭ.
Средние линии -
-
-
-
5 слайд
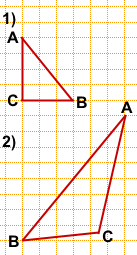
1. Проведите средние линии треугольника ABC, изображенного на рисунке.
Ответ.
Упражнения
5 -
6 слайд
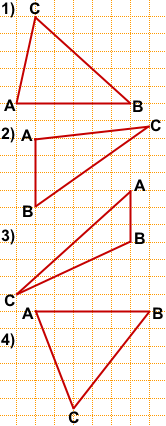
2. Изобразите треугольник, середины сторон которого отмечены на рисунке.
Ответ:
6 -
7 слайд
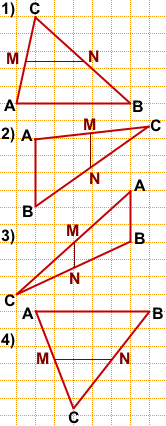
3. На рисунке изображена вершина и средняя линия треугольника. Изобразите сам треугольник.
Ответ:
7 -
8 слайд
4. Найдите длину отрезка DE. Стороны клеток равны 1
Ответ. 3.
8 -
9 слайд
5. Стороны треугольника равны 8 см, 10 см и 12 см. Найдите стороны треугольника, вершинами которого являются середины сторон данного треугольника.
Ответ: 4 см, 5 см и 6 см.
9 -
10 слайд
6. Стороны треугольника DEF равны 2 см, 3 см и 4 см. Его вершины являются серединами сторон второго треугольника ABC. Найдите периметр второго треугольника.
Ответ: 18 см.
10 -
11 слайд
7. Какую часть площади данного треугольника составляет площадь треугольника, отсекаемого его средней линией?
Ответ: 1 4 .
11 -
-
13 слайд
Упражнения
1. Проведите среднюю линию трапеции, изображенной на рисунке.
Ответ.
13 -
14 слайд
2. Изобразите трапецию, если заданы две её вершины A, C и средняя линия EF
Ответ.
14 -
15 слайд
3. Средняя линия трапеции равна 30 см, а меньшее основание равно 20 см. Найдите большее основание.
Ответ: 40 см
15 -
16 слайд
4. Основания трапеции относятся как 5:2, а их разность равна 18 см. Найдите среднюю линию трапеции.
Ответ: 21 см.
16 -
17 слайд
5. Основания трапеции ABCD равны 6 и 4. Найдите отрезки, на которые диагонали этой трапеции делят её среднюю линию EF.
Ответ: 2, 1, 2.
17 -
18 слайд
Ответ: 5.
6. Боковые стороны трапеции, описанной около окружности, равны 4 и 6. Найдите среднюю линию этой трапеции.
18 -
19 слайд
7. Может ли средняя линия трапеции пройти через точку пересечения диагоналей?
Решение. Нет. Действительно, пусть ABCD – трапеция, E – точка пересечения диагоналей, FG – средняя линия. Предположим, что средняя линия проходит через точку E. Тогда FE – средняя линия треугольника ABD, следовательно, равна половине AB. EG – средняя линия треугольника ABC, следовательно, равна половине AB. Значит средняя линия FG равна стороне AB. В этом случае четырёхугольник ABCD был бы параллелограммом.
19 -
20 слайд
8. Основания трапеции равны 14 см и 20 см. Одна из боковых сторон разделена на три равные части и через точки деления проведены прямые, параллельные основаниям трапеции. Найдите отрезки этих прямых, заключенные внутри трапеции.
Ответ: 16 и 18.
20
Слайд 1Подготовка
к ОГЭ
модуль «Геометрия»
Учитель математики
МБОУ СОШ № 43 г. Новосибирска
Картопольцева Т.Н.
Средняя
линия треугольника.
Средняя линия трапеции.
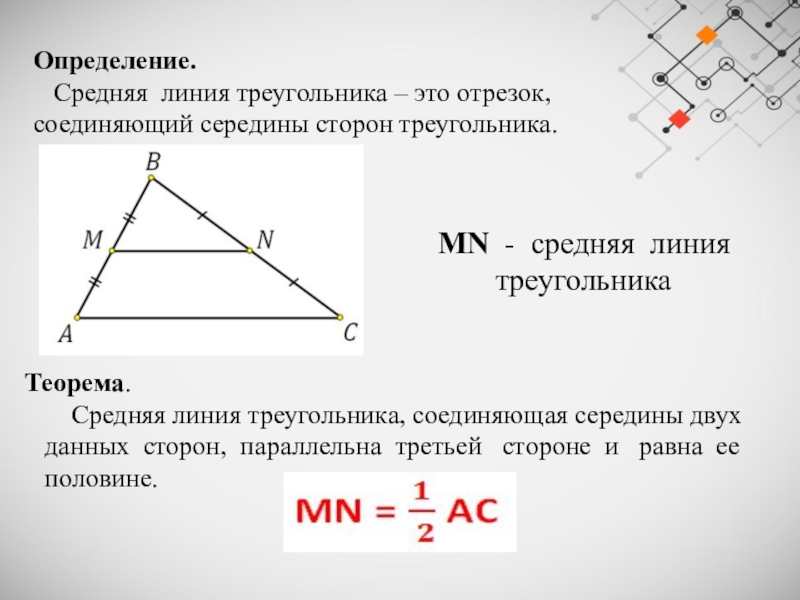
Слайд 2Определение.
Средняя линия треугольника – это отрезок, соединяющий середины
сторон треугольника.
MN — средняя линия треугольника
Теорема.
Средняя линия треугольника, соединяющая середины двух
данных сторон, параллельна третьей стороне и равна ее
половине.
Слайд 3 10 клеток
Средняя линия треугольника :
10 : 2 =
5
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.
Найдите длину
его средней линии,
параллельной стороне AC.
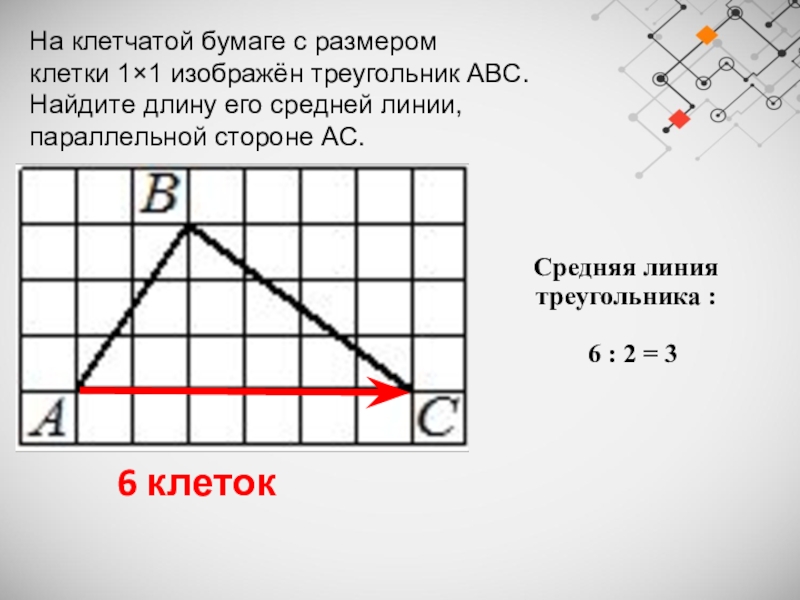
Слайд 4На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его
средней линии, параллельной стороне AC.
6 клеток
Средняя линия треугольника
:
6 : 2 = 3
Слайд 5
Тест
«Средняя
линия треугольника»
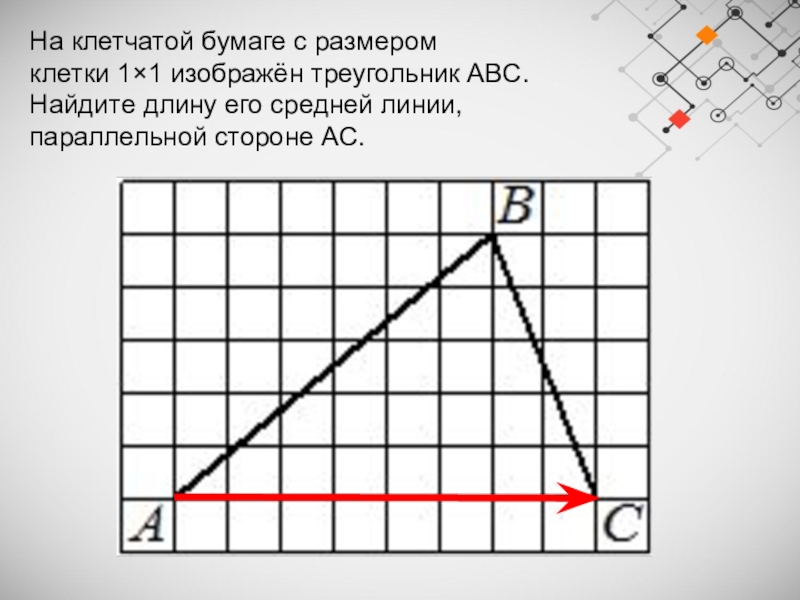
Слайд 6На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его
средней линии, параллельной стороне AC.
Слайд 7На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его
средней линии, параллельной стороне AC.
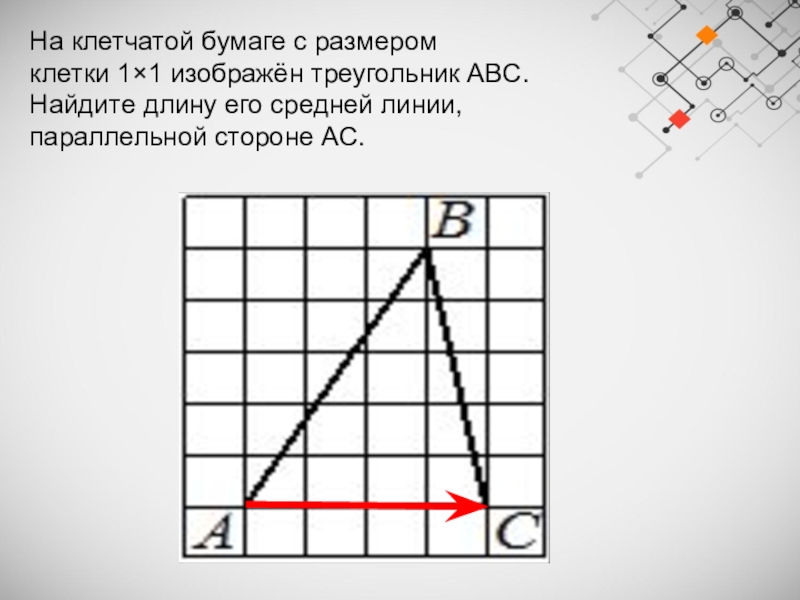
Слайд 8На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его
средней линии, параллельной стороне AC.
С
В
А
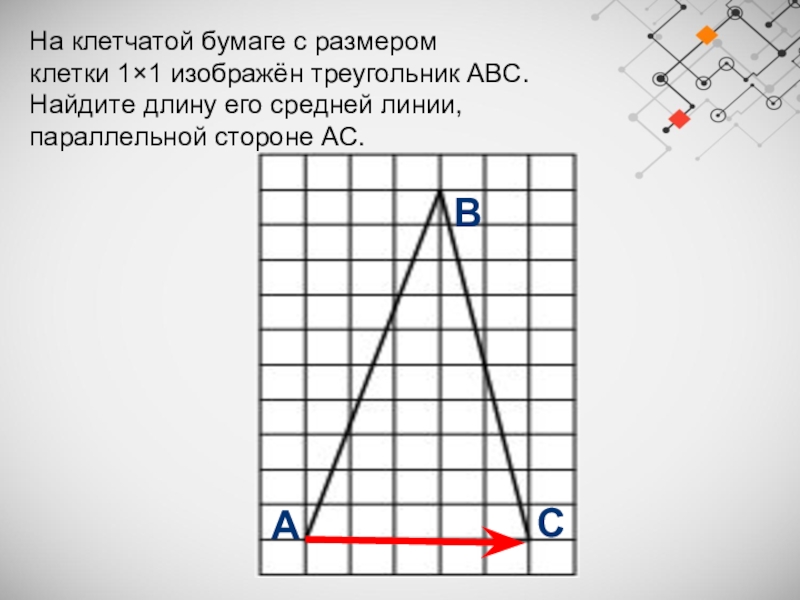
Слайд 9На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его
средней линии, параллельной стороне AC.
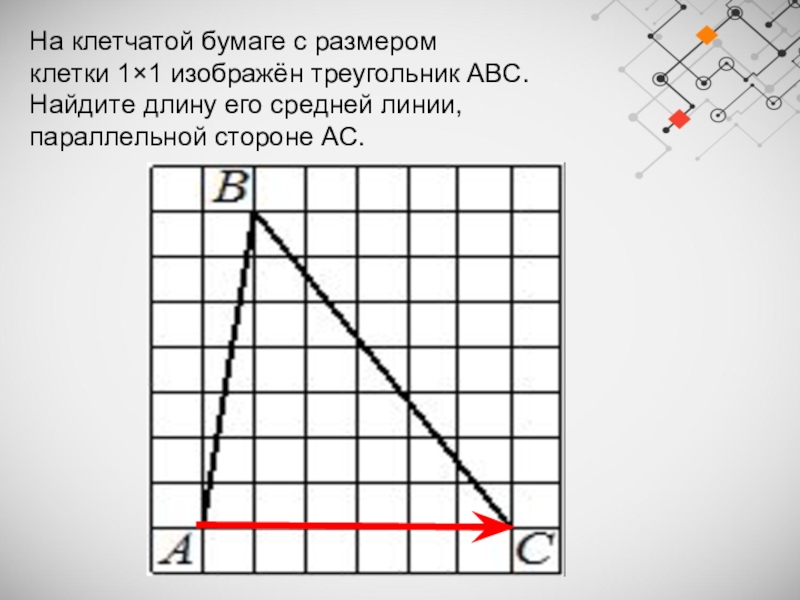
Слайд 10На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его
средней линии, параллельной стороне AC.
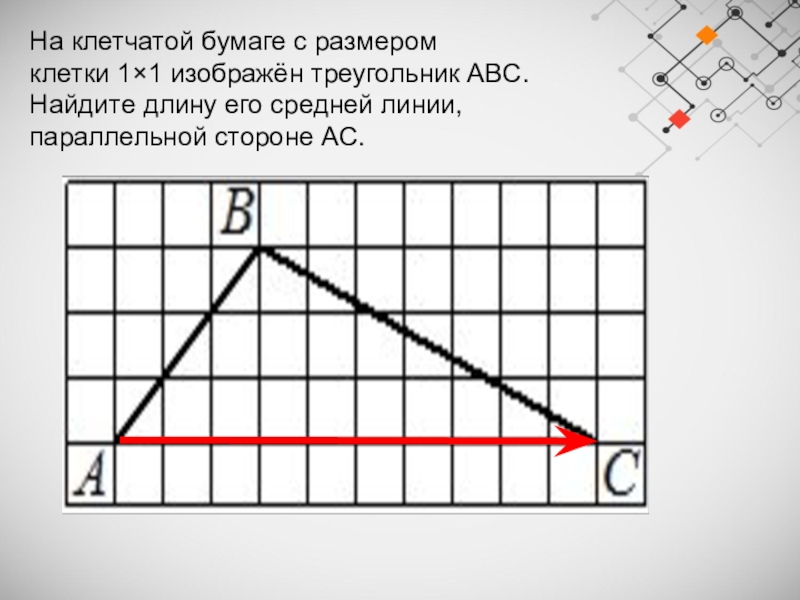
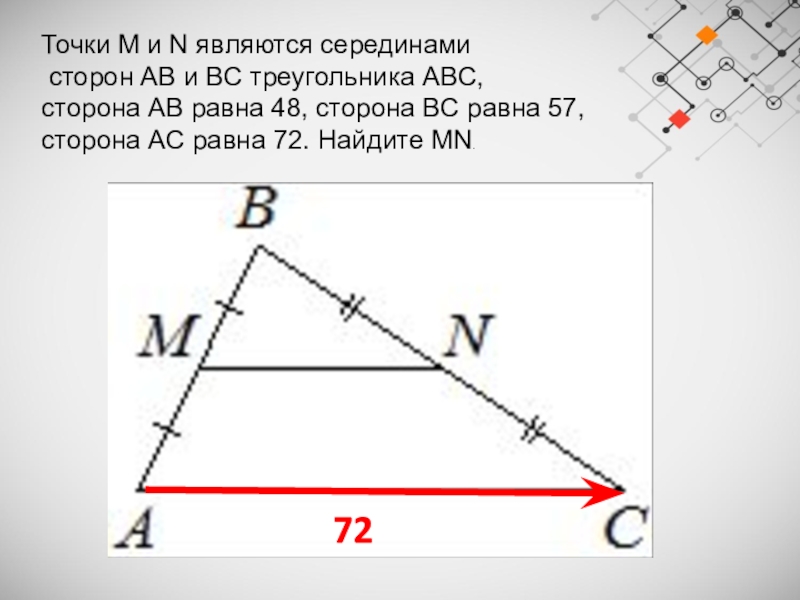
Слайд 11Точки M и N являются серединами
сторон AB и BC треугольника ABC,
сторона AB равна 48, сторона BC равна 57,
сторона AC равна 72. Найдите MN.
72
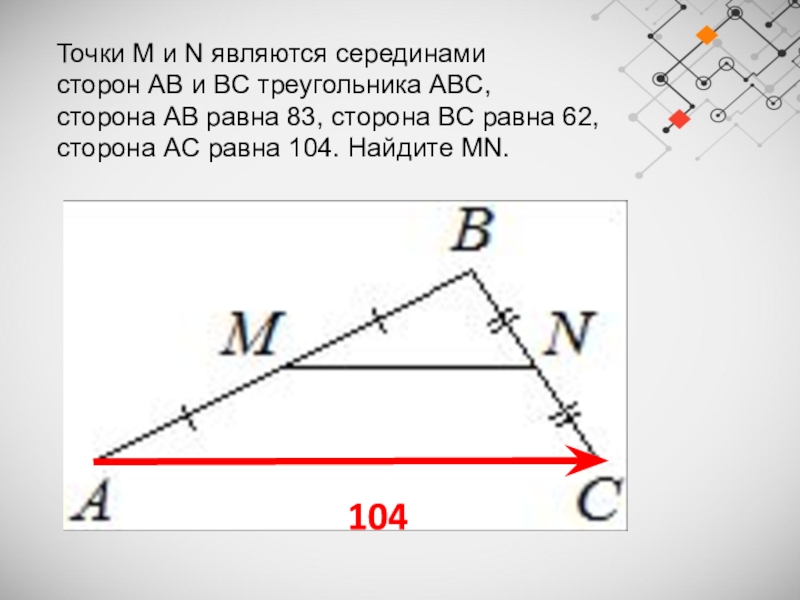
Слайд 12Точки M и N являются серединами сторон AB и BC треугольника ABC,
сторона AB равна 83, сторона BC равна 62, сторона AC равна 104. Найдите MN.
104
Слайд 13Определение.
Средняя линия трапеции – это отрезок, соединяющий середины
боковых сторон трапеции.
EF — средняя линия
трапеции
Теорема.
Средняя линия трапеции параллельна ее основаниям
и равна их полусумме.
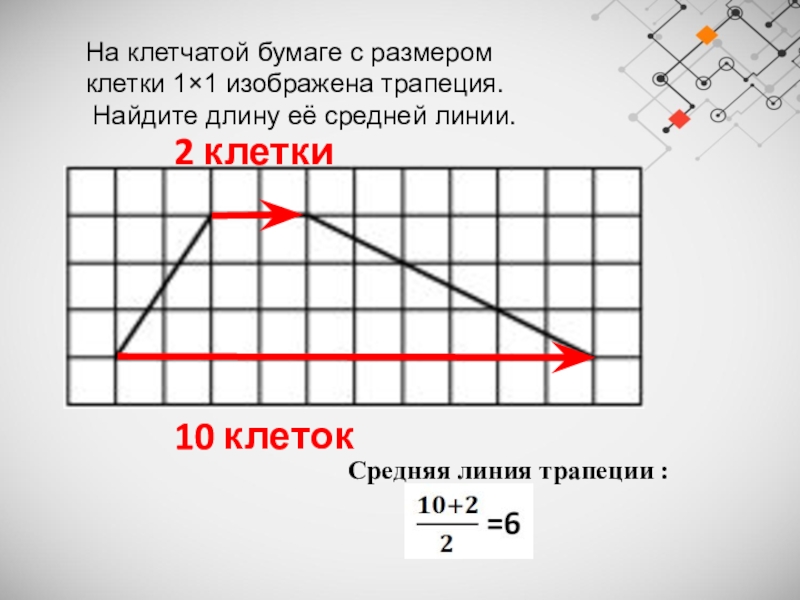
Слайд 14На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её
средней линии.
10 клеток
2 клетки
Средняя линия трапеции
:
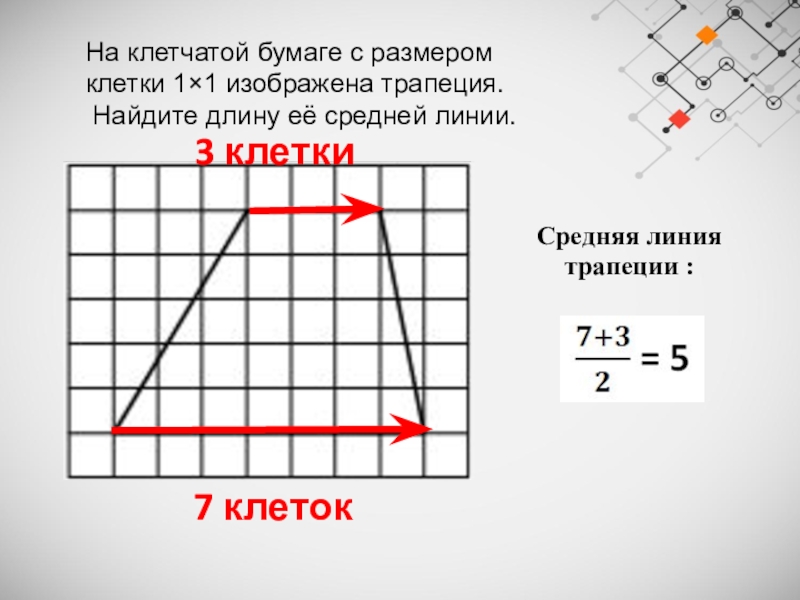
Слайд 15На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её
средней линии.
7 клеток
3 клетки
Средняя линия
трапеции :
Слайд 17На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её
средней линии.
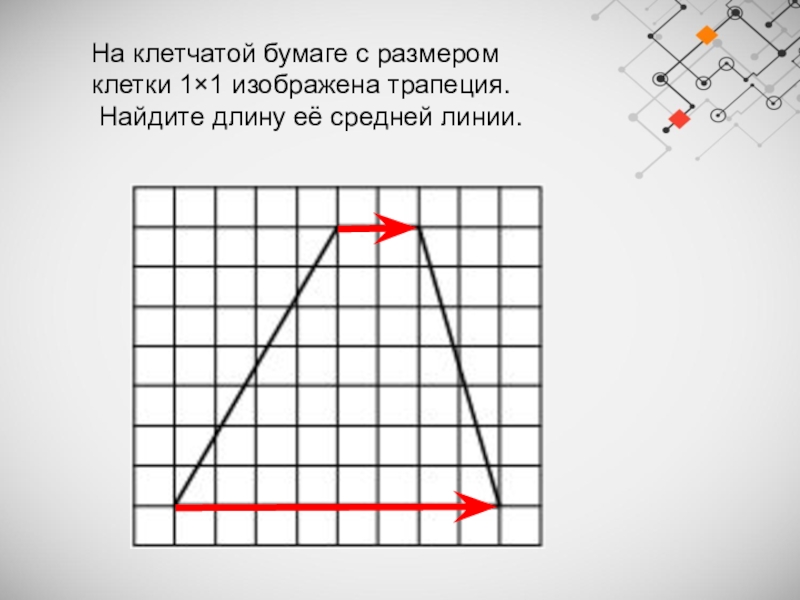
Слайд 18На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её
средней линии.
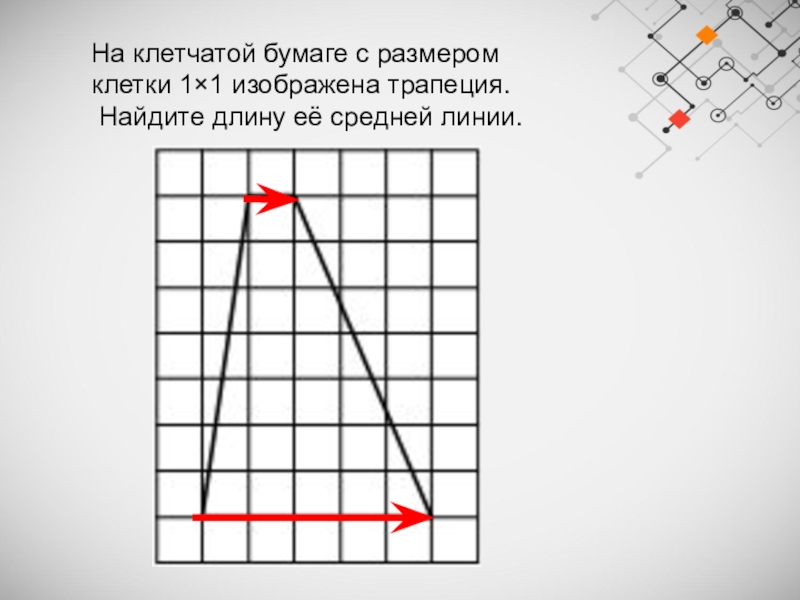
Слайд 19На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её
средней линии.
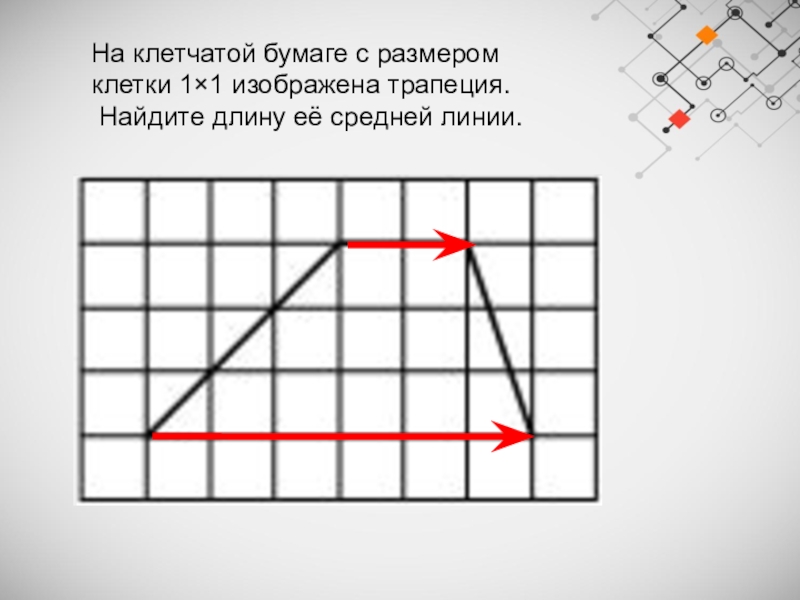
Слайд 20На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её
средней линии.
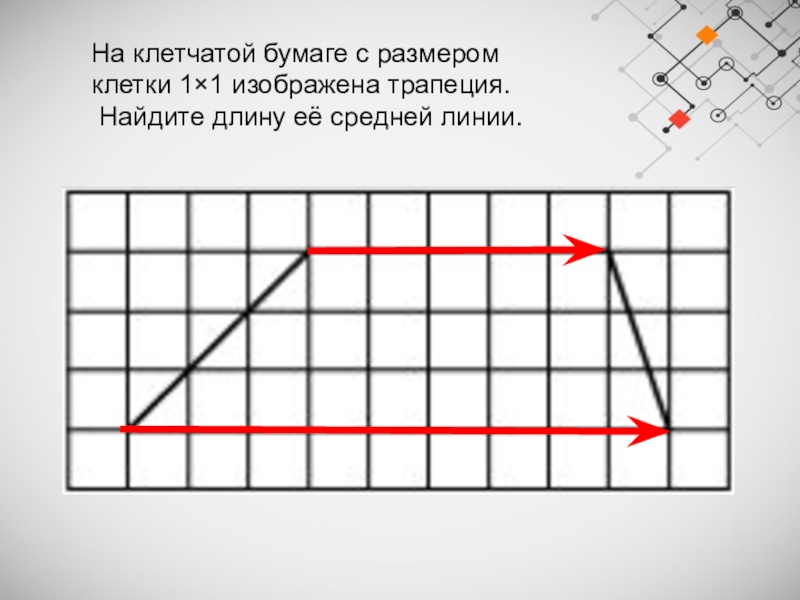
Слайд 21На клетчатой бумаге с размером клетки 1×1 изображена трапеция.
Найдите длину её
средней линии.
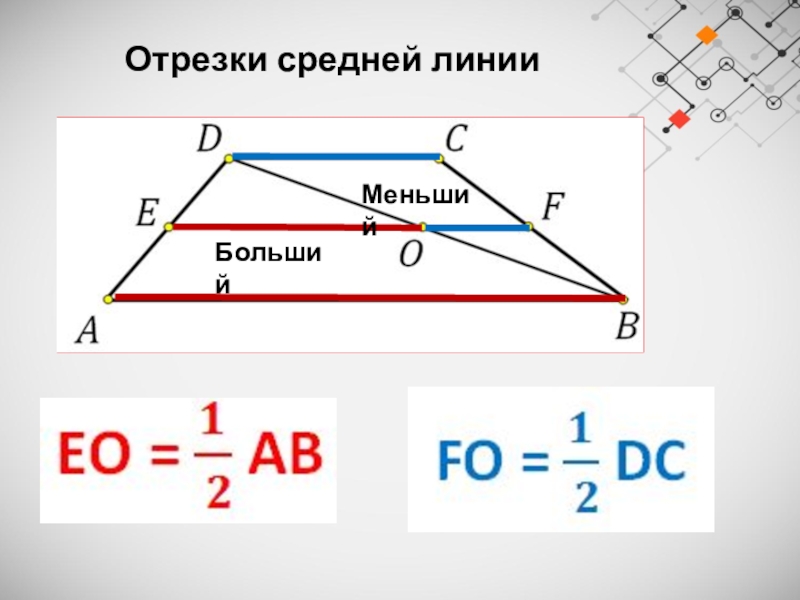
Слайд 22Отрезки средней линии
Больший
Меньший
Слайд 23Основания трапеции равны 1 и 11.
Найдите больший из отрезков,
на которые делит среднюю линию этой трапеции одна из её
диагоналей.
11
1
Слайд 24Основания трапеции равны 14 и 19.
Найдите меньший из отрезков,
на которые делит среднюю линию этой трапеции одна из её
диагоналей.
14
19
Слайд 25
Тест
«Отрезки средней
линии трапеции»
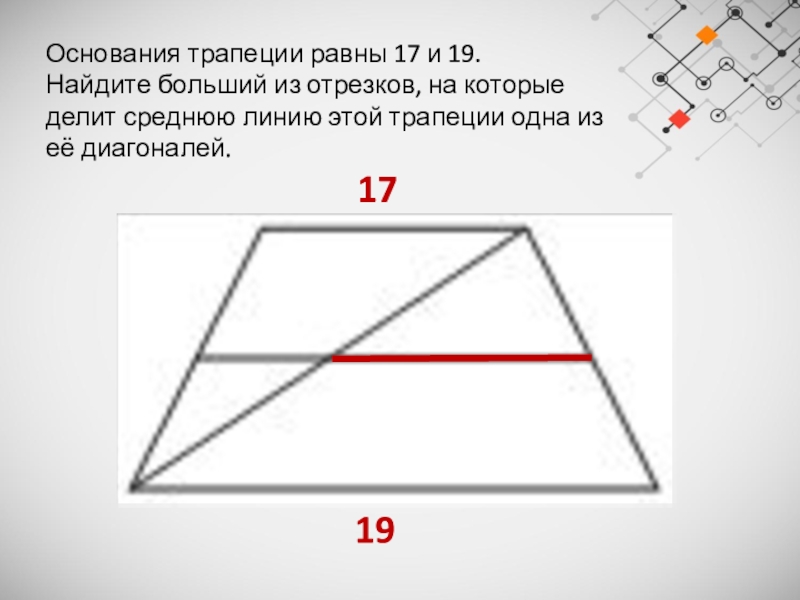
Слайд 26Основания трапеции равны 17 и 19.
Найдите больший из отрезков,
на которые делит среднюю линию этой трапеции одна из её
диагоналей.
19
17
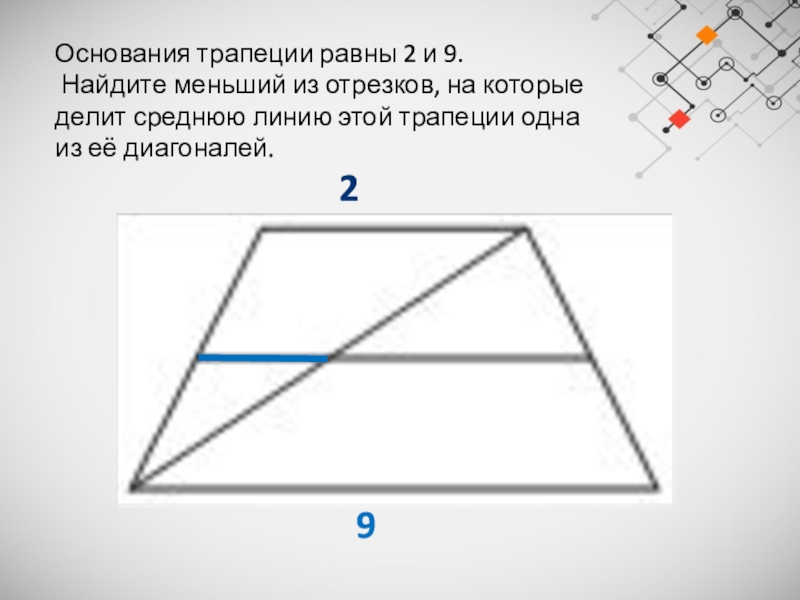
Слайд 27Основания трапеции равны 2 и 9.
Найдите меньший из отрезков,
на которые делит среднюю линию этой трапеции одна из её
диагоналей.
9
2
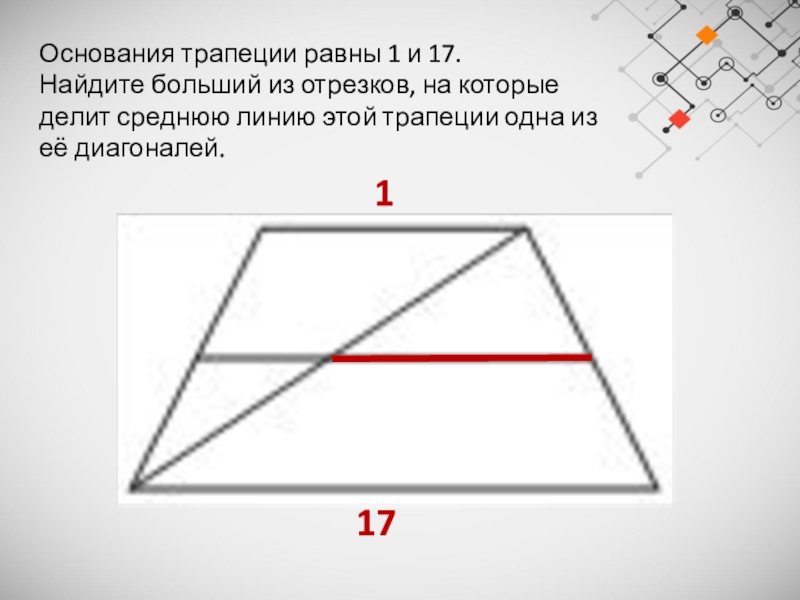
Слайд 28Основания трапеции равны 1 и 17.
Найдите больший из отрезков,
на которые делит среднюю линию этой трапеции одна из её
диагоналей.
1
17
Слайд 29Основания трапеции равны 8 и 17.
Найдите меньший из отрезков,
на которые делит среднюю линию этой трапеции одна из её
диагоналей.
17
8
Слайд 30Источники:
Шаблон презентации:
http://powerpointstore.com/286-treugolniki-v-pautine.html
Задания:
http://www.fipi.ru/content/otkrytyy-bank-zadaniy-oge
На клетчатой бумаге с размером 1х1… Найдите длину его…
Условие задачи:
На клетчатой бумаге с размером 1х1 изображен треугольник АВС (рис.1). Найдите длину его средней линии, параллельной стороне АС.
Решение задачи:
- 1
- 2
- 3
- 4
- 5
Оценка: 3.0 из 1
Комментарии
Всего комментариев
: 0
Задание:
На клетчатой бумаге с размером клетки 1 x 1 изображён треугольник АВС. Найдите длину его средней линии, параллельной стороне АВ.
Решение:
Длина средней линии MN равна половине длины стороны AB, равной 6. MN = 1/2*AB = 1/2 * 6 = 3.
Ответ: 3.
1.
На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С.
Найдите расстояние от точки А до середины отрезка ВС.
Ответ выразите в сантиметрах.
2.
Найдите тангенс угла A треугольника ABC,
изображённого на рисунке.
3.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник.
Найдите его площадь.
4.
На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный
треугольник. Найдите длину его большего катета.
5.
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите
площадь этого ромба.
6.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC.
Найдите длину его средней линии, параллельной стороне AC.
7.
На рисунке изображена
трапеция ABCD. Используя рисунок, найдите синус угла BAH.
8.
В равнобедренном треугольнике боковая сторона равна 10, основание — 
, а угол,
лежащий напротив основания, равен 120°. Найдите площадь треугольника, деленную
на 
1.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите
её площадь.
2.
На клетчатой бумаге с размером клетки 1х1 изображён ромб. Найдите
длину его большей диагонали.
3.
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм.
Найдите его площадь.
4.
На клетчатой бумаге с размером клетки 1см ✕ 1см отмечены точки A, B и C.
Найдите расстояние от точки A до середины отрезка BC .
Ответ выразите в сантиметрах.
5.
Найдите тангенс угла AOB, изображённого на рисунке.
6.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите
длину её средней линии.
7.
На рисунке изображен
параллелограмм ABCD. Используя рисунок, найдите синус угла HBA.
8.
В равнобедренном треугольнике боковая сторона равна 17,
основание — 
, а угол,
лежащий напротив основания, равен 120°. Найдите площадь треугольника, деленную
на
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
Источник: ОГЭ Ященко 2022 (36 вар)
Решение:
Средняя линия трапеции равна полусумме её оснований:
frac{2+6}{2}=frac{8}{2}=4
Ответ: 4.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.4 / 5. Количество оценок: 11
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:01.10.2021
- Рубрика записи18. Фигуры на квадратной решётке
- Автор записи:Андрей Манякин
Рассмотрим, как может быть найдена средняя линия треугольника по рисунку на клетчатой бумаге.
Задача 1
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.
Найдите длину его средней линии, параллельной стороне AB.
Решение:
Как правило, в таких заданиях на чертеже треугольник расположен таким образом, что по клеточкам посчитать длину средней линии невозможно.
Но задача легко разрешима с применением свойства средней линии треугольника:
средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.
Следовательно, чтобы найти длину средней линии, параллельной стороне AB, надо найти длину отрезка AB.
Длина искомой средней линии равна её половине.
1) AB=6,
![[ MN = frac{1}{2}AB = frac{1}{2} cdot 6 = 3; ]](http://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-a13d20a63bd1b527624c8a479799f4be_l3.png "Rendered by QuickLaTeX.com")
![[ 2)MN = frac{1}{2}AB = frac{1}{2} cdot 4 = 2; ]](http://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-3491a3e55aa59584796708674640510a_l3.png "Rendered by QuickLaTeX.com")
![[ 3)MN = frac{1}{2}AB = frac{1}{2} cdot 3 = 1,5; ]](http://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-4be9fa450f846f55b1676a9fc2df3ad4_l3.png "Rendered by QuickLaTeX.com")
![[ 4)MN = frac{1}{2}AB = frac{1}{2} cdot 6 = 3. ]](http://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-79cb6899163a4edd55bc93db62d70c5a_l3.png "Rendered by QuickLaTeX.com")
А как быть, если длину стороны треугольника посчитать по клеточкам не получается?
Возможно, в этом случае сторону треугольника можно найти с помощью теоремы Пифагора.
Задача 2
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.
Найдите длину его средней линии, параллельной стороне AB.
Решение:
1)В прямоугольном треугольнике ABC AB — гипотенуза.
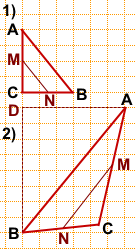
AC=4, BC=3.
По теореме Пифагора
![[ AB^2 = AC^2 + BC^2 , ]](http://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-3ad537a98fb7f4cc4a47fded3220b32e_l3.png "Rendered by QuickLaTeX.com")
![[ AB = sqrt {4^2 + 3^2 } = 5. ]](http://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-ab8741d7f0ff329e1adf541dd871e565_l3.png "Rendered by QuickLaTeX.com")
Средняя линия MN равна половине гипотенузы:
![[ MN = frac{1}{2}AB = frac{1}{2} cdot 5 = 2,5.]](http://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-d6c16c5ee46541ec875fc741e5b9ca25_l3.png "Rendered by QuickLaTeX.com")
2)Достроим по клеточкам прямоугольный треугольник ABD с гипотенузой AB.
По теореме Пифагора
![[AB^2 = AD^2 + BD^2 ,]](http://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-0189b04dd4d13cbf5d2dd17b6c3b6d2f_l3.png "Rendered by QuickLaTeX.com")
![[AB = sqrt {6^2 + 8^2 } = 10,]](http://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-242c27df451245ba230ee826fd4bb4d1_l3.png "Rendered by QuickLaTeX.com")
![[ MN = frac{1}{2}AB = frac{1}{2} cdot 10 = 5. ]](http://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-53d26275ac81facc0478c040f55b4ce2_l3.png "Rendered by QuickLaTeX.com")