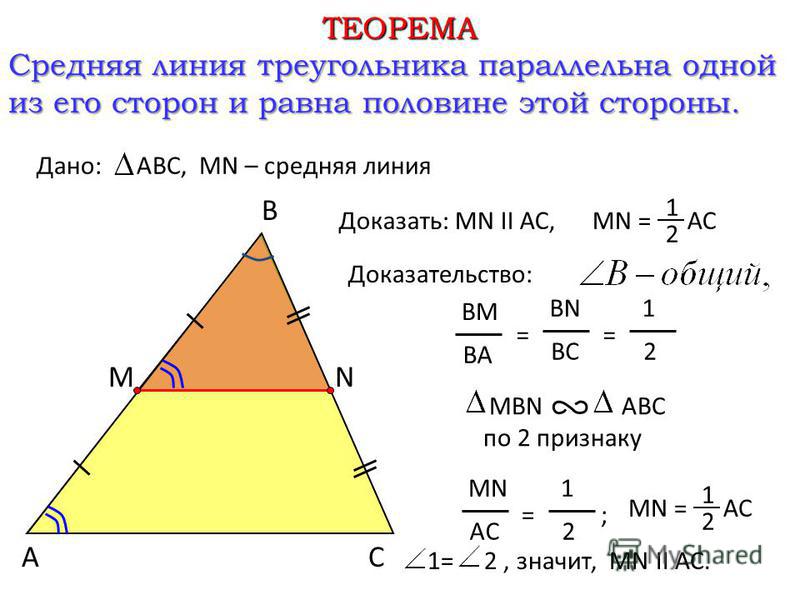
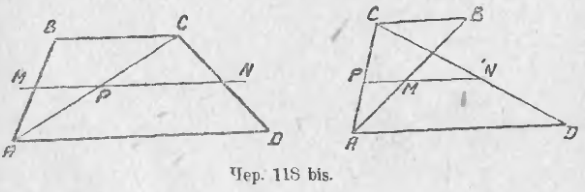Определение . Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).
На рисунке 1 средней линией является отрезок DE .
Утверждение 1 . Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.
Доказательство . Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .
Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.
Первую часть утверждения 1 мы доказали.
Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).
что и требуется доказать.
Доказательство утверждения 1 закончено.
Напомним, что трапецией трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.
Параллельные стороны трапеции называют основаниями , а непараллельные стороны – боковыми сторонами трапеции.
Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.
Определение . Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).
На рисунке 5 средней линией трапеции является отрезок EF .
Утверждение 2 . Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.
Доказательство . Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому
что и требовалось доказать.
Задача 1 . Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.
Решение . Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.
Задача 2 . Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.
Решение . Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:
что и требовалось доказать.
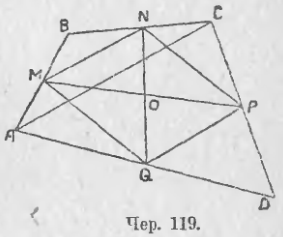
Утверждение 3 . Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.
Доказательство . Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:
откуда вытекает, что точки N и L совпадают. Доказательство завершено.
Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.
Утверждение 4 . Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.
Следствие . Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.
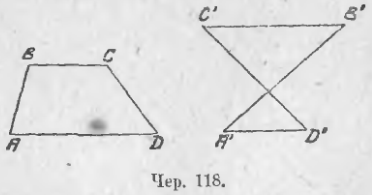
Определение . Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.
Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).
На рисунке 10 средние линии – это отрезки EF и GH .
Замечание 1 . Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.
На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .
Замечание 2 . Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.
Замечание 3 . В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.
Теорема Вариньона . Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограмма параллелограмма .
Доказательство . Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.
Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограмма признака параллелограмма признака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.
Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).
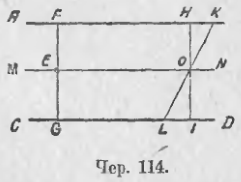
Утверждение 5 . Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).
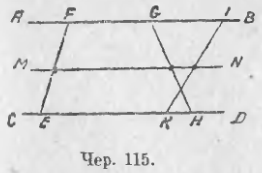
Утверждение 6 . Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:
что и требовалось доказать.
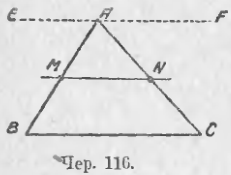
Следствие . Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.
Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапецией трапецией , а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.
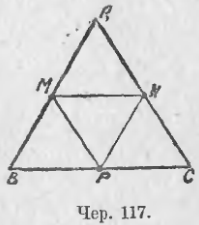
Тетраэдром называют произвольную треугольную пирамиду (рис.17).
У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер . На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых .
Определение . Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.
У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.
Утверждение 7 . Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.
Доказательство . Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).
Определение . Точку пересечения средних линий тетраэдра называют центроидом тетраэдра .
Утверждение 8 . Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:
1.Параллелограмм
Параллелограмм — это геометрическая фигура, у которой диагонали пересекаются в точке, делящей их пополам, а противолежащие стороны параллельны.
Теорема: если диагонали четырехугольника пересекаются и делятся этой точкой пересечения пополам, то такой четырехугольник называется параллелограммом.
Доказательство. Пусть АВСD данный четырехугольник. Точка О — точка пересечения его диагоналей (рис.1). Тогда треугольники Δ АОD и Δ ВOC равны по двум сторонам и углу между ними. А следовательно, угол ODA равен углу CBO и угол OAD равен углу BCO. Таким образом, эти углы являются внутренними накрест лежащими для прямых AD и BC и секущей AC. А по признаку параллельности прямых, прямые AD и BC параллельны. Аналогично можно доказать, что прямая АВ параллельна ВС. Теорема доказана.
Рис.1 Теорема. Параллелограмм.
Теорема. если четырехугольник является параллелограммом, то его диагонали делятся точкой пересечения пополам.
Доказательство. Пусть дан параллелограмм АВСD. (Рис. 2)
Тогда его стороны AD и BC равны и лежат на параллельных прямых а и b. Если мы проведем секущие с и d так, чтобы прямая с проходила через точку А и С, а прямая d проходила через точку B и D, то угол ОАD будет равен углу ОСВ, а угол ОDА будет равен углу ОВС, как внутренние накрест лежащие. Следовательно, треугольники АОD и ВОС равны по стороне и прилегающим к ней углам. А отсюда следует и равенство сторон этих треугольников. Т.е. АО = ОС, а ВО = ОD. Сумма этих сторон и есть диагонали параллелограмма.
Пример 1
Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что ее отрезок, заключенный между параллельными сторонами, делится этой точкой пополам. (Рис.9)
Доказательство:
Пусть ABCD данный параллелограмм. EF данный отрезок, проходящий через точку О пересечения диагоналей.
Рассмотрим треугольники COF и AOE. Сторона АО треугольника АОЕ равна стороне ОС треугольника COF по свойству параллелограмма. Угол при вершине А треугольника АОЕ равен углу при вершине С треугольника COF, как внутренние накрест лежащие углы. Углы при вершине О у обоих треугольников равны как вертикальные.
Отсюда можно сделать вывод, что треугольники АОЕ и COF равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Следовательно, отрезки OF и ОЕ равны.
Рис.9 Задача. Через точку пересечения диагоналей.
Пример 2
Две стороны параллелограмма относятся как 3:4, а его периметр равен 2,8 м. Найдите стороны параллелограмма. (Рис.10)
Решение:
Пусть ABCD данный параллелограмм. Обозначим сторону АВ как 3х, а сторону ВС как 4х. Тогда составим следующее соотношение:
Рис.10 Задача. Две стороны параллелограмма.
Пример 3
В параллелограмме ABCD перпендикуляр, опущенный из вершины В на сторону AD, делит ее пополам. Найдите диагональ BD и стороны параллелограмма, если периметр параллелограмма равен 4 м, а периметр треугольника ABD равен 3 м. (Рис.11)
Решение:
Так как перпендикуляр BE, опущенный на сторону AD, делит ее пополам, то треугольники ABE и BED равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). У них сторона АЕ равна стороне ED, сторона BE — общая, а углы при вершине Е равны 90°.Отсюда следует, что диагональ BD равна стороне АВ.
Обозначим сторону АВ как х, а сторону AD — как 2y. Тогда можно составить следующие соотношения:
PABCD = 2*(х + 2y) = 4, PABD = 2x +2y = 3
PABCD = 2х + 4y = 4, а 2х = 4 — 4y.
Тогда подставим 4 — 4y во второе уравнение:
4 — 4y + 2y = 3 и,следовательно, y = 0,5, а х = 1
Рис.11 Задача. В параллелограмме ABCD перпендикуляр.
Пример 4
В прямоугольный треугольник, каждый катет которого равен 8 см, вписан прямоугольник, имеющий с треугольником общий угол. Найдите периметр прямоугольника.(Рис.12)
Решение:
Пусть АВС данный треугольник. АВ = АС = 8 см. Тогда углы при вершинах В и С равны 45°. А следовательно, углы при вершине Е в треугольниках FEC и BDE также равны 45°. Если обозначить часть катета АF как х, то FC будет равно 8 — х.
Отсюда следует, что FE = AD = 8-х, а BD = х.
Теперь можно составить следующее соотношение:
РADEF = 2*(х + 8 — х) = 16 см.
Периметр прямоугольника ADEF равен 16 см.
Рис.12 Задача. В прямоугольный треугольник.
Пример 5
Докажите, что если у параллелограмма диагонали перпендикулярны, то он является ромбом.(Рис.13)
Доказательство:
Пусть АВСD данный параллелограмм. По свойству параллелограмма, у него противоположные стороны параллельны и равны. Следовательно, стороны АВ и CD можно рассматривать как параллельные прямые, а диагональ BD — как секущую. Тогда в треугольниках АВО и DOC углы при вершинах B и D равны как внутренние накрест лежащие. Так же как и углы при вершинах А и С.
Отсюда следует, что эти треугольники равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Сторона АВ = DC и внутренние накрест лежащие углы при них равны. Следовательно, АО = ОС, а ВО = OD.
Теперь рассмотрим треугольники AOD и DOC. Они также равны, но по первому признаку равенства треугольников. Сторона АО = ОС, а сторона OD у них общая. Углы при вершине О равны 90°. Т.е. по двум сторонам и углу между ними.
Следовательно, можно сделать вывод, что сторона AD = DC = AB = BC, т.е. данный параллелограмм является ромбом.
Рис.13 Задача. Докажите, что если у параллелограмма.
Плоские геометрические фигуры: свойства и основные формулы

Плоские геометрические фигуры:
Четырехугольник (общее для всех четырехугольников)
Квадрат
Прямоугольник
Параллелограмм
Трапеция
Треугольник
Окружность
Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.
Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.
Четырёхугольник
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.
Основные свойства:
- Сумма углов четырёхугольника равна 360°
- Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
- Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
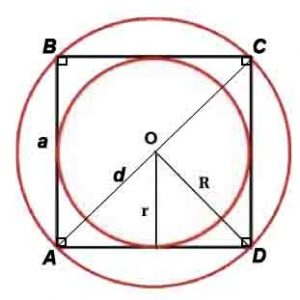
Квадрат
Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Основные формулы:
Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a 2 или S=d 2 /2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.
Свойства:
- Все стороны равны, все углы равны и составляют 90°;
- Диагонали квадрата равны и перпендикулярны;
- У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
- Квадрат является одновременно частным случаем ромба и прямоугольника.
Прямоугольник
Прямоугольник — четырехугольник, у которого все углы прямые.
Основные формулы:
Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a 2 +b 2 )/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a 2 +b 2 )/2 (теорема Пифагора)
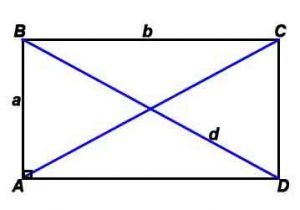
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a 2 +b 2 ) – корень квадратный из (a 2 +b 2 ).
Свойства:
- Диагонали прямоугольника равны и делятся точкой пересечения пополам.
- Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.
Параллелограмм
Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Определения:
Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.
Основные формулы:
Стороны и диагональ связаны соотношением: (d1) 2 +(d2) 2 =(a 2 +b 2 )*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d1*d2)/2*sin γ
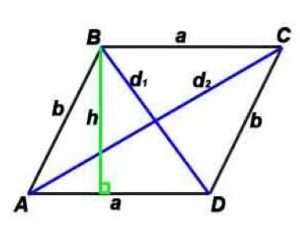
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).
Свойства:
- У параллелограмма противоположные стороны равны и противоположные углы равны.
- Сумма любых двух соседних углов параллелограмма равна 180°.
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит параллелограмм на два равных треугольника.
- Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
- Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Основные формулы:
Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d1*d2)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d1*d2)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a 2 · sin α
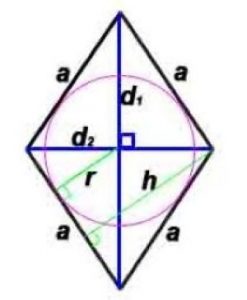
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба
Свойства:
- Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
- В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d1*d2/4a.
Трапеция
Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.
Определения:
- Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
- Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
- Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
- Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
- Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
- Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.
Основные формулы:
Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2
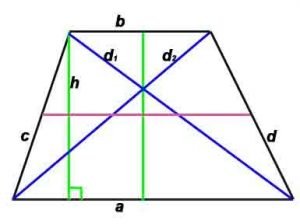
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне
Свойства:
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
Треугольник
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
Определения:
- Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
- Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
- Медиана треугольника— отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
- Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
- Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
- Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
- Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
- Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
Основные формулы:
Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c 2 =a 2 +b 2 (Теорема Пифагора)
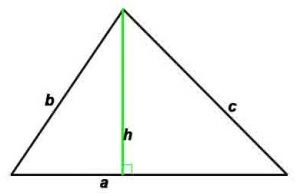
d1, d2 –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности
Свойства:
- В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
- Сумма углов треугольника равна 180°:
- Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| 2 =a 2 +b 2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.
Окружность
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.
Определения:
- Радиус — отрезок, который соединяет центр окружности с любой её точкой.
- Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
- Диаметр — хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
- Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
- Секущая — прямая, которая пересекает окружность в двух различных точках.
Основные формулы:
Длина окружности: L = 2πR
Площадь круга: S = π*r 2 или S = π*d 2 /4
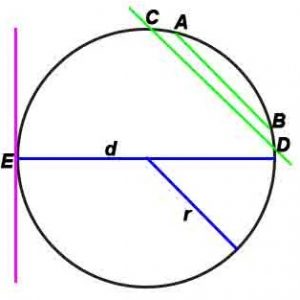
где r-радиус, d –диаметр, L – длина окружности, S-площадь.
http://www.mathtask.ru/0052-planimetry.php
| Главная > Учебные материалы > Математика: Планиметрия. Страница 4 | |||||||
| 1 2 3 4 5 6 7 8 9 10 11 12 | |||||||
| 2.Свойство диагоналей параллелограмма | |||||||
|
Рис.2 Теорема. Свойство диагоналей параллелограмма. 3.РомбРомб — это геометрическая фигура, у которой все стороны равны. Теорема. диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов. Доказательство. Пусть АВСD — ромб.(Рис. 3). Тогда треугольник АВС — равнобедренный. А это значит, что отрезок ВО, который является половиной диагонали, является биссектрисой медианой и высотой. Следовательно диагонали ромба АС и ВD пересекаются под прямым углом. |
Рис.3 Теорема. Свойство диагоналей ромба. ЗадачаВ параллелограмме АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. Необходимо найти отрезки ВЕ и ЕС, если АВ = 9 см, АD = 14 см (рис.4) Решение. Так как прямая АЕ биссектриса, то это значит, что треугольники АВЕ и АЕР равны. Так как угол ВАЕ равен углу АЕР, а угол ЕАР равен углу ВЕА как внутренние накрест лежащие. Следовательно АВЕР — ромб, так как угол ВАЕ равен углу ЕАР ( по условию). Отсюда следует, что АВ = ВЕ = 9 см, а ЕС = 5 см. |
4.Теорема ФалесаТеорема: параллельные прямые, пересекающие стороны угла и отсекающие на одной его стороне равные отрезки, отсекают равные отрезки и на другой его стороне. Доказательство. Пусть дан угол и пересекающие его параллельные прямые (рис.5). Точки А 1 А 2 А 3 А 4 и В 1 В 2 В 3 В 4 — точки пересечения. Проведем прямую ОЕ. Тогда А 1 ЕОА 3 — параллелограмм. И ОЕ = А 1 А 3 Треугольники В 1 В 2 Е и ОВ 2 В 3 равны по стороне (ОВ 2 = ЕВ 2 ) и прилегающим к ней углам. Из равенства треугольников следует, что В 1 В 2 = В 2 В 3 . |
Рис.5 Теорема Фалеса. 5.Средняя линия треугольникаТеорема. средняя линия треугольника, которая соединяет середины двух данных сторон, параллельна третьей его стороне и равна ее половине. Доказательство. Пусть АВС — треугольник. Отрезок ЕР соединяет середины сторон АВ и ВС (Рис. 5). Тогда по теореме Фалеса отрезок ЕР параллелен основанию АС, так как он делит стороны АВ и ВС на равные части. |
Рис.5 Теорема. Средняя линия треугольника. 6.ТрапецияТрапеция — это геометрическая фигура, у которой только две противолежащие стороны параллельны. Теорема. средняя линия трапеции параллельна двум своим основаниям и равна их полусумме. Доказательство. Пусть АВСD — трапеция.(Рис. 6). Проведем прямую от вершины В через середину стороны СD точку Н к основанию, т.е. достроим треугольник АВО. Тогда треугольники ВСН и DHO равны по сторонам СН и НD и прилегающим к ним углам. Следовательно отрезок АО равен сумме оснований АD и ВС. Рассмотрим треугольник АВО. ЕН это средняя линия треугольника, которая равна половине основания АО, т.е. полусумме оснований трапеции АD и ВС. |
Рис.6 Теорема. Средняя линия трапеции. 7.Теорема о пропорциональных отрезкахТеорема. параллельные прямые, которые пересекают стороны угла, отсекают от его сторон пропорциональные отрезки. Доказательство. Пусть дан угол и пересекающие его параллельные прямые. Разобьем угол ВAС параллельными прямыми на n частей. Тогда АВ = ns, a AB1 = ms. Где s — отрезок некоторой длины. По теореме Фалеса эти прямые разбивают сторону AС также на равные части. Тогда: |
Рис.7 Теорема о пропорциональных отрезках. Отложим на луче АС отрезок АС 2 1 , который равен АС 2 = АС*АВ 1 /АВ (Рис.8). Если отрезок АС разбить на большое число частей, то между точками С 1 и С 2 будут деления. Одно из них обозначим как x и y. Т.е. мы пришли к противоречию, так как изначально мы взяли отрезок АС 2 = АС*АВ 1 /АВ. |
Рис.8 Теорема о пропорциональных отрезках. |
Средняя линия треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией этого треугольника.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
В каждом треугольнике — три средних линии.
Средние линии (DE), (EF), (DF).
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией этой трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
У трапеции — только одна средняя линия.
Источники:
Рис. 1-3. Треугольник, трапеция, © ЯКласс.
������� �����
�������� �����: �����������, �������, ������� �����, ����� �������, ������� ����� ������������, ������� ����� ��������, ������� ����� ����������������
�������, ����������� �������� �������������� ������ ����������������, ���������� ������� ������ ����������������.
���� � �������� ���������������� ������,
���������� ����� �������� ���� ��������������� ������,
�������� ������ ���� � ����������� ����������������, �� ��������� �����.
������� ����� ������������ — ��� �������, ����������� �������� ���� ��� ������.
������� ����� ������������ ����������� ������� �������, � �� ����� ����� �������� ����� ���� �������.
�������, ����������� �������� ������� ������ ��������, ���������� ������� ������ ��������.
�������. ������� ����� �������� ����������� ����������, � ����� �� ����� ��������� ���� ���������. �������. �������� ������ �������������� �������� �������� ��������� �����.
��. �����:
�����������,
�������,
������������� �����������,
�������������� �����������,
�������������� �����������
Средняя линия прямоугольного треугольника формула. Трапеция
Как найти середину треугольника: задачка по геометрии. Основные элементарные задачи по Евклидовой геометрии пришли к нам из античности. В них заключается сама первичная сущность и необходимые базовые знания о восприятии человеком пространственных форм. Одной из таких задач является проблема нахождения середины треугольника. Сегодня эта задачка рассматривается как учебный прием развития интеллектуальных способностей школьников. В древнем же мире, знание того, как найти середину треугольника, применялось и на практике: в землеустройстве, при изготовлении разнообразных механизмов и т.д. В чем же состоит сущность этого геометрического ребуса?
Что такое медиана? Перед решением задачи необходимо ознакомиться с простейшей геометрической терминологией, касающейся треугольников. Прежде всего, у каждого треугольника есть три вершины, три стороны и три угла, от чего и происходит название данной геометрической фигуры. Важно знать, как называются линии, соединяющие вершины с противоположными сторонами: высота, биссектриса и медиана.
Высота − линия перпендикулярная стороне, противоположной вершине, из которой она проводится; биссектриса − делит угол пополам; медиана же делит противоположную исходящей вершине сторону пополам. Для решения этой задачи нужно знать, как найти координаты середины отрезка, ведь именно точка пересечения медиан треугольника и является его серединой.
Находим середины сторон треугольника. Нахождение середины отрезка тоже является классической геометрической задачей, для решения которой понадобится циркуль и линейка без делений. Ставим иглу циркуля в точку окончания отрезка и чертим полукруг, больший половины отрезка в середине последнего. Проделываем то же самое с другой стороны отрезка. Полученные полуокружности обязательно пересекутся в двух точках, ведь их радиусы больше половины исходного отрезка.
Соединяем две точки пересечения окружности прямой линией при помощи линейки. Эта линия пересекает исходный отрезок точно в его середине. Теперь, зная то, как найти середину отрезка, проделываем это с каждой стороной треугольника.
После нахождения всех середин сторон треугольника всё готово для построения его собственной середины.
Строим середину треугольника. Соединив прямыми линиями вершины треугольника с серединами противоположных им сторон, получаем три медианы. Может кого-то это и удивит, но одним из законов гармонии этой геометрической фигуры является то, что все три медианы всегда пересекаются в одной точке. Именно эта точка и будет искомой серединой треугольника, которую не так трудно найти, если знать;как построить середину отрезка.
Интересно и то, что точка пересечения медиан представляет собой не только геометрическую, но и «физическую» середину треугольника. То есть, если, к примеру, вырезать треугольник из фанеры, найти его середину и поместить эту точку на кончик иглы, то в идеале такая фигура будет балансировать и не упадет. Элементарная геометрия несет в себе множество подобных захватывающих «тайн», знание которых помогает постигать гармонию окружающего мира и природу более сложных вещей.
Понятие средней линии треугольника
Введем понятие средней линии треугольника.
Определение 1
Это отрезок, соединяющий середины двух сторон треугольника (Рис. 1).
Рисунок 1. Средняя линия треугольника
Теорема о средней линии треугольника
Теорема 1
Средняя линия треугольника параллельна одной из его сторон и равна её половине.
Доказательство.
Пусть нам дан треугольник $ABC$. $MN$ — средняя линия (как на рисунке 2).
Рисунок 2. Иллюстрация теоремы 1
Так как $frac{AM}{AB}=frac{BN}{BC}=frac{1}{2}$, то треугольники $ABC$ и $MBN$ подобны по второму признаку подобия треугольников. Значит
Также, отсюда следует, что $angle A=angle BMN$, значит $MN||AC$.
Теорема доказана.
Следствия из теоремы о средней линии треугольника
Следствие 1:
Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.
Доказательство.
Рассмотрим треугольник $ABC$, где ${AA}_1, {BB}_1, {CC}_1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 3).
Рисунок 3. Иллюстрация следствия 1
По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда
Аналогично доказывается, что
Теорема доказана.
Следствие 2:
Три средние линии треугольника делят его на 4 треугольника, подобных исходному треугольнику с коэффициентом подобия $k=frac{1}{2}$.
Доказательство.
Рассмотрим треугольник $ABC$ со средними линиями $A_1B_1, { A}_1C_1, B_1C_1$ (рис. 4)
Рисунок 4. Иллюстрация следствия 2
Рассмотрим треугольник $A_1B_1C$. Так как $A_1B_1$ — средняя линия, то
Угол $C$ — общий угол этих треугольников. Следовательно, треугольники $A_1B_1C$ и $ABC$ подобны по второму признаку подобия треугольников с коэффициентом подобия $k=frac{1}{2}$.
Аналогично доказывается, что треугольники $A_1C_1B$ и $ABC$, и треугольники $C_1B_1A$ и $ABC$ подобны с коэффициентом подобия $k=frac{1}{2}$.
Рассмотрим треугольник $A_1B_1C_1$. Так как $A_1B_1, { A}_1C_1, B_1C_1$ — средние линии треугольника, то
Следовательно, по третьему признаку подобия треугольников, треугольники $A_1B_1C_1$ и $ABC$ подобны с коэффициентом подобия $k=frac{1}{2}$.
Теорема доказана.
Примеры задачи на понятие средней линии треугольника
Пример 1
Дан треугольник со сторонами $16$ см, $10$ см и $14$ см. Найти периметр треугольника , вершины которого лежат в серединах сторон данного треугольника.
Решение.
Так как вершины искомого треугольника лежат в серединах сторон данного треугольника, то его стороны — средние линии исходного треугольника. По следствию 2, получим, что стороны искомого треугольника равны $8$ см, $5$ см и $7$ см.
Ответ:
$20$ см.
Пример 2
Дан треугольник $ABC$.
Рисунок 5.
Периметр треугольника $BMN=14$ см. Найти периметр треугольника $ABC$.
Решение.
Так как $N и M$ — середины сторон $BC$ и $AB$, то $MN$ — средняя линия. Значит
По теореме 1, $AC=2MN$. Получаем:
Порой темы, которые объясняют в школе, могут быть не всегда понятны с первого раза. Особенно это касается такого предмета, как математика. Но все становится намного сложнее, когда эта наука начинает подразделяться на две части: алгебру и геометрию.
Каждый ученик может обладать способностью к одному из двух направлений, но особенно в начальных классах важно понять базу и алгебры, и геометрии. В геометрии одной из главных тем принято считать раздел о треугольниках.
Как находить среднюю линию треугольника? Давайте разбираться.
Основные понятия
Для начала чтобы разобраться, как находить среднюю линию треугольника, важно понимать, что же это.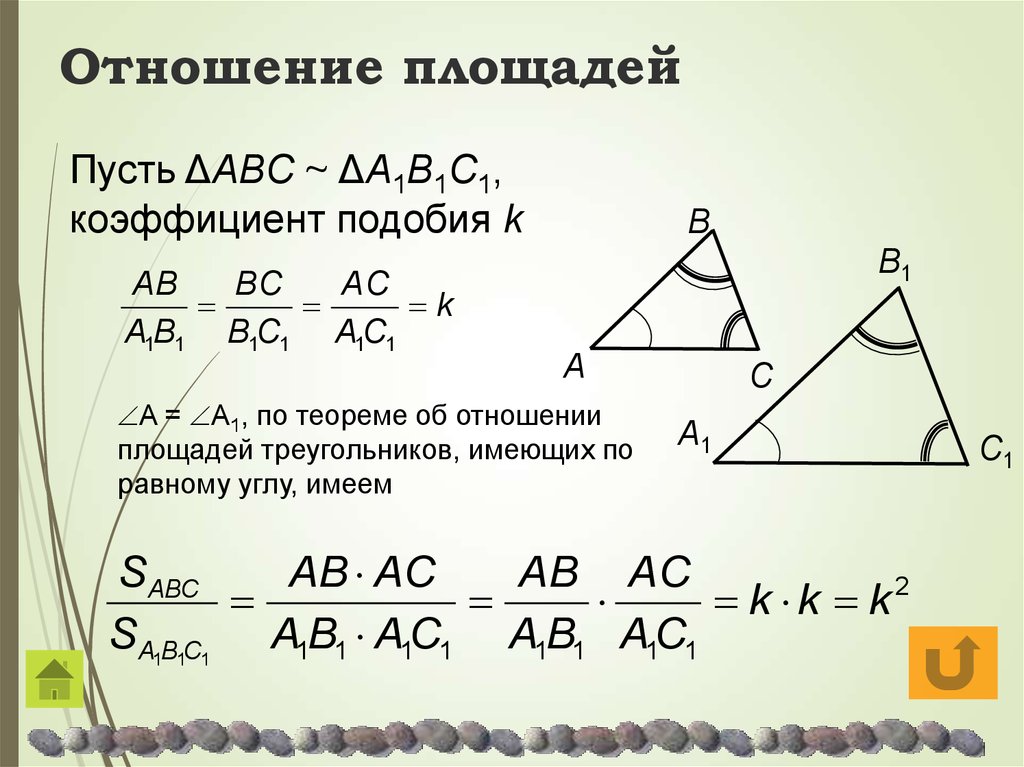
Для проведения средней линии нет ограничений: треугольник может быть любым (равнобедренным, равносторонним, прямоугольным). И все свойства, которые относятся к средней линии, будут действовать.
Средняя линия треугольника является отрезком, соединяющим середины 2-х его сторон. Следовательно, любой треугольник может иметь 3 таких линии.
Свойства
Чтобы знать, как находить среднюю линию треугольника, обозначим ее свойства, которые необходимо запомнить, иначе без них будет невозможным решение задач с необходимостью обозначить длину средней линии, поскольку все полученные данные необходимо обосновать и аргументировать теоремами, аксиомами или свойствами.
Таким образом, чтобы ответить на вопрос: «Как найти среднюю линию треугольника АВС?», достаточно знать одну из сторон треугольника.
Приведем пример
Взгляните на рисунок. На нем представлен треугольник ABC со средней линией DE. Обратим внимание, что она параллельна основанию AC в треугольнике.
Вот такими несложными способами можно понять, как находить среднюю линию треугольника. Запомните ее основные свойства и определение, и тогда у вас никогда не возникнет проблем с нахождением ее значения.
Четырёхугольник, у которого только две стороны параллельны называются трапецией
.
Параллельные стороны трапеции называются её основаниями
, а те стороны, которые не параллельны, называются боковыми сторонами
. Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DC
AM = MD; BN = NC
MN
средняя линия, AB
и CD
— основания, AD
и BC
— боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.
Основная задача
: Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема
: Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
AM = MC and BN = NC
=>
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.
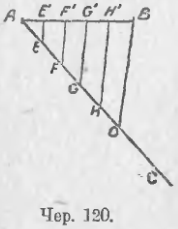
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B. Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2
В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.
[{Large{text{Подобие треугольников}}}]
Определения
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).
Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.
Определение
Периметр треугольника – это сумма длин всех его сторон.
Теорема
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
Доказательство
Рассмотрим треугольники (ABC)
и (A_1B_1C_1)
со сторонами (a,b,c)
и (a_1, b_1, c_1)
соответственно (см. рисунок выше).
Тогда (P_{ABC}=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=kcdot
P_{A_1B_1C_1})
Теорема
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Доказательство
Пусть треугольники (ABC)
и (A_1B_1C_1)
подобны, причём (dfrac{AB}{A_1B_1} = dfrac{AC}{A_1C_1} = dfrac{BC}{B_1C_1} = k)
.
— angle A_1 — angle B_1 = angle C_1)
, то есть углы треугольника (ABC)
соответственно равны углам треугольника (A_1B_1C_1)
.
Так как (angle A = angle A_1)
и (angle B = angle B_1)
, то (dfrac{S_{ABC}}{S_{A_1B_1C_1}} = dfrac{ABcdot AC}{A_1B_1cdot
A_1C_1})
и (dfrac{S_{ABC}}{S_{A_1B_1C_1}} = dfrac{ABcdot
BC}{A_1B_1cdot B_1C_1})
.
Из этих равенств следует, что (dfrac{AC}{A_1C_1} =
dfrac{BC}{B_1C_1})
.
Аналогично доказывается, что (dfrac{AC}{A_1C_1} =
dfrac{AB}{A_1B_1})
(используя равенства (angle B = angle B_1)
, (angle C = angle C_1)
).
В итоге, стороны треугольника (ABC)
пропорциональны сходственным сторонам треугольника (A_1B_1C_1)
, что и требовалось доказать.
Теорема (второй признак подобия треугольников)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Доказательство
Рассмотрим два треугольника (ABC)
и (A»B»C»)
, таких что (dfrac{AB}{A»B»}=dfrac{AC}{A»C»})
, (angle BAC = angle A»)
.
и (A»B»C»)
– подобны. Учитывая первый признак подобия треугольников, достаточно показать, что (angle B = angle B»)
.
Рассмотрим треугольник (ABC»»)
, у которого (angle 1 = angle A»)
, (angle 2 = angle B»)
. Треугольники (ABC»»)
и (A»B»C»)
подобны по первому признаку подобия треугольников, тогда (dfrac{AB}{A»B»} =
dfrac{AC»»}{A»C»})
.
С другой стороны, по условию (dfrac{AB}{A»B»} = dfrac{AC}{A»C»})
. Из последних двух равенств следует, что (AC = AC»»)
.
Треугольники (ABC)
и (ABC»»)
равны по двум сторонам и углу между ними, следовательно, (angle B = angle 2 = angle B»)
.
Теорема (третий признак подобия треугольников)
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Доказательство
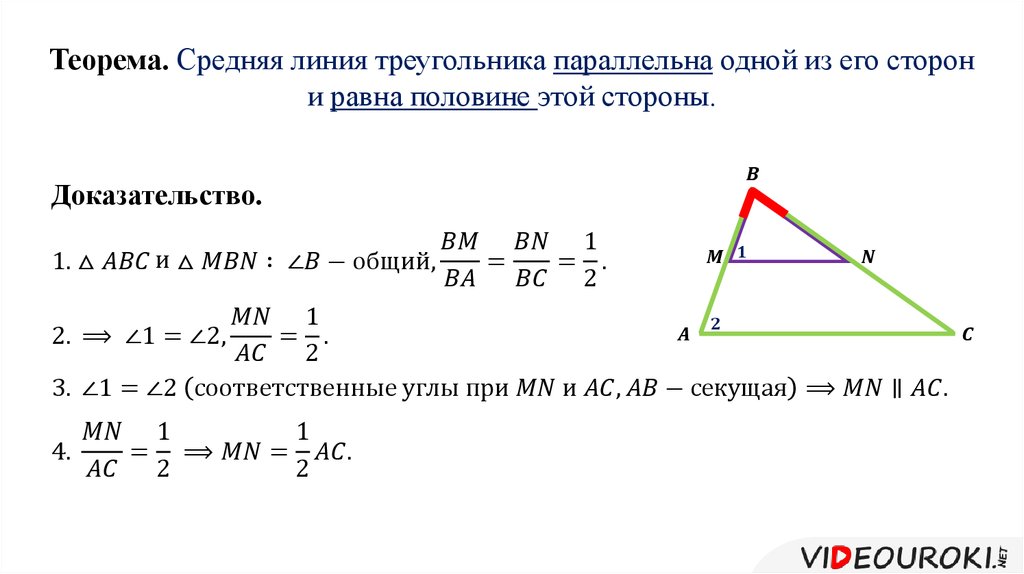
Пусть стороны треугольников (ABC)
и (A»B»C»)
пропорциональны: (dfrac{AB}{A»B»} = dfrac{AC}{A»C»} = dfrac{BC}{B»C»})
.
и (A»B»C»)
подобны.
Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что (angle BAC = angle A»)
.
Рассмотрим треугольник (ABC»»)
, у которого (angle 1 = angle A»)
, (angle 2 = angle B»)
.
Треугольники (ABC»»)
и (A»B»C»)
подобны по первому признаку подобия треугольников, следовательно, (dfrac{AB}{A»B»} = dfrac{BC»»}{B»C»}
= dfrac{C»»A}{C»A»})
.
Из последней цепочки равенств и условия (dfrac{AB}{A»B»} =
dfrac{AC}{A»C»} = dfrac{BC}{B»C»})
вытекает, что (BC = BC»»)
, (CA
=
C»»A)
.
Треугольники (ABC)
и (ABC»»)
равны по трем сторонам, следовательно, (angle BAC = angle 1 = angle A»)
.
[{Large{text{Теорема Фалеса}}}]
Теорема
Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
Доказательство
Докажем сначала лемму:
Если в (triangle OBB_1)
через середину (A)
стороны (OB)
проведена прямая (aparallel BB_1)
, то она пересечет сторону (OB_1)
также в середине.
Через точку (B_1)
проведем (lparallel OB)
. Пусть (lcap a=K)
. Тогда (ABB_1K)
— параллелограмм, следовательно, (B_1K=AB=OA)
и (angle
A_1KB_1=angle ABB_1=angle OAA_1)
; (angle AA_1O=angle KA_1B_1)
как вертикальные. Значит, по второму признаку (triangle
OAA_1=triangle B_1KA_1 Rightarrow OA_1=A_1B_1)
. Лемма доказана.
Перейдем к доказательству теоремы. Пусть (OA=AB=BC)
, (aparallel
bparallel c)
и нужно доказать, что (OA_1=A_1B_1=B_1C_1)
.
Таким образом, по данной лемме (OA_1=A_1B_1)
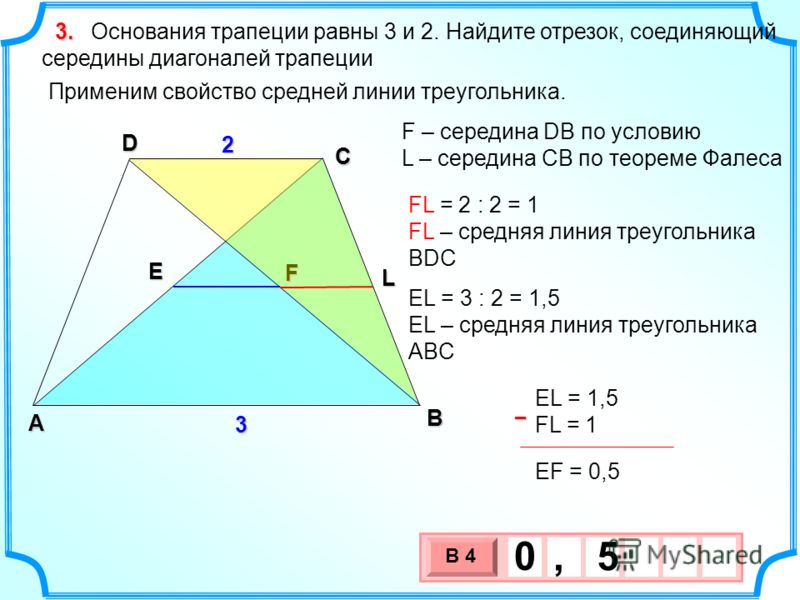
. Докажем, что (A_1B_1=B_1C_1)
. Проведем через точку (B_1)
прямую (dparallel OC)
, причем пусть (dcap a=D_1, dcap c=D_2)
. Тогда (ABB_1D_1, BCD_2B_1)
— параллелограммы, следовательно, (D_1B_1=AB=BC=B_1D_2)
. Таким образом, (angle A_1B_1D_1=angle C_1B_1D_2)
как вертикальные, (angle
A_1D_1B_1=angle C_1D_2B_1)
как накрест лежащие, и, значит, по второму признаку (triangle A_1B_1D_1=triangle C_1B_1D_2
Rightarrow A_1B_1=B_1C_1)
.
Теорема Фалеса
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
Доказательство
Пусть параллельные прямые (pparallel qparallel rparallel s)
разбили одну из прямых на отрезки (a, b, c, d)
. Тогда вторую прямую эти прямые должны разбить на отрезки (ka, kb, kc, kd)
соответственно, где (k)
– некоторое число, тот самый коэффициент пропорциональности отрезков.
Проведем через точку (A_1)
прямую (pparallel OD)
((ABB_2A_1)
— параллелограмм, следовательно, (AB=A_1B_2)
). Тогда (triangle OAA_1
sim triangle A_1B_1B_2)
по двум углам. Следовательно, (dfrac{OA}{A_1B_2}=dfrac{OA_1}{A_1B_1} Rightarrow A_1B_1=kb)
.
Аналогично проведем через (B_1)
прямую (qparallel OD Rightarrow
triangle OBB_1sim triangle B_1C_1C_2 Rightarrow B_1C_1=kc)
и т.д.
[{Large{text{Средняя линия треугольника}}}]
Определение
Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.
Теорема
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Доказательство
1) Параллельность средней линию основанию следует из доказанной выше леммы
.
2) Докажем, что (MN=dfrac12 AC)
.
Через точку (N)
проведем прямую параллельно (AB)
. Пусть эта прямая пересекла сторону (AC)
в точке (K)
. Тогда (AMNK)
— параллелограмм ((AMparallel NK, MNparallel AK)
по предыдущему пункту). Значит, (MN=AK)
.
Т.к. (NKparallel AB)
и (N)
– середина (BC)
, то по теореме Фалеса (K)
– середина (AC)
. Следовательно, (MN=AK=KC=dfrac12 AC)
.
Следствие
Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом (frac12)
.
Как найти среднюю линию всех фигур. Трапеция, средняя линия трапеции, треугольник. Свойства серединных перпендикуляров треугольника
1
Дополнительное построение, ведущее к теореме о средней линии треугольника, трапеции и свойствам подобия треугольников.
И она равна половине гипотенузы
.
Следствие 1.
Следствие 2.
2
Все прямоугольные треугольники с одинаковым острым углом — подобны. Взгляд на тригонометрические функции.
3
Пример дополнительного построения — высота, опущенная на гипотенузу. Вывод теоремы Пифагора на основе подобия треугольников.
Отсюда видно, что
1
Все прямоугольные треугольники с одинаковым острым углом — подобны. Взгляд на тригонометрические функции.
Треугольники со сторонами штрихованными и с не штрихованными подобны по равенству двух углов. Поэтому откуда
Это значит, что указанные отношения зависят лишь от острого угла прямоугольного треугольника и по сути определяют его. Это одно из оснований появления тригонометрических функций:
Часто запись тригонометрических функций угла в подобных прямоугольных треугольниках наглядней записи соотношений подобия!
2
Пример дополнительного построения — высота, опущенная на гипотенузу.
Опустим на гипотенузу AB высоту CH. Имеем три подобных треугольника ABC, AHC и CHB. Запишем выражения для тригонометрических функций:
Отсюда видно, что . Складывая, получаем теорему Пифагора, поскольку :
Другое доказательство теоремы Пифагора см.в комментарии к задаче 4.
3
Важный пример дополнительного построения – построение угла, равного одному из углов треугольника.
Проводим из вершины прямого угла отрезок прямой, составляющий с катетом CA угол, равный углу CAB заданного прямоугольного треугольника ABC. В результате получим равнобедренный треугольник ACM с углами при основании . Но другой треугольник, получающийся при таком построении, также будет равнобедренным, поскольку каждый его угол при основании равен (по свойству углов прямоугольного треугольника и по построению — из прямого угла «вычли» угол ). В силу того, что треугольники BMC и AMC равнобедренные с общей стороной MC имеем равенство MB=MA=MC, т.
, и она равна половине гипотенузы
.
Следствие 1.
Середина гипотенузы является центром окружности, описанной вокруг этого треугольника, поскольку получилось, что середина гипотенузы равноудалена от вершин прямоугольного треугольника.
Следствие 2.
Средняя линия прямоугольного треугольника, соединяющая середину гипотенузы и середину катета, параллельна противоположному катету и равна его половине.
Опустим в равнобедренных треугольниках BMC и AMC высоты MH и MG на основания. Поскольку в равнобедренном треугольнике, высота, опущенная на основание, является также и медианой (и биссектрисой), то MH и MG –линии прямоугольного треугольника, соединяющие середину гипотенузы с серединами катетов. По построению они оказываются параллельными противоположным катетам и равные их половинам, поскольку треугольники равны MHC и MGC равны (причем MHCG – прямоугольник). Этот результат является основанием для доказательства теоремы о средней линии произвольного треугольника и, далее, средней линии трапеции и свойства пропорциональности отрезков, отсекаемых параллельными прямыми на двух пересекающих их прямых.
Найти геометрическое место точек (ГМТ) пересечения медиан всевозможных прямоугольных треугольников, гипотенуза АВ которых зафиксирована.
Точка пересечения медиан любого треугольника отсекает от медианы одну треть, считая от точки ее пересечения с соответствующей стороной. В прямоугольном треугольнике медиана, проведенная из прямого угла, равна половине гипотенузы. Поэтому искомое ГМТ есть окружность радиуса, равной 1/6 от длины гипотенузы, с центром в середине этой (фиксированной) гипотенузы.
Тема урока
Средняя линия треугольника
Цели урока
Закрепить знания школьников о треугольниках;
Познакомить учащихся с таким понятием, как средняя линия треугольника;
Сформировать знания учеников о свойствах треугольников;
Продолжать обучать детей применению свойств фигур при решении задач;
Развивать логическое мышление, усидчивость и внимание учеников.
Задачи урока
Формировать знания школьников о средней линии треугольников;
Проверить знания учащихся по пройденным темам о треугольниках;
Проверить умение учащихся решать задачи.
Развивать у школьников интерес к точным наукам;
Продолжать формировать умение учащихся излагать свои мысли и владеть математическим языком;
План урока
1. Средняя линия треугольника. Основные понятия.
2. Средняя линия треугольника, теоремы и свойства.
3. Повторение ранее изученного материала.
4. Основные линии треугольника и их свойства.
5. Интересные факты из области математики.
6. Домашнее задание.
Средняя линия треугольника
Средней линией треугольника называют такой отрезок, который соединяет середины двух сторон данного треугольника.
В каждом треугольнике есть три средние линии, которые образуют еще один новый треугольник, расположенный внутри.
Вершины вновь образованного треугольника находятся на срединах сторон данного треугольника.
В каждом треугольнике есть возможность провести три средние линии.
Теперь давайте более детально остановимся на этой теме. Посмотрите на рисунок треугольника вверху.
Свойства средней линии треугольника
Каждая средняя линия треугольника, соединяющая середины его сторон, обладает следующими свойствами:
1. Средняя линия треугольника параллельна его третей стороне и равна её половине.
Таким образом, мы видим, что сторона АС параллельна MN, которая в два раза меньше, чем сторона АС.
2. Средние линии треугольника делят его на четыре равных треугольника.
Если мы посмотрим на треугольник АВС, то увидим, что средние линии MN, MP и NP разделили его на четыре равных треугольника, и в итоге образовались треугольники MBN, PMN, NCP и AMP.
3. Средняя линия треугольника отсекает от данного треугольника подобный, площадь которого равняется одной четвертой исходного треугольника.
Так, например, в треугольнике АВС средняя линия MP отсекает от данного треугольника, образуя треугольник AMP, площадь которого равна одной четвертой треугольника АВС.
Треугольники
В предыдущих классах вы уже изучали такую геометрическую фигуру, как треугольник и знаете, какие бывают виды треугольников, чем они отличаются и какими свойствами обладают.
Треугольник относится к простейшим геометрическим фигурам, которые имеют три стороны, три угла и их площадь ограничена тремя точками и тремя отрезками, которые попарно соединяют эти точки.
Вот мы вспомнили определение треугольника, а сейчас давайте повторим все что вы знаете об этой фигуре, ответив на вопросы:
4. Какие виды треугольников вы уже изучили? Перечислите их.
5. Дайте определения каждому из видов треугольников.
6. Чему равна площадь треугольника?
7. Чему равна сумма углов этой геометрической фигуры?
8. Какие типы треугольников вам известны? Назовите их.
9. Какие вы знаете треугольники по типу равных сторон?
10. Дайте определение гипотенузы.
11. Сколько острых углов может быть в треугольнике?
Основные линии треугольника
К основным линиям треугольника относятся: медиана, биссектриса, высота и срединный перпендикуляр.
Медиана
Медианой треугольника называют отрезок, который соединяет вершину треугольника с серединой противолежащей стороны данного треугольника.
Свойства медиан треугольника
1. Она делит треугольник на два других, равных по площади;
2. Все медианы данной фигуры пересекаются в одной точке. Эта точка делит их в отношении два к одному, начиная отсчет от вершины, и называется центром тяжести треугольника;
3. Медианы разделяют данный треугольник на шесть равновеликих.
Биссектриса
Луч, который выходит из вершины и, проходя между сторонами угла, делит его пополам, называется биссектрисой этого угла.
А если отрезок биссектрисы угла соединяет его вершину с точкой, которая лежит на противолежащей стороне треугольника, то он называется биссектрисой треугольника.
Свойства биссектрис треугольника
1. Биссектрисой угла является геометрическое место точек, которые равноудалены от сторон данного угла.
2.
3. Центром окружности, вписанной в треугольник, является точка пересечения биссектрис данной фигуры.
Высота
Перпендикуляр, который проведен с вершины к фигуры к прямой, которая является противоположной стороной треугольника, называется его высотой.
Свойства высот треугольника
1. Высота, проведенная из вершины прямого угла, делит треугольник на два подобных.
2. Если треугольник является остроугольным, то его две высоты отсекают от данного треугольника ему подобные.
Срединный перпендикуляр
Срединным перпендикуляром треугольника называют прямую, которая проходит через середину отрезка, который расположен перпендикулярно к этому отрезку.
Свойства серединных перпендикуляров треугольника
1. Любая точка серединного перпендикуляра к отрезку, равноудалена от его концов.
2. Точка пересечения серединных перпендикуляров, которые проведены к сторонам треугольника, есть центром окружности, которая описана около этого треугольника.
Интересные факты из области математики
Будет ли для вас новостью узнать, что за расшифровку секретной переписки правительства Испании, Франсуа Виета хотели отправить на костер, так как считали, что узнать шифр мог только дьявол, а человеку это не по силам.
Известно ли вам, что первым человеком, который предложил нумеровать кресла, ряды и места, был Рене Декарт? Аристократы-театралы даже просили короля Франции дать за это Декарту награду, но, увы, король отказал, так как считал, что давать награды философу – это ниже его достоинства.
Из-за учащихся, которые могли запомнить теорему Пифагора, но не смогли ее понять, эту теорему называли «ослиным мостом». Это значило, что ученик «осел», который не смог преодолеть мост. В данном случае мостом считали теорему Пифагора.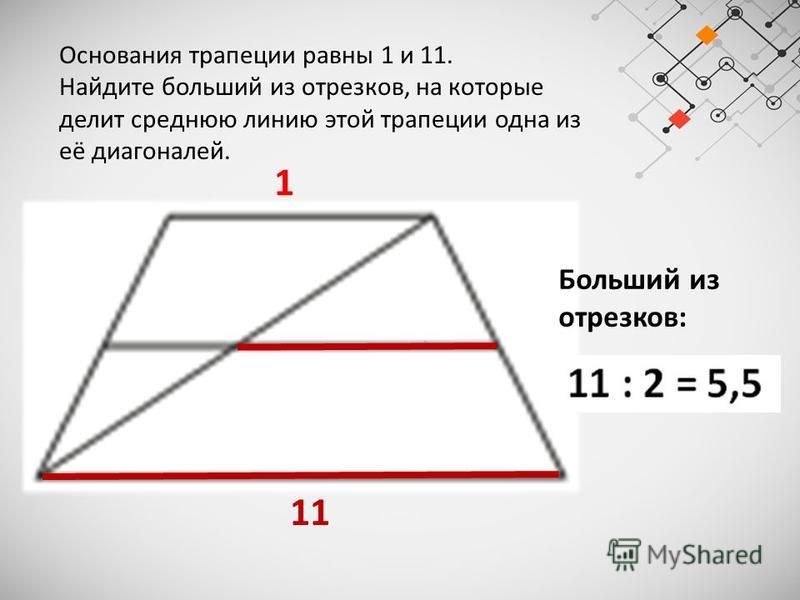
Писатели сказочники посвящали свои произведения не только мифическим героям, людям и зверюшкам, но и математическим символам. Так, например, автор знаменитой «Красной Шапочки», написал сказку о любви циркуля и линейки.
Домашнее задание
1. Перед вами изображены три треугольника, дайте ответ, являются ли проведенные в треугольниках линии средними?
2. Сколько средних линий можно построить в одном треугольнике?
3. Дан треугольник АВС. Найдите стороны треугольника АВС, если его средние линии имеют такие размеры: OF = 5,5 см, FN = 8 см, ON = 7 см.
Средняя линия трапеции, а особенно ее свойства, очень часто используются в геометрии для решения задач и доказательства тех или иных теорем.
– это четырехугольник, у которого только 2 стороны параллельны друг другу. Параллельные стороны называют основаниями (на рисунке 1 — AD
и BC
), две другие – боковыми (на рисунке AB
и CD
).
Средняя линия трапеции
– это отрезок, соединяющий середины ее боковых сторон (на рисунке 1 — KL
).
Свойства средней линии трапеции
Доказательство теоремы о средней линии трапеции
Доказать
, что средняя линия трапеции равна полусумме ее оснований и параллельна этим основаниям.
Дана трапеция ABCD
со средней линией KL
. Для доказательства рассматриваемых свойств требуется провести прямую через точки B
и L
. На рисунке 2 это прямая BQ
. А также продолжить основание AD
до пересечения с прямой BQ
.
Рассмотрим полученные треугольники LBC
и LQD
:
- По определению средней линии KL
точка L
является серединой отрезка CD
. Отсюда следует, что отрезки CL
и LD
равны. - ∠ BLC
= ∠ QLD
, так как эти углы вертикальные. - ∠ BCL
= ∠ LDQ
, так как эти углы накрест лежащие при параллельных прямых AD
и BC
и секущей CD
.
Из этих 3 равенств следует, что рассмотренные ранее треугольники LBC
и LQD
равны по 1 стороне и двум прилежащим к ней углам (см.
= ∠ LQD
, BC=DQ
и самое главное — BL=LQ
=> KL
, являющаяся средней линией трапеции ABCD
, также является и средней линией треугольника ABQ
. Согласно свойству средней линией треугольника ABQ
получаем.
В решении планиметрических задач, помимо сторон и углов фигуры, нередко активное участие принимают и другие величины – медианы, высоты, диагонали, биссектрисы и прочие. К их числу относится и средняя линия.
Если исходный многоугольник – трапеция, то что представляет собой его средняя линия? Данный отрезок представляет собой часть прямой, которая пересекает боковые стороны фигуры посередине и располагается параллельно двум другим сторонам – основаниям.
Как найти среднюю линию трапеции через линию средины и основания
Если известны величина верхнего и нижнего оснований, то рассчитать неизвестное поможет выражение:
a, b – основания, l – средняя линия.
Как найти среднюю линию трапеции через площадь
Если в исходных данных присутствует значение площади фигуры, то с помощью данной величины также можно вычислить длину линии средины трапеции.
S – площадь,
h – высота,
a, b – основания.
Но, так как l = (a+b)/2, то S = l*h, а значит l=S/h.
Как найти среднюю линию трапеции через основание и углы при нем
При наличии длины большего основания фигуры, ее высоты, а также известных градусных мер углов при нем, выражение для нахождения линии средины трапеции будет иметь следующий вид:
l=a – h*(ctgα+ctgβ)/2, при этом
l – искомая величина,
a – большее основание,
α, β – углы при нем,
h – высота фигуры.
Если известно значение меньшего основания (при тех же остальных данных), найти линию средины поможет соотношение:
l=b+h*(ctgα+ctgβ)/2,
l – искомая величина,
b – меньшее основание,
α, β – углы при нем,
h – высота фигуры.
Найти среднюю линию трапеции через высоту, диагонали и углы
Рассмотрим ситуацию, когда в условиях задачи присутствуют значения диагоналей фигуры, углы, которые они образуют, пересекаясь друг с другом, а также высота.
l=(d1*d2)/2h*sinγ или l=(d1*d2)/2h*sinφ,
l – линия средины,
d1, d2 – диагонали,
φ, γ – углы между ними,
h – высота фигуры.
Как найти среднюю линию трапецииДля равнобедренной фигуры
В случае, если базовая фигура – трапеция равнобедренная, приведенные выше формулы будут иметь следующий вид.
- При наличии значений оснований трапеции изменений в выражении не произойдет.
l = (a+b)/2, a, b – основания, l – средняя линия.
- Если известны высота, основание и углы, к нему прилегающие, то:
l=a-h*ctgα,
l=b+h*ctgα,
l – линия средины,
a, b – основания (b
α – углы при нем,
h – высота фигуры.
- Если известна боковая сторона трапеции и одно из оснований, то определить искомую величину можно, обратившись к выражению:
l=a-√(c*c-h*h),
l=b+√(c*c-h*h),
l – линия средины,
a, b – основания (b
h – высота фигуры.
- При известных значениях высоты, диагоналей (а они равны между собой) и углах, образованных в результате их пересечения, линию средины можно найти следующим образом:
l=(d*d)/2h*sinγ или l=(d*d)/2h*sinφ,
l – линия средины,
d – диагонали,
φ, γ – углы между ними,
h – высота фигуры.
- Известны площадь и высота фигуры, тогда:
l=S/h,
S – площадь,
h – высота.
- Если перпендикуляр-высота неизвестен, его можно определить с помощью определения тригонометрической функции.
h=c*sinα, поэтому
l=S/c*sinα,
l – линия средины,
S – площадь,
c – боковая сторона,
α- угол у основания.
Средняя линия треугольника интересный характеризующий отрезок, так как обладает несколькими свойствами, позволяющими найти простое решение для казалось бы сложной задачи. Поэтому рассмотрим основные свойства средней линии и поговорим о том, как найти длину этого отрезка в треугольнике.
Треугольник и его характеризующие отрезки
Треугольник это фигура, состоящая из трех сторон и трех углов. В зависимости от углов треугольники делятся на:
- Остроугольные
- Тупоугольные
- Прямоугольные
Рис. 1. Виды треугольников
Основными характеризующими отрезками треугольника являются:
- Медиана
– отрезок, соединяющий вершину с серединой противоположной стороны. - Биссектриса
– отрезок, делящий угол пополам - Высота
— перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
Рис. 2. Высота, медиана и биссектриса в треугольнике
Для каждого из характеризующих отрезков существует своя точка пересечения. При соединении трех точек пересечения медиан, биссектрис и высот получается золотое сечение треугольника.
Однако существует и ряд дополнительных характеризующих отрезков:
- Серединный перпендикуляр
— высота восстановленная из середины высоты. Как правило серединный перпендикуляр продолжается до пересечения с другой стороной. - Средняя линия
— отрезок, соединяющий середины смежных сторон. - Радиус вписанной окружности
. Вписанная окружность — окружность, которая касается каждой из сторон треугольника. - Радиус описанной окружности.
Описанная окружность — окружность, содержащая в себе все стороны треугольника.
Смежными сторонами треугольников называют стороны, которые имеют общую вершину. В геометрии существует понятие противоположных сторон, т.е. сторон, которые лежат друг напротив друга и не имеют общих вершин. Но это понятие для треугольников не применимо — любая пара сторон в треугольнике является смежной.
Свойство средней линии
Свойств средней линии не так много, но все они имеют значение при решении задач. Дело в том, что задач на нахождение длины средней линии мало, а потому некоторые из них способны построить ученика в ступор при всей своей простоте.
Поэтому приведем и обсудим все свойства средней линии треугольника:
- Средняя линия равна половине основания. Вообще правильнее сказать не половине основания, а половине противолежащей стороны. Так как сторон в треугольнике 3, а основание всего одно. Но в общем случае, основанием можно считать любую из сторон треугольника, так что подобная формулировка считается допустимой. К тому же ее проще выучить.
В общем случае по этому свойству и определяется длина средней линии треугольника.
- Средняя линия параллельна основанию. С понятием основания здесь та же ситуация, что и в прошлом свойстве.
- Средняя линия отсекает от треугольника малый подобный треугольник с коэффициентом подобия, равным 0,5
- Три средние линии делят треугольник на 4 равных треугольника, подобных большому треугольнику с коэффициентом подобия 0,5
Рис. 3. Средние линии в треугольнике
Собственно формула длины средней линии вытекает из второго свойства:
$m=1over{2}*a$- где m — средняя линия, а- сторона противоположная средней линии.
Что мы узнали?
Мы поговорили о второстепенных характеризующих отрезках, выделив среднюю линию. Привели свойства средних линий и поговорили о особенностях формулировки этих свойств. Рассказали, как выводится формула длины средней линии треугольника и как средняя линия разбивает треугольник. Все эти свойства используются при решении треугольников.
Тест по теме
Оценка статьи
Средняя оценка: 4.3
. Всего получено оценок: 174.
Треугольник для школьников и студентов
Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
По величине углов
Остроугольный треугольник
— все углы треугольника острые.
Тупоугольный треугольник
— один из углов треугольника тупой (больше 90°).
Прямоугольный треугольник
— один из углов треугольника прямой (равен 90°).
По числу равных сторон
Разносторонний треугольник
— все три стороны не равны.
Равнобедренный треугольник
— две стороны равны.
Равносторонний (правильный) треугольник
— все три стороны равны.
Вершины, углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°
α+β+γ=180°
В треугольнике против большей стороны лежит больший угол, и обратно.
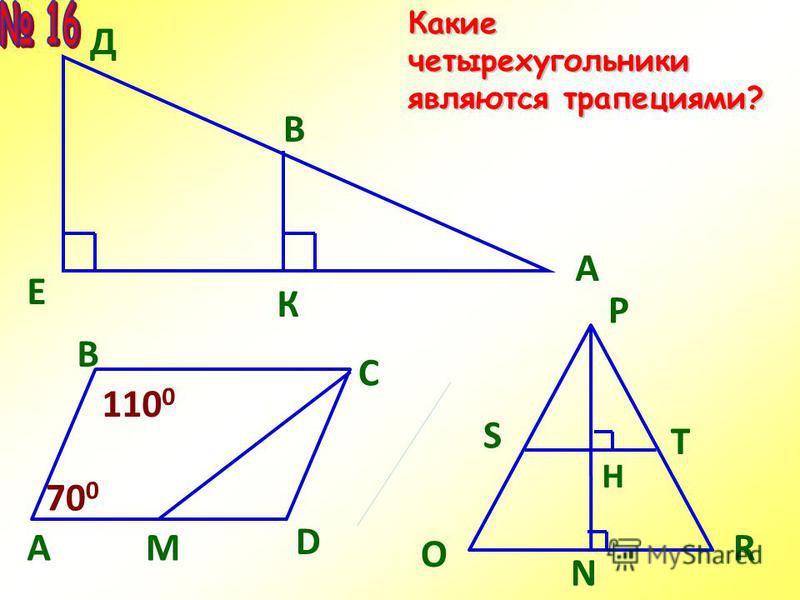
- если α>β, тогда a>b
- если α=β, тогда a=b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны
a+b>c
b+c>a
c+a>b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
asinα=bsinβ=csinγ
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.
a2=b2+c2-2bc·cosα
b2=a2+c2-2ac·cosβ
c2=a2+b2-2ab·cosγ
Теорема о проекциях
Для остроугольного треугольника:
a=bcosγ+ccosβ
b=acosγ+ccosα;
c=acosβ+bcosα;
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианы
a=232mb2+mc2-ma2
b=232ma2+mc2-mb2
c=232ma2+mb2-mc2
Медианы треугольника
Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.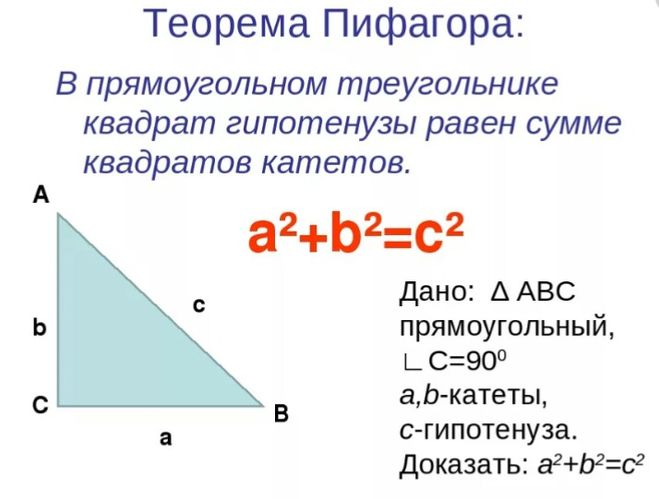
Свойства медиан треугольника
- Медианы треугольника пересекаются в одной точке. Точка пересечения медиан называется центроидом.
- В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AOOD=BOOE=COOF=21 - Медиана треугольника делит треугольник на две равновеликие части
S∆ABD=S∆ACD
S∆BEA=S∆BEC
S∆CBF=S∆CAF
- Треугольник делится тремя медианами на шесть равновеликих треугольников
S∆AOF=S∆AOE=S∆BOF=S∆BOD=S∆COD=S∆COE
- Из векторов, образующих медианы, можно составить треугольник
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma=122b2+2c2-a2
mb=122a2+2c2-b2
mc=122a2+2b2-c2
Биссектрисы треугольника
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника
- Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.
- Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AEAB=ECBC - Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°
Угол между lc и lc’=90°
- Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны
la=2bcpp-ab+c
lb=2acpp-ba+c
lc=2abpp-ca+b
где p=a+b+c2 — полупериметр треугольника.
Формулы биссектрис треугольника через две стороны и угол
la=2bccosα2b+c
lb=2accosβ2a+c
lc=2abcosγ2a+b
Высоты треугольника
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться:
- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
- Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
- Если в треугольнике две высоты равны, то треугольник — равнобедренный.
- ha:hb:hc=1a:1b:1c=BC:AC:AB
- 1ha:1hb:1hc=1r
Формулы высот треугольника
Формулы высот треугольника через сторону и угол
ha=bsinγ=csinβ
hb=csinα=asinγ
hc=asinβ=bsinα
Формулы высот треугольника через сторону и площадь
ha=2Sa
hb=2Sb
hc=2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности
ha=bc2R
hb=ac2R
hc=ab2R
Окружность вписанная в треугольник
Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
- Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
- В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру
r=Sp
Радиус вписанной в треугольник окружности через три стороны
r=a+b-cb+c-ac+a-b4a+b+c
Формулы высот треугольника через две стороны и радиус описанной окружности
1r=1ha+1hb+1hc
Окружность описанная вокруг треугольника
Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
- Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
- Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.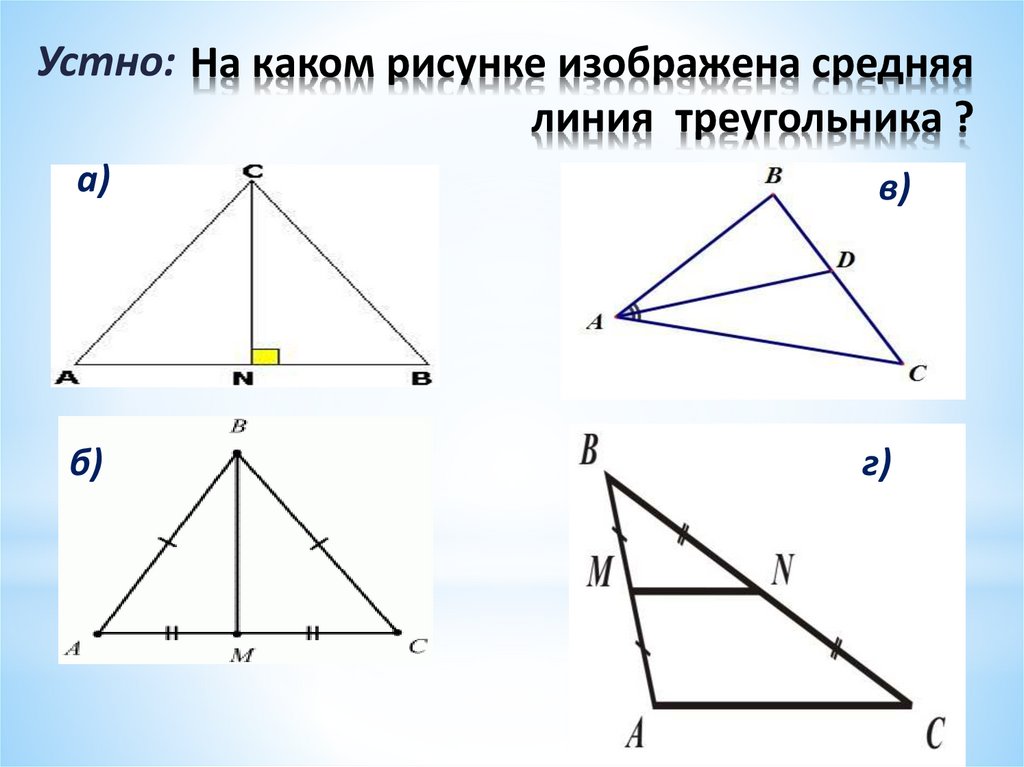
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь
R=abc4S
Радиус описанной окружности через площадь и три угла
R=S2sinαsinβsinγ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов)
R=a2sinα+b2sinβ+c2sinγ
Связь между вписанной и описанной окружностями треугольника
Формулы радиуса окружности описанной вокруг треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то
d2=R2-2Rr
Радиус описанной окружности через площадь и три угла
rR=4sinα2sinβ2sinγ2=cosα+cosβ+cosγ
2Rr=abca+b+c
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
Признаки
Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.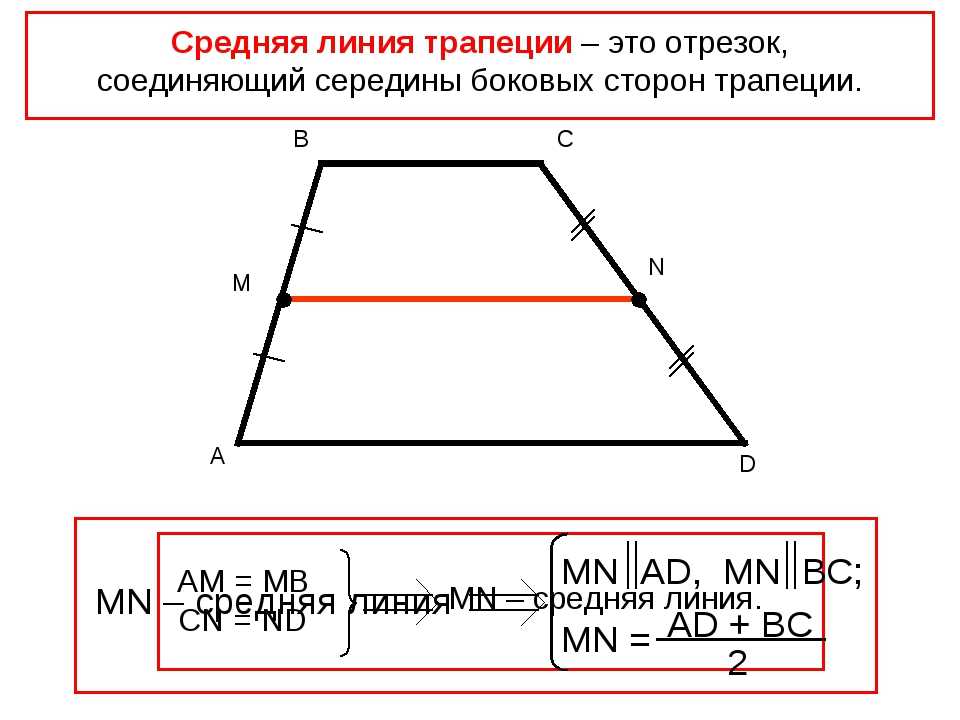
Периметр треугольника
Периметр треугольника ∆ABC равен сумме длин его сторон.
P=a+b+c
Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
S=12a·ha ,
S=12b·hb ,
S=12c·hc ,
где a, b, c — стороны треугольника,
ha, hb, hc — высоты, проведенные к сторонам a, b, c треугольника.
Формула площади треугольника по трем сторонам
Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c.
S=pp-ap-bp-c,
где p — полупериметр треугольника: p=a+b+c2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.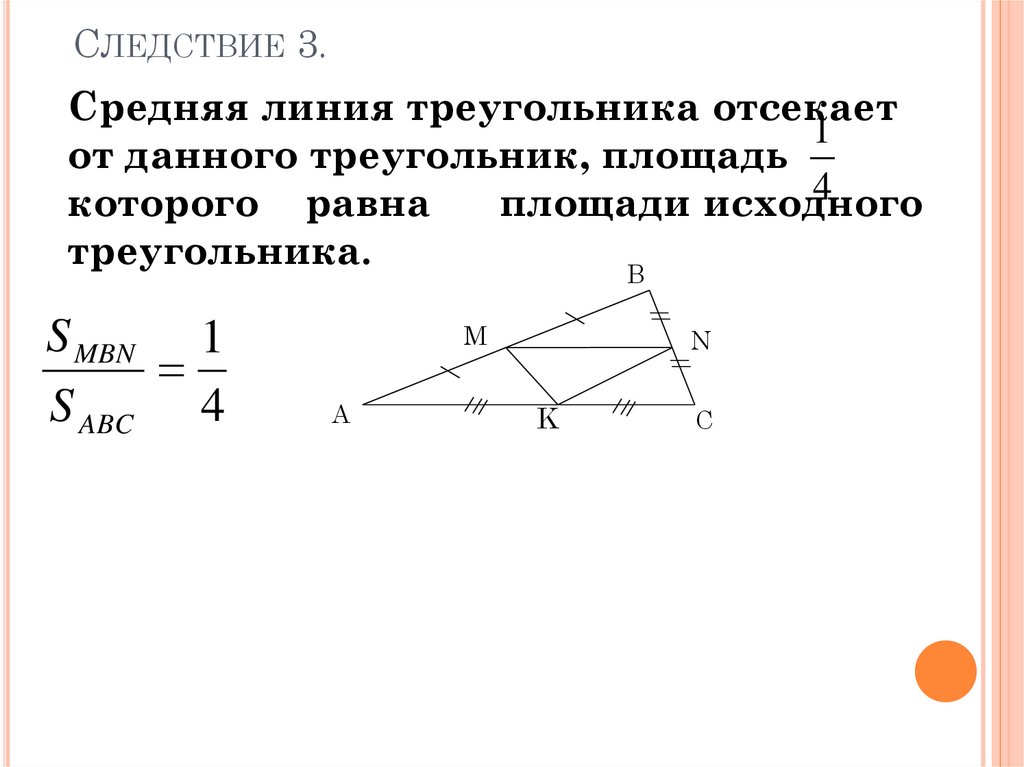
S=12a·b·sinγ ,
S=12b·c·sinα ,
S=12a·c·sinβ ,
где a, b, c — стороны треугольника,
γ — угол между сторонами a и b,
α — угол между сторонами b и c,
β — угол между сторонами a и c.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
S=a·b·c4R ,
a, b, c — стороны треугольника,
R — радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
S=p·r ,
где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p=a+b+c2
Равенство треугольников
Определение
Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.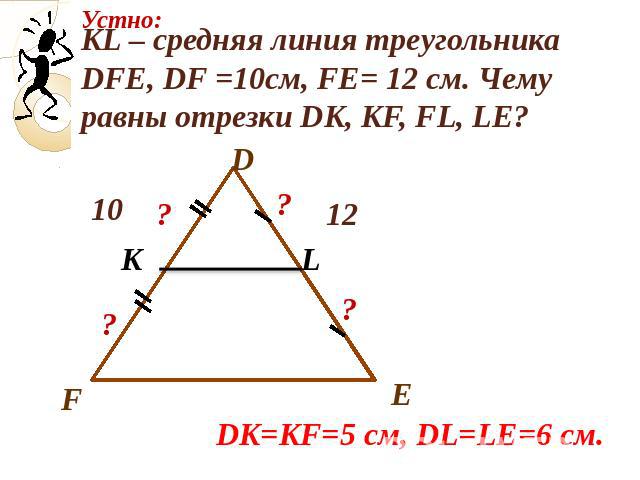
Свойства
У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).
Признаки равенства треугольников
По двум сторонам и углу между ними
Теорема.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
По стороне и двум прилежащим углам
Теорема.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
По трем сторонам
Теорема.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Подобие треугольников
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
∆АВС~∆MNK=>α=α1,β=β1,γ=γ1 и ABMN=BCNK=ACMK=k
где k — коэффициент подобия.
Признаки подобия треугольников
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
S∆АВСS∆MNK=k2
Прямоугольные треугольники
Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).
Свойства прямоугольного треугольника
-
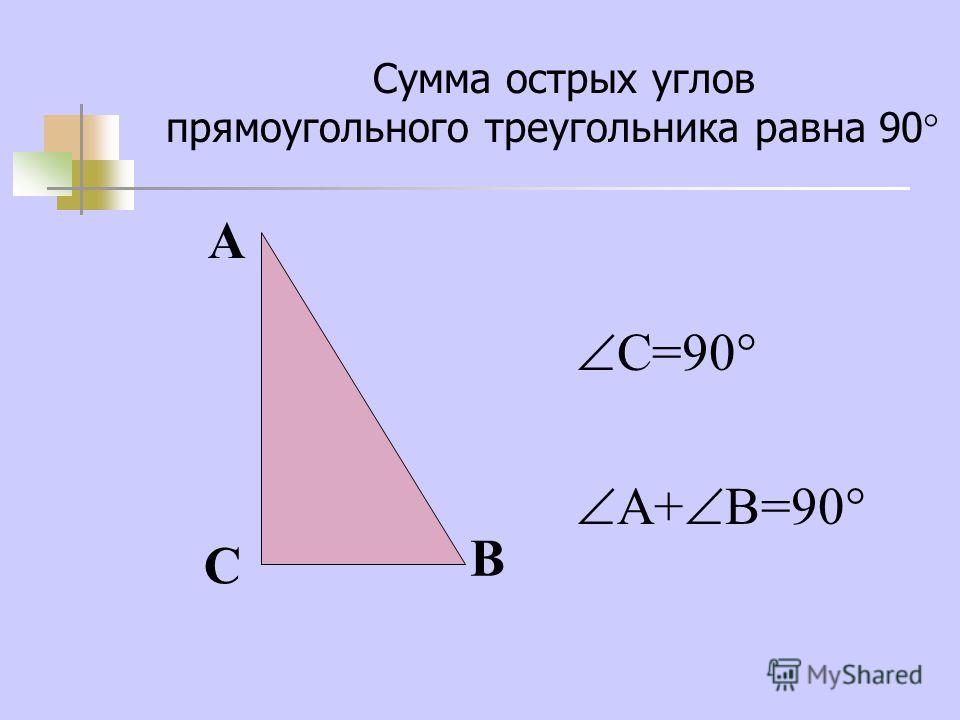
Сумма двух острых углов прямоугольного треугольника равна 90°.
Сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника ∠ 1+∠ 2=90°. -
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).
Рассмотрим прямоугольный треугольник ABC, в котором ∠ A — прямой, ∠ B = 30°, и значит, что ∠ C = 60°.
Докажем, что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD , как показано на рисунке.
Получим треугольник BCD, в котором ∠ B = ∠ D = 60° , поэтому DC = BC. Но DC = 2AC. Следовательно, BC = 2AC.Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.
Признаки равенства прямоугольных треугольников
Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
S∆АВСS∆MNK=k2
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
Срединная линия на высоте прямоугольного треугольника Калькулятор
|
✖Основание прямоугольного треугольника — это длина основания прямоугольного треугольника, примыкающего к перпендикулярной стороне. |
AU длиныствораАнгстремарпанастрономическая единицаАттометрЯчменное зерноМиллиардный светБор РадиусКабель (Международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля-Луна РасстояниеЗемли Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Положение)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрНавигационный лига (INT)Навигационный лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Радиус СолнцаТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
+10% -10% |
|
|
✖Высота прямоугольного треугольника равна длине перпендикулярной стороны прямоугольного треугольника, примыкающей к основанию. |
AU длиныствораАнгстремарпанастрономическая единицаАттометрЯчменное зерноМиллиардный светБор РадиусКабель (Международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля-Луна РасстояниеЗемли Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Положение)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрНавигационный лига (INT)Навигационный лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Радиус СолнцаТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
+10% -10% |
|
✖Медиана высоты прямоугольного треугольника — это отрезок, соединяющий середину высоты с противоположной ему вершиной. |
AU длиныствораАнгстремарпанастрономическая единицаАттометрЯчменное зерноМиллиардный светБор РадиусКабель (Международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Cubit (Великобритания)ДекаметрДециметрЗемля-Луна РасстояниеЗемли Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Положение)Световой годСсылкаДлинные CubitДлинные РидМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрНавигационный лига (INT)Навигационный лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаточкаполюскварталРидпрутРоман Actusканатныйрусский АрчинSpan (ткань)Радиус СолнцаТераметртвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Срединная линия на высоте прямоугольного треугольника Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.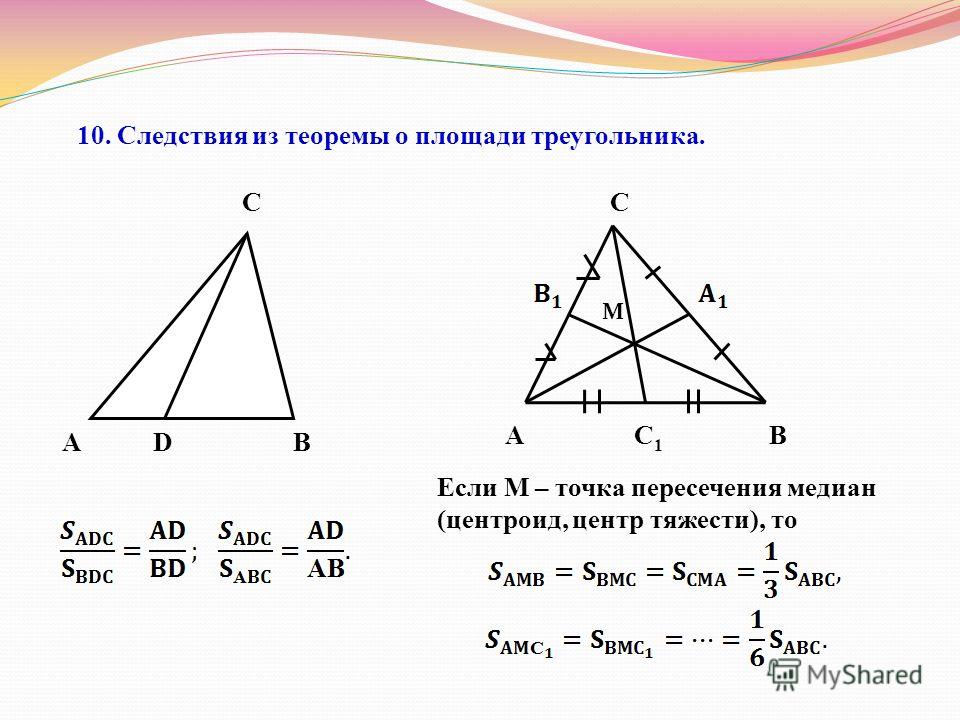
Что такое прямоугольный треугольник?
Прямоугольный треугольник или прямоугольный треугольник, или, более формально, ортогональный треугольник — это треугольник, в котором один угол является прямым. Соотношение между сторонами и углами прямоугольного треугольника является основой тригонометрии. Сторона, противолежащая прямому углу, называется гипотенузой.
Что такое медиана?
Медиана треугольника – это линия, проведенная от одной из вершин к середине противоположной стороны. В случае прямоугольного треугольника медиана гипотенузы имеет то свойство, что ее длина равна половине длины гипотенузы.
Share
Copied!
Чему равна средняя линия прямоугольного треугольника формула. Как найти среднюю линию трапеции
Средняя линия треугольника – это отрезок, соединяющий середины 2-х его сторон.
Квадратный треугольник больше верно именуется прямоугольным треугольником. Соотношения между сторонами и углами этой геометрической фигуры детально рассматриваются в математической дисциплине тригонометрии.
Вам понадобится
- – лист бумаги;
- – ручка;
- – таблицы Брадиса;
- – калькулятор.
Инструкция
1.
Обнаружьте сторону
прямоугольного треугольника
с поддержкой теоремы Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов: с2 = a2+b2 , где с – гипотенуза треугольника
, a и b – его катеты. Дабы применить это уравнение, надобно знать длину всяких 2-х сторон прямоугольного треугольника
.
2.
Если по условиям заданы размеры катетов, разыщите длину гипотенузы. Для этого с поддержкой калькулятора извлеките квадратный корень из суммы катетов, всякий из которых заранее возведите в квадрат.
3.
Вычислите длину одного из катетов, если вестимы размеры гипотенузы и иного катета.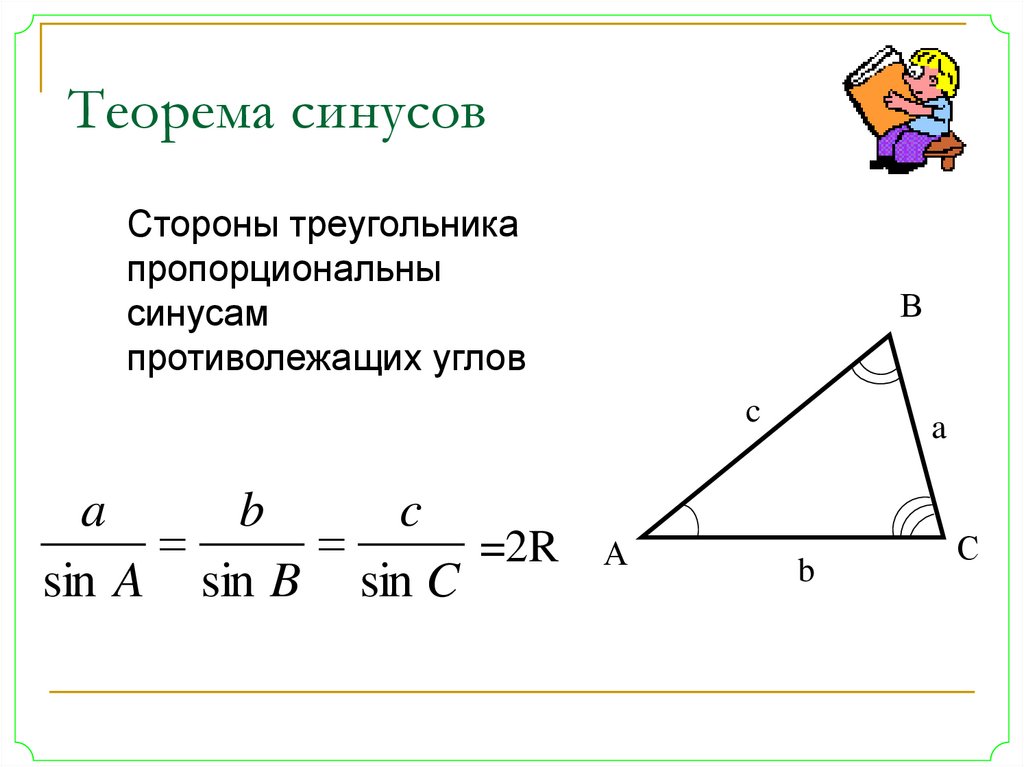
4.
Если в задаче заданы гипотенуза и один из прилежащих к ней острых углов, используйте таблицы Брадиса. В них приведены значения тригонометрических функций для большого числа углов. Воспользуйтесь калькулятором с функциями синуса и косинуса, а также теоремами тригонометрии, которые описывают соотношения между сторонами и углами прямоугольного треугольника
.
5.
Обнаружьте катеты при помощи основных тригонометрических функций: a = c*sin ?, b = c*cos ?, где а – катет, противолежащий к углу?, b – катет, прилежащий к углу?. Сходственным образом посчитайте размер сторон треугольника
, если заданы гипотенуза и иной острый угол: b = c*sin ?, a = c*cos ?, где b – катет, противолежащий к углу?, а – катет, прилежащий к углу?.
6.
В случае, когда вестим катет a и прилежащий к нему острый угол?, не забывайте, что в прямоугольном треугольнике сумма острых углов неизменно равна 90°: ? + ? = 90°.
7.
Если вестим катет а и противолежащий к нему острый угол?, при помощи таблиц Брадиса, калькулятора и тригонометрических функций вычислите гипотенузу по формуле: c=a*sin ?, катет: b=a*tg ?.
Видео по теме
Перед тем как перейти к нахождению средней линии треугольника нужно вспомнить второй признак подобия треугольников и свойства параллельности прямых.
Как найти среднюю линию треугольника – второй признак подобия треугольников
На рисунке 1 показаны два треугольника. Треугольник ABC подобен треугольнику A1B1C1. И прилежащие стороны пропорциональны, то есть AB относится к A1B1 также как AC относится к A1C1. Их этих двух условий и следует подобие треугольников.
Как найти среднюю линию треугольника – признак параллельности прямых
На рисунке 2 показаны прямые a и b, секущая c.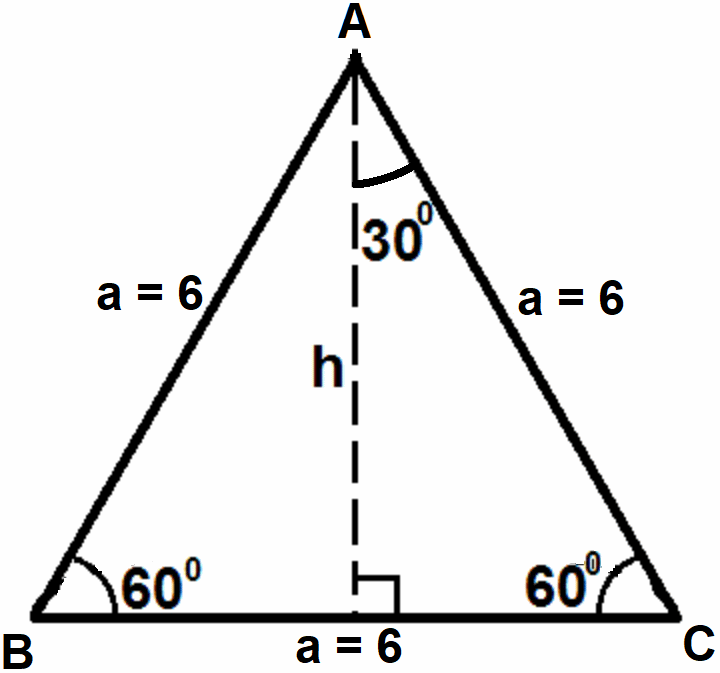
Как найти среднюю линию треугольника
На рисунке 3, M середина AB, а N середина AC, BC основание. Отрезок MN – называется средней линии треугольника. Сама же теорема гласит – Средняя линия треугольника параллельная основанию и равна его половине.
Для того чтобы доказать, что MN – средняя линия треугольника, нам понадобится второй признак подобия треугольников и признак параллельности прямых.
Треугольник AMN подобен треугольнику ABC, по второму признаку. В подобных треугольниках соответственные углы равны, угол 1 равен углу 2, а эти углы являются соответственными при пересечении двух прямых секущей, следовательно, прямые параллельны, MN параллельно BC. Угол A общий, AM/AB = AN/AC = ½
Коэффициент подобия этих треугольников ½, из этого следует что ½ = MN/BC, MN = ½ BC
Вот мы и нашли среднюю линию треугольника, и доказали теорему о средней линии треугольника, если вам до сих пор не понятно, как найти среднюю линию, смотрите видео ниже.
[{Large{text{Подобие треугольников}}}]
Определения
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).
Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.
Определение
Периметр треугольника – это сумма длин всех его сторон.
Теорема
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
Доказательство
Рассмотрим треугольники (ABC)
и (A_1B_1C_1)
со сторонами (a,b,c)
и (a_1, b_1, c_1)
соответственно (см. рисунок выше).
Тогда (P_{ABC}=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=kcdot
P_{A_1B_1C_1})
Теорема
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Доказательство
Пусть треугольники (ABC)
и (A_1B_1C_1)
подобны, причём (dfrac{AB}{A_1B_1} = dfrac{AC}{A_1C_1} = dfrac{BC}{B_1C_1} = k)
.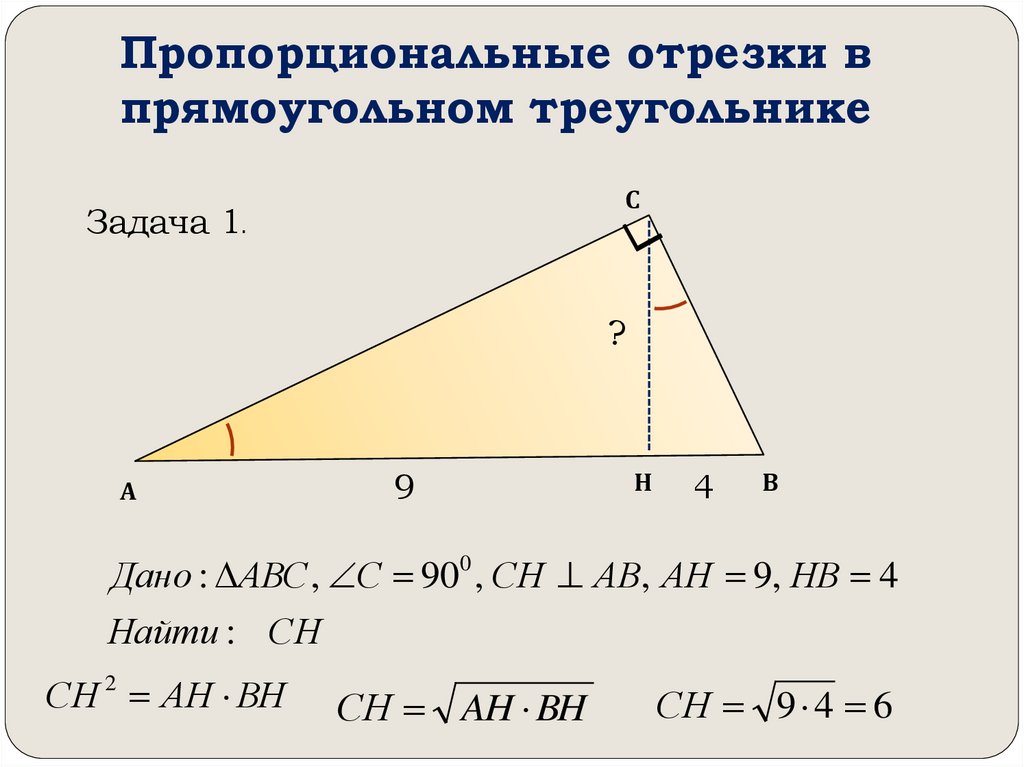
— angle A_1 — angle B_1 = angle C_1)
, то есть углы треугольника (ABC)
соответственно равны углам треугольника (A_1B_1C_1)
.
Так как (angle A = angle A_1)
и (angle B = angle B_1)
, то (dfrac{S_{ABC}}{S_{A_1B_1C_1}} = dfrac{ABcdot AC}{A_1B_1cdot
A_1C_1})
и (dfrac{S_{ABC}}{S_{A_1B_1C_1}} = dfrac{ABcdot
BC}{A_1B_1cdot B_1C_1})
.
Из этих равенств следует, что (dfrac{AC}{A_1C_1} =
dfrac{BC}{B_1C_1})
.
Аналогично доказывается, что (dfrac{AC}{A_1C_1} =
dfrac{AB}{A_1B_1})
(используя равенства (angle B = angle B_1)
, (angle C = angle C_1)
).
В итоге, стороны треугольника (ABC)
пропорциональны сходственным сторонам треугольника (A_1B_1C_1)
, что и требовалось доказать.
Теорема (второй признак подобия треугольников)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Доказательство
Рассмотрим два треугольника (ABC)
и (A»B»C»)
, таких что (dfrac{AB}{A»B»}=dfrac{AC}{A»C»})
, (angle BAC = angle A»)
.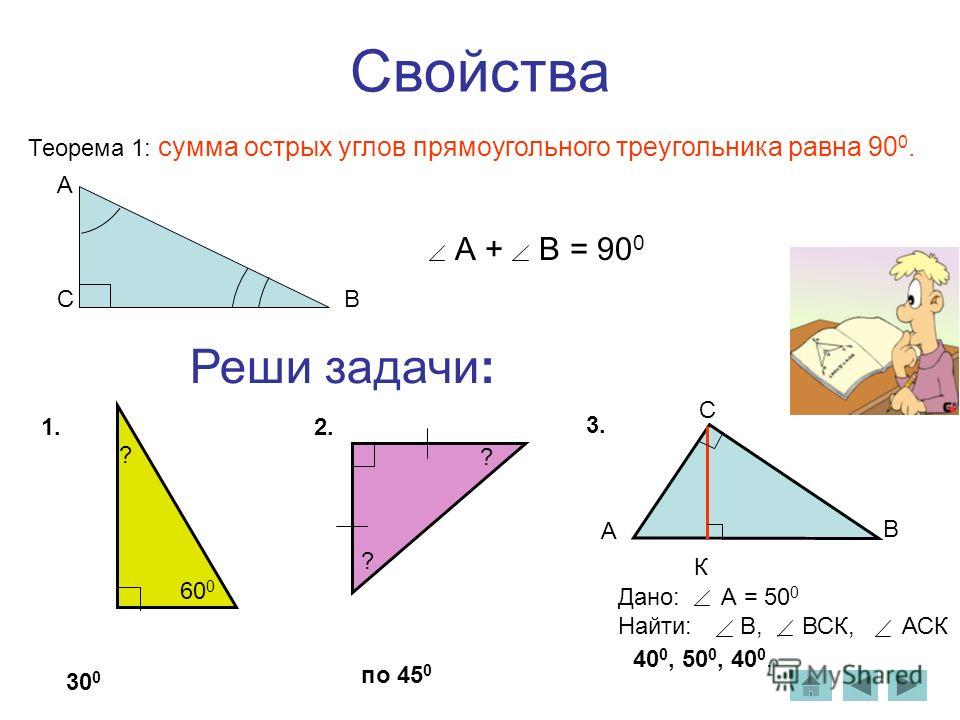
и (A»B»C»)
– подобны. Учитывая первый признак подобия треугольников, достаточно показать, что (angle B = angle B»)
.
Рассмотрим треугольник (ABC»»)
, у которого (angle 1 = angle A»)
, (angle 2 = angle B»)
. Треугольники (ABC»»)
и (A»B»C»)
подобны по первому признаку подобия треугольников, тогда (dfrac{AB}{A»B»} =
dfrac{AC»»}{A»C»})
.
С другой стороны, по условию (dfrac{AB}{A»B»} = dfrac{AC}{A»C»})
. Из последних двух равенств следует, что (AC = AC»»)
.
Треугольники (ABC)
и (ABC»»)
равны по двум сторонам и углу между ними, следовательно, (angle B = angle 2 = angle B»)
.
Теорема (третий признак подобия треугольников)
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Доказательство
Пусть стороны треугольников (ABC)
и (A»B»C»)
пропорциональны: (dfrac{AB}{A»B»} = dfrac{AC}{A»C»} = dfrac{BC}{B»C»})
.
и (A»B»C»)
подобны.
Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что (angle BAC = angle A»)
.
Рассмотрим треугольник (ABC»»)
, у которого (angle 1 = angle A»)
, (angle 2 = angle B»)
.
Треугольники (ABC»»)
и (A»B»C»)
подобны по первому признаку подобия треугольников, следовательно, (dfrac{AB}{A»B»} = dfrac{BC»»}{B»C»}
= dfrac{C»»A}{C»A»})
.
Из последней цепочки равенств и условия (dfrac{AB}{A»B»} =
dfrac{AC}{A»C»} = dfrac{BC}{B»C»})
вытекает, что (BC = BC»»)
, (CA
=
C»»A)
.
Треугольники (ABC)
и (ABC»»)
равны по трем сторонам, следовательно, (angle BAC = angle 1 = angle A»)
.
[{Large{text{Теорема Фалеса}}}]
Теорема
Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
Доказательство
Докажем сначала лемму:
Если в (triangle OBB_1)
через середину (A)
стороны (OB)
проведена прямая (aparallel BB_1)
, то она пересечет сторону (OB_1)
также в середине.
Через точку (B_1)
проведем (lparallel OB)
. Пусть (lcap a=K)
. Тогда (ABB_1K)
— параллелограмм, следовательно, (B_1K=AB=OA)
и (angle
A_1KB_1=angle ABB_1=angle OAA_1)
; (angle AA_1O=angle KA_1B_1)
как вертикальные. Значит, по второму признаку (triangle
OAA_1=triangle B_1KA_1 Rightarrow OA_1=A_1B_1)
. Лемма доказана.
Перейдем к доказательству теоремы. Пусть (OA=AB=BC)
, (aparallel
bparallel c)
и нужно доказать, что (OA_1=A_1B_1=B_1C_1)
.
Таким образом, по данной лемме (OA_1=A_1B_1)
. Докажем, что (A_1B_1=B_1C_1)
. Проведем через точку (B_1)
прямую (dparallel OC)
, причем пусть (dcap a=D_1, dcap c=D_2)
. Тогда (ABB_1D_1, BCD_2B_1)
— параллелограммы, следовательно, (D_1B_1=AB=BC=B_1D_2)
. Таким образом, (angle A_1B_1D_1=angle C_1B_1D_2)
как вертикальные, (angle
A_1D_1B_1=angle C_1D_2B_1)
как накрест лежащие, и, значит, по второму признаку (triangle A_1B_1D_1=triangle C_1B_1D_2
Rightarrow A_1B_1=B_1C_1)
.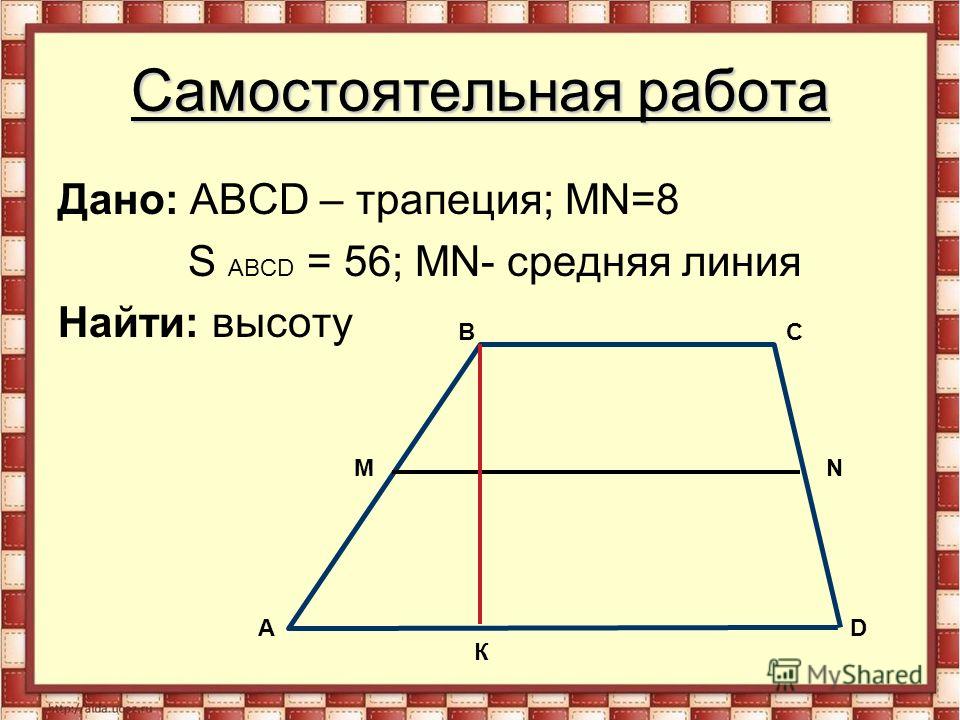
Теорема Фалеса
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
Доказательство
Пусть параллельные прямые (pparallel qparallel rparallel s)
разбили одну из прямых на отрезки (a, b, c, d)
. Тогда вторую прямую эти прямые должны разбить на отрезки (ka, kb, kc, kd)
соответственно, где (k)
– некоторое число, тот самый коэффициент пропорциональности отрезков.
Проведем через точку (A_1)
прямую (pparallel OD)
((ABB_2A_1)
— параллелограмм, следовательно, (AB=A_1B_2)
). Тогда (triangle OAA_1
sim triangle A_1B_1B_2)
по двум углам. Следовательно, (dfrac{OA}{A_1B_2}=dfrac{OA_1}{A_1B_1} Rightarrow A_1B_1=kb)
.
Аналогично проведем через (B_1)
прямую (qparallel OD Rightarrow
triangle OBB_1sim triangle B_1C_1C_2 Rightarrow B_1C_1=kc)
и т.д.
[{Large{text{Средняя линия треугольника}}}]
Определение
Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.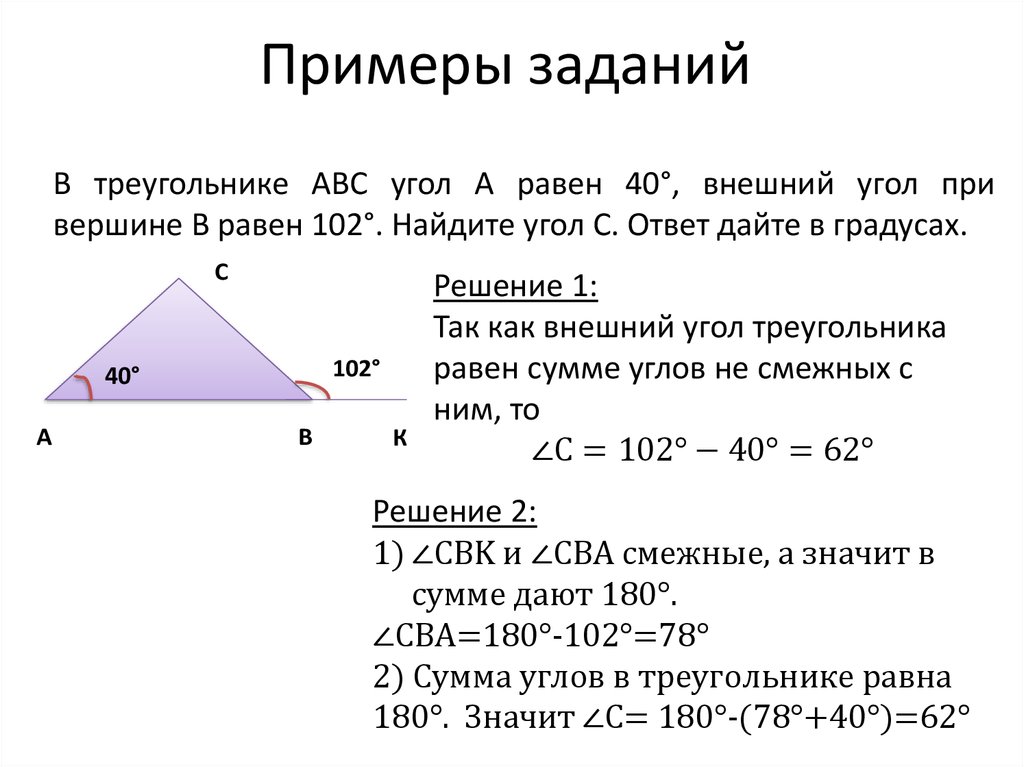
Теорема
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Доказательство
1) Параллельность средней линию основанию следует из доказанной выше леммы
.
2) Докажем, что (MN=dfrac12 AC)
.
Через точку (N)
проведем прямую параллельно (AB)
. Пусть эта прямая пересекла сторону (AC)
в точке (K)
. Тогда (AMNK)
— параллелограмм ((AMparallel NK, MNparallel AK)
по предыдущему пункту). Значит, (MN=AK)
.
Т.к. (NKparallel AB)
и (N)
– середина (BC)
, то по теореме Фалеса (K)
– середина (AC)
. Следовательно, (MN=AK=KC=dfrac12 AC)
.
Следствие
Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом (frac12)
.
Трапеция
— это четырехугольник, имеющий две параллельные стороны, являющиеся основаниями и две не параллельные стороны, являющиеся боковыми сторонами.
Также встречаются такие названия, как равнобокая
или равнобочная
.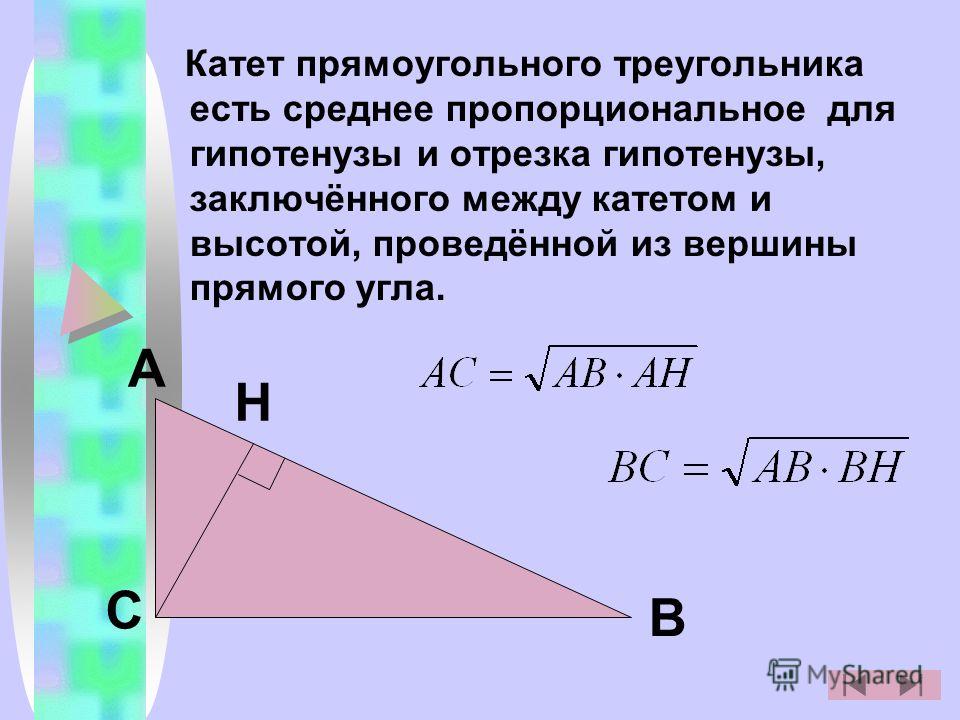
— это трапеция, у которой углы при боковой стороне прямые.
Элементы трапеции
a, b
— основания трапеции
(a
параллельно b
),
m, n
— боковые стороны
трапеции,
d 1 , d 2
— диагонали
трапеции,
h
— высота
трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),
MN
— средняя линия
(отрезок, соединяющий середины боковых сторон).
Площадь трапеции
- Через полусумму оснований a, b
и высоту h
: S = frac{a + b}{2}cdot h - Через среднюю линию MN
и высоту h
: S = MNcdot h - Через диагонали d 1 , d 2
и угол (sin varphi
) между ними: S = frac{d_{1} d_{2} sin varphi}{2}
Свойства трапеции
Средняя линия трапеции
Средняя линия
параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:
MN || a, MN || b, MN = frac{a + b}{2}
Сумма углов трапеции
Сумма углов трапеции
, прилежащих к каждой боковой стороне, равна 180^{circ}
:
alpha + beta = 180^{circ}
gamma + delta =180^{circ}
Равновеликие треугольники трапеции
Равновеликими
, то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB
и DOC
, образованные боковыми сторонами.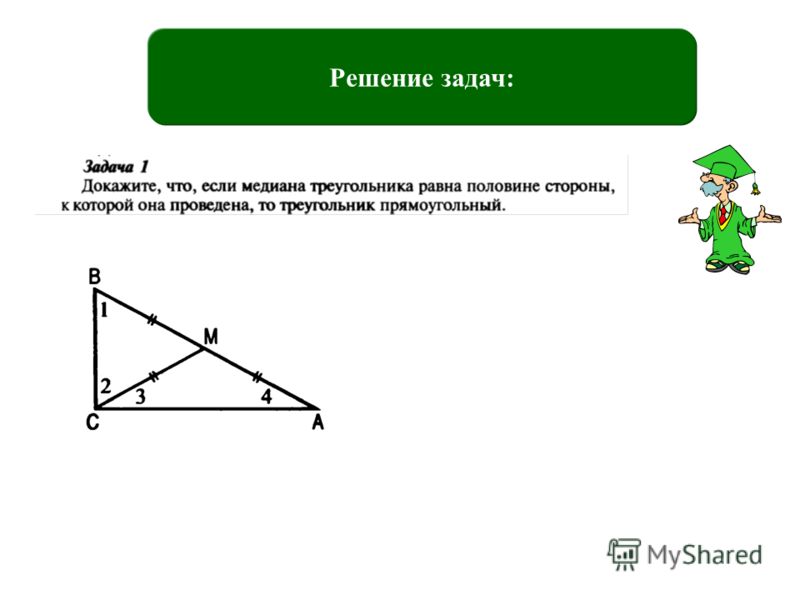
.
Отношение длин отрезков и оснований
Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:
frac{OX}{OY} = frac{BC}{AD}
Это будет являться справедливым и для высоты с самими диагоналями.
Порой темы, которые объясняют в школе, могут быть не всегда понятны с первого раза. Особенно это касается такого предмета, как математика. Но все становится намного сложнее, когда эта наука начинает подразделяться на две части: алгебру и геометрию.
Каждый ученик может обладать способностью к одному из двух направлений, но особенно в начальных классах важно понять базу и алгебры, и геометрии. В геометрии одной из главных тем принято считать раздел о треугольниках.
Как находить среднюю линию треугольника? Давайте разбираться.
Основные понятия
Для начала чтобы разобраться, как находить среднюю линию треугольника, важно понимать, что же это.
Для проведения средней линии нет ограничений: треугольник может быть любым (равнобедренным, равносторонним, прямоугольным).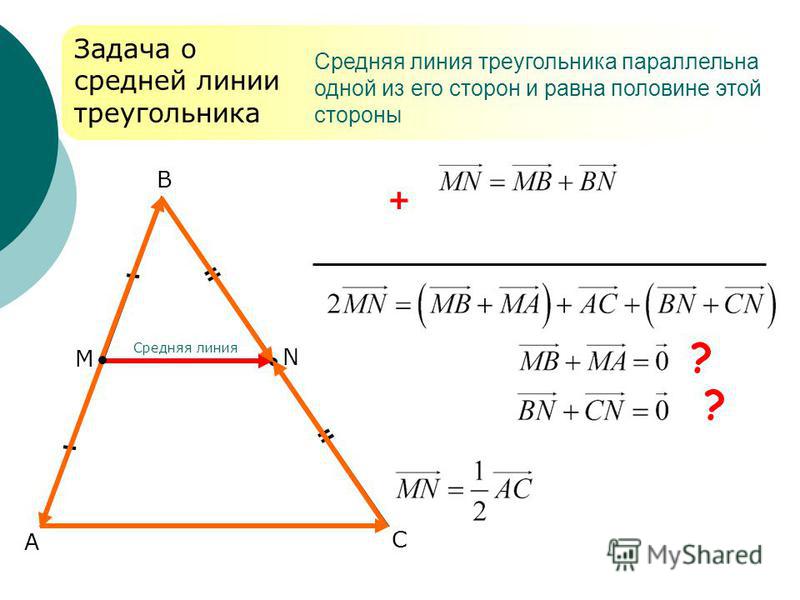
Средняя линия треугольника является отрезком, соединяющим середины 2-х его сторон. Следовательно, любой треугольник может иметь 3 таких линии.
Свойства
Чтобы знать, как находить среднюю линию треугольника, обозначим ее свойства, которые необходимо запомнить, иначе без них будет невозможным решение задач с необходимостью обозначить длину средней линии, поскольку все полученные данные необходимо обосновать и аргументировать теоремами, аксиомами или свойствами.
Таким образом, чтобы ответить на вопрос: «Как найти среднюю линию треугольника АВС?», достаточно знать одну из сторон треугольника.
Приведем пример
Взгляните на рисунок. На нем представлен треугольник ABC со средней линией DE. Обратим внимание, что она параллельна основанию AC в треугольнике. Следовательно, каким бы ни было значение AC, средняя линия DE будет в два раза меньше. К примеру, AC=20, значит DE=10 и т. д.
Вот такими несложными способами можно понять, как находить среднюю линию треугольника.
Как найти среднюю линию прямоугольного треугольника формула. Средняя линия треугольника
Как найти середину треугольника: задачка по геометрии. Основные элементарные задачи по Евклидовой геометрии пришли к нам из античности. В них заключается сама первичная сущность и необходимые базовые знания о восприятии человеком пространственных форм. Одной из таких задач является проблема нахождения середины треугольника. Сегодня эта задачка рассматривается как учебный прием развития интеллектуальных способностей школьников. В древнем же мире, знание того, как найти середину треугольника, применялось и на практике: в землеустройстве, при изготовлении разнообразных механизмов и т.д. В чем же состоит сущность этого геометрического ребуса?
Что такое медиана? Перед решением задачи необходимо ознакомиться с простейшей геометрической терминологией, касающейся треугольников.
Высота − линия перпендикулярная стороне, противоположной вершине, из которой она проводится; биссектриса − делит угол пополам; медиана же делит противоположную исходящей вершине сторону пополам. Для решения этой задачи нужно знать, как найти координаты середины отрезка, ведь именно точка пересечения медиан треугольника и является его серединой.
Находим середины сторон треугольника. Нахождение середины отрезка тоже является классической геометрической задачей, для решения которой понадобится циркуль и линейка без делений. Ставим иглу циркуля в точку окончания отрезка и чертим полукруг, больший половины отрезка в середине последнего. Проделываем то же самое с другой стороны отрезка. Полученные полуокружности обязательно пересекутся в двух точках, ведь их радиусы больше половины исходного отрезка.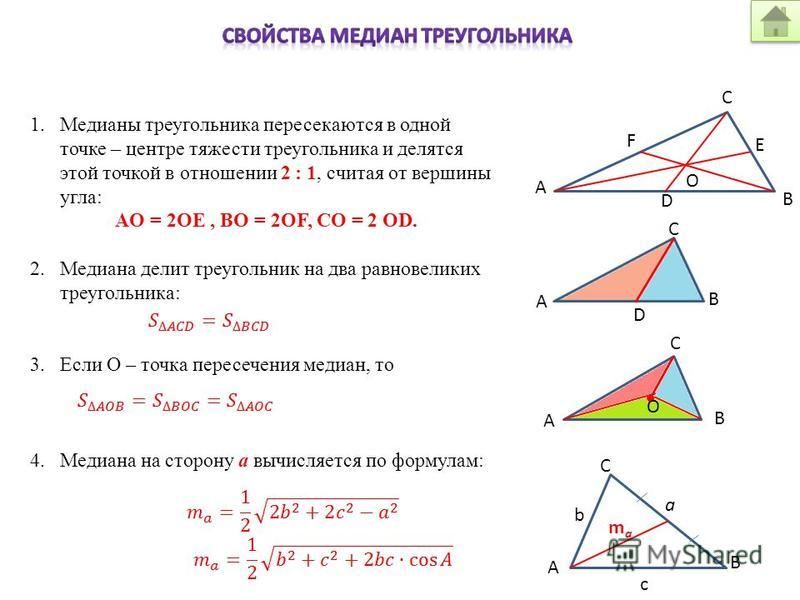
Соединяем две точки пересечения окружности прямой линией при помощи линейки. Эта линия пересекает исходный отрезок точно в его середине. Теперь, зная то, как найти середину отрезка, проделываем это с каждой стороной треугольника. После нахождения всех середин сторон треугольника всё готово для построения его собственной середины.
Строим середину треугольника. Соединив прямыми линиями вершины треугольника с серединами противоположных им сторон, получаем три медианы. Может кого-то это и удивит, но одним из законов гармонии этой геометрической фигуры является то, что все три медианы всегда пересекаются в одной точке. Именно эта точка и будет искомой серединой треугольника, которую не так трудно найти, если знать;как построить середину отрезка.
Интересно и то, что точка пересечения медиан представляет собой не только геометрическую, но и «физическую» середину треугольника. То есть, если, к примеру, вырезать треугольник из фанеры, найти его середину и поместить эту точку на кончик иглы, то в идеале такая фигура будет балансировать и не упадет.
[{Large{text{Подобие треугольников}}}]
Определения
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).
Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.
Определение
Периметр треугольника – это сумма длин всех его сторон.
Теорема
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
Доказательство
Рассмотрим треугольники (ABC)
и (A_1B_1C_1)
со сторонами (a,b,c)
и (a_1, b_1, c_1)
соответственно (см. рисунок выше).
Тогда (P_{ABC}=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=kcdot
P_{A_1B_1C_1})
Теорема
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.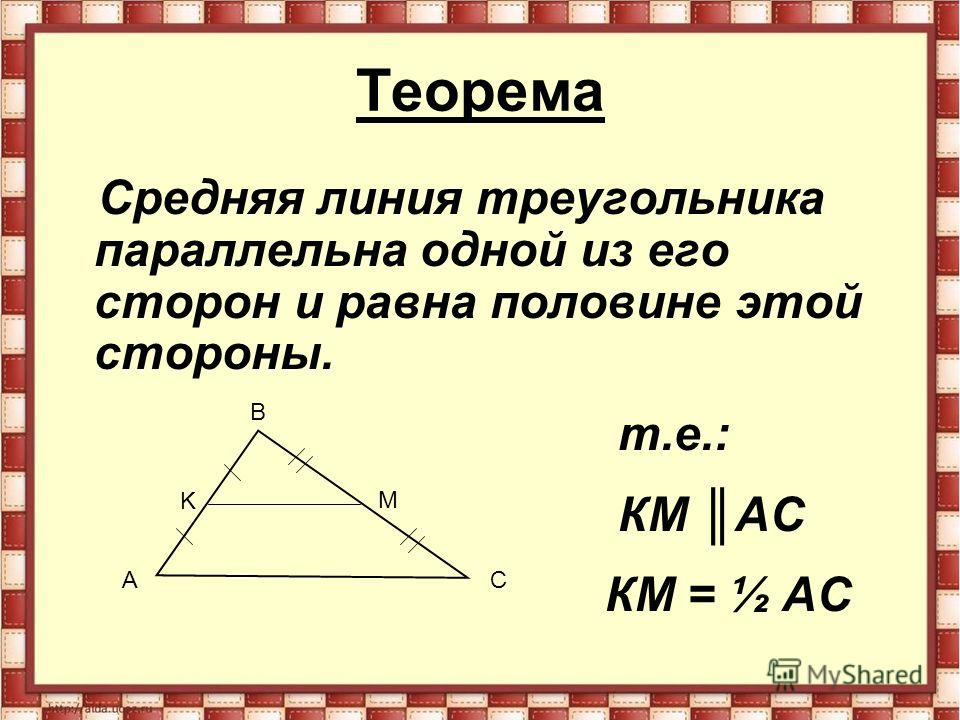
— angle A_1 — angle B_1 = angle C_1)
, то есть углы треугольника (ABC)
соответственно равны углам треугольника (A_1B_1C_1)
.
Так как (angle A = angle A_1)
и (angle B = angle B_1)
, то (dfrac{S_{ABC}}{S_{A_1B_1C_1}} = dfrac{ABcdot AC}{A_1B_1cdot
A_1C_1})
и (dfrac{S_{ABC}}{S_{A_1B_1C_1}} = dfrac{ABcdot
BC}{A_1B_1cdot B_1C_1})
.
Из этих равенств следует, что (dfrac{AC}{A_1C_1} =
dfrac{BC}{B_1C_1})
.
Аналогично доказывается, что (dfrac{AC}{A_1C_1} =
dfrac{AB}{A_1B_1})
(используя равенства (angle B = angle B_1)
, (angle C = angle C_1)
).
В итоге, стороны треугольника (ABC)
пропорциональны сходственным сторонам треугольника (A_1B_1C_1)
, что и требовалось доказать.
Теорема (второй признак подобия треугольников)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Доказательство
Рассмотрим два треугольника (ABC)
и (A»B»C»)
, таких что (dfrac{AB}{A»B»}=dfrac{AC}{A»C»})
, (angle BAC = angle A»)
.
и (A»B»C»)
– подобны. Учитывая первый признак подобия треугольников, достаточно показать, что (angle B = angle B»)
.
Рассмотрим треугольник (ABC»»)
, у которого (angle 1 = angle A»)
, (angle 2 = angle B»)
. Треугольники (ABC»»)
и (A»B»C»)
подобны по первому признаку подобия треугольников, тогда (dfrac{AB}{A»B»} =
dfrac{AC»»}{A»C»})
.
С другой стороны, по условию (dfrac{AB}{A»B»} = dfrac{AC}{A»C»})
. Из последних двух равенств следует, что (AC = AC»»)
.
Треугольники (ABC)
и (ABC»»)
равны по двум сторонам и углу между ними, следовательно, (angle B = angle 2 = angle B»)
.
Теорема (третий признак подобия треугольников)
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Доказательство
Пусть стороны треугольников (ABC)
и (A»B»C»)
пропорциональны: (dfrac{AB}{A»B»} = dfrac{AC}{A»C»} = dfrac{BC}{B»C»})
.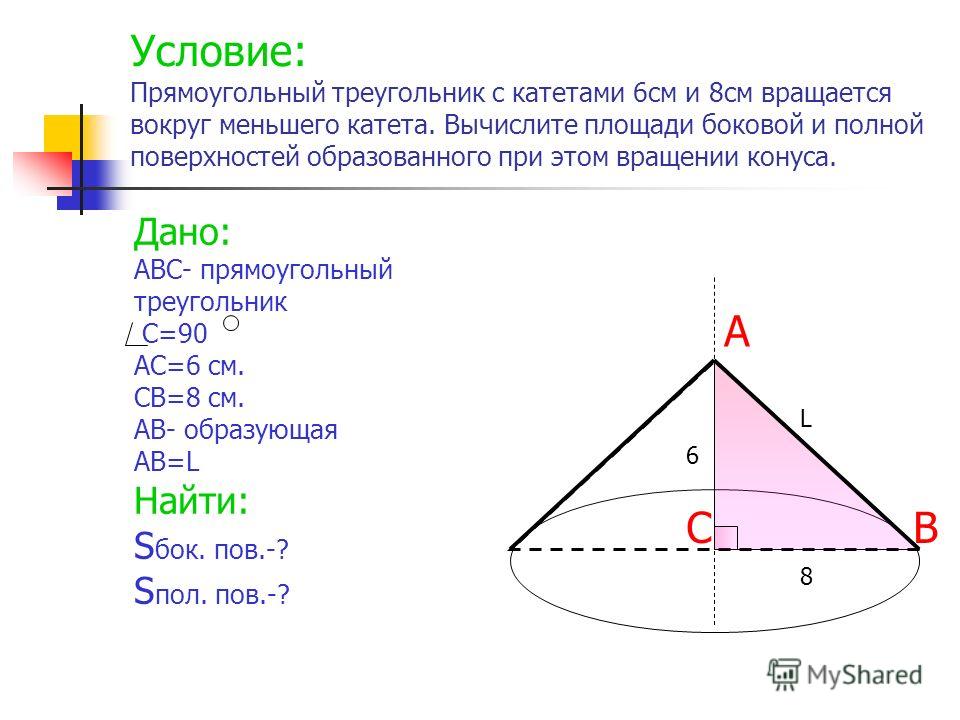
и (A»B»C»)
подобны.
Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что (angle BAC = angle A»)
.
Рассмотрим треугольник (ABC»»)
, у которого (angle 1 = angle A»)
, (angle 2 = angle B»)
.
Треугольники (ABC»»)
и (A»B»C»)
подобны по первому признаку подобия треугольников, следовательно, (dfrac{AB}{A»B»} = dfrac{BC»»}{B»C»}
= dfrac{C»»A}{C»A»})
.
Из последней цепочки равенств и условия (dfrac{AB}{A»B»} =
dfrac{AC}{A»C»} = dfrac{BC}{B»C»})
вытекает, что (BC = BC»»)
, (CA
=
C»»A)
.
Треугольники (ABC)
и (ABC»»)
равны по трем сторонам, следовательно, (angle BAC = angle 1 = angle A»)
.
[{Large{text{Теорема Фалеса}}}]
Теорема
Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
Доказательство
Докажем сначала лемму:
Если в (triangle OBB_1)
через середину (A)
стороны (OB)
проведена прямая (aparallel BB_1)
, то она пересечет сторону (OB_1)
также в середине.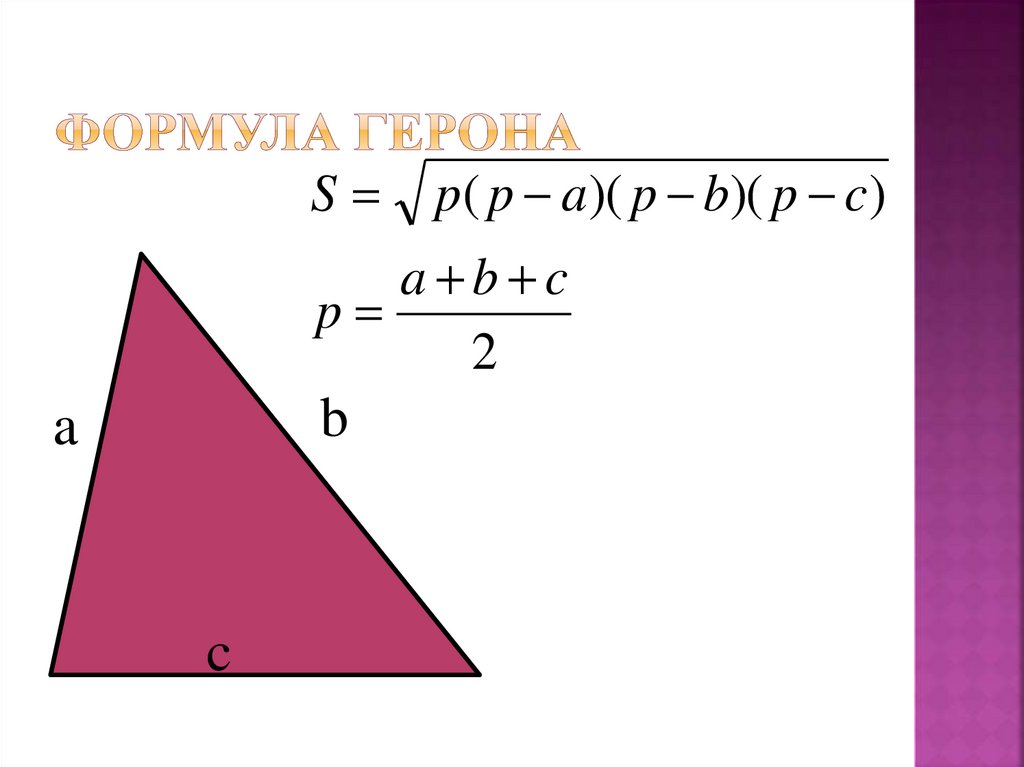
Через точку (B_1)
проведем (lparallel OB)
. Пусть (lcap a=K)
. Тогда (ABB_1K)
— параллелограмм, следовательно, (B_1K=AB=OA)
и (angle
A_1KB_1=angle ABB_1=angle OAA_1)
; (angle AA_1O=angle KA_1B_1)
как вертикальные. Значит, по второму признаку (triangle
OAA_1=triangle B_1KA_1 Rightarrow OA_1=A_1B_1)
. Лемма доказана.
Перейдем к доказательству теоремы. Пусть (OA=AB=BC)
, (aparallel
bparallel c)
и нужно доказать, что (OA_1=A_1B_1=B_1C_1)
.
Таким образом, по данной лемме (OA_1=A_1B_1)
. Докажем, что (A_1B_1=B_1C_1)
. Проведем через точку (B_1)
прямую (dparallel OC)
, причем пусть (dcap a=D_1, dcap c=D_2)
. Тогда (ABB_1D_1, BCD_2B_1)
— параллелограммы, следовательно, (D_1B_1=AB=BC=B_1D_2)
. Таким образом, (angle A_1B_1D_1=angle C_1B_1D_2)
как вертикальные, (angle
A_1D_1B_1=angle C_1D_2B_1)
как накрест лежащие, и, значит, по второму признаку (triangle A_1B_1D_1=triangle C_1B_1D_2
Rightarrow A_1B_1=B_1C_1)
.
Теорема Фалеса
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
Доказательство
Пусть параллельные прямые (pparallel qparallel rparallel s)
разбили одну из прямых на отрезки (a, b, c, d)
. Тогда вторую прямую эти прямые должны разбить на отрезки (ka, kb, kc, kd)
соответственно, где (k)
– некоторое число, тот самый коэффициент пропорциональности отрезков.
Проведем через точку (A_1)
прямую (pparallel OD)
((ABB_2A_1)
— параллелограмм, следовательно, (AB=A_1B_2)
). Тогда (triangle OAA_1
sim triangle A_1B_1B_2)
по двум углам. Следовательно, (dfrac{OA}{A_1B_2}=dfrac{OA_1}{A_1B_1} Rightarrow A_1B_1=kb)
.
Аналогично проведем через (B_1)
прямую (qparallel OD Rightarrow
triangle OBB_1sim triangle B_1C_1C_2 Rightarrow B_1C_1=kc)
и т.д.
[{Large{text{Средняя линия треугольника}}}]
Определение
Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.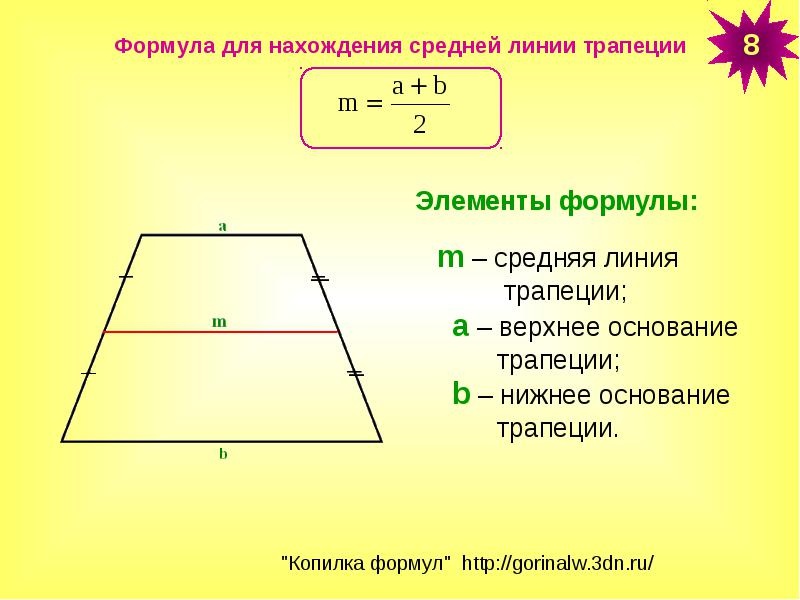
Теорема
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Доказательство
1) Параллельность средней линию основанию следует из доказанной выше леммы
.
2) Докажем, что (MN=dfrac12 AC)
.
Через точку (N)
проведем прямую параллельно (AB)
. Пусть эта прямая пересекла сторону (AC)
в точке (K)
. Тогда (AMNK)
— параллелограмм ((AMparallel NK, MNparallel AK)
по предыдущему пункту). Значит, (MN=AK)
.
Т.к. (NKparallel AB)
и (N)
– середина (BC)
, то по теореме Фалеса (K)
– середина (AC)
. Следовательно, (MN=AK=KC=dfrac12 AC)
.
Следствие
Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом (frac12)
.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике.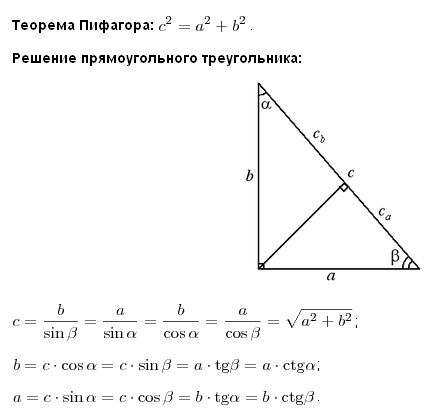
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий.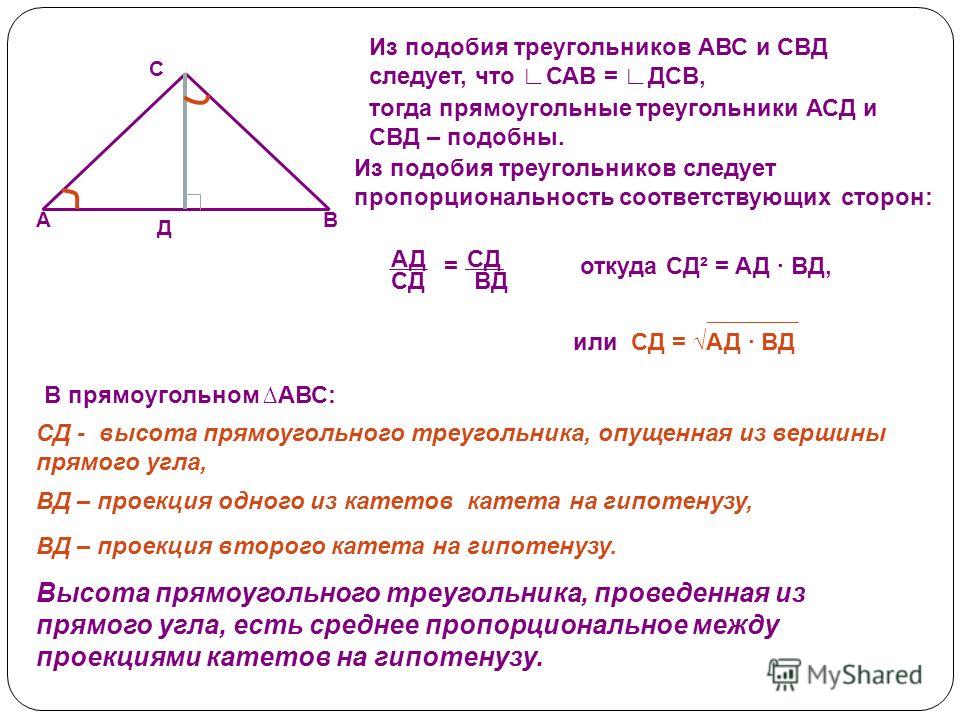
Средняя линия треугольника. Здравствуйте, друзья! Сегодня теоретический материал, связан он с треугольником. В составе экзамена имеется группа заданий, в которых используется свойство его средней линии. Причём не только в задачах с треугольниками, но и с трапециями. Была , в которой сии факты я предлагал просто запомнить, теперь подробнее…
Что такое средняя линия треугольника и каковы её свойства?
Определение.
Средняя линия треугольника – это отрезок, соединяющий середины сторон треугольника.
Понятно, что средних линий в треугольнике три. Покажем их:
Без всяких доказательств вы уже, наверное, заметили, что все четыре образованные треугольника равны. Это так, но подробнее об этом поговорим далее.
Теорема
. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
Доказательство:
1. Давайте рассмотрим треугольники BMN и BAC. По условию у нас BM=MA, BN=NC. Можем записать:
Следовательно треугольники подобны по двум пропорциональным сторонам и углу между ними (второй признак подобия). Что из этого следует? А то что:
По признаку параллельности прямых MN||AC.
2. Также из подобия треугольников следует, что
То есть MN в два раза меньше. Доказано!
Решим типичную задачу.
В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC. Найти периметр треугольника ABC, если MN=12, MK=10, KN=8.
Решение. Конечно, прежде всего следует проверить существование треугольника MNK (а значит и существование треугольника АВС). Сумма двух меньших сторон должна быть более третьей стороны, записываем 10+8>12. Выполнятся, следовательно треугольник существует.
Построим эскиз:
Таким образом периметр треугольника АВС равен 24+20+16=60.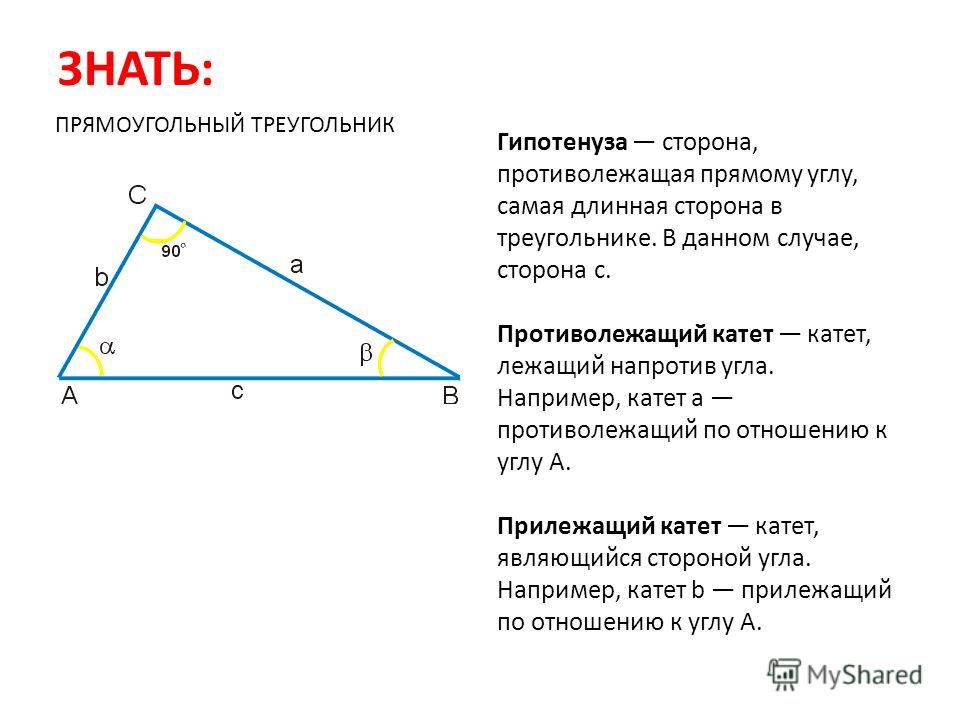
*Теперь подробнее о треугольниках полученных при построении всех трёх средних линий. Их равенство легко доказывается. Посмотрите:
Равны они по трём сторонам. Конечно, и другие признаки здесь применимы. Получаем, что
Как это свойство используется в заданиях включённых в состав экзамена? Особо хочется заострить внимание на задачах по стереометрии. Есть такие типы, в которых речь идет о треугольной призме.
Например, сказано что плоскость проходит через середины сторон основания и она параллельна третьему ребру основания. Ставятся вопросы о изменении площади поверхности призмы, её объёма и другие.
Так вот. Зная и понимая информацию изложенную выше вы сразу же определите, что эта плоскость отсекает от основания указанной призмы одну четвёртую часть и задачу решите устно. Вот с такими задачами.
На этом всё! Всего доброго!
Скачать материал статьи
С уважением, Александр Крутицких.
1
Дополнительное построение, ведущее к теореме о средней линии треугольника, трапеции и свойствам подобия треугольников.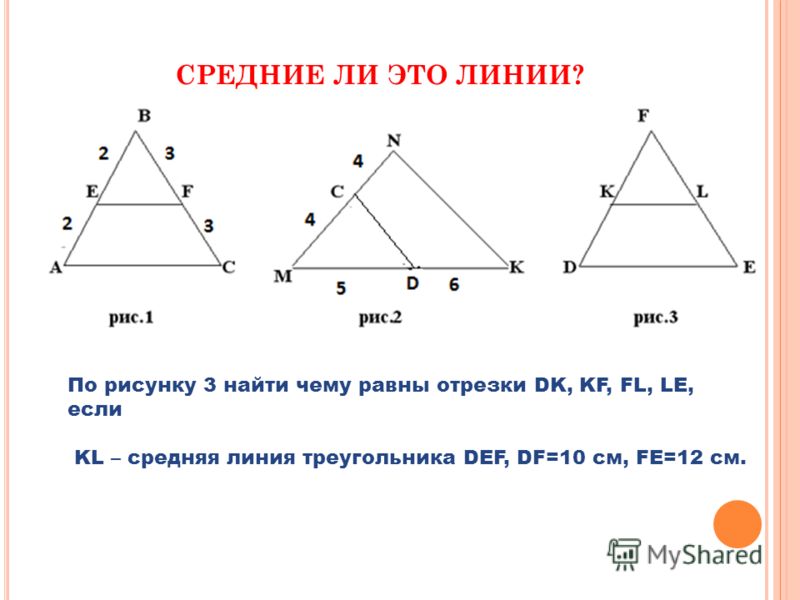
И она равна половине гипотенузы
.
Следствие 1.
Следствие 2.
2
Все прямоугольные треугольники с одинаковым острым углом — подобны. Взгляд на тригонометрические функции.
3
Пример дополнительного построения — высота, опущенная на гипотенузу. Вывод теоремы Пифагора на основе подобия треугольников.
Отсюда видно, что
1
Все прямоугольные треугольники с одинаковым острым углом — подобны. Взгляд на тригонометрические функции.
Треугольники со сторонами штрихованными и с не штрихованными подобны по равенству двух углов. Поэтому откуда
Это значит, что указанные отношения зависят лишь от острого угла прямоугольного треугольника и по сути определяют его. Это одно из оснований появления тригонометрических функций:
Часто запись тригонометрических функций угла в подобных прямоугольных треугольниках наглядней записи соотношений подобия!
2
Пример дополнительного построения — высота, опущенная на гипотенузу.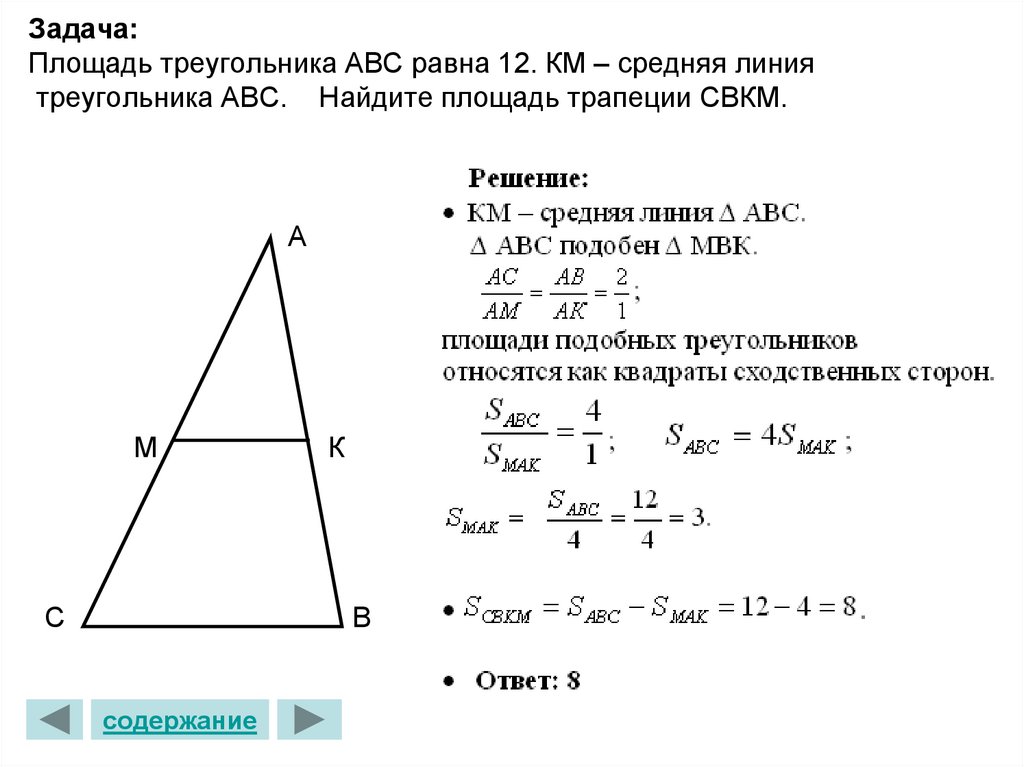
Опустим на гипотенузу AB высоту CH. Имеем три подобных треугольника ABC, AHC и CHB. Запишем выражения для тригонометрических функций:
Отсюда видно, что . Складывая, получаем теорему Пифагора, поскольку :
Другое доказательство теоремы Пифагора см.в комментарии к задаче 4.
3
Важный пример дополнительного построения – построение угла, равного одному из углов треугольника.
Проводим из вершины прямого угла отрезок прямой, составляющий с катетом CA угол, равный углу CAB заданного прямоугольного треугольника ABC. В результате получим равнобедренный треугольник ACM с углами при основании . Но другой треугольник, получающийся при таком построении, также будет равнобедренным, поскольку каждый его угол при основании равен (по свойству углов прямоугольного треугольника и по построению — из прямого угла «вычли» угол ). В силу того, что треугольники BMC и AMC равнобедренные с общей стороной MC имеем равенство MB=MA=MC, т.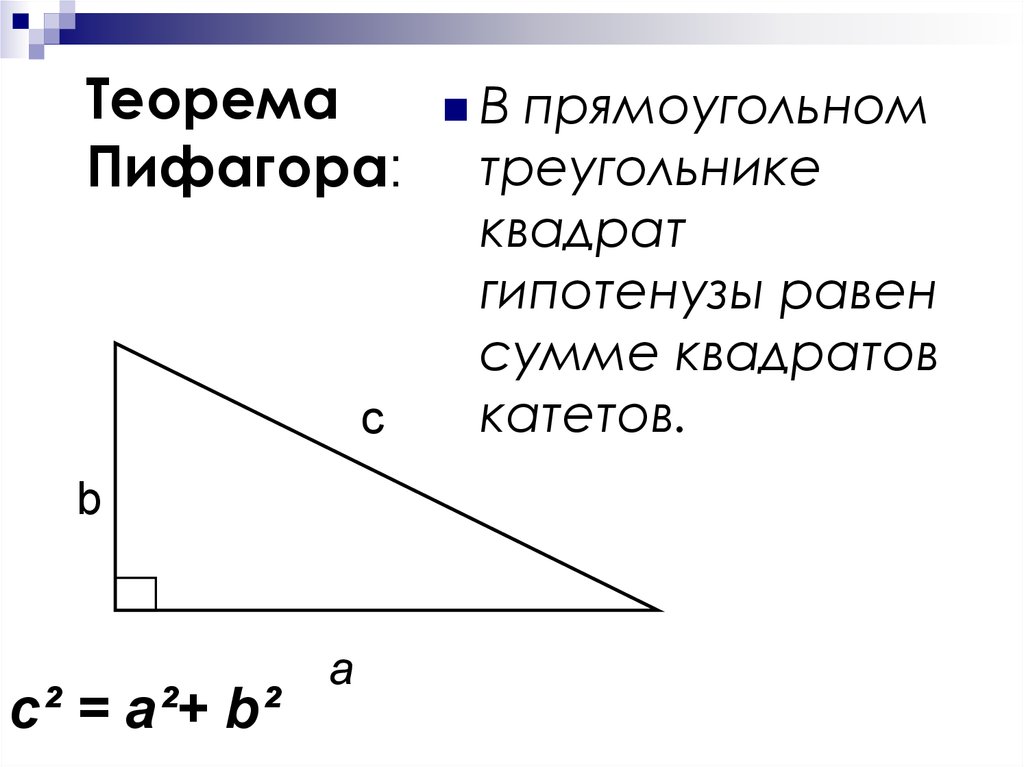
, и она равна половине гипотенузы
.
Следствие 1.
Середина гипотенузы является центром окружности, описанной вокруг этого треугольника, поскольку получилось, что середина гипотенузы равноудалена от вершин прямоугольного треугольника.
Следствие 2.
Средняя линия прямоугольного треугольника, соединяющая середину гипотенузы и середину катета, параллельна противоположному катету и равна его половине.
Опустим в равнобедренных треугольниках BMC и AMC высоты MH и MG на основания. Поскольку в равнобедренном треугольнике, высота, опущенная на основание, является также и медианой (и биссектрисой), то MH и MG –линии прямоугольного треугольника, соединяющие середину гипотенузы с серединами катетов. По построению они оказываются параллельными противоположным катетам и равные их половинам, поскольку треугольники равны MHC и MGC равны (причем MHCG – прямоугольник). Этот результат является основанием для доказательства теоремы о средней линии произвольного треугольника и, далее, средней линии трапеции и свойства пропорциональности отрезков, отсекаемых параллельными прямыми на двух пересекающих их прямых.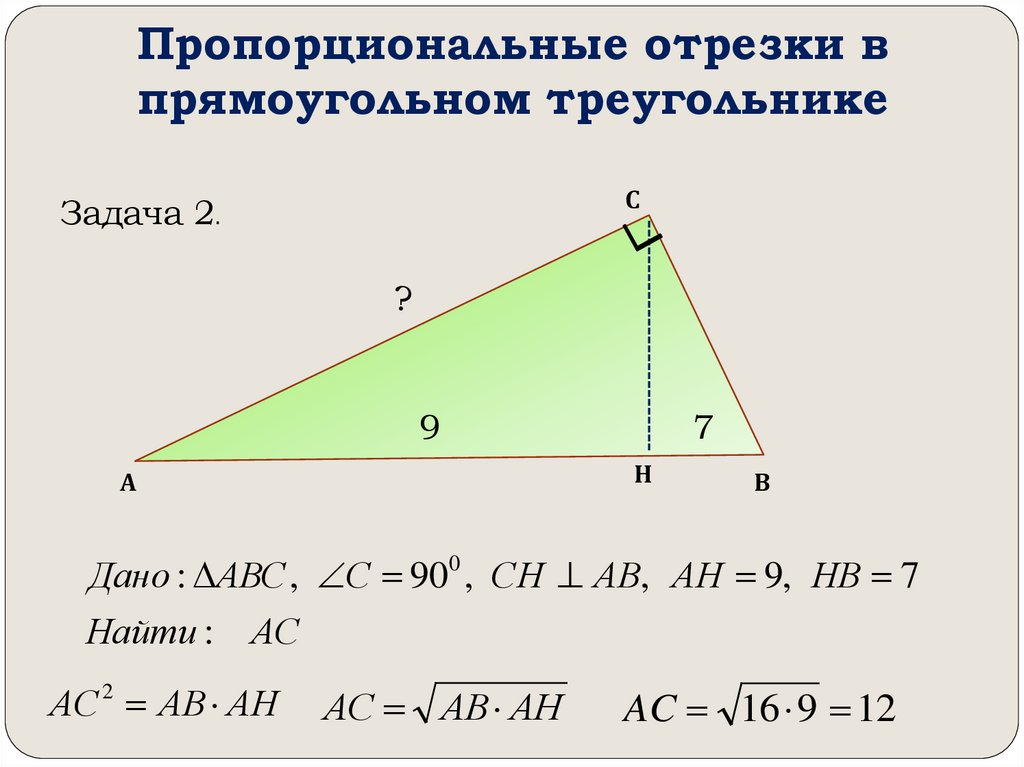
Найти геометрическое место точек (ГМТ) пересечения медиан всевозможных прямоугольных треугольников, гипотенуза АВ которых зафиксирована.
Точка пересечения медиан любого треугольника отсекает от медианы одну треть, считая от точки ее пересечения с соответствующей стороной. В прямоугольном треугольнике медиана, проведенная из прямого угла, равна половине гипотенузы. Поэтому искомое ГМТ есть окружность радиуса, равной 1/6 от длины гипотенузы, с центром в середине этой (фиксированной) гипотенузы.
Формула прямоугольного треугольника
— Что такое формула прямоугольного треугольника? Примеры
Треугольник – это замкнутая фигура или фигура с 3 сторонами, 3 углами и 3 вершинами. Для формул прямоугольного треугольника свойства должны быть более конкретными. Если какой-либо из углов треугольника является прямым углом (составляет 90º), треугольник называется прямоугольным треугольником или просто прямоугольным треугольником. Формулы прямоугольного треугольника помогут вам выполнять различные вычисления, связанные с периметром, площадью и т.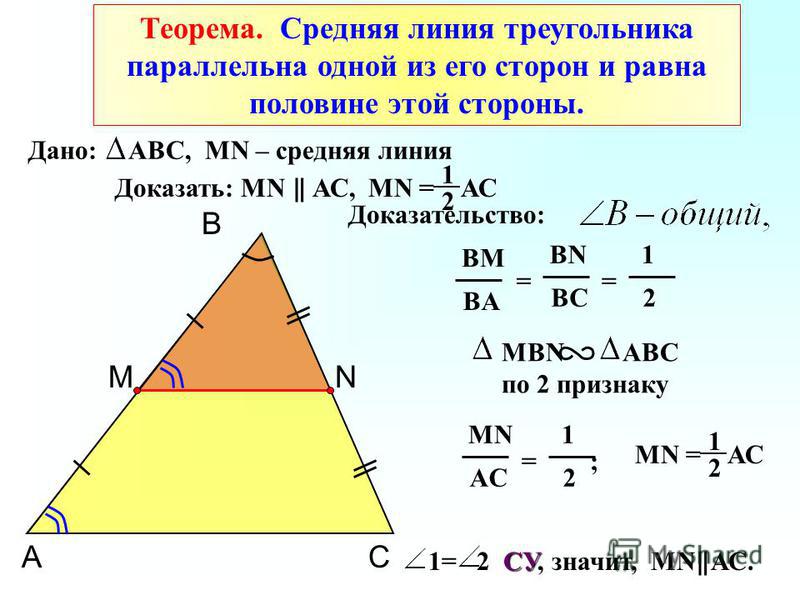
Что такое формулы прямоугольного треугольника?
Прямоугольный треугольник — это треугольник, один из внутренних углов которого равен 90 градусов. Формулы прямоугольного треугольника используются для вычисления периметра, площади, высоты и т. д. прямоугольного треугольника с использованием трех его сторон.
Формула прямоугольного треугольника
Различные формулы, связанные с прямоугольным треугольником:
- Теорема Пифагора — Формула
Определение теоремы Пифагора показывает отношение между тремя сторонами прямоугольного треугольника. Квадрат гипотенузы равен сумме квадратов двух других катетов.
(Гипотенуза) 2 = (Перпендикуляр) 2 + (Основание) 2
- Формула площади прямоугольного треугольника
Формула для вычисления площади прямоугольного треугольника задается следующим образом:
Площадь = 1/2 × Основание × Высота = 1/2 × b × h
, где высота,h равна длине перпендикуляра сторона треугольника.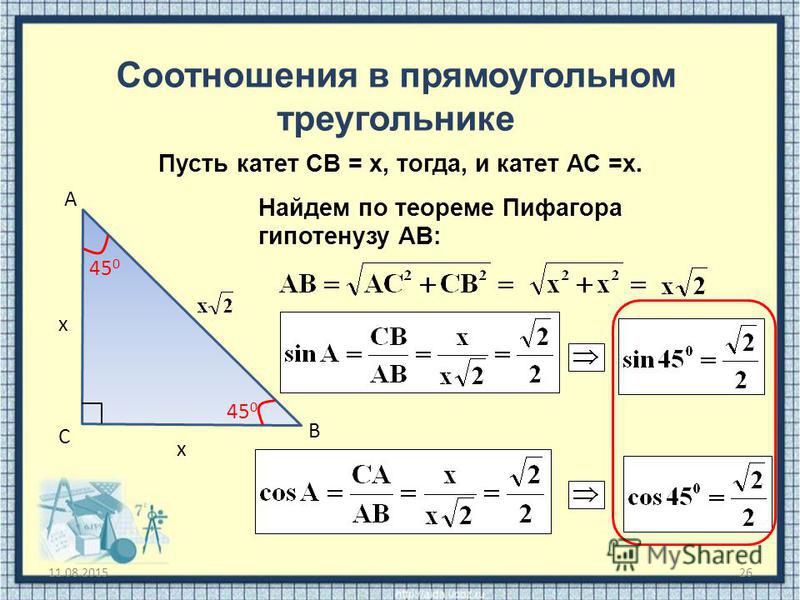
- Формула периметра прямоугольного треугольника
Формула для вычисления площади прямоугольного треугольника задается как:
Периметр = a + b + c
, где a, b и c — три стороны треугольника.
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Примеры использования формул прямоугольного треугольника
Пример 1: Длина основания и перпендикуляра прямоугольного треугольника составляет 6 дюймов и 8 дюймов соответственно. Найти:
- Длина гипотенузы
- Периметр треугольника
- Площадь треугольника
Решение:
Чтобы найти:
Дано: длина основания = 6 дюймов, длина перпендикуляра = 8 дюймов 2 + (Перпендикуляр) 2
(Гипотенуза) 2 = 6 2 + 8 2 = 100
Гипотенуза = √100 = 10 из
ii) Используя формулу периметра прямоугольного треугольника,
Периметр = сумма всех сторон
Периметр = 6 + 8 + 10 = 24 из
2 iii) Используя формула площади треугольника 10 дм, периметр прямоугольного треугольника = 24 дм, а площадь прямоугольного треугольника = 24 дм
2 .
Пример 2: Высота и гипотенуза прямоугольного треугольника равны 12 дюймам и 13 дюймам соответственно. Найдите его площадь.
Решение:
Чтобы найти: площадь прямоугольного треугольника
Дано: высота = 12 дюймов, гипотенуза = 13 в
Используя теорему Пифагора,
2 09
2 + (12) 2
(база) 2 = (13) 2 — (12) 2 = 25
Основание = √25 = 5 в
Используя формулу площади треугольника,
Площадь = (1/2) × b × h
Площадь = (1/2) × 5 × 12
Площадь = 30 в 2
Ответ: Площадь прямоугольного треугольника = 30 в 2
30 единиц, высота 12 единиц, гипотенуза 13 единиц
Решение:
Чтобы найти: Площадь прямоугольного треугольника
Дано: периметр = 30 единиц, гипотенуза = 13 единиц, высота = 12 единиц
Мы знаем, что периметр = основание + гипотенуза + высота
30 единиц = 13 + 12 + основание
Следовательно, основание = 30 — 25 = 5 единиц
Площадь = 1/2bh = 1/2 (5 × 12) = 30 квадратных единиц.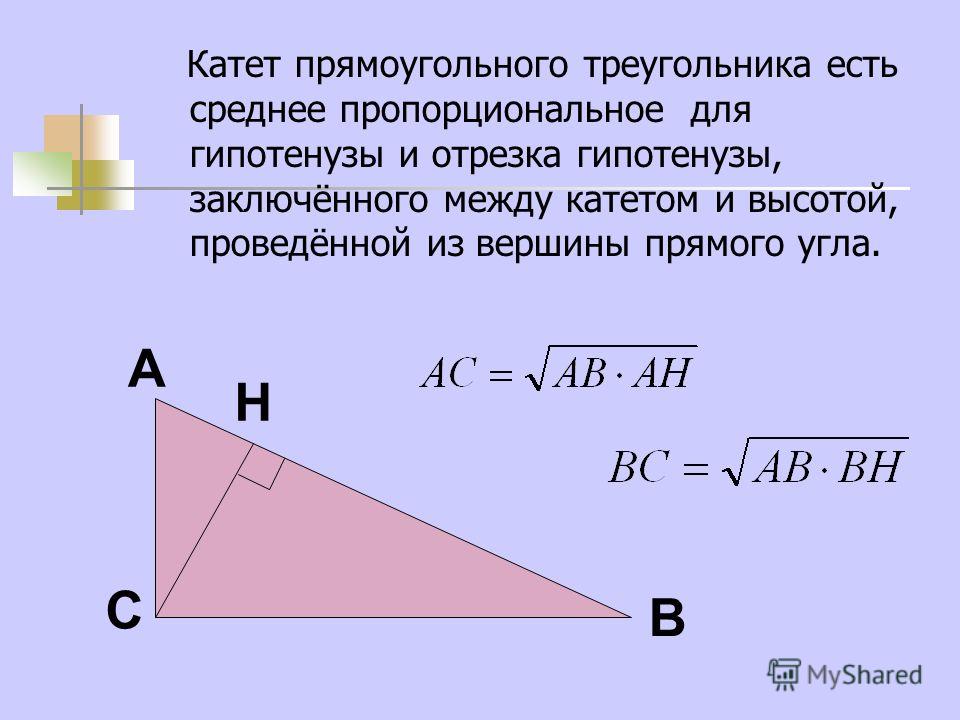
Ответ: Площадь прямоугольного треугольника = 30 единиц 2
Часто задаваемые вопросы о формулах прямоугольного треугольника
Что такое формула прямоугольного треугольника в геометрии?
В геометрии формулы прямоугольного треугольника — это формулы прямоугольного треугольника, которые используются для вычисления периметра, площади, высоты и т. д. треугольника с использованием трех его сторон — основания, высоты и гипотенузы. Эти формулы задаются следующим образом:
- Теорема Пифагора — Формула: (Гипотенуза) 2 = (Перпендикуляр) 2 + (Основание) 2
- Формула площади прямоугольного треугольника: Площадь = 1/2 × Основание × Высота
- Формула периметра прямоугольного треугольника = Сумма длин трех сторон
Каково применение формулы прямоугольного треугольника?
Существует множество применений прямоугольного треугольника в реальной жизни, наиболее распространенным является его использование в области тригонометрии, поскольку отношение между его углами и сторонами составляет основу тригонометрии.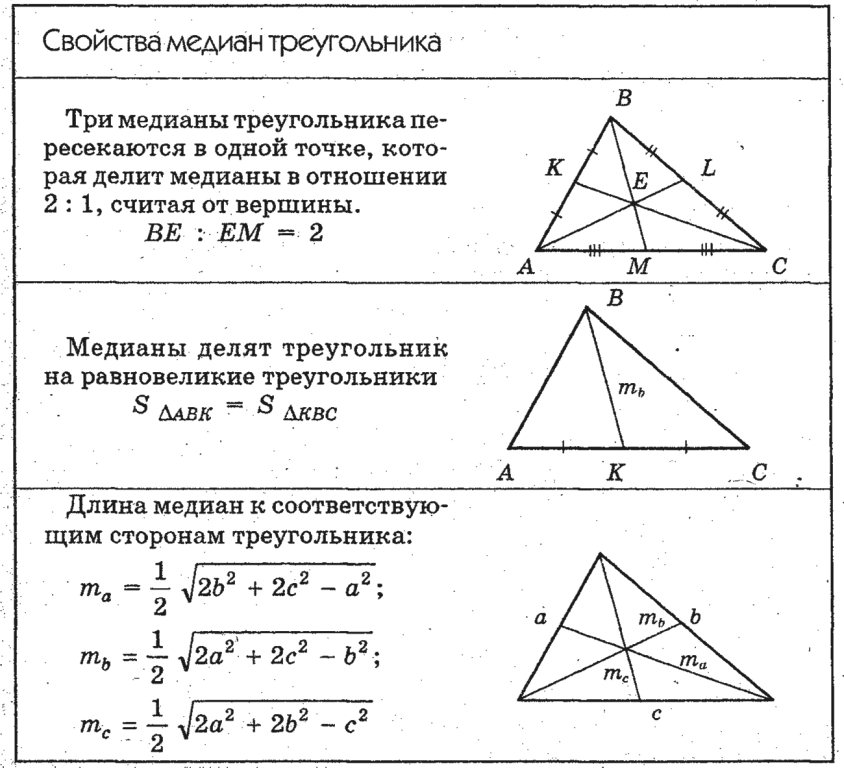
Как рассчитать площадь прямоугольного треугольника, используя формулу прямоугольного треугольника, когда известны его периметр, высота и основание?
Для того, чтобы вычислить площадь прямоугольного треугольника, когда известны его периметр, высота и основание, будем учитывать только два параметра — высоту и основание.
- Шаг 1: Проверьте заданные значения.
- Шаг 2. Подставьте значения высоты h и основания b в формулу площади (1/2)bh
Как найти формулу высоты прямоугольного треугольника?
Высоту прямоугольного треугольника можно рассчитать, учитывая длину основания и высоту. Формула прямоугольного треугольника может быть рассчитана с использованием теоремы Пифагора как, (Гипотенуза) 2 = (Высота) 2 + (База) 2 . Подставьте известные значения и найдите высоту или перпендикуляр прямоугольного треугольника.
прямоугольных треугольников
прямоугольных треугольников
Давайте снова согласимся со стандартным правилом обозначения частей прямоугольного треугольника.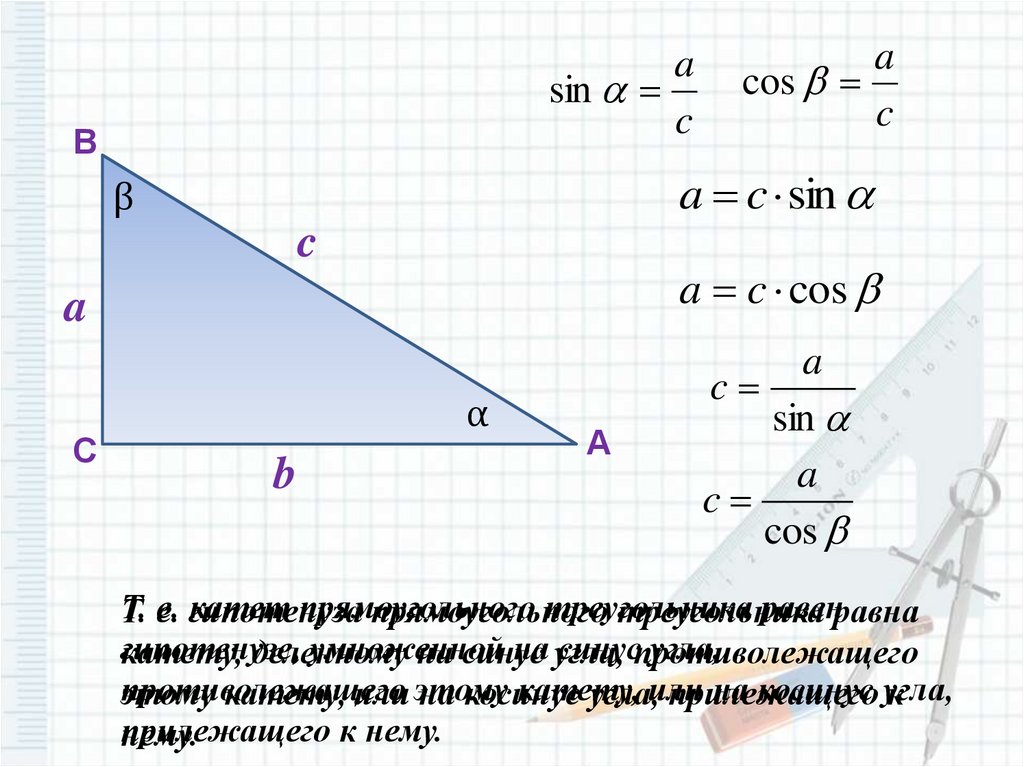
Решение прямоугольных треугольников
Мы можем использовать теорему Пифагора и свойства синусов, косинусов и тангенсов для решения треугольника, то есть для нахождения неизвестных частей через известные части.
- Теорема Пифагора: a 2 + b 2 = c 2 .
- Синусы: sin A = a/c, sin B = b/c.
- Косинусы: cos A = b/c, cos B = a/c.
- Касательные: tan A = a/b, tan B = b/a.
Давайте сначала рассмотрим некоторые случаи, когда мы не знаем всех сторон. Предположим, мы не знаем гипотенузу, но знаем две другие стороны.
Теперь предположим, что мы знаем гипотенузу и одну сторону, но должны найти другую. Например, если b = 119 и C = 169, затем A 2 = C 2 — B 2 = 169 2 — 119 2 = 28561 — 14116161616161616161616161616 гг. равно 120, поэтому a = 120.
Мы можем знать только одну сторону, но мы также знаем угол. Например, если сторона a = 15 и угол A = 41°, мы можем использовать синус и тангенс, чтобы найти гипотенузу и другую сторону.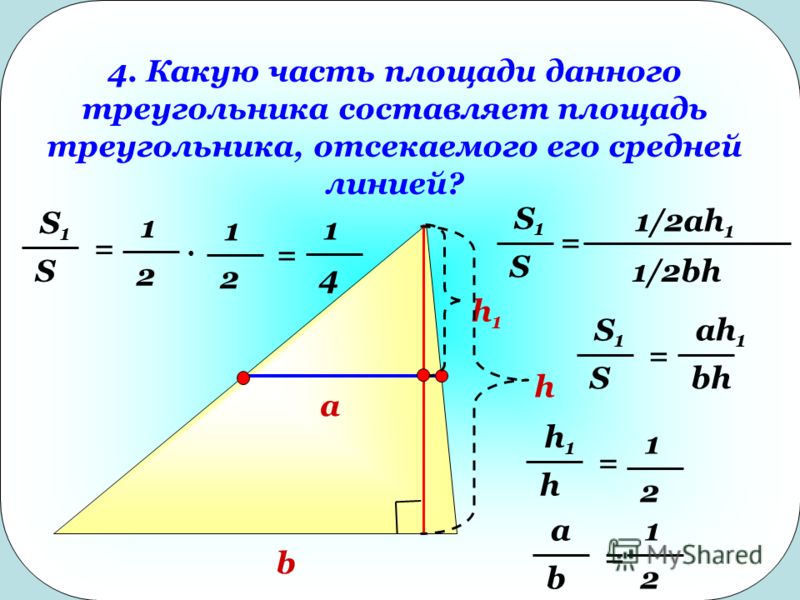
Обратные триггерные функции: арксинус, арккосинус и арктангенс
Теперь давайте рассмотрим задачу нахождения углов, если известны стороны. Опять же, вы используете триггерные функции, но наоборот. Вот пример. Предположим a = 12,3 и b = 50,1. Тогда тангенс A = a/b = 12,3/50,1 = 0,2455. Раньше, когда люди использовали таблицы триггерных функций, они просто смотрели в таблицу тангенсов, чтобы увидеть, какой угол имеет тангенс 0,2455. На калькуляторе мы используем обратные триггерные функции, называемые арктангенс, арксинус и арккосинус. Обычно на калькуляторе есть кнопка с надписью «inv» или «arc», которую вы нажимаете перед нажатием соответствующей кнопки триггера.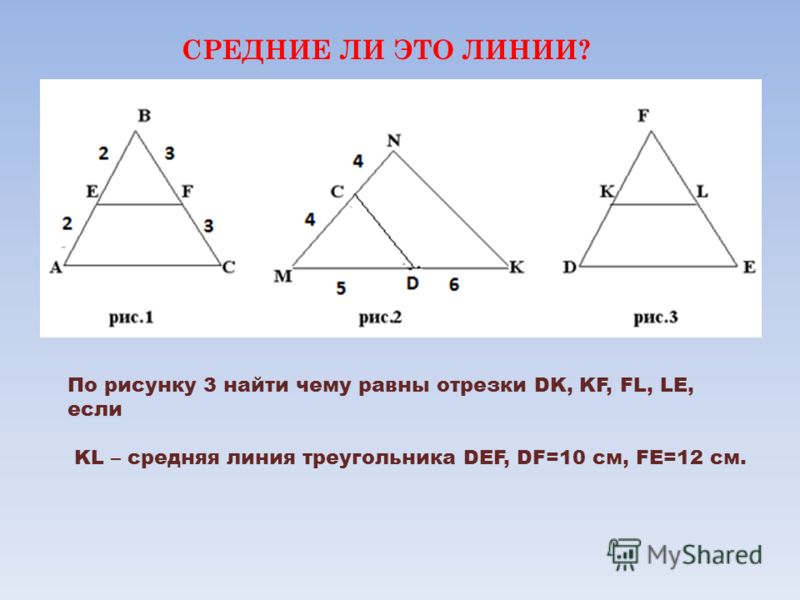
Вот и все.
Остальные три тригонометрические функции: котангенс, секанс и косеканс
Для большинства целей достаточно трех триггерных функций: синуса, косинуса и тангенса. Однако бывают случаи, когда нужны какие-то другие. В исчислении часто используется секанс. Вы можете спросить: «Почему шесть триггерных функций?» Это своего рода симметрия. Есть шесть способов сделать отношения двух сторон прямоугольного треугольника, и это дает шесть функций:
- sin A = a/c (opp/hyp)
- cos A = b/c (adj/hyp)
- tan A = a/b (opp/adj)
- детская кроватка A = b/a (adj/opp)
- сек A = c/b (hyp/adj)
- csc A = c/a (hyp/opp)
Из листинга видно, что котангенс (сокращенно cot или иногда ctn) является величиной, обратной величине тангенса, секанс (сокращенно sec) является величиной, обратной величине косинуса, а косеканс (сокращенно csc или иногда cosec) является величиной, обратной величине синуса.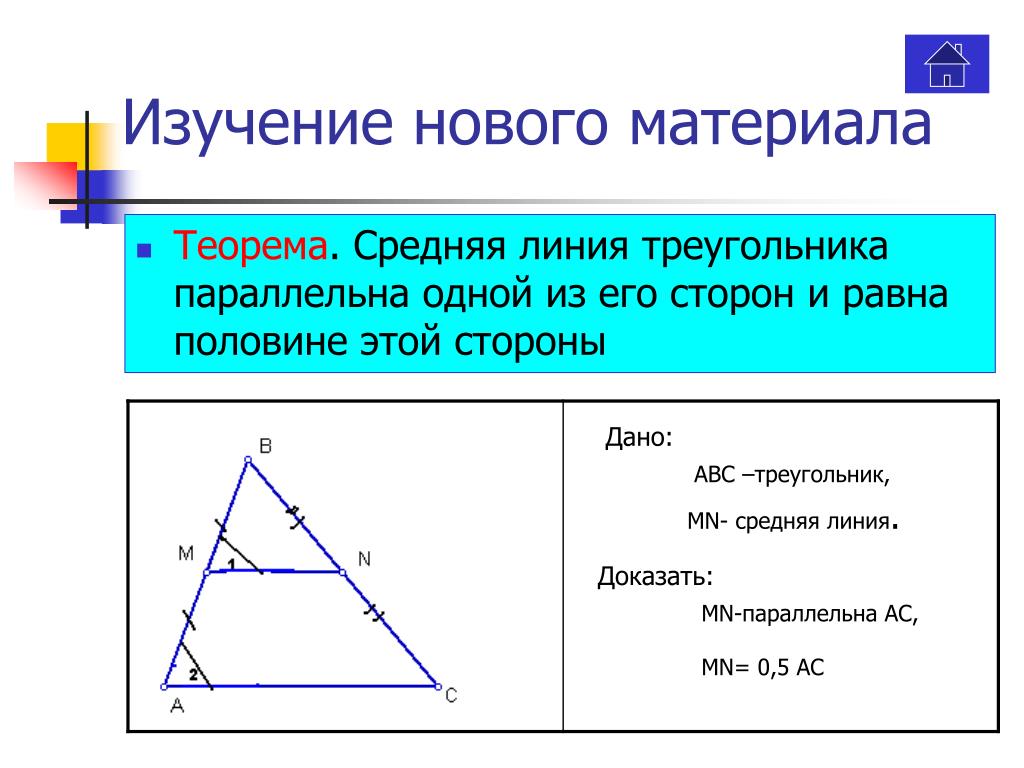
Эти три другие функции также можно интерпретировать с помощью единичной круговой диаграммы.
Мы рассматриваем угол AOB. Напомним, что его касательной является линия AC. По симметрии тангенсом угла ФОБ является линия ФГ, а FOB является дополнительным углом AOB, , следовательно, котангенс AOB равен FG.
Далее, интерпретировать секущие геометрически. Угол AOB появляется в треугольнике COA как угол AOC, so sec AOB = sec AOC = hyp/adj = OC/OA = OC . Вот оно: секанс — это линия, проведенная из центра круга к касательной AC.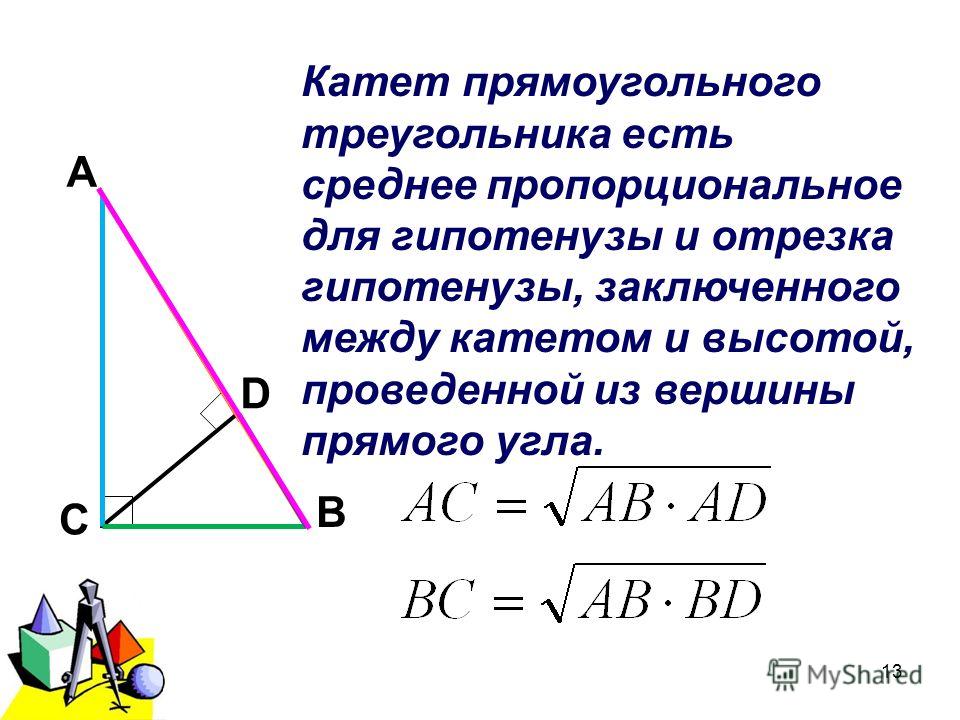
Аналогично, косекансом угла AOB является прямая OG , проходящая от центра окружности до линии котангенса FG.
Упражнения
Примечание: как обычно, во всех упражнениях на прямоугольные треугольники c обозначают гипотенузу, a и b — перпендикулярные стороны, а A и B — углы, противоположные a и б соответственно.
26. В каждом из следующих прямоугольных треугольников, две стороны которых заданы, вычислите sin, cos и тангенс углов A и B. Выразите результаты в виде обыкновенных дробей.
(и). c = 41, a = 9.
(ii). c = 37, a = 35.
(iii). a = 24, b = 7.
31.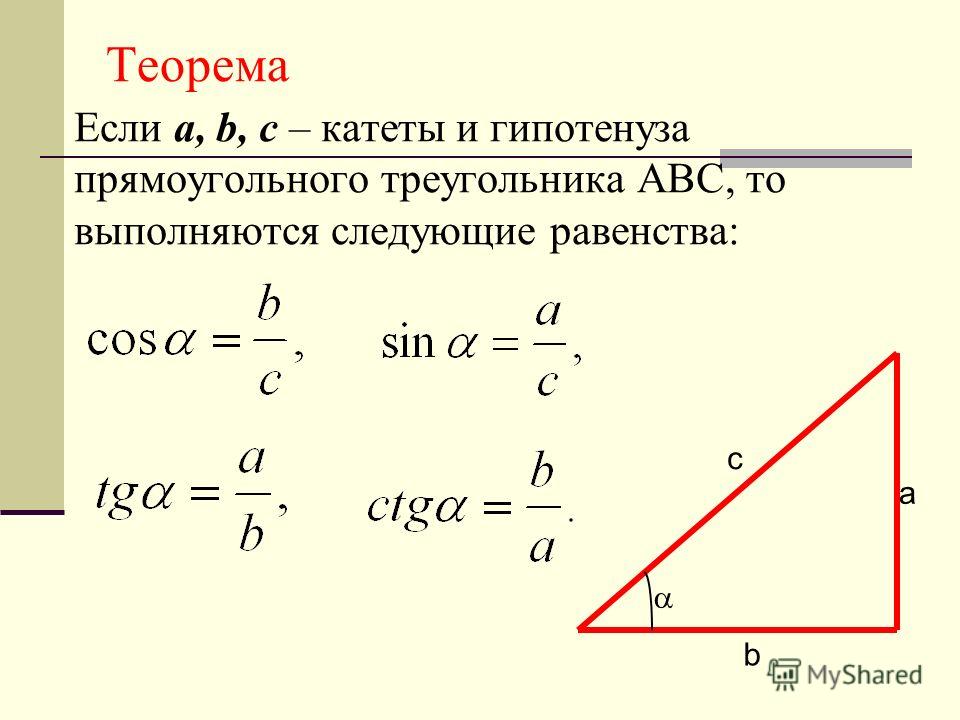
34. a = 1,2, b = 2,3. Найти A и c.
42. a = 10,11, b = 5,14. Найти B и c.
В следующих нескольких задачах треугольники не являются прямоугольными, но вы можете решить их, используя свои знания о прямоугольных треугольниках.
61. В косом треугольнике ABC, A = 30°, B = 45°, а перпендикуляр от C к AB имеет длину 12 дюймов. Найдите длину АВ.
67. Если сторона равностороннего треугольника равна а, найдите высоту и радиусы описанной и вписанной окружностей.
202. От вершины здания высотой 50 футов углы возвышения и углубления вершины и низа другого здания равны 19° 41′ и 26° 34′ соответственно. Каковы высота и расстояние до второго здания.
207. С вершины маяка высотой 175 футов углы наклона вершины и низа флагштока составляют 23° 17′ и 42° 38′ соответственно. Какой высоты столб?
214. В двух точках на расстоянии 65 футов друг от друга на одной стороне дерева и на одной линии с ним углы возвышения вершины дерева составляют 21° 19′ и 16° 20′. Найдите высоту дерева.
215. Когда воздушный шар проходит между двумя точками A, и B, находящимися на расстоянии 2 миль друг от друга, углы места воздушного шара в этих точках составляют 27° 19′ и 41° 45′ соответственно. Найдите высоту воздушного шара. Возьмите A и B на одном уровне.
233. Верхняя часть маяка находится на высоте 230 футов над уровнем моря. Как далеко находится объект, который находится «на горизонте»? [Предположим, что Земля представляет собой сферу радиусом 3956 миль.]
234. На какой высоте должен находиться наблюдатель, чтобы он мог видеть объект на Земле на расстоянии тридцати миль? Предположим, что Земля представляет собой гладкий шар.
В каждой из фигур, названных в следующих нескольких задачах, объект должен выразить свою площадь (i) через радиус R, , то есть радиус описанной окружности, (ii) через апофема r, то есть радиус вписанной окружности, и (iii) по стороне а.
251. Равносторонний треугольник. [См. задачу 67 выше.]
252. Квадрат.
253. Правильный пятиугольник.
254. Правильный шестигранник.
255. Правильный восьмиугольник.
Советы
26. Вам нужны только sin, cos и тангенс углов A и B ; вам не нужны сами углы. Таким образом, вам нужна только третья сторона, которую вы можете вычислить с помощью теоремы Пифагора, а затем взять отношения двух сторон.
31. Вы знаете c и tan B. К сожалению, tan B — это отношение двух неизвестных вам сторон, а именно b/a. Существует несколько способов решения этой проблемы.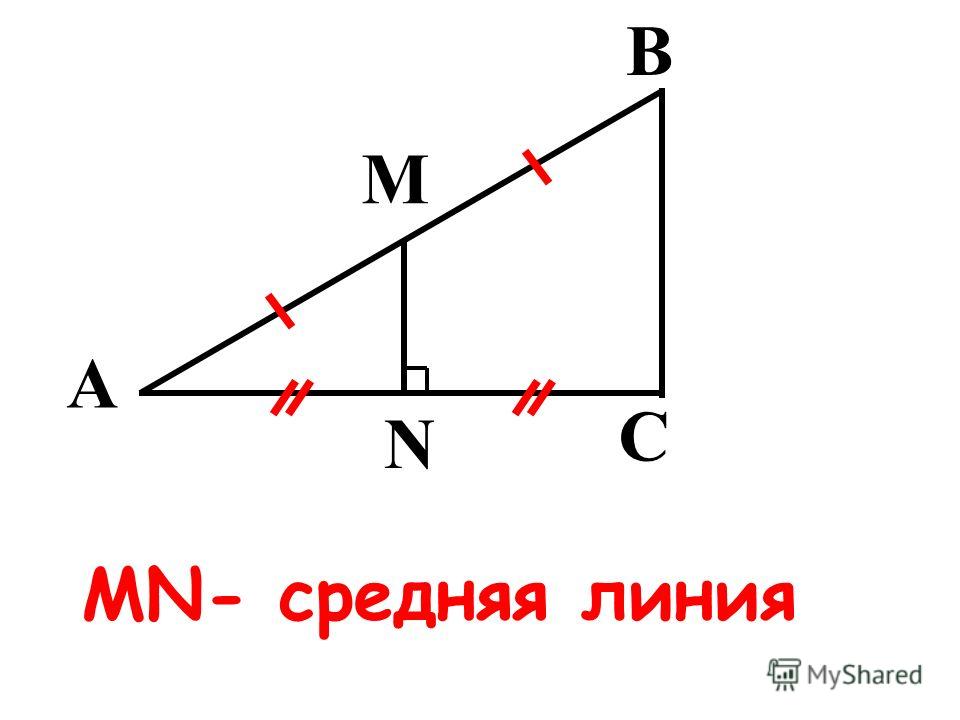
Метод 1. Возьмем уравнение 1.2 = tan B = b/a, , чтобы получить отношение между a и b, , а именно b = 1,2 a. Тогда теорема Пифагора дает 6,25 2 = а 2 + 1,44 а 2 , из которых можно определить а, и затем найти б.
Способ 2. Из тангенса B, можно определить угол B (используйте арктангенс). Отсюда вы можете найти cos B, и затем a, и вы можете найти sin B, и затем b.
34. Поскольку у вас есть a и b, вы можете использовать тангенсы, чтобы найти A и теорему Пифагора, чтобы найти c.
42. Найдите B по касательной и c по теореме Пифагора.
61. Начните с рисования фигуры. Хотя треугольник ABC не является прямоугольным, он распадается на два прямоугольных треугольника.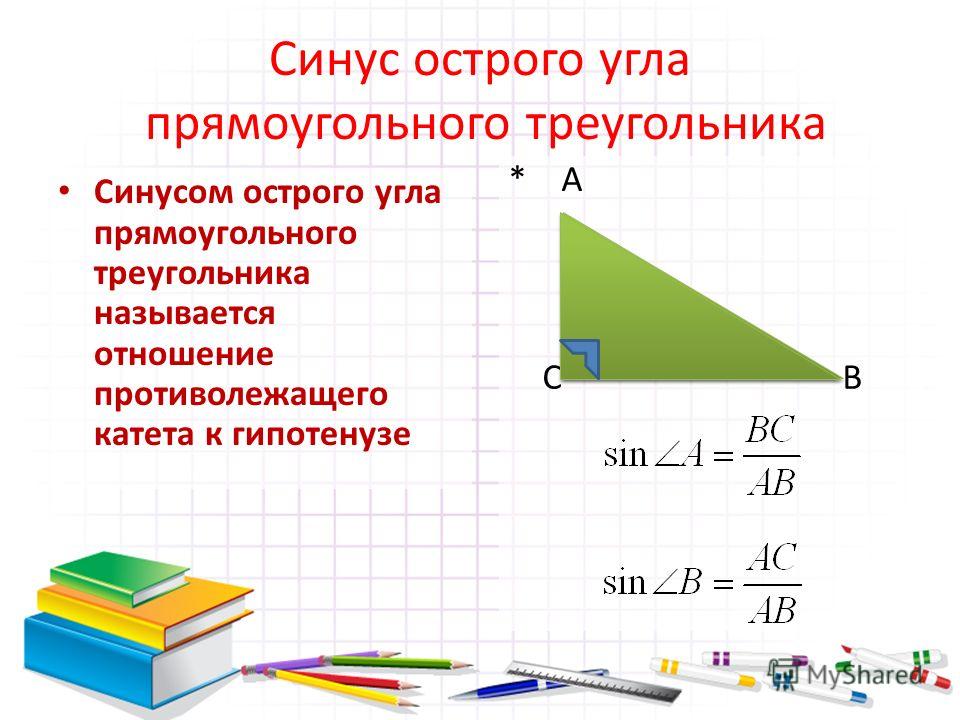
67. Равносторонний треугольник ABC имеет три угла при вершине по 60°. Отбросьте перпендикуляр из одной вершины, скажем, вершины C, , и вы получите два конгруэнтных прямоугольных треугольника ACF и BCF, , и вы можете найти длину этого перпендикуляра, а это высота равностороннего треугольника. Описанная окружность — это та, которая проходит через три вершины, а вписанная окружность — это та, которая касается внутри трех сторон. Отбрасывая перпендикуляры из другой вершины равностороннего треугольника и применяя тригонометрию к полученным маленьким треугольникам, можно найти радиусы этих двух окружностей.
202. Поскольку вы знаете высоту своего здания и угол наклона к основанию другого здания, вы можете определить, как далеко оно находится. Тогда угол подъема на вершину другого здания скажет вам, насколько оно выше вашего.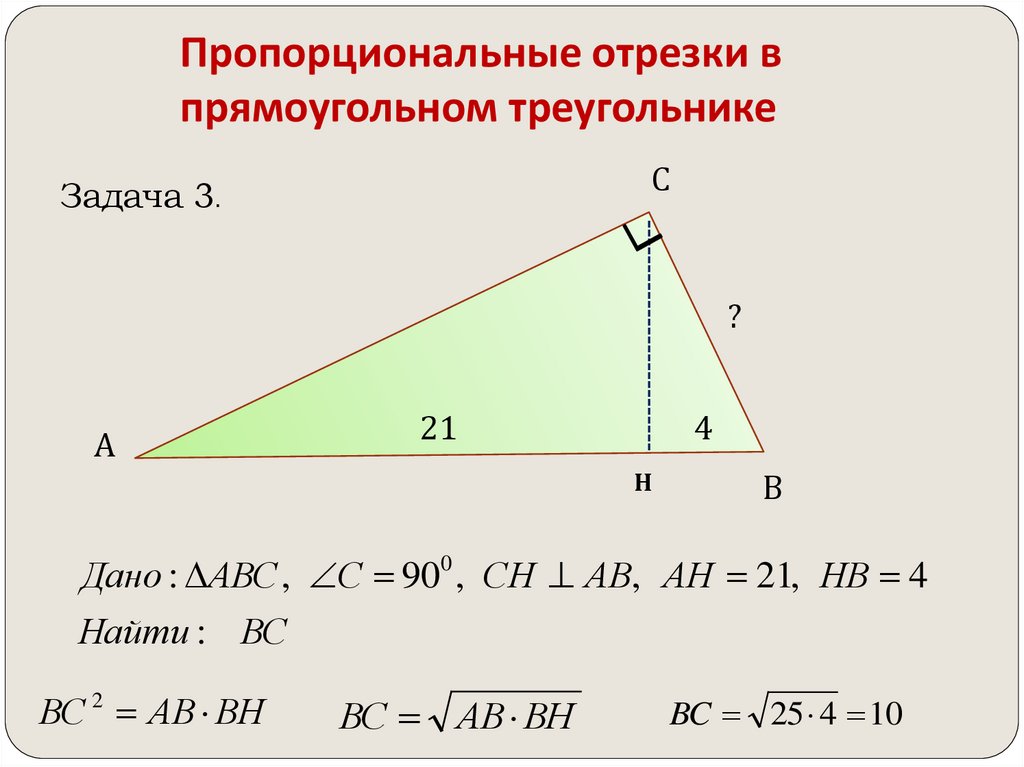
207. Подсказка похожа на 202. Смотрите, триггер может быть полезен, если вы одинокий смотритель маяка и не знаете, что делать!
214. Это полезная задача. Вы можете использовать его, чтобы найти высоты недоступных вещей. Нарисуйте фигуру. Есть два неизвестных: высота х дерева и расстояние х ближайшей точки к дереву. Дальнейшая точка будет 90 247 x 90 248 + 65 футов от дерева. Используя тангенсы известных углов, вы можете составить два уравнения, которые можно решить для определения y и x.
215. Это похоже на 214, но в этой задаче шарик лежит между двумя точками. Нарисуйте фигуру. Определите свои переменные. Составьте уравнения и решите их.
233. Очень интересная задача. Различные его обратные значения использовались на протяжении веков для вычисления радиуса Земли. В этой задаче мы предполагаем, что знаем о Земле. Все, что вам нужно здесь, это теорема Пифагора. Одна сторона прямоугольного треугольника равна 90 247 r, 90 248 — радиус Земли, а гипотенуза — 90 247 r 90 248 + 90 247 h 90 248, где 90 247 h 90 248 — высота маяка.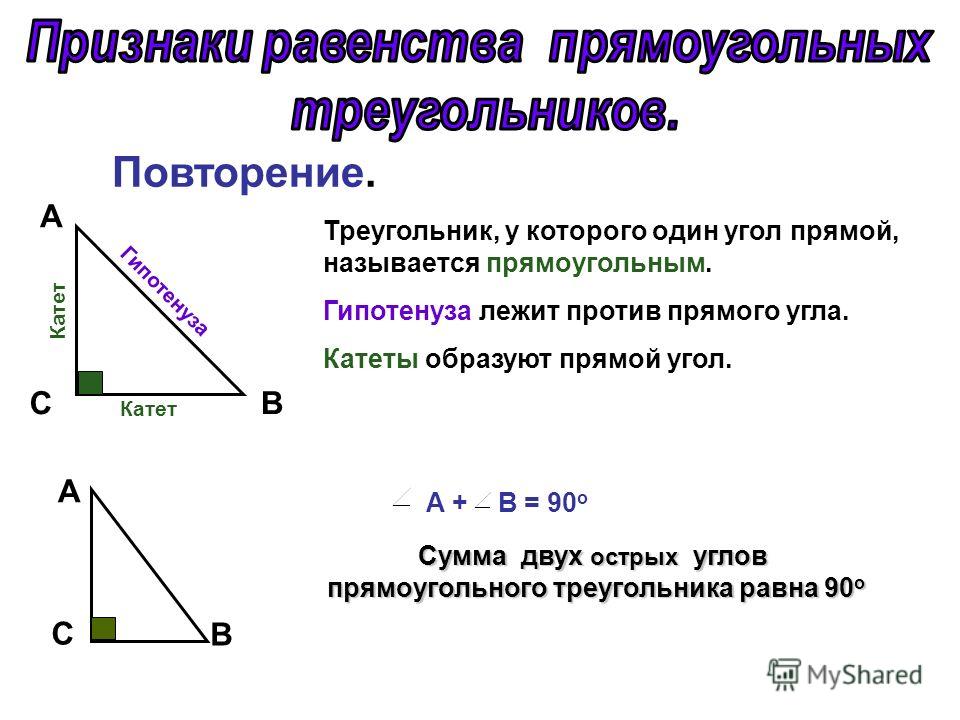
234. Поставьте эту задачу аналогично 233, но известны другие переменные.
251–255. Вы можете сделать все это сразу, оставив вычисления напоследок. Пусть n — количество сторон правильного многоугольника. Проведите линии от центра фигуры к вершинам и к серединам сторон. У вас получится 2 n маленьких треугольников. Каждый из них представляет собой прямоугольный треугольник с гипотенузой 90 247 R, 90 248 катетом р, и другая нога и /2. Угол в центре равен 360°/(2 n ) = 180°/ n. Используя тригонометрию, вы можете легко написать уравнения, связывающие площадь правильного многоугольника по мере необходимости.
Ответы
26. (и). B = 40. Итак, SIN A = COS B = 9/41, COS A = SIN B = 40/41, TAN A = 9/40, TAN B = 408 = 408 = 408 = 408 = 408 = 408 = 408 = 40248 = 40248 a = 9/40.
(ii). B = 12. Итак, SIN A = COS B = 35/37, COS A = SIN B = 12/37, TAN A = 35/12, TAN B a = 35/12, TAN B a = 35/12. /37.
(iii). C = 25. Итак, SIN A = COS B = 24/25, COS A = SIN B = 7/25, TAN A = 24/7, TAN B = 7 = 7 = 7 = 7 = 7 a = 24/7, TAN B = 7 = 7 = 70248 = 24/7, TAN B = 70247 A = 24/7, TAN B = 70247 A = 24/7, TAN B = 7. /24.
31. a = 4 фута, b = 4,8 фута, около 4 футов 10 дюймов.
34. A = 27,55°, около 28°. c = 2,6.
42. B = 26,95° или 26°57′. c = 11,3.
61. AB = 12/тангенс A + 12/тангенс B = 12(√3 + 1) дюймов, около 33 дюймов.
67. ( a √3)/2, ( a √3)/3 и ( a √3)/6 соответственно.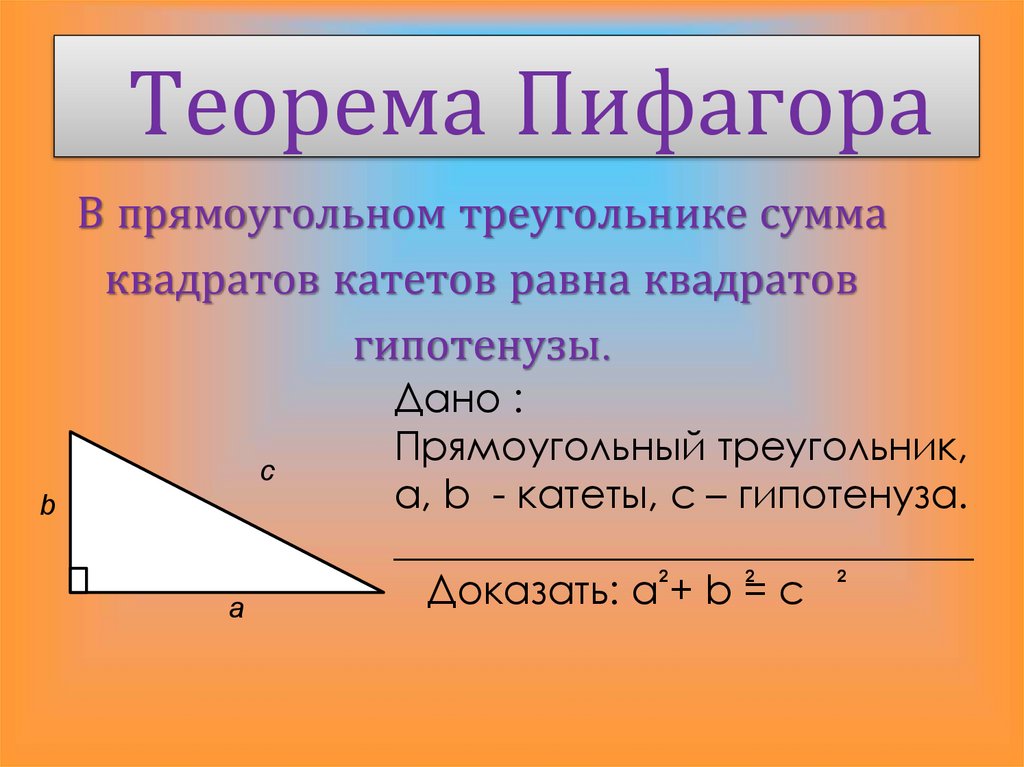
202. Расстояние = 50/тангенс 26°34′ = 100 футов. Высота = 50 + 100 tan 19°41′ = 85,8′ = 85’9″.
207. Расстояние = 175/тангенс 42°38′ = 190 футов. Рост = 175 — 190 тангенс 23°17′ = 93,23′ = 9’3″.
214. Два уравнения
- 0,2
= тангенс 16°20′ =
ч /(65 + x ), и
0,3
= тангенс 21°19′ = ч/х .
где x — расстояние от ближайшей точки до основания дерева. Вы можете решить их одновременно за х и ч.
Расстояние х = 196 футов. Высота ч = 76,5′.
215. Если h — это высота воздушного шара, а x — это расстояние по земле от точки A до точки непосредственно под воздушным шаром, то два уравнения
- тангенс 27°19′ = ч/х , и
тангенс 41°45′ = ч / (2 — x )
Вы можете решить эту пару уравнений на х и ч.
Высота = 0,654 мили = 3455 футов.
233. Мелочь больше 18,5 миль.
234. 600 футов.
251–255. Площадь правильного n -угольника равна A = nra /2. Чтобы найти A через R, r, или a, , используйте соотношения
- cos 180°/ n = r/R, и
тангенс 180°/ n = a /(2 r ).
затем
- (i) в пересчете на R, площадь A = nR 2 cos 180°/ n sin 180°/ n ,
(ii) в пересчете на r, площадь A = nr 2 tan 180°/ n , и
(iii) в пересчете на а, площадь А = na 2 /(4tan 180°/ и ).
| Problem | shape | (i) R | (ii) r | (iii) a |
|---|---|---|---|---|
| 251 | triangle | (3 R 2 √3)/4 | 3 р 2 √3 | ( a 2 √3)/4 |
| 252 | квадратный | 2 Р 2 | 4 р 2 | a 2 |
| 253 | пятиугольник | (5 R 2 sin 108°)/2 | 5 r 2 tan 36° | (5 a 2 tan 54°)/4 |
| 254 | шестигранник | (3 R 2 √3)/2 | 2 р 2 √3 | (3 a 2 √3)/2 |
| 255 | восьмиугольник | 2 Р 2 √2 | 8 r 2 tan 22°30′ | 2 a 2 tan 67°30′ |
Отступление от троек Пифагора
Это не имеет ничего общего с тригонометрией, но это интересно.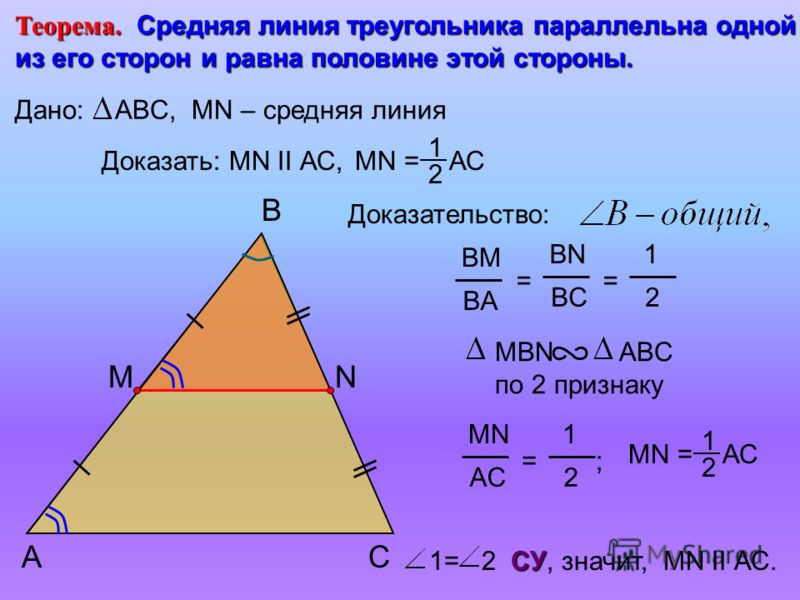
Итак, существуют ли другие специальные прямоугольные треугольники, все стороны которых являются целыми числами? Да и изучались они давно. Три числа a, b, и c такие, что a 2 + b 2 = c 2 образуют пифагорейскую тройку , в честь Пифагора. Он жил около 550 г. до н. э. и, вероятно, знаю немало из них. Но древние вавилоняне около 1800 г. до н. э. знали их все, и многие были известны в других древних цивилизациях, таких как Китай и Индия.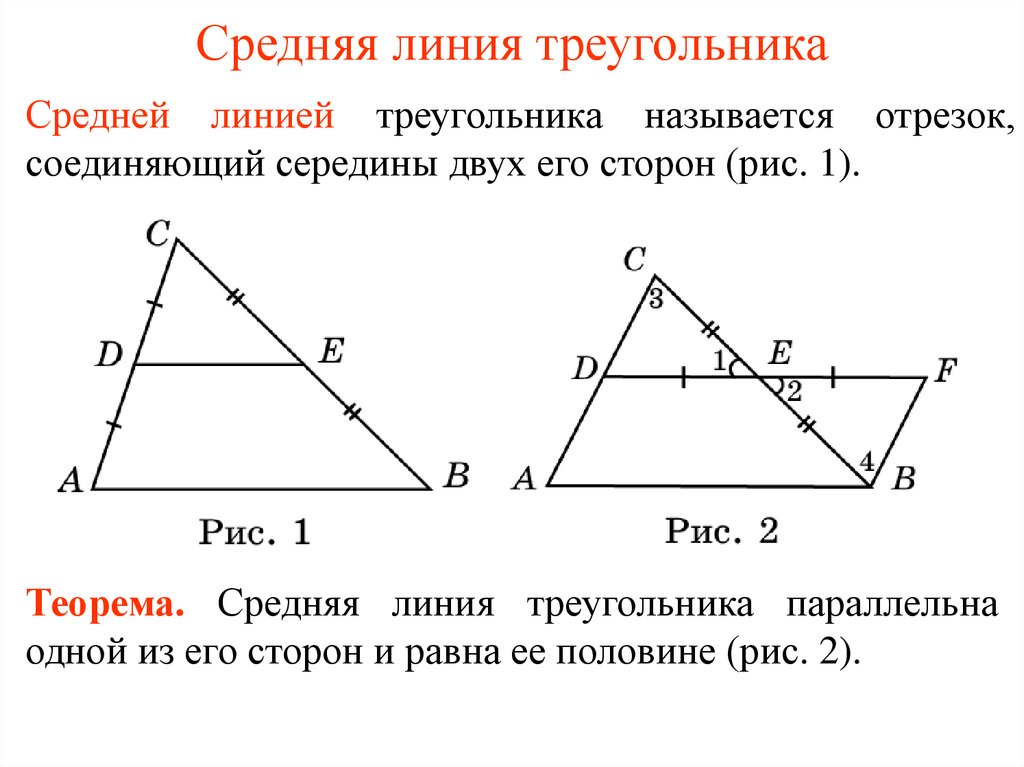
Прежде чем читать абзац, посмотрите, сможете ли вы найти еще несколько пифагорейских троек. Не считайте за новые те, у которых есть общий множитель, например 6:8:10, так как они будут похожи на меньшие.
В « Элементах » Евклида есть описание всех возможных пифагорейских троек. Вот современный парафраз Евклида. Возьмем любые два нечетных числа 90 247 m 90 248 и 90 247 n, 90 248 с 90 247 m 90 248 n и взаимно простые (то есть без общих множителей). Let a = mn, let b = ( n 2 – m 2 )/2, and let c = ( n 2 + m 2 )/2. Тогда a : b : c — пифагорейская тройка. Например, если взять m = 1, а n = 3, то получится наименьшая пифагорейская тройка 3:4:5.
Математическая сцена — Треугольники — Урок 1
Урок 1 Правила
для треугольников
Вершины треугольника принято обозначать заглавными буквами.
буквы и стороны с маленькими буквами.
Также принято обозначать сторону, противоположную углу А, знаком
малый a, сторона противоположная углу B с малым b и сторона противоположная углу C
с маленькой с (см. схему).
Стороны, образующие стороны угла А, называются смежными с А.
Сторона, на которой стоит треугольник, называется основанием треугольника.
сумма углов треугольника равна 180°. В этом легко убедиться, проведя прямую
прямую, проходящую через угол B и параллельную стороне b. (см. схему).
Углы, образованные этой прямой, равны A, B и C (по правилу
что противоположные углы между параллельными прямыми равны).
Также A + B + C = 180, так как вместе они образуют прямую линию.
Прямая, проведенная из угла B перпендикулярно базовой линии b, называется
высота треугольника. На приведенной ниже диаграмме высота обозначена буквой h.
Ранее вы узнали, что площадь треугольника определяется
формула.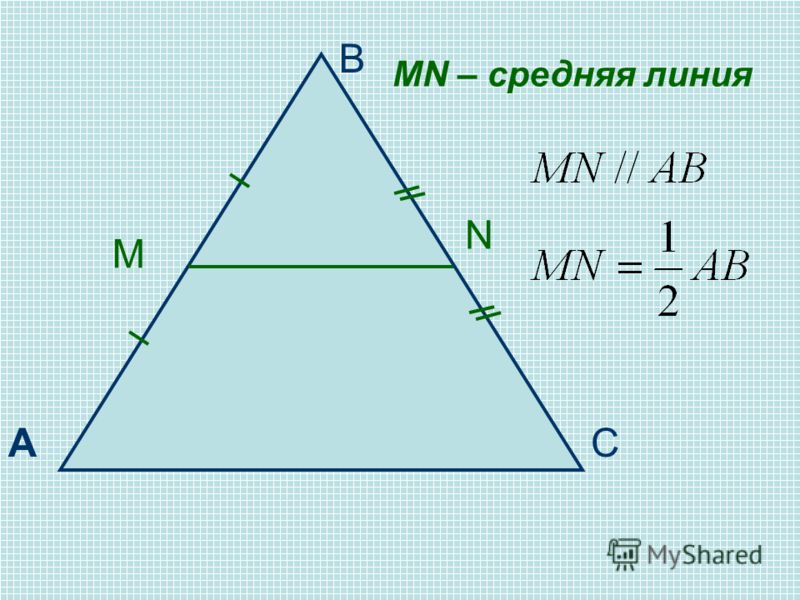
Площадь F = ×b×h
Буква G используется здесь для обозначения точки, где высота и
основание пересекается. Эту точку иногда называют перпендикулярной проекцией
точку B на линию b.
Два
треугольники называются подобными, если все углы одного треугольника равны
все углы другого. Если мы хотим показать, что два треугольника подобны
достаточно показать, что два угла равны. Если два угла равны, то
очевидно, что третий угол в каждом должен быть равен.
Треугольники на приведенной выше диаграмме
похожи. Отсюда следует, что отношения между соответствующими сторонами равны
такой же.
Другими словами:
Сейчас мы сделаем несколько примеров, используя эти соотношения.
Пример
1
Треугольники на схеме подобны с равными
углы отмечены таким же образом.
обозначены х и у.
Начнем с обозначения треугольников, чтобы лучше видеть
легко, какие стороны соответствуют друг другу.
Мы можем записать следующие отношения:
б/к
= 36/33 = 24/г = б/к
Это означает, что у/24 = 33/36
и, следовательно, y = 24×33/36 = ·22 см.
Также a/b =
х/36 = 20/24 = а/б
Что дает нам x =
36×20/24 = 30 см.
Другое правило, использующее пропорции в треугольниках
можно вывести.
Проводим прямую линию, пересекающую две стороны
треугольника и параллельна третьей стороне. Эта линия разделяет
треугольник на две части, верхняя часть представляет собой треугольник, подобный АВС,
оригинальный треугольник. Обозначим стороны этого меньшего треугольника знаком
буквы x, y и z. Следующее
теперь правда:
Проведенная линия делит сторону c
на две части, x и r, а сторону a на z и t.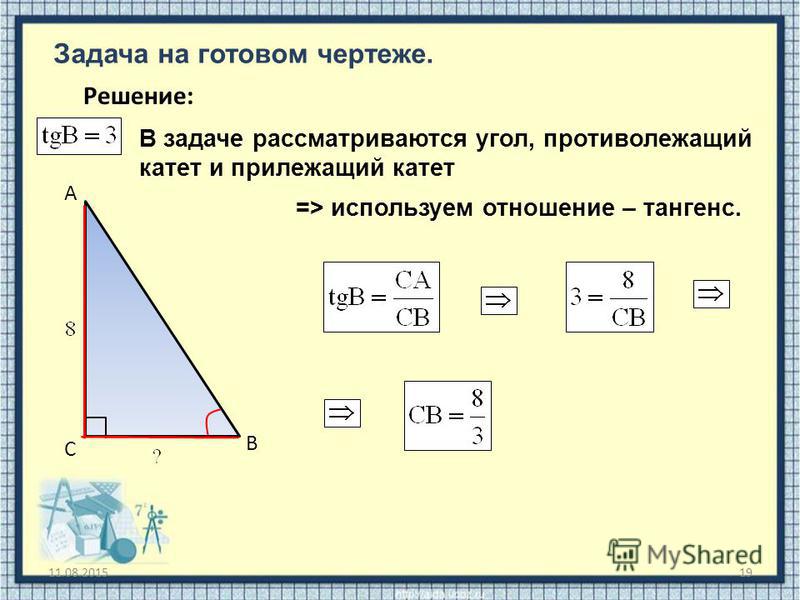
c и z + t in для a в приведенном выше уравнении мы получаем следующий результат:
Мы показали, что любая линия
через две стороны треугольника и параллельно третьей стороне делит эти две
стороны в том же соотношении.
Пример
2
Две стороны треугольника ABC, AB и BC равны 30 см.
длина и третья сторона АС, линия основания, 42 см. Через точку X на АВ проведем прямую, параллельную основанию и длиной 14 см. Найдите длину линий BX
и АКС.
14 / 42 = XB / 30
XB = 30×14 / 42 = 10
см
АХ = 30 — 10 = 20
см
В большинстве случаев, если мы хотим найти размер
углов треугольника нам нужно либо нарисовать точную диаграмму, либо
измерить углы или воспользоваться правилами тригонометрии.
Равносторонний.
Равнобедренный.
Прямоугольный.
В равностороннем
треугольник все стороны равны и все углы равны 60.
В равнобедренном треугольнике
две стороны имеют одинаковую длину и два угла (углы, образованные с основанием
линия) равны. Зная один угол в равнобедренном треугольнике, мы можем найти
другие углы. Перпендикуляр из вершины к базовой линии (высоте) в
равнобедренный треугольник делит треугольник на два равных прямоугольных
треугольники.
Стороны справа
треугольник ABC удовлетворяет правилу Пифагора, то есть a 2 + b 2 = c 2 .
Также обратное
истинный. Если выполняется правило Пифагора, то треугольник прямоугольный.
Мы можем проверить, что
Третий треугольник на приведенной выше диаграмме является прямым углом по правилу Пифагора.
5 2 + (53) 2 = 10 2
25 + 75 = 100
Обратите внимание, что длина
гипотенуза (10 см) в этом треугольнике в два раза больше длины самой короткой стороны (5
см).
В этом случае углы треугольника всегда равны 30,
60 и 90°.
Пример 3
Найдите площадь равностороннего треугольника со стороной 20 см.
Начнем с рисования высоты h треугольника. Это разделяет
треугольник на два равных прямоугольных треугольника. Используя правило Пифагора, мы можем
рассчитать ч.
ч 2 + 5 2 = 10 2
ч 2 = 10 2 − 5 2 = 100
− 25 = 75 = 5 2 × 3
ч = 53
≈ 8,7
Площадь A = ×10×h ≈ ×10×8,7 ≈ 43 см 2
Пример
4
Длина сторон равнобедренного треугольника 30 см.
в длину, а базовая линия 42
см. Найдите длину прямой, проведенной через две равные стороны параллельно
основания и 10 см от основания.
Сначала делим треугольник на два прямоугольных
угловые треугольники, рисуя высоту h от вершины до основания.
мы используем правило Пифагора, чтобы вычислить высоту.
ч 2 + 21 2 = 30 2
ч 2 = 30 2 − 21 2 = 459
ч ≈ 21,4
у = ч — 10 ≈ 21,4 — 10 ≈
11,4 см
Используя правило соотношения для
подобных треугольников получаем:
г / ч = x / 21
x ≈ 21×11,4 / 21,4 ≈ 11 см
Следовательно, длина
параллельная линия. 22 см .
Хорошо нарисуйте прямоугольный треугольник, используя
гипотенуза AB в качестве базовой линии, так что угол при вершине C равен 90. Мы
затем проведите высоту от C до AB, как показано на диаграмме:
Эта линия делит угол при вершине на два
частей (не равны, если треугольник не равнобедренный). Если одна часть равна х,
тогда другое должно быть 90−x.
Легко видеть, что два угла при основании должны быть равны 90 − x (на
справа) и x (слева) как
сумма углов любого треугольника всегда равна 180.
Обратите внимание, что все углы как в меньшем, так и в
треугольников, а также в исходном треугольнике ABC равны и равны 90,
х и
90 — х. Следовательно, эти три треугольника подобны.
Для всех прямоугольных
треугольники:
высота, проведенная из вершины к гипотенузе, делит прямоугольный треугольник
на два треугольника, которые оба подобны исходному треугольнику.
Это приводит к трем наборам соотношений.
Используя греческие буквы а для обозначения стороны, противоположной
угол
с маркировкой x и b для стороны, противоположной углу с маркировкой 90− х, как показано на
на диаграмме получаем следующее:
Два меньших треугольника подобны, поэтому
Исходный треугольник и треугольник с углом x при вершине
похожи поэтому
Исходный треугольник и
треугольник с углом 90−x
аналогичный поэтому
Пример
5
Дан прямоугольный треугольник с
две более короткие стороны длиной 7 см и 10 см.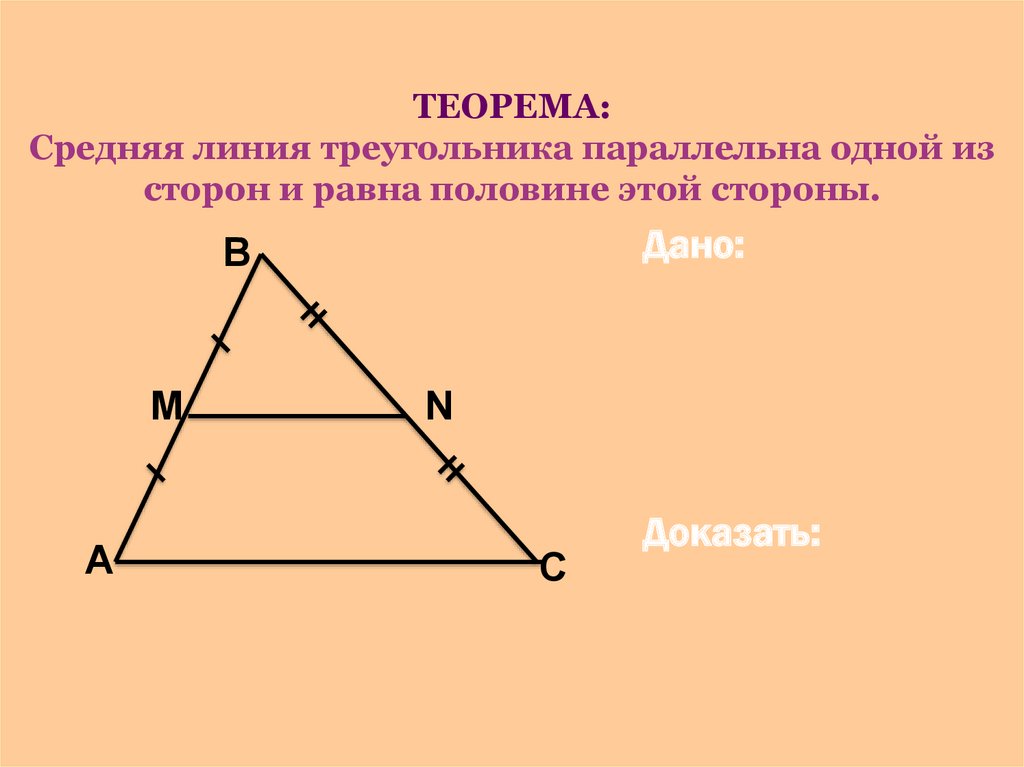
делит треугольник на два треугольника. Найдите площади этих двух треугольников.
Сначала мы используем Pythagoras
вычислить длину гипотенузы, c.
c 2 = 10 2 + 7 2 = 149, Тогда c ≈ 12,2 см
Затем мы используем одно из приведенных выше соотношений для расчета a.
a / c = a / a
a = a 2 / c ≈ 10 2 / 12,2 ≈ 8,2 см
А потом б.
б ≈ 12,2 − 8,2
≈ 4 см
Теперь нам нужно вычислить высоту h.
б / в = ч / а
ч = аб / с ≈ 10×7 / 12,2 ≈ 5,7 см
Области теперь легко найти.
Площадь F 1 = ×b×h ≈ ×4×5,7
≈ 11,4 см 2
Площадь F 2 = ×a×h ≈ ×8,2×5,7
≈ 23,4 см 2
Попробуйте пройти викторину 1 по треугольникам.
Не забудьте использовать контрольный список для
следить за своей работой.
Как найти периметр прямоугольного треугольника
Все ресурсы по базовой геометрии
9 Диагностические тесты
164 практических теста
Вопрос дня
Карточки
Learn by Concept
← Предыдущая 1 2 3 4 5 6 Следующая →
Справка по базовой геометрии »
Плоская геометрия »
Треугольники »
Прямоугольные треугольники »
Как найти периметр прямоугольного треугольника
На рисунке ниже прямоугольный треугольник имеет гипотенузу 6. Если и , найдите периметр треугольника .
Возможные ответы:
Правильный ответ:
Объяснение:
Для нахождения периметра прямоугольного треугольника используются три основных метода.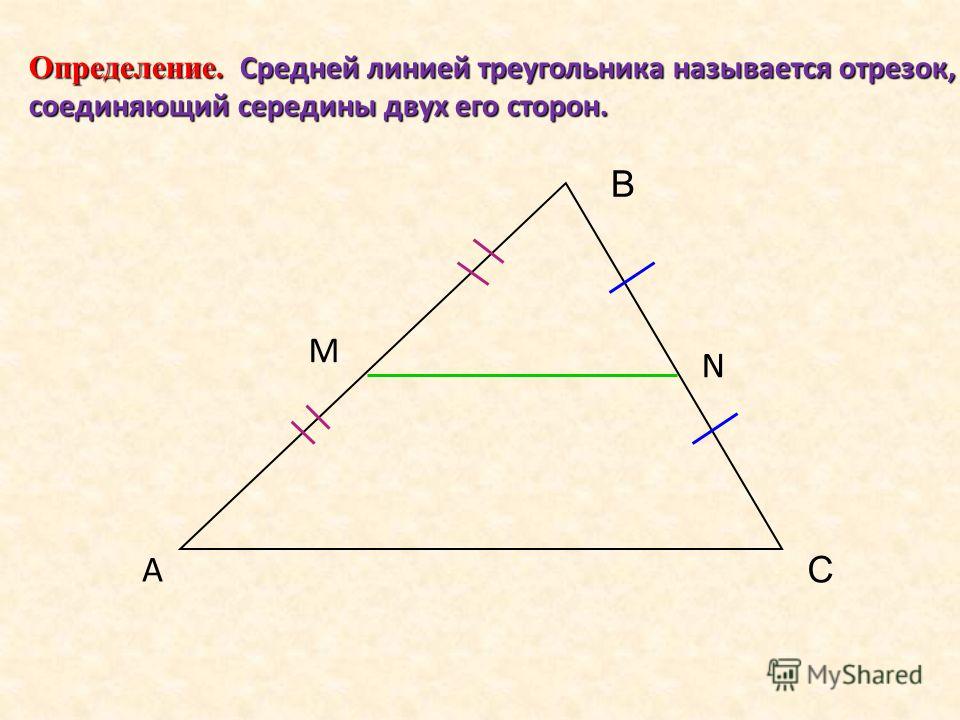
- Когда указаны длины сторон, сложите их вместе.
- Найдите недостающую сторону по теореме Пифагора.
- Если мы знаем информацию о стороне и углу, найдите недостающую сторону, используя закон косинусов.
Метод 1:
Этот метод покажет вам, как вычислить периметр треугольника, когда известны длины всех сторон. Рассмотрим следующий рисунок:
Если известны длины сторон , , и , то мы можем просто сложить их вместе, чтобы найти периметр треугольника. Важно отметить несколько вещей. Во-первых, нам нужно убедиться, что все заданные единицы совпадают друг с другом. Во-вторых, когда известны длины всех сторон, формулу периметра можно использовать для всех типов треугольников (например, прямоугольных, остроугольных, тупоугольных, равносторонних, равнобедренных и разносторонних). Формально формула периметра записывается в следующем формате:
Метод 2:
В прямоугольных треугольниках мы можем вычислить периметр треугольника, когда нам известны только две стороны.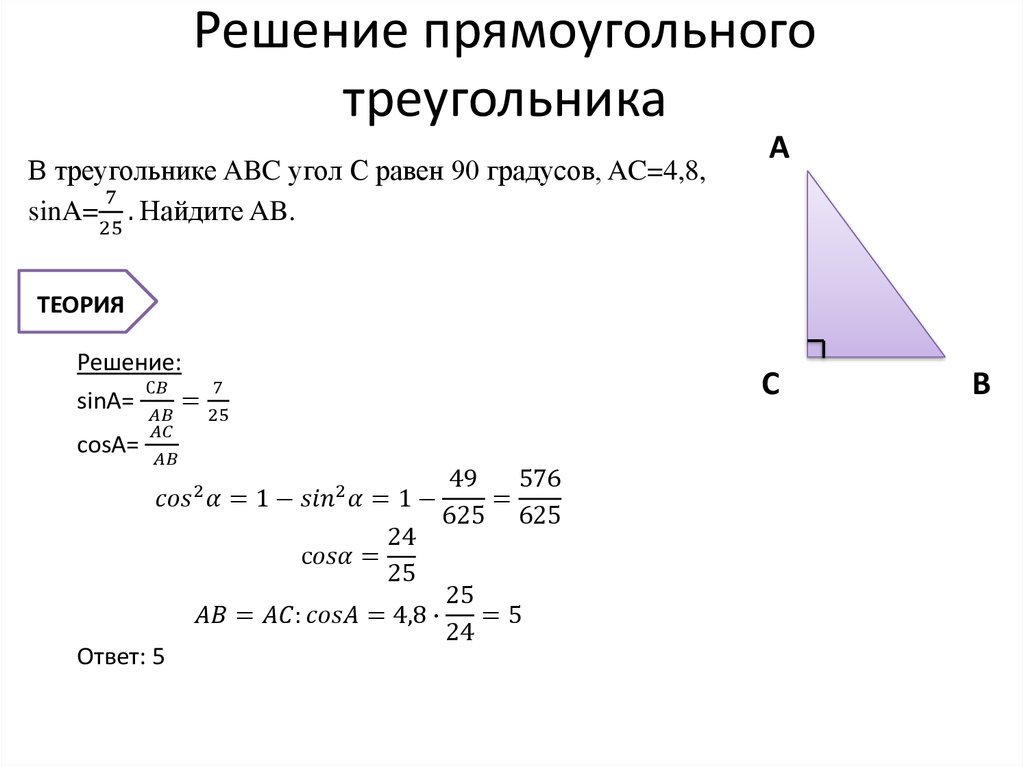
Если треугольник имеет такой формат, то мы можем использовать теорему Пифагора, чтобы найти любую отсутствующую сторону. Эта формула записывается следующим образом:
Мы можем переставить ее несколькими способами для решения каждой из сторон треугольника. Давайте перестроим его, чтобы найти гипотенузу, .
Переставьте и извлеките квадратный корень из обеих частей.
Упрощение.
Теперь давайте воспользуемся теоремой Пифагора, чтобы найти одну из ножек, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Наконец, давайте воспользуемся теоремой Пифагора, чтобы найти смежный отрезок, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Важно отметить, что мы можем использовать следующие формулы для определения недостающей стороны прямоугольного треугольника только тогда, когда известны две другие стороны: , мы можем использовать формулу периметра для вычисления периметра треугольника.
Метод 3:
Этот метод является наиболее сложным и может использоваться только тогда, когда мы знаем длины двух сторон треугольника, а также величину угла между ними. Когда мы знаем информацию о стороне и углу (SAS), мы можем использовать закон косинусов, чтобы найти недостающую сторону. Чтобы эта формула точно вычислила недостающую сторону, нам нужно пометить треугольник следующим образом:
Когда треугольник помечен таким образом, каждая сторона прямо соответствует углу, прямо противоположному ей. Если мы тщательно разметим наш треугольник, то мы можем использовать следующие формулы, чтобы найти недостающие стороны в любом треугольнике с учетом информации SAS:
корень обеих сторон, чтобы получить окончательную длину недостающей стороны. Наконец, нам нужно использовать формулу периметра, чтобы получить расстояние длин сторон многоугольника.
Решение:
Теперь, когда мы обсудили три метода, используемые для вычисления периметра треугольника, мы можем использовать эту информацию для решения задачи.
Во-первых, нам нужно использовать теорему Пифагора, чтобы найти .
Поскольку мы имеем дело с треугольником, единственное верное решение – это отсутствие отрицательных значений.
После того, как вы нашли , подключите его, чтобы найти периметр. Не забудьте упростить все квадратные корни!
Сообщить об ошибке
Найдите периметр треугольника ниже.
Возможные ответы:
Правильный ответ:
Объяснение:
Для нахождения периметра прямоугольного треугольника используются три основных метода.
- Когда указаны длины сторон, сложите их вместе.
- Найдите недостающую сторону по теореме Пифагора.
- Если мы знаем информацию о стороне и углу, найдите недостающую сторону, используя закон косинусов.
Метод 1:
Этот метод покажет вам, как вычислить периметр треугольника, когда известны длины всех сторон. Рассмотрим следующий рисунок:
Если известны длины сторон , , и , то мы можем просто сложить их вместе, чтобы найти периметр треугольника. Важно отметить несколько вещей. Во-первых, нам нужно убедиться, что все заданные единицы совпадают друг с другом. Во-вторых, когда известны длины всех сторон, формулу периметра можно использовать для всех типов треугольников (например, прямоугольных, остроугольных, тупоугольных, равносторонних, равнобедренных и разносторонних). Формально формула периметра записывается в следующем формате:
Метод 2:
В прямоугольных треугольниках мы можем вычислить периметр треугольника, когда нам известны только две стороны. Мы можем сделать это, используя теорему Пифагора. Давайте сначала обсудим прямоугольные треугольники в общем смысле. Прямоугольный треугольник — это треугольник, у которого есть один угол. Это особый треугольник, и его необходимо пометить соответствующим образом. Катеты треугольника образуют угол и обозначены буквами и . Сторона треугольника, противоположная углу и соединяющая два катета, называется гипотенузой. Гипотенуза — самая длинная сторона треугольника, обозначенная как .
Если треугольник имеет такой формат, то мы можем использовать теорему Пифагора, чтобы найти любую отсутствующую сторону. Эта формула записывается следующим образом:
Мы можем переставить ее несколькими способами для решения каждой из сторон треугольника. Давайте перестроим его, чтобы найти гипотенузу, .
Переставьте и извлеките квадратный корень из обеих частей.
Упрощение.
Теперь давайте воспользуемся теоремой Пифагора, чтобы найти одну из ножек, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Наконец, давайте воспользуемся теоремой Пифагора, чтобы найти смежный отрезок, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Важно отметить, что мы можем использовать следующие формулы для определения недостающей стороны прямоугольного треугольника только тогда, когда известны две другие стороны: , мы можем использовать формулу периметра для вычисления периметра треугольника.
Метод 3:
Этот метод является наиболее сложным и может использоваться только тогда, когда мы знаем длины двух сторон треугольника, а также величину угла между ними. Когда мы знаем информацию о стороне и углу (SAS), мы можем использовать закон косинусов, чтобы найти недостающую сторону. Чтобы эта формула точно вычислила недостающую сторону, нам нужно пометить треугольник следующим образом:
Когда треугольник помечен таким образом, каждая сторона прямо соответствует углу, прямо противоположному ей. Если мы тщательно разметим наш треугольник, то мы можем использовать следующие формулы, чтобы найти недостающие стороны в любом треугольнике с учетом информации SAS:
корень обеих сторон, чтобы получить окончательную длину недостающей стороны. Наконец, нам нужно использовать формулу периметра, чтобы получить расстояние длин сторон многоугольника.
Решение:
Теперь, когда мы обсудили три метода, используемые для вычисления периметра треугольника, мы можем использовать эту информацию для решения задачи. Периметр треугольника — это просто сумма трех его сторон. Наша проблема в том, что мы знаем только две стороны. Ключевым моментом для нас является тот факт, что у нас есть прямоугольный треугольник (на что указывает квадратик в одном из углов). Знание двух сторон прямоугольного треугольника и потребность в третьей — классический случай использования теоремы Пифагора. Проще говоря (вроде как), теорема Пифагора говорит, что сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины его гипотенузы.
Каждый прямоугольный треугольник имеет три стороны и прямой угол. Сторона напротив прямого угла (также самая длинная) называется гипотенузой. Каждая из двух других сторон называется ногами. Это означает, что в нашем треугольнике сторона с длиной 17 является гипотенузой, а сторона с длиной 8 и та, которую нам нужно найти, являются катетами.
Теорема Пифагора говорит нам, что если мы возведем в квадрат длины наших двух катетов и сложим эти два числа вместе, мы получим то же число, что и при возведении в квадрат длины нашей гипотенузы. Поскольку нам неизвестна длина второй ноги, мы можем идентифицировать ее с помощью переменной .
Это позволяет составить следующее алгебраическое уравнение:
, которое в упрощенном виде становится
Чтобы решить это уравнение, нам сначала нужно получить переменную саму по себе, что можно сделать, вычитая 64 из обеих частей, что дает us
Отсюда мы просто извлекаем квадратный корень из обеих частей.
Технически это также будет квадратным корнем из 225, но поскольку длина стороны треугольника может быть только положительной, мы ограничимся ответом 15.
Но мы еще не закончили. Теперь мы знаем длину недостающей стороны, но нам все еще нужно сложить длины трех сторон, чтобы найти периметр.
Наш ответ: 40.
Сообщить об ошибке
Учитывая, что две стороны прямоугольного треугольника равны и , а гипотенуза неизвестна, найдите периметр треугольника.
Возможные ответы:
Правильный ответ:
Объяснение:
Существует три основных метода нахождения периметра прямоугольного треугольника.
- Когда указаны длины сторон, сложите их вместе.
- Найдите недостающую сторону по теореме Пифагора.
- Если мы знаем информацию о стороне и углу, найдите недостающую сторону, используя закон косинусов.
Метод 1:
Этот метод покажет вам, как вычислить периметр треугольника, когда известны длины всех сторон. Рассмотрим следующий рисунок:
Если мы знаем длины сторон , и , то мы можем просто сложить их вместе, чтобы найти периметр треугольника. Важно отметить несколько вещей. Во-первых, нам нужно убедиться, что все заданные единицы совпадают друг с другом. Во-вторых, когда известны длины всех сторон, формулу периметра можно использовать для всех типов треугольников (например, прямоугольных, остроугольных, тупоугольных, равносторонних, равнобедренных и разносторонних). Формально формула периметра записывается в следующем формате:
Метод 2:
В прямоугольных треугольниках мы можем вычислить периметр треугольника, когда нам известны только две стороны. Мы можем сделать это, используя теорему Пифагора. Давайте сначала обсудим прямоугольные треугольники в общем смысле. Прямоугольный треугольник — это треугольник, у которого есть один угол. Это особый треугольник, и его необходимо пометить соответствующим образом. Катеты треугольника образуют угол и обозначены буквами и . Сторона треугольника, противоположная углу и соединяющая два катета, называется гипотенузой. Гипотенуза — самая длинная сторона треугольника, обозначенная как .
Если треугольник имеет такой формат, то мы можем использовать теорему Пифагора, чтобы найти любую отсутствующую сторону. Эта формула записывается следующим образом:
Мы можем переставить ее несколькими способами для решения каждой из сторон треугольника. Давайте перестроим его, чтобы найти гипотенузу, .
Переставьте и извлеките квадратный корень из обеих частей.
Упрощение.
Теперь давайте воспользуемся теоремой Пифагора, чтобы найти одну из ножек, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Наконец, давайте воспользуемся теоремой Пифагора, чтобы найти смежный отрезок, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Важно отметить, что мы можем использовать следующие формулы для определения недостающей стороны прямоугольного треугольника только тогда, когда известны две другие стороны: , мы можем использовать формулу периметра для вычисления периметра треугольника.
Метод 3:
Этот метод является наиболее сложным и может использоваться только тогда, когда мы знаем длины двух сторон треугольника, а также величину угла между ними. Когда мы знаем информацию о стороне и углу (SAS), мы можем использовать закон косинусов, чтобы найти недостающую сторону. Чтобы эта формула точно вычислила недостающую сторону, нам нужно пометить треугольник следующим образом:
Когда треугольник помечен таким образом, каждая сторона прямо соответствует углу, прямо противоположному ей. Если мы тщательно разметим наш треугольник, то мы можем использовать следующие формулы, чтобы найти недостающие стороны в любом треугольнике с учетом информации SAS:
корень обеих сторон, чтобы получить окончательную длину недостающей стороны. Наконец, нам нужно использовать формулу периметра, чтобы получить расстояние длин сторон многоугольника.
Решение:
Теперь, когда мы обсудили три метода, используемые для вычисления периметра треугольника, мы можем использовать эту информацию для решения задачи.
Чтобы вычислить периметр, нам нужно найти длину гипотенузы, используя теорему Пифагора.
Переставить.
Подставьте известные значения.
Теперь, когда мы нашли недостающую сторону, мы можем подставить значения в формулу периметра и решить.
Сообщить об ошибке
Найти периметр.
Возможные ответы:
Правильный ответ:
Объяснение:
Для нахождения периметра прямоугольного треугольника используются три основных метода.
- Когда указаны длины сторон, сложите их вместе.
- Найдите недостающую сторону по теореме Пифагора.
- Если мы знаем информацию о стороне и углу, найдите недостающую сторону, используя закон косинусов.
Метод 1:
Этот метод покажет вам, как вычислить периметр треугольника, когда известны длины всех сторон. Рассмотрим следующий рисунок:
Если известны длины сторон , , и , то мы можем просто сложить их вместе, чтобы найти периметр треугольника. Важно отметить несколько вещей. Во-первых, нам нужно убедиться, что все заданные единицы совпадают друг с другом. Во-вторых, когда известны длины всех сторон, формулу периметра можно использовать для всех типов треугольников (например, прямоугольных, остроугольных, тупоугольных, равносторонних, равнобедренных и разносторонних). Формально формула периметра записывается в следующем формате:
Метод 2:
В прямоугольных треугольниках мы можем вычислить периметр треугольника, когда нам известны только две стороны. Мы можем сделать это, используя теорему Пифагора. Давайте сначала обсудим прямоугольные треугольники в общем смысле. Прямоугольный треугольник — это треугольник, у которого есть один угол. Это особый треугольник, и его необходимо пометить соответствующим образом. Катеты треугольника образуют угол и обозначены буквами и . Сторона треугольника, противоположная углу и соединяющая два катета, называется гипотенузой. Гипотенуза — самая длинная сторона треугольника, обозначенная как .
Если треугольник имеет такой формат, то мы можем использовать теорему Пифагора, чтобы найти любую отсутствующую сторону. Эта формула записывается следующим образом:
Мы можем переставить ее несколькими способами для решения каждой из сторон треугольника. Давайте перестроим его, чтобы найти гипотенузу, .
Переставьте и извлеките квадратный корень из обеих частей.
Упрощение.
Теперь давайте воспользуемся теоремой Пифагора, чтобы найти одну из ножек, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Наконец, давайте воспользуемся теоремой Пифагора, чтобы найти смежный отрезок, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Важно отметить, что мы можем использовать следующие формулы для определения недостающей стороны прямоугольного треугольника только тогда, когда известны две другие стороны: , мы можем использовать формулу периметра для вычисления периметра треугольника.
Метод 3:
Этот метод является наиболее сложным и может использоваться только тогда, когда мы знаем длины двух сторон треугольника, а также величину угла между ними. Когда мы знаем информацию о стороне и углу (SAS), мы можем использовать закон косинусов, чтобы найти недостающую сторону. Чтобы эта формула точно вычислила недостающую сторону, нам нужно пометить треугольник следующим образом:
Когда треугольник помечен таким образом, каждая сторона прямо соответствует углу, прямо противоположному ей. Если мы тщательно разметим наш треугольник, то мы можем использовать следующие формулы, чтобы найти недостающие стороны в любом треугольнике с учетом информации SAS:
корень обеих сторон, чтобы получить окончательную длину недостающей стороны. Наконец, нам нужно использовать формулу периметра, чтобы получить расстояние длин сторон многоугольника.
Решение:
Теперь, когда мы обсудили три метода, используемые для вычисления периметра треугольника, мы можем использовать эту информацию для решения задачи.
Вспомним, как найти периметр треугольника:
Данному треугольнику нужна одна из трех сторон. Используя теорему Пифагора, найдите длину третьей стороны.
Вспомним теорему Пифагора:
Так как мы находим длину стороны, перепишем уравнение.
Подставьте значения и .
Теперь подставьте все три значения в уравнение, чтобы найти периметр. Воспользуйтесь калькулятором и округлите до десятичных знаков.
Сообщить об ошибке
Найти периметр.
Возможные ответы:
Правильный ответ:
Объяснение:
Для нахождения периметра прямоугольного треугольника используются три основных метода.
- Когда указаны длины сторон, сложите их вместе.
- Найдите недостающую сторону по теореме Пифагора.
- Если мы знаем информацию о стороне и углу, найдите недостающую сторону, используя закон косинусов.
Метод 1:
Этот метод покажет вам, как вычислить периметр треугольника, когда известны длины всех сторон. Рассмотрим следующий рисунок:
Если известны длины сторон , , и , то мы можем просто сложить их вместе, чтобы найти периметр треугольника. Важно отметить несколько вещей. Во-первых, нам нужно убедиться, что все заданные единицы совпадают друг с другом. Во-вторых, когда известны длины всех сторон, формулу периметра можно использовать для всех типов треугольников (например, прямоугольных, остроугольных, тупоугольных, равносторонних, равнобедренных и разносторонних). Формально формула периметра записывается в следующем формате:
Метод 2:
В прямоугольных треугольниках мы можем вычислить периметр треугольника, когда нам известны только две стороны. Мы можем сделать это, используя теорему Пифагора. Давайте сначала обсудим прямоугольные треугольники в общем смысле. Прямоугольный треугольник — это треугольник, у которого есть один угол. Это особый треугольник, и его необходимо пометить соответствующим образом. Катеты треугольника образуют угол и обозначены буквами и . Сторона треугольника, противоположная углу и соединяющая два катета, называется гипотенузой. Гипотенуза — самая длинная сторона треугольника, обозначенная как .
Если треугольник имеет такой формат, то мы можем использовать теорему Пифагора, чтобы найти любую отсутствующую сторону. Эта формула записывается следующим образом:
Мы можем переставить ее несколькими способами для решения каждой из сторон треугольника. Давайте перестроим его, чтобы найти гипотенузу, .
Переставьте и извлеките квадратный корень из обеих частей.
Упрощение.
Теперь давайте воспользуемся теоремой Пифагора, чтобы найти одну из ножек, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Наконец, давайте воспользуемся теоремой Пифагора, чтобы найти смежный отрезок, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Важно отметить, что мы можем использовать следующие формулы для определения недостающей стороны прямоугольного треугольника только тогда, когда известны две другие стороны: , мы можем использовать формулу периметра для вычисления периметра треугольника.
Метод 3:
Этот метод является наиболее сложным и может использоваться только тогда, когда мы знаем длины двух сторон треугольника, а также величину угла между ними. Когда мы знаем информацию о стороне и углу (SAS), мы можем использовать закон косинусов, чтобы найти недостающую сторону. Чтобы эта формула точно вычислила недостающую сторону, нам нужно пометить треугольник следующим образом:
Когда треугольник помечен таким образом, каждая сторона прямо соответствует углу, прямо противоположному ей. Если мы тщательно разметим наш треугольник, то мы можем использовать следующие формулы, чтобы найти недостающие стороны в любом треугольнике с учетом информации SAS:
корень обеих сторон, чтобы получить окончательную длину недостающей стороны. Наконец, нам нужно использовать формулу периметра, чтобы получить расстояние длин сторон многоугольника.
Решение:
Теперь, когда мы обсудили три метода, используемые для вычисления периметра треугольника, мы можем использовать эту информацию для решения задачи.
Вспомним, как найти периметр треугольника:
Данному треугольнику нужна одна из трех сторон. Используя теорему Пифагора, найдите длину третьей стороны.
Вспомним теорему Пифагора:
Так как мы находим длину стороны, перепишем уравнение.
Подставьте значения и .
Теперь подставьте все три значения в уравнение, чтобы найти периметр. Воспользуйтесь калькулятором и округлите до десятичных знаков.
Сообщить об ошибке
Найти периметр.
Возможные ответы:
Правильный ответ:
Объяснение:
Для нахождения периметра прямоугольного треугольника используются три основных метода.
- Когда указаны длины сторон, сложите их вместе.
- Найдите недостающую сторону по теореме Пифагора.
- Если мы знаем информацию о стороне и углу, найдите недостающую сторону, используя закон косинусов.
Метод 1:
Этот метод покажет вам, как вычислить периметр треугольника, когда известны длины всех сторон. Рассмотрим следующий рисунок:
Если известны длины сторон , , и , то мы можем просто сложить их вместе, чтобы найти периметр треугольника. Важно отметить несколько вещей. Во-первых, нам нужно убедиться, что все заданные единицы совпадают друг с другом. Во-вторых, когда известны длины всех сторон, формулу периметра можно использовать для всех типов треугольников (например, прямоугольных, остроугольных, тупоугольных, равносторонних, равнобедренных и разносторонних). Формально формула периметра записывается в следующем формате:
Метод 2:
В прямоугольных треугольниках мы можем вычислить периметр треугольника, когда нам известны только две стороны. Мы можем сделать это, используя теорему Пифагора. Давайте сначала обсудим прямоугольные треугольники в общем смысле. Прямоугольный треугольник — это треугольник, у которого есть один угол. Это особый треугольник, и его необходимо пометить соответствующим образом. Катеты треугольника образуют угол и обозначены буквами и . Сторона треугольника, противоположная углу и соединяющая два катета, называется гипотенузой. Гипотенуза — самая длинная сторона треугольника, обозначенная как .
Если треугольник имеет такой формат, то мы можем использовать теорему Пифагора, чтобы найти любую отсутствующую сторону. Эта формула записывается следующим образом:
Мы можем переставить ее несколькими способами для решения каждой из сторон треугольника. Давайте перестроим его, чтобы найти гипотенузу, .
Переставьте и извлеките квадратный корень из обеих частей.
Упрощение.
Теперь давайте воспользуемся теоремой Пифагора, чтобы найти одну из ножек, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Наконец, давайте воспользуемся теоремой Пифагора, чтобы найти смежный отрезок, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Важно отметить, что мы можем использовать следующие формулы для определения недостающей стороны прямоугольного треугольника только тогда, когда известны две другие стороны: , мы можем использовать формулу периметра для вычисления периметра треугольника.
Метод 3:
Этот метод является наиболее сложным и может использоваться только тогда, когда мы знаем длины двух сторон треугольника, а также величину угла между ними. Когда мы знаем информацию о стороне и углу (SAS), мы можем использовать закон косинусов, чтобы найти недостающую сторону. Чтобы эта формула точно вычислила недостающую сторону, нам нужно пометить треугольник следующим образом:
Когда треугольник помечен таким образом, каждая сторона прямо соответствует углу, прямо противоположному ей. Если мы тщательно разметим наш треугольник, то мы можем использовать следующие формулы, чтобы найти недостающие стороны в любом треугольнике с учетом информации SAS:
корень обеих сторон, чтобы получить окончательную длину недостающей стороны. Наконец, нам нужно использовать формулу периметра, чтобы получить расстояние длин сторон многоугольника.
Решение:
Теперь, когда мы обсудили три метода, используемые для вычисления периметра треугольника, мы можем использовать эту информацию для решения задачи.
Вспомним, как найти периметр треугольника:
Данному треугольнику нужна одна из трех сторон. Используя теорему Пифагора, найдите длину третьей стороны.
Вспомним теорему Пифагора:
Так как мы находим длину стороны, перепишем уравнение.
Подставьте значения и .
Теперь подставьте все три значения в уравнение, чтобы найти периметр. Воспользуйтесь калькулятором и округлите до десятичных знаков.
Сообщить об ошибке
Найти периметр.
Возможные ответы:
Правильный ответ:
Объяснение:
Для нахождения периметра прямоугольного треугольника используются три основных метода.
- Когда указаны длины сторон, сложите их вместе.
- Найдите недостающую сторону по теореме Пифагора.
- Если мы знаем информацию о стороне и углу, найдите недостающую сторону, используя закон косинусов.
Метод 1:
Этот метод покажет вам, как вычислить периметр треугольника, когда известны длины всех сторон. Рассмотрим следующий рисунок:
Если известны длины сторон , , и , то мы можем просто сложить их вместе, чтобы найти периметр треугольника. Важно отметить несколько вещей. Во-первых, нам нужно убедиться, что все заданные единицы совпадают друг с другом. Во-вторых, когда известны длины всех сторон, формулу периметра можно использовать для всех типов треугольников (например, прямоугольных, остроугольных, тупоугольных, равносторонних, равнобедренных и разносторонних). Формально формула периметра записывается в следующем формате:
Метод 2:
В прямоугольных треугольниках мы можем вычислить периметр треугольника, когда нам известны только две стороны. Мы можем сделать это, используя теорему Пифагора. Давайте сначала обсудим прямоугольные треугольники в общем смысле. Прямоугольный треугольник — это треугольник, у которого есть один угол. Это особый треугольник, и его необходимо пометить соответствующим образом. Катеты треугольника образуют угол и обозначены буквами и . Сторона треугольника, противоположная углу и соединяющая два катета, называется гипотенузой. Гипотенуза — самая длинная сторона треугольника, обозначенная как .
Если треугольник имеет такой формат, то мы можем использовать теорему Пифагора, чтобы найти любую отсутствующую сторону. Эта формула записывается следующим образом:
Мы можем переставить ее несколькими способами для решения каждой из сторон треугольника. Давайте перестроим его, чтобы найти гипотенузу, .
Переставьте и извлеките квадратный корень из обеих частей.
Упрощение.
Теперь давайте воспользуемся теоремой Пифагора, чтобы найти одну из ножек, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Наконец, давайте воспользуемся теоремой Пифагора, чтобы найти смежный отрезок, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Важно отметить, что мы можем использовать следующие формулы для определения недостающей стороны прямоугольного треугольника только тогда, когда известны две другие стороны: , мы можем использовать формулу периметра для вычисления периметра треугольника.
Метод 3:
Этот метод является наиболее сложным и может использоваться только тогда, когда мы знаем длины двух сторон треугольника, а также величину угла между ними. Когда мы знаем информацию о стороне и углу (SAS), мы можем использовать закон косинусов, чтобы найти недостающую сторону. Чтобы эта формула точно вычислила недостающую сторону, нам нужно пометить треугольник следующим образом:
Когда треугольник помечен таким образом, каждая сторона прямо соответствует углу, прямо противоположному ей. Если мы тщательно разметим наш треугольник, то мы можем использовать следующие формулы, чтобы найти недостающие стороны в любом треугольнике с учетом информации SAS:
корень обеих сторон, чтобы получить окончательную длину недостающей стороны. Наконец, нам нужно использовать формулу периметра, чтобы получить расстояние длин сторон многоугольника.
Решение:
Теперь, когда мы обсудили три метода, используемые для вычисления периметра треугольника, мы можем использовать эту информацию для решения задачи.
Вспомним, как найти периметр треугольника:
Данному треугольнику нужна одна из трех сторон. Используя теорему Пифагора, найдите длину третьей стороны.
Вспомним теорему Пифагора:
Так как мы находим длину стороны, перепишем уравнение.
Подставьте значения и .
Теперь подставьте все три значения в уравнение, чтобы найти периметр. Воспользуйтесь калькулятором и округлите до десятичных знаков.
Сообщить об ошибке
Найти периметр.
Возможные ответы:
Правильный ответ:
Объяснение:
Для нахождения периметра прямоугольного треугольника используются три основных метода.
- Когда указаны длины сторон, сложите их вместе.
- Найдите недостающую сторону по теореме Пифагора.
- Если мы знаем информацию о стороне и углу, найдите недостающую сторону, используя закон косинусов.
Метод 1:
Этот метод покажет вам, как вычислить периметр треугольника, когда известны длины всех сторон. Рассмотрим следующий рисунок:
Если известны длины сторон , , и , то мы можем просто сложить их вместе, чтобы найти периметр треугольника. Важно отметить несколько вещей. Во-первых, нам нужно убедиться, что все заданные единицы совпадают друг с другом. Во-вторых, когда известны длины всех сторон, формулу периметра можно использовать для всех типов треугольников (например, прямоугольных, остроугольных, тупоугольных, равносторонних, равнобедренных и разносторонних). Формально формула периметра записывается в следующем формате:
Метод 2:
В прямоугольных треугольниках мы можем вычислить периметр треугольника, когда нам известны только две стороны. Мы можем сделать это, используя теорему Пифагора. Давайте сначала обсудим прямоугольные треугольники в общем смысле. Прямоугольный треугольник — это треугольник, у которого есть один угол. Это особый треугольник, и его необходимо пометить соответствующим образом. Катеты треугольника образуют угол и обозначены буквами и . Сторона треугольника, противоположная углу и соединяющая два катета, называется гипотенузой. Гипотенуза — самая длинная сторона треугольника, обозначенная как .
Если треугольник имеет такой формат, то мы можем использовать теорему Пифагора, чтобы найти любую отсутствующую сторону. Эта формула записывается следующим образом:
Мы можем переставить ее несколькими способами для решения каждой из сторон треугольника. Давайте перестроим его, чтобы найти гипотенузу, .
Переставьте и извлеките квадратный корень из обеих частей.
Упрощение.
Теперь давайте воспользуемся теоремой Пифагора, чтобы найти одну из ножек, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Наконец, давайте воспользуемся теоремой Пифагора, чтобы найти смежный отрезок, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Важно отметить, что мы можем использовать следующие формулы для определения недостающей стороны прямоугольного треугольника только тогда, когда известны две другие стороны: , мы можем использовать формулу периметра для вычисления периметра треугольника.
Метод 3:
Этот метод является наиболее сложным и может использоваться только тогда, когда мы знаем длины двух сторон треугольника, а также величину угла между ними. Когда мы знаем информацию о стороне и углу (SAS), мы можем использовать закон косинусов, чтобы найти недостающую сторону. Чтобы эта формула точно вычислила недостающую сторону, нам нужно пометить треугольник следующим образом:
Когда треугольник помечен таким образом, каждая сторона прямо соответствует углу, прямо противоположному ей. Если мы тщательно разметим наш треугольник, то мы можем использовать следующие формулы, чтобы найти недостающие стороны в любом треугольнике с учетом информации SAS:
корень обеих сторон, чтобы получить окончательную длину недостающей стороны. Наконец, нам нужно использовать формулу периметра, чтобы получить расстояние длин сторон многоугольника.
Решение:
Теперь, когда мы обсудили три метода, используемые для вычисления периметра треугольника, мы можем использовать эту информацию для решения задачи.
Вспомним, как найти периметр треугольника:
Данному треугольнику нужна одна из трех сторон. Используя теорему Пифагора, найдите длину третьей стороны.
Вспомним теорему Пифагора:
Так как мы находим длину стороны, перепишем уравнение.
Подставьте значения и .
Теперь подставьте все три значения в уравнение, чтобы найти периметр. Воспользуйтесь калькулятором и округлите до десятичных знаков.
Сообщить об ошибке
Найти периметр.
Возможные ответы:
Правильный ответ:
Объяснение:
Для нахождения периметра прямоугольного треугольника используются три основных метода.
- Когда указаны длины сторон, сложите их вместе.
- Найдите недостающую сторону по теореме Пифагора.
- Если мы знаем информацию о стороне и углу, найдите недостающую сторону, используя закон косинусов.
Метод 1:
Этот метод покажет вам, как вычислить периметр треугольника, когда известны длины всех сторон. Рассмотрим следующий рисунок:
Если известны длины сторон , , и , то мы можем просто сложить их вместе, чтобы найти периметр треугольника. Важно отметить несколько вещей. Во-первых, нам нужно убедиться, что все заданные единицы совпадают друг с другом. Во-вторых, когда известны длины всех сторон, формулу периметра можно использовать для всех типов треугольников (например, прямоугольных, остроугольных, тупоугольных, равносторонних, равнобедренных и разносторонних). Формально формула периметра записывается в следующем формате:
Метод 2:
В прямоугольных треугольниках мы можем вычислить периметр треугольника, когда нам известны только две стороны. Мы можем сделать это, используя теорему Пифагора. Давайте сначала обсудим прямоугольные треугольники в общем смысле. Прямоугольный треугольник — это треугольник, у которого есть один угол. Это особый треугольник, и его необходимо пометить соответствующим образом. Катеты треугольника образуют угол и обозначены буквами и . Сторона треугольника, противоположная углу и соединяющая два катета, называется гипотенузой. Гипотенуза — самая длинная сторона треугольника, обозначенная как .
Если треугольник имеет такой формат, то мы можем использовать теорему Пифагора, чтобы найти любую отсутствующую сторону. Эта формула записывается следующим образом:
Мы можем переставить ее несколькими способами для решения каждой из сторон треугольника. Давайте перестроим его, чтобы найти гипотенузу, .
Переставьте и извлеките квадратный корень из обеих частей.
Упрощение.
Теперь давайте воспользуемся теоремой Пифагора, чтобы найти одну из ножек, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Наконец, давайте воспользуемся теоремой Пифагора, чтобы найти смежный отрезок, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Важно отметить, что мы можем использовать следующие формулы для определения недостающей стороны прямоугольного треугольника только тогда, когда известны две другие стороны: , мы можем использовать формулу периметра для вычисления периметра треугольника.
Метод 3:
Этот метод является наиболее сложным и может использоваться только тогда, когда мы знаем длины двух сторон треугольника, а также величину угла между ними. Когда мы знаем информацию о стороне и углу (SAS), мы можем использовать закон косинусов, чтобы найти недостающую сторону. Чтобы эта формула точно вычислила недостающую сторону, нам нужно пометить треугольник следующим образом:
Когда треугольник помечен таким образом, каждая сторона прямо соответствует углу, прямо противоположному ей. Если мы тщательно разметим наш треугольник, то мы можем использовать следующие формулы, чтобы найти недостающие стороны в любом треугольнике с учетом информации SAS:
корень обеих сторон, чтобы получить окончательную длину недостающей стороны. Наконец, нам нужно использовать формулу периметра, чтобы получить расстояние длин сторон многоугольника.
Решение:
Теперь, когда мы обсудили три метода, используемые для вычисления периметра треугольника, мы можем использовать эту информацию для решения задачи.
Вспомним, как найти периметр треугольника:
Данному треугольнику нужна одна из трех сторон. Используя теорему Пифагора, найдите длину третьей стороны.
Вспомним теорему Пифагора:
Так как мы находим длину стороны, перепишем уравнение.
Подставьте значения и .
Теперь подставьте все три значения в уравнение, чтобы найти периметр. Воспользуйтесь калькулятором и округлите до десятичных знаков.
Сообщить об ошибке
Найти периметр.
Возможные ответы:
Правильный ответ:
Объяснение:
Для нахождения периметра прямоугольного треугольника используются три основных метода.
- Когда указаны длины сторон, сложите их вместе.
- Найдите недостающую сторону по теореме Пифагора.
- Если мы знаем информацию о стороне и углу, найдите недостающую сторону, используя закон косинусов.
Метод 1:
Этот метод покажет вам, как вычислить периметр треугольника, когда известны длины всех сторон. Рассмотрим следующий рисунок:
Если известны длины сторон , , и , то мы можем просто сложить их вместе, чтобы найти периметр треугольника. Важно отметить несколько вещей. Во-первых, нам нужно убедиться, что все заданные единицы совпадают друг с другом. Во-вторых, когда известны длины всех сторон, формулу периметра можно использовать для всех типов треугольников (например, прямоугольных, остроугольных, тупоугольных, равносторонних, равнобедренных и разносторонних). Формально формула периметра записывается в следующем формате:
Метод 2:
В прямоугольных треугольниках мы можем вычислить периметр треугольника, когда нам известны только две стороны. Мы можем сделать это, используя теорему Пифагора. Давайте сначала обсудим прямоугольные треугольники в общем смысле. Прямоугольный треугольник — это треугольник, у которого есть один угол. Это особый треугольник, и его необходимо пометить соответствующим образом. Катеты треугольника образуют угол и обозначены буквами и . Сторона треугольника, противоположная углу и соединяющая два катета, называется гипотенузой. Гипотенуза — самая длинная сторона треугольника, обозначенная как .
Если треугольник имеет такой формат, то мы можем использовать теорему Пифагора, чтобы найти любую отсутствующую сторону. Эта формула записывается следующим образом:
Мы можем переставить ее несколькими способами для решения каждой из сторон треугольника. Давайте перестроим его, чтобы найти гипотенузу, .
Переставьте и извлеките квадратный корень из обеих частей.
Упрощение.
Теперь давайте воспользуемся теоремой Пифагора, чтобы найти одну из ножек, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Наконец, давайте воспользуемся теоремой Пифагора, чтобы найти смежный отрезок, .
Вычтите из обеих частей уравнения.
Извлеките квадратный корень из обеих сторон.
Упрощение.
Важно отметить, что мы можем использовать следующие формулы для определения недостающей стороны прямоугольного треугольника только тогда, когда известны две другие стороны: , мы можем использовать формулу периметра для вычисления периметра треугольника.
Метод 3:
Этот метод является наиболее сложным и может использоваться только тогда, когда мы знаем длины двух сторон треугольника, а также величину угла между ними. Когда мы знаем информацию о стороне и углу (SAS), мы можем использовать закон косинусов, чтобы найти недостающую сторону. Чтобы эта формула точно вычислила недостающую сторону, нам нужно пометить треугольник следующим образом:
Когда треугольник помечен таким образом, каждая сторона прямо соответствует углу, прямо противоположному ей. Если мы тщательно разметим наш треугольник, то мы можем использовать следующие формулы, чтобы найти недостающие стороны в любом треугольнике с учетом информации SAS:
корень обеих сторон, чтобы получить окончательную длину недостающей стороны. Наконец, нам нужно использовать формулу периметра, чтобы получить расстояние длин сторон многоугольника.
Решение:
Теперь, когда мы обсудили три метода, используемые для вычисления периметра треугольника, мы можем использовать эту информацию для решения задачи.
Вспомним, как найти периметр треугольника:
Данному треугольнику нужна одна из трех сторон. Используя теорему Пифагора, найдите длину третьей стороны.
Вспомним теорему Пифагора:
Так как мы находим длину стороны, перепишем уравнение.
Подставьте значения и .
Теперь подставьте все три значения в уравнение, чтобы найти периметр. Воспользуйтесь калькулятором и округлите до десятичных знаков.
Сообщить об ошибке
← Назад 1 2 3 4 5 6 Далее →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты
164 практических теста
Вопрос дня
Карточки
Учитесь по концепции
Простой справочник по треугольнику 30-60-90
Острый, тупоугольный, равнобедренный, равносторонний… Когда дело доходит до треугольников, существует множество их разновидностей, но лишь немногие являются «особенными». Эти специальные треугольники имеют стороны и углы, которые постоянны и предсказуемы, и их можно использовать для быстрого решения задач по геометрии или тригонометрии. И треугольник 30-60-90 — произносится как «тридцать шестьдесят девяносто» — действительно является очень особым типом треугольника.
В этом руководстве мы расскажем вам, что такое треугольник 30-60-90, почему он работает и когда (и как) использовать ваши знания о нем. Итак, приступим!
Что такое треугольник 30-60-90?
Треугольник 30-60-90 — это особый прямоугольный треугольник (прямоугольный треугольник — это любой треугольник, содержащий угол в 90 градусов), углы которого всегда равны 30, 60 и 90 градусов. Поскольку это особый треугольник, у него также есть значения длин сторон, которые всегда находятся в постоянном соотношении друг с другом.
Основное соотношение треугольника 30-60-90:
Сторона, противоположная углу 30°: $x$
Сторона, противоположная углу 60°: $x * √3$
Сторона, противоположная углу 90°: $2 x
Например, треугольник 30-60-90 градусов может иметь боковую длину:
2, 2√3, 4
7, 7√3, 14
√3, 3, 2√3
(Почему более длинная сторона равна 3? В этом треугольнике самая короткая сторона ($x$) равна $√3$, поэтому для более длинной стороны $x√ 3 = √3 * √3 = √9= 3$. А гипотенуза в 2 раза больше кратчайшего катета, или $2√3$)
И так далее.
Сторона, противоположная углу 30°, всегда является наименьшей , потому что 30 градусов — это наименьший угол. Сторона, противоположная углу 60°, будет средней длиной , потому что 60° — средний угол в градусах в этом треугольнике. И, наконец, сторона, противоположная углу 90°, всегда будет наибольшей стороной (гипотенуза) , потому что 90 градусов — это наибольший угол.
Хотя он может быть похож на другие типы прямоугольных треугольников, треугольник 30-60-90 настолько особенный, что вам нужно всего три элемента информации, чтобы найти все остальные измерения. Пока вы знаете значение двух углов и длины одной стороны (неважно, какой стороны), вы знаете все, что вам нужно знать о своем треугольнике.
Например, мы можем использовать формулу треугольника 30-60-90, чтобы заполнить все оставшиеся информационные пробелы треугольников ниже.
Пример 1
Мы видим, что это прямоугольный треугольник, в котором гипотенуза вдвое больше длины одного из катетов. Это означает, что это должен быть треугольник 30-60-90 и меньшая заданная сторона противоположна 30°.
Следовательно, более длинная сторона должна располагаться напротив угла 60° и иметь размер $6 * √3$, или $6√3$.
Пример 2
Мы можем видеть, что это должен быть треугольник 30-60-90, потому что мы видим, что это прямоугольный треугольник с одним заданным измерением, 30°. Тогда немаркированный угол должен быть равен 60°.
Так как 18 — это мера, противоположная углу 60°, она должна быть равна $x√3$. Тогда самая короткая нога должна быть равна $18/√3$.
(Обратите внимание, что длина ноги на самом деле будет $18/{√3} * {√3}/{√3} = {18√3}/3 = 6√3$, потому что знаменатель не может содержать радикальный/квадратный корень ).
А гипотенуза будет равна $2(18/√3)$
(Обратите внимание, что в знаменателе снова не может быть радикала, так что окончательный ответ действительно будет в 2 раза больше длины катета $6√3$ = > $12√3$).
Пример 3
Опять же, нам даны два измерения угла (90° и 60°), поэтому третье измерение будет равно 30°. Поскольку это треугольник 30-60-90, а гипотенуза равна 30, самый короткий катет будет равен 15, а более длинный катет будет равен 15√3.
Не нужно обращаться к волшебной восьмерке — эти правила всегда работают.
Почему это работает: 30-60-90 Доказательство теоремы о треугольнике
Но почему этот особый треугольник работает именно так? Откуда мы знаем, что эти правила законны? Давайте пройдемся по тому, как именно 30-60-9Теорема треугольника 0 работает и доказывает, почему эти длины сторон всегда будут постоянными.
Во-первых, давайте на секунду забудем о прямоугольных треугольниках и посмотрим на равносторонний треугольник .
Равносторонний треугольник — это треугольник, у которого все стороны равны и все углы равны. Поскольку сумма внутренних углов треугольника всегда равна 180°, а $180/3 = 60$, равносторонний треугольник всегда будет иметь три угла по 60°.
Теперь опустим высоту от самого верхнего угла к основанию треугольника.
Итак, мы создали два прямых угла и два конгруэнтных (равных) треугольника.
Откуда мы знаем, что это равные треугольники? Поскольку мы отбросили высоту от равностороннего треугольника 90 247 90 248, мы разделили основание ровно пополам. Новые треугольники также имеют одну общую длину стороны (высоту), и каждый из них имеет одинаковую длину гипотенузы. Поскольку они имеют три общие длины сторон (SSS), это означает, что треугольники конгруэнтны.
Примечание: два треугольника конгруэнтны не только на основе принципов длины стороны-стороны-стороны, или SSS, но также на основе мер стороны-угла-стороны (SAS), угла-угла-стороны (AAS) и угол-бок-угол (ASA). В принципе? Они определенно конгруэнтны.
Теперь, когда мы доказали конгруэнтность двух новых треугольников, мы можем видеть, что каждый верхний угол должен быть равен 30 градусам (поскольку каждый треугольник уже имеет углы 90° и 60° и должен в сумме составлять 180°). ). Это означает мы сделали два треугольника 30-60-90.
А поскольку мы знаем, что мы разрезаем основание равностороннего треугольника пополам, мы можем видеть, что сторона, противоположная углу в 30° (самая короткая сторона) каждого из наших треугольников 30-60-90, составляет ровно половину длины гипотенузы.
Итак, назовем исходную длину стороны $x$, а нашу длину, разделенную пополам, $x/2$.
Теперь все, что нам осталось сделать, это найти длину средней стороны двух треугольников. Для этого мы можем просто использовать теорему Пифагора. 92}/4$
$b = {√3x}/2$
Итак, у нас осталось: $x/2, {x√3}/2, x$
Теперь давайте умножим каждую меру на 2. , просто чтобы облегчить жизнь и избежать всех дробей. Таким образом, у нас остается:
$x$, $x√3$, $2x$
Таким образом, мы можем видеть, что треугольник 30-60-90 будет всегда иметь постоянную длину стороны $ x$, $x√3$ и $2x$ (или $x/2$, ${√3x}/2$ и $x$).
К счастью для нас, мы можем доказать 30-60-90 правил треугольника истинны без всего. .. этого.
Когда использовать правила треугольника 30-60-90
Знание правил треугольника 30-60-90 поможет вам сэкономить время и энергию при решении множества различных математических задач, а именно самых разнообразных геометрических и задачи по тригонометрии.
Геометрия
Правильное понимание треугольников 30-60-90 позволит вам решить вопросы геометрии, которые либо невозможно решить, не зная этих правил соотношения, либо, по крайней мере, потребуется значительное время и усилия для их решения. решить «длинный путь».
С помощью специальных соотношений треугольников вы можете определить отсутствующие высоты треугольников или длины катетов (без использования теоремы Пифагора), найти площадь треугольника, используя недостающую информацию о высоте или длине основания, и быстро вычислить периметры.
Каждый раз, когда вам нужно быстро ответить на вопрос, вам пригодится запоминание таких сокращений, как ваши правила 30-60-90.
Тригонометрия
Запоминание и понимание соотношения треугольников 30-60-90 также позволит вам решать многие задачи по тригонометрии без использования калькулятора или необходимости аппроксимировать ответы в десятичной форме.
Треугольник 30-60-90 имеет довольно простые синусы, косинусы и тангенсы для каждого угла (и эти измерения всегда будут согласованы).
Синус 30° всегда будет $1/2$.
Косинус 60° всегда равен $1/2$.
Хотя другие синусы, косинусы и тангенсы довольно просты, эти два проще всего запомнить, и они, скорее всего, появятся на тестах. Так что знание этих правил позволит вам найти эти тригонометрические измерения как можно быстрее.
Советы по запоминанию правил 30-60-90
Вы знаете, что эти правила соотношения 30-60-90 полезны, но как удержать информацию в голове? Чтобы запомнить правила треугольника 30-60-90, нужно помнить соотношение 1: √3 : 2 и знать, что самая короткая сторона всегда находится напротив самого короткого угла (30°), а самая длинная сторона всегда находится напротив угла. наибольший угол (90°).
Некоторые люди запоминают соотношение, думая: « $bi x$, $bo 2 bi x$, $bi x bo √ bo3$, «, потому что последовательность «1, 2, 3», как правило, легко запомнить. Единственная мера предосторожности при использовании этого метода состоит в том, чтобы помнить, что самая длинная сторона на самом деле равна $2x$, , а не $x$, умноженному на $√ 3$.
Еще один способ запомнить ваши пропорции — использовать мнемоническую игру слов с соотношением 1: корень 3: 2 в правильном порядке. «: один, корень три, два. (И это настоящий факт из истории бейсбола!)
Поэкспериментируйте со своими мнемоническими приемами, если они вас не устраивают, — спойте отношение к песне, найдите свои собственные фразы «один, корень три, два» или придумайте стихотворение с отношением. Вы даже можете просто вспомнить, что треугольник 30-60-90 — это половина равностороннего треугольника, и вычислить измерения оттуда, если вам не нравится их запоминать.
Однако вам имеет смысл запомнить эти правила 30-60-90, держите эти отношения в голове для будущих вопросов по геометрии и тригонометрии.
Запоминание — ваш друг, но вы можете его заставить.
Пример 30-60-90 Вопросы
Теперь, когда мы рассмотрели как и почему треугольники 30-60-90, давайте поработаем над некоторыми практическими задачами.
Геометрия
Строитель прислоняет 40-футовую лестницу к стене здания под углом 30 градусов от земли. Земля ровная, а сторона здания перпендикулярна земле. Как далеко вверх по зданию доходит лестница с точностью до ближайшего фута?
Не зная наших специальных правил треугольника 30-60-90, нам пришлось бы использовать тригонометрию и калькулятор, чтобы найти решение этой проблемы, поскольку у нас есть только одна сторона треугольника. Но поскольку мы знаем, что это особый треугольник , мы можем найти ответ за считанные секунды.
Если здание и земля перпендикулярны друг другу, это должно означать, что здание и земля образуют прямой (90°) угол. Также известно, что лестница касается земли под углом 30°. Таким образом, мы видим, что оставшийся угол должен быть равен 60°, что делает его равным 30-60-9.0 треугольник.
Теперь мы знаем, что гипотенуза (самая длинная сторона) этого числа 30-60-90 равна 40 футам, а это значит, что самая короткая сторона будет вдвое меньше. (Помните, что самая длинная сторона всегда в два раза — $2x$ — длиннее самой короткой стороны.) Поскольку самая короткая сторона находится напротив угла в 30°, а этот угол — градусная мера лестницы от земли, это означает, что верхняя часть лестницы ударяется о здание в 20 футах от земли.
Наш окончательный ответ: 20 футов.
Тригонометрия
Если в прямоугольном треугольнике sin Θ = $1/2$ и длина кратчайшего катета равна 8. Какова длина недостающей стороны, которая НЕ является гипотенузой?
Поскольку вы знаете правила 30-60-90, вы можете решить эту задачу, не прибегая ни к теореме Пифагора, ни к калькулятору.
Нам сказали, что это прямоугольный треугольник, а из наших специальных правил прямоугольного треугольника мы знаем, что синус 30° = $1/2$. Таким образом, недостающий угол должен составлять 60 градусов, что делает это 30-60-9.0 треугольник.
И поскольку это треугольник 30-60-90, и нам сказали, что самая короткая сторона равна 8, гипотенуза должна быть равна 16, а недостающая сторона должна быть равна $8 * √3$, или $8√3$.
Наш окончательный ответ 8√3.
Выводы
Запоминание правил для треугольников 30-60-90 поможет вам быстрее решать различные математические задачи . Но имейте в виду, что хотя знание этих правил и является удобным инструментом, который можно всегда носить на поясе, вы все же можете решить большинство проблем без них.
Следите за правилами $x$, $x√3$, $2x$ и 30-60-90 любым удобным для вас способом и старайтесь соблюдать их, если можете, но не паникуйте, если ваш разум отключается, когда наступает решающий момент. В любом случае, у вас есть это.
А если вам нужно больше практики, пройдите этот тест на треугольник 30-60-90. Удачной сдачи теста!
Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша проверенная база данных репетиторов включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
У вас есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Кортни Монтгомери
Об авторе
Кортни набрала 99-й процентиль по SAT в старшей школе и закончила Стэнфордский университет со степенью в области культурной и социальной антропологии. Она увлечена тем, чтобы предоставить образование и инструменты для достижения успеха учащимся из всех слоев общества и слоев общества, поскольку она считает, что открытое образование является одним из величайших социальных уравнителей. Имеет многолетний опыт репетиторства, в свободное время пишет творческие работы.
Прямоугольные треугольники | GMAT Free
Прямоугольные треугольники — это треугольники, в которых один из внутренних углов равен 90 градусов, то есть прямой угол. Поскольку три внутренних угла треугольника в сумме составляют 180 градусов, в прямоугольном треугольнике, поскольку один угол всегда равен 90 градусам, два других всегда должны в сумме давать 90 градусов (они дополняют друг друга).
Сторона, противолежащая прямому углу, называется гипотенузой. Стороны, примыкающие к прямому углу, являются катетами. При использовании теоремы Пифагора гипотенуза или ее длина часто обозначаются строчными буквами 9.0247 с . Ноги (или их длины) обычно маркируются a и b .
Любой из катетов можно считать основанием, а другой катет считать высотой (или высотой), потому что прямой угол автоматически делает их перпендикулярными. Если известны длины обоих катетов, то, приняв одну из этих сторон за основание 90 247 b 90 248, а другую за высоту 90 247 h 90 248 , площадь прямоугольного треугольника легко вычислить по стандартной формуле для треугольника. площадь:
Это интуитивно логично, потому что против него можно расположить другой конгруэнтный прямоугольный треугольник так, что гипотенузы будут одним и тем же отрезком, образуя прямоугольник со сторонами, имеющими длину b и ширину h . Площадь прямоугольника равна ( b )( h ), поэтому любой из образующих его конгруэнтных прямоугольных треугольников имеет площадь, равную половине этого прямоугольника.
Теорема Пифагора
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин двух других сторон.
The Pythagorean Theorem
The sides that we referred to as b and h above are now labeled as b and a , since the custom when using the Pythagorean Theorem is to используйте переменные a, b и c . Тем не менее, важно признать, что обе формулы относятся к одним и тем же сторонам. Например, в типичном вопросе GMAT вы можете использовать теорему Пифагора, чтобы определить основание и высоту треугольника, а затем, в конечном итоге, найти его площадь.
Довольно часто на GMAT вы оказываетесь в ситуации, когда знаете, что конкретный треугольник является прямоугольным, и знаете длины двух из трех сторон. Затем вы сможете найти длину третьей стороны, подставив две известные длины в
Ранее мы обсуждали, как можно использовать теорему Пифагора для вычисления расстояния между любыми двумя точками на координатной плоскости.
Общие пифагорейские тройки
Определенные тройки чисел, удовлетворяющие теореме Пифагора, часто появляются на GMAT. Вы должны запомнить хотя бы первые три тройки здесь. Вам не нужно знать углы этих треугольников, только отношения длин сторон:
На GMAT вы должны знать углы и отношения сторон для 45-45-90 и 30 -60-90 треугольников, но вы , а не должны запомнить или быть в состоянии определить углы для пифагорейских троек, перечисленных выше; Вы можете определить длины сторон, просто используя формулу Пифагора.
45-45-90 Треугольник
Поскольку прямоугольный треугольник является особым треугольником, треугольник 45-45-90 особенный вдвойне. К нему применимы все общие правила треугольника, к нему применима теорема Пифагора, а затем он обладает некоторыми собственными особыми свойствами.
Треугольник 45-45-90
Треугольник 45-45-90 — это то, что вы получите, если у вас равнобедренный прямоугольный треугольник. Если треугольник прямоугольный и равнобедренный, то сумма двух сторон, отличных от прямого угла, должна быть равна 9.0 градусов, и они должны быть равны, поэтому каждый должен равняться 45 градусам.
Кроме того, поскольку это прямоугольный треугольник, мы знаем, что
верно, но если a = b (поскольку мы говорим о равнобедренном треугольнике), мы можем подставить это в теорему Пифагора, чтобы получить :
Если вы попытаетесь установить a = 1, то вы получите c = √2, как на диаграмме выше. Стороны в каждом треугольнике 45-45-90 имеют длины в соотношении 1:1:√2.
Отношение сторон не означает, что стороны, противоположные углам в 45 градусов, обязательно равны 1, как указано выше. Скорее, любая длина, находящаяся напротив 45 градусов, назовем ее длиной 90 247 x 90 248 , будет сопровождаться напротив гипотенузы стороной, которая в √2 больше, или 90 247 x 90 248 √2.
Треугольник 30-60-90
Треугольник 30-60-90 похож на треугольник 45-45-90 тем, что это «двойной особый» прямоугольный треугольник. Также, как и в случае с 45-45-90 треугольник, когда у нас есть один из этих треугольников, мы знаем меру углов и знаем отношение длин сторон.
Треугольник 30-60-90 внутри равностороннего треугольника
Треугольник 30-60-90 имеет углы, которые измеряют 30 градусов, 60 градусов и 90 градусов, и стороны, обращенные к этим углам с длинами в отношении 1: √3:2 соответственно. Как и в случае с любым отношением, мы можем представить, что отсутствует число x , так что длины равны x 9. 0248 : х √3: 2 х .
Если мы попытаемся подставить эти длины в теорему Пифагора, мы получим следующее:
Наш результат подтверждает, что теорема верна — и это лучше, поскольку мы имеем дело с прямоугольным треугольником.
Вы можете запомнить, какая сторона проходит через какой угол, используя тот факт, что большие длины сторон в треугольнике обращены к большим углам. Это означает, что сторона, расположенная напротив угла 30 градусов, будет наименьшей стороной, сторона, расположенная напротив угла 60 градусов, будет стороной средней длины, а сторона, расположенная напротив угла 9 градусов.Угол 0 градусов будет самой длинной стороной. При использовании этого трюка с памятью иногда люди задаются вопросом, что больше: √3 или 2. Вы можете помнить, что √3 меньше 2, потому что 2 равно √4, а √3 меньше √4.
На рисунке выше показано свойство, которое иногда встречается на GMAT: обратите внимание, что изображенный треугольник 30-60-90 находится внутри равностороннего треугольника.
Средние линии треугольников и четырехугольников
107. Мы знаем (п. 102), что геометрическим местом точек, равноотстоящих от двух данных параллельных прямых, служит средняя параллельная. Если таким образом AB и CD (чер. 114) суть две параллельные и MN для них средняя параллельная, то расстояния любой точки E этой средней параллельной от AB и CD равны между собою, т. е., построив EF ⊥ AB и EG ⊥ CD, получим, что EF = EG.
Ясно, что построенные перпендикуляры EF и EG составляют продолжение друг друга и образуют один отрезок FG, перпендикулярный к нашим параллельным AB и CD, причем этот отрезок делится среднею параллельною (в точке E) пополам. Итак, всякий отрезок, перпендикулярный к двум параллельным и заключенный между ними, делится среднею параллельною пополам.
Возникает теперь вопрос: не будет ли также делиться пополам среднею параллельною какой-нибудь отрезок KL, не перпендикулярный к AB и CD. Пусть KL пересекается с MN в точке O. Построим через точку O перпендикулярный к прямым AB и CD отрезок HI. Тогда OH = OI. Так как, кроме того, ∠HOK = ∠IOL, как вертикальные, то прямоугольные треугольники OHK и OIL равны, откуда следует, что OK = OL. Итак, оказывается, что и любой отрезок, заключенный между двумя параллельными, делится среднею параллельною пополам.
Пусть AB || CD (чер. 115). Построив между ними ряд каких-либо отрезков EF, GH, KI и т. д., мы, согласно предыдущему, найдем, что середины этих отрезков лежат на средней параллельной MN. В общем итоге мы приходим к следующему заключению:
Геометрическим местом середин всевозможных отрезков, заключенных между двумя параллельными, служит средняя параллельная.
Отсюда возникают возможности различных построений средней параллельной для двух данных параллельных прямых: 1) мы можем, построим любой отрезок EF, заключенный между двумя данными параллельными AB и CD, разделить его пополам и через его середину построить прямую MN || AB || CD — это прямая MN и должна служить среднею параллельною, и она должна делить пополам всевозможные отрезки (напр., GH, KI и т. д.), заключенные между AB и CD. 2) Мы можем построить два отрезка, напр., EH и KI, заключенные между AB и CD, разделить каждый из них пополам и через их середины построить прямую MN — она и должна служить среднею параллельною.
108. Применим свойства средней параллельной к знакомым нам фигурам и прежде всего треугольнику.
Пусть имеем ∆ABC (чер. 116). Здесь непосредственно мы не имеем двух параллельных, но мы всегда можем их получить, напр., построив через вершину A прямую EF || BC (эту прямую EF можно было бы и не рисовать на чертеже, так как она существенной роли не играет в дальнейшем и так как достаточно лишь знать, что она существует). Тогда мы имеем две параллельных BC и EF и два отрезка AB и AC, заключенных между ними. Разделив их пополам в точках M и N (AM = MB и AN = NC) и построив через M и N прямую MN, мы получим среднюю параллельную MN, т. е. MN || BC (и || EF, но это для нас не существенно). Из этого заключаем:
прямая, соединяющая середины двух сторон треугольника, параллельна его третьей стороне.
Отрезок, соединяющий середины двух сторон треугольника, называют среднею линиею треугольника. Итак, у нас отрезок MN есть средняя лини нашего треугольника.
Пусть имеем ∆ABC (чер. 117). Разделим пополам каждую из его сторон: пусть M есть середина AB (сл. AM = MB), N — середина AC (AN = NC) и P — середина BC (BP = PC); соединим точки M, N и P отрезками MN, MP и PN, — каждый из этих отрезков является среднею линиею для нашего треугольника. Таким образом в треугольнике имеется три средних линии.
Согласно предыдущему, будем иметь: MN || BC, MP || AC и NP || AB. Поэтому AMPN, BMNP и PMNC суть параллелограммы. Так как в параллелограмме противоположные стороны равны, то имеем: MN = BP (из параллелограмма BMNP), но BP = BC/2 (ибо точка P есть середина BC); поэтому MN = BC/2. Также из параллелограмма AMPN получим: MP = AN = AC/2 и из параллелограмма AMPN — PN = AM = AB/2. Отсюда заключаем:
каждая средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей и равна ее половине.
109. Перейдем теперь к четырехугольникам и остановимся сначала на таких четырехугольниках, у которых две стороны параллельны. Принято называть такие четырехугольники трапециями. На чер. 118 изображены два различных вида трапеций: 1) трапеция ABCD, где BC || AD, но AB не параллельна CD, — эта трапеция имеет площадь (см. п. 79) и 2) трапеция A’B’C’D’, где A’D’ || B’C’, — эта трапеция не имеет площади (п. 79).
Рассмотрим сначала трапецию ABCD (чер. 118 bis), имеющую площадь. Здесь BD || AD. Поэтому мы имеем две параллельных BC и AD и между ними отрезки AB и CD. Разделив эти отрезки пополам в точках M и N (AM = MB и CN = ND) и соединив их прямою MN, получим среднюю параллельную MN для BC и AD, т. е. MN || BC || AD. Отрезок MN этой прямой называется средней линиею трапеции (следует добавить: «соединяющей середины непараллельных сторон», потому что в трапеции, как и во всяком четырехугольнике, можно рассматривать 6 средних линий, что имеет место в п. 110). Итак, мы получили, что MN || BC || AD. Далее, построив диагональ AC, получим еще третий отрезок AC, заключенный между параллельными BC и AD — его середина должна лежать (п. 107) на средней параллельной, т. е. точка P, где пересекаются MN и AC, есть середина отрезка AC. Поэтому MP есть средняя линия треугольника ABC и PN — средняя линия ∆ACD. На основании предыдущего, имеем: MP = BC/2 и PN = AD/2. Отсюда получаем: MN = MP + PN = BC/2 + AD/2 или MN = (BC + AD)/2. Итак,
средняя линия, соединяющая середины непараллельных сторон трапеции, имеющей площадь, параллельна ее параллельным сторонам и равна их полусумме.
Пусть теперь имеем трапецию ABCD (чер. 118 bis), неимеющую площади. Здесь также BC || AD и поэтому середины M и N сторон AB и CD лежат на средней параллельной, т. е. здесь также имеем: MN || BC || AD. Построив диагональ AC, получим отрезок AC, заключенный между параллельными BC и AD, и его середина, точка P, должна лежать на средней параллельной. Поэтому PM есть средняя линия треугольника ABC и, следовательно PM = BC/2; также PN есть средняя линия ∆ABC и, след., PN = AD/2. Так как MN = PN – PM, то получим MN = PN – PM = AD/2 – BC/2 или MN = (AD – BC) / 2. Итак,
средняя линия, соединяющая середины непараллельных сторон трапеции, неимеющей площади, параллельна ее параллельным сторонам и равна их полуразности.
110. Пусть имеем какой-либо четырехугольник ABCD (имеющий площадь) — (чер. 119). Найдем середины M, N, P и Q его сторон и соединим их попарно. Получим 6 средних линий четырехугольника.
Вот свойства этих средних линий.
1) Средние линии, соединяющие середины последовательных сторон четырехугольника, образуют параллелограмм.
Для выяснения этого свойства построим диагональ AC. Тогда из ∆ABC имеем (п. 108) MN || AC и из ∆ACD на том же основании: PQ || AC, — следов., MN || PQ. Построив другую диагональ BD, найдем при ее помощи, что NP || MQ, следовательно, MNPQ есть параллелограмм.
2) Средние линии четырехугольника, соединяющие середины противоположных сторон, взаимно делятся пополам.
Это свойство теперь очевидно, так как MP и NQ являются диагоналями параллелограмма.
Через точку O пересечения прямых MP и NQ проходят также прямые, соединяющие середины диагоналей AC и BD (на чертеже диагональ BD не дана). Это следует из того, что AC И BD являются сторонами четырехугольника ACBD, не имеющего площади, к которому применимо все, изложенное в начале этого п.
111. Мы умели (пп. 57, 59) делить отрезок пополам и, следов., на 4, на 8 и вообще на 2n равных частей. Теперь мы можем разделить данный отрезок на 3, на 5 и вообще на сколько угодно равных частей.
Пусть, напр., требуется отрезок AB (чер. 120) разделить на 5 равных частей. Построим через точку A произвольную прямую AC (образующую с AB угол, отличный от выпрямленного) и отложим на AC пять произвольных, но равных между собою, отрезков AE = EF = FG = GH = HO. Построим прямую OB и через точки E, F, G и Н построим прямые EE’, FF’, GG’, HH’, параллельные OB.
Рассмотрим ∆AFF’, так как AE = EF, то E есть середина стороны AF и EE’ (она || FF’) есть средняя линия этого треугольника, следовательно, AE’ = E’F’.
Рассмотрим затем трапецию EE’G’G. Так как EF = FG, FF’ || EE’, то FF’ есть средняя линия трапеции EE’GG’, — следовательно, E’F’ = F’G’. Также найдем, что GG’ есть средняя линия трапеции FF’H’H и, следов., F’G’ = G’H’ и т. д. Соединяя полученные равенства, найдем AE’ = E’F’ = F’G’ = G’H’ = H’B’, т. е. отрезок AB разделился на 5 равных частей.
Из решения этой задачи можно вывести заключение:
Если на одной стороне угла отложить равные отрезки и чрез их концы построить ряд параллельных прямых, то и на другой стороне угла получим равные между собой отрезки.
Добавление. Мы откладывали равные отрезки на одной прямой подряд, начиная от точки пересечения двух прямых (AB и AC чертежа 120), но возможно к такому же результату прийти и при ином способе отложения равных отрезков. На чертеже 120 bis дано два варианта такого построения: на прямой AD (см. чер. 120 bis слева или справа) отложим два равных отрезка AB и CD и через их концы построим параллельные AA’ || BB’ || CC’ || DD’. Затем возьмем точку O, середину отрезка BC, и построим OO’ || BB’ || CC’ || AA’ || DD’. Тогда OO’ есть средняя линия трапеции BCC’B’; поэтому B’O’ = O’C (п. 109). Так как AB = CD и BO = OC, то AO также = OD; поэтому OO’ есть также средняя линия трапеции ADD’A’ (на чертеже справа эта трапеция ADD’A’ — не имеющая площади, см. п. 109) — и также A’O’ = O’D’. Отсюда имеем A’O’ – B’O’ = O’D’ – O’C’ (ибо и уменьшаемые и вычитаемые обеих разностей равны), или A’B’ = C’D’. Возможны и иные комбинации (напр., отр. CD правой фигуры отодвинуть так, чтобы точка C оказалась правее точки пересечения прямых AD и A’D’). Общее заключение таково: если построены две прямые, на одной из них отложены как-либо два равных отрезка и через концы их построены параллельные, то эти последние выделят и на другой прямой два равных между собою отрезка.
112. Упражнения.
- Через вершины данного треугольника построены прямые, параллельные его сторонам. Показать, что новый треугольник имеет стороны вдвое больше, чем стороны данного, и что вершины данного являются серединами сторон нового (сравн. упр. 7 из п. 54).
- Построить треугольник, если даны середины трех его сторон.
- Построить параллелограмм, если даны середины трех его сторон.
- Известно (п. 110), что середины четырех сторон четырехугольника являются вершинами параллелограмма. Когда этот параллелограмм обращается в ромб, когда в прямоугольник, когда в квадрат?
- Прямая, соединяющая вершину треугольника со срединою противоположной стороны (медиана) и прямая, соединяющая середины двух других сторон треугольника, взаимно делятся пополам.
- Продолжим одну сторону треугольника на отрезок, равный этой стороне, и соединим конец отрезка со срединою другой стороны. Последняя соединяющая прямая отсекает от третьей стороны треугольника отрезок, равный 1/3 этой стороны. (Построить еще прямую, параллельную последней соединяющей прямой чрез вершину треугольника, противолежащую той его стороне, которая была продолжена).
- Если на стороне AB параллелограмма ABCD отложить отрезок AM = (1/n)AB (напр., (1/7)AB) и соединить D с M, то DM пересечет диагональ AC в точке N так, что AN = (1/(n+1))AC (во взятом примере (1/8)AC).
Для выяснения этого надо на продолжении стороны AB отложить BM’ = AM и соединить C с M’; тогда C’M’ || DM, – приметь п. 111.











 В общем случае по этому свойству и определяется длина средней линии треугольника.
В общем случае по этому свойству и определяется длина средней линии треугольника.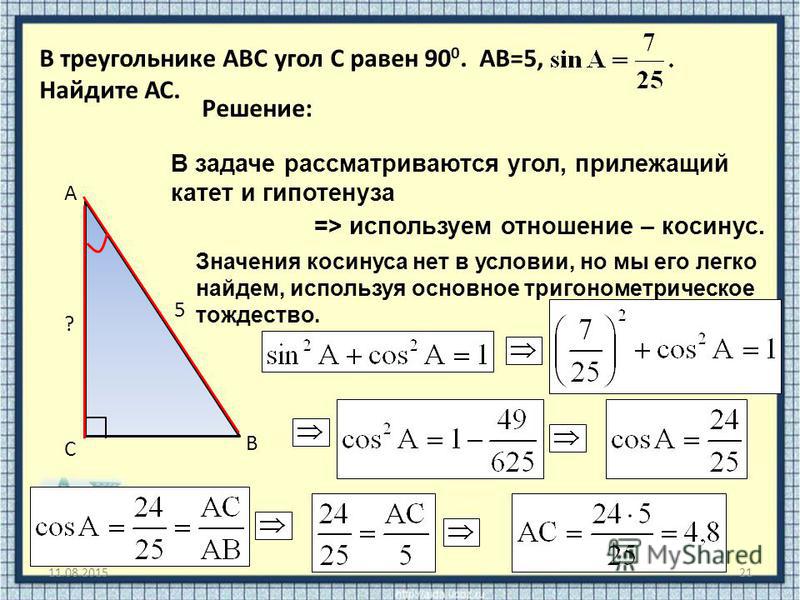

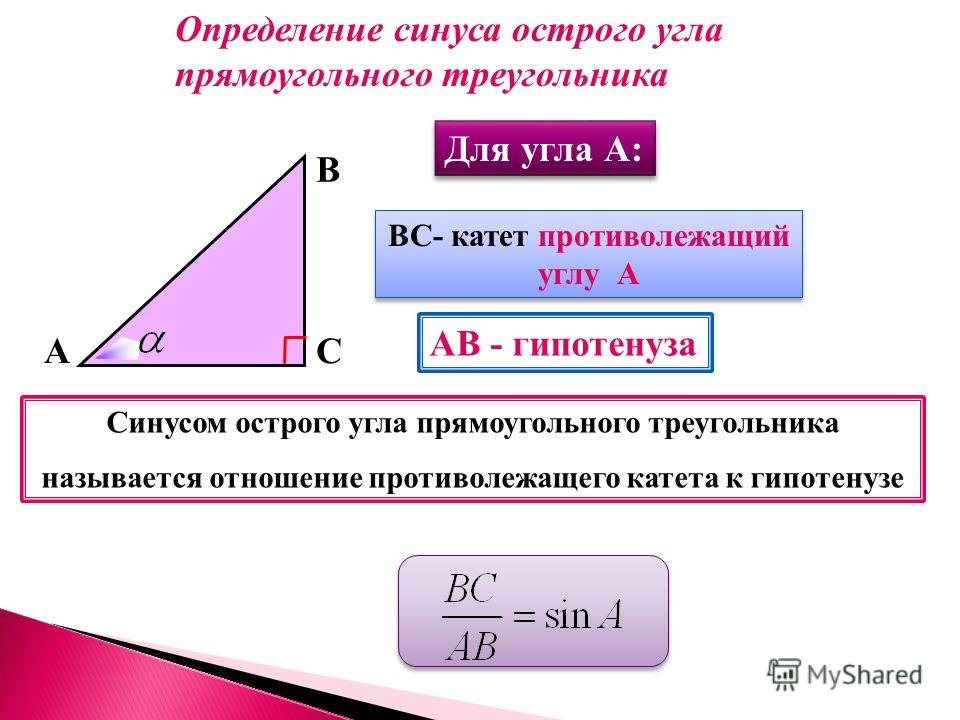
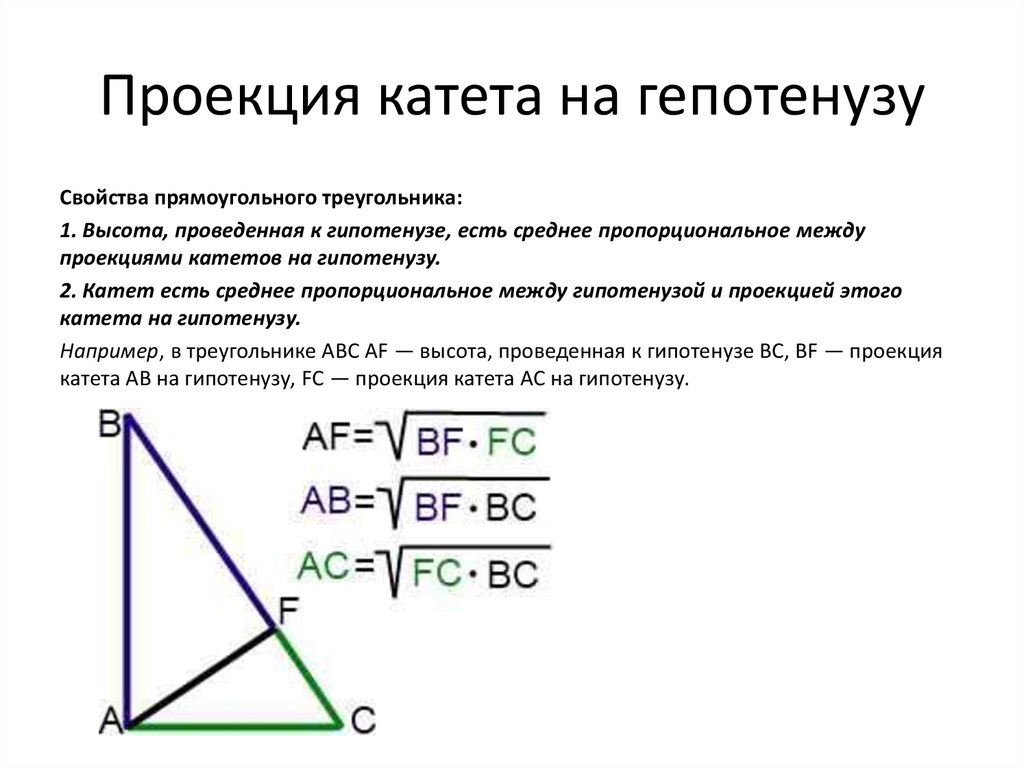
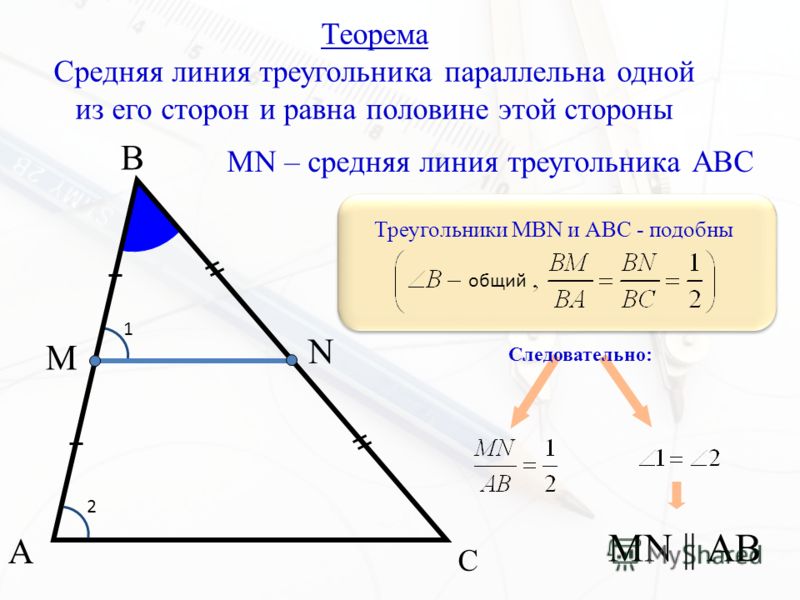 ⓘ Основание прямоугольного треугольника [b]
ⓘ Основание прямоугольного треугольника [b] ⓘ Высота прямоугольного треугольника [h]
ⓘ Высота прямоугольного треугольника [h]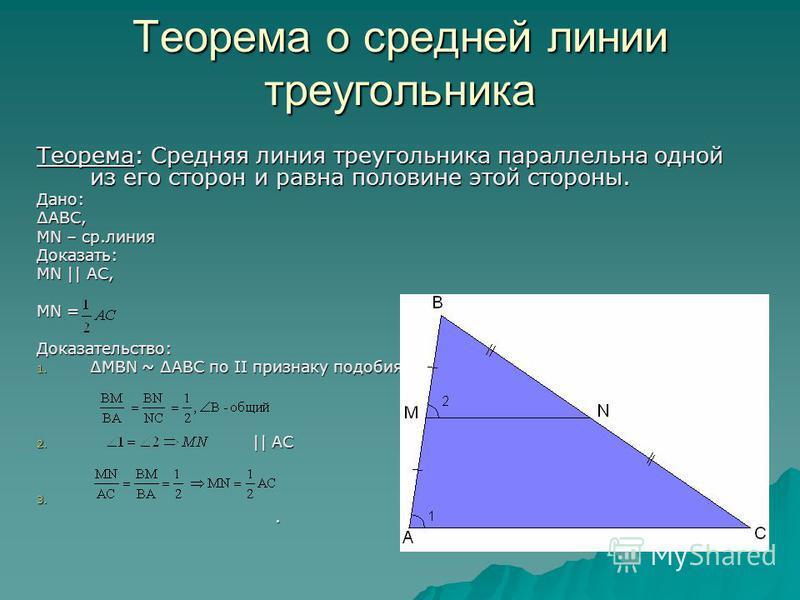 ⓘ Срединная линия на высоте прямоугольного треугольника [Mh]
ⓘ Срединная линия на высоте прямоугольного треугольника [Mh]