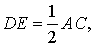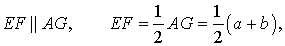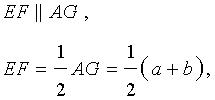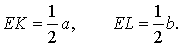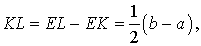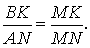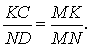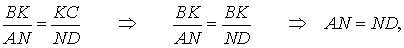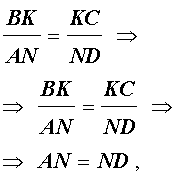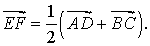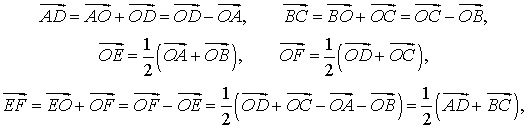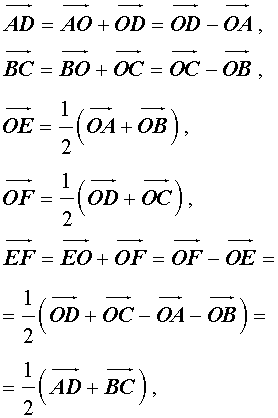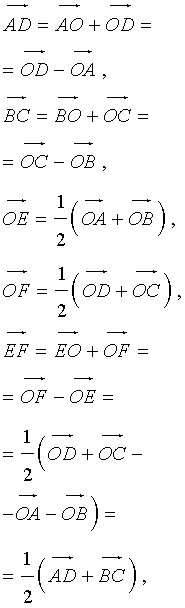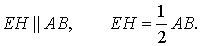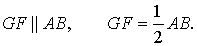Как найти среднюю линию выпуклого четырехугольника

Что такое средняя линия четырехугольника

В данной публикации мы рассмотрим определение и основные свойства средних линий выпуклого четырехугольника касательно точки их пересечения, соотношения с диагоналями и т.д.

Примечание: далее мы будем рассматривать только выпуклую фигуру.

Определение средней линии четырехугольника

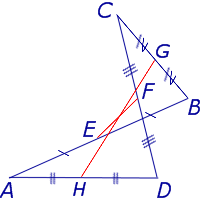
Отрезок, соединяющий середины противоположных сторон четырехугольника (т.е. не пересекающий их), называется его средней линией.

EF – средняя линия, соединяющая середины AB и CD; AE=EB, CF=FD.
GH – средняя линия, сеодиняющая середины BC и AD; BG=GC, AH=HD.

Свойства средней линии четырехугольника

Свойство 1

Средние линии четырехугольника пересекаются и в точке пересечения делятся пополам.

Примечание: Точка O является центроидом (или барицентром) четырехугольника.

Свойство 2

Точка пересечения средних линий четырехугольника является серединой отрезка, соединяющего середины его диагоналей.

Свойство 3

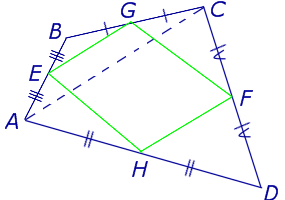
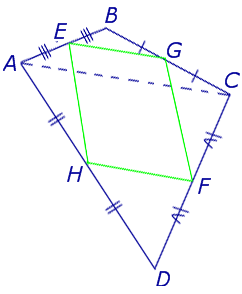
Середины сторон четырехугольника являются вершинами параллелограмма, который называется параллелограммом Вариньона.

Центром образованного таким образом параллелограмма и точкой пересечения его диагоналей является середина средних линий исходного четырехугольника, т.е. точка их пересечения – O.

Примечание: Площадь параллелограмма равняется половине площади четырехугольника.

Свойство 4

Если углы между диагоналями четырехугольника и его средней линией равны, значит диагонали имеют одинаковую длину.

Свойство 5

Средняя линия четырехугольника меньше или равна полусумме непересекающих ее сторон (при условии, что данные стороны параллельны).

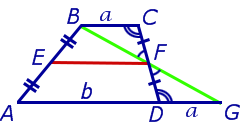
EF – средняя линия, не пересекающаяся со сторонами AD и BC.

Иначе говоря, средняя линия четырехугольника равняется половине суммы не пересекающих ее сторон тогда и только тогда, когда данный четырехугольник является трапецией. В этом случае рассматриваемые стороны являются основаниями фигуры.

Свойство 6

Для вектора средней линии произвольного четырехугольника выполняется следующее равенство:

Средние линии

Средние линии треугольника

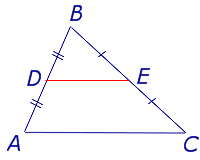
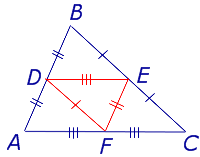
Определение . Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

На рисунке 1 средней линией является отрезок DE .

Утверждение 1 . Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.

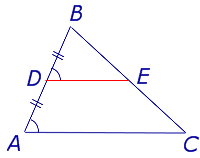
Доказательство . Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .

Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.

Первую часть утверждения 1 мы доказали.

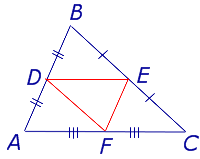
Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).

Но поскольку AF = FC , то отсюда вытекает равенство

что и требуется доказать.

Доказательство утверждения 1 закончено.

Три средних линии делят треугольник на 4 равных треугольника ADF , DBE , ECF , DEF (рис. 4).
Каждый из четырёх треугольников ADF , DBE , ECF , DEF подобен треугольнику ABC с коэффициентом подобия 0,5 .

Средняя линия трапеции

Напомним, что трапецией трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.

Параллельные стороны трапеции называют основаниями , а непараллельные стороны – боковыми сторонами трапеции.

Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.

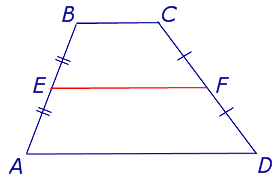
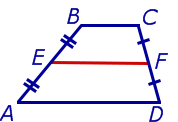
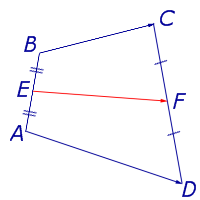
Определение . Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).

На рисунке 5 средней линией трапеции является отрезок EF .

Утверждение 2 . Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.

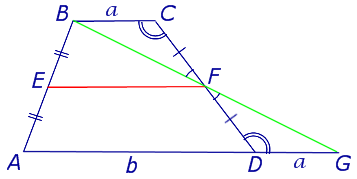
Доказательство . Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому

что и требовалось доказать.

Задача 1 . Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.

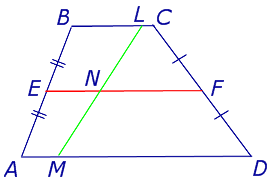
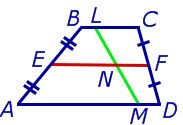
Решение . Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.

Задача 2 . Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.

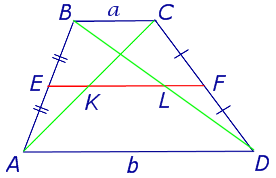
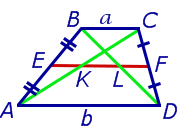
Решение . Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:

что и требовалось доказать.

Утверждение 3 . Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

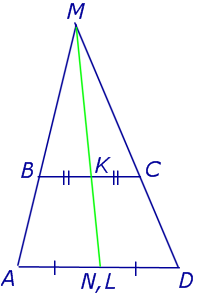
Доказательство . Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:

Из этих соотношений получаем:

откуда вытекает, что точки N и L совпадают. Доказательство завершено.

Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.

Утверждение 4 . Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.

Следствие . Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.

Средние линии четырехугольника. Теорема Вариньона

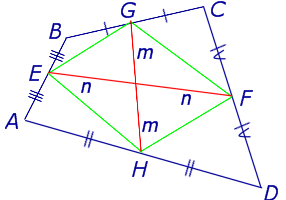
Определение . Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.

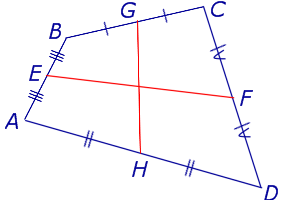
Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).

На рисунке 10 средние линии – это отрезки EF и GH .

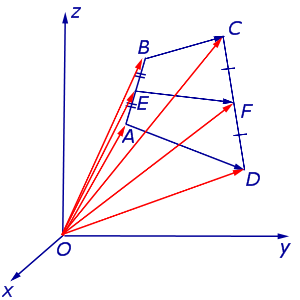
Замечание 1 . Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.

На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .

Замечание 2 . Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.

Замечание 3 . В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.

Теорема Вариньона . Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограмма параллелограмма .

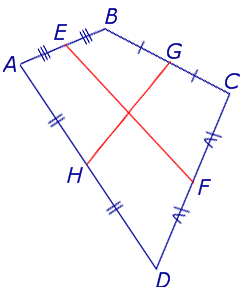
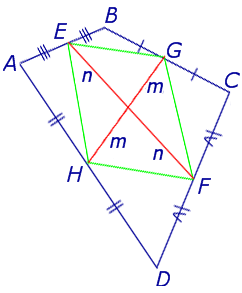
Доказательство . Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.

Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограмма признака параллелограмма признака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.

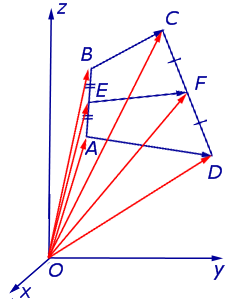
Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).

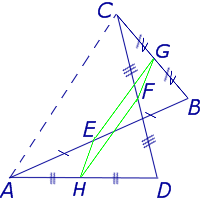
Утверждение 5 . Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).

Утверждение 6 . Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:

что и требовалось доказать.

Следствие . Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.

Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапецией трапецией , а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.

Средние линии тетраэдра

Тетраэдром называют произвольную треугольную пирамиду (рис.17).

У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер . На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых .

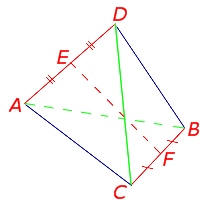
Определение . Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.

У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.

Утверждение 7 . Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.

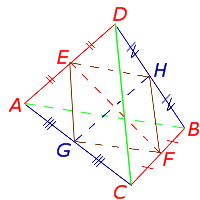
Доказательство . Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).

Заметим, что отрезок EH является средней линией треугольника ADB , поэтому

Определение . Точку пересечения средних линий тетраэдра называют центроидом тетраэдра .

Утверждение 8 . Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:

Ключевые слова: треугольник, отрезок, средняя линия, длина отрезка, средняя линия треугольника, средняя линия трапеции, средняя линия четырехугольника

Отрезок, соединяющий середины противолежащих сторон четырехугольника, называется средней линией четырехугольника.

Если в выпуклом четырехугольнике прямая, проходящая через середины двух противоположных сторон, образует равные углы с диагоналями четырехугольника, то диагонали равны.

Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.

Средняя линия треугольника параллельна третьей стороне, а ее длина равна половине длины этой стороны.

Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.

См. также:
Биссектриса, Медиана, Прямоугольный треугольник, Равнобедренный треугольник, Равносторонний треугольник

источники:

http://www.resolventa.ru/spr/planimetry/mline.htm

http://uztest.ru/abstracts/?idabstract=69

Источник

Примечание: далее мы будем рассматривать только выпуклую фигуру.

Определение средней линии четырехугольника
Свойства средней линии четырехугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6

Определение средней линии четырехугольника

EF – средняя линия, соединяющая середины AB и CD; AE=EB, CF=FD.
GH – средняя линия, сеодиняющая середины BC и AD; BG=GC, AH=HD.

Свойства средней линии четырехугольника

Свойство 1

Средние линии четырехугольника пересекаются и в точке пересечения делятся пополам.

EF и GH (средние линии) пересекаются в точке O;
EO=OF, GO=OH.

Примечание: Точка O является центроидом (или барицентром) четырехугольника.

Свойство 2

K – середина диагонали AC;
L – середина диагонали BD;
KL проходит через точку O, соединяя K и L.

Свойство 3

Примечание: Площадь параллелограмма равняется половине площади четырехугольника.

Свойство 4

EF – средняя линия;
AC и BD – диагонали;
∠ELC = ∠BMF = α, следовательно AC=BD.

Свойство 5

EF – средняя линия, не пересекающаяся со сторонами AD и BC.

Свойство 6

Для вектора средней линии произвольного четырехугольника выполняется следующее равенство:

Источник

Ястребов А.В., Шабанова М.В. Средние линии четырехугольника…

УДК 514.112.4

ЯСТРЕБОВ Александр Васильевич, кандидат физико-математических наук, доктор педагогических наук, профессор кафедры математического анализа, теории и методики обучения математике Ярославского государственного педагогического университета им. К.Д. Ушинского. Автор 147 научных публикаций, в т. ч. трех монографий

ШАБАНОВА Мария Валерьевна, доктор педагогических наук, профессор, заведующая кафедрой экспериментальной математики и информатизации образования Северного (Арктического) федерального университета имени М.В. Ломоносова. Автор 140 научных публикаций, в т. ч. 4 монографий

СРЕДНИЕ ЛИНИИ ЧЕТЫРЕХУГОЛЬНИКА,

или красивое бесполезное обобщение

Посвящается Т.М. Кориковой

Данная статья посвящена новым результатам, касающимся геометрии выпуклого четырехугольника. Если рассматривать математику как сумму знаний, то следует сказать, что авторами введены понятия «средняя линия выпуклого четырехугольника» и «середина n-го порядка выпуклого четырехугольника». Кроме того, доказана формула, выражающая площадь выпуклого четырехугольника через длины его средних линий и другие числовые характеристики. Особенность полученной формулы в том, что она связывает в единое целое 12 числовых характеристик, т. е. чрезвычайно много. Наконец, в статье сформулировано и экспериментально обосновано несколько гипотез о свойствах последовательности середин выпуклого четырехугольника. Тем самым намечено одно из возможных направлений исследования геометрии четырехугольника. Если рассматривать математику как сферу человеческой деятельности, то следует сказать, что в статье выявлена логика постановки и решения исследовательской задачи в выбранной области геометрии. По мнению авторов, для читателей представляет интерес и ценность именно демонстрация работы математика-теоретика и математика-экспериментатора. Тем самым статья возвращает читателя к экспериментальным корням математики. Если рассматривать методологию данного исследования, то следует сказать, что в нем использован комплекс дополняющих друг друга методов: соображения из области физики о деформациях фигур, сравнение различных математических формул с точки зрения их устойчивости относительно деформаций, метод теоретических обобщений, экспериментальные методы в области математики. Особо следует сказать о том, что гипотезы о свойствах выпуклого четырехугольника были получены в результате компьютерного эксперимента, проведенного в интерактивной геометрической среде «GeoGebra». Тем самым привлечение компьютеров порождает новые возможности исследования в такой, казалось бы, завершенной области, какой является элементарная геометрия.

Ключевые слова: элементарная геометрия, выпуклый четырехугольник, обобщение, компьютерный эксперимент, динамическая модель.

109

ФИЗИКА. МАТЕМАТИКА. ИНФОРМАТИКА

Постановка задачи и первое наблюдение. Хорошо известно, что площадь трапеции может быть вычислена по одной из двух формул. Как у каждого выпуклого четырехугольника, она равна половине произведения диагоналей, умноженной на синус угла между ними, а также произведению средней линии на высоту. Бросается в глаза полная разнотипность этих формул. Во-первых, их правые части не имеют ни одного общего элемента. Во-вторых, и это главное, формулы «по-разному реагируют» на вариации фигуры. Действительно, зафиксируем три вершины, а четвертую чуть-чуть «сдвинем» в направлении ее высоты. Под действием такой вариации первая формула останется справедливой, а вторая нет. При этом дело даже не в том, что два выражения окажутся неравны, а в том, что формула полностью утратит смысл, поскольку утратит смысл и понятие средней линии, и понятие высоты (они не определены для четырехугольника произвольного вида).

С точки зрения физики отмеченное обстоятельство является по меньшей мере неестественным. При малом смещении вершины — на миллиметр, микрон, ангстрем (единица длины, равная одной десятимиллиардной метра) — площадь фигуры также изменится на малую величину. При этом средняя линия превратится в другой отрезок, который хотя и не будет параллелен ни одной стороне четырехугольника, но будет мало отличаться от средней линии. В этой ситуации естественно поставить ряд вопросов, которые связаны друг с другом и, быть может, заменяют друг друга. Приведем три формулировки этих вопросов.

1. Как обобщить формулу площади трапеции на случай четырехугольника общего вида?

2. Какова формула площади четырехугольника общего вида, которая «превратится» в формулу площади трапеции при «превращении» четырехугольника в трапецию?

3. Какой геометрический образ играет в четырехугольнике общего вида ту же роль, которую играет в трапеции средняя линия?

Ответам на эти вопросы посвящена данная статья.

Частично ответ на третий вопрос подсказывает следующее наблюдение.

Пусть дана трапеция ABCD с основаниями BC и [AD] и средней линией [PQ]. Продолжим боковые стороны до их пересечения в точке F, проведем биссектрису ZAFD и рассмотрим отрезок [RT] этой биссектрисы с концами на сторонах [BC] и [AD] (рис. 1). Проведем из точки R высоту [RH]. Очевидно, что площадь трапеции вычисляется по формуле:

S = PQ-RH = PQI№n 0.

Рис 1. Иллюстрация к наводящим соображениям

Заметим, что каждая точка отрезка [PQ] равноудалена от оснований трапеции или их продолжений, а каждая точка отрезка [RT] равноудалена от боковых сторон трапеции или их продолжений. Таким образом, последняя формула показывает, что площадь трапеции является произведением длин двух отрезков, точки которых обладают неким специальным свойством, на синус угла между ними. При этом специальное свойство отрезков состоит в том, что каждая точка равноудалена от двух несмежных сторон. На этом наблюдении будет основано вводимое понятие, а с помощью этого понятия будет, в свою очередь, сформулирован основной результат.

110

Ястребов А.В., Шабанова М.В. Средние линии четырехугольника…

Понятие средней линии и основной результат.

Определение 1. Средней линией выпуклого четырехугольника, соединяющей две его противоположные стороны, назовем множество точек внутри четырехугольника, равноудаленных от двух других его сторон или их продолжений.

Согласно введенному определению средняя линия, соединяющая стороны [AB] и [CD] выпуклого четырехугольника ABCD, строится по следующему алгоритму:

1) если [BC] параллельна [AD], то средняя линия — это отрезок, соединяющий середины сторон [AB] и [CD];

2) если [BC] не параллельна [AD], то средняя линия — это отрезок биссектрисы угла, образованного продолжением сторон [BC] и [AD], который лежит внутри четырехугольника.

Всюду далее термин «средняя линия» будет употребляться в смысле определения 1. Под четырехугольником общего вида будем понимать четырехугольник, не имеющий параллельных сторон.

Заметим, что возможно иное обобщение понятия средней линии, например введение его как отрезка, соединяющего середины противоположных сторон четырехугольника [1].

Для выпуклого четырехугольника ABCD общего вида построим его средние линии [PQ] и [Я7] (рис. 2).

Основные обозначения, необходимые для формулировки основного результата, сведем в табл. 1.

Рис. 2. Иллюстрация к формулировке и доказательству теоремы

Теорема. Для любого выпуклого четырехугольника имеет место формула

S = li • l2 •sin 9 , (1)

2(1 -Pi P2 -Рз P4)

где

P 2

cd sin 8^ ab sin

da sin a ^ bc sin у y

ab sin p! cd sin 8 )

1 +

i +

sin p! sin a )

sin sin P)

sin8^ | sin у

P+sine 1

V sin y)

fi+sirn

V sin 8

л-i

( sin 8

I i + ~

V sin a

-i

, (2)

, (3) , (4)

Таблица 1

основные обозначения, необходимые для доказательства теоремы

Длины основных отрезков |AB| := a |BC| := b |CD| := c |DA| := d —

Длины вспомогательных отрезков PQ| := l |ЯГ| := l2 — — —

Углы ZA := a ZB := p ZC := у ZD := 8 ZO := 9

Примечание: символ := означает «равно по определению», причем двоеточие ставится со стороны определяемого объекта.

111

ФИЗИКА. МАТЕМАТИКА. ИНФОРМАТИКА

Р 4 =

1 +

bc sin у da sin a

1 +

sin a sin 5

1 +

sin a sin в

. (5)

a, = a

b1 = b

b2 = b

sin a

sin ^

sin в

sin a

• rV1 sin в

sin у

sin у sin в

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

у1

/ • -1

‘ sin у 1 + — ‘

sin5

sin у sin5

-1

Доказательство теоремы. Вспомогательные обозначения, необходимые для доказательства теоремы, сведем в табл. 2.

Доказательство теоремы основано на трех леммах.

Лемма 1. Концевые точки средних линий разбивают стороны четырехугольника общего вида на части, которые выражаются через длины соответствующих сторон по формулам:

r sin 5 Л

d1 = d 1 +

v sin a J

( sin a Л

dn = d 1 +

2 V sin 5 J

(9)

Доказательство.

Рассмотрим треугольник ЕАВ (рис. 2).

ТГ « EA AP |

По теореме о биссектрисе J—-L = J—1, или

EB PB

получим, что

ta1

— = —. Из системы i

u a.,

u a0

(6)

a1 + a2 = a

f u Л-1

1 + U V t J

(

(10)

1+1

(7)

V u J

Вновь рассмотрим треугольник ЕАВ. По теореме синусов получим, что

t u

(8)

sin ZABE sin ZRAE

n „ u sin(n-a) sin a откуда — = —i—L =—-.

t sin^^) sin в

Подставив полученное выражение в систему (10), получим систему (6).

Формулы (7-9) получаются аналогично, с той разницей, что для их доказательства необ-

Таблица 2

вспомогательные обозначения, необходимые для доказательства теоремы

Длины основных отрезков AB| := a BC| := b CD := c DA| := d

Длины первых частей отрезков AP := a1 BR| := b cei := c DT := d

Длины вторых частей отрезков PB| := a2 RCI := b2 6D := C2 2A| := d2

Длины вспомогательных отрезков EA| := t EB| := u FB := v FC := w

Площади отсекаемых треугольников Sabc := S1 SADC := S2 S := S BCD ‘ 3 SBAD := S4

112

Ястребов А.В., Шабанова М.В. Средние линии четырехугольника…

ходимо рассмотреть треугольники FBC, EDC и FDA соответственно.

Лемма 2. Диагонали четырехугольника разбивают его на части, площади которых выражаются через площадь четырехугольника по формулам:

51 = 5

S2 = 5

1 +

cd sin 5 ab sin в

(, ab sin вХ

1 +———

v cd sin 5 у

(

(11)

53 = 5

S4 = S

da sin a bc sin у

bc sin у

(12)

da sin a у

Доказательство. Диагональ [AC] разбивает четырехугольник на два треугольника. Пусть [BM] и [CN] — высоты треугольников ABC и ADC соответственно (рис. 3).

Рис. 3. Иллюстрация к доказательству леммы 2

Вычислим площадь треугольника ABC двумя способами: 51 = |AC| • |BM| / 2 = absinP / 2. ab sin B

Отсюда | BM |= —

I AC |

гольника ADC получим, что | DN |=

равенств

Аналогично из треу-cd sin 5

AC | следует, что

Из двух последних | DN | cd sin 5 ^

——=——-. Подставив это выражение в

| BM | ab sin в

формулы (13), получим формулы (11).

Формулы (12) получаются полностью аналогично формулам (11), с той разницей, что в четырехугольнике нужно провести другую диагональ.

Если в четырехугольнике последовательно соединить отрезками концевые точки средних линий, то эти отрезки «отсекут» от четырехугольника четыре треугольника (рис. 2). Следующая лемма показывает, как выражаются их площади через площадь четырехугольника.

Лемма 3. Площади «отсекаемых» треугольников и площадь четырехугольника общего вида связаны формулами

SPBR = 5рр SRCQ = 5р2 , SQDT = 5рз, 5TAP = 5р^ (14)

где множители р. заданы равенствами (2-5).

Доказательство. Начнем с треугольника PBR. Вычислим его площадь по стандартной

формуле: SPBR = 2 a2bx sin в. Выразив длины отрезков а и b по формулам (6) и (7), получим,

2 1 0 1 L sin в

что Spbr =- a I 1 + ——

2 I sin a

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

1 +

sin в sin у

sin в.

Очевидно, что 51 = |AC| • |BM| / 2 и 52 =

=|AC| • |DN| / 2, откуда следует, что ^ ‘

Из этого соотношения и очевидного равенства откуда БРВ1{ = 511 +

Сгруппировав некоторые сомножители последнего выражения, получим, что 1 ab sin p = SABC =:Sj,

sin в sin a

1 +

sin в sin у

. Заменив 5,

51 = 5 ( DN х-

1 +

BM )

52 = 5 ( | BM |Y

1 +

V | DN

(13)

по формуле (11) и применив определение р1, получим первое из равенств (14).

Остальные равенства доказываются аналогично. Продолжим доказательство теоремы. Сначала докажем равенство (1) для выпуклого четырехугольника общего вида.

113

ФИЗИКА. МАТЕМАТИКА. ИНФОРМАТИКА

В силу построения исходный четырехугольник разбивается на несколько многоугольников (рис. 2), поэтому справедливо равенство S — SpRQT + SpBR + SRCq + SqDT + STAp. Первое слагаемое заменим по стандартной формуле:

SPRQT = — | PQ | • | RT | — sin 0. С учетом основных Q 2 1 обозначений получим, что SPRqT =— l1 • l2 • sin 0.

Остальные слагаемые заменим по формуле

(14): S = 1 l1 • l2 • sin 0 + Sp1 + Sp2 + Sp3 + Sp4. Отсюда следует равенство (1).

Теперь докажем равенство (1) для четырехугольника, две стороны которого параллельны. Для определенности будем считать, что [BC]||[AD].

Предыдущие рассуждения не могут быть применены в полном объеме, потому что при доказательстве лемм 1 и 3 существенным образом использовалась непараллельность противоположных сторон. Поступим следующим образом.

Вычислим каждую из величин р. для того случая, когда две стороны параллельны, т. е. когда в — п — а и 5 — п — у. По определению

, cd sin 5^

1 +———

v ab sin

( sin

1 +——

V sin a )

(

1 +

sin

V sin Y)

По формуле (11) первый сомножитель в правой части равен S1/S. Подставив в два другие сомножителя в — п — а, получим, что

р,= (15)

2S sin a + sin y

. S3 sin a

Аналогично получим: р2 = ——————

2S sin a + sin y

Рз =

_S2_

sin a

sin a + sin Y

Р 4

S4 sin y

2S sin a + sin y

(16)

Вычислим теперь знаменатель формулы (1), обозначив его для краткости буквой Q:

Q — 2(1 — р1 — р2 — Рз — р4) —

2 1 S1 sin y S3 sin a

V 2S sin a+sin y 2S sin a + sin y

S2 sin a S4 sin y n 2S sin a + sin y 2S sin a + sin y,

Вынося за скобки выражение 2S(sina + + siny), получим, что

^ 2S(sin a + sin y) — S1 sin y-S3 sin a — S2 sin a — S4 sin y

S (sin a + sin y)

Пользуясь очевидной формулой 2S — S1 + S2 + S3 + S4, раскрывая скобки и приводя подобные члены, получим, что

(S1 +S4)sina + (S2 + S3)siny (17)

S (sin a + sin y)

Покажем теперь, что

S1 + S4 — S2 + S3— S. (18)

Рассмотрим трапецию ABCD, диагонали которой пересекаются в точке O. Очевидно, что

S1 + S4 — SABC + SABD — SABC + SABO + SGDA’ Хорошо

известно [2, c. 161], что в трапеции треугольники ABO и OCD равновелики, поэтому равенство приобретет вид S1 + S4 — SABC + SoCD + SODA — — SABC + SADC +S . Равенство S2 + S3 — S доказывается аналогично.

В силу соотношений (18) формула (17) приобретает вид

^ = S sin a + S sin y = 1 S (sin a + sin y)

Итак, если [BC]||[AD], то правая часть формулы (1) приобретает вид: l1 • l2 • sin 0, а в конце раздела 1 было показано, что оно равно S. Теперь теорема доказана.

Рассмотрим полученный результат с различных точек зрения. Прежде всего, формула (1) оставляет двойственное впечатление. С одной стороны, если рассматривать ее общую структуру, то она достаточно проста: площадь выпуклого четырехугольника равна произведению средних линий и синуса угла между ними, деленному на некое выражение. С другой стороны, структура делителя сложна, что делает формулу громоздкой. По-видимому, эта

114

Ястребов А.В., Шабанова М.В. Средние линии четырехугольника…

громоздкость неизбежна, потому что формула связывает в единое целое 12 (!) числовых характеристик четырехугольника: длины сторон, величины углов, длины средних линий, угол между ними и площадь. Конечно, между этими величинами существуют зависимости. Можно было бы ограничиться длинами двух смежных сторон и величинами трех прилегающих к ним углов, а затем выразить через них оставшиеся параметры, но от этого преобразования формула только усложнилась бы.

Интересно, что выражение в знаменателе формулы (1) достаточно красиво, несмотря на свою громоздкость. Стороны и углы входят в него неким регулярным образом; размерности сторон (скажем, в метрах) присутствуют в числителях и знаменателях в равных степенях и сокращаются, так что все выражение становится безразмерным; происхождение слагаемых и сомножителей нетрудно восстановить, обратившись к процессу доказательства.

Подводя итог, можно сказать, что полученная вычислительная формула не является основным результатом наших рассуждений. Главным является обобщение понятия средней линии на случай выпуклого четырехугольника.

Экспериментальная математика и задачи о средних линиях. В процессе постановки задачи мы использовали физические соображения, которые могли бы быть легко продемонстрированы посредством динамической модели, созданной в интерактивной геометрической среде, например в среде «GeoGebra». Выясним, каким образом и насколько глубоко можно исследовать средние линии четырехугольника средствами экспериментальной математики. С этой целью введем новое понятие и сформулируем несколько нерешенных задач по его изучению.

Определение 2. Серединой первого порядка выпуклого четырехугольника назовем новый четырехугольник, вершинами которого являются концевые точки средних линий исходного четырехугольника. Серединой порядка n называется середина середины порядка n — 1.

Например, на рис. 2 (см. с. 111) четырехугольник PRQT является серединой четырехугольника ABCD.

Пусть M(i), i = 1, 2, … — последовательность середин разных порядков. Очевидно, что ABCD з M(1) з M(2) з … . Почти очевидно, что линейные размеры середин стремятся к нулю. Если это так, то по теореме Кантора получим,

что существует и единственна точка Z = р| M(i).

Естественно назвать точку Z центром четырехугольника.

Приведенные рассуждения порождают ряд задач.

Задача 1 состоит из нескольких частей: 1) доказать наличие центра четырехугольника; 2) зная координаты вершин четырехугольника, найти координаты его центра; 3) выявить какую-либо зависимость между сторонами и углами четырехугольника и положением центра.

Пытаясь получить наводящие соображения, авторы построили середины четырехугольника до 10-го порядка включительно (рис. 4) и рассмотрели последовательность точек On, n = 1, 2, … , в которых пересекаются диагонали середин соответствующих порядков. При этом координаты точек On вычислялись с точностью до пяти знаков после запятой.

115

ФИЗИКА. МАТЕМАТИКА. ИНФОРМАТИКА

Эксперимент показал, что при данной точности вычислений (достаточно высокой) точки Оп и On+I становятся неразличимы начиная уже с девятого члена последовательности. Важно, что такой результат не зависит от взаимного расположения вершин исходного четырехугольника. Это подсказывает, что имеет смысл говорить о сходимости изучаемой последовательности точек. Заметим, что компьютерный эксперимент позволяет найти предел этой последовательности с любой точностью, допускаемой компьютером, однако оставляет открытым вопрос о том, как может быть построена точка, являющаяся пределом последовательности {Оп}.

Приведенные рассуждения порождают следующую задачу.

Задача 2. 1) Доказать, что предел последовательности {Оп} существует, и найти его. 2) Доказать, что искомый предел равен Z.

Визуальный анализ середин показал, что с ростом порядка середины она становится все больше и больше «похожа» на параллелограмм. Чтобы наполнить смыслом нематематическое слово «похожа», вспомним один из признаков параллелограмма: четырехугольник является параллелограммом тогда и только тогда, когда его противоположные углы равны.

Эксперимент состоял в следующем. Пусть ап, Рп, уп и 5п — это последовательно расположенные углы середины порядка п. Рассмотрим последовательность чисел {Ап}, где Лп := := тах{|ап — уп|, |Рп — 5п|} Вычисления показывают, что последовательность {Лп}, скорее всего,

стремится к нулю. Это наблюдение порождает задачу 3.

Задача 3. Доказать, что последовательность {Лп} стремится к нулю и, следовательно, середины действительно становятся похожи на параллелограмм.

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Повторимся: утверждения, сформулированные в задачах, являются не более чем гипотезами, которые, впрочем, подтверждены большим количеством примеров. Доказательство их справедливости требует повторного обращения к теоретическим методам. Однако это мы оставим за рамками данной статьи.

Вместо заключения. Вернемся к заглавию нашей статьи: «Средние линии четырехугольника, или Красивое бесполезное обобщение». Как мы уже говорили, представленная в статье формула площади выпуклого четырехугольника вряд ли будет полезна для практики вычислений, несмотря на красоту и гармоничность составляющих ее частей. Тем не менее она достаточно интересна в качестве примера полезных обобщающих рассуждений о средних линиях, которые опираются на физические соображения о динамической изменчивости фигур. По мнению авторов, использование подобных соображений в элементарной геометрии открывает новые возможности в развитии этого, казалось бы, уже завершенного раздела математики. В подтверждение нашего мнения отошлем читателей к работам В. Ненкова и С. Гроздева в области элементарной геометрии [3, 4], а также к электронной энциклопедии центров треугольников К. Кимберлинга [5].

Список литературы

1. Четырехугольники. URL: http://math4school.ru/chetyrehugolniki.html (дата обращения: 21.04.2015).

2. Рыбакова Т.Л., Суслова И.В. Математика: школ. справ. Ярославль, 1997. 333 с.

3. Grozdev S., Nenkov V Three Remarkable Points on the Medians of the Triangle. Sofia, 2012.

4. Grozdev S., Nenkov V About Orthocenter in Plane and Space. Sofia, 2012.

5. Kimberling C. Encyclopedia of Triangle Centers. URL: http://faculty.evansville.edu/ck6/encyclopedia/ETC.html (дата обращения: 21.04.2015).

116

Ястребов А.В., Шабанова М.В. Средние линии четырехугольника…

References

1. Chetyrekhugol’niki [Quadrangles]. Available at: http://math4school.ru/chetyrehugolniki.html (accessed

21.04.2015).

2. Rybakova T.L., Suslova I.V Matematika: shkol’nyy spravochnik [Mathematics: a Guide for Schools]. Yaroslavl, 1997. 333 p.

3. Grozdev S., Nenkov V. Three Remarkable Points on the Medians of the Triangle. Sofia, 2012.

4. Grozdev S., Nenkov V. About Orthocenter in Plane and Space. Sofia, 2012.

5. Kimberling C. Encyclopedia of Triangle Centers. Available at: http://faculty.evansville.edu/ck6/encyclopedia/ ETC.html (accessed 21.04.2015).

Yastrebov Aleksandr Vasil’evich

Yaroslavl State Pedagogical University named after K.D. Ushinsky (Yaroslavl, Russia)

Shabanova Mariya Valer’evna

Institute of Mathematics, Information and Space Technologies, Northern (Arctic) Federal University named after M.V. Lomonosov (Arkhangelsk, Russia)

THE QUADRANGLE MIDLINES, OR ATTRACTIVE USELESS SYNTHESIS

Dedicated to T.M. Korikova

The paper deals with new results concerning the geometry of a convex quadrangle. Considering mathematics as a body of knowledge, we introduce the concept of “the midline of a convex quadrangle” and “the n-th order middle of a convex quadrangle”. The formula expressing the area of a convex quadrangle through the lengths of its midlines and some other numerical characteristics is proved. The peculiarity of the resulting formula is a combination of 12 numerical characteristics. Several hypotheses concerning the sequence of midpoints of a convex quadrangle are formulated and experimentally-confirmed. Thus, we indicate a possible study direction of the geometry of a quadrangle. Considering mathematics as an area of human activity, the paper presents the logic of statement and solution of the investigative problem in the selected area of geometry. In the opinion of the authors the mathematician-theorist and mathematician-experimentalist activities are of great interest. The paper deals with the experimental roots of mathematics. Methodology of the paper includes a complex of complementary methods: considerations of the alteration of figures, comparison of some mathematical formulas from the viewpoint of their stability under deformations, a method of theoretical synthesis, and experimental methods. All hypotheses for the convex quadrangle properties have been obtained as a result of the computer experiment in the interactive geometric environment «GeoGebra». Hence, the use of computers generates new investigative ideas in the elementary geometry.

Keywords: elementary geometry, convex quadrangle, synthesis, computer experiment, multitemporal model.

Контактная информация: Ястребов Александр Васильевич адрес: 150000, г. Ярославль, ул. Республиканская, д. 108;

е-mail: a.yastrebov@yspu.org

Шабанова Мария Валерьевна адрес: 163060, г. Архангельск, ул. Урицкого, д. 68В;

е-mail: m.shabanova@narfu.ru

117

Источник

Слайд 1

Средние линии четырехугольников и их свойства Выполнил: Матвеев Дмитрий Учитель: Рычкова Татьяна Викторовна Лицей «Дубна» 9ИМ 2007 Средние линии и Параллелограмм Вариньона Другие свойства средней линии четырехугольника Краткий перечень всех теорем и свойств

Слайд 2

Что такое параллелограмм Вариньона? Это параллелограмм, вершины которого являются серединами сторон четырехугольника Иначе: это параллелограмм, диагоналями которого являются средние линии четырехугольника

Слайд 3

A B C D N M L K P Доказательство: Соединим точки K, L, M, N и проведем диагональ АС; В ∆ACD NM – средняя линия, значит NM  AC и NM=1/2 AC; В ∆ABC KL – средняя линия, значит KL  AC и KL=1/2 AC; NM=1/2 AC=KL, NM  AC  KL, значит четырехугольник KLMN ‑ параллелограмм. A L B M C D K P N Доказательство: Соединим точки K, L, M, N и проведем диагональ DB; В ∆CDB NM – средняя линия, значит NM  DB и NM=1/2 DB; В ∆ADC KL – средняя линия, значит KL  DB и KL=1/2 DB; NM=1/2 DB=KL, NM  DB  KL, значит четырехугольник KLMN ‑ параллелограмм. Докажем, что KLMN – параллелограмм Вариньона, при KM и NM – средних линиях ABCD.

Слайд 4

А значит… Так как четырехугольник KLMN – параллелограмм Вариньона, то его диагонали в точке пересечения делятся пополам Средние линии любого четырехугольника делятся пополам

Слайд 5

Следствия: 1. Если средние линии четырехугольника равны, то середины сторон четырехугольника (вершины параллелограмма Вариньона) лежат на одной окружности. Доказательство: Так как в параллелограмме Вариньона равные средние линии являются равными диагоналями, то этот параллелограмм – прямоугольник, а вокруг него всегда можно описать окружность, значит его вершины лежат на одной окружности.

Слайд 6

Следствия: 2. Если средние линии четырехугольника перпендикулярны, то диагонали четырехугольника равны. Доказательство: Так как NL┴KM и NL с KM диагонали в параллелограмме KLMN , то KLMN – ромб. По этому KL = LM = MN = NK . Так как AC =2 KL и BD =2 NK , то AC = BD . A K B L C M D N P O A P K C D M N L B

Слайд 7

Следствия: A K B L C M D N P O A P K C D M N L B 3. Если диагонали четырехугольника равны, то средние линии четырехугольника перпендикулярны. Доказательство: Так как AC =2 MN =2 KL , BD =2 NK =2 ML и AC = BD , то KL = LM = MN = NK . Значит KLMN – ромб, а в ромбе диагонали перпендикулярны, то есть NL┴KM.

Слайд 8

Для примера: Решая такую задачу, пришлось бы сильно потрудится, не зная одно из свойств параллелограмма Вариньона:

Слайд 9

Какова же площадь параллелограмма Вариньона? Доказательство для выпуклого четырехугольника: Рассмотрим ∆ABD и ∆ANK: а).

Слайд 10

Какова же площадь параллелограмма Вариньона? Доказательство для невыпуклого четырехугольника: Рассмотрим ∆ABD и ∆ANK: а).

Слайд 11

S KLMN =1/2 S ABCD Значит площадь параллелограмма Вариньона равна половине площади четырехугольника, чьи средние линии являются его диагоналями. Следствие: площади четырехугольников с равными средними линиями равны. Следствие: площадь четырехугольника равна произведению его средних линий на синус угла между ними.

Слайд 12

Для примера: Теперь можно решить задачу в два шага: 1. S пар. Вариньона равна 15*18=270 см в кв. 2. S ABCD = 2*270= =540 см в кв.

Слайд 13

Какова длина средней линии? A D C F B G E Пусть EF – средняя линия четырехугольника ABCD (EA=ED, FB=FC , AB не параллельна DC); Тогда : NL= ND + DA + AL и NL = NC + CB + BL Сложим эти равенства и получим: 2NL = DA + CB Значит вектора 2NL, DA и CB являются сторонами треугольника При параллельном переносе векторов DC и 2EF получатся равные им вектора BG и AG , которые вместе с вектором AB образуют ∆ AGB , где по неравенству треугольника получим: AG<=AB+BG , откуда : EF<1/2 (AB+CD). Если же AB параллельна DC , то ABCD — трапеция (или параллелограмм) с основаниями AB и DC , тогда: EF = 1/2 (AB+CD). Значит EF< = 1/2 (AB+CD) , то есть: Длина средней линии четырехугольника не превышает полусуммы длин сторон, не соединенных ею.

Слайд 14

Свойство углов Проведем отрезок KD = BC и параллельный ему. Тогда BCDK – параллелограмм. Значит CD = BK и CD  BK . Отсюда < PSC =< ABK . Соединим точки А и К, затем на середине отрезка АК поставим точку L . Рассмотрим ∆АВК: а). АВ= CD = BK , значит ∆ равнобедренный. б). Поэтому медиана BL является биссектрисой, то есть < ABL =< LBK , значит < PSC =< ABK =2*< ABL и < QSP =180°-2*< ABL . Проведем отрезок LM . Так как LM является средней линией ∆ AKD , то LM =½ KD =½ BC = BN и LM  KD  BC  BN , значит BLMN – параллелограмм, поэтому BL  MN . Отсюда < ABL =< BPM =< QPS . Рассмотрим ∆ QPS : а). < QPS =< ABL б). < QSP =180°-2*< ABL с). Значит < PQS =180°-< QSP -< QPS = =180°-(180°- 2*< ABL )-< ABL =< ABL =< BP N Q S P N C D K A B L M Если 4-хугольнике две противоположные стороны равны и не параллельны, то прямая, включающая в себя среднюю линию, не проходящую через эти стороны, образует с продолжениями этих сторон равные углы Докажем, что при AB=CD,

Слайд 15

Краткий перечень всех теорем и свойств: Средние линии любого четырехугольника делятся пополам Если средние линии четырехугольника равны, то середины сторон четырехугольника (вершины параллелограмма Вариньона) лежат на одной окружности. Если средние линии четырехугольника перпендикулярны, то диагонали четырехугольника равны. Если диагонали четырехугольника равны, то средние линии четырехугольника перпендикулярны. Значит площадь параллелограмма Вариньона равна половине площади четырехугольника, чьи средние линии являются его диагоналями. Площади четырехугольников с равными средними линиями равны. Площадь четырехугольника равна произведению его средних линий на синус угла между ними. Длина средней линии четырехугольника не превышает полусуммы длин сторон, не соединенных ею. Если 4-хугольнике две противоположные стороны равны и не параллельны, то прямая, включающая в себя среднюю линию, не проходящую через эти стороны, образует с продолжениями этих сторон равные углы

Источник

ЧЕТЫРЁХУГОЛЬНИКИ
┌─────────────┼────────────┐
невыпуклый	выпуклый	самопересекающийся

┌─────────────┼─────────────┐

вписанный	трапеция	описанный
\| ┌───────────┤	\|

равнобедренная трапеция равнобокая	параллелограмм стороны параллельны	антипараллелограмм стороны антипараллельны	выпуклый ромбоид (дельтоид) диагонали перпендикулярны

└─────┬─────┘	└─────┬─────┘
прямоугольник прямые углы	ромб равнобедренный
└──────────┬─────────┘
квадрат

Четырёхугольник (греч. τετραγωνον) — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки. Различают выпуклые и невыпуклые четырёхугольники, невыпуклый четырёхугольник может быть самопересекающимся (см. рис.). Четырёхугольник без самопересечений называется простым, часто под термином «четырёхугольник» имеется в виду только простые четырёхугольники^[1].

Содержание

1 Виды четырёхугольников
- 1.1 Некоторые обозначения и сокращения
- 1.2 Некоторые симметричные четырёхугольники
2 Полный четырёхсторонник
3 Сумма углов
4 Метрические соотношения
- 4.1 Неравенство четырёхугольника
- 4.2 Неравенство Птолемея
- 4.3 Теорема Гаусса
- 4.4 Соотношения между сторонами и диагоналями четырёхугольника
- 4.5 Соотношения Бретшнайдера
- 4.6 Теоремы о средних линиях четырёхугольника
- 4.7 Окружности девяти точек треугольников внутри четырёхугольника
5 Частные случаи четырёхугольников
- 5.1 Четырёхугольники, вписанные в окружность
- 5.2 Четырёхугольники, вписанные в окружность с перпендикулярными диагоналями (вписанные ортодиагональные четырёхугольники)
- 5.3 Четырёхугольники, описанные около окружности
- 5.4 Вписано-описанные четырёхугольники
- 5.5 Свойства
- 5.6 Четырёхугольники с перпендикулярными сторонами
- 5.7 Четырёхугольники с перпендикулярными диагоналями
6 Внеописанный четырёхугольник
- 6.1 Свойства диагоналей некоторых четырёхугольников
7 Площадь
- 7.1 История
8 См. также
9 Примечания
10 Литература

Виды четырёхугольников

Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
- Прямоугольник — четырёхугольник, у которого все углы прямые;
- Ромб — четырёхугольник, у которого все стороны равны;
- Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.
Антипараллелограмм, или контрпараллелограмм — четырёхугольник, в котором каждые две противоположные стороны равны между собою, но не параллельны, в отличие от параллелограмма. В антипараллелограмме две пары противоположных сторон антипараллельны.

Некоторые обозначения и сокращения

Вместо слова «Четырёхугольник» возможно использование некоторых обозначений и сокращений: четырёхугол, четырёхуг, 4-к, символ «» или « ♢» ^[2].

Некоторые симметричные четырёхугольники

На рис. показаны некоторые симметричные четырёхугольники, их переход друг в друга, а также дуальные к ним. Обозначения на рис.:

Kite (змей) — дельтоид (ромбоид)
Parallelogram — параллелограмм
Irregular quadrilateral — неправильный четырёхугольник
Rhombus — ромб
Rectangle — прямоугольник
Square — квадрат
Gyrational Square — вращающийся квадрат
Isosceles Trapezoid — равнобедренная трапеция

Полный четырёхсторонник

Хотя такое название может быть эквивалентно четырёхугольнику, в него часто вкладывают дополнительный смысл. Четвёрка прямых, никакие две из которых не параллельны и никакие три не проходят через одну точку, называется полным четырёхсторонником. Такая конфигурация встречается в некоторых утверждениях евклидовой геометрии (например, теорема Менелая, прямая Гаусса, прямая Обера, теорема Микеля и др.), в которых часто все прямые являются взаимозаменяемыми.

Сумма углов

Сумма углов четырёхугольника без самопересечений равна 360°.

${displaystyle sum _{i=1}^{4}alpha _{i}=(4-2)cdot 180^{circ }=2cdot 180^{circ }=360^{circ }}$

Метрические соотношения

Неравенство четырёхугольника

Модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других сторон.

Эквивалентно: в любом четырёхугольнике (включая вырожденный) сумма длин трёх его сторон не меньше длины четвёртой стороны, то есть
^[3]:

;

;

;

Равенство в неравенстве четырёхугольника достигается только в том случае, если он вырожденный, то есть все четыре его вершины лежат на одной прямой.

Неравенство Птолемея

Для сторон a,b,c,d и диагоналей выпуклого четырёхугольника выполнено неравенство Птолемея:

причём равенство достигается тогда и только тогда, когда выпуклый четырёхугольник вписан в окружность или его вершины лежат на одной прямой.

Теорема Гаусса

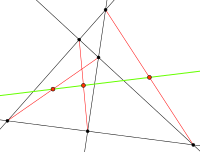
Если в четырёхугольнике две пары противоположных сторон не параллельны, то две середины его диагоналей лежат на прямой, которая проходит через середину отрезка, соединяющего две точки пересечения этих двух пар противоположных сторон (на рисунке точки показаны красным цветом). Указанная прямая называется прямой Гаусса (на рисунке она показана зелёным цветом). При этом прямая Гаусса всегда перпендикулярна прямой Обера.

Соотношения между сторонами и диагоналями четырёхугольника

Шесть расстояний между четырьмя произвольными точками плоскости, взятыми попарно, связаны соотношением:

$a^{2}c^{2}left(b^{2}+d^{2}+e^{2}+f^{2}-a^{2}-c^{2}right)+b^{2}d^{2}left(a^{2}+c^{2}+e^{2}+f^{2}-b^{2}-d^{2}right)+$

$+e^{2}f^{2}left(a^{2}+c^{2}+b^{2}+d^{2}-e^{2}-f^{2}right)=(abe)^{2}+(bcf)^{2}+(cde)^{2}+(daf)^{2}$

Это соотношение можно представить в виде определителя:

$left|{begin{matrix}0&a^{2}&e^{2}&d^{2}&1\a^{2}&0&b^{2}&f^{2}&1\e^{2}&b^{2}&0&c^{2}&1\d^{2}&f^{2}&c^{2}&0&1\1&1&1&1&0end{matrix}}right|=0$

Замечание. Последний определитель с точностью до множителя 288 представляет собой выражение для квадрата объёма тетраэдра через длины его рёбер с помощью определителя Кэли-Менгера. Если тетраэдр уложен в плоскость, то он имеет нулевой объём и превращается в четырёхугольник. Длины рёбер будут длинами сторон или диагоналей четырёхугольника.

Соотношения Бретшнайдера

Соотношения Бретшнайдера — соотношение между сторонами a, b, c, d и противоположными углами и диагоналями e, f простого (несамопересекающегося) четырёхугольника:

$e^{2}f^{2}=a^{2}c^{2}+b^{2}d^{2}-2abcdcos(angle A+angle C)$

$e^{2}f^{2}=(ac+bd)^{2}-4abcdcos ^{2}{frac {angle A+angle C}{2}}$

$e^{2}f^{2}=(ac-bd)^{2}+4abcdsin ^{2}{frac {angle A+angle C}{2}}$

Теоремы о средних линиях четырёхугольника

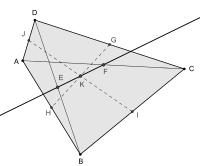
Пусть G, I, H, J — середины сторон выпуклого четырёхугольника ABCD, а E, F — середины его диагоналей. Назовем три отрезка GH, IJ, EF соответственно первой, второй и третьей средними линиями четырёхугольника. Первые две из них также называют бимедианами^[4].

Точки E, K, F лежат на одной прямой, прямой Ньютона

Обобщенная теорема Ньютона. Все три средние линии четырёхугольника пересекаются в одной точке (в центроиде вершин («vertex centroid») четырёхугольника) и делятся ею пополам.
Середины E и F двух диагоналей, а также центроид вершин K выпуклого четырёхугольника лежат на одной прямой EF. Указанная прямая называется прямой Ньютона.
Теорема Вариньона (геометрия)^[3]:
Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумма квадратов его диагоналей.
Математически для рисунка слева с серым четырёхугольником ABCD формула Эйлера записывается в виде:

$(2EF)^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}-BD^{2}-AC^{2}$ .
Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
Смотрите также свойства центроида четырёхугольника.

Окружности девяти точек треугольников внутри четырёхугольника

В произвольном выпуклом четырёхугольнике ABCD окружности девяти точек треугольников , на которые его разбивают две диагонали, пересекаются в одной точке ^[5].

Частные случаи четырёхугольников

Четырёхугольники, вписанные в окружность

Говорят, что если около четырёхугольника можно описать окружность, то четырёхугольник вписан в эту окружность, и наоборот.
Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна 180°, то есть:

${displaystyle angle A+angle C=angle B+angle D=180^{circ }}$

Две теоремы Птолемея. Для простого (несамопересекающегося) четырёхугольника, вписанного в окружность, имеющего длины пар противоположных сторон: a и c, b и d, а также длины диагоналей e и f, справедливы:

1) Первая теорема Птолемея:

;

2) Вторая теорема Птолемея:
${frac {e}{f}}={frac {acdot d+bcdot c}{acdot b+ccdot d}}.$
В последней формуле пары смежных сторон числителя a и d, b и c опираются своими концами на диагональ длиной e. Аналогичное утверждение имеет место для знаменателя.
3) Формулы для длин диагоналей (следствия первой и второй теорем Птолемея):

${displaystyle e={sqrt {frac {(ac+bd)(ad+bc)}{ab+cd}}}}$

и ${displaystyle f={sqrt {frac {(ac+bd)(ab+cd)}{ad+bc}}}}$

Если выпуклый четырёхугольник вписан в некоторую окружность, то в ту же самую окружность вписаны и пара треугольников, на которые разбивает четырёхугольник любая из его диагоналей (связь с окружностями треугольника).
Из последнего утверждения следует: если три из четырёх медиатрис (или срединных перпендикуляров), проведенных к сторонам выпуклого четырёхугольника, пресекаются в одной точке, то в той же точке пресекается и медиатриса его четвёртой стороны. Более того, такой четырёхугольник вписан в некоторую окружность, центр которой находится в точке пресечения указанных медиатрис ^[6].

Теорема Микеля-Штейнера для четырёхстронника

Выпуклый четырёхугольник (см. рис. справа), образованный четырьмя данными прямыми Микеля, вписан в окружность тогда и только тогда, когда точка Микеля M четырёхугольника лежит на прямой, соединяющей две из шести точек пересечения прямых (те, которые не являются вершинами четырёхугольника). То есть, когда M лежит на EF.
Прямая, антипараллельная стороне треугольника и пересекающая его, отсекает от него четырёхугольник, около которого всегда можно описать окружность.
Площадь вписанного в окружность четырёхугольника:
- Площадь вписанного в окружность четырёхугольника по формуле Брахмагупты равна^[7]:

где p — полупериметр четырёхугольника.

- Последняя формула следует из общей формулы (1) в рамке в параграфе «Площадь», если в ней учесть, что ${displaystyle 2theta =angle A+angle C=angle B+angle D=180^{circ }}$
- Последняя формула есть обобщение формулы Герона на случай четырёхугольника.
- Формула Брахмагупты для площади вписанного в окружность четырёхугольника может быть записана через определитель ^[6]:

$S={frac {1}{4}}{sqrt {-{begin{vmatrix}a&b&c&-d\b&a&-d&c\c&-d&a&b\-d&c&b&aend{vmatrix}}}}$

Из последней формулы при d=0 автоматически получается формула Дроздова В. ^[8]^[9] для формулы Герона:
Радиус окружности, описанной около четырёхугольника:

$R={frac {1}{4}}{sqrt {frac {(ab+cd)(ad+bc)(ac+bd)}{(p-a)(p-b)(p-c)(p-d)}}}$

Японская теорема (Japanese theorem)

Теорема^[10]. Если во вписанном в окружность четырёхугольнике провести диагональ, а в полученные два треугольника вписать две окружности, затем аналогично поступить, проведя вторую диагональ, тогда центры четырёх образовавшихся окружностей являются вершинами прямоугольника (то есть лежат на одной окружности). Эту теорему называют японской теоремой (Japanese theorem). (см. рис.). Кроме того, ортоцентры четырёх описанных здесь четырёх треугольников являются вершинами четырёхугольника, подобного исходному четырёхугольнику ABCD (то есть также лежат на другой окружности, ибо вершины исходного вписанного четырёхугольника лежат на некоторой окружности). Наконец, центроиды этих четырёх треугольников лежат на третьей окружности^[11].
Теорема ^[12]. Пусть — вписанный четырёхугольник, $A_{1}$ — основание перпендикуляра, опущенного из вершины на диагональ ; аналогично определяются точки ${displaystyle B_{1},C_{1},D_{1}}$ . Тогда точки ${displaystyle A_{1},B_{1},C_{1},D_{1}}$ лежат на одной окружности.
Условие, при котором совмещение двух треугольников с одной равной стороной даёт четырёхугольник, вписанный в окружность^[13]. Для того, чтобы два треугольника с тройками длин сторон соответственно (a, b, f) и (c, d, f) при их совмещении вдоль общей стороны с длиной, равной f, давали в итоге четырёхугольник, вписанный в окружность с последовательностью сторон (a, b, c, d), необходимо условие^[14]^:84

${displaystyle f^{2}={frac {(ac+bd)(ad+bc)}{(ab+cd)}}.}$

Последнее условие дает выражение для диагонали f четырёхугольника, вписанного в окружность, через длины четырёх его сторон (a, b, c, d). Эта формула немедленно следует при перемножении и при приравнивании друг другу левых и правых частей формул, выражающих суть первой и второй теорем Птолемея (см. выше).
Частными четырёхугольниками, вписанными в окружность, являются: прямоугольник, квадрат, равнобедренная или равнобочная трапеция, антипараллелограмм.
Подробнее о четырёхугольниках, вписанных в окружность можно почитать в статье «Вписанный четырёхугольник».

Четырёхугольники, вписанные в окружность с перпендикулярными диагоналями (вписанные ортодиагональные четырёхугольники)

Для вписанных ортодиагональных четырёхугольников справедлива теорема Брахмагупты:

Если вписанный четырёхугольник имеет перпендикулярные диагонали, пересекающиеся в точке , то две пары его антимедиатрис проходят через точку .

Замечание. В этой теореме под антимедиатрисой^[15] понимают отрезок четырёхугольника на рисунке справа (по аналогии с серединным перпендикуляром (медиатрисой) к стороне треугольника). Он перпендикулярен одной стороне и одновременно проходит через середину противоположной ей стороны четырёхугольника.

Известна теорема: Если в четырёхугольнике перпендикулярны диагонали, то на одной окружности (окружность восьми точек четырёхугольника) лежат восемь точек: середины сторон и проекции середин сторон на противоположные стороны ^[16]. Из этой теоремы и теоремы Брахмагупты следует, что концы двух пар антимедиатрис (восемь точек) вписанного ортодиагонального четырёхугольника лежат на одной окружности (окружность восьми точек четырёхугольника).
Частными вписанными ортодиагональными четырёхугольниками, вписанными в окружность, являются квадрат, дельтоид с парой перпендикулярных противоположных углов, равнобокая ортодиагональная трапеция и другие.

Четырёхугольники, описанные около окружности

Говорят, что если в четырёхугольник можно вписать окружность, то четырёхугольник описан около этой окружности, и наоборот.
Некоторые (но не все) четырёхугольники имеют вписанную окружность. Они называются описанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важным является то, что суммы противоположных сторон равны. Это утверждение называется теоремой Пито.
Иными словами, выпуклый четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны, то есть: .
Точки касания вписанной окружности с четырёхугольником отсекают равные отрезки от углов четырёхугольника.
Площадь описанного четырёхугольника

Вводя понятие полупериметра p, имеем . Следовательно, также имеем . Далее можно заметить: Следовательно, Тогда по формуле (1) в рамке в параграфе «Площадь» имеем

$S={sqrt {(p-a)(p-b)(p-c)(p-d)-abcdcos ^{2}theta }}=$

$={sqrt {abcd-abcdcos ^{2}theta }}={sqrt {abcdsin ^{2}theta }}={sqrt {abcd}}sin theta .$

- Поскольку четырёхугольник описан, то его площадь также равна половине периметра p, умноженной на радиус r вписанной окружности: .
Если выпуклый четырёхугольник — не трапеция и не параллелограмм и он описан около некоторой окружности, то около этой же самой окружности описаны и пара треугольников, которые получаются при продолжении двух его пар противоположных сторон до их пересечения (связь с окружностями треугольника).
Из последнего утверждения следует: если три из четырёх биссектрис (или биссекторов), проведенных для внутренних углов выпуклого четырёхугольника, пресекаются в одной точке, то в той же точке пресекается и биссектриса его четвёртого внутреннего угла. Более того такой четырёхугольник описан около некоторой окружности, центр которой находится в точке пресечения указанных биссектрис^[17].
Если четырёхугольник является описанным около окружности, то центр его вписанной окружности лежит на прямой Ньютона. Более точное утверждение ниже.
Во всяком описанном четырёхугольнике две середины диагоналей и центр вписанной окружности лежат на одной прямой (теорема Ньютона). На ней же лежит середина отрезка с концами в точках пересечения продолжений противоположных сторон четырёхугольника (если они не параллельны). Эта прямая называется прямой Гаусса. На рисунке (вторая группа рисунков сверху) она зелёная, диагонали красные, отрезок с концами в точках пересечения продолжений противоположных сторон четырёхугольника тоже красный.
Центр описанной около четырёхугольника окружности — точка пересечения высот треугольника с вершинами в точке пересечения диагоналей и точках пересечения противоположных сторон (теорема Брокара).
Частными четырёхугольниками, описанными около окружности, являются: ромб, квадрат, дельтоид.

Вписано-описанные четырёхугольники

Вписано-описанные четырёхугольники ABCD и EFGH и Поризм Понселе для них

Вписано-описанные четырёхугольники^[en] — четырёхугольники, которые могут быть одновременно описаны около некоторой окружности, а также вписаны в некоторую окружность. Другие их названия — бицентрические четырёхугольники (Bicentric quadrilateral), хордо-касающиеся четырёхугольники (chord-tangent quadrilateral) или двух-окружностные четырёхугольники (double circle quadrilateral).

Свойства

Любое одно из двух указанных ниже условий по отдельности является необходимым, но не достаточным условием для того, чтобы данный выпуклый четырёхугольник был вписанно-описанным для некоторых окружностей:

и ${displaystyle angle A+angle C=angle B+angle D=180^{circ }}$ .

Выполнение двух последних условий одновременно для некоторого выпуклого четырёхугольника является необходимым и достаточным для того, чтобы данный четырёхугольник был вписанно-описанным.
Площадь вписанно-описанного четырёхугольника:

${displaystyle S={frac {p^{2}}{operatorname {tg} {frac {A}{2}}+operatorname {tg} {frac {B}{2}}+operatorname {tg} {frac {C}{2}}+operatorname {tg} {frac {D}{2}}}}}$

Теорема Фусса (Fuss’ theorem).

Вписано-описанный четырёхугольник ABCD с центром I вписанной и с центром O описанной окружностей

Для радиусов R и r соответственно описанной и вписанной окружностей данного четырёхугольника и расстояния x между центрами и этих окружностей (см. рис.) выполняется соотношение, представляющее четырёхугольниковый аналог теоремы Эйлера (аналогичная формула Эйлера есть для треугольника)^[18]^[19]^[20]:

${displaystyle {frac {1}{(R+x)^{2}}}+{frac {1}{(R-x)^{2}}}={frac {1}{r^{2}}}}$

или

${displaystyle displaystyle 2r^{2}(R^{2}+x^{2})=(R^{2}-x^{2})^{2}.}$

или

${displaystyle x^{2}=R^{2}+r^{2}-r{sqrt {4R^{2}+r^{2}}}}$

или

${displaystyle x={sqrt {R^{2}+r^{2}-r{sqrt {4R^{2}+r^{2}}}}}.}$

Вписанно-описанный четырёхугольник ABCD и его внутренне-касающийся вписанный четырёхугольник WXYZ

Частным вписанно-описанным четырёхугольником является квадрат.

Четырёхугольники с перпендикулярными сторонами

Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
Если у выпуклого четырёхугольника перпендикулярны две пары смежных сторон (то есть два противоположных угла прямые), то этот четырёхугольник может быть вписан в некоторую окружность. Более того, диаметром этой окружности будет служить диагональ, на которую опираются одними концами указанные две пары смежных сторон.
Частными четырёхугольниками с перпендикулярными сторонами являются: прямоугольник и квадрат.

Четырёхугольники с перпендикулярными диагоналями

Четырёхугольники с перпендикулярными диагоналями называются ортодиагональными четырёхугольниками.
Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
Площадь ортодиагонального четырёхугольника равна половине произведения его диагоналей: ${displaystyle S={frac {1}{2}}ef.}$ .
Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.
Антимедиатрисой четырёхугольника называются отрезок прямой, выходящий из середины одной его стороны и перпендикулярный противоположной ей стороне.
Теорема Брахмагупты. Если у четырёхугольника перпендикулярны диагонали и он может быть вписан в некоторую окружность, то четыре его антимедиатрисы пересекаются в одной точке. Более того, этой точкой пересечения антимедиатрис является точка пересечения его диагоналей.
Если у четырёхугольника перпендикулярны диагонали и он может быть вписан в некоторую окружность, то учетверенный квадрат её радиуса R равен сумме квадратов любой пары противоположных его сторон: ${displaystyle a^{2}+c^{2}=b^{2}+d^{2}=4R^{2}.}$
Если у четырёхугольника перпендикулярны диагонали и он может быть описан около некоторой окружности, то у него равны произведения двух пар противоположных сторон:
Параллелограмм Вариньона с вершинами в серединах сторон ортодиагонального четырёхугольника является прямоугольником.
Если в четырёхугольнике перпендикулярны диагонали, то на одной окружности (окружность восьми точек четырёхугольника) лежат восемь точек: середины сторон и проекции середин сторон на противоположные стороны ^[16].
Частными ортодиагональными четырёхугольниками являются: ромб, квадрат, дельтоид.
Если у выпуклого четырёхугольника перпендикулярны диагонали, то середины четырёх его сторон являются вершинами прямоугольника (следствие теоремы Вариньона). Верно и обратное. Кроме того, у прямоугольника равны диагонали. Следовательно, у выпуклого четырёхугольника диагонали перпендикулярны тогда и только тогда, когда у него равны между собой длины двух его бимедиан (длины двух отрезков, соединяющих середины противоположных сторон)^[22].
Таблица сравнения свойств описанного и ортодиагонального четырёхугольника:

Их метрические свойства очень похожи (см. табл.)^[22] Здесь обозначены: a, b, c, d — длины их сторон, R₁, R₂, R₃, R₄, и радиусы описанных окружностей, проведенных через эти стороны и через точку пересечения диагоналей, h₁, h₂, h₃, h₄ — высоты, опущенные на них из точки пересечения диагоналей.

описанный четырёхугольник	ортодиагональный четырёхугольник
	${displaystyle a^{2}+c^{2}=b^{2}+d^{2}}$
${displaystyle R_{1}+R_{3}=R_{2}+R_{4}}$	${displaystyle R_{1}^{2}+R_{3}^{2}=R_{2}^{2}+R_{4}^{2}}$
${displaystyle {frac {1}{h_{1}}}+{frac {1}{h_{3}}}={frac {1}{h_{2}}}+{frac {1}{h_{4}}}}$	${displaystyle {frac {1}{h_{1}^{2}}}+{frac {1}{h_{3}^{2}}}={frac {1}{h_{2}^{2}}}+{frac {1}{h_{4}^{2}}}}$

Кроме того, для медиан на стороны ортодиагонального четырёхугольника, опущенных из из точки пересечения диагоналей, верно: ${displaystyle m_{1}^{2}+m_{3}^{2}=m_{2}^{2}+m_{4}^{2}}$ .

Внеописанный четырёхугольник

Внеописанный четырёхугольник — это выпуклый четырёхугольник, продолжения всех четырёх сторон которого являются касательными к окружности (вне четырёхугольника)^[23]. Окружность называется вневписанной. Центр вневписанной окружности лежит на пересечении шести биссектрис.
Замечание. Вписанную, описанную, а также вневписанную окружности можно провести не у всякого четырёхугольника. Если противоположные стороны выпуклого четырёхугольника ABCD пересекаются в точках E и F, то условием его внеописанности является любое из двух условий ниже:

{displaystyle AB+BC=AD+DCquad Leftrightarrow quad AE+EC=AF+FC.}

Свойства диагоналей некоторых четырёхугольников

В следующей таблице указано, есть ли у диагоналей некоторых из самых основных четырёхугольников деление пополам в точке их пересечения, есть ли перпендикулярность диагоналей, есть ли равенство длин диагоналей, и есть ли деление ими углов пополам.^[24] Список относится к наиболее общих случаев, и исчерпывает собой названные подмножества четырёхугольников.

Четырёхугольник	Деление диагоналей пополам в точке их пересечения	Перпендикулярность диагоналей	Равенство длин диагоналей	Деление углов пополам диагоналями
Трапеция	Нет	См. замечание 1	Нет	Нет
Равнобедренная трапеция	Нет	См. замечание 1	Да	Хотя бы двух противоположных углов
Параллелограмм	Да	Нет	Нет	Нет
Дельтоид	См. замечание 2	Да	См. замечание 2	См. замечание 2
Прямоугольник	Да	Нет	Да	Нет
Ромб	Да	Да	Нет	Да
Квадрат	Да	Да	Да	Да

Замечание 1: Наиболее общие трапеции и равнобедренные трапеций не имеют перпендикулярных диагоналей, но есть бесконечное число (неподобных) трапеций и равнобедренных трапеций, которые действительно имеют перпендикулярные диагонали и не похожи на какой-либо другой названный четырёхугольник.
Замечание 2: У дельтоида одна диагональ делит пополам другую. Другая же диагональ делит его противоположные углы пополам. Наиболее общий дельтоид имеет неодинаковые диагонали, но есть бесконечное число (неподобных) дельтоидов, у которых диагонали равны по длине (и дельтоиды не являются каким-либо другим из названных четырёхугольников).

Площадь

$S={frac {d_{1}d_{2}sin alpha }{2}}$

${displaystyle S_{ABCD}=GHcdot IJsin phi }$

Замечание. Первая и вторая средние линии четырёхугольника — отрезки, соединяющие середины его противоположных сторон

Площадь произвольного выпуклого четырёхугольника равна^[7]:

$16S^{2}=4d_{1}^{2}d_{2}^{2}-left(b^{2}+d^{2}-a^{2}-c^{2}right)^{2}$

, где $d_{1}$

, $d_{2}$

— длины диагоналей, a, b, c, d — длины сторон.

Площадь произвольного выпуклого четырёхугольника также равна

$S={sqrt {(p-a)(p-b)(p-c)(p-d)-abcdcos ^{2}theta }},$ (1)

где p — полупериметр, а $theta ={frac {angle A+angle C}{2}}$ есть полусумма противоположных углов четырёхугольника (Какую именно пару противоположных углов взять роли не играет, так как если полусумма одной пары противоположных углов равна theta , то полусумма двух других углов будет $180^{circ }-theta$ и $cos ^{2}(180^{circ }-theta )=cos ^{2}theta$ ). Из этой формулы для вписанных 4-угольников следует формула Брахмагупты.

Площадь произвольного выпуклого четырёхугольника по формуле (1) в рамке выше с учетом одного из соотношений Бретшнайдера (см. выше) может быть записана в виде:

$S={sqrt {(p-a)(p-b)(p-c)(p-d)+textstyle {1 over 4}((ef)^{2}-(ac+bd)^{2})}}=$

где p — полупериметр, e и f -диагонали четырёхугольника.

История

В древности египтяне и некоторые другие народы использовали для определения площади четырёхугольника неверную формулу — произведение полусумм его противоположных сторон a, b, c, d^[25]:

$S={frac {a+c}{2}}cdot {frac {b+d}{2}}$

Для непрямоугольных четырёхугольников эта формула даёт завышенное значение площади. Можно предположить, что она использовалась только для определения площади почти прямоугольных участков земли. При неточном измерении сторон прямоугольника эта формула позволяет повысить точность результата за счет усреднения исходных измерений.

См. также

Глоссарий планиметрии
категория «Окружности»
Лемма о шестой окружности
Неравенство Птолемея
Окружность
Прямая Гаусса
Прямая Обера
Параллелограмм Вариньона
Теорема Тебо 1
Соотношение Бретшнайдера
Теорема Кейси
Теорема косинусов для четырёхугольника
Теорема Ньютона (планиметрия)
Теорема о бабочке
Теорема Птолемея
Точка Микеля
Треугольник
Вписанный четырёхугольник

Примечания

↑ Яков Понарин. Элементарная геометрия. Том 1: Планиметрия, преобразования плоскости. — Litres, 2018-07-11. — С. 52. — 312 с.
↑ Стариков, 2016, с. 95—97.
↑ ¹ ² Четырёхугольники.
↑ E.W. Weisstein. Bimedian. MathWorld – A Wolfram Web Resource.
↑ Заславский, Пермякова и др., 2009, с. 118, задача 9.
↑ ¹ ² Стариков, 2014, с. 38, правая колонка, пункт 7.
↑ ¹ ² Понарин, с. 74.
↑ Дроздов, 1995, с. обложка.
↑ Мухлаев, 2006, с. 8.
↑ Ayeme, с. 6, Упр. 8, рис. 13.
↑ Andreescu, Titu & Enescu, Bogdan (2004), «2.3 Cyclic quads», Mathematical Olympiad Treasures, Springer, сс. 44–46, 50, ISBN 978-0-8176-4305-8
↑ Ayeme, с. 5, Упр. 7, рис. 11, следствие.
↑ См. подраздел «Диагонали» статьи «Вписанный четырёхугольник»
↑ Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ. Co., 2007
↑ Стариков, 2014, с. 7—39.
↑ ¹ ² Заславский, Пермякова и др., 2009, с. 118, задача 11.
↑ Стариков, 2014, с. 39, левая колонка, последний абзац.
↑ Dörrie, Heinrich. 100 Great Problems of Elementary Mathematics: Their History and Solutions. — New York : Dover, 1965. — P. 188–193. — ISBN 978-0-486-61348-2.
↑ Yiu, Paul, Euclidean Geometry, [1], 1998, pp. 158—164.
↑ Salazar, Juan Carlos (2006), «Fuss’s Theorem», Mathematical Gazette Т. 90 (July): 306–307.
↑ Josefsson, Martin (2010), «Characterizations of Bicentric Quadrilaterals», Forum Geometricorum Т. 10: 165–173, <http://forumgeom.fau.edu/FG2010volume10/FG201019.pdf>.
↑ ¹ ² Josefsson, Martin (2012), «Characterizations of Orthodiagonal Quadrilaterals», Forum Geometricorum Т. 12: 13–25, <http://forumgeom.fau.edu/FG2012volume12/FG201202.pdf>.
↑ Radic, Kaliman, Kadum, 2007, с. 33—52.
↑ Jennifer Kahle, Geometry: Basic ideas (англ. яз.).Геометрия: Основные идеи [2], accessed 28 December 2012.
↑ Г. Г. Цейтен История математики в древности и в средние века, ГТТИ, М-Л, 1932.

Литература

Болтянский В., Четырёхугольники. Квант, № 9,1974.
Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 74. — ISBN 5-94057-170-0.
Стариков В. Н. Исследования по геометрии// Сборник публикаций научного журнала Globus по материалам V-й международной научно-практической конференции «Достижения и проблемы современной науки» г. Санкт-Петербург: сборник со статьями (уровень стандарта, академический уровень). // Научный журнал Globus. — С-П., 2016.
Стариков В. Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. / Гл. ред. Романова И. В.. — Чебоксары: ЦДИП «INet», 2014. — Вып. 1.
Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду / Под редакцией А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова, М. Б. Скопенкова и А. В. Шаповалова.. — Москва: МЦНМО, 2009. — ISBN 978-5-94057-477-4.
Jean-Louis Ayeme. Feurbach’s theorem. A new purely synthetic proof. (рус.). Несколько расширенный перевод — «Вокруг задачи Архимеда»
Дроздов В. Геронов определитель. Занимательная страница // Математика в школе. — 1995. — Вып. 5.
Мухлаев А. 38–я открытая областная научная конференция учащихся. — Омск, 2006.
Mirko Radic, Zoran Kaliman, Vladimir Kadum. A condition that a tangential quadrilateral is also a chordal one // Mathematical Communications. — 2007. — Вып. 12.
D. Fraivert, A. Sigler and M. Stupel. Common properties of trapezoids and convex quadrilaterals // Journal of Mathematical Sciences: Advances and Applications. — 2016. — Т. 38. — P. 49–71. — DOI:10.18642/jmsaa_7100121635.

Источник