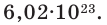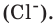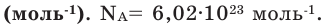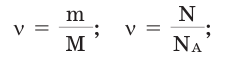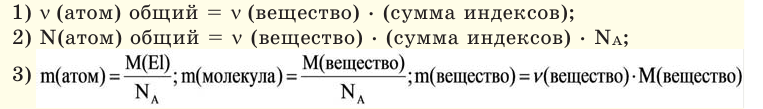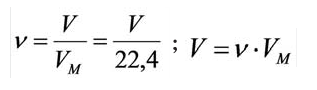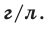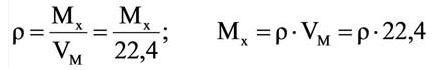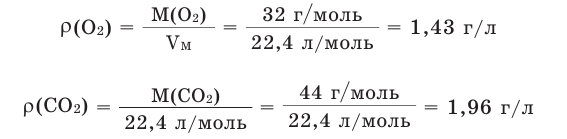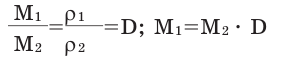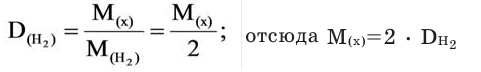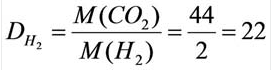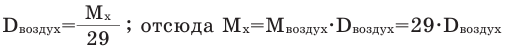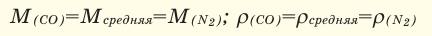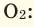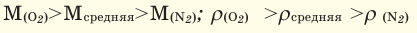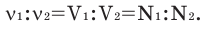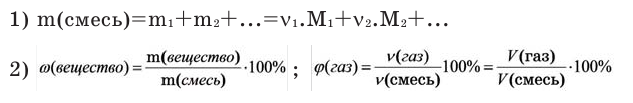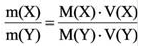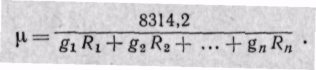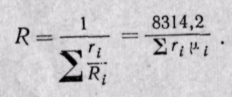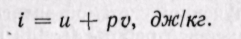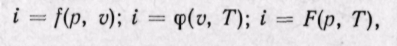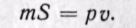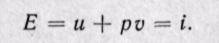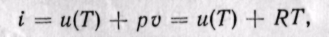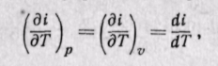Как найти среднюю молекулярную массу газа

Одним из основных
показателей, определяющих тип пластового
флюида, является его молекулярная масса,
она напрямую связана с его физическими
свойствами, и по ней можно охарактеризовать
состав природного газа, чем она больше,
тем выше в нем концентрация углеводородов
с большими молекулярными массами.
Молекулярная масса газовой смеси
состоящей в основном из метана (на 98
об.%), в пластовых условиях и на поверхности
приблизительно одинакова.

Кроме выше
перечисленной классификации углеводородов
(природный газ, газоконденсат и нефть),
существуют также классификации
подразделяющие их на сухой газ, жирный
газ, газоконденсат сухого газа,
газоконденсат жирного газа, летучая
нефть, нефть с высокой степенью усадки,
нелетучая нефть и тяжелая нефть.
Молекулярная масса жирного газа,
газоконденсата, в пластовых условиях
обычно больше, чем при нормальных
поверхностных условиях, что связано с
выпадением конденсирующихся, более
высокомолекулярных углеводородов в
пласте. В таблице 2.2 приведены диапазоны
молекулярных масс классифицирующих
углеводородные пластовые флюиды как
газы, газоконденсаты или нефти. Данные
интервалы являются приблизительными,
так как существуют некоторые исключения.

Таблица 2.2 –
Углеводородные пластовые флюиды

показатели	Жирный и сухой газ	Газокон-денсаты Сухого Газа	Конденса-ты жирного газа	Летучие нефти	Нефть с высокой степенью усадки	Нелетучая нефть	Тяжелая Нефть и гудроны
Молекуляр-ная масса	не более 20	20-25	25-40	30-60	50-90	75-150	более 150
Цвет	бесцвет-ный	от жел-товатого до проз-рачного	от оран-жевого до желто-го	от зеле- новато- го до оран- жевого	от корич- неватого до светло- зеленого	от корич- невого до темно-зе- леновато- го	черный
Доля С7+	0-1	1-6	6-12	10-30	25-35	30-50	Более 50

В таблице 2.3
приведены значения молекулярной массы
смеси углеводородов и составы пластовых
флюидов некоторых чисто газовых,
газоконденсатных и нефтяных месторождений.

Таблица 2.3 –
Состав пластовых флюидов чисто газовых,
газоконденсатных и нефтяных месторождений

Месторождение	тип	тип флюида	Молекул- лярная масса	Состав газа, % объемные
CH4	С2Н6	C3H8	С4Н10	С5H12+ высшие	СО2	N2
Медвежье (Россия)	газовое	сухой газ	16,27	98,56	0,17	0,01	0,02	0,02	0,22	1,0
Новопортовское (Россия)	газовое	жирный газ	18,60	88,1	6,6	2,2	0,94	0,52	0,4	1,5
Юбилейное (Россия)	газоконден-сатное	конденсат сухого газа кСухого	21,91	79,47	9,06	4,43	1,64	4,38	0,54	0,48
Надымское (Россия)	газоконден-сатное	конденсат жирного газа	26,32	68,45	10,99	5,66	1,65	10,72	0,88	1,66
Ромашкинское (Россия)	нефтяное	летучая нефть	32,27	38,8	19,1	17,8	8	6,8	1,5	8
Рэли (США)	нефтяное	нефть с высокой степенью усадки	76,0	45,21	7,09	4,61	4,5	35,16	1,19	0,51
Месторождение Западного Техаса (США)	нефтяное	тяжелая нефть	108,9	15,93	10,47	10,69	9,41	53,69	0,01	0,13
Каннерли (Калифорния США)	нефтяное	битуминозная нефть	268,6	22,62	1,69	0,81	0,89	73,99	0	0

В таблице 2.4
представлены молекулярные массы алканов,
которые также могут быть определены по
формуле:

(2.1)

где а
– число
атомов углевода; b
– число атомов водорода.

Таблица 2.4 –
Молекулярные массы алканов

	Метан	Этан	Пропан	Бутан	Пентан	Гексан	Гептан
Химическая формула	СН4	С2Н6	С3Н8	С4Н10	С5Н12	С6Н14	С7Н16
Молекулярная масса	16,043	30,070	44,097	58,124	72,151	86,178	100,20
Молекулярный объем 1 кмоля, м3	22,36	22,19	21,941	21,455	20,576	19,944	19,029

Таблица 2.5 –
Молекулярные массы неуглеводородных
компонентов

	Углекис-лый газ	Азот	Сероводород	Водяной пар
Химическая формула	СО2	N2	H2S	H2O
Молекулярная масса	44,010	28,013	34,082	18,015
Молекулярный объем 1 кмоля, м3	22,264	22,403	22,190	20,845

Если известен
молярный состав смеси в процентах, то
среднюю молекулярную массу можно
определить по формуле:

(2.2)

где у₁,
y₂,
…, у_n
– молярные (объемные) доли компонентов,
%; М₁,
М₂,
…, М_n
– молекулярные массы компонентов.

Упражнение 2.1.
Определить молекулярную массу смеси
газовых месторождений, представленных
в таблице 2.6.

Таблица 2.6 –
Компонентный состав природных газов
месторождений Тюменской области

	Месторождение	Продуктивный горизонт	Состав газа, «% объемные
СН4	С2Н6	С3Н8	С4Н10	С5Н12+	СО2	N2
1	Березовское	П(юрский)	94,61	0,95	0,16	0,03	—	1,04	3,20
2	Бованенковское	Сеноманский	96,44	1,44	0,17	0,14	0,06	0,18	1,61
3	Нурминское	ТП21-26	92,40	1,72	0,62	0,11	0,07	0,99	4,09
4	Губкинское	Сеноманский	96,95	0,47	0,07	—	—	0,53	1,98
5	Заполярное	Сеноманский	98,80	0,07	0,01	0,004	0,01	0,13	0,976
6	Комсомольское	Сеноманский	96,37	0,22	0,03	0,01	—	0,49	2,88
7	Ямсовейское	Сеноманский	95,0	0,08	0,006	0,01	—	0,3	4,6
8	Тазовское	Сеноманский	98,68	0,06	0,003	0,01	—	0,39	0,86
9	Ямбургское	Сеноманский	98,2	0,04	0,006	0,001	0,1	0,3	1,353
10	Уренгойское	Сеноманский	99,05	0,06	0,01	–	–	0,08	0,80

Пример расчета.
Определить
молекулярную массу смеси на Медвежьем
месторождении. Объемные составы в
процентах и молекулярные массы компонентов
представлены в таблицах (2.4), (2.5) и (2.7).

Таблица 2.7 –
Компонентный состав газовой смеси
Сеноманского продуктивного горизонта
Медвежьего месторождения

Месторождение	Продуктивный горизонт	Состав газа, % объемные
СН4	С2Н6	С3Н8	С4Н10	С5Н12+	СО2	N2
Медвежье	Сеноманский	98,56	0,17	0,01	0,02	0,02	0,22	1

Решение. Для
определения молекулярной массы смеси
используем формулу (2.2):

Определение
молекулярной массы смеси по компонентному
составу возможно, когда известны объемные
доли в процентах по каждому входящему
в состав смеси компоненту. Ввиду того,
что компоненты выше пентана объединяют
с ним в остаток С₅Н₁₂₊,
а на газоконденсатных и нефтяных
месторождениях этот остаток обычно
более 2 %, использование формулы (2.2) будет
приводить к погрешности, размер которой
тем больше чем больше объемная доля
остатка С₅Н₁₂₊.
В данном случае необходимо проводить
более расширенный хромотографический
анализ. В настоящее время существуют
приборы позволяющие определять состав
углеводородных компонентов до С₄₀
и даже более.

Газовые смеси
можно охарактеризовать не только
молярными, но и массовыми концентрациями
компонентов. Молярный и объемный составы
газовых смесей примерно совпадают друг
с другом, так как объемы 1 кмоля идеальных
газов при одинаковых нормальных
физических условиях (P=0,1013
МПа и Т=273 К) по закону Авогадро составляют
22,41 м³.
Более точные значения молярных объемов
алканов и неуглеводородных компонентов
входящих в состав природных газов
представлены в таблицах 2.4 и 2.5. Пересчет
молярных (объемных) концентраций
компонентов газовой смеси в массовые
и наоборот производится при помощи
следующих формул:

— в массовых долях;
(2.3)

— в массовых
процентах;
(2.4)

— в молярных долях;
(2.5)

— в молярных
процентах,
(2.6)

где g_i
– массовая доля i-го
компонента; М_i
– молярная
масса i-го
компонента.

Упражнение 2.2.
Пересчитать
объемные проценты в массовые проценты
по месторождениям представленным в
таблице 2.6.

Пример расчета.
Пересчитать объемные процентные в
массовые проценты на Медвежьем
месторождении. Исходные данные
представлены в примере 2.1.

Решение.
Для определения массовой доли метана
используем формулу (2.3):

EMBED Equation.3

Таким образом,
рассчитываются массовые доли всех
входящих компонентов, значения которых
представлены в таблице.

	С1	С2	С3	С4	С5+	СО2	N2
Молярная доля, %	98,56	0,17	0,01	0,02	0,02	0,22	1
Массовая доля, %	97,18	0,31	0,02	0,07	0,08	0,59	1,72

Если известен
массовый состав смеси, то ее среднюю
молекулярную массу можно определить
по формуле:

(2.7)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

Количество вещества:

В чём разница между понятиями «масса» и «количество»

Если мы будем производить подобные расчеты, соответствующие этому заданию, для простых веществ, образованных различными элементами, то всякий раз получим одно и то же число —

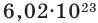
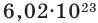
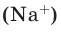
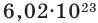
Например, в 1 моле водородного газа содержится молекул, в 1 моле поваренной соли (NaCI) ионов натрия и ионов хлора

Количество частиц, содержащихся в 1 моле химических веществ ( 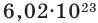), называется постоянной Авогадро (Na). Постоянная Авогадро отличается от числа Авогадро тем, что измеряется определенной единицей

Количество вещества можно вычислить по следующей формуле:

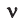
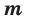
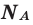
Здесь — количество вещества, — масса, М — молярная масса, N — заданное количество молекул, — постоянная Авогадро. Все представленные в формуле величины нам уже известны. Кроме понятия молярной массы. Давайте выясним сущность этого понятия.

Молярная масса

Молярной массой называют массу 1 моля вещества, выраженного в граммах. Молярная масса обозначается
буквой М, единицей измерения является г/моль.

При выражении молярной массы вещества в граммах, она численно бывает равна его относительной молекулярной массе (если состоит из молекул). Для сравнения запишем (таблица 1):

Как видно из сравнений, молярная масса веществ по своей единице отличается от относительной молекулярной массы. То есть молярная масса — измеряемая величина.

Как видно из вышесказанного, понятие молярная масса применяется как к химическим элементам, так и к простым и сложным веществам с молекулярным и немолекулярным строением.

На основе количества вещества (моль) можно производить следующие вычисления. Если известно мольное количество вещества:

Закон Авогадро и молярный объём газов

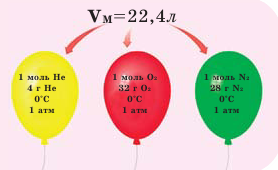
Обратите внимание на рисунки. Почему, несмотря на разные массы газов, они занимают одинаковый объём?

В начале XIX века итальянский ученый Авогадро, проведя наблюдения над свойствами газов в различных условиях и проанализировав открытые прежде законы о газах (Бойля-Мариотта, Гей-Люссака и др.) в 1811 году сформулировал новый закон о газах. Закон Авогадро звучит следующим образом: в равных объемах различных газов при одинаковых условиях (одинаковых температуре и давлении) содержится одинаковое число молекул.

Итальянский ученый. В 1811 году им был открыт закон о газах, который впоследствии был назван его именем.

Мы уже знаем, что 1 моль любого вещества содержит 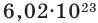молекул. Согласно закону Авогадро, можно утверждать, что одинаковое число молекул в 2 г водорода, 32 г кислорода, 28 г азота, 44 г углекислого газа занимает одинаковый объём.

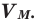
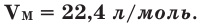
Было вычислено, что при нормальных условиях объем 1 моля любого газа или смеси газов составляет примерно 22,4 л. Объем 1 моля газа при нормальных условиях (н.у.) называют молярным объемом данного газа, выраженным знаком . При измерении объема газа в литрах молярный объём составит Зависимость между количеством вещества и молярным объёмом газа можно выразить следующей формулой:

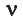
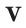
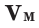
Здесь — количество вещества, — объём газа, — молярный объем.

На основе закона Авогадро и молярного объёма газов можно вычислить плотность газов при нормальных условиях и относительную плотность одного газа по отношению к другому газу. Плотность обозначается буквой 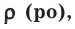её единица
измерения —

Нормальные условия означают: температура 0°С, 1 атм давления 1атм — 101,3 кПа

Для вычисления плотности какого-либо газа X в нормальных условиях (н.у.), следует его молярную массу разделить на молярный объем:

Например, вычислим плотности кислорода и углекислого газа при нормальных условиях:

Плотность твёрдых и жидких веществ при н.у. вычисляется по формуле .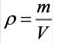

Для того, чтобы определить, масса какого из газов с одинаковыми объемами и при одинаковых условиях бывает тяжелее, пользуются понятием относительной плотности. Отношение плотностей различных газов при одинаковых условиях равно отношению их молярных масс. Относительная плотность обозначается буквой D и не имеет единицы измерения. Формула относительной плотности следующая:

Относительную плотность газов в большинстве случаев вычисляют по самому легкому газу — водороду и воздуху:

В таком случае, относительная плотность углекислого газа по водороду вычисляется следующим образом:

Так как средняя молярная масса воздуха, состоящего из смеси газов, примерно равна 29 г/моль, то формула его относительной плотности следующая:

Способы вычисления средней молярной массы газовой смеси

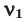
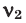
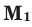
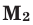
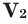
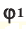
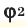
Здесь: и количество молей газов, и — молярные массы газов, и — объем газов в н.у., (и — доля газов в объеме газовой смеси.

Среднюю молярную массу 1 моля смеси из двух различных газов можно вычислить по следующей формуле: .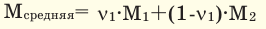

При смешивании газов с одинаковыми молярными массами, которые при одинаковом давлении не вступают друг с другом в реакцию, плотность газовой смеси (при н.у.), а также их средняя молярная масса остаются неизменными. Например, при смешивании 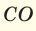и

При смешивании газов с различными молярными массами, при одинаковом давлении, средняя молярная масса (при н.у.) и плотность полученной газовой смеси приобретают значение между молярными массами и плотностями смешиваемых газов. Например, при смешивании 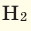и

При добавлении газа с большей молярной массой в тот или иной газ при постоянном давлении плотность газовой смеси увеличивается, а при добавлении газа с меньшей молярной массой — уменьшается.

Закон объемных отношений

В химических реакциях соотношение объемов, вступающих в реакцию, и полученных газов равно соотношению их коэффициентов. Например:

(объёмное соотношение 2:1:2)

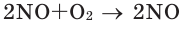
Численное соотношение объемов, молей и молекул газов равно друг другу.

Можно производить следующие вычисления по смесям:

  3)    Массовое соотношение двух газов:  

2.1. Основные понятия и формулы

Количество вещества — число структурных элементов (молекул, атомов, ионов и т. п.), содержащихся в теле или системе. Количество вещества выражается в молях. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в 0,012 кг изотопа углерода 12 C. Количество вещества тела (системы)

,

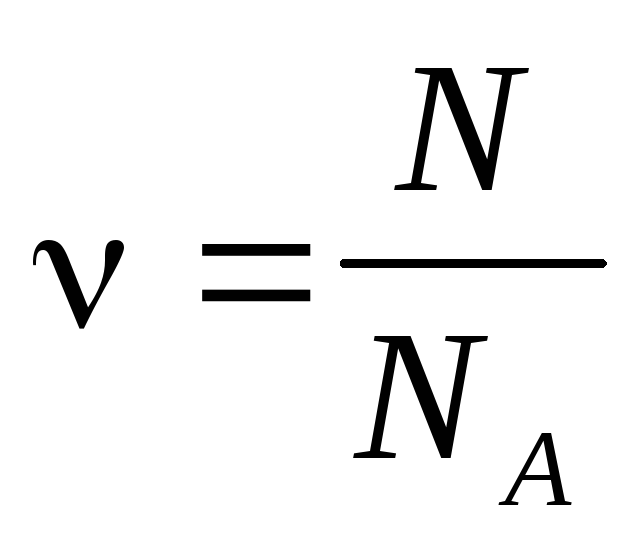
где N — число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему). Постоянная Авогадро N_А=6,0210 23 моль -1 .

Молярная масса вещества ,

где m—масса однородного тела (системы); —количество вещества (число молей) этого тела (системы). Выражается в единицах г/моль (или кг/моль).

Единица массы, равная 1/12 массы атома углерода 12 C, называется атомной единицей массы (а.е.м.). Массы атомов или молекул выраженные в атомных единицах массы называют соответственно относительной атомной или относительной молекулярной массой вещества. Относительная молекулярная масса вещества состоит из относительных атомных масс химических элементов, составляющих молекулу вещества. Относительные атомные массы химических элементов приводятся в таблице Д. И. Менделеева (см. также таблицу 8 приложения данного пособия).

Молярная масса вещества численно равна относительной атомной или молекулярной массе данного вещества, если размерность а.е.м. заменить на размерность г/моль.

Количество вещества смеси n газов

или ,

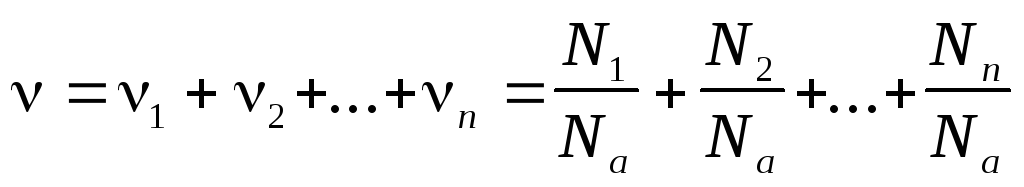
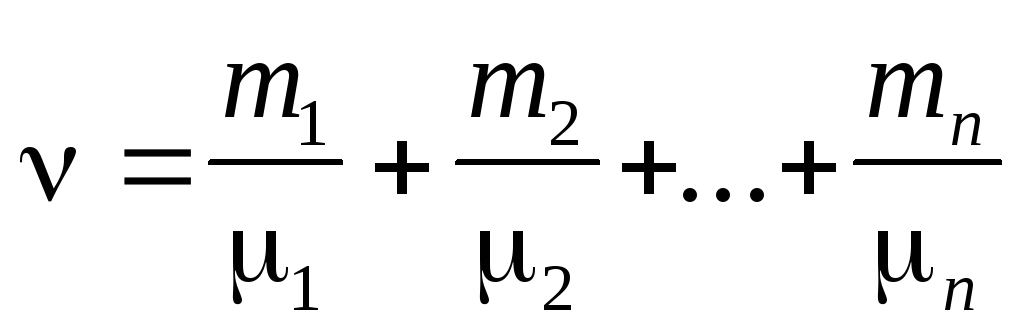
Уравнение Менделеева — Клапейрона (уравнение состояния идеального газа)

,

где т — масса газа,  — молярная масса газа, R — универсальная газовая постоянная, ν — количество вещества, Т — термодинамическая температура.

Опытные газовые законы, являющиеся частными случаями уравнения Менделеева — Клапейрона для изопроцессов:

а) закон Бойля—Мариотта (изотермический процесс: T=const, m=const)

или для двух состояний газа, обозначенных цифрами 1 и 2,

,

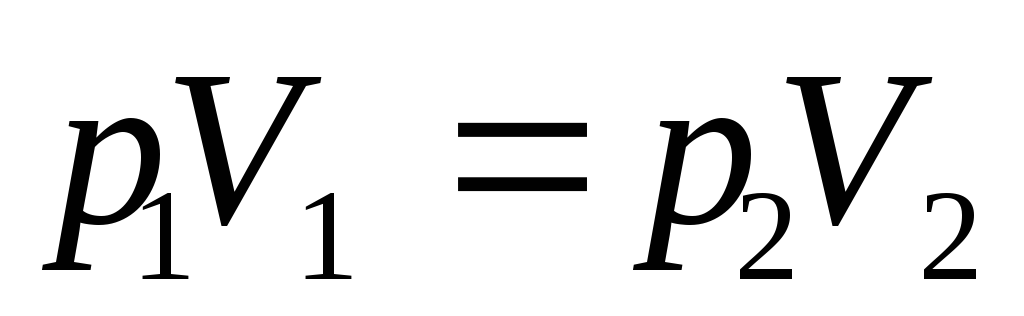
б) закон Гей-Люссака (изобарический процесс: р=const, m=const)

или для двух состояний ,

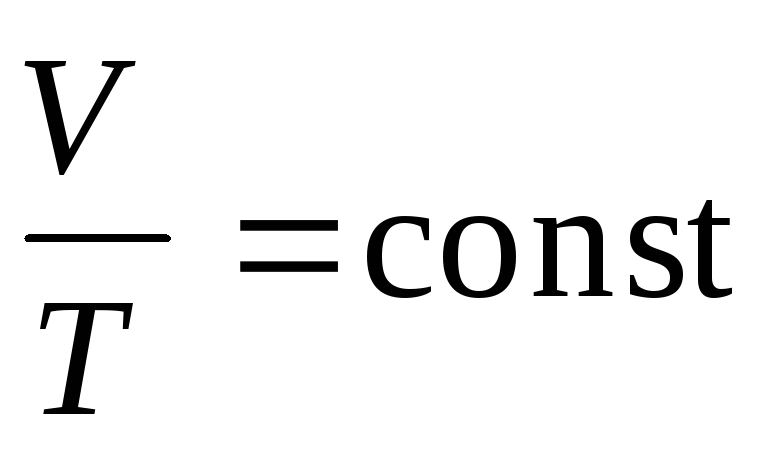
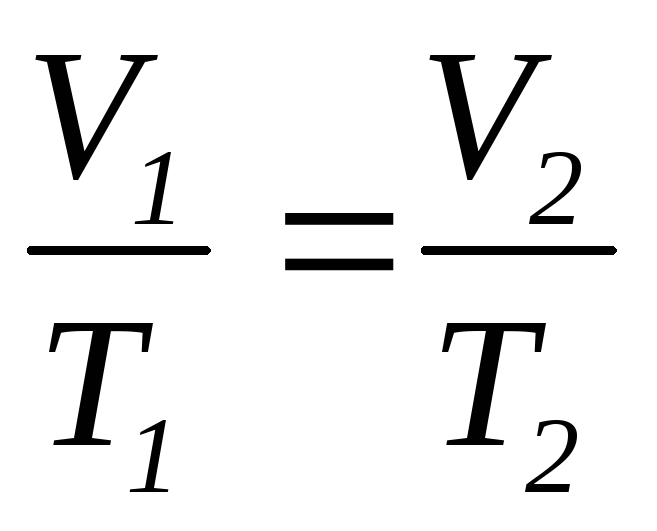
в) закон Шарля (изохорический процесс: V=const, m=const)

или для двух состояний ,

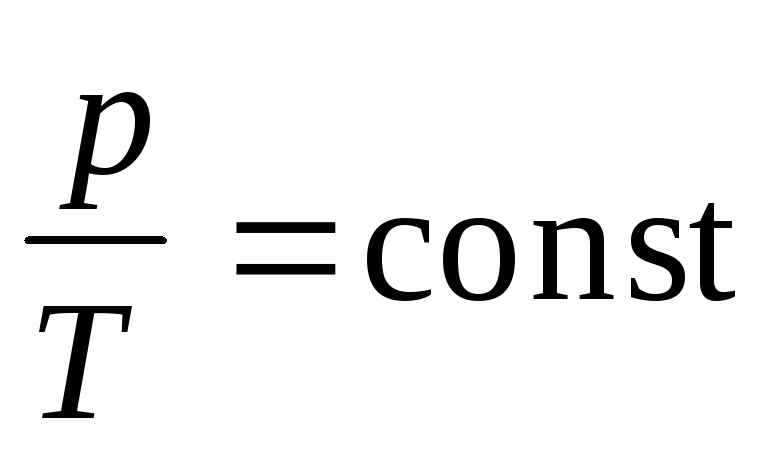
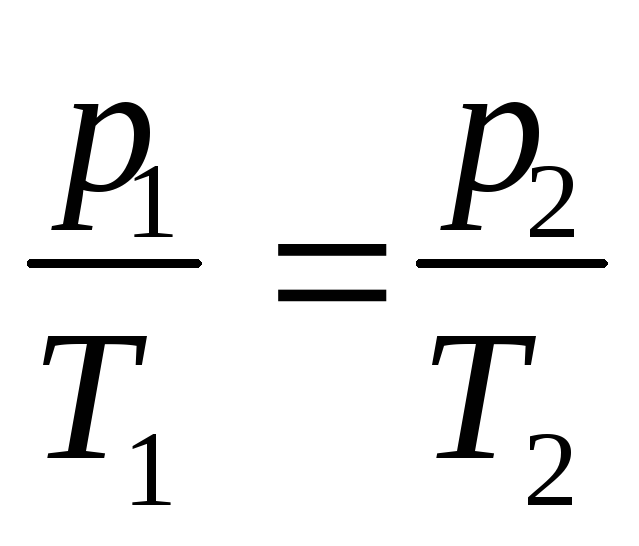
г) объединенный газовый закон (m=const)

или для двух состояний .

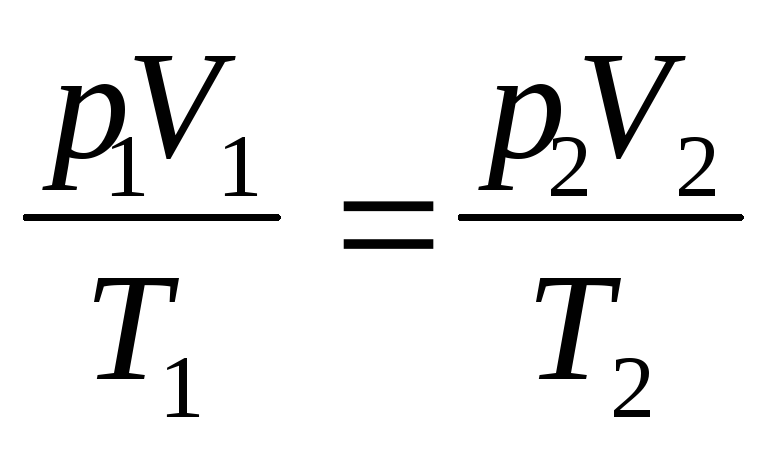
Под нормальными условиями понимают давление p_o=1 атм (1,01310 5 Па), температуру 0 о С (T=273 K).

Закон Дальтона, определяющий давление смеси n газов.

,

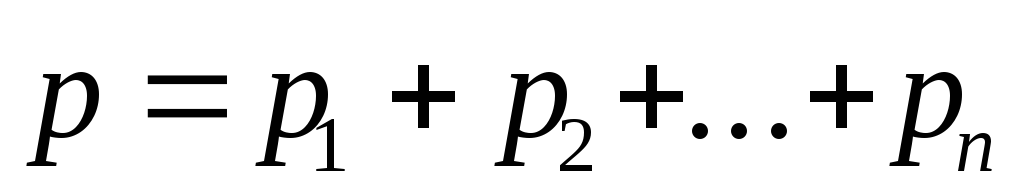
где p_i — парциальные давления компонентов смеси (i=1,2,…,n). Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.

Молярная масса смеси n газов

.

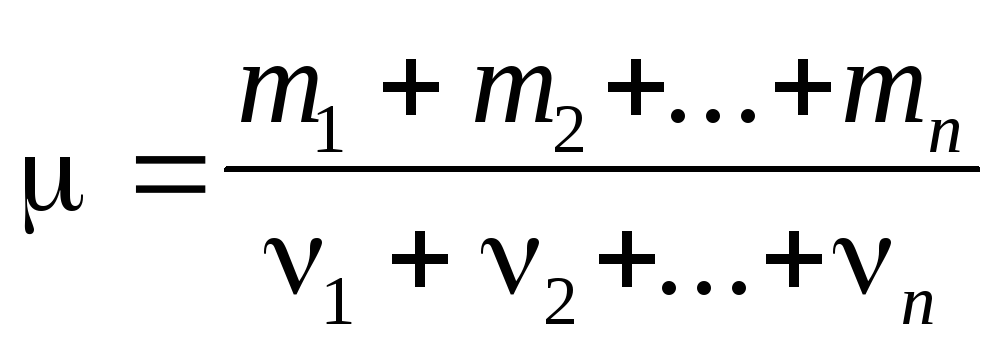
Массовая доля i-го компонента смеси газа (в долях единицы или процентах)

,

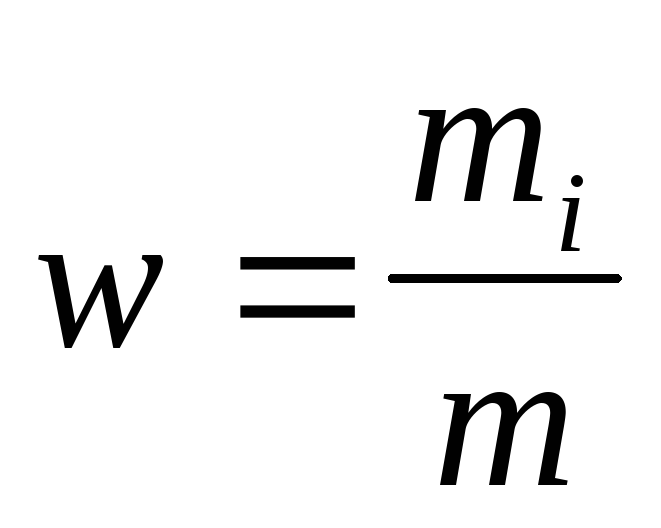
Концентрация молекул

,

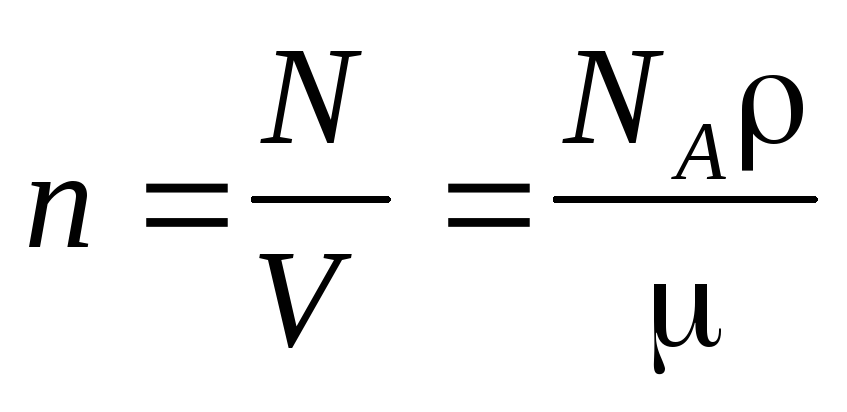
где N — число молекул, содержащихся в данной системе;  — плотность вещества в системе; V — объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

Уравнение Ван-дер-Ваальса для реального газа

,

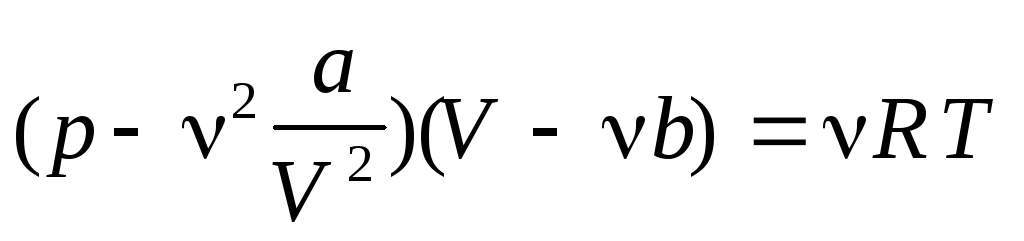
где a и b — коэффициенты Ван-дер-Ваальса

Для идеального газа уравнение Ван-дер-Ваальса переходит в уравнение Менделеева — Клапейрона.

Основное уравнение молекулярно — кинетической теории газов

,

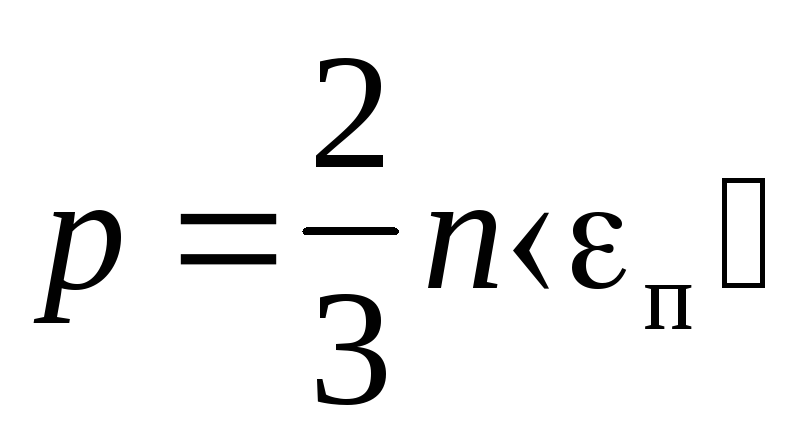
где _п — средняя кинетическая энергия поступательного движения молекулы.

Средняя молекулярная масса представляет собой условную величину и относится к такому однородному газу, у которого число молекул и общая масса равны числу молекул и массе смеси газов.

Если известна величина газовой постоянной смеси, то

(3-7)

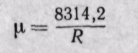
Заменяя газовые постоянные R₁, R₂, . R_n их значениями из уравнения Клапейрона, получаем выражение для средней молекулярной массы, если смесь задана массовыми долями:

(3-8)

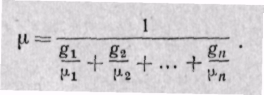
Если смесь задана объемными долями, то, как следует из уравнения (3-6),

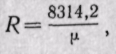
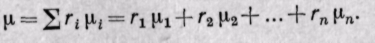
Поскольку то

(3-9)

Средняя молекулярная масса смеси газов равна сумме произведений объемных долей на молекулярные массы отдельных газов, составляющих смесь.

Парциальные давления

Парциальное давление газа может быть определено через массовые доли из уравнения Клапейрона, если известны основные параметры газа:

(3-10)

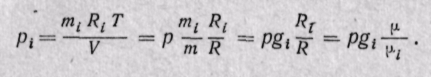
Для нахождения парциального давления каждого газа при задании смеси объемными долями можно воспользоваться законом Бойля — Мариотта, из которого следует, что при постоянной температуре

(3-11)

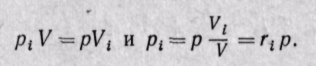
Парциальное давление каждого газа равно произведению общего давления смеси газов на его объемную долю.

Уравнением (3-11) обычно пользуются при технических расчетах и при испытаниях тепловых установок. Объемные доли газов определяют специальными аппаратами — газоанализаторами.

Удельная энтальпия, т. е. энтальпия, отнесенная к 1 кг, обозначается буквой i и представляет собой по определению сложную функцию вида

Дифференциал энтальпии di есть элементарное количество теплоты, участвующее в процессе при постоянном давлении. Вся теплота в процессе при постоянном давлении расходуется на изменение энтальпии:

(5-15)

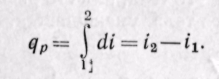
Из уравнения (5-12) следует, что

(5-16)

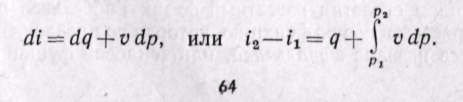
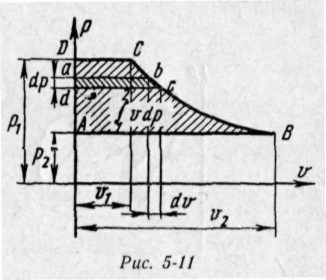
Энтальпия больше внешней теплоты на величину работы vdp, которая на рv-диаграмме изображается элементарной площадкой abed (рис. 5-11). Очевидно, вся пл. ABCD определяется выражением

, которое называется располагаемой, или полезной, работой.

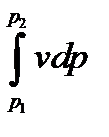
Изменение энтальпии полностью определяется начальным и конечным состоянием рабочего тела и не зависит от промежуточных состояний. Изменение энтальпии газа в циклах равно нулю, т. е.

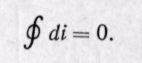
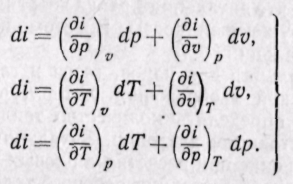
Поскольку энтальпия является функцией основных параметров состояния, то di есть полный дифференциал этой функции при любых независимых переменных, характеризующих состояние газа;

(5-17)

Изменение энтальпии во всех процессах, протекающих между двумя точками А и В, будет одинаковым (рис. 5-12).

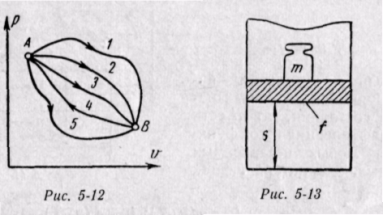
Физический смысл энтальпии будет понятен из рассмотрения следующего примера. На перемещающийся поршень в цилиндре с 1 кг газа помещена гиря массой т кг (рис. 5-13). Площадь поршня /; внутренняя энергия рабочего тела и. Потенциальная энергия гири равна произведению массы гири т на высоту S. Так как давление газа р уравновешивается массой гири, то потенциальную энергию ее можно 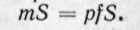выразить иначе:

Произведение /S есть удельный объем газа. Отсюда

Произведение давления на объем есть работа, которую надо затратить, чтобы ввести газ объемом v во внешнюю среду с давлением р. Таким образом, работа pv есть потенциальная энергия газа, зависящая от сил, действующих на поршень. Чем больше эти внешние силы, тем больше давление р и тем больше потенциальная энергия давления pv.

Если рассматривать газ, находящийся в цилиндре и поршень с грузом как одну систему, которую будем называть расширенной системой, то полная энергия Е этой системы складывается из внутренней энергии газа и и потенциальной энергии поршня с грузом, равной pv:

Отсюда видно, что энтальпия i равна энергии расширенной системы — тела и окружающей среды. В этом и заключается физический смысл энтальпии.

Значения энтальпий для паров, газов и газовых смесей приводятся в технической и справочной литературе. Пользуясь этими данными, можно определять количество теплоты, участвующее в процессе при постоянном давлении. Энтальпия получила большое значение и применение при расчетах тепловых и холодильных установок и, как параметр состояния рабочего тела, значительно упрощает тепловые расчеты. Она позволяет [применять графические методы при исследовании всевозможных термодинамических процессов и циклов.

Энтальпией особенно целесообразно пользоваться тогда, когда в качестве основных параметров принимают р и Т. Это наглядно можно видеть, если энтальпию i сравнить с внутренней энергией и. При v = const уравнение первого закона термодинамики dq = = du + pdv превращается в dq_v = du, или q_v — u₂—u₁ а при р = const q_p = i₃ — i₁.

Энтальпия идеального газа,’ так же как и внутренняя энергия, является функцией температуры и не зависит от других параметров. Действительно, для идеального газа

следовательно (поскольку оба слагаемых зависят только от температуры), i = f(T).

Тогда по аналогии с внутренней энергией будем иметь

т. е. в любом процессе изменения состояния идеального газа производная от изменения энтальпии по температуре будет полной производной.

Численные значения энтальпий идеальных газов приведены в приложении, табл. XIII.

Дата добавления: 2018-02-15 ; просмотров: 1423 ; ЗАКАЗАТЬ РАБОТУ

Электронное учебное пособие
Москва 2013

2. Ocновные понятия и законы химии. Атомно-молекулярное учение

2.10. Примеры решения задач

2.10.1. Расчет относительных и абсолютных масс атомов и молекул

Относительные массы атомов и молекул определяются с использованием приведенных в таблице Д.И. Менделеева величин атомных масс. При этом, при проведении расчетов для учебных целей значения атомных масс элементов обычно округляются до целых чисел (за исключением хлора, атомная масса которого принимается равной 35,5).

Пример 1. Относительная атомная масса кальция А_r(Са)=40; относительная атомная масса платины А_r(Pt)=195.

Относительная масса молекулы рассчитывается как сумма относительных атомных масс составляющих данную молекулу атомов с учетом количества их вещества.

Пример 2. Относительная молярная масса серной кислоты:

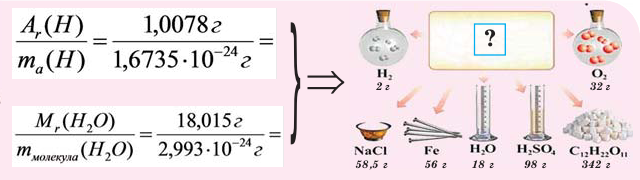
Величины абсолютных масс атомов и молекул находятся делением массы 1 моль вещества на число Авогадро.

Пример 3. Определите массу одного атома кальция.

Решение. Атомная масса кальция составляет А_r(Са)=40 г/моль. Масса одного атома кальция окажется равной:

m(Ca)= А_r(Ca) : N_A =40 : 6,02·10 23 = 6,64·10 -23 г.

Пример 4. Определите массу одной молекулы серной кислоты.

Решение. Молярная масса серной кислоты равна М_r(H₂SO₄) = 98. Масса одной молекулы m(H₂SO₄) равна:

2.10.2. Расчет количества вещества и вычисление числа атомных и молекулярных частиц по известным значениям массы и объема

Количество вещества определяется путем деления его массы, выраженной в граммах, на его атомную (молярную) массу. Количество вещества, находящегося в газообразном состоянии при н.у., находится делением его объема на объем 1 моль газа (22,4 л).

Пример 5. Определите количество вещества натрия n(Na), находящегося в 57,5 г металлического натрия.

Решение. Относительная атомная масса натрия равна А_r(Na)=23. Количество вещества находим делением массы металлического натрия на его атомную массу:

Пример 6 . Определите количество вещества азота, если его объем при н.у. составляет 5,6 л.

Решение. Количество вещества азота n(N ₂) находим делением его объема на объем 1 моль газа (22,4 л):

Число атомов и молекул в веществе определяется умножением количества вещества атомов и молекул на число Авогадро.

Пример 7. Определите число молекул, содержащихся в 1 кг воды.

Решение. Количество вещества воды находим делением ее массы (1000 г) на молярную массу (18 г/моль):

Число молекул в 1000 г воды составит:

N(Н₂О) = 55,5·6,02·10 23 = 3,34·10 24 .

Пример 8. Определите число атомов, содержащихся в 1 л (н.у.) кислорода.

Решение. Количество вещества кислорода, объем которого при нормальных условиях составляет 1 л равно:

n(О₂) = 1 : 22,4 = 4,46·10 -2 моль.

Число молекул кислорода в 1 л (н.у.) составит:

N(О₂) = 4,46·10 -2 · 6,02·10 23 = 2,69·10 22 .

Следует отметить, что 26,9·10 22 молекул будет содержаться в 1 л любого газа при н.у. Поскольку молекула кислорода двухатомна, число атомов кислорода в 1 л будет в 2 раза больше, т.е. 5,38·10 22 .

2.10.3. Расчет средней молярной массы газовой смеси и объемной доли
содержащихся в ней газов

Средняя молярная масса газовой смеси рассчитывается на основе молярных масс составляющих эту смесь газов и их объемных долей.

Пример 9. Полагая, что содержание (в объемных процентах) азота, кислорода и аргона в воздухе соответственно составляет 78, 21 и 1, рассчитайте среднюю молярную массу воздуха.

Решение.

М_возд = 0,78·М_r(N₂)+0,21·М_r (O₂)+0,01·М_r(Ar)= 0,78·28+0,21·32+0,01·40 = 21,84+6,72+0,40=28,96

или приблизительно 29 г/моль.

Пример 10. Газовая смесь содержит 12 л NH₃, 5 л N₂ и 3 л Н₂, измеренных при н.у. Рассчитать объемные доли газов в этой смеси и ее среднюю молярную массу.

Решение. Общий объем смеси газов равен V=12+5+3=20 л. Объемные доли j газов окажутся равными:

Средняя молярная масса рассчитывается на основе объемных долей составляющих эту смесь газов и их молекулярных масс:

М=0,6·М(NH₃)+0,25·M(N₂)+0,15·M(H₂) = 0,6·17+0,25·28+0,15·2 = 17,5.

2.10.4. Расчет массовой доли химического элемента в химическом соединении

Массовая доля ω химического элемента определяется как отношение массы атома данного элемента Х, содержащегося в данной массе вещества к массе этого вещества m. Массовая доля – безразмерная величина. Ее выражают в долях от единицы:

ω(X) = m(X)/m (0 Пример 11. Рассчитайте массовую долю марганца в оксиде марганца (VII).

Решение. Молярные массы веществ равны: М(Mn) = 55 г/моль, М(О) = 16 г/моль, M(Mn₂O₇)=2М(Mn)+7М(О)= 222 г/моль. Следовательно, масса Mn₂O₇ количеством вещества 1 моль составляет:

Из формулы Mn₂O₇следует, что количество вещества атомов марганца в два раза больше количества вещества оксида марганца (VII). Значит,

m(Mn)= n(Mn)·M(Mn) = 2·55 = 110 г.

Таким образом, массовая доля марганца в оксиде марганца(VII) равна:

2.10.5. Установление формулы химического соединения по его элементному составу

Простейшая химическая формула вещества определяется на основании известных величин массовых долей входящих в состав этого вещества элементов.

Допустим имеется образец вещества Na_xP_yO_z массой m_o г. Рассмотрим как определяется его химическая формула, если известны количества вещества атомов элементов, их массы или массовые доли в известной массе вещества. Формула вещества определяется отношением:

x : y : z = N(Na) : N(P) : N(O).

Это отношение не изменится, если каждый его член разделить на число Авогадро:

Таким образом, для нахождения формулы вещества необходимо знать соотношение между количествами веществ атомов в одной и той же массе вещества:

Если разделить каждый член последнего уравнения на массу образца m_o, то получим выражение, позволяющее определить состав вещества:

Пример 12. Вещество содержит 85,71 масс. % углерода и 14,29 масс. % водорода. Молярная его масса равна 28 г/моль. Определите простейшую и истинную химические формулы этого вещества.

Решение. Соотношение между количеством атомов в молекуле С_хН_у определяется делением массовых долей каждого элемента на его атомную массу:

х : у = 85,71/12 : 14,29/1 = 7,14:14,29 = 1 : 2.

Таким образом простейшая формула вещества — СН₂. Простейшая формула вещества не всегда совпадает с его истинной формулой. В данном случае формула СН₂ не соответствует валентности атома водорода. Для нахождения истинной химической формулы необходимо знать молярную массу данного вещества. В данном примере молярная масса вещества равна 28 г/моль. Разделив 28 на 14 (сумму атомных масс, отвечающих формульной единице СН₂), получаем истинное соотношение между числом атомов в молекуле:

Получаем истинную формулу вещества: С₂Н₄— этилен.

Вместо молярной массы для газообразных веществ и паров в условии задачи может быть указана плотность по какому-либо газу или по воздуху.

В рассматриваемом случае плотность газа по воздуху составляет 0,9655. На основании этой величины может быть найдена молярная масса газа:

М = М_возд·D_возд = 29·0,9655 = 28.

В этом выражении М – молярная масса газа С_хН_у, М_возд – средняя молярная масса воздуха, D_возд — плотность газа С_хН_у по воздуху. Полученная величина молярной массы используется для определения истинной формулы вещества.

В условии задачи может не указываться массовая доля одного из элементов. Она находится вычитанием из единицы (100%) массовых долей всех остальных элементов.

Пример 13. Органическое соединение содержит 38,71 масс. % углерода, 51,61 масс. % кислорода и 9,68 масс. % водорода. Определить истинную формулу этого вещества, если плотность его паров по кислороду составляет 1,9375.

Решение. Рассчитываем соотношение между количеством атомов в молекуле С_хН_yО_z:

х : у : z = 38,71/12 : 9,68/1 : 51,61/16 = 3,226 : 9,68 : 3,226= 1:3:1.

Молярная масса М вещества равна:

М = М(O₂)·D(O₂) = 32·1,9375 = 62.

Простейшая формула вещества СН₃О. Сумма атомных масс для этой формульной единицы составит 12+3+16=31. Делим 62 на 31 и получаем истинное соотношение между количеством атомов в молекуле:

х : у : z = 2 : 6 : 2.

Таким образом, истинная формула вещества С₂Н₆О₂. Эта формула отвечает составу двухатомного спирта – этиленгликоля: СН₂(ОН)-СН₂(ОН).

2.10.6. Определение молярной массы вещества

Молярная масса вещества может быть определена на основе величины плотности его паров по газу с известной величиной молярной массы.

Пример 14 . Плотность паров некоторого органического соединения по кислороду равна 1,8125. Определите молярную массу этого соединения.

Решение. Молярная масса неизвестного вещества М_x равна произведению относительной плотности этого вещества D на молярную массу вещества M, по которому определено значение относительной плотности:

М_x = D·M = 1,8125·32 = 58,0.

Веществами с найденным значением молярной массы могут быть ацетон, пропионовый альдегид и аллиловый спирт.

Молярная масса газа может быть рассчитана с использованием величины молярного его объема при н.у.

Пример 15. Масса 5,6 л газа при н.у. составляет 5,046 г. Рассчитайте молярную массу этого газа.

Решение. Молярный объем газа при н.у равен 22,4 л. Следовательно, молярная масса искомого газа равна

М = 5,046·22,4/5,6 = 20,18.

Искомый газ – неон Ne.

Уравнение Клапейрона–Менделеева используется для расчета молярной массы газа, объем которого задан при условиях, отличающихся от нормальных.

Пример 16. При температуре 40 о С и давлении 200 кПа масса 3,0 л газа составляет 6,0 г. Определите молярную массу этого газа.

Решение. Подставляя известные величины в уравнение Клапейрона–Менделеева получаем:

М = mRT/PV = 6,0·8,31·313/(200·3,0)= 26,0.

Рассматриваемый газ – ацетилен С₂Н₂.

Пример 17. При сгорании 5,6 л (н.у.) углеводорода получено 44,0 г углекислого газа и 22,5 г воды. Относительная плотность углеводорода по кислороду равна 1,8125. Определите истинную химическую формулу углеводорода.

Решение. Уравнение реакции сгорания углеводорода можно представить следующим образом:

Количество углеводорода составляет 5,6:22,4=0,25 моль. В результате реакции образуется 1 моль углекислого газа и 1,25 моль воды, которая содержит 2,5 моль атомов водорода. При сжигании углеводорода количеством вещества 1 моль получается 4 моль углекислого газа и 5 моль воды. Таким образом, 1 моль углеводорода содержит 4 моль атомов углерода и 10 моль атомов водорода, т.е. химическая формула углеводорода С₄Н₁₀. Молярная масса этого углеводорода равна М=4·12+10=58. Его относительная плотность по кислороду D=58:32=1,8125 соответствует величине, приведенной в условии задачи, что подтверждает правильность найденной химической формулы.

© Факультет естественных наук РХТУ им. Д.И. Менделеева. 2013 г.