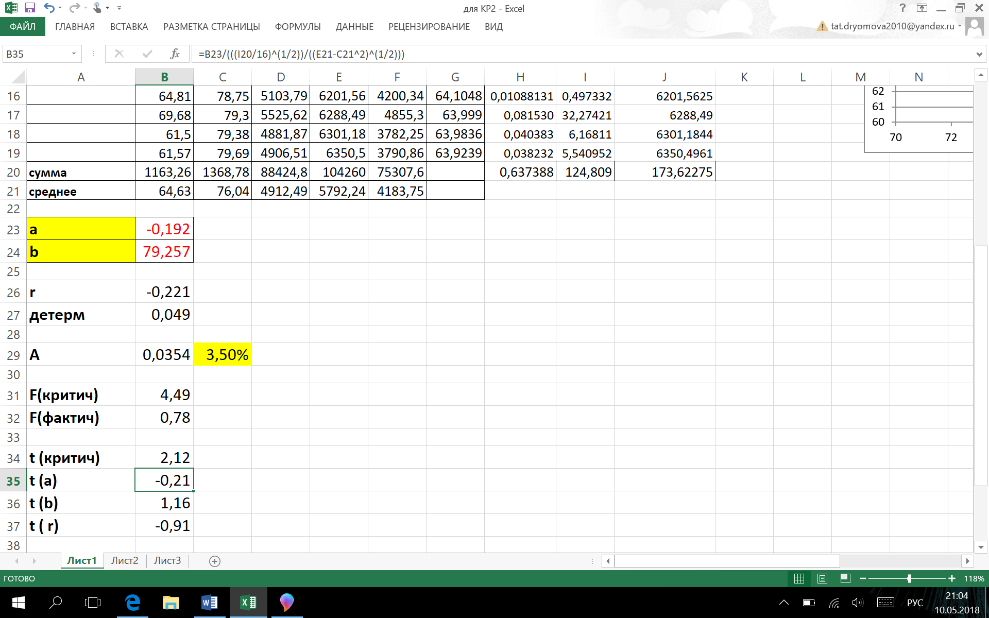
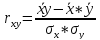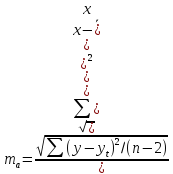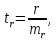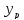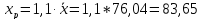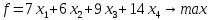Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
Означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: 
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее , и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа . В главном меню последовательно выберите: Файл/Параметры/Надстройки .
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа , а затем нажмите кнопку ОК .
Если Пакет анализа отсутствует в списке поля Доступные надстройки , нажмите кнопку Обзор , чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да , чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия , а затем нажмите кнопку ОК .
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y — диапазон, содержащий данные результативного признака;
Входной интервал X — диапазон, содержащий данные факторного признака;
Метки — флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа — ноль — флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал — достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист — можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК .
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как не превышает 8 — 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н 0 о статистически незначимом отличии показателей от нуля:


На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
где 
Данные для расчёта возьмём из таблицы на Рисунке 7.
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н 0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций : в главном меню выберете Формулы / Вставить функцию .
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК .
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2003. — 192 с.: ил.
Для общей оценки качества построенной эконометрической определяются такие характеристики как коэффициент детерминации, индекс корреляции, средняя относительная ошибка аппроксимации, а также проверяется значимость уравнения регрессии с помощью F -критерия Фишера. Перечисленные характеристики являются достаточно универсальными и могут применяться как для линейных, так и для нелинейных моделей, а также моделей с двумя и более факторными переменными. Определяющее значение при вычислении всех перечисленных характеристик качества играет ряд остатков ε i , который вычисляется путем вычитания из фактических (полученных по наблюдениям) значений исследуемого признака y i значений, рассчитанных по уравнению модели y рi .
показывает, какая доля изменения исследуемого признака учтена в модели. Другими словами коэффициент детерминации показывает, какая часть изменения исследуемой переменной может быть вычислена, исходя из изменений включённых в модель факторных переменных с помощью выбранного типа функции, связывающей факторные переменные и исследуемый признак в уравнении модели.
Коэффициент детерминации R 2 может принимать значения от 0 до 1. Чем ближе коэффициент детерминации R 2 к единице, тем лучше качество модели.
Индекс корреляции можно легко вычислить, зная коэффициент детерминации:
Индекс корреляции R характеризует тесноту выбранного при построении модели типа связи между учтёнными в модели факторами и исследуемой переменной. В случае линейной парной регрессии его значение по абсолютной величине совпадает с коэффициентом парной корреляции r (x, y) , который мы рассмотрели ранее, и характеризует тесноту линейной связи между x и y . Значения индекса корреляции, очевидно, также лежат в интервале от 0 до 1. Чем ближе величина R к единице, тем теснее выбранный вид функции связывает между собой факторные переменные и исследуемый признак, тем лучше качество модели.

выражается в процентах и характеризует точность модели. Приемлимая точность модели при решении практических задач может определяться, исходя из соображений экономической целесообразности с учётом конкретной ситуации. Широко применяется критерий, в соответствии с которым точность считается удовлетворительной, если средняя относительная погрешность меньше 15%. Если E отн.ср. меньше 5%, то говорят, что модель имеет высокую точность. Не рекомендуется применять для анализа и прогноза модели с неудовлетворительной точностью, то есть, когда E отн.ср. больше 15%.
F-критерий Фишера используется для оценки значимости уравнения регрессии. Расчётное значение F-критерия определяется из соотношения:

Критическое значение F -критерия определяется по таблицам при заданном уровне значимости α и степенях свободы (можно использовать функцию FРАСПОБР в Excel). Здесь, по-прежнему, m – число факторов, учтённых в модели, n – количество наблюдений. Если расчётное значение больше критического, то уравнение модели признаётся значимым. Чем больше расчётное значение F -критерия, тем лучше качество модели.
Определим характеристики качества построенной нами линейной модели для Примера 1 . Воспользуемся данными Таблицы 2. Коэффициент детерминации :
Следовательно, в рамках линейной модели изменение объёма продаж на 90,1% объясняется изменением температуры воздуха.

Значение индекса корреляции в случае парной линейной модели как мы видим, действительно по модулю равно коэффициенту корреляции между соответствующими переменными (объём продаж и температура). Поскольку полученное значение достаточно близко к единице, то можно сделать вывод о наличии тесной линейной связи между исследуемой переменной (объём продаж) и факторной переменноё (температура).
Критическое значение F кр при α = 0,1; ν 1 =1; ν 2 =7-1-1=5 равно 4,06. Расчётное значение F -критерия больше табличного, следовательно, уравнение модели является значимым.
Средняя относительная ошибка аппроксимации
Построенная линейная модель парной регрессии имеет неудовлетворительную точность (>15%), и её не рекомендуется использовать для анализа и прогнозирования.
В итоге, несмотря на то, что большинство статистических характеристик удовлетворяют предъявляемым к ним критериям, линейная модель парной регрессии непригодна для прогнозирования объёма продаж в зависимости от температуры воздуха. Нелинейный характер зависимости между указанными переменными по данным наблюдений достаточно хорошо виден на Рис.1. Проведённый анализ это подтвердил.
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
В конкретно нашем случае формула принимает такой вид:
Величина достоверности аппроксимации у нас равна 0,9418 , что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
Общий вид функции сглаживания при этом такой:
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
В общем виде формула сглаживания выглядит так:
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
В конкретно нашем случае она выглядит так:
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844 ), наименьший уровень достоверности у линейного метода (0,9418 ). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Контрольная работа: Парная регрессия
Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х1 , Х2 , … Хр и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение функции). Переменные Х мы будем называть факторами, а Y – откликом.
Наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай называется парной (простой) регрессией.
Парная регрессия – уравнение связи двух переменных у иx :
,
где у – зависимая переменная (результативный признак);
х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия:.
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
• полиномы разных степеней
•равносторонняя гипербола
Регрессии, нелинейные по оцениваемым параметрам:
• степенная ;
• показательная
• экспоненциальная
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических минимальна, т.е.
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно а и b :
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии
и индекс корреляции — для нелинейной регрессии ():
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
Допустимый предел значений – не более 8 – 10%.
Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
где – общая сумма квадратов отклонений;
– сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
–остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R 2 :
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
F -тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F -критерия Фишера. F факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
п – число единиц совокупности;
т – число параметров при переменных х.
Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.
Если Fтабл Fфакт , то гипотеза Н0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t -критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и критическое (табличное) значения t-статистики – tтабл и tфакт – принимаем или отвергаем гипотезу Hо .
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством
Если tтабл tфакт , то гипотеза Но не отклоняется и признается случайная природа формирования a , b или .
Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:
Формулы для расчета доверительных интервалов имеют следующий вид:
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения . Вычисляется средняя стандартная ошибка прогноза :
где
и строится доверительный интервал прогноза:
где
По 22 регионам страны изучается зависимость розничной продажи телевизоров, y от среднедушевых денежных доходов в месяц, x (табл. 1):
| Название: Парная регрессия Раздел: Рефераты по математике Тип: контрольная работа Добавлен 13:41:57 15 апреля 2011 Похожие работы Просмотров: 3780 Комментариев: 22 Оценило: 4 человек Средний балл: 4.5 Оценка: неизвестно Скачать |
| № региона | X | Y |
| 1,000 | 2,800 | 28,000 |
| 2,000 | 2,400 | 21,300 |
| 3,000 | 2,100 | 21,000 |
| 4,000 | 2,600 | 23,300 |
| 5,000 | 1,700 | 15,800 |
| 6,000 | 2,500 | 21,900 |
| 7,000 | 2,400 | 20,000 |
| 8,000 | 2,600 | 22,000 |
| 9,000 | 2,800 | 23,900 |
| 10,000 | 2,600 | 26,000 |
| 11,000 | 2,600 | 24,600 |
| 12,000 | 2,500 | 21,000 |
| 13,000 | 2,900 | 27,000 |
| 14,000 | 2,600 | 21,000 |
| 15,000 | 2,200 | 24,000 |
| 16,000 | 2,600 | 34,000 |
| 17,000 | 3,300 | 31,900 |
| 19,000 | 3,900 | 33,000 |
| 20,000 | 4,600 | 35,400 |
| 21,000 | 3,700 | 34,000 |
| 22,000 | 3,400 | 31,000 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
5. Качество уравнений оцените с помощью средней ошибки аппроксимации.
6. С помощью F-критерия Фишера определите статистическую надежность результатов регрессионного моделирования. Выберите лучшее уравнение регрессии и дайте его обоснование.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
1. Поле корреляции для:
· Линейной регрессии y=a+b*x:
Гипотеза о форме связи: чем больше размер среднедушевого денежного дохода в месяц (факторный признак), тем больше при прочих равных условиях розничная продажа телевизоров (результативный признак). В данной модели параметр b называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признаках на одну единицу.
· Степенной регрессии :
Гипотеза о форме связи : степенная функция имеет вид Y=ax b .
Параметр b степенного уравнения называется показателем эластичности и указывает, на сколько процентов изменится у при возрастании х на 1%. При х = 1 a = Y.
· Экспоненциальная регрессия :
· Равносторонняя гипербола :
Гипотеза о форме связи: В ряде случаев обратная связь между факторным и результативным признаками может быть выражена уравнением гиперболы: Y=a+b/x.
· Обратная гипербола :
· Полулогарифмическая регрессия :
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
· Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:
По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x 2 , ∑y 2 (табл. 2):
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp | Y-Y^cp | Ai |
| 1 | 2,800 | 28,000 | 78,400 | 7,840 | 784,000 | 25,719 | 2,281 | 0,081 |
| 2 | 2,400 | 21,300 | 51,120 | 5,760 | 453,690 | 22,870 | -1,570 | 0,074 |
| 3 | 2,100 | 21,000 | 44,100 | 4,410 | 441,000 | 20,734 | 0,266 | 0,013 |
| 4 | 2,600 | 23,300 | 60,580 | 6,760 | 542,890 | 24,295 | -0,995 | 0,043 |
| 5 | 1,700 | 15,800 | 26,860 | 2,890 | 249,640 | 17,885 | -2,085 | 0,132 |
| 6 | 2,500 | 21,900 | 54,750 | 6,250 | 479,610 | 23,582 | -1,682 | 0,077 |
| 7 | 2,400 | 20,000 | 48,000 | 5,760 | 400,000 | 22,870 | -2,870 | 0,144 |
| 8 | 2,600 | 22,000 | 57,200 | 6,760 | 484,000 | 24,295 | -2,295 | 0,104 |
| 9 | 2,800 | 23,900 | 66,920 | 7,840 | 571,210 | 25,719 | -1,819 | 0,076 |
| 10 | 2,600 | 26,000 | 67,600 | 6,760 | 676,000 | 24,295 | 1,705 | 0,066 |
| 11 | 2,600 | 24,600 | 63,960 | 6,760 | 605,160 | 24,295 | 0,305 | 0,012 |
| 12 | 2,500 | 21,000 | 52,500 | 6,250 | 441,000 | 23,582 | -2,582 | 0,123 |
| 13 | 2,900 | 27,000 | 78,300 | 8,410 | 729,000 | 26,431 | 0,569 | 0,021 |
| 14 | 2,600 | 21,000 | 54,600 | 6,760 | 441,000 | 24,295 | -3,295 | 0,157 |
| 15 | 2,200 | 24,000 | 52,800 | 4,840 | 576,000 | 21,446 | 2,554 | 0,106 |
| 16 | 2,600 | 34,000 | 88,400 | 6,760 | 1156,000 | 24,295 | 9,705 | 0,285 |
| 17 | 3,300 | 31,900 | 105,270 | 10,890 | 1017,610 | 29,280 | 2,620 | 0,082 |
| 19 | 3,900 | 33,000 | 128,700 | 15,210 | 1089,000 | 33,553 | -0,553 | 0,017 |
| 20 | 4,600 | 35,400 | 162,840 | 21,160 | 1253,160 | 38,539 | -3,139 | 0,089 |
| 21 | 3,700 | 34,000 | 125,800 | 13,690 | 1156,000 | 32,129 | 1,871 | 0,055 |
| 22 | 3,400 | 31,000 | 105,400 | 11,560 | 961,000 | 29,992 | 1,008 | 0,033 |
| Итого | 58,800 | 540,100 | 1574,100 | 173,320 | 14506,970 | 540,100 | 0,000 | |
| сред значение | 2,800 | 25,719 | 74,957 | 8,253 | 690,808 | 0,085 | ||
| станд. откл | 0,643 | 5,417 |
Система нормальных уравнений составит:
Ур-ие регрессии: = 5,777+7,122∙x. Данное уравнение показывает, что с увеличением среднедушевого денежного дохода в месяц на 1 тыс. руб. доля розничных продаж телевизоров повышается в среднем на 7,12%.
· Рассчитаем параметры уравнений степенной парной регрессии. Построению степенной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
где
Для расчетов используем данные табл. 3:
| № рег | X | Y | XY | X^2 | Y^2 | Yp^cp | y^cp |
| 1 | 1,030 | 3,332 | 3,431 | 1,060 | 11,104 | 3,245 | 25,67072 |
| 2 | 0,875 | 3,059 | 2,678 | 0,766 | 9,356 | 3,116 | 22,56102 |
| 3 | 0,742 | 3,045 | 2,259 | 0,550 | 9,269 | 3,004 | 20,17348 |
| 4 | 0,956 | 3,148 | 3,008 | 0,913 | 9,913 | 3,183 | 24,12559 |
| 5 | 0,531 | 2,760 | 1,465 | 0,282 | 7,618 | 2,827 | 16,90081 |
| 6 | 0,916 | 3,086 | 2,828 | 0,840 | 9,526 | 3,150 | 23,34585 |
| 7 | 0,875 | 2,996 | 2,623 | 0,766 | 8,974 | 3,116 | 22,56102 |
| 8 | 0,956 | 3,091 | 2,954 | 0,913 | 9,555 | 3,183 | 24,12559 |
| 9 | 1,030 | 3,174 | 3,268 | 1,060 | 10,074 | 3,245 | 25,67072 |
| 10 | 0,956 | 3,258 | 3,113 | 0,913 | 10,615 | 3,183 | 24,12559 |
| 11 | 0,956 | 3,203 | 3,060 | 0,913 | 10,258 | 3,183 | 24,12559 |
| 12 | 0,916 | 3,045 | 2,790 | 0,840 | 9,269 | 3,150 | 23,34585 |
| 13 | 1,065 | 3,296 | 3,509 | 1,134 | 10,863 | 3,275 | 26,4365 |
| 14 | 0,956 | 3,045 | 2,909 | 0,913 | 9,269 | 3,183 | 24,12559 |
| 15 | 0,788 | 3,178 | 2,506 | 0,622 | 10,100 | 3,043 | 20,97512 |
| 16 | 0,956 | 3,526 | 3,369 | 0,913 | 12,435 | 3,183 | 24,12559 |
| 17 | 1,194 | 3,463 | 4,134 | 1,425 | 11,990 | 3,383 | 29,4585 |
| 19 | 1,361 | 3,497 | 4,759 | 1,852 | 12,226 | 3,523 | 33,88317 |
| 20 | 1,526 | 3,567 | 5,443 | 2,329 | 12,721 | 3,661 | 38,90802 |
| 21 | 1,308 | 3,526 | 4,614 | 1,712 | 12,435 | 3,479 | 32,42145 |
| 22 | 1,224 | 3,434 | 4,202 | 1,498 | 11,792 | 3,408 | 30,20445 |
| итого | 21,115 | 67,727 | 68,921 | 22,214 | 219,361 | 67,727 | 537,270 |
| сред зн | 1,005 | 3,225 | 3,282 | 1,058 | 10,446 | 3,225 | |
| стан откл | 0,216 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: . Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата y .
· Рассчитаем параметры уравнений экспоненциальной парной регрессии. Построению экспоненциальной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
где
Для расчетов используем данные табл. 4:
| № региона | X | Y | XY | X^2 | Y^2 | Yp | y^cp |
| 1 | 2,800 | 3,332 | 9,330 | 7,840 | 11,104 | 3,225 | 25,156 |
| 2 | 2,400 | 3,059 | 7,341 | 5,760 | 9,356 | 3,116 | 22,552 |
| 3 | 2,100 | 3,045 | 6,393 | 4,410 | 9,269 | 3,034 | 20,777 |
| 4 | 2,600 | 3,148 | 8,186 | 6,760 | 9,913 | 3,170 | 23,818 |
| 5 | 1,700 | 2,760 | 4,692 | 2,890 | 7,618 | 2,925 | 18,625 |
| 6 | 2,500 | 3,086 | 7,716 | 6,250 | 9,526 | 3,143 | 23,176 |
| 7 | 2,400 | 2,996 | 7,190 | 5,760 | 8,974 | 3,116 | 22,552 |
| 8 | 2,600 | 3,091 | 8,037 | 6,760 | 9,555 | 3,170 | 23,818 |
| 9 | 2,800 | 3,174 | 8,887 | 7,840 | 10,074 | 3,225 | 25,156 |
| 10 | 2,600 | 3,258 | 8,471 | 6,760 | 10,615 | 3,170 | 23,818 |
| 11 | 2,600 | 3,203 | 8,327 | 6,760 | 10,258 | 3,170 | 23,818 |
| 12 | 2,500 | 3,045 | 7,611 | 6,250 | 9,269 | 3,143 | 23,176 |
| 13 | 2,900 | 3,296 | 9,558 | 8,410 | 10,863 | 3,252 | 25,853 |
| 14 | 2,600 | 3,045 | 7,916 | 6,760 | 9,269 | 3,170 | 23,818 |
| 15 | 2,200 | 3,178 | 6,992 | 4,840 | 10,100 | 3,061 | 21,352 |
| 16 | 2,600 | 3,526 | 9,169 | 6,760 | 12,435 | 3,170 | 23,818 |
| 17 | 3,300 | 3,463 | 11,427 | 10,890 | 11,990 | 3,362 | 28,839 |
| 19 | 3,900 | 3,497 | 13,636 | 15,210 | 12,226 | 3,526 | 33,978 |
| 20 | 4,600 | 3,567 | 16,407 | 21,160 | 12,721 | 3,717 | 41,140 |
| 21 | 3,700 | 3,526 | 13,048 | 13,690 | 12,435 | 3,471 | 32,170 |
| 22 | 3,400 | 3,434 | 11,676 | 11,560 | 11,792 | 3,389 | 29,638 |
| Итого | 58,800 | 67,727 | 192,008 | 173,320 | 219,361 | 67,727 | 537,053 |
| сред зн | 2,800 | 3,225 | 9,143 | 8,253 | 10,446 | ||
| стан откл | 0,643 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: . Выполнив его потенцирование, получим:
Для расчета теоретических значений y подставим в уравнение значения x .
· Рассчитаем параметры уравнений полулогарифмической парной регрессии. Построению полулогарифмической модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем замены:
где
Для расчетов используем данные табл. 5:
| № региона | X | Y | XY | X^2 | Y^2 | y^cp |
| 1 | 1,030 | 28,000 | 28,829 | 1,060 | 784,000 | 26,238 |
| 2 | 0,875 | 21,300 | 18,647 | 0,766 | 453,690 | 22,928 |
| 3 | 0,742 | 21,000 | 15,581 | 0,550 | 441,000 | 20,062 |
| 4 | 0,956 | 23,300 | 22,263 | 0,913 | 542,890 | 24,647 |
| 5 | 0,531 | 15,800 | 8,384 | 0,282 | 249,640 | 15,525 |
| 6 | 0,916 | 21,900 | 20,067 | 0,840 | 479,610 | 23,805 |
| 7 | 0,875 | 20,000 | 17,509 | 0,766 | 400,000 | 22,928 |
| 8 | 0,956 | 22,000 | 21,021 | 0,913 | 484,000 | 24,647 |
| 9 | 1,030 | 23,900 | 24,608 | 1,060 | 571,210 | 26,238 |
| 10 | 0,956 | 26,000 | 24,843 | 0,913 | 676,000 | 24,647 |
| 11 | 0,956 | 24,600 | 23,506 | 0,913 | 605,160 | 24,647 |
| 12 | 0,916 | 21,000 | 19,242 | 0,840 | 441,000 | 23,805 |
| 13 | 1,065 | 27,000 | 28,747 | 1,134 | 729,000 | 26,991 |
| 14 | 0,956 | 21,000 | 20,066 | 0,913 | 441,000 | 24,647 |
| 15 | 0,788 | 24,000 | 18,923 | 0,622 | 576,000 | 21,060 |
| 16 | 0,956 | 34,000 | 32,487 | 0,913 | 1156,000 | 24,647 |
| 17 | 1,194 | 31,900 | 38,086 | 1,425 | 1017,610 | 29,765 |
| 19 | 1,361 | 33,000 | 44,912 | 1,852 | 1089,000 | 33,351 |
| 20 | 1,526 | 35,400 | 54,022 | 2,329 | 1253,160 | 36,895 |
| 21 | 1,308 | 34,000 | 44,483 | 1,712 | 1156,000 | 32,221 |
| 22 | 1,224 | 31,000 | 37,937 | 1,498 | 961,000 | 30,406 |
| Итого | 21,115 | 540,100 | 564,166 | 22,214 | 14506,970 | 540,100 |
| сред зн | 1,005 | 25,719 | 26,865 | 1,058 | 690,808 | |
| стан откл | 0,216 | 5,417 |
Рассчитаем a и b:
Получим линейное уравнение: .
· Рассчитаем параметры уравнений обратной парной регрессии. Для оценки параметров приведем обратную модель к линейному виду, заменив , тогда
Для расчетов используем данные табл. 6:
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 2,800 | 0,036 | 0,100 | 7,840 | 0,001 | 24,605 |
| 2 | 2,400 | 0,047 | 0,113 | 5,760 | 0,002 | 22,230 |
| 3 | 2,100 | 0,048 | 0,100 | 4,410 | 0,002 | 20,729 |
| 4 | 2,600 | 0,043 | 0,112 | 6,760 | 0,002 | 23,357 |
| 5 | 1,700 | 0,063 | 0,108 | 2,890 | 0,004 | 19,017 |
| 6 | 2,500 | 0,046 | 0,114 | 6,250 | 0,002 | 22,780 |
| 7 | 2,400 | 0,050 | 0,120 | 5,760 | 0,003 | 22,230 |
| 8 | 2,600 | 0,045 | 0,118 | 6,760 | 0,002 | 23,357 |
| 9 | 2,800 | 0,042 | 0,117 | 7,840 | 0,002 | 24,605 |
| 10 | 2,600 | 0,038 | 0,100 | 6,760 | 0,001 | 23,357 |
| 11 | 2,600 | 0,041 | 0,106 | 6,760 | 0,002 | 23,357 |
| 12 | 2,500 | 0,048 | 0,119 | 6,250 | 0,002 | 22,780 |
| 13 | 2,900 | 0,037 | 0,107 | 8,410 | 0,001 | 25,280 |
| 14 | 2,600 | 0,048 | 0,124 | 6,760 | 0,002 | 23,357 |
| 15 | 2,200 | 0,042 | 0,092 | 4,840 | 0,002 | 21,206 |
| 16 | 2,600 | 0,029 | 0,076 | 6,760 | 0,001 | 23,357 |
| 17 | 3,300 | 0,031 | 0,103 | 10,890 | 0,001 | 28,398 |
| 19 | 3,900 | 0,030 | 0,118 | 15,210 | 0,001 | 34,844 |
| 20 | 4,600 | 0,028 | 0,130 | 21,160 | 0,001 | 47,393 |
| 21 | 3,700 | 0,029 | 0,109 | 13,690 | 0,001 | 32,393 |
| 22 | 3,400 | 0,032 | 0,110 | 11,560 | 0,001 | 29,301 |
| Итого | 58,800 | 0,853 | 2,296 | 173,320 | 0,036 | 537,933 |
| сред знач | 2,800 | 0,041 | 0,109 | 8,253 | 0,002 | |
| стан отклон | 0,643 | 0,009 |
Рассчитаем a и b:
Получим линейное уравнение: . Выполнив его потенцирование, получим:
Для расчета теоретических значений y подставим в уравнение значения x .
· Рассчитаем параметры уравнений равносторонней гиперболы парной регрессии. Для оценки параметров приведем модель равносторонней гиперболы к линейному виду, заменив , тогда
Для расчетов используем данные табл. 7:
| № региона | X=1/z | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 0,357 | 28,000 | 10,000 | 0,128 | 784,000 | 26,715 |
| 2 | 0,417 | 21,300 | 8,875 | 0,174 | 453,690 | 23,259 |
| 3 | 0,476 | 21,000 | 10,000 | 0,227 | 441,000 | 19,804 |
| 4 | 0,385 | 23,300 | 8,962 | 0,148 | 542,890 | 25,120 |
| 5 | 0,588 | 15,800 | 9,294 | 0,346 | 249,640 | 13,298 |
| 6 | 0,400 | 21,900 | 8,760 | 0,160 | 479,610 | 24,227 |
| 7 | 0,417 | 20,000 | 8,333 | 0,174 | 400,000 | 23,259 |
| 8 | 0,385 | 22,000 | 8,462 | 0,148 | 484,000 | 25,120 |
| 9 | 0,357 | 23,900 | 8,536 | 0,128 | 571,210 | 26,715 |
| 10 | 0,385 | 26,000 | 10,000 | 0,148 | 676,000 | 25,120 |
| 11 | 0,385 | 24,600 | 9,462 | 0,148 | 605,160 | 25,120 |
| 12 | 0,400 | 21,000 | 8,400 | 0,160 | 441,000 | 24,227 |
| 13 | 0,345 | 27,000 | 9,310 | 0,119 | 729,000 | 27,430 |
| 14 | 0,385 | 21,000 | 8,077 | 0,148 | 441,000 | 25,120 |
| 15 | 0,455 | 24,000 | 10,909 | 0,207 | 576,000 | 21,060 |
| 16 | 0,385 | 34,000 | 13,077 | 0,148 | 1156,000 | 25,120 |
| 17 | 0,303 | 31,900 | 9,667 | 0,092 | 1017,610 | 29,857 |
| 19 | 0,256 | 33,000 | 8,462 | 0,066 | 1089,000 | 32,564 |
| 20 | 0,217 | 35,400 | 7,696 | 0,047 | 1253,160 | 34,829 |
| 21 | 0,270 | 34,000 | 9,189 | 0,073 | 1156,000 | 31,759 |
| 22 | 0,294 | 31,000 | 9,118 | 0,087 | 961,000 | 30,374 |
| Итого | 7,860 | 540,100 | 194,587 | 3,073 | 14506,970 | 540,100 |
| сред знач | 0,374 | 25,719 | 9,266 | 0,146 | 1318,815 | |
| стан отклон | 0,079 | 25,639 |
Рассчитаем a и b:
Получим линейное уравнение: . Получим уравнение регрессии: .
3. Оценка тесноты связи с помощью показателей корреляции и детерминации :
· Линейная модель. Тесноту линейной связи оценит коэффициент корреляции. Был получен следующий коэффициент корреляции rxy =b=7,122*, что говорит о прямой сильной связи фактора и результата. Коэффициент детерминации r²xy =(0,845)²=0,715. Это означает, что 71,5% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Степенная модель. Тесноту нелинейной связи оценит индекс корреляции. Был получен следующий индекс корреляции =, что говорит о очень сильной тесной связи, но немного больше чем в линейной модели. Коэффициент детерминации r²xy =0,7175. Это означает, что 71,75% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Экспоненциальная модель. Был получен следующий индекс корреляции ρxy =0,8124, что говорит о том, что связь прямая и очень сильная, но немного слабее, чем в линейной и степенной моделях. Коэффициент детерминации r²xy =0,66. Это означает, что 66% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Полулогарифмическая модель. Был получен следующий индекс корреляции ρxy =0,8578, что говорит о том, что связь прямая и очень сильная, но немного больше чем в предыдущих моделях. Коэффициент детерминации r²xy =0,7358. Это означает, что 73,58% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Гиперболическая модель. Был получен следующий индекс корреляции ρxy =0,8448 и коэффициент корреляции rxy =-0,1784 что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy =0,7358. Это означает, что 73,5% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Обратная модель. Был получен следующий индекс корреляции ρxy =0,8114 и коэффициент корреляции rxy =-0,8120, что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy =0,6584. Это означает, что 65,84% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Вывод: по полулогарифмическому уравнению получена наибольшая оценка тесноты связи: ρxy =0,8578 (по сравнению с линейной, степенной, экспоненциальной, гиперболической, обратной регрессиями).
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
Рассчитаем коэффициент эластичности для линейной модели:
· Для уравнения прямой:y = 5,777+7,122∙x
· Для уравнениястепенноймодели :
· Для уравненияэкспоненциальноймодели :
Для уравненияполулогарифмическоймодели :
· Для уравнения обратной гиперболической модели :
· Для уравнения равносторонней гиперболической модели :
Сравнивая значения , характеризуем оценку силы связи фактора с результатом:
·
·
·
·
·
·
Известно, что коэффициент эластичности показывает связь между фактором и результатом, т.е. на сколько% изменится результат y от своей средней величины при изменении фактора х на 1% от своего среднего значения. В данном примере получилось, что самая большая сила связи между фактором и результатом в полулогарифмической модели, слабая сила связи в обратной гиперболической модели.
5. Оценка качества уравнений с помощью средней ошибки аппроксимации.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения . Найдем величину средней ошибки аппроксимации :
В среднем расчетные значения отклоняются от фактических на:
· Линейная регрессия. =*100%= 8,5%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Степенная регрессия. =*100%= 8,2%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Экспоненциальная регрессия. =*100%= 9%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Полулогарифмическая регрессия. =*100%= 7,9 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Гиперболическая регрессия. =*100%= 9,3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Обратная регрессия. =*100%= 9,9 3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
6. Рассчитаем F-критерий:
· Линейная регрессия. = *19= 47,579
http://welom.ru/srednyaya-oshibka-approksimacii-v-excel-ocenka-kachestva-uravneniya/
http://www.bestreferat.ru/referat-268496.html
Вариант
5
1
задание
-
Постройте
поле корреляции и сформулируйте гипотезу
о форме связи.
-
Введу
значения Y
и X
в таблицу, отсортирую их по возрастанию
по X:Y
X
68,77
70,5
64,19
70,64
65,78
70,93
63,35
71,61
67,67
73,37
60,95
75,93
61,21
76,31
65,96
76,37
67,47
76,72
61,13
77,18
65,55
77,43
62,47
77,79
64,53
78,38
66,67
78,5
64,81
78,75
69,68
79,3
61,5
79,38
61,57
79,69
-
Построю
поле корреляции по данным из таблицы:
-
Сказать
о форме связи достаточно тяжело, потому
что точки располагаются неравномерно.
Возможно, здесь линейная форма связи.
-
Рассчитайте
параметры уравнения линейной регрессии.
-
Чтобы
рассчитать параметры уравнения линейной
регрессии, необходимо написать само
уравнение: y=ax+b,
а также нужно записать формулу для
коэффициентов а и b.
-
Введу
в таблицу новые показатели: x*y,
x^2,
сумму, среднее значение и рассчитаю
их, а затем по формулам рассчитаю
коэффициенты а и b.
|
|
||||
|
|
||||
-
Оцените
тесноту связи с помощью показателей
корреляции и детерминации.
-
С
помощью формулы линейного коэффициента
парной корреляции определю тесноту
связи
R=-0,221
-
Коэффициент
детерминации – это коэффициент
корреляции в квадрате.
Он
равен = 0,049
Вывод:
связь слабая.
-
Оцените
с помощью средней ошибки аппроксимации
качество уравнений.
Средняя
ошибка аппроксимации – среднее отклонение
расчетных значений от фактических:
Для
данных расчётов мне необходимо значение

которое в Excel
назову y(t).
По формуле рассчитала показатель А.
Средняя
ошибка аппроксимации равна 3,5%. Величина
ошибки аппроксимации говорит о высоком
качестве модели.
-
Оцените
с помощью F -критерия Фишера и t -критерия
Стьюдента статистическую значимость
результатов регрессионного моделирования.
-
Рассчитаю
F-критерий
Фишера по формулам
Критическое
значение рассчитала по специальной
статистической формуле в Excel
F.ОБР.ПХ.
(вероятность 0,05; степени свободы1 =1;
степени свободы2 = 16). F(критич)
= 4,49
Фактическое
значение рассчитала по формуле:

где n-
количество исследуемых точек.
F
(фактич) = 0,78
Так
как F
(критич) больше F
(фактич), то можно сделать вывод, что
уравнение связи является статистически
незначимым.
-
Рассчитаю
критический t-критерий
Стьюдента по статистической формуле
в Excel
СТЬЮДЕНТ.ОБР.2Х (вероятность = 0,05; степени
свободы (18-2) =16). t (критич) = 2,12.
Фактическое
значение считаю для каждого параметра:
Параметр
а:
,
Параметр
b:
Параметр
r:
t(a)
= -0,01
t(b)
= 1,16
t(r
) = -0,91
Так
как все фактические критерии параметров
меньше критического t-критерия,
значит все параметры статистически не
значимые.
-
По
значениям характеристик, рассчитанным
в пп. 3-5, выберите лучшее уравнение
регрессии и дайте его обоснование.
Наше
уравнение линейной регрессии обладает
такими свойствами:
-
Связь
слабая (по коэффициенту парной корреляции) -
Высокое
качество модели (по средней ошибке
аппроксимации) -
Уравнение
связи и все его параметры являются
статистически незначимыми (на основании
F-критерия
Фишера и t-критерия
Стьюдента)
-
Рассчитайте
прогнозное значение результата, если
значение фактора увеличится на 10% от
его среднего уровня. Определите
доверительный интервал прогноза для
уровня значимости α= 0,05
Прогнозное
значение
определяется путём подстановки в
уравнение регрессии
соответствующего (прогнозного) значения

Вычисляется средняя стандартная ошибка
прогноза
:
где
и
строится доверительный интервал
прогноза:
-
Найду
прогнозное значение результативного
фактора
при значении признака-фактора,
составляющем 110% от среднего уровня
-
Найду
доверительный интервал прогноза. Ошибка
прогноза
Доверительный
интервал рассчитывается:

Здесь:
(двухстороннее значение t-критерия
Стьюдента): t
(0,05; 18-2) = 2,12
Доверительный
интервал: (63,16- 9,81*2,12; 63,16+ 9,81*2,12) = (42,38;
83,95)
Истинное
значение прогноза (63,16) попадает в этот
интервал.
2
задание
Разработайте
план погашения кредита, полученного на
следующих условиях: Сумма кредита – Р
тысяч рублей, срок кредита – n лет,
процентная ставка по кредиту – i% годовых,
количество платежей в год –m раз. Данные
для каждого варианта приводятся в
таблице ниже:
|
Сумма |
Срок |
Процентная |
Количество |
|
675 |
5 |
28 |
1 |
-
Составлю
таблицу «План погашения кредита»
|
№ п/п |
Сумма |
Годовая |
Процентные |
Осталось |
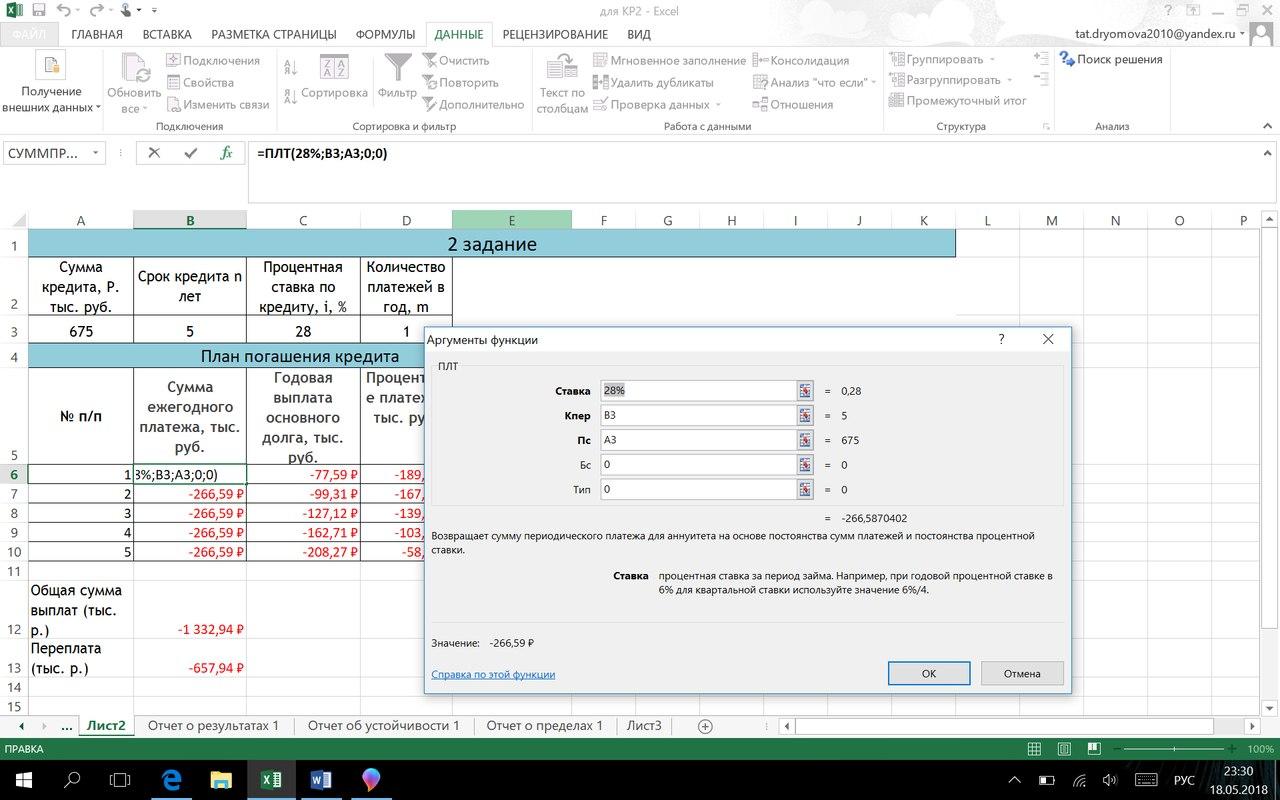
-
Для
начала рассчитаю сумму ежегодного
платежа (тыс. руб.). Для этого выберу
финансовую функцию ПЛТ в Excel:
ПЛТ(28%; В3; А3; 0; 0)
Ежегодный
платёж на протяжении 5-ти лет будет
равным. Поэтому можно рассчитать общую
сумму выплат (долг + проценты) и переплату:
-
Общая
сумма выплат = сумма ежегодного платежа
* срок кредита = 266, 59 тыс. р. * 5 лет = 1332,94
тыс. р. -
Переплата
составит = общая сумма выплат – сумма
кредита = 1332,59 тыс. р. – 675 тыс. р. = 657, 94
тыс. р.
-
Рассчитаю
годовую выплату основного долга:
Для
этого использую функцию ОСПЛТ в Excel:
ОСПЛТ (28%; период; $B$3;
$A$3;
0) – период соответственно каждой строке
(1-5)
Годовая
выплата по кредиту для каждого года
составила:
-
Далее
рассчитаю сколько процентных платежей
уплачивается за каждый период. Для
этого из суммы ежегодного платежа вычту
годовую выплату основного долга
(результаты этих вычислений на фото
таблицы Excel
выше). -
Чтобы
посчитать последний столбец «осталось
выплатить» проделаю следующую операцию:
-
для
первого периода: =$A$3+СУММ($C$6:C6), где $A$3
– первоначальная сумма кредита, $C$6:C6
– годовая выплата основного долга в
рассматриваемый период; -
для
второго периода: =$E$6+СУММ($C$7:C7), где $E$6
– осталось выплатить в предыдущем
периоде; -
для
остальных периодов первое слагаемое
будет равно «осталось выплатить» в
предыдущем периоде, а второе слагаемое
– годовая выплата основного долга в
рассматриваемом периоде.
В
конце последнего периода «осталось
выплатить» становится равным 0, так как
мы полностью погасили долг.
План
погашения кредита разработан.
3
задание
-
определить
оптимальный план выпуска, максимизирующий
прибыль; -
насколько
изменится оптимальное решение, если
продукция будет измеряться в шт.
(целочисленное). -
насколько
изменится оптимальное решение, если
задана нижняя граница плана выпуска
по каждому изделию (договорные
обязательства) -
Провести
анализ чувствительности оптимального
решения.
|
Нормы |
Запасы |
||||
|
Изделие |
Изделие |
Изделие |
Изделие |
||
|
Сырьё |
5 |
1 |
8 |
7 |
745 |
|
Сырьё |
1 |
5 |
5 |
6 |
610 |
|
Сырьё |
7 |
5 |
7 |
4 |
768 |
|
Цена |
7 |
6 |
9 |
14 |
-
Составлю
таблицу в Excel:
создала сроку «коэф. цф», где написала
коэффициенты переменных из первого
уравнения и столбец «знач. цф». Через
функцию СУММПРОИЗВ посчитала «знач.
цф». Затем, нажав ячейку «знач. цф»,
нажму «поиск решения» и введу ограничения,
а также выберу метод поиска решений.
Таким образом определила оптимальный
план выпуска, максимизирующий прибыль.
-
Для
ответа на второй вопрос задачи оставлю
эту же таблицу. В графе поиска решений
добавлю ограничение на значения
переменных – они должны быть целыми.
Значение переменных изменится
незначительно (округлится до целых
чисел), а в столбце на пересечении стоки
«огранич» и столбца «знач. цф» произойдут
изменения с 745 до 741 (на 4 ед.) и с 768 до 764
(на 4 ед.)
-
Задам
произвольную нижнюю границу: 1 и добавлю
это условие в ограничения на поиск
решений. При этом значения переменных
изменятся следующим образом:
Х1
уменьшится на 3 ед., Х2 уменьшится на 3
ед., Х3 увеличится на 1 ед., Х4 увеличится
на 2 ед.
-
Отчёты:
Согласно
отчёту о результатах все ресурсы являются
дефицитными (состояние – привязка).
Согласно
отчёту об устойчивости:
Х1: допустимое
увеличение =6,741, допустимое уменьшение
= 0,172
Х2: допустимое увеличение =6,894,
допустимое уменьшение = 0,217
Х3:
допустимое увеличение =5,306, допустимое
уменьшение = 1Е+30
Х4: допустимое увеличение
=0,208, допустимое уменьшение = 7,271.
F10:
допустимое увеличение =348, 774, допустимое
уменьшение = 242,896
F11:
допустимое увеличение =620,75, допустимое
уменьшение = 306,26
F9:
допустимое увеличение =185,368, допустимое
уменьшение = 496,6
Соседние файлы в предмете Компьютерный практикум
- #
20.03.201819.8 Кб2701 курс КП 11.xlsx
- #
20.03.201836.24 Кб1601 курс КП 6.xlsx
- #
20.03.201821.95 Кб1111 курс КП 8.xlsx
- #
20.03.201822.76 Кб1361 курс КП 9.xlsx
- #
1. Настройка пакета для выполнения регрессионного анализа
Процедуры корреляционно-регрессионного анализа выполняются в табличном процессоре с помощью модуля «Пакет анализа». Для подключения этого модуля с помощью команды СЕРВИС – НАДСТРОЙКИ выведите окно НАДСТРОЙКИ и включите надстройку ПАКЕТ АНАЛИЗА.
Рис. 11. Диалоговое окно Надстройки меню Сервис.
После выполнения этой процедуры в ниспадающем меню пункта СЕРВИС появится команда АНАЛИЗ ДАННЫХ.
Рис. 12. Лист ППП «Excel» пункт меню Сервис команда Анализ данных.
2. Расчет показателей описательной статистики
Для проверки требований, предъявляемых к исходным данным, следует рассчитать ряд показателей, характеризующих эти данные (среднее значение, дисперсия и т. д.). Эти характеристики данных можно получить, воспользовавшись функцией СЕРВИС — АНАЛИЗ ДАННЫХ – ОПИСАТЕЛЬНАЯ СТАТИСТИКА.
Рис. 13. Диалоговое окно АНАЛИЗ ДАННЫХ.
После выбора требуемой функции откроется окно ОПИСАТЕЛЬНАЯ СТАТИСТИКА.
Рис. 14. Диалоговое окно ОПИСАТЕЛЬНАЯ статистика.
Для расчета показателей описательной статистики в окне «Входной интервал» укажите область ячеек электронной таблицы, где расположены анализируемые данные (исследуемый показатель и все факторы). Желательно в эту область включить ячейки с обозначениями переменных (Х0, Х1, …, Хр) для комфортного восприятия результатов вычислений. Если метки данных (обозначения переменных) учтены, то в области ВХОДНЫЕ ДАННЫЕ включите опцию «Метки в первой строке». Затем в области «Параметры вывода» укажите, куда должны быть выведены результаты расчетов (Новый лист либо Выходной интервал И верхняя левая ячейка области электронной таблицы, где должны быть размещены результаты).
В области «Параметры вывода» включите опцию «Итоговая статистика» и выполните процедуру.
В полученных результатах расчетов удалите повторяющуюся информацию (многократное повторение названий статистик) и рассчитайте для каждого показателя коэффициенты вариации (по среднему значению и стандартному отклонению).
3. Выявление тесноты связи и закона зависимости между факторами и результирующим показателем (анализ полей корреляции)
Для построения полей корреляции (диаграмм рассеивания) используйте команду ВСТАВКА – ДИАГРАММА – ТОЧЕЧНАЯ (вариант без соединения точек) либо мастер диаграмм. В результате выполнения этой команды появится окно МАСТЕР ДИАГРАММ (шаг 2 из 4):
Рис. 15. Диалоговое окно Мастера диаграмм.
В окне Диапазон укажите область столбца электронной таблицы, где находится массив данных для фактора, и через точку с запятой область данных по результирующему показателю. Щелкните мышкой по кнопке ДАЛЕЕ. В результате появится окно следующего 3 шага. В соответствующих окнах введите заголовок графика и названия осей; разместите график на рабочем листе. Постройте графики, отражающие влияние каждого фактора на исследуемый показатель.
Рис. 16. Диалоговое окно Мастера диаграмм – Параметры диаграммы.
Элементы корреляционной матрицы получите, воспользовавшись функцией СЕРВИС — АНАЛИЗ ДАННЫХ — КОРРЕЛЯЦИЯ. В результате будет открыто окно АНАЛИЗ ДАННЫХ.
Рис. 17. Диалоговое окно Анализ данных.
После выбора требуемой функции откроется окно КОРРЕЛЯЦИЯ.
Рис. 18. Диалоговое окно Корреляция.
В окне «Входной интервал» задайте область ячеек электронной таблицы, где расположены анализируемые данные (исследуемый показатель и все факторы). В эту область так же включите ячейки с обозначениями переменных (Х0, Х1, …, Хр). Если метки учтены в области данных, то в окне КОРРЕЛЯЦИЯ включите опцию «Метки в первой строке». Затем в области «Параметры вывода» укажите левую верхнюю ячейку области электронной таблицы, куда должна быть выведена корреляционная матрица.
Анализируя корреляционную матрицу, сделайте выводы о том, как сильно связаны факторы между собой и с исследуемым показателем. Если обнаружены коллинеарные (мультиколлинеарные) факторы, то для дальнейшего анализа следует оставить только один из этих факторов. Проводя анализ взаимосвязей показателей по корреляционной матрице, необходимо помнить о том, что парные коэффициенты корреляции — это показатели тесноты связи для линейных зависимостей.
4. Расчет параметров регрессионной модели
Вид регрессионной модели обосновывают двумя путями: теоретическим и эмпирическим. В первом случае используют качественные рассуждения о законе связи между исследуемым показателем и каждым из факторов, а также результаты других исследователей по построению аналогичных регрессионных моделей. При эмпирическом подходе выводы о форме связи делают на основе анализа фактических данных, представленных в виде первичных полей корреляции.
Чаще всего для анализа используют линейный вид модели или модель, которую можно привести к линейному виду путем некоторых преобразований и замены переменных.
Для расчета параметров регрессионной модели воспользуйтесь функцией СЕРВИС — АНАЛИЗ ДАННЫХ — РЕГРЕССИЯ. В результате появится окно АНАЛИЗ ДАННЫХ. В этом окне выберите инструмент анализа РЕГЕРССИЯ.
Рис. 19. Диалоговое окно Анализ данных.
После щелчка мышкой по кнопке ОК на экране появится окно РЕГРЕССИЯ.
Рис. 20. Диалоговое окно Регрессия.
В этом окне в области «Входной интервал Y» укажите область ячеек, где находятся данные исследуемого показателя, в области «Входной интервал X» — область ячеек с данными по всем факторам. Желательно при этом учитывать обозначения переменных. Если метки данных включены при определении области переменных, то включите опцию «Метки».
Чтобы получить данные для расчета средней относительной ошибки аппроксимации, в этом диалоговом окне поставьте флажок рядом с опцией ОСТАТКИ.
В результате использования функции СЕРВИС — АНАЛИЗ ДАННЫХ — РЕГРЕССИЯ будут получены не только параметры модели, но и показатели, позволяющие оценить надежность построенной модели.
5. Исключение из модели факторов, оказывающих несущественной влияние
Все факторы, влияние которых на исследуемый показатель несущественно, должны быть исключены из модели. Влияние фактора следует считать несущественным, если соответствующий коэффициент регрессии статистически не значим, то есть его можно приравнять нулю. Коэффициент регрессии следует считать статистически значимым (не равным нулю), если фактическая величина критерия Стьюдента будет больше табличного значения этого критерия. Табличное значение критерия Стьюдента можно найти, воспользовавшись в Excel мастером функций
.
После обращения к мастеру функций на экране появится окно «Мастер функций – шаг 1 из 2».
Рис. 21. Диалоговое окно Мастера функций.
В левой части этого окна выберите категорию функций «Статистические», в правой части, используя бегунок, выберите функцию «СТЬЮДРАСПРОБР» и щелкните мышкой по кнопке ОК. В результате появится окно для задания параметров этой функции. В этом окне «Вероятность» – уровень значимости (
= 1-
, где
— доверительная вероятность).
Рис. 22. Диалоговое окно функции Стьюдраспобр.
Уровень значимости обычно принимают равным 0,05; число степеней свободы
=
(где
— число наблюдений,
— число параметров регрессионной модели).
Если в модели присутствует несколько несущественных факторов, то первым следует исключить тот фактор, для которого табличное значение критерия Стьюдента намного больше
. Несущественно влияющий фактор убирают из совокупности наблюдений и пересчитывают параметры регресcионной модели и ее характеристики. Для модели, полученной на втором шаге, заново проверяют статистическую значимость коэффициентов регресcии. Если вновь обнаружен фактор, оказывающий несущественное влияние на анализируемый показатель, то этот фактор также исключают из модели. Отсев факторов из модели выполняют до тех пор, пока в ней останутся только факторы, оказывающие сильное влияние на
.
Чтобы убедиться в том, что из модели были исключены факторы, оказывающие слабое влияние на исследуемый показатель, сравните величины коэффициентов детерминации первого и последнего шагов. Их различие будет незначительным.
6. Проверка надежности регрессионной модели
Вывод о статистической значимости модели в целом делают по — критерию. Если фактическая величина критерия Фишера окажется больше табличного значения, то полученная модель статистически значима и полно описывает изменение исследуемого показателя под действием факторов, присутствующих в модели.
Теоретическое значение — критерия также можно получить с помощью мастера функций
. Для этого в окне «Мастер функций – шаг 1 из 2» следует выбрать функцию FРАСПОБР.
Рис. 23. Диалоговое окно Мастера функций.
В окне выбранной функции задайте требуемые параметры.
Рис. 24. Диалоговое окно функции Fраспобр.
«Вероятность» – уровень значимости (обычно принимают равным 0,05); «Число_степеней свободы1» — это число факторов, присутствующих в модели, «Число_степеней свободы2» определяют как разность между числом наблюдений и числом параметров модели.
Если Fрасч > Fтабл, то построенная модель считается статистически надежной, а следовательно, правильно отражает закон изменения исследуемого показателя под действием факторов, присутствующих в модели.
7. Проверка адекватности регрессионной модели
Среднюю относительную ошибку аппроксимации пользователь должен рассчитать самостоятельно по формуле 
фактические (расчетные) значения исследуемого показателя.
Если модель используют для целей анализа, допустима величина средней относительной ошибки до 10%, при применении модели для прогнозирования ошибка не должна быть больше 4%.
Для этого рядом с остатками следует добавить столбец фактических значений исследуемого показателя и выполнить ряд промежуточных расчетов.
8. Интерпретация полученных результатов
На этом этапе разрабатывают рекомендации об использовании результатов регрессионного анализа. Анализируют коэффициенты регрессии в натуральном и стандартизованном масштабе, а также коэффициенты эластичности.
Коэффициент регрессии в натуральном масштабе показывает, на сколько своих единиц измерения в среднем изменится исследуемый показатель
при увеличении
— го фактора на единицу своего измерения. При этом влияние остальных факторов находится на среднем уровне; свободный член уравнения характеризует изменение показателя за счет изменения факторов, неучтенных в модели.
В связи с тем, что факторы имеют различный физический смысл и различные единицы измерения, коэффициенты регрессии нельзя сравнивать между собой и, следовательно, невозможно определить, какой из факторов оказывает наибольшее влияние. Для устранения различий в единицах измерения применяют частные коэффициенты эластичности, рассчитываемые по формуле:

— средние значения
— го фактора и исследуемого показателя,
— коэффициент регрессии, стоящий при переменной
в многофакторном уравнении регрессии. Как известно, коэффициент эластичности характеризующие на сколько % в среднем изменится
При увеличении j-го фактора на 1% при фиксированном положении других факторов.
При определении степени влияния отдельных факторов необходим показатель, который бы учитывал влияние анализируемых факторов с учетом различий в уровне их колеблемости. Таким показателем является коэффициент регрессии в стандартизированном масштабе 
показывает на какую часть своего среднеквадратического отклонения изменится
при изменении j-го фактора на одно свое среднеквадратическое отклонение при фиксированном значении остальных факторов. Уравнение регрессии в стандартизированном масштабе :
где
Границы влияния фактора на исследуемый показатель рассчитываются по формуле (левая граница)
(правая граница), где
— доверительные полуинтервалы.
| < Предыдущая | Следующая > |
|---|
Средняя относительная ошибка аппроксимации.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
Рассмотрим каждый из вариантов более подробно в отдельности.
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
В конкретно нашем случае формула принимает такой вид:
Величина достоверности аппроксимации у нас равна 0,9418 , что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
В конкретно нашем случае формула приняла следующую форму:
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
где ln – это величина натурального логарифма. Отсюда и наименование метода.
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
5. С использованием F- критерия установлено, что полученное уравнение парной регрессии в целом является статистически незначимым, и неадекватно описывает изучаемое явление связи величины ежемесячной пенсии у с величиной прожиточного минимума х.
Сформирована эконометрическая модель множественной линейной регрессии, связывающая величину чистого дохода условной фирмы у с оборотом капитала х1 и использованным капиталом х2
7. Путем расчета коэффициентов эластичности показано, что при изменении оборота капитала на 1% величина чистого дохода копании изменяется на 0,0008%, а при изменении использованного капитала на 1% величина чистого дохода компании изменяется на 0,56%.
8. С использованием t-критерия выполнена оценка статистической значимости коэффициентов регрессии Установлено, что объясняющая переменная х 1 является статистически незначимой и ее можно исключить из уравнения регрессии, в тоже время объясняющая переменная х 2 является статистически значимой.
9. С использованием F-критерия установлено, что полученное уравнение парной регрессии в целом является статистически значимым, и адекватно описывает изучаемое явление связи величины чистого дохода условной фирмы у с оборотом капитала х 1 и использованным капиталом х 2 .
10. Рассчитана средняя ошибка аппроксимации статистических данных линейным уравнением множественной регрессии, которая составила 29,8%. Показано, за счет какого наблюдения в статистической базе величина данной ошибки превышает допустимое значение.
14. Построение модели парной регрессии без использования EXCEL.
Используя статистический материал, приведенный в таблице 3.5 необходимо:
2.Оценить тесноту связи с помощью показателей корреляции и детерминации.
3.Используя коэффициент эластичности, определить степень связи факторного признака с результативным.
5.Оценить с помощью F-критерия Фишера статистическую надежность моделирования.
Доля денежных доходов, направленных на прирост сбережений во вкладах, займах, сертификатах и на покупку валюты, в общей сумме среднедушевого денежного дохода, %
Для определения неизвестных параметров b 0 , b 1 уравнения парной линейной регрессии используем стандартную систему нормальных уравнений, которая имеет вид
(3.7)
Для решения этой системы вначале необходимо определить значения величин Sх 2 и Sху. Эти значения определяем из таблицы исходных данных, дополняя ее соответствующими колонками (таблица 3.6).
Выражая из первого уравнения b 0 и подставляя полученное выражение во второе уравнение получим:
Производя почленное умножение и раскрывая скобки, получим:
Окончательно уравнение парной линейной регрессии, связывающее величину доли денежных доходов населения, направленных на прирост сбережений у с величиной среднемесячной начисленной заработной платы х имеет вид:
Так, как построено уравнение парной линейной регрессии, то определяем линейный коэффициент корреляции по зависимости:
где- значения среднеквадратических отклонений соответствующих параметров.
Для расчета линейного коэффициента корреляции по зависимости (3.9) выполним промежуточные расчеты.
Подставляя значения найденных параметров в выражение (3.9) получим
.
Полученное значение линейного коэффициента корреляции свидетельствует о наличии слабой обратной статистической связи между величиной доли денежных доходов населения, направленных на прирост сбережений у и величины среднемесячной начисленной заработной платы х.
Коэффициент детерминации равен , что означает, что только 9,6% объясняется регрессией объясняющей переменнойх на величину у. Соответственно величина 1-равная 90,4 % характеризует долю дисперсии переменнойу, вызванную влиянием всех остальных, неучтенных в эконометрической модели объясняющих переменных.
Полученное значение превышает (12…15)%, что свидетельствует о существенности среднего отклонения расчетных данных от фактических, по которым построена эконометрическая модель.
Надежность статистического моделирования выполним на основе F-критерия Фишера. Теоретичное значение критерия Фишера F расч определяется из соотношения значений факторной и остаточнойдисперсий, рассчитанных на одну степень свободы по формуле
m-число объясняющих переменных (для рассматриваемого примераm m =1).
Критическое значение F крит определяется по статистическим таблицам и для уровня значимости a = 0, 05 равняется 10,13. Так как F расч F крит, то нулевая гипотеза отвергается, и полученное уравнение регрессии принимается статистически значимым.
Оценка статистической значимости коэффициентов регрессии ипоt-критерию сводится к сопоставлению численного значения этих коэффициентов с величиной их случайных ошибок ипо зависимости:
Рабочая формула для расчета теоретического значения t-статистики имеет вид:
, (3.13)
где парные коэффициенты корреляции и коэффициент множественной корреляции рассчитываются по зависимостям:
Тогда теоретические (расчетные) значения t-статистик соответственно равны:
Таблица 3.10. К расчету средней ошибки аппроксимации.
Полученное значение не превышает допустимого предела равного (12…15)%.
Номера домов также измерены в порядковой шкале — они показывают, в каком порядке стоят дома вдоль улицы. Номера томов в собрании сочинений писателя или номера дел в архиве предприятия обычно связаны с хронологическим порядком их создания.
При оценке экологических воздействий первая, наиболее обобщенная оценка — обычно порядковая, например: природная среда стабильна — природная среда угнетена (деградирует). Аналогична эколого-медицинская шкала: нет выраженного воздействия на здоровье людей — отмечается отрицательное воздействие на здоровье.
Порядковая шкала используется и в других областях. В эконометрике это прежде всего различные методы экспертных оценок.
Только для абсолютной шкалы результаты измерений — числа в обычном смысле слова, например, число людей в комнате. Для абсолютной шкалы допустимым является только тождественное преобразование.
Сформулируем основное требование к алгоритмам анализа данных в ТИ: выводы, сделанные на основе данных, измеренных в шкале определенного типа, не должны меняться при допустимом преобразовании шкалы измерения этих данных. Другими словами, выводы должны быть инвариантны по отношению к допустимым преобразованиям шкалы.
Для наблюдающихся в реальной жизни распределений доходов и заработной платы справедлива та же закономерность: мода меньше медианы, а медиана меньше среднего арифметического.
С помощью математической теории, развитой в 1970-х годах, удается описать вид допустимых средних в основных шкалах. Понятно, что для данных, измеренных в шкале наименований, качестве среднего годится только мода.
Рассмотрим обработку мнений экспертов, измеренных в порядковой шкале. Справедливо следующее утверждение.
Теорема 1 . Из всех средних по Коши допустимыми средними в порядковой шкале являются только члены вариационного ряда (порядковые статистики).
Есть ли средние по Колмогорову, которыми нельзя пользоваться в шкале отношений? Конечно, есть. Например F(x) = е х.
Аналогично средним величинам могут быть изучены и другие статистические характеристики — показатели разброса, связи, расстояния и др. . Нетрудно показать, например, что коэффициент корреляции не меняется при любом допустимом преобразовании в пиале интервалов, как и отношение дисперсий, дисперсия не меняется в шкале разностей, коэффициент вариации — в шкале отношений, и т.д.
Парная регрессия представляется уравнением связи двух переменных у и х следующего вида:
где у – зависимая переменная (результативный признак), а х – независимая переменная (объясняющая переменная, или признак-фактор). Бывает линейная регрессия и нелинейная регрессия. Линейная регрессия описывается уравнением вида:
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации, который есть не что иное как отношение суммы квадратов отклонений, обусловленной регрессией к общей сумме квадратов отклонений (первого слагаемого ко всей сумме).
23. Математические условия Гаусса-Маркова и их применение.
Чтобы регрессионный анализ, основанный на обычном МНК давал наилучшие результаты, случайный член должен удовлетворять четырем условиям Гаусса-Маркова.
Дисперсия случайного члена постоянна для всех наблюдений.
Ковариация значений случайных величин, образующих выборку должна быть равна нулю, т.е. отсутствует систематическая связь между значениями случайного члена в любых двух конкретных наблюдениях. Случайные члены должны быть независимы друг от друга.
Закон распределения случайного члена должен быть независим от объясняющих переменных.
Более того, во многих применениях объясняющие переменные не являются стохастическими, т.е. не имеют случайной составляющей. Значение любой независимой переменной в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии.
Однако поскольку коэффициенты были определены с определенной погрешностью, то интерес представляет не точечная оценка (точечный прогноз) для результативного признака, а знание того в каких пределах с определенной вероятностью будут лежать значения результативного признака, соответствующее взятому значению фактора х.
По существу формула стандартной ошибки независимо от того каким образом и в каком виде она получена характеризует ошибку положения линии регрессии. Величина стандартной ошибки достигает минимума при совпадении значения фактора х со средним значением фактора.
24. Статистическая проверка гипотез и оценка значимости линейной регрессии по критерию Фишера.
Общая сумма квадратов отклонений индивидуальных значений результативного признака у от среднего значения у вызвана влиянием множества факторов.
Для заданного набора значений переменных Y и Х расчетное значение среднего величины Y является в линейной регрессии функцией только одного параметра – коэффициента регрессии. В соответствии с этим факторная сумма квадратов отклонений имеет число степеней свободы, равное 1. А число степеней свободы остаточной суммы квадратов отклонений при линейной регрессии равно n-2.
В случае, если величина отношения оказывается меньше табличного, то вероятность нулевой гипотезы оказывается выше заданного уровня(который выбирался изначально) и нулевая гипотеза не может быть отклонена без заметной опасности получить неверный вывод о наличии связи. Соответственно уравнение регрессии считается при этом незначимым.
Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента выполняется посредством сопоставления значений этих величин и величины стандартной ошибки. Величинаошибки параметров линейной регрессии и коэффициента корреляции определяется по следующим формулам:
где S – среднеквадратичноеостаточное выборочное отклонение,
Соответственно величина стандартной ошибки, предсказываемой по линии регрессии, дается формулой:
В линейной регрессии ∑(y x -y ср) 2 =b 2 ∑(x-x ср) 2 . В этом нетрудно убедиться, обратившись к формуле линейного коэффициента корреляции: r 2 ху = b 2 *σ 2 x /σ 2 y
σ 2 x — дисперсия признака у обусловленная фактором х. Соответственно сумма квадратов отклонений, обусловленных линейной регрессией, составит:
Поскольку при заданном объеме наблюдений по х и у факторная сумма квадратов при линейной регрессии зависит только от одной константы коэффициента регрессии b, то данная сумма квадратов имеет одну степень свободы. Рассмотрим содержательную сторону расчетного значения признака у т.е. у х. Величина у х определяется по уравнению линейной регрессии: у х =а+bх.
Параметр а можно определить, как а=у-bх. Подставив выражение параметра а в линейную модель, получим: y x =y-bx+bx ср =y-b(x-x ср).
При заданном наборе переменных у и х расчетное значение у х является в линейной регрессии функцией только одного параметра — коэффициента регрессии. Соответственно и факторная сумма квадратов отклонений имеет число степеней свободы, равное 1.
25. Оценка значимости отдельных параметров уравнения регрессии и коэффициентов по критерию Стьюдента.
27. Линейная и нелинейная регрессии и методы их исследования.
Ее параметры хорошо оцениваются по МНК и сама такая зависимость характеризует связь удельных расходов сырья, топлива, материалов с объемом выпускаемой продукции, временем обращением товаров и всех этих факторов с величиной товарооборота. Например, кривая Филипса характеризует нелинейное соотношение между нормой безработицы и процентом прироста заработной платы.
Вернемся к зависимостям, приводимым к линейным. Если они нелинейны и по параметрам и по переменным, например, вида у = а умноженному на степень Х, показатель которой и есть параметр – (бета):
Очевидно, такое соотношение легко преобразуется в линейное уравнение простым логарифмированием.
Для существенно нелинейной регрессии невозможно применение обычной процедуры оценивания регрессии, поскольку соответствующая зависимость не может быть преобразована в линейную. Общая схема действий при этом такова:
1. Принимаются некоторые правдоподобные исходные значения параметров;
2. Вычисляются предсказанные значения Y по фактическим значениям Х с использованием этих значений параметров;
3. Вычисляются остатки для всех наблюдений в выборке и затем сумма квадратов остатков;
4. Вносятся небольшие изменения в одну или более оценку параметров;
5. Вычисляются новые предсказанные значения Y, остатки и сумма квадратов остатков;
6. Если сумма квадратов остатков меньше, чем прежде, то новые оценки параметров лучше прежних и их следует использовать в качестве новой отправной точки;
7. Шаги 4, 5 и 6 повторяются вновь до тех пор, пока не окажется невозможным внести такие изменения в оценки параметров, которые привели бы к изменению суммы остатков квадратов;
8. Делается вывод о том, что величина суммы квадратов остатков минимизирована и конечные оценки параметров являются оценками по методу наименьших квадратов.
Вычисляется среднее геометрическое значений Y в выборке, совпадающее с экспонентой среднего арифметического значений логарифма от Y;
Пересчитываются наблюдения Y таким образом, что они делятся на полученное на первом шаге значение;
Оценивается регрессия для линейной модели с использованием пересчитанных значений Y вместо исходных значений Y и для логарифмической модели с использованием логарифма от пересчитанных значений Y. Теперь значения СКО для двух регрессий сравнимы и поэтому модель с меньшей суммой квадратов отклонений обеспечивает лучшее соответствие с истинной зависимостью наблюденных значений;
Для проверки того, что одна из моделей не обеспечивает значимо лучшее соответствие, можно использовать произведение половины числа наблюдений на логарифм отношения значений СКО в пересчитанных регрессиях с последующим взятием абсолютного значения этой величины.
30. Поняти интеркорреляции и мультиколлинеарности факоров.
Напротив, гетероскедастичность заключается в нарушении такого постоянства дисперсии для различных наблюдений. В этом случае априорная (до наблюдений) вероятность получения сильно отклоненных величин с различным теоретическим распределением случайного члена для различных наблюдений в выборке будет относительно высока.
35. Гомоскедастичность и гетероскедастичность, автокорреляция остатков, обобщенный метод наименьших квадратов (ОМНК).
37. Понятие о тесте Бреуша-Пагана, тесте Гольдфельдта-Квандта
«Комплексный анализ взаимосвязи финансово-экономических показателей деятельности предприятий»
Средняя относительная ошибка аппроксимации.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
[expert_bq id=»1570″]На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
2. Выполнить команду Диаграмма, Добавить линию тренда или переместить указатель на ряд данных, щелкнуть правой кнопкой мыши, а затем в контекстном меню выбрать команду Добавить линию тренда . В появившемся окне Линия тренда раскрыть вкладку Тип (рис. 29)
Средняя относительная ошибка аппроксимации считают по формуле. Метод аппроксимации в Microsoft Excel
10. Рассчитана средняя ошибка аппроксимации статистических данных линейным уравнением множественной регрессии, которая составила 29,8%. Показано, за счет какого наблюдения в статистической базе величина данной ошибки превышает допустимое значение.
Значение ошибки аппроксимации должно быть. Метод аппроксимации в Microsoft Excel
показывает, какая доля изменения исследуемого признака учтена в модели. Другими словами коэффициент детерминации показывает, какая часть изменения исследуемой переменной может быть вычислена, исходя из изменений включённых в модель факторных переменных с помощью выбранного типа функции, связывающей факторные переменные и исследуемый признак в уравнении модели.
Коэффициент детерминации R 2 может принимать значения от 0 до 1. Чем ближе коэффициент детерминации R 2 к единице, тем лучше качество модели.
Индекс корреляции можно легко вычислить, зная коэффициент детерминации:
F-критерий Фишера используется для оценки значимости уравнения регрессии. Расчётное значение F-критерия определяется из соотношения:
Определим характеристики качества построенной нами линейной модели для Примера 1 . Воспользуемся данными Таблицы 2. Коэффициент детерминации :
Следовательно, в рамках линейной модели изменение объёма продаж на 90,1% объясняется изменением температуры воздуха.
Критическое значение F кр при α = 0,1; ν 1 =1; ν 2 =7-1-1=5 равно 4,06. Расчётное значение F -критерия больше табличного, следовательно, уравнение модели является значимым.
Построенная линейная модель парной регрессии имеет неудовлетворительную точность (>15%), и её не рекомендуется использовать для анализа и прогнозирования.
В итоге, несмотря на то, что большинство статистических характеристик удовлетворяют предъявляемым к ним критериям, линейная модель парной регрессии непригодна для прогнозирования объёма продаж в зависимости от температуры воздуха. Нелинейный характер зависимости между указанными переменными по данным наблюдений достаточно хорошо виден на Рис.1. Проведённый анализ это подтвердил.
Ошибка аппроксимации — один из наиболее часто возникающих вопросов при применении тех или иных методов аппроксимации исходных данных. Есть разного рода ошибки аппроксимации:
Ошибки, связанные с несоответствием аппроксимирующей модели структуре аппроксимируемых данных.
В Excel есть хорошо разработанная функция Линейн, предназначенная для обработки данных и аппроксимаций, в которой задействован отлаженный математический аппарат. Для того, чтобы иметь о ней представление, обратимся (через F1) к описательной части этой разработки, которую приводим с сокращениями и некоторыми изменениями обозначений.
Расчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива.
Массив x — известные значеня x. Массив x может содержать одно или несколько множеств переменных.
Конст — это логическое значение, которое указывает, требуется ли, чтобы свободный член a был равен 0.
Если аргумент конст имеет значение ИСТИНА, 1 или опущено, то a вычисляется обычным образом. Если аргумент конст имеет значение ЛОЖЬ или 0, то a полагается равным 0.
Статистика — это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если аргумент статистика имеет значение ИСТИНА или 1, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Если аргумент статистика имеет значение ЛОЖЬ, 0 или опущена, то функция ЛИНЕЙН возвращает только коэффициенты и свободный член.
se1,se2. sen — стандартные значения ошибок для коэффициентов b1,b2. bn.
sea — стандартное значение ошибки для постоянной a (sea = #Н/Д, если конст имеет значение ЛОЖЬ).
F-статистика, или F-наблюдаемое значение. F-статистика используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет.
df — степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели нужно сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН.
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.
Выборочную информацию из функции можно получить через функцию ИHДЕКС, например:
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемая функцией ЛИНЕЙН. Функция ЛИНЕЙН использует метод наименьших квадратов для определения наилучшей аппроксимации данных.
Заметьте, что значения y, предсказанные с помощью уравнения регрессии, возможно не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
Эмпирические коэффициенты регрессии b 0 , b 1 будем определять с помощью инструмента «Регрессия» надстройки «Анализ данных» табличного процессораMS Excel.
Алгоритм определения коэффициентов состоит в следующем.
1. Вводимисходные данные в табличный процессор MS Excel.
4. Заполняем соответствующие позиции окна Регрессия (рисунок 4).
5. Нажимаем кнопку ОК окна Регрессия и получаем протокол решения задачи (рисунок 5)
Из рисунка 5 видно, что эмпирические коэффициенты регрессии соответственно равны
Тогда уравнение парной линейной регрессии, связывающая величину ежемесячной пенсии у с величиной прожиточного минимумахимеет вид
На следующем этапе, в соответствии с заданием необходимо определить степень связи объясняющей переменной х с зависимой переменной у, используя коэффициент эластичности. Коэффициент эластичности для модели парной линейной регрессии определяется в виде:
Следовательно, при изменении прожиточного минимума на 1% величина ежемесячной пенсии изменяется на 0,000758%.
Для этого исходную таблицу 1 дополняем двумя колонками, в которых определяем значения, рассчитанные с использованием зависимости (3.2) и значения разности .
Таблица 3.2. Расчет средней ошибки аппроксимации.
Из практики известно, что значение средней ошибки аппроксимации не должно превышать (12…15)%
На последнем этапе выполним оценкустатистической надежности моделирования спомощью F – критерия Фишера. Для этого выполним проверку нулевой гипотезы Н 0 о статистической не значимости полученного уравнения регрессиипо условию:
если при заданном уровне значимости a = 0,05 теоретическое (расчетное) значение F-критерия больше его критического значения F крит (табличного), то нулевая гипотеза отвергается, и полученное уравнение регрессии принимается значимым.
Из рисунка 5 следует, что F расч = 0,0058. Критическое значение F-критерия определяем с помощью использования статистической функции FРАСПОБР (рисунок 6). Входными параметрами функции является уровень значимости (вероятность) и число степеней свободы 1 и 2. Для модели парной регрессии число степеней свободы соответственно равно 1 (одна объясняющая переменная) и n-2 = 6-2=4.
Из рисунка 6 видно, что критическое значение F-критерия равно 7,71.
Так как F расч Fтеор — уравнение регрессии адекватно.
n — число наблюдений (уровней ряда), m — число параметров уравнения (модели) регрессии.
Проверка адекватности уравнения регрессии (качества модели в целом) осуществляется с помощью средней ошибки аппроксимации, величина которой не должна превышать 10-12% (рекомендовано).
«Комплексный анализ взаимосвязи финансово-экономических показателей деятельности предприятий»
1. Составление корреляционной матрицы. Отбор факторов
2. Построение уравнения множественной линейной регрессии. Интерпретация параметров уравнения
4.Оценка качества уравнения множественной линейной регрессии
4.2.Проверка статистической значимости уравнения множественной регрессии в целом с помощью F-критерия Фишера
4.3.Проверка статистической значимости параметров уравнения множественной регрессии. Интервальные оценки параметров
5.2.Частные коэффициенты эластичности и средние частные коэффициенты эластичности
6.Анализ остатков регрессионной модели (проверка предпосылок теоремы Гаусса-Маркова)
Заданы значения 6 показателей, характеризующих экономическую деятельность 53 предприятий. Требуется:
1. Составить корреляционную матрицу. Скорректировать набор независимых переменных (отобрать 2 фактора).
4.2. Проверить статистическую значимость уравнения множественной регрессии в целом с помощью F-критерия Фишера. Сделать выводы
4.3. Проверить статистическую значимость параметров уравнения множественной регрессии. Построить интервальные оценки параметров. Сделать выводы.
5.1. Используя построенное уравнение, дать точечный прогноз. Найти значение исследуемого параметра y, если значение первого фактора (наиболее тесно связанного с у) составит 110% от его среднего значения, значение второго фактора составит 80% от его среднего значения. Дать экономическую интерпретацию результата.
5.2. Найти частные коэффициенты эластичности и средние частные коэффициенты эластичности. Интерпретировать результаты. Сделать выводы.
6. Провести анализ остатков регрессионной модели (проверить требования теоремы Гаусса-Маркова):
6.2. Проверить наличие автокорреляции в остатках. Сделать вывод.
7. Разделите выборку на две равные части. Рассматривая первые и последние наблюдения как независимые выборки, проверить гипотезу о возможности объединения их в единую выборку по критерию Грегори-Чоу.
Составление корреляционной матрицы. Отбор факторов
1.Составить корреляционную матрицу. Скорректировать набор независимых переменных (отобрать 2 фактора).
Рассмотрим результативный признак Y3 и факторные признаки Х10, X12, Х5, Х7, Х13 .
Составим корреляционную матрицу с помощью опции «Анализ данных→Корреляция» в MS Excel:
| Y3 | X10 | X12 | X5 | X7 | X13 | |
| Y3 | 1,0000 | 0,3653 | 0,0185 | 0,2891 | 0,1736 | 0,0828 |
| X10 | 0,3653 | 1,0000 | -0,2198 | -0,0166 | -0,2061 | -0,0627 |
| X12 | 0,0185 | -0,2198 | 1,0000 | 0,2392 | 0,3796 | 0,6308 |
| X5 | 0,2891 | -0,0166 | 0,2392 | 1,0000 | 0,4147 | 0,0883 |
| X7 | 0,1736 | -0,2061 | 0,3796 | 0,4147 | 1,0000 | 0,1939 |
| X13 | 0,0828 | -0,0627 | 0,6308 | 0,0883 | 0,1939 | 1,0000 |
Таким образом, в следующих пунктах работа будет производиться с факторами X10 , X5.
Построение уравнения множественной линейной регрессии. Интерпретация параметров уравнения.
2. Построить уравнение множественной линейной регрессии. Дать интерпретацию параметров уравнения.
Составим регрессионную модель с помощью пакета анализа «Анализ данных→Регрессия» в MS Excel:
| Коэффициенты | |
| Y | -20,7163 |
| X 10 | 5,7169 |
| X 5 | 34,9321 |
Уравнение регрессии будет выглядеть следующим образом:
Коэффициент детерминации, множественный коэффициент корреляции
3. Найти коэффициент детерминации, множественный коэффициент корреляции. Сделать выводы.
В регрессионном анализе, выполненном с помощью пакета анализа «Анализ данных→Регрессия» в MS Excel, найдём таблицу «Регрессионная статистика»:
R-квадрат-22,05% вариации признака Y объясняется вариацией признаков X10 и X5
Оценка качества уравнения множественной линейной регрессии
4. Оценить качество уравнения множественной линейной регрессии:
Рассчитаем прогнозные значения для каждого наблюдения или воспользуемся столбцом «Предсказанное У» в таблице «Вывод остатка» в регрессионном анализе, выполненном с помощью пакета анализа «Анализ данных→Регрессия» в MS Excel)
Вычислим относительные ошибки для каждого наблюдения по формуле:
Вычислим среднюю относительную ошибку аппроксимации по формуле:
Михаил Серяков Бухара — один из немногих городов в мировой истории, который все время находился и развивался на одном и том же месте, в 7-ом веке на эту территорию распространился арабский халифат и.
Легендарные сокровища алимхана Что ел эмир бухарский саид алимхан
[expert_bq id=»1570″]Если изменение уровней ряда характеризуется равномерным увеличением уменьшением уровней, когда абсолютные цепные приросты близки по величине, тенденцию развития характеризует уравнение прямой линии. Если же вы хотите что-то уточнить, обращайтесь ко мне![/expert_bq]
1. Если изменение уровней ряда характеризуется равномерным увеличением (уменьшением) уровней, когда абсолютные цепные приросты близки по величине, тенденцию развития характеризует уравнение прямой линии.
10. Затем щелкаем по любой из линий диапазонов погрешностей правой кнопкой мыши, выбираем в контекстном меню «Формат полос погрешностей…» и в окне «Формат планок погрешностей» на вкладке «Вид» настраиваем цвет и толщину линий.
| Y3 | X10 | X12 | X5 | X7 | X13 | |
| Y3 | 1,0000 | 0,3653 | 0,0185 | 0,2891 | 0,1736 | 0,0828 |
| X10 | 0,3653 | 1,0000 | -0,2198 | -0,0166 | -0,2061 | -0,0627 |
| X12 | 0,0185 | -0,2198 | 1,0000 | 0,2392 | 0,3796 | 0,6308 |
| X5 | 0,2891 | -0,0166 | 0,2392 | 1,0000 | 0,4147 | 0,0883 |
| X7 | 0,1736 | -0,2061 | 0,3796 | 0,4147 | 1,0000 | 0,1939 |
| X13 | 0,0828 | -0,0627 | 0,6308 | 0,0883 | 0,1939 | 1,0000 |
Средняя ошибка аппроксимации
Решение проводим при помощь онлайн калькулятора Линейное уравнение регрессии.
а) линейное уравнение регрессии;
Использование графического метода.
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
Для наших данных система уравнений имеет вид
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = -0.35, a = 76.88
Уравнение регрессии:
y = -0.35 x + 76.88
| x | y | x 2 | y 2 | x • y | y(x) | (y i -y cp ) 2 | (y-y(x)) 2 | |y — y x |:y |
| 45,1 | 68,8 | 2034,01 | 4733,44 | 3102,88 | 61,28 | 119,12 | 56,61 | 0,1094 |
| 59 | 61,2 | 3481 | 3745,44 | 3610,8 | 56,47 | 10,98 | 22,4 | 0,0773 |
| 57,2 | 59,9 | 3271,84 | 3588,01 | 3426,28 | 57,09 | 4,06 | 7,9 | 0,0469 |
| 61,8 | 56,7 | 3819,24 | 3214,89 | 3504,06 | 55,5 | 1,41 | 1,44 | 0,0212 |
| 58,8 | 55 | 3457,44 | 3025 | 3234 | 56,54 | 8,33 | 2,36 | 0,0279 |
| 47,2 | 54,3 | 2227,84 | 2948,49 | 2562,96 | 60,55 | 12,86 | 39,05 | 0,1151 |
| 55,2 | 49,3 | 3047,04 | 2430,49 | 2721,36 | 57,78 | 73,71 | 71,94 | 0,172 |
| 384,3 | 405,2 | 21338,41 | 23685,76 | 22162,34 | 405,2 | 230,47 | 201,71 | 0,5699 |
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(45.1) = -0.35*45.1 + 76.88 = 61.28
y(59) = -0.35*59 + 76.88 = 56.47
. . .
Ошибка аппроксимации
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических:
F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
Поскольку фактическое значение F b
в) показательная регрессия;
г) модель равносторонней гиперболы.
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
7a + 0.1291b = 405.2
0.1291a + 0.0024b = 7.51
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 1054.67, a = 38.44
Уравнение регрессии:
y = 1054.67 / x + 38.44
Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Метод аппроксимации в Microsoft Excel
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Выполнение аппроксимации
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
- Для построения графика, прежде всего, выделяем столбцы «Себестоимость единицы продукции» и «Прибыль». После этого перемещаемся во вкладку «Вставка». Далее на ленте в блоке инструментов «Диаграммы» щелкаем по кнопке «Точечная». В открывшемся списке выбираем наименование «Точечная с гладкими кривыми и маркерами». Именно данный вид диаграмм наиболее подходит для работы с линией тренда, а значит, и для применения метода аппроксимации в Excel.
Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».
Если же вы выбрали все-таки первый вариант действий с добавлением через контекстное меню, то откроется окно формата.
В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.
Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.
После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
В конкретно нашем случае формула принимает такой вид:
Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
- Для того, чтобы изменить тип линии тренда, выделяем её кликом правой кнопки мыши и в раскрывшемся меню выбираем пункт «Формат линии тренда…».
После этого запускается уже знакомое нам окно формата. В блоке выбора типа аппроксимации устанавливаем переключатель в положение «Экспоненциальная». Остальные настройки оставим такими же, как и в первом случае. Щелкаем по кнопке «Закрыть».
Общий вид функции сглаживания при этом такой:
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
- Тем же способом, что и в предыдущий раз через контекстное меню запускаем окно формата линии тренда. Устанавливаем переключатель в позицию «Логарифмическая» и жмем на кнопку «Закрыть».
В общем виде формула сглаживания выглядит так:
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
- Переходим в окно формата линии тренда, как уже делали не раз. В блоке «Построение линии тренда» устанавливаем переключатель в позицию «Полиномиальная». Справа от данного пункта расположено поле «Степень». При выборе значения «Полиномиальная» оно становится активным. Здесь можно указать любое степенное значение от 2 (установлено по умолчанию) до 6. Данный показатель определяет число максимумов и минимумов функции. При установке полинома второй степени описывается только один максимум, а при установке полинома шестой степени может быть описано до пяти максимумов. Для начала оставим настройки по умолчанию, то есть, укажем вторую степень. Остальные настройки оставляем такими же, какими мы выставляли их в предыдущих способах. Жмем на кнопку «Закрыть».
Линия тренда с использованием данного метода построена. Как видим, она ещё более изогнута, чем при использовании экспоненциальной аппроксимации. Уровень достоверности выше, чем при любом из использованных ранее способов, и составляет 0,9724.
Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:
В нашем случае формула приняла такой вид:
y=0,0015*x^2-1,7202*x+507,01
Теперь давайте изменим степень полиномов, чтобы увидеть, будет ли отличаться результат. Возвращаемся в окно формата. Тип аппроксимации оставляем полиномиальным, но напротив него в окне степени устанавливаем максимально возможное значение – 6.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
- Перемещаемся в окно «Формат линии тренда». Устанавливаем переключатель вида сглаживания в позицию «Степенная». Показ уравнения и уровня достоверности, как всегда, оставляем включенными. Жмем на кнопку «Закрыть».
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
В конкретно нашем случае она выглядит так:
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Мы рады, что смогли помочь Вам в решении проблемы.
Помимо этой статьи, на сайте еще 11905 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.