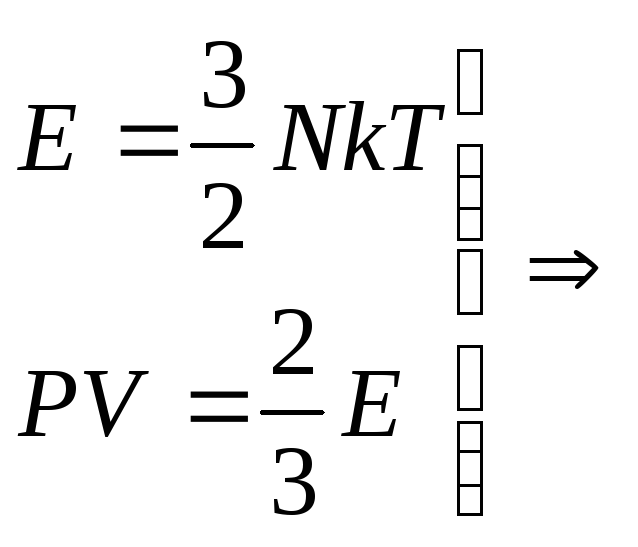Как найти среднюю скорость движения молекул газа - Исправление недочетов и поиск решений вместе с Examum.ru

Средняя скорость молекул

В физике выделяют 2 скорости, характеризующие движение молекул: средняя скорость движения молекул и средняя квадратичная скорость.

Средняя скорость движения молекул

Средняя скорость движения молекул называется также скоростью теплового движения молекул.

Определение 1

Формула средней относительной скорости молекул в физике представлена следующим выражением:

υotn=28kTπm0=2υ.

Средняя квадратичная скорость

Средняя квадратичная скорость движения молекул газа это следующая величина:

υkυ=1N∑i=1Nυi2

Формулу средней квадратичной скорости можно переписать так:

υkυ2=∫0∞υ2Fυdυ.

Проводя интегрирование, аналогичное интегрированию при получении связи средней скорости с температурой газа, получаем:

υkυ=3kTm0=3RTμ

Именно средняя квадратичная скорость поступательного движения молекул газа входит в состав основного уравнения молекулярно-кинетической теории:

p=13nm0υkυ,

где n=NV – это концентрация частиц вещества, N – это количество частиц вещества, V – это объем.

Пример 1

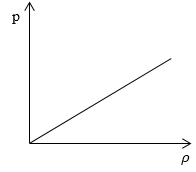
Необходимо определить, как изменяется средняя скорость движения молекул идеального газа с увеличением давления в процессе, изображенном на графике (рисунок 1).

Рисунок 1

Решение

Запишем выражение для средней скорости движения молекул газа следующим образом:

υ=8kTπm0

Из графика видно, что p~ρ или p=Cρ, где C – это некоторая константа.

m0=ρn, p=nkT=Cρ→kT=Cρn

Подставив m0=ρn, p=nkT=Cρ→kT=Cρn в υ=8kTπm0, получаем:

υ=8kTπm0=8Cρπnnρ=8Cπ

Ответ: В процессе, представленном на графике, с увеличением давления средняя скорость движения молекул не меняется.

Пример 2

Можно ли найти среднюю квадратичную скорость молекулы идеального газа, если известно: давление газа (p), молярная масса газа (μ), а также концентрация молекул газа (n)?

Решение

Применим выражение для υkυ:

υkυ=3RTμ

Помимо этого, из уравнения Менделеева-Клайперона и зная, что mμ=NNA:

pV=mμRT=NNART.

Поделим правую и левую части pV=mμRT=NNART на V, и зная NV=n, получаем:

p=nNART→RT=pNAn

Подставляем p=nNART→RT=pNAn в выражение для среднеквадратичной скорости υkυ=3RTμ, получаем:

υkυ=3pNAμn

Ответ: По заданным в условии задачи параметрам среднеквадратичная скорость движения молекул газа вычисляется при помощи формулы υkυ=3pNAμn.

Источник

Определение средней квадратичной скорости молекул газа

Содержание:

Средняя квадратичная скорость молекул газа — что это за параметр
От каких величин зависит в идеальном газе
Формула средней квадратичной скорости молекул
- Как посчитать в зависимости от природы газа и температуры?

Средняя квадратичная скорость молекул газа — что это за параметр

Молекулы любого газа пребывают в постоянном движении. Его можно охарактеризовать с точки зрения средней их скорости или средней квадратичной скорости. Первое понятие имеет специальный термин — скорость теплового движения. Второе — средняя квадратичная скорость — величина, для которой существует специальная формула.

Для того, чтобы полностью разобраться в понятии средней квадратичной скорости молекул газа, вводится условный участник процесса — идеальный газ.

Определение

Идеальный газ — это математическая модель, потенциальную энергию которой принимают за ноль, а кинетическую характеризуют в полном объеме. Идеальный газ подходит в качестве модели окружающих нас газов, например, обычного воздуха.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Определение

Средняя квадратичная скорость — физическая величина, отличная от средней арифметической скорости молекул, определяемая по формуле: корень квадратный из средней арифметической квадратов скоростей различных молекул.

Кинетическая энергия определяется скоростью движения молекул, поэтому зависит от температуры. Скорости молекул одного газа не одинаковы. Часть молекул движутся очень быстро, часть — с незначительной скоростью. Однако для большинства существует некое среднее значение. Если изобразить это на графике в виде параболы, такие молекулы со средней скоростью будут составлять ее верхнюю часть.

В единице объема газа содержится огромное число молекул. Поэтому, например, его давление на стенки сосуда — величина постоянная. В ином случае, если бы в единицу времени о стенку ударялось различное количество молекул, давление бы «скакало».

Из изложенного можно сделать вывод: скорость — свойство отдельной молекулы газа, а давление — характеристика их совокупности.

От каких величин зависит в идеальном газе

Для идеального газа средняя квадратичная скорость прямо пропорциональна его температуре и обратно пропорциональна молярной массе газа.

В математическом выражении данная зависимость выражается через корень квадратный:

(V=surd(3RT/mu)
)

где R — универсальная постоянная величина, Т — температура газа, μ — молярная масса.

Из формулы видно, что искомая величина (средняя квадратичная скорость) зависит от природных свойств газа и его температуры.

Формула средней квадратичной скорости молекул

Математическое выражение формулы выглядит следующим образом:

(V_{ср;кв}=surd(V_{12}+V_{22}+V_{n2})/N)

В формуле присутствуют следующие условные обозначения: V₁, V₂, V_n — скорости молекул, а N — их количество.

Формула может иметь и другой вид:

(V_{ср;кв}=surd1/Nastsum V_2)

или

(V_{ср;кв}=int V_2F(V)dV)

Как посчитать в зависимости от природы газа и температуры?

Проведенное интегрирование формулы, цель которого определить зависимость искомой единицы от природных свойств иттемпературы газа, приводит расчеты к формуле:

(V_{ср;кв}=surd(3kT/mo))

или

(V_{ср;кв}=surd(3RT/mu))

При поступательном движении молекул газа V_{ср кв} — составляющая уравнения для молекулярно-кинетической теории.

Если n=N/V, где N — число частиц, а V — объем, то концентрация частиц n получает следующее формульное выражение:

(p=1/3ast nmo(V_{ср;кв})^2)

Насколько полезной была для вас статья?

Рейтинг: 2.33 (Голосов: 3)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа

$Large vecupsilon =sqrt{frac{3kT}{m}}=sqrt{frac{3RT}{M}}$

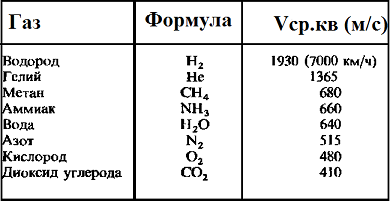
Таблица значений средней квадратичной скорости молекул некоторых газов

Для того чтоб понять, откуда же у нас получается эта формула, мы выведем среднюю квадратичную скорость молекул. Вывод формулы начинается с основного уравнения молекулярно кинетический теории (МКТ):

Где у нас количество вещества, для более легкого доказательства, возьмем на рассмотрение 1 моль вещества, тогда у нас получается:

Если посмотреть, то PV это две третьих средней кинетической энергии всех молекул (а у нас взят 1 моль молекул):

$large PV=frac{2}{3}vec E_k$

Тогда, если приравнять правые части, у нас получается, что для 1 моля газа средняя кинетическая энергия будет равняться:

$large vec E_k =frac{3}{2}RT$

Но средняя кинетическая энергия, так же находится, как :

$large vec E_k =frac{1}{2}N_a m vecupsilon^2$

А вот теперь, если мы приравняем правые части и выразим из них скорость и возьмем квадрат,Число Авогадро на массу молекулы , получается Молярная масса то у нас и получится формула для средней квадратичной скорости молекулы газа:

$Large vecupsilon =sqrt{frac{3RT}{M}}$

А если расписать универсальную газовую постоянную, как , и за одно молярную массу , то у нас получится?

$Large vecupsilon =sqrt{frac{3kT}{m}}$

В Формуле мы использовали :

— Средняя квадратичная скорость молекул

$k=1.38cdot10^{-23}$ — Постоянная Больцмана

— Температура

— Масса одной молекулы

— Универсальная газовая постоянная

— Молярная масса

— Количество вещества

— Средняя кинетическая энергия молекул

$N_a=6,02cdot10^{23}$ — Число Авогадро

Источник

Значительная часть явлений молекулярной физики определяется скоростями молекул. Несмотря на это, нахождение скоростей молекул газа приобретает как теоретического, так и практического значения.

Виды скоростей молекул газа

Скорости газовых молекул в результате их хаотического движения отличаются как по величине, так и по направлению. Скорость данной молекулы газа в данный момент времени есть величина случайная. В молекулярно-кинетической теории газов пользуются понятиями средней (vv), средней квадратичной (vквv_{кв}) и наиболее вероятной (νHν_H) скоростей. Эти скорости задаются для равновесных состояний газа.

Средняя (или среднеарифметическая) скорость определяется уравнением

v=1n∑i=1nviv=frac{1}{n}sumlimits_{i=1}^{n}{{{v}_{i}}}

где viv_i – скорость ii-й молекулы;

nn –количество молекул.

Средняя квадратичная скорость определяется как:

vкв=v2=3kTm{{v}_{кв}}=sqrt{{{v}^{2}}}=sqrt{frac{3kT}{m}}

По этой формуле можно вычислить также скорость броуновских частиц. Конечно, при этом mm –масса броуновской частицы.

Выражению vквv_{кв} можно придать более удобный вид, умножив числитель и знаменатель под корнем на число Авогадро и учитывая, что kN=RkN = R и mN=МmN = М,

vкв=3RTM{{v}_{кв}}=sqrt{frac{3RT}{M}}

Среднюю квадратичную скорость называют еще тепловой. Значение vкв для газов достаточно велики. Так, для водорода при комнатной температуре vкв=1,9⋅103v_{кв} = 1,9 · 10^3 м/с, то есть около 2 км/с.

Тепловая скорость, как видно из уравнения, пропорциональна корню температуры и обратно пропорциональна корню массы. Это обстоятельство определяет, что тепловое движение– достаточно интенсивно для молекул, заметно для микроскопически малых частиц, которые осуществляют броуновское движение, и совершенно незаметно для тяжелых тел.

Экспериментальное определение скоростей газовых молекул

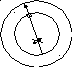
Большой интерес представляет непосредственное экспериментальное определение скоростей газовых молекул. Оно является прямым подтверждением многих результатов и положений молекулярно-кинетической теории. Впервые такое исследование провел А. Штерн в 1920 г. Источником атомов, скорость которых измерялась, в опыте Штерна был молекулярный пучок атомов серебра Ag. Схема установки приведены на рис. 1. На оси системы двух коаксиальных цилиндрических поверхностей натянуто платиновый провод, покрытый слоем серебра.

Примечание

В других опытах использовали также висмут, кадмий, цезий.

Проволока разогревается электрическим током. Так, при температуре около 1300°С серебро с поверхности проволоки испаряется. Таким образом создавался линейный источник «Ag-лучей» и в камере цилиндров, воздух из которой предварительно откачивался при давлении 1,3 · 10^-4 Па, образовывался одноатомный газ серебра. Часть атомов серебра через диафрагмы s₁ и s₂ проходила, образуя молекулярный пучок, к поверхности внешнего цилиндра, где оседала на прозрачной пластинке, создавая слой в виде узкой полосы.

Рис. 1

На первой стадии опыта Штерна установка находится в состоянии покоя. При достижении равновесного состояния (температура проволоки достигала определенного значения, которое определяли по её свечению) атомы серебра оседали у точки а₁. На второй стадии опыта оба цилиндра приводились в достаточно быстрое вращение с частотой 41,7 с^-1.

При этом атомы серебра, двигаясь в вакууме прямолинейно, оседали у точки b. Смещение полосы объясняется тем, что пока атомы серебра пролетают по инерции путь r, внешний цилиндр успевает вернуться на угол φ=ωtφ = ωt, то есть каждая точка внешнего цилиндра смещается на расстояние Δs=ωrtΔs = ωrt, где ωω –угловая скорость его вращения; tt –время, за который атомы серебра проходят путь r. Таким образом,

t=rv=Δsωrt=frac{r}{v}=frac{Delta s}{omega r}

где vv – скорость атомов серебра.

Отсюда

v=ωr2Δsv=frac{omega {{r}^{2}}}{Delta s}

Измеряя смещение полос атомов серебра ΔsΔs и угловую скорость вращения прибора, можно определить скорость атомов серебра. Она приблизительно описывалась выражением

(3,5kTm)12{{left( 3,5frac{kT}{m} right)}^{frac{1}{2}}}

что согласуется со средней скоростью молекул, которые определяются по формуле

v=8kTπmv=sqrt{frac{8kT}{pi m}}

Результаты опытов Штерна показали, что на самом деле картина структуры полосы сложнее.

Смещенная возле точки b полоса была не резко ограниченной, а размытой (рис. 2).

Рис. 2

Несмотря на то, что атомы серебра имеют разные скорости, более быстрым атомам должны соответствовать меньшие смещения, а тем более медленным – большие. Таким образом, результаты опыта Штерна вполне передают реальную картину теплового движения молекул.

Тест по теме «Скорость движения молекул»

Источник

Так как
,
то, следовательно,
…(11.12)

где
–
кинетическая энергия всех молекул газа.

Массу газа можно
выразить как
,
тогда (12.12) запишется как
;
для одного моля газа, то есть m
= M, а V = V_


,
отсюда

Так как молярную
массу можно выразить через массу одной
молекулы m₀
и число Авогадро —
,
то квадратичную скорость можно представить
как

где

— постоянная Больцмана.

При комнатной
температуре молекулы кислорода, например,
имеют среднеквадратическую скорость
480м/с, водорода – 1900м/с.

6. Средняя кинетическая энергия поступательного движения молекул газа.

Средняя кинетическая
энергия поступательного движения одной
молекулы идеального газа

– она пропорциональна термодина-мической
температуре и зависит только от нее, то
есть
температура тела есть количественная
мера энергии движения молекул, из которых
состоит это тело. Кроме
того, связи между абсолютной температурой
и средней кинетической энергией
показывает, что при
одинаковой температуре средние
кинетические энергии молекул всех газов
одинаковы, несмотря на различие масс
молекул разных газов.

Кинетическая
энергия газа состоящего из

молекул, равна

,
то есть
,
отсюда
,
где

— концентрация молекул, тогда

– получили уравнение состояния идеального
газа. Из этих выражений видно, что если

то <E₀>
= 0, то есть прекращается поступательное
движение молекул идеального газа, а, ,
его давление равно нулю.

Не следует думать,
что при абсолютном нуле температуры,
прекращается всякое движение частиц
вещества. Даже если все молекулы газа
остановятся, то внутри них будут двигаться
электроны, будут участвовать в движении
протоны и нейтроны ядер.

Абсолютный ноль
температур означает для реальной системы
не отсутствие движения, но такое состояние
тела, при котором дальнейшее уменьшение
интенсивности этого движения за счет
отдачи его энергии окружающим телам
невозможно. Следовательно, при абсолютном
нуле система находится в состоянии с
наименьшей возможной энергией.
Характер этого состояния зависит от
конкретных свойств составляющих систему
частиц.

7. Любая
молекулярная система состоит из большого
числа составных частиц (идеальный газ).
Эти частицы беспорядочно движутся.
Скорости каждой частицы в произвольный
момент времени неизвестны. Но, оказываются
разные
скорости различных частиц встречаются
с разными вероятностями.
В этом можно убедится на опыте Штерна
(1888 – 1970):

	Раскаленная током нить расположена на оси двух имеющих общую ось цилиндров. Нить покрыта серебром., атомы которого
испаряясь, покидают нить и по радиусу разлетаются в разные
стороны. Во внутреннем цилиндре сделана узкая щель. Только
те атомы, которые попали в щель, достигают внутренней

поверхности
внешнего цилиндра, они создают изображение
щели, которое можно увидеть, если через
некоторое время развернуть внутреннюю
поверхность большого цилиндра. Если
прибор привести во вращение вокруг
общей оси, то атомы серебра, прошедшие
сквозь щель, будут оседать не прямо
напротив него, а с некоторым смещением.
Если бы всех молекул серебра была
одинакова, то и это смещение было бы
одинаковым, но опыт показал распределение
по скоростям.

	Существует некая скорость
около которой расположе-
ны наиболее населенные
интервалы, она называется
наиболее вероятной скоро-
стью U_в и ей соответству-
ет максимум на рисунке.

Чем больше скорость
частиц отличается от U_в,
тем меньше число таких частиц. С
увеличением

возрастает наиболее вероятная скорость,
больше появится быстрых частиц, вся
кривая сместится вправо. Однако площадь
под кривой остается постоянной (так как
постоянно число частиц), кривая
растягивается. Сама кривая называется:
распределение
Максвелла молекул по скоростям.