Как найти среднюю скорость когда известно ускорение - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Чтобы вычислить среднюю скорость, необходимо знать значение перемещения и общее время. Помните, что скорость задается как численным значением, так и направлением (поэтому указывайте направление в ответе). Если в задаче дано постоянное ускорение, вычислить среднюю скорость будет еще проще.

1
Помните, что скорость задается как численным значением, так и направлением. Скорость описывает быстроту изменения положения тела, а также направление, в котором движется это тело. Например, 100 м/с (на юг).
- Величины, которые задаются как численным значением, так и направлением, называются векторными величинами.^[1] Над векторными величинами ставится значок в виде стрелки. Они отличаются от скалярных величин, которые задаются исключительно численным значением. Например, v^→ – это скорость.^[2]
- В научных задачах рекомендуется использовать метрические единицы измерения перемещения (метры, километры и так далее), а в повседневной жизни пользуйтесь любыми удобными единицами измерения.
2
Найдите общее перемещение, то есть расстояние и направление между начальной и конечной точками пути. В качестве примера рассмотрим тело, движущееся с постоянной скоростью в одном направлении.
- Например, ракета была запущена в северном направлении и двигалась в течение 5 минут с постоянной скоростью 120 метров в минуту. Чтобы вычислить общее перемещение, воспользуйтесь формулой s = vt: (5 минут) (120 м/мин) = 600 м (на север).
- Если в задаче дано постоянное ускорение, воспользуйтесь формулой s = vt + ½at² (в следующем разделе описывается упрощенный способ работы с постоянным ускорением).
3
Найдите общее время в пути. В нашем примере ракета перемещается в течение 5 минут. Среднюю скорость можно выразить в любых единицах измерения, но в международной системе единиц скорость измеряется в метрах в секунду (м/с). Конвертируйте минуты в секунды: (5 минут) х (60 секунд/минута) = 300 секунд.
- Если даже в научной задаче время дано в часах или других единицах измерения, лучше сначала вычислить скорость, а затем преобразовать ее в м/с.
4
Вычислите среднюю скорость. Если вы знаете значение перемещения и общее время в пути, вычислить среднюю скорость можно по формуле v_ср = Δs/Δt. В нашем примере средняя скорость ракеты равна 600 м (на север) / (300 секунд) = 2 м/с (на север).
- Не забудьте указать направление движения (например, «вперед» или «на север»).
- В формуле v_ср = Δs/Δt символ «дельта» (Δ) означает «изменение величины», то есть Δs/Δt означает «изменение положения к изменению времени».
- Средняя скорость может быть записана как v_ср или как v с горизонтальной чертой сверху.
5
Решение более сложных задач, например, если тело вращается или ускорение не является постоянным. В этих случаях средняя скорость по-прежнему вычисляется как отношение общего перемещения к общему времени. Не имеет значения, что происходит с телом между начальной и конечной точками пути. Вот несколько примеров задач с одинаковым общим перемещением и общим временем (а, следовательно, и одинаковой средней скоростью).
- Анна идет на запад со скоростью 1 м/с в течение 2 секунд, затем мгновенно ускоряется до 3 м/с и продолжает идти на запад в течение 2 секунд. Ее общее перемещение составляет (1 м/с)(2 с) + (3 м/с)(2 с) = 8 м (на запад). Общее время в пути: 2 с + 2 с = 4 с. Ее средняя скорость: 8 м / 4 с = 2 м/с (на запад).
- Борис идет на запад со скоростью 5 м/с в течение 3 секунд, затем разворачивается и идет на восток со скоростью 7 м/с в течение 1 секунды. Мы можем рассматривать движение на восток как «отрицательное движение» на запад, поэтому общее перемещение равно (5 м/с)(3 с) + (-7 м/с)(1 с) = 8 метров. Общее время равно 4 с. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад).
- Юля проходит 1 метр на север, затем проходит 8 метров на запад, а затем проходит 1 метр на юг. Общее время в пути составляет 4 секунды. Нарисуйте схему этого движения на бумаге, и вы увидите, что оно заканчивается в 8 метрах к западу от начальной точки, то есть общее перемещение равно 8 м. Общее время в пути составило 4 секунды. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад).
Реклама

1
Обратите внимание на начальную скорость и постоянное ускорение. Например: велосипедист начинает движение направо со скоростью 5 м/с и с постоянным ускорением 2 м/с². Если общее время в пути составило 5 секунд, то какова средняя скорость велосипедиста?
- Если вы не понимаете единицу измерения м/с², запишите ее как м/с/с или как метр в секунду за секунду.^[3] Ускорение 2 м/с/с означает, что скорость велосипедиста увеличивается на 2 м/с за каждую секунду.
2
Используя ускорение, найдите конечную скорость. Ускорение – это быстрота изменения скорости. Можно нарисовать таблицу и, используя значение ускорения, найти конечную скорость в различные промежутки времени. В нашем примере требуется найти скорость при t = 5 с, но мы построим большую таблицу, чтобы вы лучше уяснили процесс.
- В начале (t = 0) велосипедист едет со скоростью 5 м/с.
- Спустя 1 с (t = 1), велосипедист едет со скоростью 5 м/с + at = 5 м/с + (2 м/с²)(1 с) = 7 м/с.
- Спустя 2 с (t = 2), велосипедист едет со скоростью 5 + (2)(2) = 9 м/с.
- Спустя 3 с (t = 3), велосипедист едет со скоростью 5 + (2)(3) = 11 м/с.
- Спустя 4 с (t = 4), велосипедист едет со скоростью 5 + (2)(4) = 13 м/с.
- Спустя 5 с (t = 5), велосипедист едет со скоростью 5 + (2)(5) = 15 м/с.
3
Используйте следующую формулу, чтобы вычислить среднюю скорость. Только если ускорение постоянно, то средняя скорость равна половине суммы начальной и конечной скоростей: (v_н + v_к)/2. В нашем примере начальная скорость v_н = 5м/с, а конечная скорость v_к = 15 м/с. Средняя скорость велосипедиста равна (15 м/с + 5 м/с) / 2 = (20 м/с) / 2 = 10 м/с (вправо).
- Не забудьте указать направление (в данном случае «вправо»).
- Начальную скорость можно обозначить как v₀, а конечную как v.
4

Объяснение формулы. Чтобы найти среднюю скорость, необходимо вычислить скорость тела в каждый промежуток времени, сложить полученные результаты и разделить эту сумму на число временных промежутков. Однако это долго и утомительно. Вместо этого давайте найдем среднею скорость всего в двух (любых) временных промежутках.
5
Используйте приведенную выше таблицу конечных скоростей в различные моменты времени. Рассмотрим некоторые пары временных промежутков: (t = 0, t = 5), (t = 1, t = 4) или (t = 2, t = 3). Если хотите, проверьте процесс при дробных значениях t.
- Независимо от того, какую пару временных промежутков вы выберите, вы получите одно и то же значение средней скорости. Например, (5 + 15)/2 = (7 + 13)/2 = (9 + 11)/2 = 10 м/с (вправо).
6
Если бы мы вычислили скорость тела в каждый промежуток времени, мы бы получили среднюю скорость в первой половине пути и среднюю скорость во второй половине пути. Так как временных промежутков в каждой половине равное количество, то вы не потеряете ни одного значения скорости на всем протяжении пути (то есть в результате все значения скоростей будут учтены).
- Так как средняя скорость между любыми двумя промежутками времени остается постоянной, то общая средняя скорость равна средней скорости между любыми двумя промежутками времени.
- Мы можем найти общую среднюю скорость, рассмотрев скорости в любых двух промежутках времени, например, начальную и конечную скорости. В нашем примере: (5 + 15) / 2 = 10 м/с (вправо).
7
Математическое обоснование формулы. Далее изложен математический вывод формулы.^[4]
- s = v_нt + ½at² (правильнее писать Δs and Δt).
- Средняя скорость v_ср = s/t.
- v_ср = s/t = v_н + ½at
- at = v_к — v_н
- v_ср = v_н + ½(v_к — v_н).
- v_ср = v_н + ½v_к — ½v_н = ½v_н + ½v_к = (v_н + v_к)/2.
Реклама

Советы

Скорость отличается от «значения скорости», потому что скорость является векторной величиной. Векторные величины определяются и значением, и направлением, а скалярные величины только значением.
Если тело движется вперед и назад, можно использовать положительные числа, чтобы представить одно направление (например, вперед), и отрицательные числа, чтобы представить движение в другом направлении (например, назад). Запишите это в верхней части вашей работы, чтобы преподаватель понял ваши вычисления.

Об этой статье

Эту страницу просматривали 35 081 раз.

Была ли эта статья полезной?

Источник

Как вычислить среднюю скорость

Вычислить среднюю скорость нетрудно. Для этого необходимо просто разделить длину пройденного пути на время. Однако на практике и при решении задач иногда возникают дополнительные вопросы. Например, что считать пройденным путем? Показания спидометра или реальное смещение объекта? Что считать временем в пути, если объект половину времени никуда не двигался? Без учета всех этих нюансов невозможно правильно вычислить среднюю скорость.

Вам понадобится

калькулятор или компьютер, спидометр

Инструкция

Для вычисления средней скорости равномерного движения объекта, просто измерьте его скорость в любой точке пути. Так как скорость движения постоянна, то она и будет средней скоростью.
Еще проще эта зависимость выглядит в виде формулы:Vср=V, где
Vср – средняя скорость, а
V – скорость равномерного движения.

Чтобы вычислить среднюю скорость равноускоренного движения, найдите среднее арифметическое начальной и конечной скорости. Для этого найдите сумму этих скоростей и разделите на два. Полученное число и будет средней скоростью объекта.
Нагляднее это выглядит в виде следующей формулы:Vср = (Vкон + Vнач) / 2, где
Vср – средняя скорость,
Vкон – конечная скорость,
Vнач – начальная скорость.

Если задана величина ускорения и начальная скорость, а конечная скорость неизвестна, то преобразуйте вышеприведенную формулу следующим образом:
Так как при равноускоренном движении Vкон = Vнач + a*t, где а – ускорение объекта, а t – время, то имеем:Vср = (Vкон + Vнач) / 2 = (Vнач + a*t + Vнач) / 2 = Vнач + a*t / 2

Если же, наоборот, известны конечная скорость и ускорение тела, но начальная скорость не задана, то преобразуйте формулу к следующему виду:Vср = (Vкон + Vнач) / 2 = (Vкон + Vкон — a*t) / 2 = Vкон — a*t / 2

Если заданы длина пройденного телом пути, а также время, которое понадобилось на прохождение этого расстояния, то просто разделите этот путь на затраченное время. То есть используйте общую формулу:Vср = S / t, где S – общая длина пройденного пути.Время, затраченное на прохождение пути учитывается независимо от того, двигался объект непрерывно или останавливался.

Если в условиях задачи специально не указано, какую именно среднюю скорость необходимо вычислить, то подразумевается средняя путевая скорость.
Чтобы вычислить среднюю путевую скорость, берется общая длина пройденного пути, т.е. его траектория. Если во время движения объект возвращался в пройденные точки пути, то это расстояние также учитывается. Так, например, для автомобиля длина пути, необходимая для вычисления средней путевой скорости, будет соответствовать показаниям спидометра (разности показаний).

Если необходимо вычислить среднюю скорость перемещения (смещения), то под пройденным путем подразумевается то расстояние, на которое тело действительно переместилось.
Так как перемещение всегда происходит в определенном направлении, то смещение (S) величина векторная, т.е. характеризуется как направлением, так и абсолютной величиной. Следовательно, и значение средней скорости смещения будет величиной векторной. В связи с этим, при решении подобных задач обязательно узнайте: какую именно скорость требуется вычислить. Среднюю путевую скорость, числовое значение средней скорости смещения или вектор средней скорости смещения.
В частности, если тело в процессе движения возвращается в исходную точку, то считается, что его средняя скорость смещения равна нулю.

Источник

В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.

Определение средней скорости

Средней скоростью движения $upsilon_{cp}$ тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело:

$[ upsilon_{cp} = frac{s}{t}. ]$

Научимся ее находить на примере следующей задачи:

Тело двигалось 3 мин. со скоростью 5 м/с, после чего 7 мин. двигалось со скоростью 3 м/с. Найти среднюю скорость движения тела.

Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей и , которое равно:
$frac{upsilon_1+upsilon_1}{2} = 4$ м/с.

Частные случаи нахождения средней скорости

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

$[ upsilon_{cp} = frac{s}{t_1+t_2} = frac{s}{frac{s}{2upsilon_1}+frac{s}{2upsilon_2}} = frac{2upsilon_1upsilon_2}{upsilon_1+upsilon_2}. ]$

2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

$[ upsilon_{cp} = frac{s_1+s_2}{t} = frac{upsilon_1frac{t}{2}+upsilon_2frac{t}{2}}{t} = frac{upsilon_1+upsilon_2}{2}. ]$

Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Пройденный телом путь составляет: $s = upsilon_{cp}t = 80$ м. Можно найти также путь, который прошло тело за последние с своего движения: $s_2 = upsilon_{cp2}t_2 = 40$ м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила:
$upsilon_{cp1} = frac{s_1}{t_1} = 2.5$ м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Репетитор по физике на Юго-Западной
Сергей Валерьевич

Источник

Средняя скорость

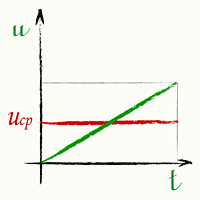
Средняя скорость для равномерно ускоренного движения без начальной скорости

Средняя скорость u_сред движения равна среднему арифметическому начальной и конечной скоростей

[ u_{сред} = frac{0+u}{2} = frac{u}{2} ]

Здесь:
u — скорость тела через промежуток времени t,

средняя скорость, график скорости - Равномерно ускоренное движение без начальной скорости

Также средняя скорость выражается через ускорение

[ u_{сред} = frac{at}{2} ]

Здесь:
a — ускорение тела, постоянное в течение времени t

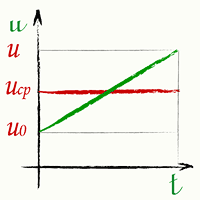
Средняя скорость для равномерно ускоренного движения с начальной скоростью

Средняя скорость u_сред движения равна среднему арифметическому начальной и конечной скоростей

[ u_{сред} = frac{u_0+u}{2} ]

Здесь:
u₀ — начальная скорость тела в момент времени t=0,
u — скорость тела через промежуток времени t,

средняя скорость, график скорости - Равномерно ускоренное движение с начальной скоростью

Также средняя скорость выражается через ускорение

[ u_{сред} = u_0 + frac{at}{2} ]

Здесь:
a — ускорение тела, постоянное в течение времени t

Средняя скорость	стр. 401

Источник

План урока:

Закон сложения скоростей

Мгновенная скорость, направление мгновенной скорости

Ускорение. Касательное ускорение. Центростремительное ускорение

Равноускоренное движение

Свободное падение

Равномерное движение точки по окружности

Закон сложения скоростей

Как уже упоминалось в предыдущем уроке, скорость тела зависит от выбранной наблюдателем системы отсчета. Разберем следующий пример: в безветренную погоду пчела летит со скоростью относительно земли. Это будет собственная скорость пчелы. Затем погода меняется и начинает дуть ветер, перпендикулярный скорости пчелы. Скорость ветра обозначена (см. рисунок 1).

Рисунок 1 – Первоначальная скорость пчелы и ветра

Естественно, что ветер начнет сдувать пчелу с первоначального курса. Собственная скорость не изменяется, так как это характеристика самой пчелы, но ее скорость относительно земли (по модулю и направлению) изменится и станет (см. рисунок 2):

Рисунок 2 – Изменившаяся скорость пчелы

Систему отсчета, связанную с землей, можно считать неподвижной. Если же рассматривать движение пчелы относительно воздуха, можно говорить о движущейся со скоростью v₂ системе отсчета.

Рисунок 3 – Векторы скорости и перемещений при движении пчелы при ветре

Мгновенная скорость, направление мгновенной скорости

Средняя скорость. Средняя путевая скорость

Так как в реальной жизни тела редко движутся с постоянной скорость, но необходимо как-то описывать их движение и скорость, ввели понятие мгновенной скорости.

Мгновенная скорость – это скорость тела в выбранный конкретный момент времени.

Если по определению скорости разделить перемещение на суммарное время пути, можно получить средняя скорость:

Фактически, это та же формула, которая используется при расчетах для прямолинейного равномерного движения.

То есть средняя скорость движения – это такая скорость, с которой тело должно было бы двигаться, если бы оно перемещалось из начальной точки в конечную равномерно и прямолинейно. Из выражения для вычисления средней скорости можно увидеть, что средняя скорость сонаправлена вектору перемещения.

Касательно же мгновенной скорости, чтобы ее найти, необходимо разделить общее время Δt на одинаковые отрезки Δt₁, Δt₂,…Δt_n, и найти средние скорости за эти отрезки времени:

А куда направлена мгновенная скорость? Из рисунка 5 видно, что при уменьшении отрезков времени Δt_b направление вектора перемещения ему соответствующее постепенно приближается к направлению касательной к траектории. Значит, мгновенная скорость направлена по касательной к линии траектории.

Еще одна важная характеристика, использующаяся в кинематике – средняя путевая скорость. Из названия вытекает, что средняя путевая скорость – это отношение пути (S), пройденного телом, к отрезку времени (t), за которое оно этот путь прошло:

Именно о путевой скорости идет речь, когда говорят, что автомобиль ехал из одного города в другой со скоростью 70 км/ч, например.

Ускорение. Касательное ускорение. Центростремительное ускорение

Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.

Единицы измерения ускорения:

Рисунок 6 – Тело перемещается из точки 1 в точку 2 (в верхнем правом углу дана иллюстрация к разности векторов)

Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить на маленькие отрезки времени и рассматривать ускорение на каждом из них.

Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).

Рисунок 7 – Полное, касательно и центростремительное ускорение тела, движущегося из точки 1 в точку 2

Равноускоренное движение

Прямолинейное равноускоренное движение. Определение скорости при равноускоренном движении. Уравнения движения при равноускоренном движении

Когда движение тела происходит с постоянным по модулю и направлению ускорением, такой тип движения называют равноускоренным. Для него справедливо выражение:

Частный случай равноускоренного движения – прямолинейное равноускоренное движение. Как следует из названия, это движение вдоль прямой линии с постоянным ускорением.

При условии, что ускорение сонаправлено начальной скорости, формула для вычисления скорости при прямолинейном равноускоренном движении записывается в скалярном виде:

v = v₀ + a * t

Если же ускорение противонаправлено начальной скорости, это выражение станет таким:

v = v₀ — a * t

Рассмотрим график зависимости скорости от времени при равноускоренном движении (см. рисунок 8). Считаем, что тело совершает движение вдоль оси ОХ, а все величины – начальная скорость (v_ox) , ускорение (a_x) – взяты в проекции на эту ось.

Рисунок 8 – График зависимости скорости от времени при прямолинейном равноускоренном движении

Как известно из предыдущего курса физики, путь, который прошло тело, можно найти как площадь фигуры под графиком зависимости скорости движения от времени. Общую площадь под графиком можно найти как сумму площадей прямоугольника ABCD и треугольника ADE.

Свободное падение

Движение тела, брошенного вертикально вверх. Движение тела, брошенного под углом к горизонту. Криволинейное равноускоренное движение

Примерами движения с постоянным ускорением может служить свободное падение, движение брошенного вертикально вверх тела, движение тела, брошенного под углом к горизонту. Поговорим об этих видах движения подробнее.

Свободное падение

Представим, что какое-то небольшое, но тяжелое тело подняли на высоту h, а затем отпустили (см. рисунок 9).

Рисунок 9 – Свободное падение тела

Тело начнет падать. Принимаем допущение, что на это тело воздействует одна только сила тяжести (силой сопротивления воздуха и силой ветра пренебрегаем). Тогда тело будет двигаться вертикально вниз, а его ускорение будет равняться ускорению свободного падения:

Движение тела, брошенного вертикально вверх

Представим, что тело подкинули вертикально наверх с начальной скоростью v₀ (см. рисунок 10).

Рисунок 10 – Тело бросили вертикально вверх

Очевидно, что тело сначала будет лететь вверх, постепенно замедляясь, пока его скорость не уменьшится до нуля. Затем тело полетит вниз, постепенно ускоряясь. Получается, что максимальной своей скорости тело будет достигать два раза – у земли, и эта скорость будет равно начальной скорости v₀(вообще нужно было бы писать v_oy, но так как рассматривается движение вдоль только одной оси OY, опустим индекс y).

Отсюда можно найти полное время полета:

Движение тела, брошенного под углом к горизонту

Данный тип движения чуть сложнее, чем предыдущие два, так как придется рассматривать движение сразу вдоль двух осей OX и OY (см. рисунок 11). Этот тип движения относится к криволинейному равноускоренному движению. Будем считать, что тело подбросили с начальной скоростью под углом α к горизонту.

Рисунок 11 – Тело брошено под углом к горизонту

Уравнения движения в общем виде по двум осям выглядят так:

Еще время полета можно посчитать, учитывая что в двух моментах – в начале полета и в конце. Значит можно посчитать:

Равномерное движение точки по окружности

Центростремительное ускорение

Представим себе равномерное движение по окружности: во время этого типа движения скорость не меняется по модулю, однако меняется по направлению (см. рисунок 12).

Рисунок 12 – Изменение направления скорости при равномерном движении по окружности

За изменение направления скорости отвечает центростремительное ускорение ( Оно, так же как и скорость, постоянно по модулю, но меняется по направлению – в любой точке окружности оно направлено к ее центру. Центростремительное ускорение можно найти по формуле:

где R – радиус окружности, по которой циклически движется тело.

Источник

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Как вычислить среднюю скорость

Определение средней скорости

Частные случаи нахождения средней скорости

Средняя скорость

Средняя скорость для равномерно ускоренного движения без начальной скорости

Средняя скорость для равномерно ускоренного движения с начальной скоростью

Средняя скорость

Закон сложения скоростей

Мгновенная скорость, направление мгновенной скорости

Средняя скорость. Средняя путевая скорость

Ускорение. Касательное ускорение. Центростремительное ускорение

Равноускоренное движение

Прямолинейное равноускоренное движение. Определение скорости при равноускоренном движении. Уравнения движения при равноускоренном движении

Свободное падение

Движение тела, брошенного вертикально вверх. Движение тела, брошенного под углом к горизонту. Криволинейное равноускоренное движение

Равномерное движение точки по окружности

Центростремительное ускорение