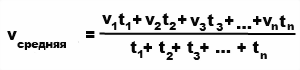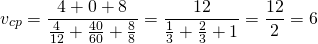Как найти среднюю скорость когда неизвестно время - Исправление недочетов и поиск решений вместе с Examum.ru

Средняя скорость

Главная
/
Физика
/
Средняя скорость

Чтобы найти среднюю скорость воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Средняя скорость на протяжении всего пути

Расстояние (путь)

S =

Время

t =

Средняя скорость

V_ср =

Округление ответа:

Средняя скорость через несколько скоростей

Средняя скорость

V_ср =

Округление ответа:

Просто введите значения скоростей на разных участках пути и получите среднюю скорость. Для того чтобы добавить в ряд более двух чисел воспользуйтесь зелёной кнопкой «+».

Теория

Как найти среднюю скорость зная расстояние (путь) и время

Чему равна средняя скорость V_ср если известны путь S и время t за которое этот путь преодолён?

Формула

V_ср = ^S⁄_t

Пример

К примеру, поезд преодолел расстояние в 1000 км за 16 часов. Посчитаем с какой средней скоростью он двигался:

V_ср = 1000/16 = 62.5 км/ч

Как найти среднюю скорость зная скорости на участках пути

Чтобы найти среднюю скорость V_ср на протяжении всего пути, зная показатели скорости на его участках (V₁ , V₂ , … V_n), следует найти среднее гармоническое этих скоростей.

Формула

V_ср	=	n
¹⁄_V₁ + ¹⁄_V₂ + … + ¹⁄_{V_n}

Пример

Средняя скорость через две скорости

Автомобиль проехал некий путь, при этом первые полпути он ехал со скоростью 80 км/ч, а вторые полпути — со скоростью 20 км/ч. Определим среднюю скорость этого автомобиля:

V_ср	=	2	=	2	= 32
¹⁄₈₀ + ¹⁄₂₀	0.0125 + 0.05

Средняя скорость автомобиля равна 32 км/ч.

Источник

Загрузить PDF

Чтобы вычислить среднюю скорость, воспользуйтесь простой формулой: ${text{Скорость}}={frac {{text{Пройденный путь}}}{{text{Время}}}}$ . Но в некоторых задачах даются два значения скорости — на разных участках пройденного пути или в различные промежутки времени. В этих случаях нужно пользоваться другими формулами для вычисления средней скорости. Навыки решения подобных задач могут пригодиться в реальной жизни, а сами задачи могут встретиться на экзаменах, поэтому запомните формулы и уясните принципы решения задач.

1
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:
- длина пути, пройденного телом;
- время, за которое тело прошло этот путь.
- Например: автомобиль проехал 150 км за 3 ч. Найдите среднюю скорость автомобиля.
2

Запишите формулу для вычисления средней скорости. Формула: $v={frac {s}{t}}$ , где — средняя скорость, — пройденный путь, — время, за которое пройден путь.^[1]
3
В формулу подставьте пройденный путь. Значение пути подставьте вместо .
- В нашем примере автомобиль проехал 150 км. Формула запишется так: $v={frac {150}{t}}$ .
4
В формулу подставьте время. Значение времени подставьте вместо .
- В нашем примере автомобиль ехал в течение 3 ч. Формула запишется так: $v={frac {150}{3}}$ .
5

Разделите путь на время. Вы найдете среднюю скорость (как правило, она измеряется в километрах в час).

Реклама

1
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:
- несколько значений пройденных участков пути;
- несколько значений времени, за которые был пройден каждый участок пути.^[2]
- Например: автомобиль проехал 150 км за 3 ч, 120 км за 2 ч, 70 км за 1 ч. Найдите среднюю скорость автомобиля на всем протяжении пути.
2

Запишите формулу для вычисления средней скорости. Формула: $v={frac {s}{t}}$ , где — средняя скорость, — общий пройденный путь, — общее время, за которое пройден путь.^[3]
3

Вычислите общий пройденный путь. Для этого сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо ).
4

Вычислите общее время в пути. Для этого сложите значения времени, за которые был пройден каждый участок пути. В формулу подставьте общее время (вместо ).
5

Разделите общий путь на общее время. Вы найдете среднюю скорость.

Реклама

1
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины:
- несколько значений скоростей, с которыми двигалось тело;
- несколько значений времени, в течение которого тело двигалось с соответствующей скоростью.^[4]
- Например: автомобиль двигался со скоростью 50 км/ч в течение 3 ч, со скоростью 60 км/ч в течение 2 ч, со скоростью 70 км/ч в течение 1 ч. Найдите среднюю скорость автомобиля на всем протяжении пути.
2

Запишите формулу для вычисления средней скорости. Формула: $v={frac {s}{t}}$ , где — средняя скорость, — общий пройденный путь, — общее время, за которое пройден путь.^[5]
3

Вычислите общий путь. Для этого умножьте каждую скорость на соответствующее время. Так вы найдете длину каждого участка пути. Чтобы вычислить общий путь, сложите значения пройденных участков пути. В формулу подставьте общий пройденный путь (вместо ).
4

Вычислите общее время в пути. Для этого сложите значения времени, за которые был пройден каждый участок пути. В формулу подставьте общее время (вместо ).
5

Разделите общий путь на общее время. Вы найдете среднюю скорость.

Реклама

1
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины и условия:
- два или несколько значений скоростей, с которыми двигалось тело;
- тело двигалось с определенными скоростями в течение равных промежутков времени.
- Например: автомобиль двигался со скоростью 40 км/ч в течение 2 ч и со скоростью 60 км/ч в течение других 2 ч. Найдите среднюю скорость автомобиля на всем протяжении пути.
2
3
4

Сложите значения двух скоростей. Затем сумму разделите на два. Вы найдете среднюю скорость на всем протяжении пути.

Реклама

1
Посмотрите на данные величины. Воспользуйтесь этим методом, если даны следующие величины и условия:
- два или несколько значений скоростей, с которыми двигалось тело;
- тело двигалось с определенными скоростями и прошло равные участки пути.
- Например: автомобиль проехал 150 км со скоростью 40 км/ч, а затем вернулся обратно (то есть проехал те же 160 км) со скоростью 60 км/ч. Найдите среднюю скорость автомобиля на всем протяжении пути.
2
Запишите формулу для вычисления средней скорости, если даны две скорости и одинаковые значения участков пути. Формула: $v={frac {2ab}{a+b}}$ , где — средняя скорость, — скорость тела, с которым оно двигалось на первом участке пути, — скорость тела, с которым оно двигалось на втором (таком же, как первый) участке пути.
^[7]
- Зачастую в условиях таких задач дано, что тело прошло определенный путь и вернулось обратно.
- В таких задачах значения участков пути не важны — главное, чтобы они были равны.
- Если даны три скорости и равные участки пути, перепишите формулу так: $v={frac {3abc}{ab+bc+ca}}$ .^[8]
3
4

Произведение двух скоростей умножьте на 2. Полученный результат запишите в числителе дроби.
5

Сложите две скорости. Полученный результат запишите в знаменателе дроби.
6

Сократите дробь. Вы найдете среднюю скорость на всем протяжении пути.

Реклама

Об этой статье

Эту страницу просматривали 170 881 раз.

Была ли эта статья полезной?

Источник

В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.

Определение средней скорости

Средней скоростью движения $upsilon_{cp}$ тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело:

$[ upsilon_{cp} = frac{s}{t}. ]$

Научимся ее находить на примере следующей задачи:

Тело двигалось 3 мин. со скоростью 5 м/с, после чего 7 мин. двигалось со скоростью 3 м/с. Найти среднюю скорость движения тела.

Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей и , которое равно:
$frac{upsilon_1+upsilon_1}{2} = 4$ м/с.

Частные случаи нахождения средней скорости

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

$[ upsilon_{cp} = frac{s}{t_1+t_2} = frac{s}{frac{s}{2upsilon_1}+frac{s}{2upsilon_2}} = frac{2upsilon_1upsilon_2}{upsilon_1+upsilon_2}. ]$

2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

$[ upsilon_{cp} = frac{s_1+s_2}{t} = frac{upsilon_1frac{t}{2}+upsilon_2frac{t}{2}}{t} = frac{upsilon_1+upsilon_2}{2}. ]$

Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Пройденный телом путь составляет: $s = upsilon_{cp}t = 80$ м. Можно найти также путь, который прошло тело за последние с своего движения: $s_2 = upsilon_{cp2}t_2 = 40$ м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила:
$upsilon_{cp1} = frac{s_1}{t_1} = 2.5$ м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Репетитор по физике на Юго-Западной
Сергей Валерьевич

Источник

Download Article

Often calculating the average speed is simple using the formula ${text{speed}}={frac {{text{distance}}}{{text{time}}}}$ . But sometimes you are given two different speeds used for some periods of time, or over some distances. In these instances, other formulas exist for calculating the average speed. These types of problems might be useful to you in real life, and often appear on standardized tests, so it is helpful to learn these formulas and methods.

1
Assess what information you are given. Use this method if you know:
- the total distance covered by one person or vehicle; and
- the total time it took that person or vehicle to cover the distance.
- For example:^[1] If Ben traveled 150 miles in 3 hours, what was his average speed?
2

Set up the formula for speed. The formula is $S={frac {d}{t}}$ , where equals the average speed, equals the total distance, and equals the total time.^[2]

Advertisement
3
Plug the distance into the formula. Remember to substitute for the variable .
- For example, if Ben drives 150 total miles, your formula will look like this: $S={frac {150}{t}}$ .
4
Plug the time into the formula. Remember to substitute for the variable .
- For example, if Ben drives for 3 hours, your formula will look like this: $S={frac {150}{3}}$ .
5

Divide the distance by the time. This will give you the average speed per unit of time, usually hour.

1
Assess what information you are given. Use this method if you know:
- multiple distances that were traveled; and
- the amount of time it took to travel each of those distances.^[3]
- For example: If Ben traveled 150 miles in 3 hours, 120 miles in 2 hours, and 70 miles in 1 hour, what was his average speed for the entire trip?
2

Set up the formula for average speed. The formula is $S={frac {d}{t}}$ , where equals the average speed, equals the total distance, and equals the total time.^[4]
3

Determine the total distance. To do this, add up the number of miles traveled during the entire trip. Substitute this value for in the formula.
4

Determine the total time. To do this, add up the times, usually hours, that were spent traveling. Substitute this value for in the formula.
5

Divide the total distance traveled by the total time spent traveling. This will give you your average speed.

1
Assess what information you are given. Use this method if you know:
- multiple speeds used to travel; and
- the amount of time each of those speeds was traveled for.^[5]
- For example: For example: If Ben traveled 50 mph for 3 hours, 60 mph for 2 hours, and 70 mph for 1 hour, what was his average speed for the entire trip?
2

Set up the formula for average speed. The formula is $S={frac {d}{t}}$ , where equals the average speed, equals the total distance, and equals the total time.^[6]
3

Determine the total distance. To do this, separately multiply each speed by each time period. This will give you the distance traveled for each section of the trip. Add up these distances. Substitute this sum for in the formula.
4

Determine the total time. To do this, add up the times, usually hours, that were spent traveling. Substitute this value for in the formula.
5

Divide the total distance traveled by the total time spent traveling. This will give you your average speed.

1
Assess what information you are given. Use this method if you know:
- two or more different speeds; and
- that those speeds were traveled for the same amount of time.
- For example, if Ben drives 40 mph for 2 hours, and 60 mph for another 2 hours, what is his average speed for the entire trip?
2
3
4

Add the two speeds together. Then, divide the sum by two. This will give you the average speed for the entire trip.

1
Assess what information is given. Use this method if you know:
- two different speeds; and
- that those speeds were used for the same distance.
- For example, if Ben drives the 160 miles to the waterpark at 40 mph, and returns the 160 miles home driving 60 mph, what is his average speed for the entire trip?
2
3
4

Multiply the product of the two speeds by 2. This number should be the numerator of your fraction.
5

Add the two speeds together. This number should be the denominator of your fraction.
6

Simplify the fraction. This will give you the average speed for the entire trip.

Calculator, Practice Problems, and Answers

Add New Question

Question

An athlete runs in a circular path with a radius of 14m. The athlete completes 10 rounds in 10 minutes. How do I calculate his speed in m/s?

To know how far he runs, you first have to calculate the circumference of the circle. The formula for circumference is 2(pi)(r). So 2(3.14)(14) = 87.92.

Since he runs ten rounds, you have to multiply the circumference by 10: 87.92 x 10 = 879.2 (879 rounded)

Next, it says he completed the run in 10 minutes, but the answer needs to be in seconds, so convert by multiplying 10 x 60 = 600.

Now, you can set up the speed ratio: s = d/t; s = 879/600

Finally, simplify the ratio by dividing 879/600 = 1.47.

So his average speed was 1.47 m/s
Question

How can I find an average speed of a car if it moves from point A To B at a speed of 30 kilometers per hour and returns at a speed of 50 kilometers per hour?

Since you have two different speeds for half the distance (A to B = half; B to A = half), use the formula given in method 5: 2ab/a+b. So:

(2)(30)(50)/30+50
3000/80
37.5

So, the average speed is 37.5 km/hr
Question

Does steepness matter when you’re finding the average speed?

No, the formula for average speed is the same regardless of steepness. If you were calculating velocity, then the direction/incline of the motion would matter.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Thanks for submitting a tip for review!

About This Article

Article SummaryX

If you need to calculate average speed and you know the total distance covered and the total time it took to cover that distance, divide the distance into the total time. If the fraction doesn’t simplify into a whole number, convert it to a decimal. The result will be the average speed per unit of time, usually an hour. If you want to learn how to calculate average speed if there are multiples distances or amounts of time, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 1,206,557 times.

Did this article help you?

Источник

Как находить среднюю скорость

Повторим, как находить среднюю скорость, и рассмотрим конкретные примеры.

Чтобы найти среднюю скорость, надо:

1) найти весь пройденный путь;

2) найти все время движения;

3) весь пройденный путь разделить на все время движения:

На примерах посмотрим, как находить среднюю скорость.

1) Пешеход прошел 2 часа со скоростью 7 км/ч и 3 часа со скоростью 5 км/ч. Найти среднюю скорость движения пешехода на всем пути.

Находим весь пройденный путь: 2∙7 + 3∙5 = 29 км.

Находим все время движения: 2+3=5 часов.

Чтобы найти среднюю скорость, весь пройденный путь делим на все время движения: 29:5=5,8 км/ч.

2) Автомобиль проехал 2 часа по шоссе со скоростью 100 км/ч, 1,5 часа по грунтовой дороге со скоростью 40 км/ч и 30 минут по проселочной дороге со скоростью 26 км/ч. Найти среднюю скорость автомобиля на всем пути.

Переведем минуты в часы: 30 минут = 0,5 часа.

Найдем весь пройденный автомобилем путь:

2∙100 + 1,5∙40 + 0,5∙26 = 200 + 60 + 13= 273 км.

Находим все время движения:

Чтобы найти среднюю скорость движения автомобиля, разделим весь пройденный путь на все время движения:

3) Велосипедист проехал 3 часа со скоростью 12 км/ч, затем отдохнул час, после чего продолжил путь со скоростью 9 км/ч и проехал еще 2 часа. Найти среднюю скорость движения велосипедиста на всем пути.

Найдем весь путь велосипедиста:

3∙12 + 1∙0 + 2∙9 = 54 км.

Найдем все время движения:

Чтобы найти среднюю скорость движения велосипедиста, весь путь делим на все время движения:

самый лучший сайт по математике спасибо огромное

Илья, спасибо за теплые слова!

Велосипедист проехал со скоростью 12 км/ч 4 км,остановился на 40 мин и продолжил движение со скоростью 8 км/ч и проехал 8 км. Найдите скорость велосипедиста на протяжении всей дороги? Пожалуйста,помогите,очень важно

Валерий, эта задача — на движение по водному пути. Но ее можно решить логически.
Поскольку известно, что скорость катера по течению реки в два раза больше скорости против течения, при этом расстояние туда и обратно — одинаковое, то время, затраченное катером на путь по течению, в два раза меньше времени против течения (скорость и время — обратно пропорциональные величины. Если скорость увеличить в несколько раз, то при том же расстоянии время уменьшится во столько же раз).
Таким образом, все время можно разделить на 3 части, одну часть которого катер потратил на путь по течению, две — на путь против течения. Так как на весь путь было потрачено 2 часа=120 минут, то из них на путь по течению — 1/3 от 120 — это 40 минут=2/3 часа. Чтобы найти скорость, надо расстояние разделить на время: 20:(2/3)=30 км/ч — это скорость катера по течению. Она в два раза больше скорости против течения, следовательно, скорость против течения 30:2=15 км/ч.

Девушка ехала на работу со средней скоростью 40 миль в час, обратно домой ехала со средней скоростью 30 миль в час, весь путь от дома до работы и обратно занял 1 час, сколько миль проехала девушка?

Это — задача на движение. Пусть на работу девушка ехала х часов,тогда обратный путь занял у нее (1-х) часов. По формуле пути путь на работу равен 40х миль, обратный путь — 30(1-х) миль. Так как туда и обратно девушка проехала одинаковое расстояние, составляем уравнение: 40х=30(1-х). Отсюда х=3/7, путь на работу 40∙(3/7)=120/7 миль, туда и обратно — 2∙(120/7)=240/7=38 2/7 мили.

Источник

Формула нахождения значений скорости, времени и расстояния

С древних времен людей беспокоит мысль о достижении сверх скоростей, так же как не дают покоя раздумья о высотах, летательных аппаратах. На самом деле это два очень сильно связанных между собой понятия. То, насколько быстро можно добраться из одного пункта в другой на летательном аппарате в наше время, зависит полностью от скорости. Рассмотрим же способы и формулы расчета этого показателя, а также времени и расстояния.

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

Можно записать использовать и такой вид вычислений:

Но можно записать эту же формулу и в более точном варианте:

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Другие способы вычисления

Существую и другие способы и методы, которые помогают вычислить значения рассматриваемого параметра. В пример можно привести формулу вычисления мощности:

Способы вычисления расстояния и времени

Можно и наоборот, зная скорость, найти значение расстояния или времени. Например:

Таким образом вычисляется значение расстояния.

Или вычисляем значение времени, за которое пройдено расстояние:

Для нахождения средних значений этих параметров существует довольно много представлений как данной формулы, так и всех остальных. Главное, знать основные правила перестановок и вычислений. А еще главнее знать сами формулы и лучше наизусть. Если же запомнить не получается, тогда лучше записывать. Это поможет, не сомневайтесь.

Пользуясь такими перестановками можно с легкостью найти время, расстояние и другие параметры, используя нужные, правильные способы их вычисления.

И это еще не предел!

Видео

В нашем видео вы найдете интересные примеры решения задач на нахождение скорости, времени и расстояния.

Источник

Средняя скорость пути

Известно, что средняя скорость V равна пути S, деленному на время t средней скорости. Средняя скорость не всегда находится так легко. В случае, если автомобиль движется равномерно с постоянной скоростью, например 45 км/час, то, очевидно, средняя скорость и постоянная скорость одинаковы, т. е. 45 км/час. Если же автомобиль трогается с места (начальная скорость равна 0) и развивает скорость постепенно, то среднюю скорость можно найти следующим способом: нужно записать сумму всех скоростей и поделить ее на число отсчетов скоростей. Важно — временные интервалы должны быть одинаковые (например: записывать скорость каждые 5 секунд, или каждые 7 минут).

Калькулятор средней скорости пути

Складывая скорости, введенные вами, мы находим их сумму. Разделив эту сумму на количество равных временных отсчетов, мы узнаем среднюю скорость.

Единицы скорости

Скорость обычно определяют как путь, пройденный за единицу времени. Поэтому, если скорость автомобиля 90 км/час, то он за минуту должен пройти 1,5 км, а в секунду 1500 : 60, или 25 м. Следовательно, скорость 90 км/час может быть выражена различными способами в зависимости от выбора единиц времени и пути:

90 км/час = 1.5 км/мин =25 м/сек.

Поскольку скорость может быть выражена в различных единицах, то надо внимательно следить за выбором единиц в формуле S=vt. Если скорость выбираем в км/час, то время надо брать в часах, если — в м/сек, то время должно быть выражено в секундах.

Источник

Как посчитать среднюю скорость движения автомобиля

Средняя скорость – не самое сложное понятие в кинематике. Однако для многих учащихся простота этого понятия оказывается обманчивой.
Известно, что средняя скорость – это величина, равная отношению пути, пройденного телом, ко времени, за которое пройден этот путь: Краткость и простота определения скрывают от некоторых учеников важные для решения задач вопросы и ответы на них.
1. Какое время следует учитывать при расчете средней скорости, если тело в пути делало остановки?
В определении указано: “. ко времени, за которое пройден этот путь”, то есть ко всему промежутку времени с момента, когда тело тронулось в этот путь (представьте, что Вы включили секундомер), до момента, когда тело преодолело этот путь (только в этот момент Вы останавливаете секундомер!). О том, что время на остановки не следует учитывать, в определении ничего не сказано (поэтому секундомер на промежуточных остановках не выключайте!). Таким образом, при расчете средней скорости следует учитывать всё время, которое ушло на преодоление пути (в том числе и время, потраченное на остановки).

2. Как правильно рассчитать среднюю скорость тела, которое начало движение в пункте А, окончило его в пункте В, но по дороге из А в В поворачивало назад (может быть ни один раз!), а затем вновь продолжало движение к пункту В?
В определении указано “. равная отношению пути, пройденного телом. ”, значит, при расчете средней скорости определяющим является не расстояние между точками (пунктами) начала и окончания движения, а реальный путь, которое прошло тело.

Пример 1. Найти среднюю скорость человека на пути от дома до станции, расстояние между которыми l =800 м, если, пройдя четверть пути, он вернулся домой (например, проверить, хорошо ли закрыта дверь) и через мин продолжил путь на станцию. Скорость движения человека постоянна и равна v =4 км/ч.

Решение. Началом движения человека, конечно, следует считать момент времени, когда он первый раз вышел из дома. Четверть пути составляет расстояние l_1/4 =l : 4 =800 : 4 =200 м. При возвращении домой человек прошел путь 2l_1/4 =400 м. После этого он вышел из дома второй раз и дошел до станции. Путь, пройденный человеком с начала движения, составит:

Время t, которое затрачено на преодоление этого пути, складывается из времени пребывания дома и времени Т, в течение которого человек двигался по маршруту “из дома–к дому–на станцию”. Поскольку скорость движения человека постоянна (v =4 км/ч) и проделанный путь известен, то время движения составляет:

1,2 км : 4 км/ч =0,3 ч =18 мин.
Тогда все время, затраченное человеком, составляет:

t = + T = 2 + 18 =20 мин =1/3 ч.
Найдем среднюю скорость:

1,2 км : ч =3,6 км/ч.

Среднюю скорость движения человек оценивает довольно часто, но судит о ней, глядя на часы. Торопящийся человек соотносит расстояние, которое ещё осталось преодолеть, и время, отпущенное ему на это, после чего делает вывод (хотя числовое значение средней скорости вряд ли при этом находится): “Ну, теперь можно идти помедленнее” или “Придется еще поднажать, иначе не успею”.

Вернемся к рассмотренному примеру. Будем считать, что скорость v₀ =4 км/ч выбрана человеком не случайно. проходя от дома до станции ежедневно, человек замечает, что расстояние l ==800 м, он проходит за время t₀ =12 мин =0,2 ч:

= 0,8 км : 0,2 ч =4 км/ч.

По существу, это – средняя скорость, поскольку доподлинно неизвестно, с какой скоростью человек идет в каждый момент времени. Двигаясь с такой скоростью и затрачивая время t₀, человек ежедневно успевает на станцию вовремя. Если приходится возвращаться домой (увеличивать путь, который надо преодолеть и на это требуется дополнительное время) или останавливаться (увеличивая время, необходимое на преодоление пути), выбранная скорость движения v₀ не подходит: можно опоздать на станцию. Значит, надо увеличивать скорость движения. Но как это сделать без напрасных затрат сил?

Пример 2. Человек обычно доходит из дома до станции за время t₀ =12 мин, проходя расстояние l =800 м. Однажды, пройдя четверть пути, он вспоминает, что не выключил электроприборы, и возвращается домой, выключает электроприборы, затрачивая время = 2 мин, и снова идет на станцию. С какой наименьшей скоростью надо двигаться человеку, после того как он повернул домой, чтобы успеть на станцию в обычное время (и не опоздать на электричку).

1. Обычно человек двигается со скоростью

м/мин =4 км/ч.

2. Пройдя с такой скоростью четверть пути, он затратил время : 4 км/ч =0,05 ч =3 мин. Значит, в его распоряжении осталось время Т₂ =t₀ – T₁ =12 – 3 =9 мин.

3. За время Т₂ человек должен преодолеть путь до дома, а затем снова до станции:
м =1 км и, кроме того, часть времени ( = 2 мин) потратить дома. Поэтому путь S человеку придется преодолевать за время

ч,

то есть со скоростью, не меньшей, чем

1 км : ч = км/ч = км/ч » 8,6 км/ч.

Проверьте, что добежав до дома со скоростью км/ч, а затем шагая со скоростью v₂ =2v₀ =8 км/ч, человек придет на станцию вовремя.
Ответ: человеку необходимо двигаться со скоростью, не меньшей, чем км/ч. Обратите внимание, что средняя скорость за время (t =12 минут) от начала движения до его окончания составляет

м/мин =100 м/мин =6 км/ч.

Найденное значение v_ср в полтора раза выше, чем v₀, и показывает, с какой начальной скоростью следует выходить человеку из дома, если он забывчив.

На рис.1 показан график зависимости скорости человека от времени для примера 2 в случае, если человек бежит домой со скоростью v₁ =3v₀ ==12 км/ч, а затем идет до станции очень быстрым шагом со скоростью v₂ =2v₀ =8 км/ч. Штрихпунктирной линией указан график движения со скоростью v₀, а тонкой линией – со скоростью v_ср =6 км/ч.

Подсчитаем среднее арифметическое для значений скорости v₀, v₁, v₂:

км/ч.

Это значение не равно значению средней скорости v_ср. Убедитесь в этом и не совершайте в дальнейшем распространенную ошибку: не пытайтесь искать среднюю скорость как среднее арифметическое значение (оно не имеет физического смысла!).

Пример 3. Автомобиль проезжает первую треть пути равномерно со скоростью v₁ =108 км/ч, а остальные две трети пути – со скоростью v₂ =72 км/ч. Найти среднюю скорость автомобиля.
Решение. Неверно считать, что средняя скорость совпадает со средним арифметическим значением v₁ и v₂, которое составляет

км/ч.

1. Найдем время t₁ движения со скоростью v₁, полагая, что весь путь равен L [км]. Из условия ясно, что

2. Время t₂ движения на оставшемся участке пути составляет

3. Итак, время на продолжение пути L составляет

4. По определению средней скорости

км/ч.

Ответ : средняя скорость v_ср =81 км/ч.

Значение средней скорости совпадает со средним арифметическим значением скорости только в одном частном случае, когда тело двигается с различными скоростями так, что между последовательными моментами изменения (переключения) скорости проходит одинаковое время Т. Таким образом, тело двигается со скоростью v₁ в течение времени t₁=T, со скоростью v₂ в течение времени t₂=T, со скоростью v₃ в течение времени t₃=T и т.д. Если на протяжении пути скорость изменялась n раз, то пройденный путь

Время t, за которое пройден путь, составляет

Не запрещено для этого частного случая двигаться со скоростью v₀=0, т.е. делать остановки. Но время остановки должно составлять t₀ =T.

Пример 4. Вертолет пролетает без остановок равномерно и прямолинейно над пунктами А, В, С (в указанном порядке) и возвращается в А. Пункты А, В, С являются как бы вершинами треугольника. Расстояние между А и В составляет L_AB =150 км, между В и С L_BC =200 км, между С и А L_CA =100 км. Время, за которое вертолет пролетает от одного пункта до другого, составляет полчаса. Найти среднюю скорость движения вертолета на маршруте АВСА. Изменится ли средняя скорость, если L_CA =200 км и всё расстояние вертолет преодолеет за 1 ч?

Решение. 1. Находим скорость движения вертолета на каждом участке:

км/ч;

км/ч.

2. Поскольку t =0,5 ч одинаково для всех участков движения, то

км/ч.

Источник

Среднее арифметическое

Чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество.

Обозначим среднее арифметическое буквой « m ». По определению выше найдем сумму всех чисел.

Разделим полученную сумму на количество взятых чисел. У нас по условию три числа.

В итоге мы получаем формулу среднего арифметического:

Для чего нужно среднее арифметическое?

Кроме того, что его постоянно предлагают найти на уроках, нахождение среднего арифметического весьма полезно и в жизни.

Например, вы решили продавать футбольные мячи. Но так как вы новичок в этом деле, совершенно непонятно по какой цене вам продавать мячи.

Тогда вы решаете узнать, по какой цене в вашем районе уже продают футбольные мячи конкуренты. Узнаем цены в магазинах и составим таблицу.

Магазин	Цена футбольного мяча
«Спорт-товары»	290 руб.
«Adidas»	360 руб.
«Все для футбола»	310 руб.

Цены на мячи в магазинах оказались совсем разные. Какую цену для продажи футбольного мяча нам лучше выбрать?

Если выбрать самую низкую ( 290 руб.), то мы будем продавать товар себе в убыток. Если выбрать самую высокую ( 360 руб.), то покупатели не будут приобретать футбольные мячи у нас.

Нам нужна средняя цена. Здесь на помощь приходит среднее арифметическое.

Вычислим среднее арифметическое цен на футбольные мячи:

Таким образом, мы получили среднюю цену ( 320 руб.), по которой мы можем продавать футбольный мяч не слишком дёшево и не слишком дорого.

Средняя скорость движения

Со средним арифметическим тесно связано понятие средней скорости движения.

Наблюдая за движением транспорта в городе, можно заметить, что машины, то разгоняются и едут с большой скоростью, то замедляются и едут с маленькой скоростью.

Таких участков на пути следования автотранспорта бывает много. Поэтому для удобства расчётов, используют понятие средней скорости движения.

Средняя скорость движения — это весь пройденный путь разделить на всё время движения.

Рассмотрим задачу на среднюю скорость.

Задача № 1503 из учебника «Виленкин 5 класс»

Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем 1,5 ч по грунтовой дороге со скоростью 45 км/ч, наконец 0,3 ч по просёлочной дороге со скоростью 30 км/ч. Найдите среднюю скорость движения автомобиля на всём пути.

Для расчёта средней скорости движения нужно знать весь путь, пройденный автомобилем, и всё время, которое автомобиль двигался.

S₁ = 90 · 3,2 = 288 (км) — шоссе.

S₂ = 45 · 1,5 = 67,5 (км) — грунтовая дорога.

S₃ = 30 · 0,3 = 9 (км) — просёлочная дорога.

S = 288 + 67,5 + 9 = 364,5 (км) — весь путь, пройденный автомобилем.

t = 3,2 + 1,5 + 0,3 = 5 (ч) — всё время.

V_ср = 364,5 : 5 = 72,9 (км/ч) — средняя скорость движения автомобиля.

Ответ: V_ср = 72,9 (км/ч) — средняя скорость движения автомобиля.

Источник