Enter the height at which an object is being dropped into the calculator to determine the impact velocity. This calculator can also calculate the height when given the impact velocity.
- Final Velocity Calculator
- Free Fall Velocity Calculator
- Initial Velocity Calculator
- Maximum Height of a Projectile Calculator
- Angle of Impact Calculator
- Falling Force Calculator
- Impact G Force Calculator
- Average Impact Force Calculator
- Force From Height Calculator
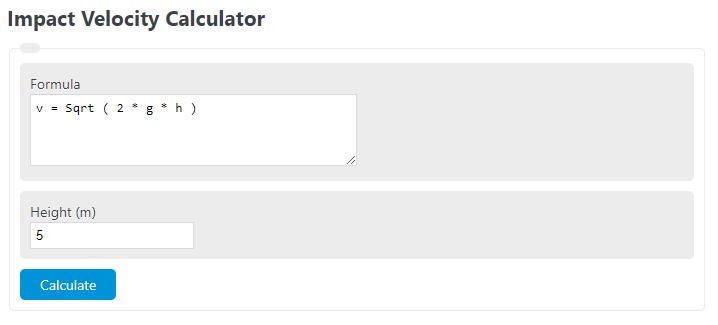
Impact Velocity Formula
The following formula is used to calculate an impact velocity.
- Where v is the impact velocity (m/s)
- g is the acceleration due to gravity (9.8 m/s^2)
- h is the height of the object (m)
To calculate impact velocity, multiply the height by 2 times the acceleration due to gravity, then take the square root of the result.
Impact Velocity Definition
An impact velocity is the total speed of an object when it makes an impact with the ground or another object after falling from a certain distance.
Impact Velocity Example
How to calculate impact velocity?
The following example goes over the necessary steps to calculate the impact velocity of a falling object given the height of the object and assuming that there is no air resistance and no other forces acting on the object.
The first step is to determine or measure the height that the object is going to be dropped from.
For this example, the height of the object is 10 meters (m).
The next and last step is to use the formula above to calculate the impact velocity:
v = Sqrt ( 2 * g * h )
v = Sqrt ( 2 * 9.81 * 10 )
v = 14.007 m/s.
FAQ
What is an impact velocity?
An impact velocity is a measure of the speed of an object when it impacts another surface. It’s most often used when analyzing objects that are dropped from a certain height.

2.1
Расчет скорости шарика до удара.
Формула
:
1=2*Sin(
i
/
2)*g*L
L
– Длинна
нити.
g
– Скорость свободного падения.
1
–
Скорость
шарика до удара.
I
– Угол
отклонения шарика.
2.2
Расчет скорости шарика после удара.
Формула
:
2=2*Sin(<
i>
/
2)*g*L
<i>
— Среднее
значение угла отскока шарика.
Производим
вычисления :
1
= 2*Sin(200/2)*9,81*0,315
= 0,605 (м/с).
2= 2*Sin(17.50/2)*
9,81*0,315
= 0,532 (м/с).
1
= 2*Sin(300/2)*9,81*0,315
= 0,905 (м/с).
2
= 2*Sin(26.50/2)*9,81*0,315
= 0,802 (м/с).
1
= 2*Sin(400/2)*9,81*0,315
= 1,197 (м/с).
2
= 2*Sin(35.50/2)*9,81*0,315
= 1,067 (м/с).
1= 2*Sin(500/2)*
9,81*0,315
= 1,479 (м/с).
2
= 2*Sin(430/2)*9,81*0,315
= 1,282 (м/с).
1
= 2*Sin(600/2)*9,81*0,315
= 1,757 (м/с).
2
= 2*Sin(500/2)*9,81*0,315
= 1,479 (м/с).
Результаты расчетов
сведем в таблицу
Таблица
5
|
|
|
|
|
|
|
|
|
0,605 |
0,905 |
1,197 |
1,479 |
1,757 |
|
|
0,532 |
0,802 |
1,067 |
1,282 |
1,479 |
3. Расчет среднего значения силы удара
Формула
:
<
F >
=
<F>
— Среднее
значение силы удара.
m – Масса
шарика.
1
—
скорость
шарика до удара.
2
— скорость
шарика после удара.
–время удара.
Производим
вычисления :
<F1>
= 0,0195*(0,605-0,532)
/
0,0000309 = 46,06 H.
<F2>
= 0,0195*(0,905-0,802)
/ 0,0000287 = 69,98 H.
<F3>
= 0,0195*(1,197-1,067)
/ 0,0000269 = 94,23 H.
<F4>
= 0,0195*(1,479-1,282)
/ 0,0000217 = 177,02 H.
<F5>
= 0,0195*(1,757-1,479)
/ 0,0000191 = 283,82 H.
4. Расчет коэффициента восстановления.
Формула
:
ε
=
2
/
1
ε
— коэффициент восстановления.
ε
1 = 0,532 / 0,605
= 0,878 ε
5 = 1,479 / 1,757
= 1,187
ε
2 = 0,802 / 0,905
= 0,886
ε
3 = 1,067
/ 1,197 = 0,891
ε
4 = 1,282 / 1,479
= 0,866
5.Расчет погрешностей прямых измерений.
5.1
Определяем стандартную погрешность
измерения угла отскока шарика.
Формула
:
SI
=
(
S/I
)2
+
(
S//2
)2.
SI
— среднеквадратичное
отклонение.
S/I
— стандартная
случайная погрешность.
S//2
= 0, 5 — стандартная
систематическая погрешность.
S/I
=
∑(
I
—
<i>)2
/
N
( N
— 1 )
N=10
количество
измерений угла.
S/1=
(180-17.50)2+(17.50-17.50)2+(170-17.50)2+(180-17.50)2+(18.50-17.50)2+(170-17.50
)2
+(17.50-17.50)2+(170-17.50)2+(180-17.50)2+(180-17.50)2
/ 10( 10-1) = 0,176;
S=
(0,
5)2+(0,176)2
= 0,530;
S/2=
(270-26.50)2+(27.50+26.50)2+(260-26.50)2+(26.50-26.50)2+(270-26.50)2+(
270-26.50)2+(26.50-26.50)2+(
270-26.50)2+(
26.50-26.50)2+(
26.50-26.50)2
/ 10( 10-1) = 0,148;
S=
(0,
5)2+(0,148)2
= 0,521;
S/3=
(350-35.50)2+(35.50-35.50)2+(35.50-35.50)2+(360-35.50)2+(
35.50-35.50)2+(35.50-35.50)2+(
350-35.50)2+
(350-35.50)2+(
350-35.50)2+(
35.50-35.50)2
/ 10( 10-1) = 0,104
S=
(0,
5)2+(0,104)2
= 0,510;
S/4=
(43-43)2+(43-43)2+(43.5-43)2+(42-43)2+
(43-43)2+(
43.5-43)2+(
42.5-43)2+
(43-43)+ (43-43)2
+( 42.5-43) / 10( 10-1) = 0,139
S=
(0,
5)2+(0,139)2
= 0,518;
S/5=
(500-500)2+(500.5-500)2+
(500-500)2+(50.50-500)2+
(50.50-500)2+
(50.50-500)2+
(510-500)2+
(500-500)2+(49.50-500)2+
(50.50-500)2
/ 10( 10-1) = 0,158;
S=
(0,
5)2+(0,158)2
= 0,524
5.2
Расчет абсолютной погрешности угла
отклонения шарика
∆i
Формула
:
∆i
=
(kn
*
S/i)2+(1/3*k*S//
2
)2
kn
= 2.3 — соответствующий
коэффициент Стьюдента;
k
=
2.0
— соответствующий
коэффициент Стьюдента;
Производим
вычисления :
∆1=
(2.3*0,176)2+
(1/3*2.0*0, 5)2=
0,524
∆2=
(2.3*0,148)2+
(1/3*2.0*0, 5)2=
0,476
∆3=
(2.3*0,104)2+
(1/3*2.0*0, 5)2=
0,410
∆4=
(2.3*0,139)2+
(1/3*2.0*0, 5)2=
0,461
∆5=
(2.3*0,158)2+
(1/3*2.0*0, 5)2=
0,493
5.2
Определяем относительную погрешность
измерения угла отскока шарика.
Формула
:
εi=
∆I
/
<i>
ε1
=
0,524
/
17,50
= 0,029;
ε2
=
0,476
/
26,50
= 0,016;
ε3
=
0,410
/
35,50
= 0,012;
ε4
= 0,461
/ 43,00
= 0,011;
ε5
= 0,493
/ 50,00
=
0,010;
5.3
Определяем относительную и абсолютную
погрешность измерения угла отклонения
шарика .
Формулы
:
∆i
=
(kn
*
S/i)2+(1/3*k*S//
2
)2
ε
i=
∆I
/
<i>
т.к.
(kn
*
S/i)2
=
0
, то
∆i
=
(1/3*k*S//
2
)2.
Производим
вычисления :
∆I
=(1/3*2.0*0.5)2
= 0,33
ε1
=
0,33/20
= 0,016;
ε2
=
0,33/30
= 0,011;
ε3
=
0,33/40
= 0,008;
ε4
=
0,33/50
= 0,007;
ε5
=
0,33/60 = 0,006;
5.4
Рассчитаем относительную погрешность
измерения времени соударения шарика.
Формула
:
SI
=
∑(
i—
<i>)2
/
N ( N — 1 )
Производим
вычисления
:
S1=10-7*
(321-309)2+(312-309)2+(304-309)2+(312-309)2+(303-309)2+(307-309)2+(315-309)2+(309-309)2+(302-309)2+(311+309)2
/ 10( 10-1) =1,8*10-7
S2=10-7*
(272-287)2+(288-287)2+(271-287)2+(297-287)2+(287-287)2+(301-279)2+(286-287)2
+(291-287)2+(300-287)2
+(279-287)2
/ 10( 10-1) =3,37*10-7
S3=10-7*
(262-269)2+(267-269)2+(269-269)2+(262-269)2+(258-269)2+(252-269)2+(261-269)2
+(243-269)2+(255-269)2+
(261-269)2
/ 10( 10-1) = 4,10*10-7
S4=10-7*
(217+217)2+(216-217)2+(208-217)2+(212-217)2+(206-217)2+(231-217)2+(214-
-217)2+
(227-217)2+(221-217)2+(211-217)2
/ 10( 10-1) = 2,71*10-7
S5=10-7*
(
191-191)2+(189-191)2+(192-191)2+(184-191)2+(190-191)2+(183-191)2+(202-
191)2+
(193-191)2+(201-191)2+(186-191)2
/ 10( 10-1) = 2,27*10-7
5.5
Определим абсолютную погрешность
измерения времени соударения шарика.
Формула
:
∆I
=
(kn*S
)2+(1/3*k*
S/)2
S
—
стандартная
случайная погрешность.
S/
=1*10-7
—
стандартная
систематическая погрешность.
Производим
вычисления :
∆1
=
10-7*(2,3*1,8)2+(1/3*2,0*1)2
= 4,14*10-7;
∆2
=
10-7*(2,3*3,37)2+(1/3*2,0*1)2
= 7,75*10-7;
∆3
=
10-7*(2,3*4,10)2+(1/3*2,0*1)2
= 9,43*10-7;
∆4
=
10-7*(2,3*2,71)2+(1/3*2,0*1)2
= 6,23*10-7;
∆5
=
10-7*(2,3*2,27)2+(1/3*2,0*1)2
= 2,28*10-7;
5.6
Определим относительную погрешность
измерения времени соударения шарика.
Формула
:
ε=
∆I
/
<i>
ε1=
4,
14*10-7
/ 309 * 10-7
= 0,013;
ε2=
7,
75*10-7
/ 287* 10-7
= 0,027;
ε3=
9,
43*10-7
/ 269 *10-7
= 0,035;
ε4=
6,
23*10-7
/ 217* 10-7
= 0,028;
ε5=
2,
28*10-7
/ 191* 10-7
= 0,012;
Соседние файлы в папке Отчёты 1 семестр
- #
- #
28.03.2015126.98 Кб47маятник максвела(1).doc
- #
- #
- #
28.03.2015560.13 Кб44Мех. удар(1).doc
- #
- #
- #
28.03.2015891.39 Кб43Мех.удар(1).doc
- #
- #
- #
Условие задачи:
Мяч массой 0,15 кг ударяется о гладкую стенку под углом 30° к ней и отскакивает без потери скорости. Найти среднюю силу, действующую на мяч со стороны стенки, если скорость мяча 10 м/с, а продолжительность удара 0,1 с.
Задача №2.1.37 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=0,15) кг, (alpha=30^circ), (upsilon=10) м/с, (Delta t=0,1) с, (F-?)
Решение задачи:
[F = frac{{Delta p}}{{Delta t}};;;;(1)]
В этой формуле (Delta p) – это изменение импульса мяча вследствие удара о стенку, (Delta t) – известное из условия время взаимодействия.
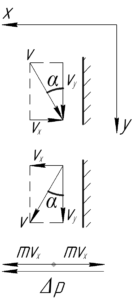
Найдем изменение импульса мяча. На рисунке изображены моменты непосредственно перед ударом и сразу после удара. Так как потерь скорости нет, то удар считается абсолютно упругим, поэтому мяч отскочит под тем же углом. Проецируем скорость мяча перед ударом и после удара на оси (x) и (y).
Видно, что по оси (y) проекции скорости (upsilon_y) равны до и после удара (upsilon cos alpha), поэтому изменения импульса мяча в этом направлении не было, а значит, в этом направлении и не действует сила.
По оси (x) модуль изменения импульса составит (смотри нижнюю часть схемы):
[Delta p = 2m{upsilon _x} = 2mupsilon sin alpha ;;;;(2)]
Подставим (2) в (1), получим решение задачи в общем виде.
[F = frac{{2mupsilon sin alpha }}{{Delta t}}]
Подставляем данные задачи в эту формулу, считаем численный ответ.
[F = frac{{2 cdot 0,15 cdot 10 cdot sin 30^circ }}{{0,1}} = 15; Н]
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.36 Металлический шарик массой 100 г падает на горизонтальную плоскость с высоты 20 см
2.1.38 Вор, масса которого вместе с добычей 125 кг, убегая, налетает на камень. Столкновение
2.1.39 Два автомобиля с одинаковыми массами m движутся со скоростями v и 2v
В мире физики скорость (v), положение (x), ускорение (a) и время (t) являются четырьмя ключевыми составляющими в решении уравнений движения. Вы можете получить ускорение, начальную скорость (v 0) и истекшее время частицы, и вам нужно будет определить окончательную скорость (v f). Возможен ряд других перестановок, применимых к бесчисленным сценариям реального мира. Эти понятия фигурируют в четырех основных уравнениях:
1. x = v 0 t + (1/2) при 2
2. v f 2 = v 0 2 + 2ax
3. v f = v 0 + при
4. х = (v 0/2 + v f / 2) (т)
Эти уравнения полезны при расчете скорости (эквивалентной скорости для настоящих целей) частицы, движущейся с постоянным ускорением в тот момент, когда она ударяется о неприступный объект, такой как земля или твердая стена. Другими словами, вы можете использовать их для расчета скорости удара или в терминах приведенных выше переменных, v f.
Шаг 1: Оцените ваши переменные
Если ваша проблема связана с тем, что объект падает из покоя под действием силы тяжести, то v 0 = 0 и a = 9, 8 м / с 2, и вам нужно знать только время t или пройденное расстояние x (см. Шаг 2). Если, с другой стороны, вы можете получить значение ускорения a для автомобиля, движущегося горизонтально на заданном расстоянии x или в течение заданного времени t, требующего решения промежуточной задачи перед определением v f (см. Шаг 3).
Шаг 2: Падающий объект
Если вы знаете, что объект, упавший с крыши, падал в течение 3, 7 секунд, как быстро он будет двигаться?
Из приведенного выше уравнения 3 вы знаете, что v f = 0 + (9, 
Если вам не дано время, но вы знаете, что объект упал на 80 метров (около 260 футов или 25 этажей), вы должны использовать вместо этого уравнение 2:
v f 2 = 0 + 2 (9, 
v f = √ 1568 = 39, 6 м / с
Вы сделали!
Шаг 3: Ускоряющаяся машина
Допустим, вы знаете, что автомобиль, который начинал с места, разгонялся со скоростью 5, 0 м / с в течение 400 метров (около четверти мили) перед тем, как проехать через большой лист бумаги, предназначенный для праздничного показа. Из приведенного выше уравнения 1
400 = 0 + (1/2) (5) t 2
400 = (2, 5) т 2
160 = т 2
t = 12, 65 секунд
Отсюда вы можете использовать уравнение 3, чтобы найти v f:
v f = 0 + (5) (12, 65)
= 63, 25 м / с
Чаевые
Всегда сначала используйте уравнение, для которого существует только одно неизвестное, которое не обязательно содержит переменную, представляющую наибольший интерес.
Как определить среднюю силу
Средняя сила – это условная величина. В случаях, когда сила, действующая на тело, меняется со временем или действие силы очень мало, то определить величину силы в каждый момент времени не представляется возможным. Поэтому в данных случаях принимают допущение, что за определенное время на тело действовала постоянная сила равная средней и рассчитывают именно ее — Fср.

Вам понадобится
- умение интегрировать
Инструкция
Пусть тело под действием некой силы F изменило свою скорость с V1 до V2 за короткий промежуток времени Δt. Ускорение данного тела будет равно a=(V2-V1)/Δt, где а, V1 и V2 – являются векторными величинами.
Подставьте данное выражение в формулу второго закона Ньютона: F=ma=m(V2-V1)/Δt=(mV2-mV1)/Δt, не забывая, что сила F – тоже векторная величина.
Запишите полученную формулу в несколько ином виде: FΔt=mΔV =Δp. Векторную величину FΔt, равную произведению силы на время ее воздействия, называют импульсом силы и измеряют в ньютонах умноженных на секунду (Н•с). А произведение массы тела на его скорость p=mV – импульсом тела или количеством движения тела. Эту векторную величину измеряют в килограммах, умноженных на метр в секунду (кг•м/с).
Т.о. второй закон Ньютона можно сформулировать иначе: импульс силы, действующей на тело равен изменению импульса тела: FΔt=Δp.
Если время воздействия силы было очень мало, например, во время удара, то среднюю силу находят так: Fср=Δp/Δt=m(V2-V1)/Δt.Пример: Мяч массой 0,26кг летел со скоростью 10м/с. После удара волейболиста, мяч увеличил скорость до 20м/с. Время удара – 0,005с. Средняя сила воздействия руки волейболиста на мяч равна в данном случае Fср=0,26•(20-10)/0,005с=520Н.
Если сила, действующая на тело, не постоянна, а меняется со временем по закону F(t), то путем интегрирования функции F(t) по времени t на промежутке от 0 до T найдите изменение импульса тела: dр=F(t)dt.
И по формуле Fср=dp/dt определите значение средней силы.Пример: Сила меняется со временем по линейному закону F=30t+2. Найдите среднюю силу воздействия за 5с. Сначала вычисляем импульс тела p=∫(30t+2)dt=15t²+2t , а затем среднюю силу: Fср=(15t²+2t)/t=15t+2=15•5+2=77Н
Видео по теме
Обратите внимание
Сила является векторной величиной. Если в результате расчетов значение Fср получилось отрицательным, это значит, что вектор силы направлен в сторону, противоположную направлению координатной оси.
Полезный совет
Не забывайте при решении задач переводить все используемые в формулах величины в СИ. Т.е. массу – в килограммы, скорость – в метры, деленные на секунду, а силу – в ньютоны.
Источники:
- Физика для углубленного изучения, Е.И. Бутиков, А.С. Кондратьев
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
