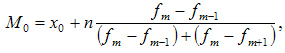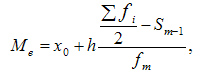Как найти среднюю сумму за год - Исправление недочетов и поиск решений вместе с Examum.ru

Для чего нужен средний заработок за год

Средний заработок за календарный год (далее – за год) – это средняя зарплата. Сведения о том, как посчитать размер среднего заработка за год, необходимы для установления сумм (ст. 114, 126, 127, 167, 178, 185 ТК РФ):

командировочных;
выходного пособия;
отпускных;
выплат при обучении с отрывом от производства;
выплат при прохождении работником курсов повышения квалификации;
оплаты труда лиц, направленных работодателем на медосмотр;
компенсации, положенной на основании ч. 1 ст. 127 ТК РФ.

Бывает, что вместо зарплаты работнику выплачивается средний заработок.

Такое возможно при следующих обстоятельствах:

ликвидация компании (ч. 1 ст. 178 ТК РФ);
сокращение штата (п. 3 постановления КС РФ «По делу о проверке» № 45-П от 19.12.2018);
зачисление сотрудника в ряды ВС РФ;
мобилизация работника в зону военных действий (п. 1 ст. 6 Закона РФ «О воинской обязанности» № 53 от 28.03.1998).

Мобилизация 2022: что делать работодателю?

21 сентября 2022 года президент России Владимир Владимирович Путин официально объявил о частичной мобилизации. Что делать если сотрудник получил повестку в военкомат? Как оплачивать такие дни? Нужно ли увольнять сотрудника в связи с призывом? Ответы на эти и другие вопросы рассмотрим в материале далее.

Подробнее

Установление расчетного периода по среднему заработку

Перед тем как высчитать средний заработок работника за год, следует иметь в виду расчетный период. Таковым является период работы за 12 месяцев, предшествующих дате расчета. Если приведенный период составляет менее 1 года, то в расчет берется период работы с первого рабочего дня.

Как вычислить средний заработок за год

При расчете среднего заработка работника в 2023 году применяется следующая формула (п. 4, 9, 10 постановления 922, ст. 139 ТК РФ):

Учет премий при подсчете среднего заработка за год имеет особенности. Как учитывают премии и вознаграждения по итогам года при расчете среднего заработка, подробно разъяснили эксперты «КонсультантПлюс». Если у вас нет доступа к справочно-правовой системе, получите пробный демодоступ и бесплатно переходите в Готовое решение.

Пример № 1: Механику Ветрову А. П. за предыдущие 12 месяцев была выплачена зарплата в размере 340 тыс. руб. Премии составили 20 тыс. руб.

Средняя зарплата Ветрова А. П. = (340 тыс. руб. + 20 тыс. руб.) / 12 месяцев = 30 тыс. руб.

В отдельных ситуациях применяется показатель среднего дневного заработка за год. Такое возможно для расчета выплаты:

отпускных – для ежегодного отпуска (ст. 115 ТК РФ);
компенсации, положенной в соответствии с ч. 1 ст. 127 ТК РФ.

Средний дневной заработок = ((Совокупный доход за год) / 12 месяцев) / 29,3. При установлении размера среднего заработка за год приведенный показатель умножается на число календарных (рабочих) дней в подлежащем оплате месяце.

Пример № 2: Механик Ветров А. П. в феврале 2022 г. был в отпуске. Его зарплата вместе с премиями за предыдущие 12 месяцев составила 360 тыс. руб. Предположим, что Ветров А. П. на протяжении последних 12 месяцев не болел. В итоге:

Средний дневной заработок Ветрова для оплаты отпуска = 360 тыс. руб. / 12 месяцев) / 29,3 = 1, 02389 тыс. руб. в день.

Как посчитать средний заработок за год по вышеприведенной формуле:

1, 02389 тыс. руб. х 30 дн. (продолжительность отпуска Ветрова А. П.) = 30, 71672 тыс. руб. Эта сумма и будет выплачена Ветрову А. П. в качестве отпускных.

Как считается средний часовой заработок за год

В отдельных ситуациях при расчетах применяется такой показатель, как средний часовой заработок. Такое возможно (п. 13 постановления 922):

при ведении организацией суммированного учета рабочего времени (ст. 104 ТК РФ);
когда при расчете размера средней зарплаты за год не устанавливается суммы по оплате отпусков, а также размер компенсации, положенной при увольнении на основании ч. 1 ст. 127 ТК РФ.

Для определения размера средней зарплаты за год приведенный показатель умножается на число часов по графику работы в периоде, подлежащем оплате.

Справка! Расчет среднего заработка за год производится и на онлайн-калькуляторе. Перед тем как посчитать размер среднего заработка за год на данном калькуляторе, необходимо ввести в поля необходимые сведения и нажать на кнопку расчета.

Как посчитать размер среднего заработка за 2 года

Перед тем как высчитать средний заработок за 2 последних года, необходимо иметь в виду, что на основании приведенного показателя осуществляется расчет соответствующих пособий (выплат) (п. 5 постановления Правительства РФ «Об утверждении» № 1540 от 11.09.2021, далее – постановления 1540):

Оплата отпуска по родам и беременности, ст. 255 ТК РФ (далее – декретного отпуска).
Оплата листа временной нетрудоспособности.
Оплата отпуска по уходу за ребенком (ст. 256 ТК РФ).

При расчете приведенных выплат работнику необходимо вычислить средний дневной заработок за 2 года (п. 12, 13 постановления 1540). Данный показатель рассчитывается по формуле:

совокупный доход за 2 последних года / (число дней за 2 предыдущих года – число дней, приходящихся на исключаемые периоды) – при расчете суммы среднего заработка за 2 года для расчета пособия по уходу за ребенком (ежемесячного), декретного;
совокупный доход за 2 предыдущих года / 730 – при установлении размера пособия по временной нетрудоспособности.

В первом случае при расчете среднего заработка за последние 2 года к исключаемым относятся периоды:

декретного отпуска;
освобождения от работы на основании ст. 170 ТК РФ, то есть с сохранением зарплаты – если такой доход не подлежал обложению страховыми взносами;
отпуска по уходу за ребенком (ст. 256 ТК РФ);
временной нетрудоспособности.

Что включается в совокупный доход при расчете среднего заработка за год

При расчете размера среднего заработка за год (за два года) учитываются все виды выплат работнику, прописанные в трудовом договоре (контракте), договоре ГПХ. К таковым относятся (п. 2 постановления 922):

зарплата;
денежное содержание (вознаграждение);
доплаты, надбавки, например, за выслугу лет;
выплаты, положенные работнику в связи с условиями труда, приведенные в приказе ФНС РФ «О введении условий оплаты» № ММ-7-5/114@ от 12.03.2009;
премии;
выплата за работу в ночное время;
выплата за работу в праздники, выходные, сверхурочную;
вознаграждения;
гонорар, постановочное (авторское) вознаграждение – если они положены сотрудникам редакций СМИ и работникам организаций искусства.

В формулу расчета суммы среднего заработка за год не включаются социальные выплаты (п. 3 постановления 922). К таковым относится, например, матпомощь или оплата проезда, услуг ЖКХ, стоимости продуктов.

Нерабочие дни при установлении среднего заработка за год

Нерабочие дни – это период, в который (п. 4, 5, 10 постановления 922):

Была проведена забастовка, из-за которой работник не имел возможности присутствовать на своем рабочем месте – при этом он не участвовал в ней.
Были оплачены дополнительные выходные – при уходе за инвалидом с детства, детьми-инвалидами.
Было начислено пособие по временной нетрудоспособности (выплата в декретном отпуске).
Был простой, но не по вине работника.
За работником сохранялся средний заработок на основании ч. 3 ст. 220 ТК РФ, кроме тридцатиминутных перерывов от работы на кормление ребенка (ст. 258 ТК РФ).

В формулу расчета суммы среднего заработка за год (в том числе на калькуляторе) не включатся и суммы, начисленные в нерабочие дни.

Дни отсутствия работника на работе в расчетном периоде

При наличии периодов отсутствия работника на работе средний дневной заработок считается по отдельной формуле (п. 10 постановления 922):

Средний дневной заработок = Совокупный доход / (29,3 × Число полностью отработанных месяцев + Х),

где

Х = (29,3 / Число дней в месяце) × Число отработанных дней в одном месяце.

Пример № 3: Механик Ветров А. П. был на больничном с 03.08.2022 по 13.08.2022. После закрытия больничного он получил выплату в размере 30 тыс. руб.

Совокупный доход за 1 год = 360 тыс. руб. – 30 тыс. руб. = 330 тыс. руб.

Количество дней = 29,3 дн. × 11 месяцев + ((29,3 дн. / 30 дн. в августе 2022) × 13 отработанных в августе дн.) = 334,7 дн.

Средняя дневная зарплата (заработок) Ветрова А. П. = 330 тыс. руб. / 334,7 дн. = 985,95 руб.

Отпускные Ветрова А. П. = 985,95 руб. × 30 дней отпуска в феврале 2023 г. = 29 578,50 руб.

Как узнать средний заработок за год – вознаграждения и премии

В случае установления размера среднего заработка за год в расчет включаются (п. 15 постановления 922):

вознаграждение за год – по итогам работы;
вознаграждение за выслугу лет – единовременное;
премии и вознаграждения, начисляемые за месяц, – в размере одной выплаты за каждый месяц и один критерий выплаты. В частности, для продавца-консультанта это может быть премия за перевыполнение плана по выручке и за привлечение новых клиентов;
квартальная премия – применяется при расчете средней зарплаты за 3 месяца (годовой бонус – за год);
вознаграждения и премии, положенные работнику более чем за месяц, – в размере части, положенной за месяц, за каждый месяц расчетного периода – если период начисления приведенных выплат больше расчетного.

Как узнать средний заработок за 2 года – вознаграждения и премии

В формулу расчета среднего заработка за 2 предыдущих года также включаются премии и вознаграждения. При этом приведенные выплаты включаются в заработок (п. 10 постановления №1540):

в размере сумм, начисленных в расчетном периоде, – премии (годовые, квартальные), вознаграждения, в том числе единовременное за выслугу лет;
того месяца, в котором были начислены премии, вознаграждения, – касается ежемесячных премий, выплачиваемых вместе с зарплатой.

Где можно посмотреть расчет среднего заработка за 2 года: постановление № 1540.

Вывод

Таким образом, знать о том, как рассчитывается средний заработок за 1 (2) года, необходимо для расчета выплат в пользу работников за неотработанное время (например, после пребывании на больничном). Этот показатель также применяется в случае установления размера отпускных и иных выплат, приведенных в ст. 114, 126, 127, 167, 178, 185 ТК РФ. Как рассчитать средний заработок за год на калькуляторе, можно узнать на приведенном в этой статье сайте.

Источник

Ситуации, при которых применяется показатель средней зарплаты
Основные правила расчёта средней зарплаты
Формула расчёта среднего заработка
Учитываемые выплаты и исключаемые периоды
Пошаговая инструкция при расчёте средней зарплаты

Ситуации, при которых применяется показатель средней зарплаты

В законодательстве в сфере трудовых отношений имеется перечень ситуаций, при которых для начисления выплаты денежных средств осуществляется расчёт среднемесячной заработной платы. Наиболее распространённые обстоятельства:

уход в отпуск (ст. 114 ТК);
компенсация за отпуск — при прекращении трудовых отношений или при превышении отпускного периода 28 дней (ст. 126, 127 ТК);
командировка (ст. 167 ТК);
выходное пособие (ст. 178 ТК);
обучение с отрывом от работы (ст. 173-176, 187 ТК).

Также существуют и менее распространённые ситуации, при которых учитывается показатель средней зарплаты, к примеру:

Когда используется	Статья ТК
Простой из-за работодателя	157
Невыполнение работы из-за работодателя	155
Перевод физлица на нижеоплачиваемую работу по медицинским показаниям	182
Медосмотр	185
Диспансеризация	185.1
Донорство	186
Приостановка функционирования компании	220
Перерыв для кормления ребёнка	258
Дополнительные выходные по уходу за детьми-инвалидами	262

Таблица 1 — Ситуации, при которых оплата производится на основании среднего заработка

Важно! Средняя зарплата определяется и в случае, если нужно заполнить справку для постановки на учёт бывшего сотрудника в качестве безработного.

Основные правила расчёта средней зарплаты

По ст. 139 ТК установлено, как рассчитать среднюю заработную плату по стандартным правилам. В первую очередь необходимо ориентироваться на основное — средняя зарплата считается по фактической зарплате и отработанному времени за 12 месяцев. Этот период берётся непосредственно до месяца, в котором считается средняя зарплата.

Формула расчёта среднего заработка

Основная формула для исчисления выглядит так:

Среднемесячная зарплата = Среднедневной заработок * Кол-во дней оплаты

Для решения вопроса, как посчитать среднюю заработную плату, принимают во внимание некоторые особенности. Главная из них заключается в том, что неодинаковые правила исчисления предусмотрены для:

отпуска и компенсации за него;
остальных ситуаций.

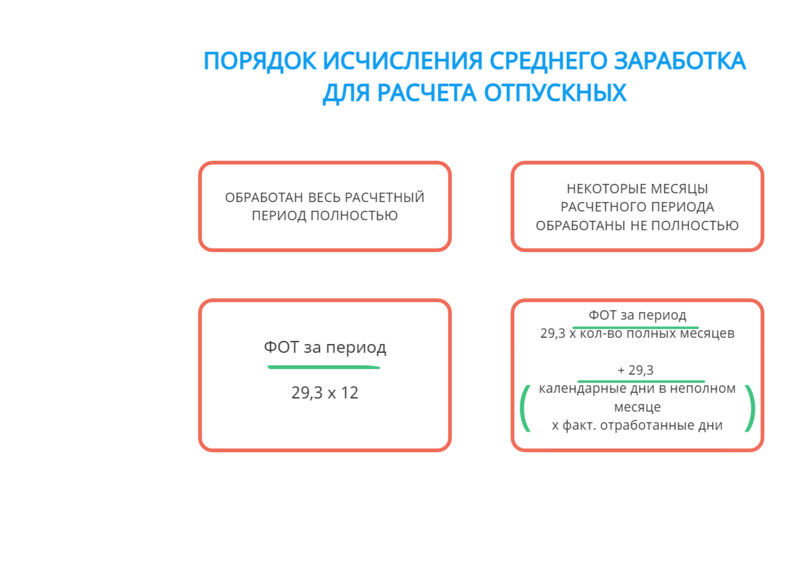
При расчёте средней зарплаты по отпускным выплатам необходимо ориентироваться на формулы:

Формулы расчёта средней зарплаты для отпуска и компенсации за него

В этом случае средний заработок — частное от деления зарплаты за расчётный период на 12 мес. и на 29,3. Когда некоторые месяцы сотрудник отработал не в полном объёме или когда есть исключаемые периоды, рассчитывать нужно делением зарплаты на показатель — (29,3 * полные мес. + 29,3 / календ. дни в мес. * отработ. дни).

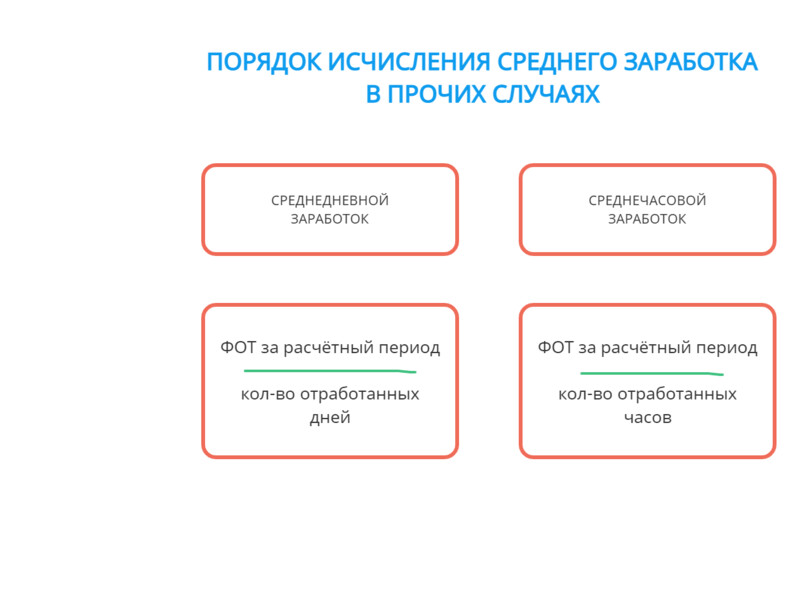
В остальных случаях формула среднемесячной заработной платы выглядит так:

Формулы расчёта средней зарплаты в иных обстоятельствах

Средний заработок исчисляется как зарплата за расчётный период (обычно 12 мес.), делённая на фактически выработанные дни. Если отработано меньше 12 мес., то расчётный период — время трудовой деятельности по факту.

Учитываемые выплаты и исключаемые периоды

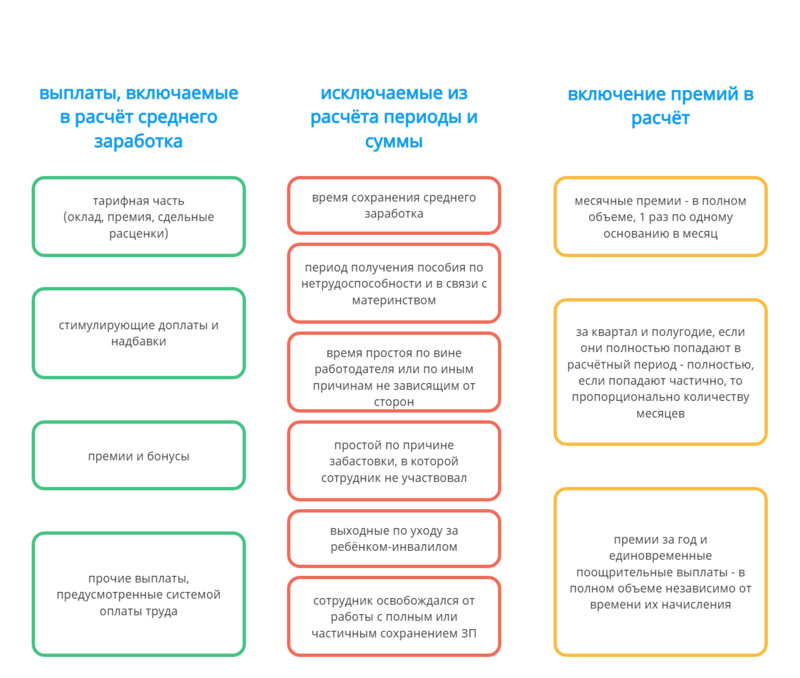
Когда есть проблема, как рассчитать среднемесячную заработную плату, нужно знать, что при исчислении берутся все выплаты по системе оплаты работы в организации. К примеру, ими являются:

зарплата в любой форме;
стимулирующие надбавки;
премии и другие вознаграждения;
иные выплаты по профессиональной деятельности.

В расчёте не применяются выплаты, имеющие социальную направленность, к примеру, матпомощь, компенсация проезда или питания, оплата коммунальных платежей и т.д.

Также из расчёта убираются периоды, к которым относятся:

период сохранения за человеком среднего заработка;
болезнь;
декрет;
простой из-за работодателя или форс-мажора;
забастовка, в которой человек не принимал участия, но из-за этого не работал;
выходные по уходу за ребёнком-инвалидом и др.

Учитываемые выплаты и исключаемые периоды

Пошаговая инструкция при расчёте средней зарплаты

Для решения задачи о том, как рассчитывается средняя заработная плата, воспользуйтесь такой пошаговой инструкцией.

Шаг 1 — Определить период, который используется для расчёта

hidden>

Расчётный период — 12 календарных месяцев до месяца, в котором рассчитывается выплата. К примеру, сотрудник идёт в отпуск 21 февраля 2022 года. Соответственно, нужно брать расчётный период с 1 февраля 2021 года по 31 января 2022 года.

Такая ситуация наблюдается и при расторжении трудовых отношений, когда нужно рассчитать компенсацию за неиспользованный отпуск. Если работник будет увольняться 21 февраля 2022 года, расчётный период будет аналогичный, как и при указанном выше отпуске. Однако здесь есть исключение: если день расторжения трудового договора приходится на последний календарный день месяца, тогда именно этот месяц нужно включать в расчёт. К примеру, увольнение 28 февраля 2022 года, тогда период — с 1 марта 2021 года по 28 февраля 2022 года.

Шаг 2 — Установить исключаемые периоды

hidden>

Ранее мы указывали, какие периоды не нужно использовать при расчёте. Соответственно, если за них были какие-то выплаты, их также не надо учитывать.

Например, сотрудник идёт в отпуск 21 февраля 2022 года. В 2021 году он с 1 по 30 сентября был на больничном. Соответственно, из расчёта нужно полностью исключить сентябрь и выплату по листку нетрудоспособности.

При этом нужно учесть особые ситуации:

сотрудник отработал меньше 12 месяцев — началом периода считается месяц заключения трудового договора;
за расчётный период нет заработка — для исчисления нужно брать предшествующий период;
за расчётный период нет заработка, но он есть в месяце, в котором рассчитывается выплата — для расчёта берутся суммы, начисленные в этом месяце;
нет фактически отработанного расчётного периода и начисленных сумм — средняя зарплата определяется по размеру оклада.

Шаг 3 — Определить заработок для расчёта средней зарплаты

hidden>

Далее по правилам, как рассчитать среднюю зарплату, — нужно за установленный период взять все начисленные выплаты, касающиеся трудовых отношений. При этом не нужно учитывать выплаты, имеющие социальную направленность, к примеру, больничное пособие, оплачиваемые дни по уходу за ребёнком-инвалидом и др.

Также в расчете не учитываются премии, которые являются непроизводственными, например, в честь юбилея сотрудника. А если премия выплачена по результатам деятельности, то её в расчёт нужно принимать обязательно.

Шаг 4 — Рассчитать среднедневной или среднечасовой заработок

hidden>

Формулы для расчёта этих показателей представлены выше.

К примеру, как рассчитать среднюю заработную плату за год для оплаты отпуска? Для этого нужно взять всю зарплату за период, определённый на первом шаге, убрать из него периоды из второго шага, посчитать выплаты из третьего шага.

Допустим, сотрудник идёт в отпуск 21 февраля 2022 года. Берётся период с 1 февраля 2021 года по 31 января 2022 года. В каждом месяце ему начислялась зарплата — 50 тыс. руб. Соответственно, общая сумма заработка — 600 тыс. руб.

Далее эту выплату нужно разделить на 12 месяцев:

600 000 / 12 = 50 тыс. руб. в мес.

Затем результат делится на 29,3 (среднее число дней в месяце):

50 000 / 29,3 = 1 706,48 руб. Это будет среднедневной заработок.

Также можно посчитать и среднечасовой заработок, разделив результат на количество часов в дне работы (стандартно — 8 часов). Или полученный за период заработок разделить на количество отработанных по факту часов.

Шаг 5 — Определить выплату по среднему заработку

hidden>

На последнем этапе требуется определить, какая выплата положена сотруднику, если она определяется по среднему.

Для этого нужно полученный результат по среднедневному или среднечасовом заработку умножить на количество дней или часов. Допустим, в рассмотренном выше примере работник уходит в отпуск на 25 дней. Тогда ему положены отпускные:

1 706,48 руб. * 25 дн. = 42 662 руб.

Из них нужно удержать НДФЛ:

42 662 руб. * 13% = 5 546 руб.

Итого на руки сотрудник получит:

42 662 — 5 546 = 37 116 руб.

При вопросе, как посчитать средний заработок за год, нужно учесть такие важные моменты.

Если в расчётном периоде произведено повышение зарплаты, тогда проиндексировать требуется все выплаты до повышения. Коэффициент индексирования — частное от деления новой ставки или оклада на старую ставку или оклад во всех 12-ти месяцах.

Когда повышение было после расчётного периода, но до даты, на которую считается средняя зарплата, тогда индексируется посчитанный средний заработок. Применяется коэффициент, рассчитанный как частное от деления нового размера оплаты труда на старый.

Если повышение было в периоде, для оплаты которого исчислялся средний заработок, тогда выплату нужно индексировать, но с даты этого повышения и до завершения периода. Для этого используется коэффициент, рассчитанный способом, указанным в предыдущем случае.

Источник

Что такое средняя величина мы уже разобрали вот здесь. Сейчас поговорим о том, как рассчитывать среднюю величину.
В классическом виде общая теория статистики предлагает нам один вариант правил выбора средней величины.
Сначала необходимо составить правильно логическую формулу для расчета средней величины (ЛФС). Для каждой средней величины всегда есть только одна логическая формула ее расчета, поэтому ошибиться тут трудно. Но всегда надо помнить, что в числителе (это то, что сверху дроби) сумма всех явлений, а в знаменателе (то, что внизу дроби) общее количество элементов.

После того как составлена логическая формула можно пользоваться правилами (для простоты понимания упростим их и сократим):
1. Если в исходных данных (определяем по частоте) представлен знаменатель логической формулы, то расчет проводим по формуле средней арифметической взвешенной.
2. Если в исходных данных представлен числитель логической формулы, то расчет ведем по формуле средней гармонической взвешенной.
3. Если в задаче представлены сразу и числитель и знаменатель логической формулы (такое бывает редко), то расчет проводим по этой формуле или по формуле средней арифметической простой.
Это классическое представление о выборе верной формулы расчета средней величины. Далее представим последовательность действий при решении задач на расчет средней величины.

Алгоритм решения задач на расчет средней величины

А. Определяем способ расчета средней величины – простой или взвешенный. Если данные представлены в таблице то используем взвешенный способ, если данные представлены простым перечислением, то используем простой способ расчета.

Б. Определяем или расставляем условные обозначения – x – варианта, f – частота. Варианта это то, для какого явления требуется найти среднюю величину. Оставшиеся данные в таблице будут частотой.

В. Определяем форму расчета средней величины – арифметическая или гармоническая. Определение проводится по колонке частот. Арифметическая форма используется, если частоты заданы явным количеством (условно к ним можно подставить слово штук, количество элементов «штук»). Гармоническая форма используется, если частоты заданы не явным количеством, а сложным показателем (произведением осредняемой величины и частоты).

Самое сложное, это догадаться, где и какое количество задано, особенно неопытному в таких делах студенту. В такой ситуации можно воспользоваться одним из предлагаемых далее способов. Для некоторых задач (экономических) подходит наработанное годами практики утверждение (пункт В.1). В других же ситуациях придется пользоваться пунктом В.2.

В.1 Если частота задана в денежных единицах (в рублях), то используется для расчета средняя гармоническая, такое утверждение верно всегда, если выявленная частота задана в деньгах, в других ситуациях это правило не действует.

В.2 Воспользоваться правилами выбора средней величины указанными выше в этой статье. Если частота задана знаменателем логической формулы расчета средней величины, то рассчитываем по средней арифметической форме, если частота задана числителем логической формулы расчета средней величины, то рассчитываем по средней гармонической форме.

Рассмотрим на примерах использование данного алгоритма.

Задача 1. Рассчитать средний размер пенсии, если известны пенсии 12 пенсионеров – 8500, 7900, 11200, 9900, 8800, 8700, 9100, 9500, 7500, 8400, 10400, 10600 рублей.

А. Так как данные представлены в строчку то используем простой способ расчета.

Б. В. Имеем только данные по величине пенсий, именно они и будут нашей вариантой – х. Данные представлены простым количеством (12 человек), для расчета используем среднюю арифметическую простую.

Средний размер пенсии пенсионера составляет 9208,3 рубля.

Задача 2. Рассчитать средний размер детских выплат по следующим данным

А. Так как данные представлены в таблице то для расчета используем взвешенную форму.

Б. Так как требуется найти средний размер выплаты на одного ребенка, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.

В. Частота (число детей) задана явным количеством (можно подставить слово штук детей, с точки зрения русского языка неверное словосочетание, но, по сути, очень удобно проверять), значит, для расчета используется средняя арифметическая взвешенная.

Эту же задачу модно решить не формульным способом, а табличным, то есть занести все данные промежуточных расчетов в таблицу.

В результате все, что нужно теперь сделать, это разделить два итоговых данных в правильно порядке.

Средний размер выплаты на одного ребенка в месяц составил 1910 рублей.

Задача 3. Рассчитать среднюю себестоимость единицы изделия

А. Так как данные представлены в таблице то для расчета используем взвешенную форму.

Б. Так как требуется найти среднюю себестоимость единицы изделия, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.

В. Частота (себестоимость выпуска) задана неявным количеством (частота задана в рублях пункт алгоритма В1), значит, для расчета используется средняя гармоническая взвешенная. Вообще же, по сути, себестоимость выпуска это сложный показатель, который получается перемножение себестоимости единицы изделия на количество таких изделий, вот это и есть суть средней гармонической величины.

Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо себестоимости выпуска стояло число изделий с соответствующей себестоимостью.

Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 410 (120+80+210) это и есть общее количество выпущенных изделий.

Средняя себестоимость единицы изделия составила 314,4 рубля.

Задача 4. Рассчитать среднюю число пропусков одного студента

А. Так как данные представлены в таблице то для расчета используем взвешенную форму.

В. Частота (общее число пропусков) задана неявным количеством (это произведение двух показателей числа пропусков и числа студентов, имеющих такое количество пропусков), значит, для расчета используется средняя гармоническая взвешенная. Будем использовать пункт алгоритма В2.

Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо общего числа пропусков стояло число студентов.

Составляем логическую формулу расчета среднего числа пропусков одного студента.

Частота по условию задачи Общее число пропусков. В логической формуле этот показатель находится в числителе, а значит, используем формулу средней гармонической.

Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 31 (18+8+5) это и есть общее количество студентов.

Среднее число пропусков одного студента 13,8 дня.

Может еще поучимся? Загляни сюда!

Источник

Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.

Смысл коэффициента

Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:

Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.

Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.

Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.

Подсчет среднего арифметического

Формула для вычислений предельно проста:

P = (a1 + a2 + … an) / n,

где an – значение величины, n – общее количество значений.

Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.

К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.

Как считать средние для разнородных данных

В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.

Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.

Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.

Рассмотрим пару примеров

Расчет средней оценки

Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:

(3 + 3 + 5 + 4) / 4 = 3,75

Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.

Расчет съеденных конфет

Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.

Заключение

Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.

Источник

Средняя зарплата… Средняя продолжительность жизни… Практически каждый день мы с вами слышим эти словосочетания, используемые для описания множества одним единственным числом. Но как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека.

В чем проблема?

Под средним значением чаще всего подразумевается среднее арифметическое, которое очень сильно варьируется под воздействием единичных фактов или событий. И вы не получите реального представления о том, как именно распределены значения, которые вы изучаете.

Давайте обратимся к классическому примеру со средней зарплатой.

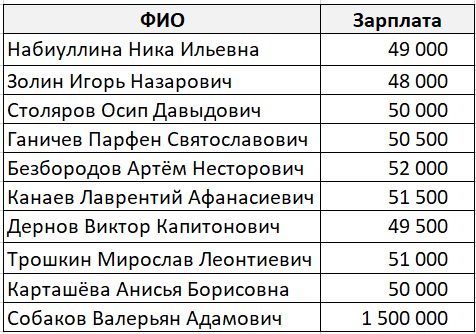
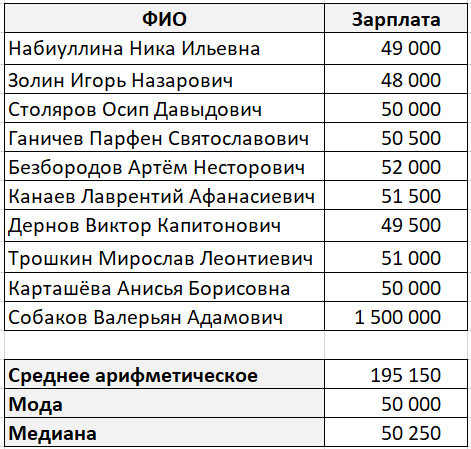
В какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).

Средним значением в данном случае будет 195 150 рублей, что согласитесь, неправильно.

Какие способы вычисления среднего бывают?

Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.

Формула:

x– среднее арифметическое;
x_n– конкретное значение;
n – количество значений.

Плюсы:

Хорошо работает при нормальном распределении значений в выборке;
Легко вычислить;
Интуитивно понятно.

Минусы:

Не дает реального представления о распределении значений;
Неустойчивая величина легко поддающаяся выбросам (как в случае с генеральным директором).

Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.

Формула:

M₀– мода;
x₀– нижняя граница интервала, который содержит моду;
n – величина интервала;
f_m– частота (сколько раз в ряду встречается то или иное значение);
f_m-1 – частота интервала предшествующего модальному;
f_m+1 – частота интервала следующего за модальным.

Плюсы:

Прекрасно подходит для получения представления об общественном мнении;
Хорошо подходит для нечисловых данных (цвета сезона, хиты продаж, рейтинги);
Проста для понимания.

Минусы:

Моды может просто не быть (нет повторов);
Мод может быть несколько (многомодальное распределение).

Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.

Формула:

M_e – медиана;
x₀– нижняя граница интервала, который содержит медиану;
h – величина интервала;
f _i– частота (сколько раз в ряду встречается то или иное значение);
S_m-1 – сумма частот интервалов предшествующих медианному;
f_m – число значений в медианном интервале (его частота).

Плюсы:

Дает самую реалистичную и репрезентативную оценку;
Устойчива к выбросам.

Минусы:

Сложнее вычислить, так как перед вычислением выборку нужно упорядочить.

Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).

А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:

СРЗНАЧ(число1;[число2];…) — функция для определения среднего арифметического;
МОДА.ОДН(число1;[число2];...) — функция моды (в более старых версиях Excel использовалась МОДА(число1;[число2];...));
МЕДИАНА(число1;[число2];...) — функция для поиска медианы.

И вот какие значения у нас получились:

В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.

Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.

Вычисляем среднее арифметическое на SQL

Тут все достаточно просто, так как в SQL предусмотрена специальная агрегатная функция AVG.

И чтобы ее использовать достаточно написать вот такой запрос:

/* Здесь и далее salary - столбец с зарплатами, а employees - таблица сотрудников в нашей базе данных */

SELECT AVG(salary) AS 'Средняя зарплата'
FROM employees

Вычисляем моду на SQL

В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.

Напишем запрос:

/* WITH TIES необходимо добавлять к TOP() если множество многомодально, то есть у множества несколько мод */
SELECT TOP(1) WITH TIES salary AS 'Мода зарплаты'
FROM employees
GROUP BY salary
ORDER BY COUNT(*) DESC

Вычисляем медиану на SQL

Как и в случае с модой, в SQL нет встроенной функции для вычисления медианы, зато есть универсальная функция для вычисления процентилей PERCENTILE_CONT.

Выглядит все это так:

/* В данном случае процентиль 0.5 и будет являться медианой */

SELECT TOP(1) PERCENTILE_CONT(0.5)
       WITHIN GROUP (ORDER BY salary)
       OVER() AS 'Медианная зарплата'
FROM employees

Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.

Какой способ все-таки использовать?

Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.

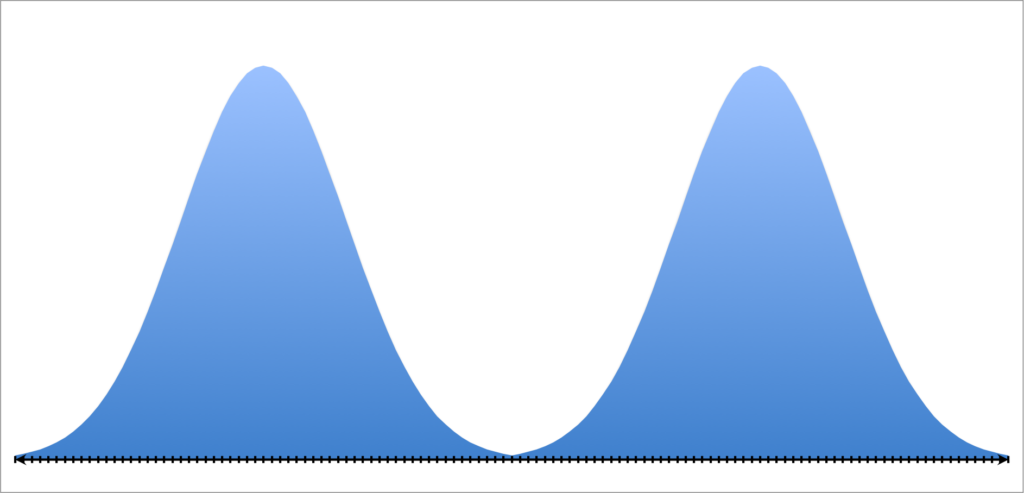
Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:

На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при голосовании на выборах.

В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.

А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.

Вывод:

При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.

Окончательный выбор меры центральной тенденции всегда лежит на аналитике.

Полезные ссылки:

SQL и теория вероятностей (YouTube)
Анализ нормальности распределения данных (YouTube)
Меры центральной тенденции

Об авторе
Свежие записи

Источник