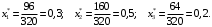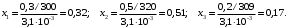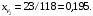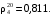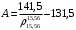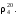Таблица
1.3 – Содержание узких фракций в
пономаревской нефти
|
Номер фракции |
Пределы |
Выход, |
|
|
суммарный |
отдельной |
||
|
0 |
до |
1,9 |
— |
|
1 |
нк-60* |
5,0 |
5,0 |
|
2 |
60-100 |
10,4 |
5,4 |
|
3 |
100-150 |
18,0 |
7,6 |
|
4 |
150-200 |
26,8 |
8,8 |
|
5 |
200-250 |
36,6 |
9,8 |
|
6 |
250-300 |
46,2 |
9,6 |
|
7 |
300-350 |
55,5 |
9,3 |
|
8 |
350-400 |
63,8 |
8,3 |
|
9 |
400-450 |
70,0 |
6,2 |
|
10 |
450-500 |
76,2 |
6,2 |
|
11 |
500 |
100 |
23,8 |
|
* |
Таблица
1.4 – Содержание узких фракций в
тархановской нефти
|
Номер фракции |
Пределы |
Выход, |
|
|
суммарный |
отдельной |
||
|
1 |
2 |
3 |
4 |
|
0 |
до |
0 |
— |
|
1 |
нк-60* |
1,5 |
1,5 |
|
2 |
60-100 |
5,0 |
3,5 |
|
3 |
100-150 |
10,2 |
5,2 |
|
4 |
150-200 |
16,0 |
5,8 |
|
5 |
200-250 |
22,4 |
6,4 |
|
6 |
250-300 |
29,6 |
7,2 |
|
7 |
300-350 |
37,0 |
7,4 |
Продолжение таблицы 1.4
|
1 |
2 |
3 |
4 |
|
8 |
350-400 |
44,5 |
7,5 |
|
9 |
400-450 |
51,5 |
7,0 |
|
10 |
450-500 |
56,3 |
4,8 |
|
11 |
500+ |
100 |
43,7 |
|
* |
Содержание фракций в % масс.
(асм)
в смеси нефтей рассчитывается по формуле:
асм =
а1 ∙
в1 +
а2 ∙
в2 ,
где а1,
а2 –
содержание одноименных фракций в каждой
нефти, % масс.;
в1,
в2 –
массовая доля нефтей в смеси.
Содержание газа в смеси:
1,9 ∙ 0,6 + 0,0 ∙ 0,4 = 1,14 %
масс.
Содержание фракции нк-60 °С
в смеси:
5,0 ∙ 0,6 + 1,5 ∙ 0,4 = 3,6 %
масс.
Содержание фракции 60-100 °С
в смеси:
5,4 ∙ 0,6 + 3,5 ∙ 0,4 = 4,64 % масс.
Содержание фракции 100-150 °С
в смеси:
7,6 ∙ 0,6 + 5,2 ∙ 0,4 = 6,64 % масс.
Содержание фракции 150-200 °С
в смеси:
8,8 ∙ 0,6 + 5,8 ∙ 0,4 = 7,6 % масс.
Содержание фракции 200-250 °С
в смеси:
9,8 ∙ 0,6 + 6,4 ∙ 0,4 = 8,44 % масс.
Содержание фракции 250-300 °С
в смеси:
9,6 ∙ 0,6 + 7,2 ∙ 0,4 = 8,64 % масс.
Содержание фракции 300-350 °С
в смеси:
9,3 ∙ 0,6 + 7,4 ∙ 0,4 = 8,54 % масс.
Содержание фракции 350-400
°С
в смеси:
8,3 ∙ 0,6 + 7,5 ∙ 0,4 = 7,98 % масс.
Содержание фракции 400-450 °С
в смеси:
6,2 ∙ 0,6 + 7,0 ∙ 0,4 = 6,52 % масс.
Содержание фракции 450-500 °С
в смеси:
6,2 ∙ 0,6 + 4,8 ∙ 0,4 = 5,64 % масс.
Содержание фракции 500 °С+
в смеси:
23,8 ∙ 0,6 + 43,7 ∙ 0,4 = 31,76 % масс.
Содержание узких фракций в
смеси нефтей приведено в таблице 1.5.
Кроме того, рассчитываются значения
средних ординат для каждой фракции,
которые понадобятся в дальнейшем для
построения кривых плотностей и молярных
масс.
Средние ординаты фракций
рассчитываются по формуле:
Хср = (ао + аƩ)
/ 2,
где ао,аƩ
– суммарные
выходы, соответствующие началу кипения
и концу кипения каждой
фракции.
Расчет и значения средних
ординат приведены в таблице 1.5.
Таблица 1.5 – Содержание узких
фракций в смеси нефтей
|
Номер фракции |
Пределы выкипания |
|
|
|
Суммарный |
Средняя |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
до |
1,9 |
0 |
1,14 |
— |
— |
|
1 |
нк-60* |
5,0 |
1,5 |
3,6 |
3,6 |
(0+3,6)/2=1,8 |
|
2 |
60-100 |
5,4 |
3,5 |
4,64 |
8,24 |
(3,6+8,24)/2=5,92 |
|
3 |
100-150 |
7,6 |
5,2 |
6,64 |
14,88 |
(8,24+14,88)/2=11,56 |
|
4 |
150-200 |
8,8 |
5,8 |
7,6 |
22,48 |
(14,88+22,48)/2=18,68 |
|
5 |
200-250 |
9,8 |
6,4 |
8,44 |
30,92 |
(22,48+30,92)/2=26,7 |
|
6 |
250-300 |
9,6 |
7,2 |
8,64 |
39,56 |
(30,92+39,56)/2=35,24 |
|
7 |
300-350 |
9,3 |
7,4 |
8,54 |
48,1 |
(39,56+48,1)/2=43,83 |
|
8 |
350-400 |
8,3 |
7,5 |
7,98 |
56,08 |
(48,1+56,08)/2=52,09 |
|
9 |
400-450 |
6,2 |
7,0 |
6,52 |
62,6 |
(56,08+62,6)/2=59,34 |
Продолжение таблицы 1.5
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
10 |
450-500 |
6,2 |
4,8 |
5,64 |
68,24 |
(62,6+68,24)/2=65,42 |
|
11 |
500+ |
23,8 |
43,7 |
31,76 |
100 |
(68,24+100)/2=84,12 |
|
*в |
Рисунок 1.1 – К расчету средней
температуры кипения остатка
Среднюю температуру
кипения остатка (toст)
можно рассчитать,
используя
подобные треугольники
ABC и
ADE.
Для данного случая AB
= 68,24 – 62,6 = 5,64; AD = 84,12 –
62,6 = 21,52

отсюда 5,64 ⋅
х = (21,52 – 5,64) ⋅
50, х = 141.
tост.=
500 + х = 500 + 141 = 641 °С
Рисунок 1.2 – К расчету начала
кипения смеси нефтей
Начало кипения смеси нефтей
определяется пересечением луча,
проведенного через точки [1,14 %; 28 °С]
и [3,6 %; 60 °С]
с осью ординат.
Начало кипения нефти (tнк)
можно рассчитать, используя подобные
треугольники ABC и ADE.

Для
нашего
случая AC
= 1,14
(выход
газа);
AE = 3,6 (см.
таблицу 1.5);
BC = x; DE
= x
+ (60 – 28)
= x
+ 32.

отсюда 1,14 ⋅
х + 1,14 ⋅
32 = 3,6 ⋅
х;
х =
= 15
tнк =
28 – х = 28 – 15 = 13 °С
Среднюю
температуру кипения фракции находим
как среднее арифметическое:
tср
=
(tнк
+
tкк)
/ 2,
где tнк
и tкк
–
температура начала и конца кипения
фракции соответственно.
Средняя
температура кипения фракции нк-60
°С:
tср1
=
(13 + 60) / 2 = 37 °С
Средняя
температура кипения фракции 60-100
°С:
tср2
=
(60 + 100) / 2 = 80 °С
Средняя
температура кипения фракции 100-150
°С:
tср3
=
(100 + 150) / 2 = 125 °С
Средняя
температура кипения фракции 150-200
°С:
tср4
=
(150 + 200) / 2 = 175 °С
Средняя
температура кипения фракции 200-250
°С:
tср5
=
(200 + 250) / 2 = 225 °С
Средняя
температура кипения фракции 250-300
°С:
tср6
=
(250 + 300) / 2 = 275 °С
Средняя
температура кипения фракции 300-350
°С:
tср7
=
(300 + 350) / 2 = 325 °С
Средняя
температура кипения фракции 350-400
°С:
tср8
=
(350 + 400) / 2 = 375 °С
Средняя
температура кипения фракции 400-450
°С:
tср9
=
(400 + 450) / 2 = 425 °С
Средняя
температура кипения фракции 450-500
°С:
tср10
=
(450 + 500) / 2 = 475 °С
По формуле Воинова рассчитываются
значения молярной массы фракций:
Мi
= 60 + 0,3 ⋅
+ 0,001⋅
где
– средняя температура кипения фракции.
Молярная масса фракции нк-60
°С:
М1 =
60 + 0,3 ⋅
37 + 0,001 ⋅
372
= 72 кг/кмоль
Молярная масса фракции 60-100
°С:
М2 =
60 + 0,3 ⋅
80 + 0,001 ⋅
802 =
90 кг/кмоль
Молярная масса фракции 100-150
°С:
М3 =
60 + 0,3 ⋅
125 + 0,001 ⋅
1252
= 113 кг/кмоль
Молярная масса фракции 150-200
°С:
М4 =
60 + 0,3 ⋅
175 + 0,001 ⋅
1752
= 143 кг/кмоль
Молярная масса фракции 200-250
°С:
М5 =
60 + 0,3 ⋅
225 + 0,001 ⋅
2252
= 178 кг/кмоль
Молярная масса фракции 250-300
°С:
М6 =
60 + 0,3 ⋅
275 + 0,001 ⋅
2752
= 218 кг/кмоль
Молярная масса фракции 300-350
°С:
М7 =
60 + 0,3 ⋅
325 + 0,001 ⋅
3252
= 263 кг/кмоль
Молярная масса фракции 350-400
°С:
М8 =
60 + 0,3 ⋅
375 + 0,001 ⋅
3752
= 313 кг/кмоль
Молярная масса фракции 400-450
°С:
М9 =
60 + 0,3 ⋅
425 + 0,001 ⋅
4252
= 368 кг/кмоль
Молярная масса фракции 450-500
°С:
М10 =
60 + 0,3 ⋅
475 + 0,001 ⋅
4752
= 428 кг/кмоль
Молярная масса фракции 500
°С+:
М11 =
60 + 0,3 ⋅
641 + 0,001 ⋅
6412
= 663 кг/кмоль
Плотность
дистиллятных фракций (при атмосферно-вакуумной
перегонке нефти – это фракции, выкипающие
до 500 °С)
рассчитывается по формуле:


(0,58 + 0,12 ⋅
(Хср)1/3),
где
– относительная плотность смеси нефтей;
= 0,6 ⋅
0,8416 + 0,4 ⋅
0,8795 = 0,8568
Хср –
средняя ордината фракций (см. таблицу
1.5).
Относительная плотность
фракции нк-60 °С:
= 0,8568 ⋅
(0,58 + 0,12 ⋅
(1,8)1/3)
= 0,622
Относительная плотность
фракции 60-100 °С:
= 0,8568 ⋅
(0,58 + 0,12 ⋅
(5,92)1/3)
= 0,683
Относительная плотность
фракции 100-150 °С:
= 0,8568 ⋅
(0,58 + 0,12 ⋅
(11,56)1/3)
= 0,730
Относительная плотность
фракции 150-200 °С:
= 0,8568 ⋅
(0,58 + 0,12 ⋅
(18,68)1/3)
= 0,770
Относительная плотность
фракции 200-250 °С:
= 0,8568 ⋅
(0,58 + 0,12 ⋅
(26,7)1/3)
= 0,804
Относительная плотность
фракции 250-300 °С:
= 0,8568 ⋅
(0,58 + 0,12 ⋅
(35,24)1/3)
= 0,834
Относительная плотность
фракции 300-350 °С:
= 0,8568 ⋅
(0,58 + 0,12 ⋅
(43,83)1/3)
= 0,860
Относительная плотность
фракции 350-400 °С:
= 0,8568 ⋅
(0,58 + 0,12 ⋅
(52,09)1/3)
= 0,881
Относительная плотность
фракции 400-450 °С:
= 0,8568 ⋅
(0,58 + 0,12 ⋅
(59,34)1/3)
= 0,898
Относительная плотность
фракции 450-500 °С:
= 0,8568 ⋅
(0,58 + 0,12 ⋅
(65,42)1/3)
= 0,911
Для остатка перегонки плотность
рассчитывается по формуле:
ρост =

[1 + 0,204 ⋅
(Xсум
/ 100)0,8],
где Xсум
– суммарный отгон дистиллятов до
получения данного остатка (в нашем
случае это суммарный выход до 500 °С
= 68,24 %).
ρост =
0,8568 ⋅
[1 + 0,204 ⋅
(68,24 / 100)0,8]
= 0,986.
Все данные по характеристикам
узких фракций сводятся в таблицу 1.6.
Таблица 1.6 – Характеристика
узких фракций смесей нефтей
|
Номер |
Пределы |
Выход фракции аi,% |
ti |
|
Мi |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
0 |
до |
1,14 |
— |
— |
— |
|
1 |
нк-60* |
3,6 |
37 |
0,622 |
72 |
|
2 |
60-100 |
4,64 |
80 |
0,683 |
90 |
Соседние файлы в папке ФАСХУД
- #
- #
- #
- #
- #
25.07.202062.46 Кб34с 70.xlsx
- #
Средняя температура — кипение — смесь
Cтраница 1
Средняя температура кипения смеси, плотность и средняя молекулярная масса которой совладает с аналогичными величинами для некоторого чистого компонента, не равна температуре кипения этого компонента так же, как и средняя молекулярная масса смеси, имеющей ту же ллотность и среднюю температуру кипения, что и чистый компонент, ие равна ( молекулярной массе этого компонента.
[2]
Температура устанавливается примерно равной средней температуре кипения смеси. При использовании большого количества жидкой фазы требуется применение высоких температур; повышение температуры необходимо также в случае жидкой фазы с большой удерживающей способностью.
[3]
Обычно температура хроматографической колонны поддерживается равной средней температуре кипения смеси.
[5]
С увеличением температуры Н увеличивается, а производительность максимальна при температуре, несколько более низкой, чем средняя температура кипения смеси.
[6]
При расширении пределов выкипания, но при постоянстве плотности и средней молекулярной массы, средняя мольная температура кипения дает Меньшие отклонения от температуры кипения индивидуального чистого компонента, чем средние массовая и объемная. Наименьшее отклонение от температуры кипения чистого компонента дает средняя средних температур кипения смеси, имеющей те же плотность и среднюю молекулярную массу, что и чистый компонент.
[8]
В СБОЮ очередь коэффициент распределения, сильно зависящий от температуры, уменьшается в два раза при повышении температуры на 30 С, что влечет за собой увеличение скорости перемещения компонента в два раза. В общем случае разделение может быть улучшено при снижении температуры. Температура устанавливается примерно равной средней температуре кипения смеси. При использовании большого количества жидкой фазы требуется применение высоких температур; повышение температуры необходимо также в случае жидкой фазы с большой удерживающей способностью. Выбирая температуру колонки, следует иметь в виду максимальную или минимальную рабочие температуры используемой жидкой фазы. Некоторые жидкости вследствие разложения не могут быть использованы выше определенных температур, другие же постепенно испаряются; это вызывает изменение процентного содержания жидкой фазы.
[9]
Температура в верхней части аппарата регулируется расходом холодной воды, а в нижней части силой тока, регулируемой через масляной трансформатор. Расход ВКП и НКП замеряется с помощью отградуированных емкостей и секундомера. Температура в концевой части аппарата поддерживалась равной средней температуре кипения смеси гептан-толуол, то есть 104 — 105 С.
[10]
Температура в верхней части аппарата регулируется расходом холодной воды, а в нижней части силой тока, регулируемой через масляндй трансформатор. Расход ВКП и НКП замеряется с помощью отградуированных емкостей и секундомера. Температура в концевой части аппарата поддерживалась равной средней температуре кипения смеси гептан-толуол, то есть 104 — 105 С.
[11]
Температура и верхней части аппарат регулируется расходом холодной воды, а в нижней части силой тока, регулируемой через масляный трансформатор. Расход ВКП и НКП замеряется с помощью отградуированных емкостей и секундомера. Температура в концевой части аппарата поддерживалась равной средней температуре кипения смеси гептан-толуол, то есть 104 — 105 С.
[12]
Температура испарителя должна поддерживаться постоянной, хотя и не столь тщательно, как температура колонок и детектора. Особенно это важно при использовании метода абсолютной калибровки. Температура в испарителе должна быть такой, чтобы компоненты пробы не разрушались. Обычно считают, что достаточна температура на 10 — 30 К выше температуры наиболее высококипящего компонента. В одной из работ [82] указано на улучшение эффективности колонки при поддерживании температуры испарителя на уровне в 1 5 — 2 раза превышающем среднюю температуру кипения смеси. Те же авторы рекомендуют при работе методом абсолютной калибровки стабилизировать температуру испарителя с точностью 0 5 К. По наблюдениям автора данной книги, подобная точность нужна лишь при использовании в качестве параметра пика высоты.
[13]
Страницы:
1
Подборка по базе: Анализ учебных заданий с точки зрения требований к формированию , Практическая работа №3. Задание Анализ учебных заданий с точки з, Практическая работа на тему _Анализ содержания УМК _Английский в, Сущность и характеристические особенности кибернетики Н. Винера., Исследовательская работа Распространение гриппа с точки зрения ф, Даны точки А.docx, Момент силы относительно точки.docx, «Анализ содержания и методического аппарата УМК Климанова с точк, Культура речи с точки зрения литературно-языковой нормы.docx, Анализ содержания и методического аппарата УМК с точки зрения тр
1.1 Характеристические точки кипения нефтяных фракций
Нефть и её фракции – это смесь различных углеводородов и их соединений, выкипающая в определённом интервале температур. Поэтому при расчетах пользуются понятием средней температуры кипения. В зависимости от способа усреднения различают средне-объемную (tср.об.), средне-молекулярную (средне-молярную) (tср.мол.), средне-массовую (tср.масс.), средне-кубическую (tср.куб.), средне-усредненную (tср.ус.) температуры кипения, но чаще всего используют для расчетов средне-молекулярную tср.мол. [2–5]. Расчеты средних температур кипения всегда ведутся в градусах Цельсия, однако, в дальнейших расчетах данная величина может быть выражена в градусах Кельвина.
Так как значение температуры кипения нефтяной фракции повсеместно используется для расчета прочих теплофизических свойств фракции, для упрощения часто среднюю температуру кипения определяют как среднее арифметическое начальной и конечной температур кипения.
Для смеси, состоящей из нескольких нефтяных фракций, средне-молекулярная температура кипения определяется следующим образом:
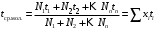
где 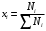
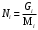
t1, t2, …, tn, (ti) – среднеарифметические значения температур кипения фракций, ºС,
N1, N2 ,…,Nn, (Ni) – моли (или % мол.) отдельных фракций,
хi – содержание отдельных фракций, мольные доли,
Мi – молекулярная масса отдельных фракций,
Gi – массы (или масс. доля %) отдельных фракций.
Если известны данные о разгонке образца нефти или узкой фракции, то приближенно среднюю температуру (tср.об) можно определить как температуру отгона 50 % образца по кривой истинных температур кипения (ИТК) или по кривой разгонки.
1.2 Характеристический фактор
Характеристический фактор К определяет химическую природу нефтепродукта. Характеристический фактор применяется для повышения точности в расчетах плотности и молекулярной массы нефтяных фракций.
Рассчитывают К по формуле
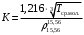
где 
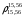
За рубежом данный параметр носит название характеристического фактора Уотсона [6].
Средние значения характеристического фактора К:
- парафинистые продукты ок. 13,0;
- нафтеновые продукты ок. 12,0;
- ароматизированные продукты ок. 10,0.
1.3 Компонентный состав
В практических расчетах состав многокомпонентной смеси выражается в долях или процентах. Соотношение между долями и процентами – 1:100.
Массовая доля 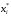
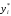
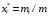
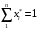
Пример.Смешали три масляные фракции в количествах: m1=96 кг; m2=160 кг; m3=64 кг. Определить массовую долю каждой фракции в смеси.
Решение. Найдем общую массу смеси
m=m1+m2+m3=96+160+64=320 кг.
Определим массовую долю каждой фракции:
Молярная (мольная) доля 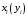
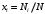
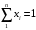
Пересчет массового состава в мольный и обратный пересчет осуществляется по формулам
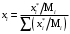
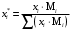
где Мi – молекулярная масса компонента.
Пример. Пересчитать массовые доли фракций 0,3; 0,5 и 0,2 в мольные, если молекулярные массы компонентов равны М1=300; М2=320; М3=390.
Решение. Определим сумму отношений массовых долей фракций к их молекулярным массам: 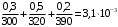
Находим молярные доли каждой фракции:
Для проверки правильности результатов суммируем мольные доли:
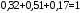
Следовательно, пересчёт выполнен верно.
Объемная доля 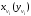

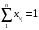
Для пересчета объемного состава в массовый и обратно необходимо знать плотность 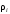
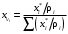
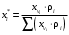
Для жидкой смеси прямой пересчет объемных долей в мольные достаточно сложен, поэтому предпочтительно его проводить с помощью массовых долей. Для газовой смеси состав, выраженный объемными и массовыми долями, одинаков.
Пример.Газовая смесь получена из 95 м3 пропана и 23 м3 этана. Плотность пропана и этана равна 2,0037 кг/м3 и 1,3560 кг/м3 соответственно. Выразить состав смеси в объемных и массовых долях.
Решение. Найдем общий объем смеси
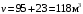
Объемные доли: пропана 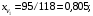
Массовые доли компонентов:
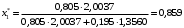
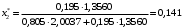
1.4 Плотность
Плотностью [1–4] называется масса единицы объема вещества (нефтепродукта, нефти). Размерность в системе СИ – кг/м3.
На практике чаще всего используют относительную плотность, представляющую собой отношение плотностей жидкого нефтепродукта и дистиллированной воды (эталонное вещество) при определенных температурах.
В России (СССР) приняты следующие стандартные температуры: нефтепродукт – 20 °С, дистиллированная вода – 4 °С (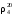

Часто в литературе наравне с буквой ρ можно встретить обозначение плотности буквой d (от англ. density — плотность).
Умножением значения относительной плотности на плотность воды при выбранной стандартной температуре можно получить плотность, выраженную в кг/м3.
Относительную плотность 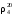
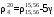
Температурную поправку рассчитывают по формуле
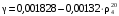
Зависимость плотности нефти и нефтепродукта от температуры основана на линейном законе (с повышением температуры их плотность снижается):
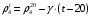
где 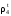
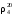
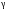
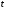
Зависимость (1.12) строго справедлива в интервале температур от 0 до 50 °С для нефтей и нефтепродуктов, содержащих относительно небольшие количества твердого парафина и ароматических углеводородов.
Значения температурной поправки даны в Прил. 1.
Плотность 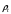
Для нефтей и дистиллятных фракций допускается расчет плотности по следующим формулам:
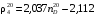
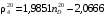
где 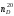
Зависимость (1.15) рекомендуется применять, если фракции парафино-нафтенового характера и имеют значения 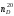
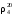
Для фракций, обогащенных ароматическими соединениями, справедлива зависимость:
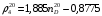
По зависимости (1.16) отклонение от экспериментальных значений составляет не более 4 %.
БашНИИНП предложена формула для расчета плотности узких нефтяных фракций
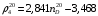
Из перечисленных формул для расчета плотности наибольшую точность даёт формула (1.17) БашНИИНП (отклонения от экспериментальных значений 0,5 %). Эта формула включена в унифицированную программу исследования нефти.
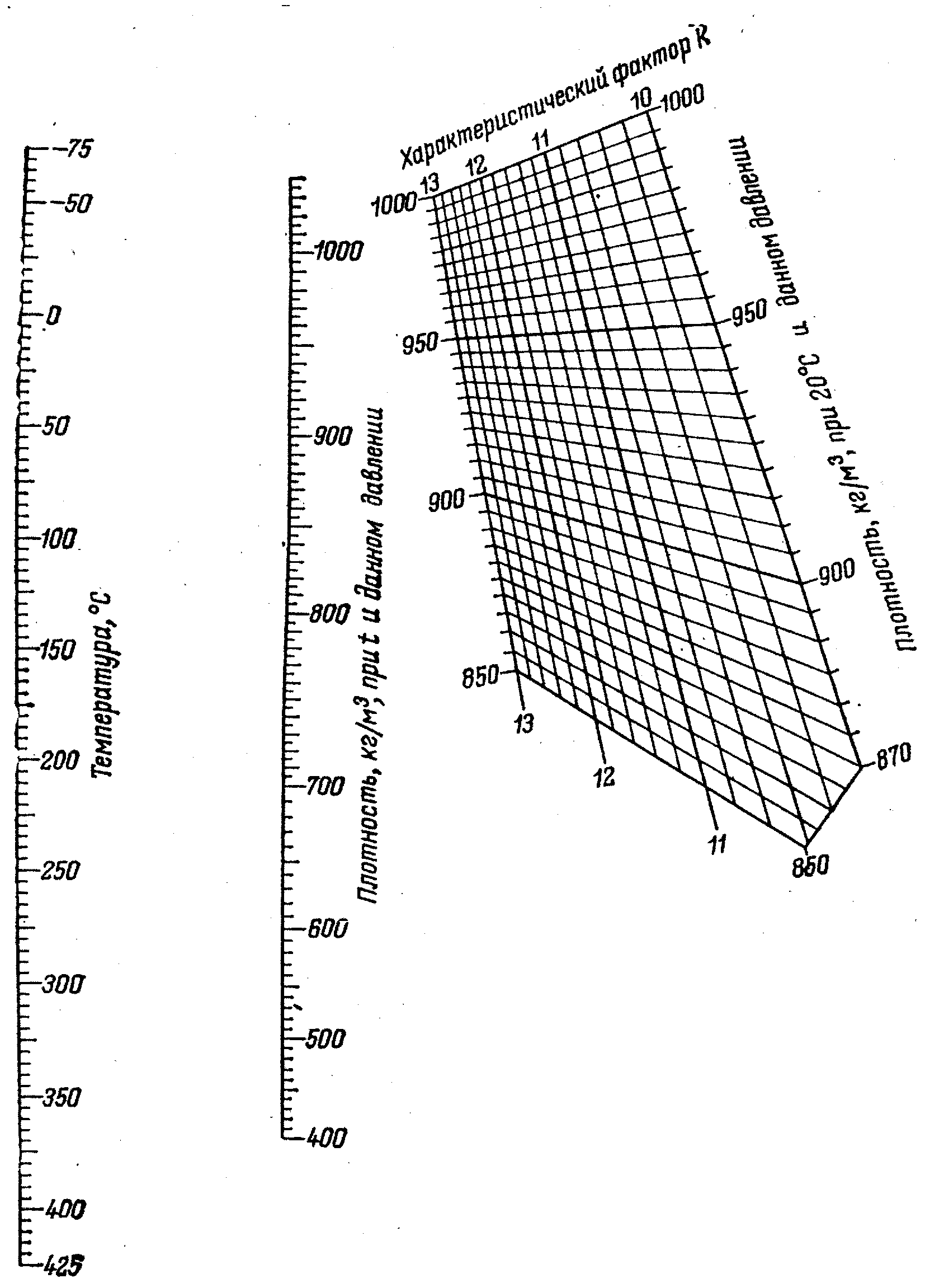
Плотность жидких нефтепродуктов при высоких температурах можно определить и по номограммам (см. Прил. 2-4). Указанные номограммы дают хорошие результаты вплоть до давлений в 1,5 МПа.
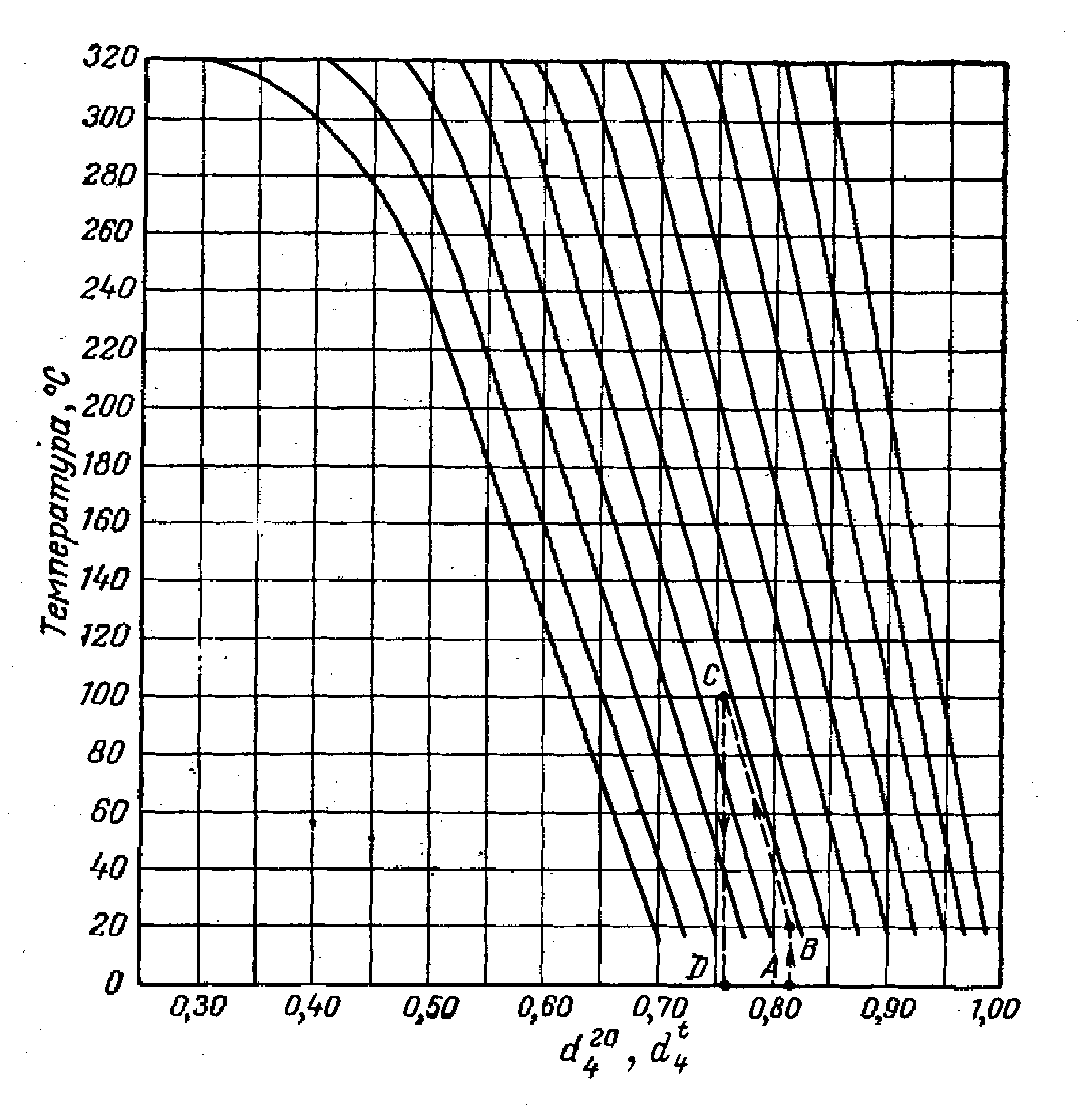
Пример.Определить относительную плотность жидкой нефтяной фракции при 100 °С, если её
Решение. Для этого воспользуемся графиком Прил. 2, который позволяет по известной плотности найти любую другую. На оси абсцисс отложим значение плотности 0,811. Из полученной точки А восстановим перпендикуляр до пересечения с горизонталью, соответствующей температуре 20 °С, при которой определена заданная плотность (точка В). Из точки В параллельно ближайшей наклонной кривой проводим линию до пересечения с горизонталью, соответствующей искомой температуре (точка С). Опустив из точки С перпендикуляр на ось абсцисс (точка Д), находим требуемую плотность 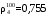
Плотность является аддитивным свойством, поэтому при смешении различных нефтепродуктов плотность смеси, в зависимости от способа выражения её состава, определяют по следующим уравнениям:
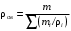
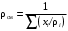
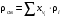
Если состав выражен в молярных долях, их следует вначале пересчитать в массовые и затем найти плотность смеси.
За рубежом плотность нефти также измеряется в градусах API (American Petroleum Institute — Американский институт нефти). Плотность Aв градусах API и относительная плотность при температуре 15,56 °C связаны уравнением:
Если плотность в градусах API больше 10, то нефть легче и плавает на поверхности воды, а если меньше 10, то тонет.
Экспериментально плотность нефти определяют стандартными методами: ареометром (нефтеденсиметром), гидростатическими весами Вестфаля-Мора и пикнометром. Наиболее точным является пикнометрический метод. Для экспрессного определения плотности используется ареометр.
Задачи
1. Определить относительную плотность нефтепродукта при 250 °С, если его 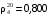
2. Нефть находится в резервуаре при температуре 12 ºС. Определить её относительную плотность в данных условиях, если 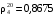
3. Определить относительную плотность смеси, состоящей из 250 кг бензина плотностью 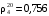
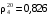
4. При перекачке нефти по нефтепроводу её температура изменяется от 8 до 15 ºС. Найти относительную плотность в начальной и конечной точках транспортировки, если её 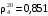
5. Определить плотность смеси следующего состава (в об. %): 25 бензина (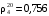
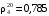
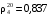
6. Нефть закачали в резервуар при температуре 15 ºС; плотность (определена денсиметром) составила 0,845. Через сутки температура нефти поднялась до 25 ºС. Определить её плотность при этой температуре.
7. Дизельная фракция 180–230 ºС на выходе из холодильника атмосферно-вакуумной трубчатки имеет температуру 30 ºС. Найти её относительную плотность при этой температуре, если 
8. Смесь состоит из 60 кг н-пентана, 50 кг н-гексана и 25 кг н-гептана. Определить среднюю плотность смеси, если для н-пентана 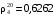
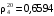
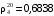
9. Самотлорская нефть имеет плотность 852,5 кг/м3 при 20 ºС. Определить её относительную плотность 
10. Плотность керосинового дистиллята (фракция 120–230 ºС) при температуре 27 ºС равна 805 кг/м3. Найти 
11. Бензиновая фракция (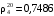
12. Средняя молекулярная температура кипения легкой нефтяной фракции равна 97 ºС, характеристический фактор – 12,3. Определить её относительную плотность
13. Температура 50 %-го отгона нефтепродукта равна 145 ºС. Найти его 
14. Мазут выходит из колонн К-2 атмосферной трубчатки (АТ) с температурой 330 ºС. Определить его плотность при этой температуре, если известны 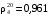
15. Для проведения испытаний приготовили пробу бензина, состоящую из 5 кг прямогонной бензиновой фракции (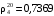
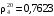
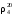
16. Ароматический концентрат представляет собой смесь, состоящую из 120 кг бензола, 75 кг толуола и 25 кг этилбензола. Найти массовый и мольный состав смеси.
17. Природный газ Северного месторождения состоит из следующих компонентов (% об.): СН4 – 96,8; С2Н6 – 0,9; С3Н8 – 0,4; С4Н10 – 0,3; N2 – 1,0; СО2 – 0,6. Найти массовый состав смеси.
18. Дана смесь двух узких бензиновых фракций самотлорской нефти:
| Температура выкипания фракции, ºС | Молекулярная масса | Массовое содержание, % |
| 105–120 | 103 | 30 |
| 120–140 | 112 | 70 |
Найти среднюю молекулярную температуру кипения смеси.
19. Имеется смесь двух нефтяных фракций:
| Температура выкипания фракции, ºС | Молярная масса, кг/кмоль | Плотность 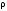 , кг/м3 , кг/м3 |
Мольная доля |
| 180–210 | 168 | 806 | 0,34 |
| 210–230 | 182 | 833 | 0,68 |
Найти объемный состав и среднюю молекулярную температуру кипения смеси.
ПРИЛОЖЕНИЯ
Приложение 1
Средние температурные поправки 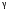
для нефти и нефтепродуктов
Плотность 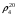 |
Поправка 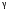 |
| 0,6900–0,6999 | 0,000910 |
| 0,7000–0,7099 | 0,000897 |
| 0,7100–0,7199 | 0,000884 |
| 0,7200–0,7299 | 0,000870 |
| 0,7300–0,7399 | 0,000857 |
| 0,7400–0,7499 | 0,000844 |
| 0,7500–0,7599 | 0,000831 |
| 0,7600–0,7699 | 0,000818 |
| 0,7700–0,7799 | 0,000805 |
| 0,7800–0,7899 | 0,000792 |
| 0,7900–0,7999 | 0,000778 |
| 0,8000–0,8099 | 0,000765 |
| 0,8100–0,8199 | 0,000752 |
| 0,8200–0,8299 | 0,000738 |
| 0,8300–0,8399 | 0,000725 |
| 0,8400–0,8499 | 0,000712 |
| 0,8500–0,8599 | 0,000699 |
| 0,8600–0,8699 | 0,000686 |
| 0,8700–0,8799 | 0,000673 |
| 0,8800–0,8899 | 0,000660 |
| 0,8900–0,8999 | 0,000647 |
| 0,9000–0,9099 | 0,000633 |
| 0,9100–0,9199 | 0,000620 |
| 0,9200–0,9299 | 0,000607 |
| 0,9300–0,9399 | 0,000594 |
| 0,9400–0,9499 | 0,000581 |
| 0,9500–0,9599 | 0,000567 |
| 0,9600–0,9699 | 0,000554 |
| 0,9700–0,9799 | 0,000541 |
| 0,9800–0,9899 | 0,000528 |
| 0,9900–1,0000 | 0,000515 |
Приложение 2
Зависимость относительной плотности жидких нефтепродуктов
от температуры
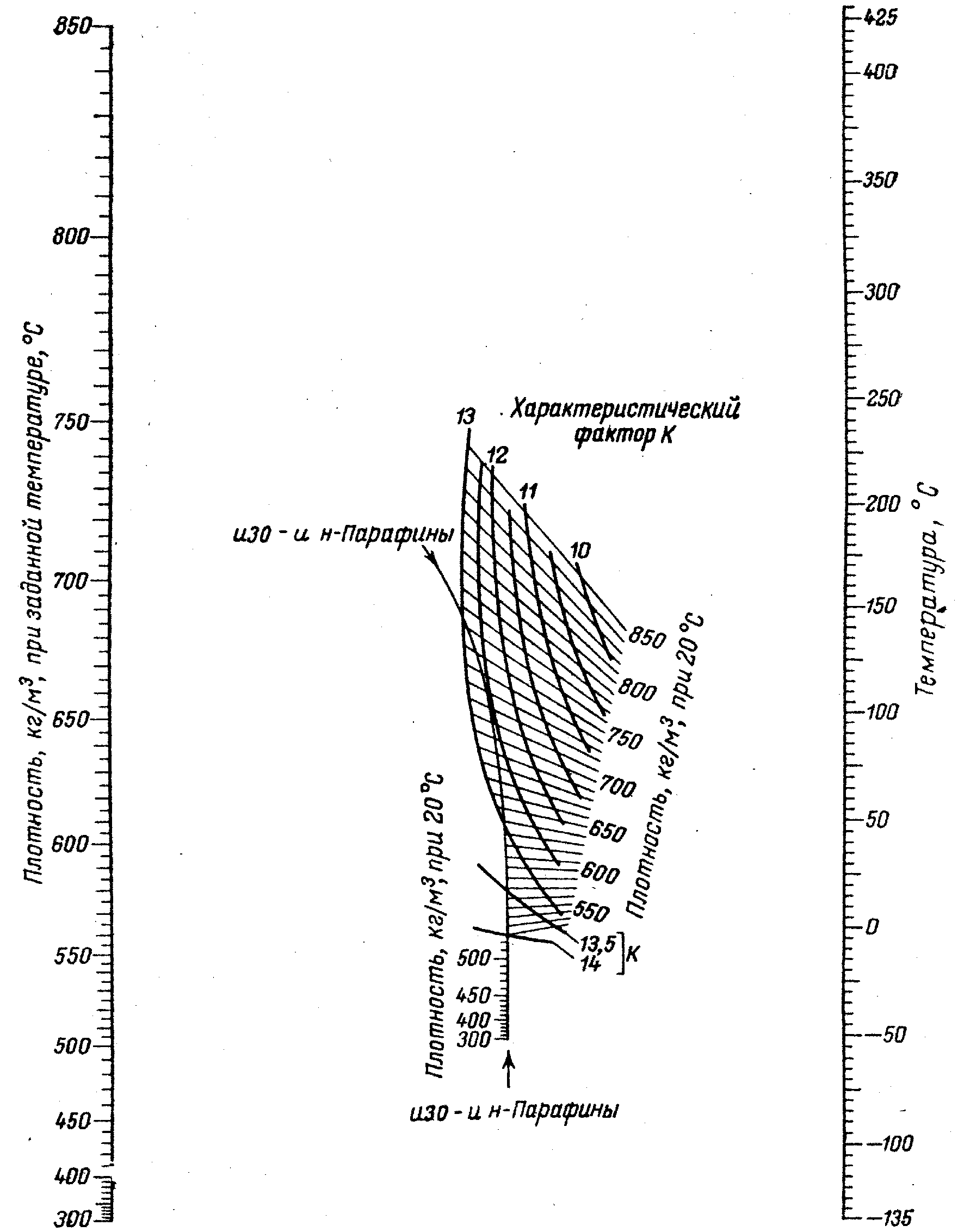
Приложение 3
Зависимость «плотность–температура»
для жидких нефтяных фракций при постоянном давлении
(область низких плотностей)
Приложение 4
Зависимость «плотность–температура»
для жидких нефтяных фракций при постоянном давлении
(область высоких плотностей)
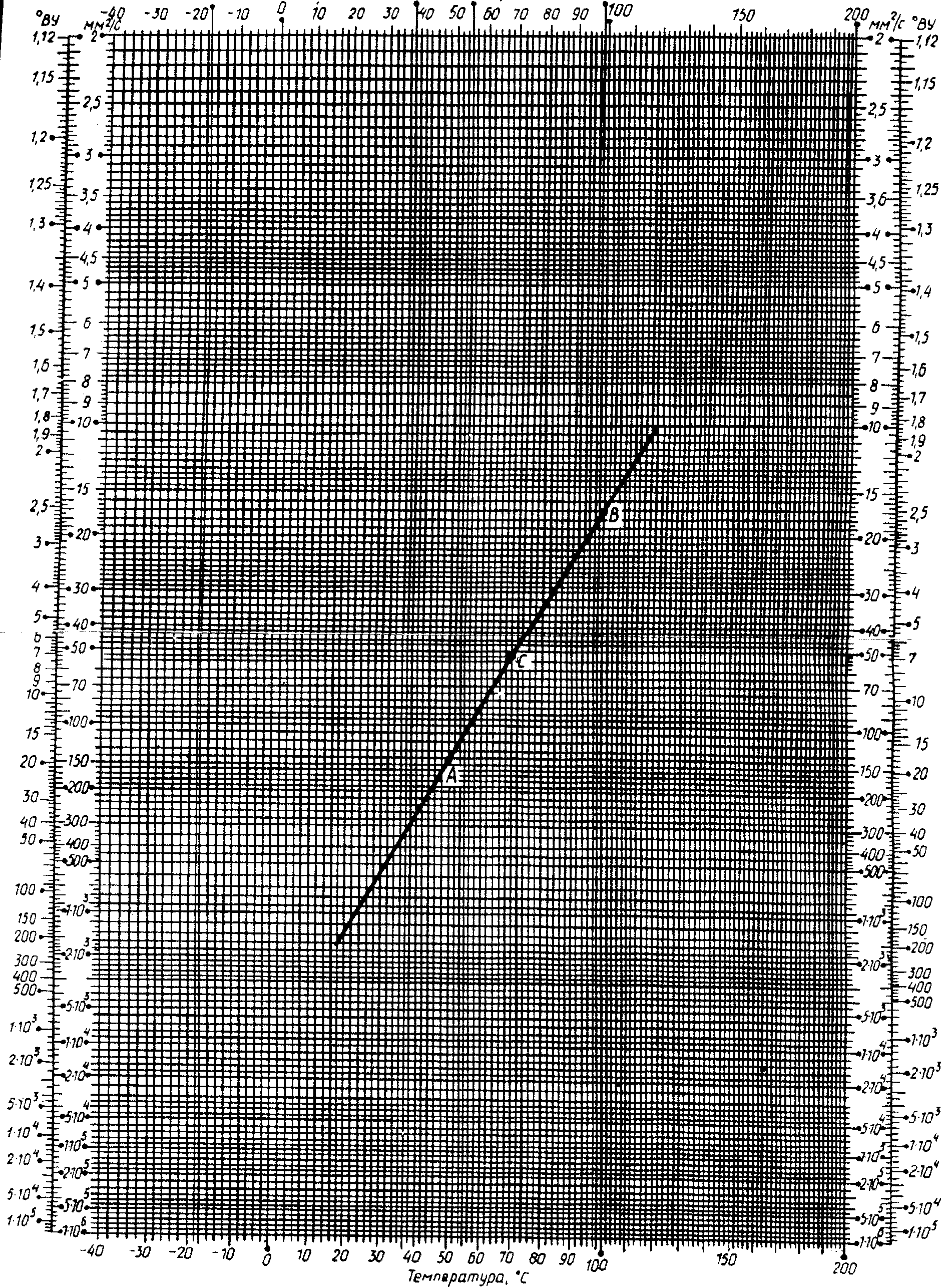
Приложение 5
Номограмма для определения вязкости нефтяных масел
в зависимости от температуры




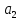





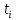












 i
i