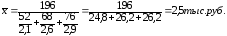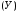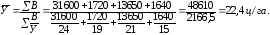Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
- Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
- средняя арифметическая;
- средняя гармоническая;
- средняя геометрическая;
- средняя квадратическая.
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
- Средняя арифметическая простая (невзвешенная) – вычисляется когда каждый вариант совокупности встречается только один раз.
- Средняя арифметическая (взвешенная) – варианты повторяются различное число раз, при этом число повторений вариантов называется частотой, или статистическим весом.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
- Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле (8.8):
(8.8 -формула средней арифметической простой)
- где хi – вариант, а n – количество единиц совокупности.
- Пример вычисления средней арифметической простой. Провели опрос о желаемом размере заработной платы у пяти сотрудников офиса. По результатам опроса выяснили, что желаемый размер заработной платы составляет соответственно для каждого сотрудника: 50000, 100000, 200000, 350000, 500000 рублей человек. Рассчитаем среднюю арифметическую простую по формуле (8.8):
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
- Средняя арифметическая взвешенная формула 8.9.
(8.9 -формула средней арифметической взвешенной)
- где хi – вариант, а fi – частота или статистический вес.
- Пример вычисления средней арифметической взвешенной. Результаты опроса всех работников офиса приведены в табл. 8.2.
Таблица 8.2 – Результаты опроса работников офиса
|
Желаемый размер заработной платы, тыс.руб хi |
Количество работников fi | хifi |
| 1 | 2 | 3 |
|
50 100 200 350 500 |
6
10 20 9 5 |
300
1000 4000 3150 2500 |
| Итого | 50 | 10950 |
Пример. Вычислим (ориентируясь на итоговые строки таблицы) желаемый размер заработной платы, 50 сотрудников офиса (используем формулу 8.9):
Пример вычисления средней арифметической взвешенной
Вывод: в среднем желаемый размер заработной платы по результатам опроса 50 человек составил 219 тысяч рублей.
Среднеарифметическая – всегда обобщающая количественная характеристика варьирующего признака совокупности.
- Средняя гармоническая вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины.
- Средняя гармоническая простая представлена ниже:
(8.10 – формула средней гармонической простой)
Средняя гармоническая взвешенная определяется по формуле
(8.11- формула средней гармонической взвешенной)
где xi – вариант, n – количество вариантов, Vi – веса для обратных значений xi.
Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, чем взвешенная. Для иллюстрации области ее применения воспользуемся упрощенным условным примером.
- Пример (вычисление средней гармонической простой (невзвешенной)).
Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 5 мин., второй – 15 мин.
- Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?
На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. если используем среднюю арифметическую простую получим: (5+15):2=10, мин.
- Проверим обоснованность такого подхода на примере одного часа (60 минут) работы. За этот час первый работник обрабатывает 12 заказов (60:5), второй – 4 заказа (60:15), что в сумме составляет 16 заказов.
Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится: (60/10) + (60/10) = 12 заказов (что не соответствует истине).
- Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов, т.е. используем среднюю гармоническую:
Пример вычисления средней гармонической простой (невзвешенной)
Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится: (60/7,5) + (60/7,5) = 16 заказов
- Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения Wj для единиц совокупности равны (в рассмотренном примере рабочий день у сотрудников одинаковый).
Пример (вычисление средней гармонической взвешенной) В ходе торгов на валютной бирже за первый час работы заключено пять сделок. Данные о сумме продажи рублей и курсе рубля по отношению к доллару США приведены в табл.8.3.
Таблица 8.3 – Данные о ходе торгов на валютной бирже (цифры условные)
Номер сделки Сумма продажи V, млн руб. Курс рубля x, руб. за 1 дол. V/x 1 2 3 4 1
2
3
4
5
455,00
327,50
528,00
266,00
332,50
65,00 65,50
66,00
66,50
66,50
7,00
5,00
8,00
4,00
5,00
итого 1909,00 – 29,00 Для того чтобы определить средний курс рубля по отношению к доллару, нужно найти соотношение между суммой продажи рублей, которые затрачены на покупку долларов в ходе всех сделок, и суммой приобретенных в результате этих сделок долларов.
- Вывод: средний курс за один доллар составил 65,83 руб.;
- Если бы для расчета среднего курса была использована средняя арифметическая простая:
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин как отношение каждого уровня ряда к предыдущему уровню.
- Средняя геометрическая простая рассчитывается по формуле 8.12
(8.12)
- Если использовать частоты m, получим формулу средней геометрической взвешенной
- Средняя геометрическая взвешенная рассчитывается по формуле 8.13
(8.13)
Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.
Для несгруппированных данных используют формулу средней квадратической простой
Средняя квадратическая простая (формула 8.14)
8.14
Для сгруппированных данных используют формулу средней квадратической взвешенной
Средняя квадратическая взвешенная (формула 8.15)
(8.15) – Формула -средняя квадратическая взвешенная
Средние арифметическая, гармоническая, геометрическая и квадратическая, рассчитанные для одного и того же ряда вариантов, отличаются друг от друга. Их численное значение возрастает с ростом показателя степени в формуле степенной средней правило мажорантности средних А.Я. Боярского, т.е.
Мода и Медиана (структурные средние) формулы и примеры вычисления см. по ссылке
Что такое средняя величина мы уже разобрали вот здесь. Сейчас поговорим о том, как рассчитывать среднюю величину.
В классическом виде общая теория статистики предлагает нам один вариант правил выбора средней величины.
Сначала необходимо составить правильно логическую формулу для расчета средней величины (ЛФС). Для каждой средней величины всегда есть только одна логическая формула ее расчета, поэтому ошибиться тут трудно. Но всегда надо помнить, что в числителе (это то, что сверху дроби) сумма всех явлений, а в знаменателе (то, что внизу дроби) общее количество элементов.
После того как составлена логическая формула можно пользоваться правилами (для простоты понимания упростим их и сократим):
1. Если в исходных данных (определяем по частоте) представлен знаменатель логической формулы, то расчет проводим по формуле средней арифметической взвешенной.
2. Если в исходных данных представлен числитель логической формулы, то расчет ведем по формуле средней гармонической взвешенной.
3. Если в задаче представлены сразу и числитель и знаменатель логической формулы (такое бывает редко), то расчет проводим по этой формуле или по формуле средней арифметической простой.
Это классическое представление о выборе верной формулы расчета средней величины. Далее представим последовательность действий при решении задач на расчет средней величины.
Алгоритм решения задач на расчет средней величины
А. Определяем способ расчета средней величины – простой или взвешенный. Если данные представлены в таблице то используем взвешенный способ, если данные представлены простым перечислением, то используем простой способ расчета.
Б. Определяем или расставляем условные обозначения – x – варианта, f – частота. Варианта это то, для какого явления требуется найти среднюю величину. Оставшиеся данные в таблице будут частотой.
В. Определяем форму расчета средней величины – арифметическая или гармоническая. Определение проводится по колонке частот. Арифметическая форма используется, если частоты заданы явным количеством (условно к ним можно подставить слово штук, количество элементов «штук»). Гармоническая форма используется, если частоты заданы не явным количеством, а сложным показателем (произведением осредняемой величины и частоты).
Самое сложное, это догадаться, где и какое количество задано, особенно неопытному в таких делах студенту. В такой ситуации можно воспользоваться одним из предлагаемых далее способов. Для некоторых задач (экономических) подходит наработанное годами практики утверждение (пункт В.1). В других же ситуациях придется пользоваться пунктом В.2.
В.1 Если частота задана в денежных единицах (в рублях), то используется для расчета средняя гармоническая, такое утверждение верно всегда, если выявленная частота задана в деньгах, в других ситуациях это правило не действует.
В.2 Воспользоваться правилами выбора средней величины указанными выше в этой статье. Если частота задана знаменателем логической формулы расчета средней величины, то рассчитываем по средней арифметической форме, если частота задана числителем логической формулы расчета средней величины, то рассчитываем по средней гармонической форме.
Рассмотрим на примерах использование данного алгоритма.
Задача 1. Рассчитать средний размер пенсии, если известны пенсии 12 пенсионеров – 8500, 7900, 11200, 9900, 8800, 8700, 9100, 9500, 7500, 8400, 10400, 10600 рублей.
А. Так как данные представлены в строчку то используем простой способ расчета.
Б. В. Имеем только данные по величине пенсий, именно они и будут нашей вариантой – х. Данные представлены простым количеством (12 человек), для расчета используем среднюю арифметическую простую.
Средний размер пенсии пенсионера составляет 9208,3 рубля.
Задача 2. Рассчитать средний размер детских выплат по следующим данным
А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти средний размер выплаты на одного ребенка, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (число детей) задана явным количеством (можно подставить слово штук детей, с точки зрения русского языка неверное словосочетание, но, по сути, очень удобно проверять), значит, для расчета используется средняя арифметическая взвешенная.
Эту же задачу модно решить не формульным способом, а табличным, то есть занести все данные промежуточных расчетов в таблицу.
В результате все, что нужно теперь сделать, это разделить два итоговых данных в правильно порядке.
Средний размер выплаты на одного ребенка в месяц составил 1910 рублей.
Задача 3. Рассчитать среднюю себестоимость единицы изделия
А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти среднюю себестоимость единицы изделия, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (себестоимость выпуска) задана неявным количеством (частота задана в рублях пункт алгоритма В1), значит, для расчета используется средняя гармоническая взвешенная. Вообще же, по сути, себестоимость выпуска это сложный показатель, который получается перемножение себестоимости единицы изделия на количество таких изделий, вот это и есть суть средней гармонической величины.
Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо себестоимости выпуска стояло число изделий с соответствующей себестоимостью.
Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 410 (120+80+210) это и есть общее количество выпущенных изделий.
Средняя себестоимость единицы изделия составила 314,4 рубля.
Задача 4. Рассчитать среднюю число пропусков одного студента
А. Так как данные представлены в таблице то для расчета используем взвешенную форму.
Б. Так как требуется найти среднюю себестоимость единицы изделия, то варианты находятся в первой колонке, туда ставим обозначение х, вторая колонка автоматически становится частотой f.
В. Частота (общее число пропусков) задана неявным количеством (это произведение двух показателей числа пропусков и числа студентов, имеющих такое количество пропусков), значит, для расчета используется средняя гармоническая взвешенная. Будем использовать пункт алгоритма В2.
Чтобы эта задача могла решаться по формуле средней арифметической необходимо, чтобы вместо общего числа пропусков стояло число студентов.
Составляем логическую формулу расчета среднего числа пропусков одного студента.
Частота по условию задачи Общее число пропусков. В логической формуле этот показатель находится в числителе, а значит, используем формулу средней гармонической.
Обратите внимание, что сумма в знаменателе, получившаяся после расчетов 31 (18+8+5) это и есть общее количество студентов.
Среднее число пропусков одного студента 13,8 дня.
Может еще поучимся? Загляни сюда!
ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ
Тема
4. СРЕДНИЕ ВЕЛИЧИНЫ
4.1.
Средние показатели
Средняя величина есть обобщающая количественная характеристика
совокупности однотипных явлений по одному варьирующему признаку.
Она отражает определённый уровень достигнутый в процессе развития
явления к определённому периоду или моменту времени.
Средняя величина – абстрактная величина. Поэтому анализ проводимый при
ней всегда дополняется показом индивидуальных величин.
Среднее может быть вычислено только для какой-то однородной
совокупности.
Расчёт средней необходимо сочетать с группировкой.
В статистике рассчитывают индивидуальные и общие средние.
Общее среднее затушёвывает существенные (существующие) отличия между
явлениями таким образом во многих случаях они становятся фиктивными.
Признак по которым находится среднее
называется усредняемое (Х). Величина усредняемого признака у каждой единицы
совокупности называется индивидуальное значение.
Значение признака, которое встречается у
крупных единиц или отдельных единиц и не повторяется называется вариантами
признака (Х1, Х2, …).
Средняя арифметическая.
Средняя
арифметическая простая (рассчитывается по несгруппированным данным):
. 
где x1 ,x2, …, xn-значение признака (варианты), n— число вариантов.
Средняя арифметическая взвешенная (рассчитывается
по сгруппированным данным):
,
где f1, f2, …, fn — веса
(частоты) значений признака.
f— частота повторения соответствующих вариантов в статистике называется
весом.
Пример: 1) Вычислить средний возраст выпуска, возраст
которого: 24,22,25,24,25,24,22,22,24,26 лет.
Расчёт по средней арифметической простой:
2)
Расчёт по средней
арифметической взвешенной.
|
Возраст (х) |
Число выпускников (f) |
Сумма возрастов (хf) |
|
22 24 25 26 |
3 4 2 1 |
66 96 50 26 |
|
Сумма |
10 |
238 |
.
Свойства средней арифметической:
1)
Сумма отклонений
значений признака от средней арифметической равно 0.

2)
Если от каждого
варианта вычесть или к каждому варианту прибавить какое-либо постоянное число,
то среднее увеличится или уменьшится на то же самое число.
3)
Если каждый вариант
умножить или разделить на какое-либо число, то среднее уменьшится или
увеличится во столько же раз.
4)
Если веса или частоты
разделить или умножить на какое-либо число, то величина средней не изменится.
Это свойство даёт возможность частоты заменять их удельными весами
,
где р – удельный вес, выраженный в процентах.
Если удельный вес выражается в доле, то
.
Средняя гармоническая.
Рассчитывается, когда 1) среднее арифметическое по
имеющимся данным рассчитать невозможно, 2) расчет средней гармонической более
удобен.
Средняя гармоническая простая: 
Средняя гармоническая взвешенная: 
Пример: требуется вычислить
производительность труда рабочей силы, если первому рабочему требуется для
изготовления единицы продукции 0,25 часа, второму – 1/3 часа, третьему – 1/2
часа.

Средняя геометрическая.
Средняя геометрическая простая:
.
Средняя геометрическая взвешенная:
.
Наиболее широкое применение этот вид средней получил в анализе динамики
для определения среднего темпа роста.
Средняя квадратическая.
Средняя квадратическая простая:

Средняя квадратическая взвешенная:

Пример: Оценка за ответ на первый вопрос – 2, на
второй вопрос – 5.
4.2.
Структурные средние
Для того чтобы определить среднее в некоторых случаях нет
необходимости, или возможности прибегать к расчёту степенных средних в этих
случаях появляется возможность или необходимость расчёта структурной средней.
Если величина средней (ср. арифметической) зависит от всех значений
признака, встречаемых в данном распределении, то значение структурной средней
определяется структурой распределения, местом распределения. Отсюда их
названия.
Медиана – значение признака, приходящееся на
середину ранжированной (упорядоченной) совокупности. Медиана делит совокупность
на две равные части.
Медиана в интервальном ряду рассчитывается следующим образом:
Для определения медианы прежде всего исчисляют её порядковый номер по
формуле
или
(для интервальных
рядов) и строят ряд накопленных частот. Накопленной частоте, которая равна
порядковому номеру медианы или первая его превышает, в дискретном вариационном
ряду соответствует вариант, являющийся медианой, а в интервальном вариационном
ряду – медианный интервал.
где Х0 – нижняя граница медианного
интервала,
d – величина медианного интервала,
fi – частота i-го интервала,
Sме-1
– сумма накопленных весов по интервалу
предшествующему медианному,
fMe
– частота медианного интервала.
Пример: Имеются
данные о з/п рабочих:
|
Месячная з/п (руб) х |
Количество рабочих, fi |
Накопленные частоты, Si |
|
До 800 |
1 |
1 |
|
800- 1000 |
2 |
3 |
|
1000- 1200 |
4 |
7 |
|
1200- 1400 |
1 |
8 |
|
1400 и более |
2 |
10 |
|
Итого |
10 |
,

Мода – значение признака, которое чаще других
встречается в данном ряду распределения.
Мода для дискретного ряда определяется как варианта, имеющая
наибольшую частоту.
Для интервального ряда:
,
где Х0 –нижняя граница модального
интервала,
d – величина модального интервала,
fMo-1 – частота (вес) интервала,
предшествующего модальному,
fMo – частота (вес) модального интервала,
fMo+1 – частота (вес) интервала, следующего за модальным.
Пример: (См. предыдущую задачу)
.
Квартили – значения признака, делящие
ранжированную совокупность на четыре равновеликие части.
Рассчитывают 1-й и 3-й квартили.

XQ1 – нижняя граница интервала, содержащего
нижний квартиль (интервал определяется по накопленной частоте, первой
превышающей 25%),
d – величина интервала,
fQ1 – частота квартильного интервала,
SQ1-1 – сумма накопленных частот в интервале, предшествующего квартильному.
Q2=Мe.

обозначения
аналогичны 1-му квартилю с изменением на верхний.
Децили – варианты, делящие ранжированный ряд
на десять равных частей.
Вычисляются они по той же схеме, что и медиана, и квартили. Обычно
рассчитывают только первый и девятый децили:


Значения признака, делящие ряд на сто частей, называются перцентилями.
Расчёт средних всегда производится одновременно с
количественным анализом, изучаемых совокупностей, средние величины
рассчитываются не всегда, когда на лицо количественная вариация признаков.
Средняя величина должна быть рассчитываема для количественно-однородной
совокупности.
Это требование состоит в том, что среднее нельзя применить к таким
совокупностям, отдельные части которых подчинены различным законам развития
относительных величин признака.
Тема 5. ПОКАЗАТЕЛИ
ВАРИАЦИИ
5.1.
Меры вариации
Колеблемость, многообразие, изменяемость величины признака у единиц
совокупности называются вариацией.
Вариация существует в пространстве и во времени.
Вариация в пространстве – колеблемость значений
признака по отдельным территориям.
Вариация во времени – изменение значений признака в
различные периоды (или моменты) времени.
Для измерения вариации используются такие показатели,
как размах вариации, среднее линейное отклонение, дисперсия, среднее
квадратическое отклонение, коэффициент вариации.
Простейший показатель – размах вариации.
R=Xmax – Xmin.
Из приведённой формы видно, что величина этого показателя целиком
зависит от случайности расположения крайних членов ряда.
Его недостаток в том, что варьирование значения признака из основной
массы членов ряда не находит отражения в этом показателе. В то же время
колеблимость признака складывается из всех его значений.
Среднее линейное отклонение:
– простая,

Показывает в среднем отклонение вариантов признака от их средней
величины.
Дисперсия:
простая,
взвешенная.

Это средняя величина квадратов отклонений.
Среднее квадратическое отклонение:

Это обобщающая характеристика размеров вариации признака в
совокупности. Оно выражается в тех же единицах измерения, что и признак.
Для расчёта дисперсии в дискретном рядах используется следующая
формула.
,
где 

Пример: Распределение коров колхозной фермы по
годовому удою молока и расчёт абсолютных показателей вариации.
|
Годовой удой молока от коровы тыс.кг. (Хi) |
Число коров, fi |
Средняя величина признака, сер. интерв. |
Хifi |
Хi–Х |
|Xi–X|fi |
(Xi–X)2 |
(Xi–X)2fi |
|
До-2 |
4 |
1,5 |
6 |
-1,3 |
5,2 |
1,69 |
6,76 |
|
2-3 |
2 |
2,5 |
5 |
-0,3 |
0,6 |
0,09 |
0,18 |
|
3-4 |
2 |
3,5 |
7 |
+0,7 |
1,4 |
0,49 |
0,98 |
|
4-5 |
1 |
4,5 |
4,5 |
+1,7 |
1,7 |
2,89 |
2,89 |
|
5 и более |
1 |
5,5 |
5,6 |
+2,1 |
2,7 |
7,29 |
7,29 |
|
Итого |
10 |
28 |
11,6 |
18,1 |
1) Находим среднюю арифметическую
2) Среднее линейное отклонение:

2)
Дисперсия

4) Среднее квадратическое отклонение:
тыс.кг.
Дисперсия обладает рядом свойств, некоторые из которых позволяют упростить
её вычисление.
1. Дисперсия постоянной величины равна 0
2. Если все варианты значений признака уменьшить на одно число то
дисперсия не изменится.
3. Если все варианты значений признака уменьшить (увеличить) в одно и тоже
число раз (в К раз), то дисперсия уменьшится (увеличится) в К2
раз.
Дисперсия и среднее квадратическое отклонение – наиболее широко
применяемые показатели вариации, т.к. они входят в большинство теорем теории
вероятности, которая служит фундаментом математической статистики.
Коэффициент вариации.
Он используется не только для сравнения оценки вариации, но и для
характеристики однородной совокупности.
Совокупность считается однородной если коэффициент вариации <=0,33.
В статистике наряду с показателем вариации количественного признака
определяется показатель вариации качественного или альтернативного
признака.
Альтернативными признаками являются признаки, которым
обладают одни единицы совокупности и не обладают другие.
При статистическом выражении колеблимости признака, наличие изучаемого
признака обозначается «1», а его отсутствие «0».
Доля вариантов обладающих изучаемым признаком обозначается р, а
доля вариантов не обладающих изучаемым признаком обозначается q.
Найдём среднее:
.
Дисперсия альтернативного признака:
.
Пример: имеется совокупность новорождённых –
205 человек, девочки – 100.
Доля девочек р=100/205=0,488
Доля мальчиков q =105/205=0,512
Дисперсия альт. призн.= 0,488·0,512= 0,2498
p+q не может быть >1
p·q не может быть >0.25
5.2. Виды дисперсий
Общая дисперсия измеряет вариацию признака во всей совокупности под
влиянием всех факторов, обусловивших эту вариацию.
Межгрупповая дисперсия отражает вариацию
изучаемого признака, которая возникает под влиянием признака фактора,
положенного в основу группировки. Она характеризует колеблимость групповых
(частных) средних около общей средней

где – среднее по определённой группе; ni
– численность отдельных групп.
Внутригрупповая дисперсия отражает случайную
вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и
не зависящую от признака-фактора, положенного в основание группировки.

Средняя из внутригрупповых дисперсий:

Правило сложения дисперсий:
.
Можно рассчитать относительные показатели.
1.
Эмпирический коэффициент детерминации
Он показывает долю (удельный вес) общей вариации изучаемого признака,
обусловленную вариацией группировочного признака.
2. Эмпирическое корреляционное отношение
Оно характеризует влияние признака, положенного в
основание группировки, на вариацию результативного признака. Чем больше это
число, тем больше зависимость результативного признака от факторов положенных
в основу группировки.
Пример:
|
Тип хозяйства |
Посевная площадь тысяч гект. |
Средняя урожайность |
Среднее |
|
1 |
300 |
20 |
2 |
|
2 |
100 |
10 |
2,5 |
1)
Находим среднюю урожайности по двум типах хозяйств
2)
Средняя из групп дисперсий
(22ּ300+2,52ּ100)/400=4,5625
3)
Определяем межгрупповую дисперсию
4)
Определяем общую дисперсию
5)
Эти данные свидетельствуют о том, что фактор положенный в основу
группировки оказывает существенное влияние на среднюю урожайность.
Выбор знака: если вариация факторного и результативного признака идёт в
одном направлении, то берётся знак «+», а если нет, то «–», сам по себе знак не
характеризует тесноту связи. Помимо расчета общей дисперсии и её составных
частей по абсолютным данным можно производить расчёт дисперсии доли.
5.3.
Теоретическое распределение в анализе вариационных рядов
При анализе изучаемых явлений в совокупности с другими, аналогичными по
своей сущности, часто удается обнаружить закономерность, связанную с их
возникновением. Наиболее часто закономерности описывают с помощью нормального
распределения:

Чем больше случайных величин действует вместе, тем точнее подчиненность
закону нормального распределения.
Примеры нормального распределения: 1) распределение отклонений в
производственном процессе при нормальном уровне организации и технологии, 2)
распределение населения определенного возраста по размеру обуви и т.д.
Соответствие эмпирического распределения нормальному можно оценивать с
помощью особых статистических показателей – критериев согласия.
Критерий согласия Пирсона (хи-квадрат)

где fэ и fт – эмпирические и теоретические частоты
соответственно.
Затем с помощью «хи-квадрат» и числа степеней свободы (n-1) находят по специальным таблицам вероятность .
При Р>0,5 считается, что эмпирическое и теоретическое распределения
близки, при 0,2<P<0,5 – удовлетворительное, в
остальных случаях – недостаточное.
Критерий Романовского (С)

где γ – число степеней свободы (число групп минус три).
При С<3 различие несущественно, эмпирическое распределение близкое к
нормальному.
Критерий Колмогорова (λ)

где D – максимальное значение разности между
накопленными эмпирическими и теоретическими частотами,
fi – эмпирические частоты.
Далее по таблицам вероятностей определяем . Чем
ближе к 1, тем лучше.
Тема 6. ИЗУЧЕНИЕ ДИНАМИКИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ
ЯВЛЕНИЙ
6.1. Понятие рядов динамики
Изучение изменения различных явлений во времени – одна из важнейших
задач статистики. Решается эта задача путем составления и анализа так
называемых рядов динамики (иногда их также называют временными или
хронологическими рядами).
Динамика – процесс развития, движения
социально-экономических явлений во времени.
Ряды динамики – ряды изменяющихся во времени
значений статистического показателя, расположенных в хронологическом порядке.
Составными элементами ряда динамики являются показатели уровней ряда и
периоды времени (годы, кварталы, месяцы, сутки) или моменты (даты) времени.
Обозначения:
y – уровни ряда,
t – моменты или периоды времени, к которым относятся уровни.
Ряды динамики, как правило, представляют в виде таблицы или графически.
При графическом изображении ряда динамики на оси абсцисс строится шкала времени
t, а на оси ординат – шкала уровней ряда у (арифметическая или иногда
логарифмическая).
Одна из первых задач изучения рядов динамики – выявить основную
тенденцию (закономерность) в изменении уровней ряда, именуемую трендом.
Закономерность в изменении уровней ряда в одних случаях проявляется довольно
наглядно, в других – может затушевываться колебаниями, вызванными случайными и
неслучайными причинами.
Виды рядов динамики.
В одних рядах уровни могут быть выражены абсолютными показателями, в
других – средними или относительными. В зависимости от вида показателей уровней
ряда ряды динамики также подразделяют на ряды абсолютных, относительных и
средних величин (показателей).
На основе рядов абсолютных величин образуются ряды динамики
относительных и средних величин, поэтому ряды абсолютных величин рассматривают
как исходные, а ряды относительных и средних величин — как производные.
Ряды относительных величин могут характеризовать: темпы роста (или
снижения) определенного показателя; изменение удельного веса того или иного
показателя в совокупности (например, удельного веса (доли) городского населения
или доли приватизированных предприятий в той или иной отрасли); изменение показателей
интенсивности отдельных явлений (например, производство продукции на душу
населения, уровень рождаемости и смертности на 1000 человек населения) и др.
Примерами рядов динамики средних величин служат данные о среднегодовой
численности занятых в экономике (или безработных), о средней заработной плате в
отдельных отраслях, о среднем размере пенсий, о средней урожайности отдельных
сельскохозяйственных культур и др.
Кроме того, уровни рядов динамики могут относиться к определенным
моментам времени (датам) или же периодам (интервалам). В соответствии с этим в
статистике различают моментные и интервальные ряды динамики
Моментным называется ряд, уровни которого характеризуют
значение показателя (явления) по состоянию на определенные моменты времени
(дату).
Интервальным называется ряд, уровни которого
характеризуют значение показателя, достигнутое за определенный период (интервал).
Отметим отличительную особенность интервальных рядов абсолютных
величин: их уровни можно дробить и складывать (суммировать). Так, зная добычу
угля по годам, можно разделить каждый уровень на 12 и получить новые данные – о
среднемесячной добыче угля за указанный период. Или же, суммируя данные о
численности родившихся по месяцам, можно получить численность родившихся за
год. Подобные действия с уровнями моментного ряда лишены смысла.
Суммируя уровни интервальных рядов абсолютных величин, можно строить
ряды с нарастающим итогом.
6.2.
Показатели изменения уровней ряда динамики
Анализ рядов динамики начинается с определения того, как именно
изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в
абсолютном и относительном выражении.
Анализ скорости и интенсивности развития явления во времени
осуществляется с помощью статистических показателей, которые получаются в
результате сравнения уровней между собой. При этом сравниваемый уровень
называют отчетным, а уровень, с которым производят сравнение, – базисным.
Чтобы проследить за направлением и размером изменений уровней во
времени, для рядов динамики рассчитывают такие показатели, как:
—
абсолютные приросты (изменения) уровней;
—
темпы роста;
—
темпы прироста (снижения) уровней.
Абсолютный прирост (Δy) характеризует размер изменения
уровня ряда за определенный промежуток времени. Он рассчитывается как разность
между двумя уровнями ряда. Абсолютный прирост показывает, на сколько (в
единицах измерения показателей ряда) уровень одного периода больше или меньше
уровня какого-либо предшествующего периода, и, следовательно, может иметь знак
«+» (при увеличении уровней) или «–» (при уменьшении уровней).
Δyi=yi – yi-1, i=1..n.
В зависимости от базы сравнения абсолютные приросты могут
рассчитываться как цепные и как базисные.
Вычитая из каждого уровня предыдущий
Δу
= yi – yi-1,
получаем
абсолютные изменения уровней ряда за отдельные периоды как цепные.
Вычитая
из каждого уровня начальный
Δу
= yi – y0,
получаем
накопленные итоги прироста (изменения) показателя с начала изучаемого периода,
т.е. абсолютные изменения рассчитываются как базисные.
Если значения цепных абсолютных изменений постоянны, то уровни ряда
изменяются равномерно. Если же абсолютные приросты от периода к периоду
возрастают (или убывают), то уровни изменяются ускоренно (или замедленно). В
этом случае рассчитывается показатель ускорения как разность между двумя
смежными цепными абсолютными приростами.
Абсолютное ускорение (Δ′) – показывает,
насколько данная скорость больше (меньше) предыдущей.
Δ′=Δyi–Δyi-1
Наряду с абсолютными изменениями уровней ряда важно измерить также их
относительное изменение.
Темп роста (Тр) – показатель интенсивности
изменения уровня ряда, относительный показатель, рассчитываемый как отношение
двух уровней ряда.
В зависимости от базы сравнения темпы роста могут рассчитываться как
цепные, когда каждый уровень сопоставляется с уровнем предыдущего периода, и
как базисные, когда все уровни сопоставляются с уровнем одного какого-то
периода, принятого за базу сравнения (часто это начальный уровень ряда). Соответственно,
цепные темпы роста характеризуют интенсивность изменения в каждом отдельном
периоде, а базисные – за отрезок времени, отделяющий данный уровень от
базисного.
Базисный темп роста:
.
Цепной темп роста:
Темпы роста как относительные величины могут выражаться в виде
коэффициентов, т.е. простого кратного отношения (если база сравнения
принимается за единицу), и в процентах (если база сравнения принимается за 100
единиц). Говоря о темпах, чаще всего имеют в виду отношение уровней в
процентах.
Выраженные в коэффициентах темпы роста показывают, во сколько раз
уровень данного периода больше уровня базы сравнения или какую часть его
составляет. При процентном выражении темп роста показывает, сколько процентов
составляет уровень данного периода по сравнению с уровнем базы сравнения.
Между цепными и базисными коэффициентами роста существует связь,
позволяющая при необходимости переходить от цепных к базисным и наоборот.
В частности:
—
произведение цепных коэффициентов роста равно
базисному;
—
результат деления двух базисных коэффициентов равен
цепному
Темп прироста (Тпр) характеризует
относительную скорость изменения уровня ряда в единицу времени, это относительный
показатель, показывающий, на сколько процентов данный уровень больше (или
меньше) другого, принимаемого за базу сравнения. Показатель Тпр
можно рассчитать двояко:
—
путем вычитания 100% из темпа роста (снижения),
—
как процентное отношение абсолютного прироста к
тому уровню, по сравнению с которым рассчитан абсолютный прирост.
Абсолютное значение одного процента прироста
Абсолютное значение 1% прироста равно одной сотой предыдущего уровня
Для базисных абсолютных приростов и темпов прироста расчет не имеет
смысла, так как при сравнении всех накопленных приростов с одним и тем же
первоначальным уровнем для всех периодов будет получаться одно и то же значение
1% прироста.
Каждый ряд динамики можно рассматривать как некую совокупность изменяющихся
во времени показателей, которые можно обобщать в виде средних величин. Такие
обобщенные (средние) показатели особенно необходимы при сравнении изменений
того или иного показателя в разные периоды, в разных странах и т. д.
Средний уровень
ряда динамики. Для разных видов
рядов динамики средний уровень рассчитывается различным образом.
Для моментного равноотстоящего ряда динамики по средней хронологической:

Для моментного ряда динамики с неравноотстоящими уровнями:

где ti – длительность интервала времени
между уровнями.
Для интервального ряда с равноотстоящими уровнями:
Для интервального ряда с неравноотстоящими уровнями:
Средний абсолютный прирост
Средний темп роста
Средний темп прироста
При анализе динамики социально-экономических явлений необходимо
параллельно использовать показатели скорости и интенсивности изменения уровней.
6.3. Анализ основной тенденции в рядах динамики
Описание тенденции в ряду динамики производится с
помощью методов сглаживания. Методы сглаживания разделяются на две основные
группы:
1)
сглаживание или
механическое выравнивание отдельных членов ряда динамики с использованием
фактических значений соседних уровней;
2)
выравнивание с применением
кривой, проведенной между конкретными уровнями таким образом, чтобы она
отображала тенденцию, присущую ряду, и освободила его от незначительных
колебаний.
Метод усреднения по левой и правой половине. Ряд динамики разделяют на две части, находят
для каждой из них среднее арифметическое значение и проводят через полученные
точки линию тренда на графике.
Метод укрупнения интервалов. Производится укрупнение периодов времени, к которым
относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется
рядом месячного выпуска продукции.
Метод скользящей средней. Вычисляется средний уровень из определенного числа
первых по порядку уровней ряда, затем – начиная со второго, далее – с третьего
и т.д.
Алгоритм расчета скользящей средней:
1.
Определяем интервал
сглаживания, т.е. число входящих в него уровней m (m<n).
2.
Вычислить среднее значение
уровней, образующих интервал сглаживания, по формуле

где m – число уровней, входящих в интервал сглаживания,
i – порядковый номер уровня в интервале сглаживания,
p – при нечетном m равно: p=(m-1)/2.
При четном m проводят центрирование:
находят среднюю из двух смежных скользящих средних для отнесения полученного
уровня к определенной дате.
3. Сдвинуть интервал сглаживания на одну точку вправо, затем вычислить все
последующие сглаженные значения, производя одновременно сдвиги.
Пример:
|
Год |
Центнеров с 1 га |
Скользящие трехлетние суммы |
Трехлетние скользящие средние |
|
1982 1983 1984 1985 1986 1987 1988 1989 |
9,5 13,7 12,1 14,0 13,2 15,6 15,4 14,0 |
— — 35,3 39,8 39,3 42,8 44,2 45 |
— 11,77 13,27 13,1 14,27 14,73 15 — |
Тема
7. ИНДЕКСНЫЕ МЕТОДЫ
7.1. Понятие индексов
В статистике под индексами понимаются относительные
величины, выражающие изменение сложных экономических явлений во времени,
пространстве и по сравнению с планом. В связи с этим различают динамические
индексы, характеризующие изменения явлений во времени; индексы выполнения
плана и территориальные индексы.
Индексы относятся либо к элементам сложного экономического явления,
либо ко всему явлению в целом. Показатели характеризующие изменение более или
менее однородных объектов входящих в состав сложных явлений называются
индивидуальные индексы
Принятые обозначения:
Q, q – физический объём;
p – цена единицы товара;
z – себестоимость единицы продукции;
pq – стоимость продукции или товарооборот;
zq – издержки производства.
7.2. Индивидуальные и общие индексы
Индивидуальные индексы (i) – это обычные относительные величины.
Индивидуальный индекс объёма:
=
,
q0 – базисный период (пояснить);
q1 – текущий период (пояснить).
Индивидуальный индекс цены:
.
Индивидуальный индекс товарооборота:
Индекс как индивидуальный так и общий получает название по названию
индексированной величины. Индексы как индивидуальные так и общие обозначаются
либо в виде коэффициента, либо в виде процентов.
Явления общественные и социальные, изучаемые в экономике состоят из
несопоставимых элементов. Таким образом, основным вопросом построения индексов,
общих и сводных состоит в том, чтобы обеспечить эту сопоставимость
Самый лёгкий способ сопоставления – сложные явления разбиваются на
простые элементы которые в известной мере являются однородными.
Общий индекс обозначается – I. Различают агрегатные и средневзвешенные индексы.
Основной формой сводного индекса является агрегатный индекс. Для
того, чтобы его построить необходимо свести различные элементы сложного явления
к такому виду, который делает их соизмеримыми.

продукции(Ласпейреса).

продукции(Пааше).




производства.
Та часть индекса, которая не изменяется, называется весом.
Веса свободного индекса в агрегатной форме выбираются исходя из
следующих данных:
Если индексируемая величина – суть количественный
показатель, то вес выбирается на уровне базисного периода.
В том случае если индексируется величина – качественный признак вес
принимается на уровне текущего периода. Такой подход к выбору весов даёт нам
возможность записать следующее равенство индексов
Итак, в целом по совокупности, состоящей из элементов, непосредственно
несоизмеримых (различные виды продукции, товарные группы и т.д.), изменение
физического объема реализации и цен характеризуется с помощью агрегатных
индексов, формулы построения которых сведены в табл. 1.
Таблица 1
Агрегатные индексы
|
Формулы индексов |
Название индексов |
|
|
Индекс физического объема и других первичных |
Индекс цен и других вторичных признаков |
|
|
По формуле Ласпейреса (по базисным весам) |
|
|
|
По формуле Пааше (по отчетным весам) |
|
|
|
Индекс Фишера |
|
|
Пример:
|
Товары |
Ед. измер |
Базисный период |
Текущий период |
Индивидуаль-ный индекс |
|||
|
P0 , (руб) |
Q0 (ед.) |
P1 |
Q1 |
|
|
||
|
Капуста |
Кг. |
17 |
350000 |
15 |
420000 |
0,882 |
1,2 |
|
Молоко |
Литры |
28 |
25400 |
35 |
23600 |
1,25 |
0,929 |
|
Яйца |
Десятки |
120 |
125 |
120 |
140 |
1 |
1,29 |
Индекс товарооборота:
Это значит товарооборот текущего периода по отношению к базисному вырос
на 7% этот показатель отражает изменение товарооборота под влиянием р и q.
Индекс физического объёма продукции (Ласпейраса):
Это значит товарооборот в текущем периоде возрос на 17% в связи с
изменением объёма реализации.
Индекс цены (Пааше):
Индекс цены показал нам, что стоимость продукции в текущем периоде по
сравнению с базисным сократился на 9% под влиянием изменения цен.
7.3.
Средние индексы
Агрегатная форма индекса – его основная форма, но не единственная в
ряде случаев для удобства расчётов в том случае если мы располагаем значениями
индивидуальных индексов на практике удобно использовать средние индексы.
Средний индекс – индекс, вычисленный как
средняя величина из индивидуальных индексов.
Средний гармонический индекс цены:
Средний арифметический индекс физического объема:
Цепные индексы – ряд индексов одного и того же
явления, вычисленных с меняющейся от индекса к индексу базой сравнения.
,
.
7.4. Индексы структурных сдвигов
При изучении динамики показателей приходится
определять изменение средней величины индексируемого показателя, которое
обусловлено взаимодействием двух факторов – изменением значения индексируемого
показателя у отдельных групп единиц и изменением структуры явления, т.е.
изменением доли отдельных групп единиц совокупности в общей их численности. Для
этого вычисляются три индекса: переменного состава, постоянного состава и
структурных сдвигов.
Индекс переменного состава – индекс,
выражающий соотношение средних уровней изучаемого явления, относящихся к разным
периодам времени. Он отражает изменение не только индексируемой величины, но и
структуры совокупности (весов).

Индекс постоянного (фиксированного) состава –
индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо
периода, и показывающий изменение только индексируемой величины. Это агрегатный
индекс.

Индекс структурных сдвигов – индекс,
характеризующий влияние изменения структуры изучаемого явления на динамику
среднего уровня этого явления.

Существует взаимосвязь между этими индексами: .
Пример: по имеющимся данным о себестоимости
единицы продукции на трех предприятиях в текущем и базисном периодах получили
следующие индексы структурных сдвигов
средняя себестоимость по трем
предприятиям снизилась в текущем периоде по сравнению с базисным на 3,25%.
себестоимость в текущем периоде по
сравнению с базисным возросла в среднем на 2,1%.
изменение доли предприятий в общем объеме
произведенной продукции привело к снижению себестоимости на 5,24%.
Рекомендуемая литература
1.
Елисеева И.И., Юзбашев М.М. Общая теория
статистики: Учебник. – М.: ИНФРА-М, 1998.
2.
Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая
теория статистики: Учебник. Изд. 2-е, испр. и доп. – М.: ИНФРА-М, 2001. – 416
с. — (Серия «Высшее образование»).
3.
Практикум по теории статистики: Учеб. Пособие / Под
ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2001.- 416 с.: ил.
4.
Теория статистики: Учебник / Под ред. проф. Р.А.
Шмойловой. – 3-е изд., перераб. – М.: Финансы и статистика, 2001.- 506 с.: ил.
5.
Теория статистики: Учебно-практическое пособие для
системы дистанционного образования /Под ред. В.Г. Минашкина. – М.: МЭСИ, 1998.
Виктория
Николаевна Шайкина
общая теория статистики
Учебное
пособие
Под ред.
В.В. Лихолетова
Технический
редактор А.В. Миних
Издательство Южно-Уральского государственного университета
Подписано
в печать
Формат
60х84 1/16. Печать офсетная. Усл. печ. л. Уч.-изд. л.
Тираж 100 экз. Заказ . Цена р.
Отпечатано
в типографии Издательства ЮУрГУ. 454080,
г. Челябинск,
пр. им. В.И.Ленина, 76
.
Статистика
изучает массовые явления и процессы.
Каждое из таких явлений обладает общими
для всей совокупности и индивидуальными
свойствами. Различие между индивидуальными
свойствами называется вариацией, а
присущая массовым явлениям близость
(похожесть) характеристик отдельных
явлений определяется средними величинами.
Наиболее часто в статистике применяется
средняя арифметическая, реже — средняя
гармоническая, средняя геометрическая
применяется только при исчислении
средних темпов динамики (см. формулы 5
и 6).
Средняя
арифметическаяприменяется в тех
случаях, когда объем варьирующего
признака для всей совокупности образуется
как сумма значений признака у отдельных
единиц. Например, общий фонд заработной
платы состоит из зарплат, начисленных
отдельным работникам. Когда имеются
отдельные несгруппированные значения
признака рассчитывается средняя
арифметическая простая по формуле:

(5)
где

значения признака, которые называют
вариантами,
единиц совокупности.
По данным,
представленным в виде рядов распределения
или группировок рассчитывается средняя
арифметическая взвешенная. Формула для
расчета средней арифметической взвешенной
имеет вид:

где


или частоты (т.е. число вариант, имеющих
одинаковое значение признака).
Рассмотрим
пример расчета средней арифметической
взвешенной на основе интервального
вариационного ряда.
Таблица
5 — Расчет средней заработной платы из
вариационного ряда
|
Группы рабочих по размеру |
Среднее значение интервалов |
Число рабочих (f) |
Произведение вариант на |
|
1500-2000 2000-2500 2500-3000 |
1750 2250 2750 |
100 220 280 |
175000 495000 770000 |
|
Итого |
600 |
1440000 |
По данным
табл.5 средняя месячная зарплата рабочих
составит:
Средняя
гармоническая— это величина, обратная
средней арифметической, из обратных
значений признака. Ее применяют тогда,
когда веса приходится не умножать, а
делить на варианты или умножать на
обратное их значение. Формулы средней
гармонической простой и взвешенной
имеют вид:

(7)

(8)
где

единиц совокупности,
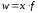
Расчет средней гармонической поясним
на примере.
Таблица
6 — Стоимость продукции и ее выработка
в рабочих бригадах
|
Номер бригады |
Стоимость произведенной ( |
Выработка на 1-го рабочего, |
|
1 2 3 |
52 68 76 |
2,1 2,6 2,9 |
|
Итого |
196 |
Варьирующим
признаком в данном примере является
средняя выработка рабочих в каждой
бригаде. Среднее значение данного
варьирующего признака равно 2,4 тыс. руб.
Эта средняя получается как средняя
гармоническая, где веса деленные на
варианты показывают численность рабочих
в бригадах, т.е.
5.4. Логическая формула для вычисления средней арифметической и средней гармонической величин
При расчете
средней величины одного и того же
показателя может использоваться как
средняя арифметическая так и средняя
гармоническая величины. Это обусловлено
одной и той же логической формулой для
искомого показателя. Но вместе с тем
данные, по которым могут быть вычислены
эти величины, должны быть различными.
Логическая
формула вытекает из сущности средней,
ее социально-экономического содержания.
Поэтому, прежде чем оперировать цифрами,
нужно выяснить, соотношением каких
показателей является средняя в данном
конкретном случае. Это исходное
соотношение необходимо записать в виде
формулы, называемой логической формулой
средней. Далее на основании логической
формулы осуществляется выбор рабочей
формулы средней в данном конкретном
случае. Приведем известный алгоритм
выбора рабочей формулы средней:
1. На основании
исходной информаций устанавливается
логическая формула для искомого
показателя средней.
2. Если имеется
ряд данных по двум взаимосвязанным
показателям, для одного из которых нужно
вычислить среднюю величину, и при этом
известны численные значения знаменателя
ее логической формулы, а значения
числителя не известны, но могут быть
найдены как произведения этих показателей,
то средняя должна вычисляться по формуле
средней арифметической взвешенной.
3. Если в
указанной постановке задачи известны
численные значения числителя логической
формулы, а значения знаменателя не
известны, но могут быть найдены как
частное от деления одного показателя
на другой, то средняя вычисляется по
формуле средней гармонической взвешенной.
4. В том
случае, когда в условии задачи даны
численные значения числителя и знаменателя
логической формулы показателя, средняя
вычисляется непосредственно по этой
формуле.
Рассмотрим
на примере порядок расчета и выбор
формулы средней величины.
Пример. На
основании следующих данных по двум
сельскохозяйственным предприятиям
необходимо определить, в каком из них
и насколько выше средняя урожайность
зерновых культур:
|
Культура |
Предприятие 1 |
Предприятие 2 |
||
|
Валовой сбор, ц |
Урожайность ц./г |
Посевная площадь, га |
Урожайность, ц/га |
|
|
Пшеница озимая Рожь Ячмень Просо |
31600 1720 13650 1640 |
24 19 21 15 |
1460 120 470 80 |
19 18 16 13 |
|
Итого |
48610 |
— |
2130 |
— |
Показатель
урожайности является вторичным признаком,
так как он задан на единицу первичного
признака ( посевной площади, выраженной
в гектарах) и может быть представлен
как отношение двух первичных признаков,
а именно валового сбора и посевной
площади:
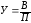
(9)
где


сбор;
площадь.
Так как нас
интересует средняя урожайность по
каждому предприятию то логическая
формула средней будет иметь вид:

(10)
Согласно
данным рассматриваемого примера, для
сельскохозяйственного предприятия 1
средняя урожайность должна определяться
по правилу 3, изложенному выше алгоритма,
т.е. по формуле средней гармонической
взвешенной:
Для
сельскохозяйственного предприятия №
2 средняя урожайность определяется по
правилу 2, т. е. По формуле средней
арифметической взвешенной:
Следовательно,
средняя урожайность зерновых культур
на предприятии № 1 по сравнению с
предприятием № 2 была выше на 4,3 ц/га.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задачи по статистике с решением — Средние величины
Решаем проверочные задачи по статистике
Тема: «Средние величины»
1. Задача на определение средней арифметической
Рассчитать средний возраст студентов в группе из 20 человек:


|
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
|
1 2 3 4 5 |
18 18 19 20 19 |
6 7 8 9 10 |
20 19 19 19 20 |
11 12 13 14 15 |
22 19 19 20 20 |
16 17 18 19 20 |
21 19 19 19 19 |
Если сгруппировать данные, то получим ряд распределения:


2. Задача на нахождение средней арифметической взвешенной
Распределение рабочих по выработке деталей
|
Выработка деталей за смену одним рабочим, шт., Хi |
18 |
19 |
20 |
21 |
22 |
Всего |
|
Число рабочих, fi |
2 |
11 |
5 |
1 |
1 |
20 |


3. Задача на вычисление средней по групповым средним или по частным средним.
Распределение рабочих по среднему стажу работы
|
Номер цеха |
Средний стаж работы, лет. |
Число рабочих, чел., fi |
|
1-й 2-й 3-й |
5 7 10 |
90 60 50 |
|
ИТОГО: |
200 |


4. Задача на вычисление средних в рядах распределения (интервальный ряд).
Распределение рабочих АО по уровню ежемесячной оплаты труда
|
Группы рабочих по оплате труда у.е. |
Число рабочих, чел. |
Середина интервала, хi |
|
До 500 |
5 |
450 |
|
500-600 |
15 |
550 |
|
600-700 |
20 |
650 |
|
700-800 |
30 |
750 |
|
800-900 |
16 |
850 |
|
900 и более |
14 |
950 |
|
Итого: |
100 |
— |

Задача 5. Вычисление средних в интервальных рядах методом моментов
Распределение малых предприятий региона по стоимости основных производственных фондов
|
Группы предприятий по стоимости ОПФ, у.е. |
Число предприятий |
Середина интервалов, х |
|
Хi*f |
|
14-16 16-18 18-20 20-22 22-24 |
2 6 10 4 3 |
15 17 19 21 22 |
-2 -1 0 1 2 |
-4 -6 0 4 6 |
|
Итого: |
25 |
— |
— |
0 |
Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот.
Один из вариантов, обладающий наибольшей частотой принимают за А, i— величина интервала.
А- начало отсчета «способ отсчета от условного нуля», «способ моментов». Все варианты уменьшим на А, затем разделим на I, получим новый вариационный ряд распределения новых вариантов хi. Средняя арифметическая их новых вариантов- момент первого порядка m i= 

Задача 6 на определение Средней гармонической.
Заработная плата предприятий АО
|
Предприятие |
Численность промышленно- производственного персонала, чел |
Месячный фонд заработной платы, тыс руб. |
Средняя заработная плата, руб. |
|
А |
1 |
2 |
3 |
|
1 2 3 |
540 275 458 |
564,84 332,75 517,54 |
1046 1210 1130 |
|
ИТОГО: |
1 273 |
1415,13 |
? |
Определить среднюю з/п по всем предприятиям.
Решение:
Составим логическую формулу средней: средняя з/п по всем предприятиям =
1) Пусть мы располагаем данными гр.1 и 2. Нам известен числитель и знаменатель логической формулы.
Искомая средняя величина определяется по средней агрегатной:

2) Пусть мы располагаем данными гр.1 и 3 , нам известен числитель логической формулы, а знаменатель числитель не известен, но может быть найден путем умножения средней з/п на численность ППП. Искомая средняя определяется по средней арифметической взвешенной.


3) Пусть мы располагаем данными гр.2 и 3 , нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления фонда з/п на среднюю з/п логической формулы. Искомая средняя определяется по средней гармонической взвешенной:
Все ответы верны.
Задача 7. Определить среднюю цену моркови по всем магазинам.
Цена и выручка от реализации по трем коммерческим магазинам.
|
№ магазина |
Цена моркови., руб за кг. |
Выручка от реализации, руб. |
|
1 2 3 |
17 20 24 |
3060 2800 1920 |
|
Итого: |
— |
7780 |
Решение.
Логическая формула средней: средняя цена моркови =
нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления выручки от реализации на цену моркови.
Искомая средняя определяется по средней гармонической взвешенной:
Задача 8 по статистике с решением: средние величины.
Информация о вкладах в банке
|
Вид вклада |
Октябрь |
Ноябрь |
||
|
Число вкладов, тыс., f |
Средний размер вклада, руб., x |
Сумма вкладов, млн. руб., F |
Средний размер вклада, x |
|
|
До востребования Срочный |
10 8 |
350 400 |
4,07 3,87 |
370 430 |
Определить средний размер вклада по двум видам.
1) Пусть в октябре известен средний размер вкладов каждого вида и число вкладов. По формуле средней арифметической взвешенной:


2) Пусть в ноябре известен средний размер вкладов каждого вида и сумма вкладов. По формуле средней гармонической взвешенной:
Задача 9: Удельная материалоемкость по двум предприятиям, изготавливающим один и тот же вид продукции составила соответственно 2,5 и 3 кг. Вычислить среднюю удельную материалоемкость изделия по двум предприятиям при условии, что каждым предприятием израсходовано на изготовления одного изделия по 60 тонн стали.
1) Решение задачи по средней арифметической простой:


2) решение по средней арифметической взвешенной



Оба решения не имеют логического смысла, чтобы правильно выбрать формулу средней величины необходимо составить логическую формулу задачи, отражающую ее смысл.
Логическая формула: средняя удельная материалоемкость по двум предприятиям = общему расходу материала на двух предприятиях/ на количество произведенных изделий→ средняя гармоническая взвешенная
3)



 Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.





 то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.




























 )
) )
)